Прикладная математика и механика, 2020, T. 84, № 4, стр. 407-425
Расчеты эволюции орбит планет
Н. И. Амелькин *
Московский физико-технический институт
Москва, Россия
* E-mail: namelkin@mail.ru
Поступила в редакцию 03.02.2020
После доработки 23.04.2020
Принята к публикации 12.05.2020
Аннотация
В рамках планетной задачи исследуется эволюция орбит планет Солнечной системы. Смещение элементов орбит определяется численным интегрированием уравнений возмущенного движения, записанных в невырождающихся переменных. Результаты представлены в виде таблиц для средних смещений элементов орбит и их колебательных составляющих на эпоху J2000, а также в виде графиков поведения элементов орбит в зависимости от времени.
Введение. Первые расчеты движения планет Солнечной системы в рамках ньютоновской механики были проведены Леверье. Им было исследовано [1, 2] движение Меркурия в гравитационном поле Солнца при учете гравитационных возмущений от других планет и обнаружено аномальное смещение перигелия Меркурия. Результаты Леверье с незначительными поправками были подтверждены в последующих работах других авторов [3, 4], а аномальное смещение перигелия Меркурия было объяснено в рамках общей теории относительности Эйнштейна [5].
При исследовании эволюции планетных орбит используются уравнения возмущенного движения, записанные в тех или иных переменных. До середины двадцатого столетия (в расчетах Леверье и других авторов) уравнения возмущенного движения исследовались аналитически с применением метода осреднения. Этот метод требует выполнения огромного числа весьма громоздких вычислительных процедур и поэтому при его использовании ограничиваются решением задачи в первом приближении теории возмущений.
Более эффективным и менее затратным представляется расчет эволюции планетных орбит по результатам численного интегрирования уравнений возмущенного движения. Этот метод широко используется в настоящее время для создания высокоточных численных эфемерид планет и других небесных тел [6, 7].
Численное интегрирование дифференциальных уравнений возмущенного движения позволяет помимо вычисления вековых смещений элементов орбит определить также и колебательные составляющие в поведении этих элементов. В рассматриваемой планетной задаче колебательные составляющие для некоторых планет характеризуются сравнительно большими амплитудами. Поэтому их необходимо учитывать при оценке точности вычисления вековых смещений по данным наблюдений и при составлении эфемерид планет. Ранее [8] на примере плоской планетной задачи показано, что среднее смещение перигелия Меркурия, найденное численным интегрированием соответствующих дифференциальных уравнений, полностью совпадает со средним смещением, вычисленным аналитически методом осреднения, и определена амплитуда колебательной составляющей в поведении перигелия Меркурия.
Ниже эволюция орбит планет Солнечной системы исследуется в рамках пространственной задачи n тел и определяется по результатам численного интегрирования дифференциальных уравнений возмущенного движения.
Элементы орбит планет определяются относительно плоскости начальной эклиптики. Для орбиты Земли в начальную эпоху наклонение относительно плоскости эклиптики равно нулю, а в уравнении для долготы восходящего узла при таком значении наклонения орбиты возникает особенность. Из-за этой особенности численное интегрирование уравнений возмущенного движения в оскулирующих элементах, как единой системы взаимосвязанных уравнений, невозможно. Из этих уравнений можно рассчитать только в первом приближении смещение всех элементов орбит планет, кроме долготы восходящего узла и наклонения для орбиты Земли, полагая, что фигурирующие в правых частях этих уравнений элементы орбит планет остаются неизменными.
Для определения смещений элементов орбит планет в точной (нелинейной) постановке в работе выведены уравнения возмущенного движения в невырождающихся переменных. В качестве таких переменных использовались векторы кинетических моментов и векторы Лапласа планет.
Основное внимание в работе уделяется исследованию вопроса о точности вычисления вековых смещений элементов орбит планет по данным наблюдений и определению интервалов времени, на которых первое приближение адекватно описывает поведение элементов орбит планет. Кроме того, проводится сопоставление результатов расчетов, полученных в рамках классической механики, с данными эфемерид на эпоху J2000, и определяется, как согласуется разница в этих данных с релятивистским эффектом, предсказываемым общей теорией относительности.
1. Уравнения возмущенного движения в оскулирующих элементах. Система состоит из Солнца массы $M$ и $n$ планет с массами ${{m}_{k}}$. Солнце и планеты рассматриваются как материальные точки.
Обозначим через ${{{\mathbf{R}}}_{k}}$ радиус-векторы, соединяющие Солнце с k-й планетой, а через ${\mathbf{R}}_{k}^{'}$ и ${{{\mathbf{R}}}_{M}}$ – радиус-векторы планет и Солнца относительно инерциального базиса $O{{{\mathbf{i}}}_{1}}{{{\mathbf{i}}}_{2}}{{{\mathbf{i}}}_{3}}$ с началом в центре масс всей системы. Эти векторы связаны формулами
(1.1)
${\mathbf{R}}_{k}^{'} = {{{\mathbf{R}}}_{k}} + {{{\mathbf{R}}}_{M}},\quad {{{\mathbf{R}}}_{M}} = - \sum\limits_{s = 1}^n {{{\varepsilon }_{s}}{\mathbf{R}}_{s}^{'}} ;\quad {{\varepsilon }_{s}} = \frac{{{{m}_{s}}}}{M}$Ускорение k-й планеты в инерциальном базисе записывается в виде
(1.2)
${\mathbf{\ddot {R}}}_{k}^{'} = {{{\mathbf{\ddot {R}}}}_{k}} + {{{\mathbf{\ddot {R}}}}_{M}} = - \frac{{\mu {{{\mathbf{R}}}_{k}}}}{{R_{k}^{3}}} - \sum\limits_{j \ne k} {\frac{{\mu {{\varepsilon }_{j}}({{{\mathbf{R}}}_{k}} - {{{\mathbf{R}}}_{j}})}}{{{{{\left| {{{{\mathbf{R}}}_{k}} - {{{\mathbf{R}}}_{j}}} \right|}}^{3}}}}} ;\quad \mu = \gamma M$Отсюда, учитывая соотношения (1.1), получим в наблюдаемых переменных ${{{\mathbf{R}}}_{k}}$ следующие уравнения:
Последняя сумма в правых частях этих уравнений обращается в нуль. Поэтому уравнения возмущенного движения записываются в виде
(1.3)
${{{\mathbf{\ddot {R}}}}_{k}} = - \frac{{{{\mu }_{k}}{{{\mathbf{R}}}_{k}}}}{{R_{k}^{3}}} + {{{\mathbf{a}}}_{k}},\quad {{\mu }_{k}} = \mu (1 + {{\varepsilon }_{k}});\quad k = 1,2,...$(1.4)
${{{\mathbf{a}}}_{k}} = \sum\limits_{j \ne k} {{{{\mathbf{a}}}_{{kj}}}} = - \mu \sum\limits_{j \ne k} {{{\varepsilon }_{j}}\left( {\frac{{{{{\mathbf{R}}}_{j}}}}{{R_{j}^{3}}} + \frac{{{{{\mathbf{R}}}_{k}} - {{{\mathbf{R}}}_{j}}}}{{{{{\left| {{{{\mathbf{R}}}_{k}} - {{{\mathbf{R}}}_{j}}} \right|}}^{3}}}}} \right)} ;\quad k = 1,2,...$Невозмущенное движение k-й планеты описывается дифференциальным уравнением
и представляет собой движение по кеплеровой эллиптической орбите вокруг Солнца, а возмущающее ускорение для k-й планеты дается формулой (1.4).В качестве инерциального базиса $O{{{\mathbf{i}}}_{1}}{{{\mathbf{i}}}_{2}}{{{\mathbf{i}}}_{3}}$ будем использовать правую ортонормированную тройку векторов, задающую ориентацию плоскости эклиптики на начальную эпоху (например, J2000). Оси ${{{\mathbf{i}}}_{1}}$ и ${{{\mathbf{i}}}_{2}}$ расположим в плоскости этой фиксированной эклиптики, причем ось ${{{\mathbf{i}}}_{1}}$ направим на точку весеннего равноденствия, а ось ${{{\mathbf{i}}}_{2}}$ – в сторону движения Земли по эклиптике. Ось ${{{\mathbf{i}}}_{3}}$ будет ортогональна плоскости указанной эклиптики [9, 10]. Положение орбиты k-й планеты относительно базиса $O{{{\mathbf{i}}}_{1}}{{{\mathbf{i}}}_{2}}{{{\mathbf{i}}}_{3}}$ задается долготой восходящего узла ${{\Omega }_{k}}$, наклонением орбиты ${{i}_{k}}$ и аргументом перицентра ${{\omega }_{k}}$. Невозмущенное движение k-й планеты описывается уравнением
(1.6)
${{{\mathbf{R}}}_{k}} = {{R}_{k}}{{{\mathbf{s}}}_{k}};\quad {{R}_{k}} = \frac{{{{P}_{k}}}}{{1 + {{e}_{k}}\cos {{\nu }_{k}}}},$(1.7)
$\begin{gathered} {{{\mathbf{s}}}_{k}} = {{{\mathbf{i}}}_{1}}{{X}_{k}} + {{{\mathbf{i}}}_{2}}{{Y}_{k}} + {{{\mathbf{i}}}_{3}}{{Z}_{k}} \\ {{X}_{k}} = \cos {{\Omega }_{k}}\cos ({{\omega }_{k}} + {{\nu }_{k}}) - \cos {{i}_{k}}\sin {{\Omega }_{k}}\sin ({{\omega }_{k}} + {{\nu }_{k}}) \\ {{Y}_{k}} = \sin {{\Omega }_{k}}\cos ({{\omega }_{k}} + {{\nu }_{k}}) + \cos {{i}_{k}}\cos {{\Omega }_{k}}\sin ({{\omega }_{k}} + {{\nu }_{k}}) \\ {{Z}_{k}} = \sin {{i}_{k}}\sin ({{\omega }_{k}} + {{\nu }_{k}}) \\ \end{gathered} $Введем также единичный вектор ${{\tau }_{k}}$, указывающий трансверсальное направление. Он определяется формулой
(1.8)
$\begin{gathered} {{\tau }_{k}} = \frac{{\partial {{{\mathbf{s}}}_{k}}}}{{\partial {{\nu }_{k}}}} = {{{\mathbf{i}}}_{1}}X_{k}^{'} + {{{\mathbf{i}}}_{2}}Y_{k}^{'} + {{{\mathbf{i}}}_{3}}Z_{k}^{'} \\ X_{k}^{'} = - [\cos {{\Omega }_{k}}\sin ({{\omega }_{k}} + {{\nu }_{k}}) + \cos {{i}_{k}}\sin {{\Omega }_{k}}\cos ({{\omega }_{k}} + {{\nu }_{k}})] \\ Y_{k}^{'} = - \sin {{\Omega }_{k}}\sin ({{\omega }_{k}} + {{\nu }_{k}}) + \cos {{i}_{k}}\cos {{\Omega }_{k}}\cos ({{\omega }_{k}} + {{\nu }_{k}}) \\ Z_{k}^{'} = \sin {{i}_{k}}\cos ({{\omega }_{k}} + {{\nu }_{k}}) \\ \end{gathered} $Здесь штрихом обозначена производная по истинной аномалии ${{\nu }_{k}}$.
Введем следующие обозначения:
(1.8)
${{r}_{{kj}}} = \frac{{{{R}_{k}}}}{{{{R}_{j}}}} = \frac{{{{P}_{k}}(1 + {{e}_{j}}\cos {{\nu }_{j}})}}{{{{P}_{j}}(1 + {{e}_{k}}\cos {{\nu }_{k}})}}$(1.9)
${{F}_{{kj}}} = {{{\mathbf{s}}}_{k}} \cdot {{{\mathbf{s}}}_{j}} = {{X}_{k}}{{X}_{j}} + {{Y}_{k}}{{Y}_{j}} + {{Z}_{k}}{{Z}_{j}}$(1.10)
$F_{{kj}}^{'} = {{\tau }_{k}} \cdot {{{\mathbf{s}}}_{j}} = X_{k}^{'}{{X}_{j}} + Y_{k}^{'}{{Y}_{j}} + Z_{k}^{'}{{Z}_{j}}$(1.11)
${{H}_{{kj}}} = \frac{1}{{{{{\left| {{{{\mathbf{s}}}_{j}} - {{{\mathbf{s}}}_{k}}{{r}_{{kj}}}} \right|}}^{3}}}} = {{(1 - 2{{F}_{{kj}}}{{r}_{{kj}}} + r_{{kj}}^{2})}^{{ - 3/2}}}$Тогда возмущающее ускорение (1.4) запишется в виде
(1.12)
${{{\mathbf{a}}}_{k}} = \mu \sum\limits_{j \ne k} {\frac{{{{\varepsilon }_{j}}}}{{R_{j}^{2}}}\left( {({{H}_{{kj}}} - 1){{{\mathbf{s}}}_{j}} - {{H}_{{kj}}}{{r}_{{kj}}}{{{\mathbf{s}}}_{k}}} \right)} ,$(1.13)
${{S}_{k}} = {{{\mathbf{a}}}_{k}} \cdot {{{\mathbf{s}}}_{k}} = \mu \sum\limits_{j \ne k} {\frac{{{{\varepsilon }_{j}}}}{{R_{j}^{2}}}\left( {({{H}_{{kj}}} - 1){{F}_{{kj}}} - {{H}_{{kj}}}{{r}_{{kj}}}} \right)} $(1.14)
${{T}_{k}} = {{{\mathbf{a}}}_{k}} \cdot {{\tau }_{k}} = \mu \sum\limits_{j \ne k} {\frac{{{{\varepsilon }_{j}}}}{{R_{j}^{2}}}({{H}_{{kj}}} - 1)F_{{kj}}^{'}} $(1.15)
${{W}_{k}} = {{{\mathbf{a}}}_{k}} \cdot {{{\mathbf{n}}}_{k}} = \mu \sum\limits_{j \ne k} {\frac{{{{\varepsilon }_{j}}}}{{R_{j}^{2}}}({{H}_{{kj}}} - 1)[({{X}_{j}}\sin {{\Omega }_{k}} - {{Y}_{j}}\cos {{\Omega }_{k}})\sin {{i}_{k}} + {{Z}_{j}}\cos {{i}_{k}}]} $Здесь ${{{\mathbf{n}}}_{k}} = {{{\mathbf{s}}}_{k}} \times {{\tau }_{k}}$ – единичный вектор нормали к плоскости орбиты планеты.
Пронумеруем планеты в порядке их удаления от Солнца (Меркурий – 1, Венера – 2, Земля – 3, Марс – 4, Юпитер – 5, Сатурн – 6, Уран – 7, Нептун – 8). Запишем уравнения возмущенного движения в оскулирующих элементах планетных орбит ${{\Omega }_{k}}$, ${{\pi }_{k}}$, ${{i}_{k}}$, ${{e}_{k}}$ и ${{P}_{k}}$. Здесь через ${{\pi }_{k}}$ обозначена долгота перигелия: ${{\pi }_{k}} = {{\Omega }_{k}} + {{\omega }_{k}}$. Учитывая закон изменения истинной аномалии со временем [9]
(1.16)
$\frac{{d{{\nu }_{k}}}}{{dt}} = \frac{{\sqrt {{{\mu }_{k}}{{P}_{k}}} }}{{R_{k}^{2}}}\left( {1 + \frac{\mu }{{{{\mu }_{k}}}}{{h}_{k}}R_{k}^{2}} \right);\quad {{h}_{k}} = \frac{1}{{{{e}_{k}}}}\left( {{{{\tilde {S}}}_{k}}\cos {{\nu }_{k}} - {{{\tilde {T}}}_{k}}\left( {1 + \frac{{{{R}_{k}}}}{{{{P}_{k}}}}} \right)\sin {{\nu }_{k}}} \right)$(1.17)
$\frac{{d{{\nu }_{k}}}}{{d{{\nu }_{3}}}} = {{\alpha }_{k}}\sqrt {\frac{{{{P}_{k}}}}{{{{P}_{3}}}}} \frac{{R_{3}^{2}}}{{R_{k}^{2}}}\frac{{(1 + {{\gamma }_{k}}R_{k}^{2}{{h}_{k}})}}{{(1 + {{\gamma }_{3}}R_{3}^{2}{{h}_{3}})}}$(1.18)
$\frac{{d{{\pi }_{k}}}}{{d{{\nu }_{3}}}} = \frac{{{{\beta }_{k}}R_{3}^{2}}}{{1 + {{\gamma }_{3}}{{h}_{3}}R_{3}^{2}}}\sqrt {\frac{{{{P}_{k}}}}{{{{P}_{3}}}}} \left( { - {{h}_{k}} + {{{\tilde {W}}}_{k}}\frac{{{{R}_{k}}}}{{{{P}_{k}}}}\sin ({{\omega }_{k}} + {{\nu }_{k}})\operatorname{tg} \frac{{{{i}_{k}}}}{2}} \right)$(1.19)
$\frac{{d{{\Omega }_{k}}}}{{d{{\nu }_{3}}}} = \frac{{{{\beta }_{k}}R_{3}^{2}}}{{1 + {{\gamma }_{3}}{{h}_{3}}R_{3}^{2}}}\sqrt {\frac{{{{P}_{k}}}}{{{{P}_{3}}}}} \frac{{{{R}_{k}}}}{{{{P}_{k}}}}\frac{{{{{\tilde {W}}}_{k}}}}{{\sin {{i}_{k}}}}\sin ({{\omega }_{k}} + {{\nu }_{k}})$(1.20)
$\frac{{d{{i}_{k}}}}{{d{{\nu }_{3}}}} = \frac{{{{\beta }_{k}}R_{3}^{2}}}{{1 + {{\gamma }_{3}}{{h}_{3}}R_{3}^{2}}}\sqrt {\frac{{{{P}_{k}}}}{{{{P}_{3}}}}} \frac{{{{R}_{k}}}}{{\,{{P}_{k}}}}{{\tilde {W}}_{k}}\cos ({{\omega }_{k}} + {{\nu }_{k}})$(1.21)
$\frac{{d{{e}_{k}}}}{{d{{\nu }_{3}}}} = \frac{{{{\beta }_{k}}R_{3}^{2}}}{{1 + {{\gamma }_{3}}{{h}_{3}}R_{3}^{2}}}\sqrt {\frac{{{{P}_{k}}}}{{{{P}_{3}}}}} \left( {{{{\tilde {S}}}_{k}}\sin {{\nu }_{k}} + {{{\tilde {T}}}_{k}}\left[ {\cos {{\nu }_{k}} + (\cos {{\nu }_{k}} + {{e}_{k}})\frac{{{{R}_{k}}}}{{{{P}_{k}}}}} \right]} \right)$(1.22)
$\frac{{d{{P}_{k}}}}{{d{{\nu }_{3}}}} = \frac{{2{{\beta }_{k}}R_{3}^{2}}}{{1 + {{\gamma }_{3}}{{h}_{3}}R_{3}^{2}}}\sqrt {\frac{{{{P}_{k}}}}{{{{P}_{3}}}}} {{R}_{k}}{{\tilde {T}}_{k}}$Здесь использованы обозначения
(1.23)
${{\tilde {S}}_{k}} = \frac{{{{S}_{k}}}}{\mu }\,,\,\,\,\,\,\,{{\tilde {T}}_{k}} = \frac{{{{T}_{k}}}}{\mu }\,,\,\,\,\,\,{{\tilde {W}}_{k}} = \frac{{{{W}_{k}}}}{\mu }$(1.24)
${{\alpha }_{k}} = \sqrt {\frac{{1 + {{\varepsilon }_{k}}}}{{1 + {{\varepsilon }_{3}}}}} \,,\,\,\,\,\,\,\,{{\beta }_{k}} = \frac{1}{{\sqrt {(1 + {{\varepsilon }_{3}})(1 + {{\varepsilon }_{k}})} }}\,,\,\,\,\,\,\,{{\gamma }_{k}} = \frac{1}{{1 + {{\varepsilon }_{3}}}}$Закон изменения большой полуоси для k-й планеты определяется из уравнения
(1.25)
$\frac{{d{{a}_{k}}}}{{d{{\nu }_{3}}}} = \frac{1}{{1 - e_{k}^{2}}}\frac{{d{{P}_{k}}}}{{d{{\nu }_{3}}}} + \frac{{2{{P}_{k}}{{e}_{k}}}}{{{{{(1 - e_{k}^{2})}}^{2}}}}\frac{{d{{e}_{k}}}}{{d{{\nu }_{3}}}}$Заметим, что для всех планет Солнечной системы коэффициенты ${{\varepsilon }_{k}}$ не превышают величины ${{10}^{{ - 3}}}$. Поэтому, если положить ${{\alpha }_{k}} = 1$, ${{\beta }_{k}} = 1$, ${{\gamma }_{k}} = 1$, то правые части уравнений будут записаны с относительной точностью до ${{10}^{{ - 3}}}$, а для внутренних планет – с относительной точностью до ${{10}^{{ - 5}}}$.
По результатам интегрирования уравнений (1.17)–(1.22) определяется поведение элементов орбит планет в “земном” времени, где изменение независимой переменной ${{\nu }_{3}}$ на $2\pi $ соответствует одному земному году.
Элементы орбит планет определяются относительно плоскости начальной эклиптики. Для орбиты Земли в начальную эпоху наклонение относительно плоскости эклиптики равно нулю (${{i}_{3}} = 0$), а в уравнении (1.19) при таком значении наклонения орбиты возникает особенность. Из-за этой особенности численное интегрирование уравнений (1.17)–(1.22), как единой системы взаимосвязанных уравнений, невозможно. Из этих уравнений можно получить только решение в первом приближении, полагая, что фигурирующие в правых частях этих уравнений элементы орбит планет остаются неизменными [9]. Тогда каждое k-е уравнение (1.18)–(1.22) интегрируется в сочетании с k-м уравнением (1.17) независимо от других уравнений. Таким образом, полагая значения элементов в правых частях уравнений постоянными, интегрированием уравнений (1.17)–(1.22), можно рассчитать в первом приближении смещение всех элементов орбит планет, кроме долготы восходящего узла и наклонения для орбиты Земли (уравнение (1.20) тоже не может быть непосредственно использовано для расчета поведения наклонения орбиты Земли относительно начальной эклиптики ввиду неопределенности значений ${{\Omega }_{3}}$ и ${{\omega }_{3}}$ при ${{i}_{3}} = 0$).
Отметим, что за счет малости возмущений (в рассматриваемой задаче малыми параметрами являются коэффициенты ${{\varepsilon }_{j}}$ в выражениях (1.12) для возмущающих ускорений) элементы орбит меняются медленно и, как будет установлено ниже, первое приближение адекватно описывает эволюцию большинства элементов планетных орбит на интервалах времени до ста лет. Но для точного определения смещений всех элементов орбит требуется точное решение уравнений возмущенного движения. Такое решение можно получить численным интегрированием уравнений, записанных в невырождающихся переменных.
2. Уравнения возмущенного движения планет в избыточных переменных. Получить систему уравнений, не имеющих особенностей при ${{i}_{k}} = 0$, можно, используя закон изменения кинетического момента и вектора Лапласа для каждой планеты.
Рассмотрим задачу о движении отдельной планеты. Пусть уравнения возмущенного движения имеют вид
где ${\mathbf{a}}$ – возмущающее ускорение. Вектор кинетического момента планеты определяется формулой где ${\mathbf{n}}$ – единичный вектор нормали к плоскости орбиты.Вектор Лапласа обозначим через ${\mathbf{\tilde {f}}}$. Он определяется формулой
(2.3)
${\mathbf{\tilde {f}}} = - \mu \frac{{\mathbf{R}}}{R} + {\mathbf{\dot {R}}} \times {\mathbf{c}} = \mu e{\mathbf{j}},$(2.5)
${\mathbf{\dot {\tilde {f}}}} = {\mathbf{a}} \times {\mathbf{c}} + {\mathbf{\dot {R}}} \times {\mathbf{\dot {c}}}\, = {\mathbf{a}} \times {\mathbf{c}} + {\mathbf{\dot {R}}} \times ({\mathbf{R}} \times \,{\mathbf{a}})$Вектор ${\mathbf{\dot {R}}}$ исключим из уравнения (2.5), используя соотношения (2.2) и (2.3). Умножив векторно обе части этих равенств на вектор ${\mathbf{R}}$ и учитывая взаимную ортогональность векторов ${\mathbf{R}}$ и ${\mathbf{c}}$, получим
Отсюда следует
(2.6)
${\mathbf{\dot {R}}} = - \frac{1}{{R_{{}}^{2}}}\left( {{\mathbf{R}} \times {\mathbf{с}} + \frac{{{\mathbf{R}}[{\mathbf{с}} \cdot ({\mathbf{R}} \times {\mathbf{\tilde {f}}})]}}{{{{c}^{2}}}}} \right)$Ниже вместо переменных (2.2) и (2.3) будем использовать переменные
(2.7)
${\mathbf{C}} = \frac{{\mathbf{с}}}{{\sqrt \mu }} = C{\mathbf{n}} = \sqrt P {\mathbf{n}},\quad {\mathbf{f}} = \frac{{{\mathbf{\tilde {f}}}}}{\mu } = f{\mathbf{j}} = e{\mathbf{j}},$в которых уравнения (2.4), (2.5) при учете (2.6) запишутся в виде
(2.9)
${\mathbf{\dot {f}}} = \frac{1}{{\sqrt \mu }}\left( {{\mathbf{a}} \times {\mathbf{C}} - \frac{1}{{{{R}^{2}}}}\left[ {\left( {{\mathbf{R}} \times {\mathbf{C}} + \frac{{{\mathbf{R}}[{\mathbf{C}} \cdot ({\mathbf{R}} \times {\mathbf{f}})]}}{{{{C}^{2}}}}} \right) \times ({\mathbf{R}} \times {\mathbf{a}})} \right]} \right)$После учета соотношений
(2.10)
$\frac{{d{\mathbf{С}}}}{{dt}} = \sqrt \mu \frac{{C[{\mathbf{C}}\tilde {T}f + \tilde {W}({\mathbf{f}}C\sin \nu - {\mathbf{C}} \times {\mathbf{f}}\cos \nu )]}}{{f(1 + e\cos \nu )}}$(2.11)
$\begin{gathered} \frac{{d{\mathbf{f}}}}{{dt}} = \sqrt \mu \left( {\frac{{{\mathbf{f}}C}}{f}\left( {\tilde {T}\left[ {\cos \nu + \frac{{\cos \nu + f}}{{1 + f\cos \nu }}} \right] + \tilde {S}\sin \nu } \right) - \frac{{{\mathbf{C}}\tilde {W}f\sin \nu }}{{1 + f\cos \nu }}} \right) + \\ + \;\sqrt \mu \frac{{{\mathbf{C}} \times {\mathbf{f}}}}{f}\left( {\tilde {T}\left[ {1 + \frac{1}{{1 + f\cos \nu }}} \right]\sin \nu - \tilde {S}\cos \nu } \right) \\ \end{gathered} $Эти уравнения дополняются уравнением для истинной аномалии
(2.12)
$\frac{{d\nu }}{{dt}} = \sqrt \mu \frac{С}{{{{R}^{2}}}}\left( {1 + h{{R}^{2}}} \right);\quad h = \frac{1}{f}\left( {\tilde {S}\cos \nu - \tilde {T}\left( {1 + \frac{R}{{{{C}^{2}}}}} \right)\sin \nu } \right)$Следует отметить, что используемые в уравнениях (2.10)–(2.12) векторы ${\mathbf{C}}$ и ${\mathbf{f}}$ задают орбиту планеты избыточным числом координат (шесть вместо пяти). Но, при этом, уравнения (2.10)–(2.12), в отличие от уравнений (1.17)–(1.22), не вырождаются ни при каких наклонениях орбиты, а скалярное произведение ${\mathbf{C}} \cdot {\mathbf{f}}$ – первый интеграл этих уравнений.
Приведем формулы, выражающие оскулирующие элементы орбиты через переменные ${\mathbf{C}}$ и ${\mathbf{f}}$. Эксцентриситет, параметр и наклонение орбиты выражаются следующими формулами:
(2.13)
$e = f,\quad P = {{C}^{2}},\quad \cos i = \frac{{{{C}_{3}}}}{C},\quad \sin i = \frac{{\sqrt {{{C}^{2}} - C_{3}^{2}} }}{C}$Для долготы восходящего узла $\Omega $, аргумента перицентра $\omega $ и долготы перицентра $\pi = \Omega + \omega $, учитывая взаимную ортогональность векторов ${\mathbf{C}}$ и f, получим
(2.14)
$\cos \Omega = - \frac{{{{C}_{2}}}}{{\sqrt {{{C}^{2}} - C_{3}^{2}} }},\quad \sin \Omega = \frac{{{{C}_{1}}}}{{\sqrt {{{C}^{2}} - C_{3}^{2}} }}$(2.15)
$\cos \omega = \frac{{{{C}_{1}}{{f}_{2}} - {{C}_{2}}{{f}_{1}}}}{{f\sqrt {{{C}^{2}} - C_{3}^{2}} }},\quad \sin \omega = \frac{{{{f}_{3}}C}}{{f\sqrt {{{C}^{2}} - C_{3}^{2}} }}$(2.16)
$\cos \pi = \frac{1}{{{{C}_{3}}f}}\left[ {{{f}_{1}}C + \frac{{{{C}_{2}}({{f}_{2}}{{C}_{1}} - {{f}_{1}}{{C}_{2}})}}{{C + {{C}_{3}}}}} \right],\quad \sin \pi = \frac{1}{{{{C}_{3}}f}}\left[ {{{f}_{2}}C + \frac{{{{C}_{1}}({{f}_{1}}{{C}_{2}} - {{f}_{2}}C_{1}^{{}})}}{{C + {{C}_{3}}}}} \right]$Смещения оскулирующих элементов вычисляются по формулам
(2.17)
$\Delta e = f - {{e}_{0}},\quad \Delta P = {{C}^{2}} - {{P}_{0}},\quad \sin \Delta i = \frac{{\sqrt {{{C}^{2}} - C_{3}^{2}} }}{C}\cos {{i}_{0}} - \frac{{{{C}_{3}}}}{C}\sin {{i}_{0}}$(2.18)
$\sin \Delta \Omega = \frac{{{{C}_{1}}}}{{\sqrt {{{C}^{2}} - C_{3}^{2}} }}\cos {{\Omega }_{0}} + \frac{{{{C}_{2}}}}{{\sqrt {{{C}^{2}} - C_{3}^{2}} }}\sin {{\Omega }_{0}}$(2.19)
$\sin \Delta \omega = \frac{{{{f}_{3}}\,C}}{{f\sqrt {{{C}^{2}} - C_{3}^{2}} }}\sin {{\omega }_{0}} - \frac{{{{C}_{1}}{{f}_{2}} - {{C}_{2}}{{f}_{1}}}}{{f\sqrt {{{C}^{2}} - C_{3}^{2}} }}\cos {{\omega }_{0}}$(2.20)
$\sin \Delta \pi = \frac{1}{{{{C}_{3}}f}}\left( {\left[ {{{f}_{2}}C + \frac{{{{C}_{1}}({{f}_{1}}{{C}_{2}} - {{f}_{2}}C_{1}^{{}})}}{{C + {{C}_{3}}}}} \right]\cos {{\pi }_{0}} - \left[ {{{f}_{1}}C + \frac{{{{C}_{2}}({{f}_{2}}{{C}_{1}} - {{f}_{1}}{{C}_{2}})}}{{C + {{C}_{3}}}}} \right]\sin {{\pi }_{0}}} \right)$Здесь начальные значения элементов обозначены нижним индексом “0”.
Отметим, что применительно к рассматриваемой задаче об эволюции планетных орбит смещения угловых элементов ввиду их малости однозначно определяются значениями синусов соответствующих углов на интервалах времени в сотни тысяч лет. Кроме того, на интервалах времени в тысячи лет синусы смещений угловых переменных с высокой точностью совпадают с самими смещениями.
Вернемся теперь к задаче об эволюции орбит планет Солнечной системы. Выбирая в качестве переменных векторы
(2.21)
${{{\mathbf{C}}}_{k}} = \frac{{{{{\mathbf{c}}}_{k}}}}{{\sqrt {{{\mu }_{k}}} }},\quad {{{\mathbf{f}}}_{k}} = \frac{{{{{{\mathbf{\tilde {f}}}}}_{k}}}}{{{{\mu }_{k}}}},$(2.22)
$\frac{{d{{\nu }_{k}}}}{{d{{\nu }_{3}}}} = {{\alpha }_{k}}\frac{{{{C}_{k}}R_{3}^{2}(1 + {{\gamma }_{k}}{{h}_{k}}R_{k}^{2})}}{{{{C}_{3}}R_{k}^{2}(1 + {{\gamma }_{3}}{{h}_{3}}R_{3}^{2})}};\quad {{h}_{k}} = \frac{1}{{{{f}_{k}}}}\left( {{{{\tilde {S}}}_{k}}\cos {{\nu }_{k}} - {{{\tilde {T}}}_{k}}\left( {1 + \frac{{{{R}_{k}}}}{{C_{k}^{2}}}} \right)\sin {{\nu }_{k}}} \right)$(2.23)
$\frac{{d{{{\mathbf{C}}}_{k}}}}{{d{{\nu }_{3}}}} = \frac{{{{\beta }_{k}}R_{3}^{2}{{C}_{k}}}}{{(1 + {{\gamma }_{3}}{{h}_{3}}R_{3}^{2}){{C}_{3}}}}\left( {\frac{{{{{\mathbf{C}}}_{k}}{{f}_{k}}{{{\tilde {T}}}_{k}} + {{{\tilde {W}}}_{k}}({{{\mathbf{f}}}_{k}}{{C}_{k}}\sin {{\nu }_{k}} - {{{\mathbf{C}}}_{k}} \times {{{\mathbf{f}}}_{k}}\cos {{\nu }_{k}})}}{{{{f}_{k}}(1 + {{f}_{k}}\cos {{\nu }_{k}})}}} \right)$(2.24)
$\begin{gathered} \frac{{d{{{\mathbf{f}}}_{k}}}}{{d{{\nu }_{3}}}} = \frac{{{{\beta }_{k}}R_{3}^{2}}}{{(1 + {{\gamma }_{3}}{{h}_{3}}R_{3}^{2}){{C}_{3}}}}\left( {\frac{{{{{\mathbf{f}}}_{k}}{{C}_{k}}}}{{{{f}_{k}}}}\left[ {{{{\tilde {S}}}_{k}}\sin {{\nu }_{k}} + {{{\tilde {T}}}_{k}}\left[ {\cos {{\nu }_{k}} + \frac{{\cos {{\nu }_{k}} + {{f}_{k}}}}{{1 + {{f}_{k}}\cos {{\nu }_{k}}}}} \right]} \right] + } \right. \\ \left. { + \;\frac{{{{{\mathbf{C}}}_{k}} \times {{{\mathbf{f}}}_{k}}}}{{{{f}_{k}}}}\left[ {{{{\tilde {T}}}_{k}}\sin {{\nu }_{k}}\left[ {1 + \frac{1}{{1 + {{f}_{k}}\cos {{\nu }_{k}}}}} \right] - {{{\tilde {S}}}_{k}}\cos {{\nu }_{k}})} \right] - \frac{{{{{\mathbf{C}}}_{k}}{{f}_{k}}{{{\tilde {W}}}_{k}}\sin {{\nu }_{k}}}}{{1 + {{f}_{k}}\cos {{\nu }_{k}}}}} \right) \\ \end{gathered} $В этих уравнениях коэффициенты ${{\alpha }_{k}}$, ${{\beta }_{k}}$, ${{\gamma }_{k}}$ определяются формулами (1.24), а функции ${{\tilde {S}}_{k}}$, ${{\tilde {T}}_{k}}$ и ${{\tilde {W}}_{k}}$ выражаются через переменные (2.21) формулами
(2.25)
$\begin{gathered} {{{\tilde {S}}}_{k}} = \sum\limits_{j \ne k} {\frac{{{{\varepsilon }_{j}}}}{{R_{j}^{2}}}\left( {({{H}_{{kj}}} - 1){{F}_{{kj}}} - {{H}_{{kj}}}{{r}_{{kj}}}} \right)} ,\quad {{{\tilde {T}}}_{k}} = \sum\limits_{j \ne k} {\frac{{{{\varepsilon }_{j}}}}{{R_{j}^{2}}}({{H}_{{kj}}} - 1)F_{{kj}}^{'}} \\ {{{\tilde {W}}}_{k}} = \sum\limits_{j \ne k} {\frac{{{{\varepsilon }_{j}}}}{{R_{j}^{2}}}({{H}_{{kj}}} - 1){{Z}_{{kj}}}} , \\ \end{gathered} $(2.26)
${{R}_{j}} = \frac{{C_{j}^{2}}}{{1 + {{f}_{j}}\cos {{\nu }_{j}}}},\quad {{r}_{{kj}}} = \frac{{{{R}_{k}}}}{{{{R}_{j}}}},\quad {{H}_{{kj}}} = {{(1 - 2{{F}_{{kj}}}{{r}_{{kj}}} + r_{{kj}}^{2})}^{{ - 3/2}}}$(2.27)
$\begin{gathered} {{F}_{{kj}}} = \frac{{{{{\mathbf{f}}}_{k}} \cdot {{{\mathbf{f}}}_{j}}\cos {{\nu }_{k}}\cos {{\nu }_{j}}}}{{{{f}_{k}}{{f}_{j}}}} + \frac{{({{{\mathbf{C}}}_{k}} \times {{{\mathbf{f}}}_{k}}) \cdot ({{{\mathbf{C}}}_{j}} \times {{{\mathbf{f}}}_{j}})\sin {{\nu }_{k}}\sin {{\nu }_{j}}}}{{{{C}_{k}}{{f}_{k}}{{C}_{j}}{{f}_{j}}}} + \\ + \;\frac{{{{{\mathbf{f}}}_{j}} \cdot ({{{\mathbf{C}}}_{k}} \times {{{\mathbf{f}}}_{k}})\sin {{\nu }_{k}}\cos {{\nu }_{j}}}}{{{{C}_{k}}{{f}_{k}}{{f}_{j}}}} + \frac{{{{{\mathbf{f}}}_{k}} \cdot ({{{\mathbf{C}}}_{j}} \times {{{\mathbf{f}}}_{j}})\cos {{\nu }_{k}}\sin {{\nu }_{j}}}}{{{{C}_{j}}{{f}_{k}}{{f}_{j}}}} \\ \end{gathered} $(2.28)
$F_{{kj}}^{'} = \frac{{\partial {{F}_{{kj}}}}}{{\partial {{\nu }_{k}}}},\quad {{Z}_{{kj}}} = \frac{{{{{\mathbf{C}}}_{k}} \cdot {{{\mathbf{f}}}_{j}}\cos {{\nu }_{j}}}}{{{{C}_{k}}{{f}_{j}}}} + \frac{{{{{\mathbf{C}}}_{k}} \cdot ({{{\mathbf{C}}}_{j}} \times {{{\mathbf{f}}}_{j}})\sin {{\nu }_{j}}}}{{{{C}_{k}}{{f}_{j}}{{C}_{j}}}}$Для восьми планет Солнечной системы уравнения (2.22)–(2.24) образуют замкнутую систему из 56 скалярных уравнений для 56 переменных ${{\nu }_{k}}$, ${{C}_{{ki}}}$, ${{f}_{{ki}}}$; $k = 1,2,...,8$, $i = 1,2,3$. Скалярные произведения ${{{\mathbf{C}}}_{k}} \cdot {{{\mathbf{f}}}_{k}}$ являются первыми интегралами этих уравнений. По результатам интегрирования этих уравнений значения и смещения оскулирующих элементов вычисляются формулами (2.13)–(2.20). Поведение большой полуоси каждой планеты определяется формулой
Отметим, что при необходимости из системы (2.23), (2.24) можно получить и первое приближение для смещений элементов орбит, положив векторы ${{{\mathbf{C}}}_{k}}$ и ${{{\mathbf{f}}}_{k}}$ в правых частях уравнений постоянными.
3. Эволюция орбит внутренних планет. Анализ эволюции планетных орбит проводился по результатам численного интегрирования уравнений возмущенного движения. При этом использовались как первое приближение для смещений элементов орбит, получаемое интегрирование уравнений (1.17)–(1.22) при постоянных значениях элементов в правых частях уравнений, так и точные решения уравнений (2.23), (2.24), которые интегрировались как единая система взаимосвязанных уравнений. Результаты расчетов по первому приближению и по точным решениям сопоставлялись друг с другом и определялись интервалы времени, в пределах которых первое приближение адекватно описывает эволюцию планетных орбит.
В качестве больших полуосей орбит планет принимались их отношения к большой полуоси орбиты Земли. При таком определении больших полуосей исследуемые уравнения представляют собой уравнения в безразмерных переменных. В расчетах использовались начальные данные на эпоху J2000 [11].
Средние смещения элементов орбит, вычисленные по первому приближению, линейно зависят от времени. Процедура вычисления среднего смещения по первому приближению состояла в следующем. Из графика поведения элемента, полученного по результатам численного интегрирования уравнений (1.17)–(1.22), вычиталась линейная функция времени, коэффициент пропорциональности в которой подбирался методом последовательных приближений таким образом, чтобы в конечном итоге с требуемой точностью получалась только колебательная составляющая. Ввиду того, что помимо среднего смещения в поведении элементов орбит имеются колебательные составляющие, значения амплитуд которых может достигать весьма больших величин, для вычисления с требуемой точностью среднего смещения интегрирование уравнений проводилось на интервалах времени в десятки тысяч лет.
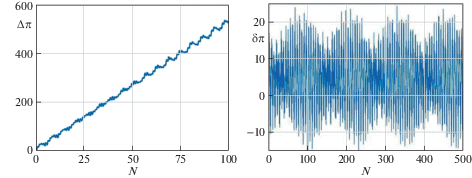
На рис. 1 приведен пример вычисления среднего смещения перигелия Меркурия. Здесь N – число земных лет, а смещение перигелия $\Delta \pi $ выражается в угловых секундах. В левой части рисунка изображен график $\Delta \pi $ в зависимости от времени, а в правой части – график колебательной составляющей, который получается при вычитании из графика $\Delta \pi $ линейной функции $5.2882''N$. Таким образом, среднее смещение перигелия Меркурия, вычисленное в первом приближении, составляет 528.82 угловых секунд за столетие. Амплитуда колебательной составляющей в поведении перигелия Меркурия составляет около $18''$ (эта составляющая названа колебательной, поскольку строгой периодичности в ней не наблюдается). Аналогичным образом вычислялись средние смещения других элементов орбиты Меркурия и всех остальных планет.
Результаты расчетов эволюции орбит внутренних планет, полученные на основе первого приближения решений уравнений (1.17)–(1.22), приведены в таблице 1. Здесь символом $\Delta $ обозначается среднее смещение элемента за столетие, а символом $\delta $ – амплитуда колебательной составляющей в поведении этого элемента.
Таблица 1.
Смещение элементов орбит внутренних планет за столетие. Эпоха J2000
| Планета | $\Delta \pi $ | $\Delta \Omega $ | $\Delta i$ | $\Delta e$ | $\Delta P$ |
|---|---|---|---|---|---|
| Меркурий | $528.82'' \pm 0.03''$ | $ - 451.50'' \pm 0.03''$ | $\begin{gathered} - 21.423'' \pm \\ \pm \;0.002'' \\ \end{gathered} $ | $\begin{gathered} 2.040 \times {{10}^{{ - 5}}} \pm \\ \pm 0.002 \times {{10}^{{ - 5}}} \\ \end{gathered} $ | $\begin{gathered} - 3.25 \times {{10}^{{ - 6}}} \pm \\ \pm \;0.005 \times {{10}^{{ - 6}}} \\ \end{gathered} $ |
| $\delta \pi = 18''$ | $\delta \Omega = 3''$ | $\delta i = 0.35''$ | $\delta e = 1.7 \times {{10}^{{ - 5}}}$ | $\delta P = 4.3 \times {{10}^{{ - 6}}}$ | |
| Венера | $15.4'' \pm 1''$ | $ - 1000.9'' \pm 0.2''$ | $\begin{gathered} - 3.083'' \pm \\ \pm \;0.002'' \\ \end{gathered} $ | $\begin{gathered} - 4.758 \times {{10}^{{ - 5}}} \pm \\ \pm \;0.002 \times {{10}^{{ - 5}}} \\ \end{gathered} $ | $\begin{gathered} 0.46 \times {{10}^{{ - 6}}} \pm \\ \pm \;0.01 \times {{10}^{{ - 6}}} \\ \end{gathered} $ |
| $\delta \pi = 1350''$ | $\delta \Omega = 13''$ | $\delta i = 0.5''$ | $\delta e = 4.2 \times {{10}^{{ - 5}}}$ | $\delta P = 1.3 \times {{10}^{{ - 5}}}$ | |
| Земля | $1146.6'' \pm 0.3''$ | – | $\begin{gathered} 46.997'' \pm \\ \pm \;0.002'' \\ \end{gathered} $ | $\begin{gathered} - 4.21 \times {{10}^{{ - 5}}} \pm \\ \pm \;0.01 \times {{10}^{{ - 5}}} \\ \end{gathered} $ | $\begin{gathered} 1.41 \times {{10}^{{ - 6}}} \pm \\ \pm \;0.01 \times {{10}^{{ - 6}}} \\ \end{gathered} $ |
| $\delta \pi = 700''$ | – | $\delta i = 0.5''$ | $\delta e = 5.5 \times {{10}^{{ - 5}}}$ | $\delta P = 2.5 \times {{10}^{{ - 5}}}$ | |
| Марс | $1591.9'' \pm 0.2''$ | $\begin{gathered} - 1062.05'' \pm \\ \pm \;0.03'' \\ \end{gathered} $ | $\begin{gathered} - 29.325'' \pm \\ \pm \;0.002'' \\ \end{gathered} $ | $\begin{gathered} 9.05 \times {{10}^{{ - 5}}} \pm \\ \pm \;0.01 \times {{10}^{{ - 5}}} \\ \end{gathered} $ | $\begin{gathered} - 2.57 \times {{10}^{{ - 5}}} \pm \\ \pm \;0.01 \times {{10}^{{ - 5}}} \\ \end{gathered} $ |
| $\delta \pi = \,320''$ | $\delta \Omega = 25''$ | $\delta i = 0.6''$ | $\delta e = 1.5 \times {{10}^{{ - 4}}}$ | $\delta P = 1.4 \times {{10}^{{ - 4}}}$ |
Обратим внимание, что средние значения параметров и эксцентриситетов всех планет меняются со временем. Но среднего смещения больших полуосей, вычисляемого интегрированием уравнения (1.25), не обнаружено.
Смещение каждого элемента орбиты возмущаемой планеты, вычисленное в первом приближения, равно сумме смещений, обусловленных влиянием отдельных возмущающих планет. Полученные по результатам интегрирования уравнений (1.17)–(1.22) данные о вкладе отдельных планет в смещение перигелия внутренних планет приведены в таблице 2.
Таблица 2.
Вклад отдельных планет в смещение перигелия внутренних планет (в угловых секундах за столетие)
| Планета | Меркурий | Венера | Земля | Марс |
|---|---|---|---|---|
| Меркурий | –150.95 | –13.73 | 0.77 | |
| Венера | 275.931 | 345.25 | 49.4 | |
| Земля | 90.115 | –574.2 | 227.5 | |
| Марс | 2.464 | 74.9 | 97.42 | |
| Юпитер | 152.91 | 657.5 | 698.2 | 1246.3 |
| Сатурн | 7.222 | 7.74 | 18.7 | 66.4 |
| Уран | 0.138 | 0.27 | 0.56 | 1.17 |
| Нептун | 0.042 | 0.11 | 0.18 | 0.35 |
| $\sum $ | 528.82 | 15.37 | 1146.58 | 1591.89 |
Из таблицы 1 видно, что помимо векового смещения в поведении элементов орбит имеются колебательные составляющие, амплитуды которых могут достигать больших значений. Например, для перигелия Венеры амплитуда колебательной составляющей почти в сто раз превышает среднее смещение за столетие. Колебательная составляющая влияет на точность вычисления среднего при расчетах смещения элементов орбит по данным наблюдений. Из всех внутренних планет точность вычисления среднего смещения перигелия по данным наблюдений для Меркурия самая высокая, а для Венеры – самая низкая.
Наличием колебательных составляющих объясняется также наблюдаемое различие между средними смещениями элементов, вычисленными по первому приближению, и линейной по времени составляющей среднего смещения, вычисленной на основе точных решений системы уравнений (2.23), (2.24).
Расчеты смещений элементов орбит планет по точным решениям уравнений возмущенного движения показали, что средние смещения нелинейно зависят от времени. При этом для внутренних планет на интервалах времени до тысячи лет доминирующей является линейная составляющая, а нелинейная составляющая вносит заметный вклад на интервалах времени в десятки тысяч лет.
Линейные по времени составляющие среднего смещения элементов орбиты рассчитывались по следующей процедуре. Из графика поведения элемента, полученного по результатам численного интегрирования системы (2.23), (2.24), вычиталась линейная функция времени, коэффициент пропорциональности в которой подбирался методом последовательных приближений таким образом, чтобы в среднем для получаемой в итоге функции момент начальной эпохи соответствовал ее стационарной точке. Точность вычисления линейной части среднего смещения по такой процедуре ниже, чем при вычислении среднего смещения по первому приближению. Ввиду того, что точные решения характеризуются нелинейным по времени поведением средних элементов орбит, увеличением интервала интегрирования уточнить линейную часть среднего смещения на начальную эпоху нет возможности. Чтобы точнее определить линейную часть среднего смещения, уравнения интегрировались как в “прямом”, так и в “обратном” времени по отношению к начальной эпохе.
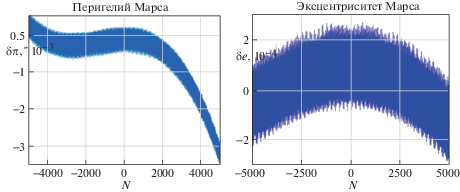
На рис. 2 приведен пример вычисления линейной части в среднем смещении перигелия и эксцентриситета Марса на эпоху J2000. В левой части рисунка изображен график функции, получаемый вычитанием из графика поведения перигелия Марса $\Delta {{\pi }_{4}}$ линейной функции $15.95''N$, а в правой части – график функции, получаемый вычитанием из графика $\Delta {{e}_{4}}$ линейной функции $8.85 \times {{10}^{{ - 7}}}N$. Для полученных функций момент времени $t = 0$ – стационарная точка. Поэтому линейная часть среднего смещения перигелия Марса на эпоху J200 составляет $1595''$ за столетие, а линейная часть среднего смещения эксцентриситета равна $8.85 \times {{10}^{{ - 5}}}$ за столетие. Графики показывают поведение нелинейных по времени составляющих в среднем смещении перигелия и эксцентриситета Марса.
По результатам численного интегрирования уравнений (2.23), (2.24) установлено, что линейные части наклонений и долгот восходящего узла для всех внутренних планет совпадают с данными таблицы 1 и данными эфемерид [11] с точностью до погрешности расчетов. Различие наблюдается в смещениях перигелиев и эксцентриситетов некоторых планет. Рассчитанные на основе уравнений (2.23), (2.24) данные для этих элементов приведены в таблице 3.
Таблица 3.
Линейная часть средних смещений элементов орбит внутренних планет на эпоху J2000 (за столетие)
| Планета | $\Delta \pi $ | $\Delta e$ |
|---|---|---|
| Меркурий | $529.1'' \pm 0.2''$ | $(2.04 \pm 0.02) \times {{10}^{{ - 5}}}$ |
| Венера | $15'' \pm 10''$ | $( - 4.75 \pm 0.03) \times {{10}^{{ - 5}}}$ |
| Земля | $1160'' \pm 3''$ | $( - 4.2 \pm 0.03) \times {{10}^{{ - 5}}}$ |
| Марс | $1595'' \pm 2''$ | $(8.85 \pm 0.03) \times {{10}^{{ - 5}}}$ |
Важно отметить, что и по результатам интегрирования уравнений (2.23), (2.24) на интервалах времени в тысячи лет векового смещения больших полуосей, определяемых формулой (2.29), не обнаружено.
Сопоставляя полученные результаты расчетов для смещений элементов орбит с данными эфемерид [11] на эпоху J2000, можно определить, как согласуется разница в этих данных с релятивистским эффектом, предсказываемым общей теорией относительности (ОТО).
Дополнительное смещение перигелия орбиты планеты по ОТО за один оборот планеты вокруг Солнца определяется формулой [5]
(3.1)
$\Delta \pi = \frac{{6\pi \mu }}{{a(1 - {{e}^{2}}){{c}^{2}}}} = \frac{{24{{\pi }^{3}}{{a}^{2}}}}{{{{T}^{2}}(1 - {{e}^{2}}){{c}^{2}}}},$(3.2)
${\mathbf{F}}({\mathbf{R}}) = - \frac{{\mu m}}{{{{R}^{2}}}}\left( {1 + \frac{{3\mu P}}{{{{c}^{2}}{{R}^{2}}}}} \right)\frac{{\mathbf{R}}}{R}$Здесь $P$ – параметр орбиты. В таком поле к ньтоновскому ускорению добавляется возмущающее ускорение, которое имеет только радиальную компоненту
Из уравнений возмущенного движения в оскулирующих элементах следует, что такое возмущение влияет только на поведение долготы перигелия и эксцентриситета орбиты. Уравнения для этих элементов принимают вид
(3.4)
$\frac{{d\pi }}{{d\nu }} = \frac{{3\mu P}}{{{{c}^{2}}{{R}^{2}}e}}\cos \nu = \frac{{3\mu }}{{{{c}^{2}}ae(1 - {{e}^{2}})}}\cos \nu {{(1 + e\cos \nu )}^{2}}$(3.5)
$\frac{{de}}{{d\nu }} = - \frac{{3\mu P}}{{{{c}^{2}}{{R}^{2}}}}\sin \nu = - \frac{{3\mu }}{{{{c}^{2}}a(1 - {{e}^{2}})}}\sin \nu {{(1 + e\cos \nu )}^{2}}$Здесь $\nu $ – истинная аномалия планеты. Из уравнений (3.4) и (3.5) следует, что обусловленное релятивистским эффектом дополнительное среднее смещение перигелия планеты за один оборот вокруг Солнца определяется формулой (3.1), а дополнительное среднее смещение эксцентриситета равно нулю.
Определяемые формулой (3.1) дополнительные средние смещения перигелия для внутренних планет за столетие имеют следующие значения:
(3.6)
${\text{Меркурий:}}\;43.03'',\quad {\text{Венера:}}\;8.64'',\quad {\text{Земля:}}\;3.83'',\quad {\text{Марс:}}\;1.35''$Разница для линейных по времени составляющих средних смещений перигелиев между данными эфемерид [11] и данными таблицы 3 составляет:
(3.7)
$\begin{gathered} {\text{Меркурий:}}\;42.81'' \pm 0.2'',\quad {\text{Венера:}}\;2.55'' \pm 10'' \\ {\text{Земля:}}\;1.24'' \pm 3'',\quad {\text{Марс:}}\;3.05'' \pm 2'' \\ \end{gathered} $Сопоставляя данные (3.6) и (3.7), можно сделать вывод, что наличие релятивистского эффекта подтверждается для смещения перигелия Меркурия. Для перигелиев остальных планет эффект, предсказываемый ОТО, находится внутри интервала погрешности расчетов. Кроме того, между данными таблицы 3 и данными эфемерид [11] имеется существенная разница в среднем смещении эксцентриситета Марса. Она составляет $(0.198 \pm 0.03) \times {{10}^{{ - 5}}}$ и не может быть объяснена с позиций ОТО, поскольку возмущение (3.3), как было показано выше, не вызывает векового смещения эксцентриситетов.
Отметим, что если сравнивать данные эфемерид [11] с данными таблицы 1, полученными на основе первого приближения решений уравнений возмущенного движения, то разница в средних смещениях перигелиев Венеры, Земли и Марса будет существенно отличаться от значений, предсказываемых ОТО.
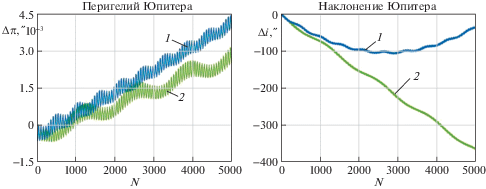
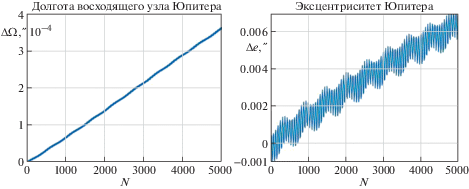
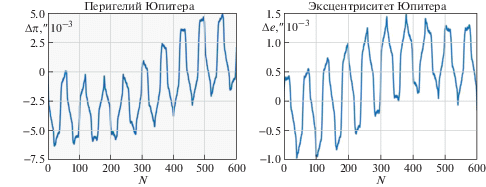
4. Эволюция орбит внешних планет. Для внешних планет, как показали расчеты, смещения элементов орбит, вычисленные на основе первого приближения и точных решений уравнений возмущенного движения, различаются более заметно, чем для внутренних планет. На рис. 3 приведены графики смещений перигелия и наклонения орбиты Юпитера на интервале времени в пять тысяч лет. Здесь цифрой 1 обозначены графики, полученные из точных решений системы (2.23), (2.24), а цифрой 2 – графики, полученные из первого приближения. На рис. 4 приведены полученные из точных решений графики смещений долготы восходящего узла и эксцентриситета орбиты Юпитера.
Из этих графиков видно, как существенно различаются смещения некоторых элементов орбиты Юпитера, вычисленные по первому приближению и по точным решениям уравнений возмущенного движения. В поведении элементов орбиты Юпитера наблюдаются ярко выраженные долгопериодические моды колебаний. При этом на точных решениях и на решениях первого приближения частоты этих мод различаются в несколько раз, а различие в средних смещениях перигелия Юпитера составляет около 20%. По точным решениям период долгопериодических мод колебаний составляет около 560 лет.
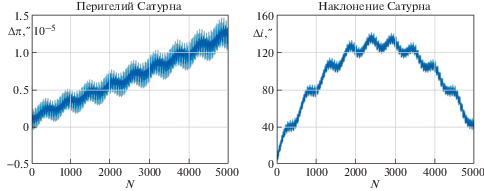
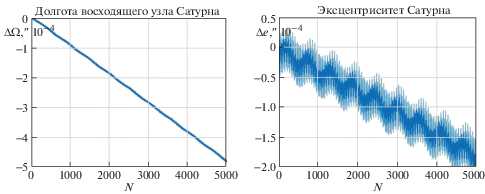
Аналогичная картина наблюдается и в поведении элементов орбиты Сатурна. На рис. 5 приведены вычисленные по точным решениям графики смещений перигелия и наклонения орбиты Сатурна, а на рис. 6 – графики смещений долготы восходящего узла и эксцентриситета. Наличие долгопериодических мод колебаний в поведении элементов орбит Юпитера и Сатурна обусловлено тем, что отношение периодов обращения этих планет близко к резонансу 2:5.
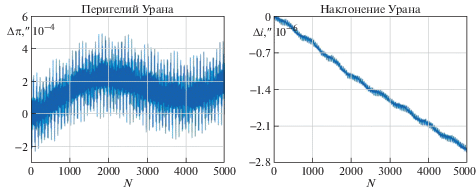
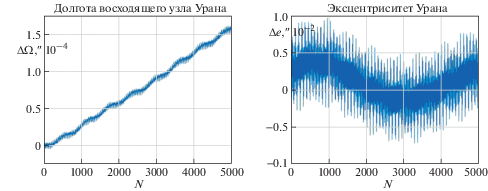
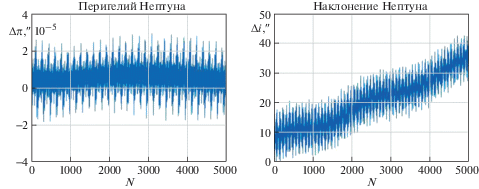
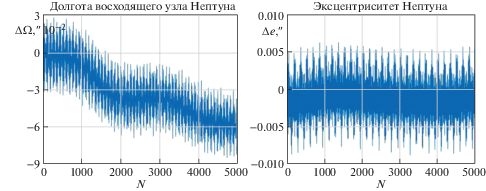
На рис. 7, 8 и 9, 10 приведены графики поведения во времени элементов орбиты Урана и Нептуна, соответственно, вычисленные по точным решениям уравнений возмущенного движения (2.23), (2.24).
Детальный анализ графиков показал, что первое приближение адекватно описывают поведение элементов орбит внешних планет только на коротких интервалах времени до ста лет. На более длинных интервалах времени эволюцию орбит следует рассчитывать, используя точные решения уравнений возмущенного движения.
Как видно из графиков на рис. 11, где показано поведение перигелия и эксцентриситета орбиты Юпитера на интервале времени в шестьсот лет, помимо долгопериодической составляющей в поведении элементов орбит внешних планет имеется еще среднепериодическая составляющая, период которой равен около 62 лет, что соответствует примерно двум периодам обращения Сатурна. Для некоторых элементов орбит амплитуда этих колебаний во много раз превышает среднее смещение за столетие. Например, для перигелия Юпитера она составляет около 0.8°, а для перигелия Сатурна – около 3.5°. А поскольку период этих колебаний сравнительно большой, то для расчета значений элементов орбит внешних планет на заданный момент времени информация о средних смещениях элементов представляется мало полезной, так как на интервалах времени в десятки лет истинное значение элемента существенно отличается от среднего.
Как показали расчеты, в эволюции орбит внешних планет доминирующим фактором является взаимодействие между самими этими планетами, т.е. влияние внутренних планет сравнительно мало, и им можно пренебречь. На основании этого из системы (1.17)–(1.22) можно исключить уравнения для внутренних планет. Тогда проблема, связанная с особенностью в уравнениях для элементов орбиты Земли, будет устранена. Оставшиеся уравнения можно уже проинтегрировать как единую систему взаимосвязанных уравнений и получить, тем самым, точные решения уравнений возмущенного движения для внешних планет. Проведенные расчеты показали полное совпадение результатов численного интегрирования этой системы с результатами численного интегрирования системы (2.23), (2.24). Это совпадение может служить свидетельством того, что при выводе уравнений (2.23), (2.24) и при их программировании никаких ошибок допущено не было.
Результаты численного интегрирования уравнений возмущенного движения на интервалах времени до пяти тысяч свидетельствуют о том, что средние значения параметров и эксцентриситетов орбит планет меняются со временем. Но их изменения носят такой характер, что средние значения больших полуосей остаются неизменными. Для внешних планет в средних значениях больших полуосей орбит наблюдаются только среднепериодические и долгопериодические колебания. Таким образом, теорема Лапласа [9] об устойчивости Солнечной системы подтверждается и результатами численного интегрирования уравнений возмущенного движения.
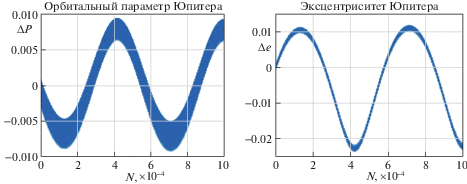
Были проведены также расчеты эволюции орбит внешних планет на больших интервалах времени до ста тысяч лет. По результатам этих расчетов также не выявлено вековых смещений в средних значениях больших полуосей орбит планет. Кроме того, установлено, что помимо долгопериодических мод колебаний в поведении элементов орбит имеются сверх долгопериодические моды, период которых составляет в зависимости от планеты от нескольких тысяч лет до нескольких десятков тысяч лет. Соответствующий пример приведен на рис. 12, где изображены графики для параметра и эксцентриситета орбиты Юпитера на интервале времени в сто тысяч лет.
Заключение. В работе получены уравнения возмущенного движения в невырождающихся переменных, численным интегрированием которых задача определения смещения элементов орбит планет решается в точной (нелинейной) постановке. В качестве таких переменных использовались векторы кинетических моментов и векторы Лапласа планет.
Определены средние смещения и амплитуды колебательных составляющих для элементов орбит всех внутренних планет Солнечной системы на эпоху J2000 (таблица 1). По результатам этих расчетов установлено, что точность вычисления вековых смещений перигелия для Меркурия самая высокая, а для Венеры – самая низкая. Определен вклад каждой планеты в среднее смещение перигелия внутренних планет (таблица 2).
Определены интервалы времени, на которых первое приближение адекватно описывает поведение элементов орбит планет. Для внутренних планет эти интервалы составляют около тысячи лет, а для внешних – не более ста лет. Установлено также, что в поведении элементов орбит внешних планет присутствуют среднепериодические (около 60 лет) и долгопериодические (около 560 лет) моды колебаний, амплитуда которых может в несколько раз превышать среднее смещение элемента за столетие. По этой причине точность вычисления вековых смещений элементов орбит внешних планет существенно ниже, чем для внутренних планет.
Проведено сопоставление результатов расчетов для средних смещений элементов орбит, полученных в рамках классической механики, с данными эфемерид на эпоху J2000 [11]. Установлено, что для Меркурия разница в этих данных хорошо согласуется с релятивистским эффектом, предсказываемым общей теорией относительности, а для остальных планет находится внутри интервала погрешности расчетов.
Результаты расчетов на интервалах времени до ста тысяч лет подтверждают теорему Лапласа об отсутствии вековых смещений в значениях больших полуосей орбит планет.
Список литературы
Le Verrier U. Théorie de mouvement de Mercure // Ann. Observ. Imp. 1859. V. 5. P. 1–96.
Le Verrier U. Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète // Comptes rendus hebdomadaires des séances de l’Académie des sciences. 1859. V. 49. P. 379–383.
Newcomb S. The Elements of the Four Inner Planets and the Fundamental Constants of Astronomy. Suppl. Am. Ephem. & Naut. Alman. for 1897. Washington, D.C.: U.S. Govt. Printing Office, 1895. ix+202 p.
Роузвер Н.Т. Перигелий Меркурия. От Леверье до Эйнштейна. М.: Мир, 1985. 244 с.
Эйнштейн А. Объяснение движения перигелия Меркурия в общей теории относительности // Собр. научн. тр. в 4 томах. Т. I. С. 439–447.
Standish E.M., Newhall X.X., Williams J.G., Folkner W.M. JPL planetary and lunar ephemerides, DE403/LE403 // Interoffice Memorandum. 1995. 314.10-127, 1–22.
Питьева Е.В. Современные численные теории движения Солнца, Луны и больших планет. СПб.: Ин-т прикл. астрон. РАН. 2003. 32 с.
Амелькин Н.И. О прецессии орбиты Меркурия // Докл. РАН. 2019. Т. 489. № 6. С. 570–575.
Дубошин Г.Н. Небесная механика. Основные задачи и методы. М.: Физматгиз, 1963. 588 с.
Дубошин Г.Н. Справочное руководство по небесной механике и астродинамике. М.: Наука, 1976. 864 с.
Simon J.L., Bretagnon P., Chapront J., Chapront-Touzé M., Francon G., Laskar J. Numerical expressions for precession formulae and mean elements for the Moon and the planets // Astron. Astrophys. 1994. V. 282. P. 663–683. neb/rw/natsat/plaorbw.htm.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика