1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 84, № 4, 2020

Прикладная математика и механика, 2020, T. 84, № 4, стр. 433-441

Переходные процессы в динамике волчка тип-топ

М. А. Муницына 1, 2, *

1 Московский физико-технический институт
Долгопрудный, Россия

2 Институт проблем управления РАН
Москва, Россия

* E-mail: munitsyna@gmail.com

Поступила в редакцию 02.03.2020
После доработки 21.04.2020
Принята к публикации 06.05.2020

Полный текст (PDF)

Аннотация

Простейшей моделью волчка тип-топ является неоднородный динамически симметричный шар, центр масс которого лежит на оси динамической симметрии, но не совпадает с геометрическим центром. Локальный анализ этой модели представлен в работах [1, 2], а глобальный качественный анализ – в работах [3–5]. Численные исследования проводились в рамках поликомпонентного сухого трения [6]. Сравнительный анализ различных моделей проведен в [7]. В работе [8] представлен метод обобщенных диаграмм Смейла [9, 10] в задаче о движении волчка тип-топ на вязкоупругой плоскости. В настоящей работе для поликомпонентных моделей сухого и вязкого трения при некотором классе начальных условий приводятся приближенные уравнения, описывающие динамику волчка и позволяющие дополнить качественный анализ количественными оценками.

Ключевые слова: трения, тип-топ, диаграммы Смейла

1. Постановка задачи. Рассмотрим задачу о движении неоднородного динамически симметричного шара на горизонтальной плоскости. Пусть $r$ – радиус шара, $s$ – расстояние между его геометрическим центром $O$ и центром масс $S$ ($s \ne 0$). Будем считать, что прямая $SO$ с единичным ортом ${\kern 1pt} e = \overline {SO} {\text{/}}s$ является осью динамической симметрии шара, а $A$ и $C$ – его экваториальный и осевой моменты инерции.

Теоремы об изменении количества движения и кинетического момента шара, условие постоянства вектора ${\kern 1pt} \gamma $ и условие безотрывности движения, отнесенные к главным центральным осям инерции шара, имеют соответственно вид

(1.1)
$\begin{gathered} m{\kern 1pt} {\mathbf{\dot {v}}} + [\omega ,m{\mathbf{v}}] = - mg\gamma + N\gamma + {\mathbf{F}},\quad \operatorname{J} \dot {\omega } + [\omega ,\operatorname{J} \omega ] = [{\mathbf{r}},N\gamma + {\mathbf{F}}] + {\mathbf{M}} \\ \dot {\gamma }[\omega ,\gamma ] = 0,\quad ({\mathbf{u}},\gamma ) = 0 \\ \end{gathered} $

Здесь $m$ – масса шара, ${\kern 1pt} {\mathbf{v}}{\kern 1pt} $ и ${\kern 1pt} \omega $ – векторы скорости его центра масс и угловой скорости, ${\mathbf{r}} = s{\mathbf{e}} - r\gamma $ и ${\kern 1pt} {\mathbf{u}} = {\mathbf{v}} + [\omega ,{\mathbf{r}}]$ – радиус-вектор и скорость нижней точки шара соответственно, $g$ – ускорение свободного падения, $N \geqslant 0$ – величина нормальной составляющей реакции опорной плоскости, $\operatorname{J} = {\text{diag}}(A,A,C)$ – центральный тензор инерции шара, F и M – сила и момент трения. При заданной модели трения

(1.2)
${\kern 1pt} {\mathbf{F}} = {\mathbf{F}}({\mathbf{v}},\omega ,\gamma ,N),\quad {\mathbf{M}} = {\mathbf{M}}({\mathbf{v}},\omega ,\gamma ,N)$
система (1.1) замкнута относительно переменных v, ω, γ и N.

Заметим, что в случае отрыва шара от плоскости ($N = 0$) для описания его динамики следует положить ${\mathbf{F}} = 0$, ${\mathbf{M}} = 0$ в первых трех уравнениях (1.1), отбросив последнее уравнение. При этом для отслеживания возвращения на контакт следует рассматривать также уравнение

(1.3)
$\dot {z} = ({\kern 1pt} {\mathbf{u}},\gamma ),$
где $z$ – высота над плоскостью нижней точки шара (в момент отрыва и при возвращении на контакт $z = 0$).

2. Плоскость с трением скольжения. Следуя [1, 4], рассмотрим случай ${\mathbf{M}} = 0$ и будем считать, что сила трения удовлетворяет условиям

(2.1)
${\kern 1pt} {\mathbf{F}} = 0\quad при\quad {\mathbf{u}} = 0;\quad ({\kern 1pt} {\mathbf{F}},{\mathbf{u}}) < 0\quad при\quad {\mathbf{u}} \ne 0$

Тогда система уравнений (1.1) имеет первый интеграл (интеграл Джелетта) вида

(2.2)
$K(\omega {\kern 1pt} ,\gamma ) = - \frac{1}{{Cr}}(\operatorname{J} \omega ,{\mathbf{r}}) = k = \operatorname{const} ,$
а для качественного анализа динамики предложенной модели волчка (неоднородного шара) явное выражение силы трения не требуется [4].

В рассматриваемом случае система уравнений (1.1) имеет решения вида

(2.3)
$\begin{array}{*{20}{c}} {{{\gamma }_{1}} = {{\gamma }_{2}} = 0,\quad {{\gamma }_{3}} = \pm 1,\quad {{\omega }_{1}} = {{\omega }_{2}} = 0,\quad {{\omega }_{3}} = \operatorname{const} ,\quad N = mg,\quad {\mathbf{v}} = 0} \end{array},$
соответствующие равномерным вращениям вокруг вертикальной оси динамической симметрии шара, и
(2.4)
$\begin{gathered} {{\omega }_{1}} = \omega sin\theta sin{{\omega }_{0}}t,\quad {{\omega }_{2}} = \omega sin\theta cos{{\omega }_{0}}t,\quad {{\omega }_{3}} = \omega cos\theta + {{\omega }_{0}} \\ {{\gamma }_{1}} = sin\theta sin{{\omega }_{0}}t,\quad {{\gamma }_{2}} = sin\theta cos{{\omega }_{0}}t,\quad {{\gamma }_{3}} = cos\theta ,\quad N = mg,\quad {\mathbf{v}} = 0, \\ \end{gathered} $
соответствующие его регулярным прецессиям вокруг неподвижного центра масс. Параметры регулярной прецессии (2.4) определяются постоянной интеграла Джелетта
(2.5)
$\begin{array}{*{20}{c}} {{{k}^{2}} = c\frac{{{{{\left( {a(1 - {{y}^{2}}) + {{{\left( {y - b} \right)}}^{2}}} \right)}}^{2}}}}{{b - (1 - a)y}},\quad \omega = \frac{k}{{a(1 - {{y}^{2}}) + {{{\left( {y - b} \right)}}^{2}}}},\quad {{\omega }_{0}} = - b\omega } \end{array}$
и справедливо равенство

(2.6)
$\omega _{3}^{2} = \frac{{{{{\left( {b - y} \right)}}^{2}}c}}{{(a - 1)y + b}}$

Здесь $y = cos\theta $ – косинус угла нутации шара, значение которого определяется первым равенством формулы (2.4), а $a$, $b$ и $c$ – параметры волчка

$a = \frac{A}{C} \in [1{\text{/}}2, + \infty ],\quad b = \frac{s}{r} \in (0,1),\quad c = \frac{{mgs}}{C} \in (0, + \infty ]$

Указанные движения представляют собой множество всех возможных движений без проскальзывания (${\kern 1pt} {\mathbf{u}} = 0$), на которых полная механическая энергия

(2.7)
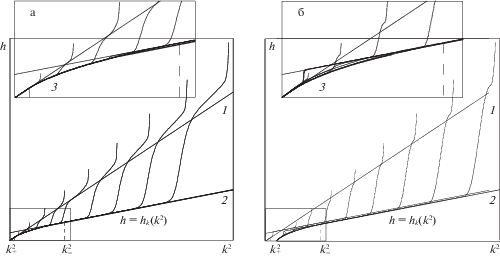
$H({\mathbf{v}},\omega ,\gamma ) = \frac{1}{2}m{{{\mathbf{v}}}^{2}} + \frac{1}{2}(\operatorname{J} \omega ,\omega ) - mg({\kern 1pt} \gamma ,{\mathbf{r}})$
сохраняется.

Полный параметрический анализ устойчивости этих решений и соответствующие диаграммы Смейла на плоскости $({{k}^{2}},h)$, где $h$ – начальное значений полной механической энергии представлен в работе [4]. Например, для волчка с параметрами

(2.8)
$a = 1,\quad b = 0.3$
диаграмма Смейла имеет вид, представленый на рис. 1. Здесь решениям (2.3), устойчивым при ${{k}^{2}} \leqslant k_{ \pm }^{2}$, соответствуют прямые 1 и 2, решениям (2.4), (2.5) соответствует кривая 3. Каждому значению $k$ соответствует ровно одно устойчивое движение (жирная кривая), точные выражения для соответствующей зависимости $h = h({{k}^{2}})$ и значения $k_{ \pm }^{2}$ представлены в [4].

Рис. 1.

Заметим, в случае абсолютно гладкой плоскости уравнения движения шара имеют еще один первый интеграл ${{\omega }_{3}} = \operatorname{const} $ и допускают что те же решения (2.3), (2.4), параметры которых определяются значениями интегралов

(2.9)
$\frac{{\left( {\left( {x - b} \right){{\omega }_{3}} - k} \right){{\omega }_{3}}}}{{(1 - {{x}^{2}})a}} + \frac{{{{{\left( {\left( {x - b} \right){{\omega }_{3}} - k} \right)}}^{2}}x}}{{{{{(1 - {{x}^{2}})}}^{2}}a}} = c,\quad \omega = \frac{{k - (x - b){\kern 1pt} {{\omega }_{3}}}}{{a(1 - {{x}^{2}})}},\quad {{\omega }_{0}} = {{\omega }_{3}} - \omega x$

Здесь $x = cos\theta $ – косинус угла нутации шара, значение которого определяется первым равенством формулы (2.9). Причем прецессии устойчивы при любых параметрах задачи [11].

3. Плоскость с трением скольжения, верчения и качения. Рассмотрим плоскость с трением скольжения, верчения и качения ${\mathbf{F}} \ne 0$, ${\mathbf{M}} \ne 0$. Тогда на решениях системы (1.1) спреведливы равенства

(3.1)
$\dot {H} = ({\kern 1pt} {\mathbf{F}},{\mathbf{u}}) + ({\mathbf{M}},\omega ),\quad \dot {K} = - \frac{1}{{Cr}}({\mathbf{M}}{\kern 1pt} ,{\mathbf{r}})$

Следуя [4] будем считать, что момент трения удовлетворяет условиям

(3.2)
$0 < \frac{{({\mathbf{M}},\omega )}}{{({\mathbf{F}},{\mathbf{u}})}} \ll 1\quad при\quad {\mathbf{u}} \ne 0;\quad \frac{{({\mathbf{M}},{\mathbf{r}})}}{{mg{{r}^{2}}}} \ll 1\quad при\quad {\mathbf{u}} \ne 0$

Эти условия позволяют провести качественный анализ динамики методом обобщенных диаграмм Смейла [9, 10]. Полная механическая энергия $H$ убывает на движения без проскальзывания значительно медленнее, чем на движениях с проскальзыванием, а величина $K$ медленно меняется на всех движениях. Следовательно [4], под действием фазового потока системы (1.1) те точки плоскости $({{K}^{2}},H)$, которые не принадлежат соответствующим (2.3) и (2.4), (2.5) решениям движутся “быстро” в сторону уменьшения $H$, и “медленно” – вдоль оси ${{K}^{2}}$. Попадая таким образом на множество $H = h({{K}^{2}})$ точка продолжает движение “медленно” вдоль него до тех пор, пока не остановится в соответсвующей устойчивому равновесию точке.

Тогда, если в начальном положении ось шара с параметрами (2.8) почти вертикальна, центр масс близок к наинизшему положению, а начальная угловая скорость почти сонаправлена с осью и достаточно велика, то начальная точка на обобщенной диаграмме Смейла находится в окрестности прямой 1 (рис. 1) в области ${{K}^{2}} > k_{ - }^{2}$, и в процессе движения ось шара сначала перевернется к вертикальному положению с наивысшем расположением центра масс после чего на некоторое время останется в этом положении. Шар будет вращаться вокруг нее с медленно убывающей по модулю угловой скоростью, пока она не уменьшится о соответствующего равенству ${{K}^{2}} = k_{ - }^{2}$ значения. После этого ось шара будет переворачиваться к начальному положению, а шар будет совершать квазипрецессионные движения. Когда центр масс займет наинизшее положение, шар будет замедленно вращаться вокруг вертикали до полной остановки.

Для исследования первого переходного процесса к множеству $H = h({{K}^{2}})$ заметим, что из системы (1.1) следует, что

(3.3)
${{\dot {\omega }}_{3}} = \frac{r}{C}([{\mathbf{F}},\gamma ],{\mathbf{e}}) + \frac{1}{C}({\kern 1pt} {\mathbf{M}},e)$

Отсюда в предположении о малости правой части следует, что ${{\omega }_{3}}$ является медленной переменной, а приближенное уравнение, описывающие ее изменение, может быть получено подстановкой вместо быстрых переменных соответствующих периодических или почти периодических решений исходной системы, найденных в предположении о постоянстве медленной переменной [12, 13], т.е. соответствующих стационарным движениям шара на абсолютно гладкой плоскости – прецессии (2.4) с учетом (2.9). При движении вдоль соответствующих (2.3) множеств величина ${{\dot {\omega }}_{3}}$ может быть определена непосредственно из уравнений движения. На движении вдоль соответствующего (2.4), (2.5) множества, медленной величиной будет также полная механическая энергия, а почти периодическими решениями, найденными в предположении ее постоянстве, будут соответствующие этому множеству решения.

Таким образом, учитывая все высказанное при вязком трении вида

(3.4)
${\kern 1pt} {\mathbf{F}} = - {{\kappa }_{f}}{\kern 1pt} {\mathbf{u}},\quad {\mathbf{M}} = - {{\kappa }_{m}}(\omega ,\gamma )\gamma {\kern 1pt} ,\quad {{\kappa }_{f}} = \operatorname{const} ,\quad {{\kappa }_{m}} = \operatorname{const} $
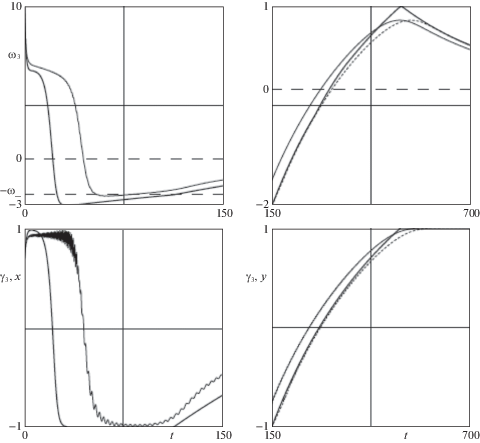
и считая малыми безразмерные параметры ${{k}_{f}}\sqrt {r{\text{/}}g} {\text{/}}m$ и ${{k}_{m}}\sqrt {r{\text{/}}g} {\text{/}}C$, получим
(3.5)
${{\dot {\omega }}_{3}} = \left\{ \begin{gathered} - \frac{{{{\kappa }_{f}}{{r}^{2}}}}{A}\Phi ({{\omega }_{3}}) - \frac{{{{\kappa }_{m}}}}{A}\Psi ({{\omega }_{3}})x,\quad H > h({{K}^{2}}) \hfill \\ - \frac{{{{\kappa }_{m}}}}{C}{{\omega }_{3}},\quad H = h({{K}^{2}}),\quad {{K}^{2}} \in [0,k_{ + }^{2}] \cup [k_{ - }^{2}, + \infty ) \hfill \\ - \frac{{{{\kappa }_{m}}c}}{C}\frac{{\varphi (y)\left( {1 - by} \right)}}{{\left( {a - 1} \right)y + b}}\frac{{y - b}}{{{{\omega }_{3}}}},\quad H = h({{K}^{2}}),\quad {{K}^{2}} \in (k_{ + }^{2},k_{ - }^{2}){\kern 1pt} , \hfill \\ \end{gathered} \right.$
где
$\varphi (y) = \frac{{\left( {by - 1} \right)\left[ {(a - 1)y + b(a + 1)} \right]}}{{(3{{{[(a - 1)y + b(a + 1)]}}^{2}} + a({{b}^{2}} - 1) + {{a}^{2}})}}$
зависимости $x = x({{\omega }_{3}})$ и $y = y({{\omega }_{3}})$ определяются соответствующими равенствами (2.9) и (2.6), а зависимости $\Phi ({{\omega }_{3}})$ и $\Psi ({{\omega }_{3}})$ имеют вид

$\Phi ({{\omega }_{3}}) = \left( {b - x} \right)K + (a(1 - {{x}^{2}}) + {{\left( {b - x} \right)}^{2}}){{\omega }_{3}},\quad \Psi ({{\omega }_{3}}) = K + \left( {b + (a - 1)x({{\omega }_{3}})} \right){{\omega }_{3}}$

Введем такие масштабы измерения масс, длин и времени, что $m = 1$, $g = 1$ и $r = 1$, численные значения параметров волчка (2.8) и трения примем следующими: $c = 1$, ${{\kappa }_{f}} = 0.25$, ${{\kappa }_{m}} = 1 \times {{10}^{{ - 3}}}$. На рис. 2 тонкими кривыми представлены результаты численного интегрирования полных уравнений движения шара при начальных условиях

(3.6)
${\kern 1pt} {\mathbf{v}}{\kern 1pt} (0) = 0,\quad {{\gamma }_{3}}(0) = 0.7,\quad {{\gamma }_{1}}(0) = 0,\quad {{\omega }_{3}}(0) = 10,\quad {{\omega }_{1}}(0) = {{\omega }_{2}}(0) = 0$
Рис. 2.

Жирным кривым на рис. 2 отмечены решение уравнения (3.5) и соответствующая ему зависимость косинуса угла нутации шара. Последние можно разделить на четыре этапа движения: на первом абсолютная величина ${{\omega }_{3}}$ уменьшается и выполнено неравенство $x > - 1$ – в этом случае интегрируется первая строчка уравнения (3.5) (этот этап соответствует первому перевороту волчка от положения с наинизшим расположением центра масс к наивысшему); на втором ${{\dot {\omega }}_{3}}$ меняет знак на противоположный, а величина $x$ ($y$) полагается равной –1 – интегрируется вторая строчка уравнения (3.5) (соответствующая вращению волчка вокруг вертикали) до тех пор, пока не достигается равенство $\omega _{3}^{2} = \omega _{ - }^{2}$ (${{K}^{2}} = k_{ - }^{2}$); затем интегрируется третья строчка (соответствующая второму перевороту волчка) и величина $y$ меняется от –1 до 1; на финальном этапе (также соответствующем вращениям волчка вокруг вертикали) снова интегрируется вторая строчка уравнения (3.5) до тех пор, пока величина ${{\omega }_{3}}$ не обратится в ноль.

При численном интегрировании уравнения (3.5) на первом этапе движения изменение величины $K$ не учитывалось, вследствие чего наблюдается различие значений ${{\omega }_{3}}$ в результате этого переходного процесса, а на следующих этапах решения отличаются сдвигом по времени (пунктиром обозначен сдвиг точного решения). При численном интегрировании уравнения (3.5) на третьем этапе учитывалось, что его правая часть имеет в точке ${{\omega }_{3}} = 0$ ($y = b$) устранимую особенность. Заметим, что в начале этого этапа решение полной системы уравнений остается в окрестности ${{\gamma }_{3}} = - 1$, а затем быстро переходит в окрестность приближенного решения, т.е. при сходе с неустойчивых вращений наблюдается затягивание потери устойчивости ([14, 15]).

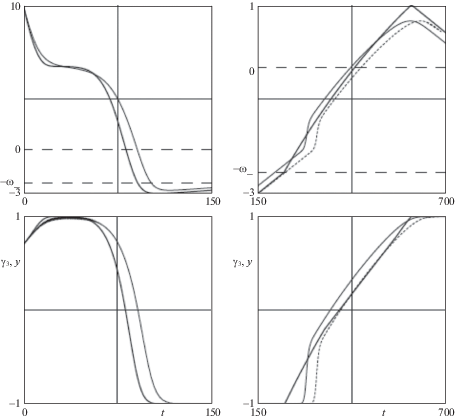
Рассмотрим модель трения вида

(3.7)
${\kern 1pt} {\mathbf{F}} = - fN\frac{{\mathbf{u}}}{{\left| {\mathbf{u}} \right| + 8\rho {\text{/}}(3\pi )\left| {(\omega ,\gamma )} \right|}},\quad {\mathbf{M}} = - \frac{{3\pi {{\rho }^{2}}f}}{{16}}N\frac{{(\omega ,\gamma )\gamma }}{{15\pi {\text{/}}(16\rho )\left| {\mathbf{u}} \right| + \left| {(\omega ,\gamma )} \right|}},$
где $f$, $\rho $ – постоянные коэффициенты. Равенства (19) соответствует аппроксимациям Паде первого порядка моделей трения [2, 10]. Тогда, считая малыми параметры $f$ и ρ/r, получим

(3.8)
$\begin{array}{*{20}{l}} {{{{\dot {\omega }}}_{3}} = \left\{ \begin{gathered} - \tfrac{{fc}}{b}\tfrac{{\Phi ({{\omega }_{3}})\sqrt {1 - {{x}^{2}}} }}{{\Phi ({{\omega }_{3}})\operatorname{sign} K + \beta \Psi ({{\omega }_{3}})\sqrt {1 - {{x}^{2}}} }} - \tfrac{\mu }{C}\tfrac{{\Psi ({{\omega }_{3}})x\sqrt {1 - {{x}^{2}}} }}{{\alpha \Phi ({{\omega }_{3}})\operatorname{sign} K + \Psi ({{\omega }_{3}})\sqrt {1 - {{x}^{2}}} }} \hfill \\ H > h({{K}^{2}}) \hfill \\ - \tfrac{{{{\kappa }_{m}}}}{C}\operatorname{sign} {{\omega }_{3}},\quad H = h({{K}^{2}}),\quad {{K}^{2}} \in [0,k_{ + }^{2}] \cup [k_{ - }^{2}, + \infty ) \hfill \\ - \tfrac{{{{\kappa }_{m}}}}{C}\varphi (y),\quad H = h({{K}^{2}}),\quad {{K}^{2}} \in (k_{ + }^{2},k_{ - }^{2}) \hfill \\ \end{gathered} \right.} \end{array}$

Результаты соответствующих численных экспериментов при следующих параметрах трения $f = 0.2$, $\rho = 0.04$, представлены на рис. 3. Качественно эти результаты совпадают с представленными на рис. 2. Параметры трения определялись из условия примерного совпадения длины временных интервалов каждого из этапов движения с аналогичными интервалами предыдущего эксперимента. В целом можно сказать, что при выбранных параметрах в рассматриваемых экспериментах качество приближения полученными уравнениями (3.5), (3.8) полной системы уравнений движения при двух рассмотренных моделях трения одинаково. К различиям можно отнести дольшее затягивание потери устойчивости при переходе с неустойчивых вращений к прецессиям в случае сухого трения.

Рис. 3.

Кривые, соответствующие численному интегрированию полных уравнений движения на обощенных диаграммах Смейла в случае моделей трения (3.4) и (3.7) представлены на рис. 1, а и рис. 1, б соответственно (начальные условия имели аналогичный (3.6) вид, начальная угловая скорость менялась от 1 до 10 с равным шагом в единицу).

Полученные уравнения (3.5), (3.8), определяют динамику шара при близких к виду (2.4) при соотношении (2.9) начальных условиях. Они интегрируются в квадратурах и аппроксимируют зависимость от времени проекции угловой скорости шара на ось его динамической симметрии, при этом равенства (2.3) или (2.4) с учетом (2.9) или (2.5) на соответствующих этапах движения описывают поведение всех остальных переменных. Точные решения полной системы уравнений движения шара представляют собой сумму плавно меняющейся траектории усредненного движения и быстро осциллирующих слагаемых. В частности, сила реакции опорной плоскости, сохраняя в среднем равное весу шара значение, может существенно отклонятся от него, в том числе принимая нулевое значение. В таком случае происходит отрыв от плоскости. Но в силу быстрой осциляции всех переменных, а следовательно и правой части равенства (1.3), ему соответствует столь же быстрое возвращение на контакт. Этим объясняется тот факт, что в соответствующем натурном эксперименте видимого отрыва от плоскости не наблюдается, а движение сопровождается звуком серии микроударов.

Следует отметить, что при добавлении к любой из рассмотренных моделей трения перпендикулярной скорости скольжения компоненты силы или момента трения полученные уравнения (3.5), (3.8) не изменятся, т.е. в рассматриваемой задаче о движении неоднородного шара на неподвижной горизонтальной плоскости эти компоненты не оказывают качественного влияния на динамику. Заметим также, что предложенный подход к исследованию динамики волчка тип-топ и других задач подобного рода (например, динамики сфероида [18, 19]) может быть использован и при других моделях взаимодействия тела с опорной поверхностью.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (19-01-00140, 18-01-00335) и Программы фундаментальных научных исследований по приоритетным направлениям, определяемым Президиумом Российской академии наук, № 7 “Новые разработки в перспективных направлениях энергетики, механики и робототехники”.

Список литературы

  1. Контенсу П. Связь между трением скольжения и трением верчения в ее учет в теории волчка // Проблемы гироскопии. М.: Мир, 1967. С. 60–77.

  2. Mагнус К. Гироскоп. теория и применение. М.: Мир, 1974. 526 с.

  3. Карапетян А.В. Качественное исследование волчка на плоскости с трением // ПММ. 1991. Т. 55. № 4. С. 698–701.

  4. Карапетян А.В. Глобальный качественный анализ динамики китайского волчка (тип-топ) // Изв. РАН. МТТ. 2008. № 3. С. 33–41.

  5. Карапетян А.В. Инвариантные множества механических систем с симметрией // Проблемы устойчивости и управления. Сб. научн. статей, посвященный 80-летию акад. В.М. Матросова. М.: Физматлит, 2013. С. 184–210.

  6. Климов Д.М., Журавлёв В.Ф. О динамике волчка Tомсона (тип-топ) на плоскости с реальным сухим трением // Изв. РАН. МТТ. 2005. № 6. С. 157.

  7. Зобова А.А. Различные модели трения в динамике двусферического волчка // Изв. РАН. МТТ. 2013. № 2. С. 21–28.

  8. Zobova A.A., Karapetyan A.V. Tippe-top on visco-elastic plane: steady-state motions, generalized Smale diagrams and overturns // Lobachevskii J. Math. 2017. V. 38. P. 1007–1013.

  9. Карапетян А.В. Качественный анализ динамики диссипативных систем с симметрией на основе метода обобщенных диаграмм Смейла // В сб.: Современные проблемы математики и механики. Т. 2. Механика. Вып. 2. М.: МГУ, 2009. С. 192–200.

  10. Карапетян А.В. Обобщенные диаграммы Cмейла и их применение к задачам динамики систем с трением // Аналитическая механика, устойчивость и управление: Тр. 10-й междунар. Четаевской конф. Казань, 2012 Казань: Изд-во Казан. гос. техн. ун-та, 2012. С. 247–258.

  11. Карапетян А.В. Об устойчивости стационарных движений тяжелого твердого тела на абсолютно гладкой горизонтальной плоскости // ПММ. 1981. Т.45. № 3. С. 504–511.

  12. Моргунов Б.И., Волосов В.М. Метод осреднения в теории нелинейных колебательных систем. М.: МГУ, 1971. 508 с.

  13. Блехман И.И. Вибрационная механика. М.: Физматлит, 1994. 400 с.

  14. Нейштадт А.И. О затягивании потери устойчивости при динамических бифуркациях. I // Дифференц. уравн. 1987. Т. 23. № 12. С. 2060–2067.

  15. Нейштадт А.И. О затягивании потери устойчивости при динамических бифуркациях. II // Дифференц. уравн. 1988. Т. 24. № 2. С. 226–233.

  16. Карапетян А.В. Двухпараметрическая модель трения и ее свойства // ПММ. 2009. Т. 73. № 5. С. 515–519.

  17. Журавлев В.Ф. О модели сухого трения в задаче качения твердых тел // ПММ. 1998. Т. 62. №. 5. С. 762–767.

  18. Муницына М.А. Динамика сфероида на плоскости с трением // ПММ. 2018. Т. 82. №. 1. С. 16–24.

  19. Муницына М.А. О переходных процессах в динамике эллипсоида вращения на плоскости c трением // Изв. РАН. МТТ. 2019. № 3. С. 69–75.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал