Прикладная математика и механика, 2020, T. 84, № 4, стр. 455-466

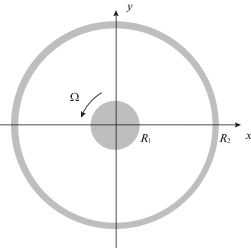
Изучается система, состоящая из двух цилиндров, вставленных один в другой, и вязкой несжимаемой жидкости между ними. Внешний цилиндр покоится, внутренний цилиндр вращается относительно своей оси с угловой скоростью $\Omega $, которая поддерживается постоянной. Ось внутреннего цилиндра упруго закреплена и может совершать колебания относительно положения равновесия, в котором цилиндры расположены коаксиально (рис. 1).

Задача об устойчивости быстро вращающегося ротора в кожухе впервые была поставлена П.Л. Капицей [1]. Было рассмотрено влияние вязкости на устойчивость ротора и показано, что трение об окружающую среду приводит к появлению неустойчивости в системе. При этом была отмечена чрезвычайная сложность определения силы, действующей на цилиндр со стороны жидкости, из уравнений гидродинамики и использовалась оценка, полученная полуэмпирическим путем. Полученные оценки для силы [1], действующей на цилиндр со стороны вязкой жидкости, используются также в более современных работах [2] для анализа способов повышения устойчивости таких систем. Имеется ряд зарубежных публикаций, посвященных влиянию потока жидкости на устойчивость быстро вращающихся роторов, в которых используются введенные несколько иные полуэмпирические оценки для сил [3], действующих на ротор.

Анализ устойчивости может быть проведен в рамках модели идеальной несжимаемой жидкости. Впервые такое исследование было выполнено для течения произвольной завихренностью [4]. Аналитически найдена сила, действующая на внутренний цилиндр, при малом отклонении осей цилиндров. С учетом выражения для силы определяются условия устойчивости в линейном приближении. Выделено несколько типов неустойчивости в зависимости от завихренности течения. Сила, действующая на внутренний цилиндр, найдена [5] для течения идеальной жидкости с постоянной завихренностью в нелинейной постановке.

Ниже устойчивость точной краевой задачи впервые проанализирована в рамках модели вязкой несжимаемой жидкости. Для этого вычисляется сила, действующая со стороны жидкости на цилиндр, найденная в приближении больших чисел Рейнольдса и предположении о ламинарности течения между цилиндрами. Задача устойчивости центральной оси ротора также решена с учетом найденного выражения для силы.

При вращении внутреннего цилиндра с постоянной угловой скоростью $\Omega $ образуется известное течение Куэтта с постоянной завихренностью [6]. Течение Куэтта будет рассматриваться как порождающее течение, которое возмущается при смещении оси внутреннего цилиндра. Решение для возмущенного течения строится в приближении больших чисел Рейнольдса.

В настоящей работе получено выражение для силы, действующей на цилиндр со стороны вязкой жидкости, и проанализировано влияние этой силы на устойчивость положения цилиндра.

1. Основные уравнения. В работе П.Л. Капицы [1] рассматривается следующая система уравнений

где $M$ – масса внутреннего цилиндра, $H > 0$ – демпфирующий фактор, $K > 0$ – коэффициент упругости, ${{F}_{x}}$ и ${{F}_{y}}$ – проекции на оси Ox и Oy силы, действующей на цилиндр со стороны жидкости, $\left( {x,y} \right)$ – координаты центра внутреннего цилиндра. Введем обозначения ${{h}_{1}} = \frac{H}{M}$, ${{\Omega }_{0}} = \sqrt {\frac{K}{M}} $ – частота собственных колебаний внутреннего цилиндра, ${{z}_{0}} = x + iy$ – комплексная координата, $f = \frac{{{{F}_{x}}}}{M} + i\frac{{{{F}_{y}}}}{M}$ – комплексная сила и перепишем систему (1.1) в комплексном виде

Далее рассматриваются три варианта определения выражения для силы $F$, действующей на цилиндр со стороны жидкости: (I) полуэмпирическая сила [1], (II) сила в приближении невязкой несжимаемой жидкости и (III) сила в приближении вязкой жидкости при больших числах Рейнольдса. Для каждого случая задача устойчивости решается в линейном приближении.

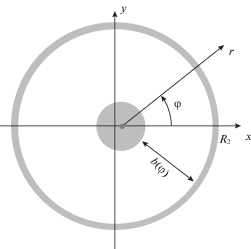
2. Решение П.Л. Капицы. Рассмотрим полученные [1] оценки силы, действующей на смещенный внутренний цилиндр, который вращается с угловой скоростью $\Omega $. Пусть внутренний цилиндр смещен на некоторую величину ${{x}_{0}}$ вдоль оси $Ox$ (рис. 2). Тогда зазор между двумя цилиндрами можно записать как

где ${{R}_{2}}$ и ${{R}_{1}}$ – радиусы внешнего и внутреннего цилиндра, соответственно.

Средняя скорость газа между цилиндрами в положении равновесия предполагается равной половине периферической скорости внутреннего цилиндра ${{\Omega {{R}_{1}}} \mathord{\left/ {\vphantom {{\Omega {{R}_{1}}} 2}} \right. \kern-0em} 2}$. При смещении внутреннего цилиндра расход считается неизменным. Откуда найдена средняя скорость в зависимости от угла $\varphi $ [1]

Сила трения, действующая на цилиндр, считается пропорциональной квадрату относительной скорости, плотности окружающей среды $\rho $ и постоянной трения $\kappa $. Тогда в проекции на ось Oy получим

Вводя обозначение $n = \frac{N}{M}$ и переходя к комплексным переменным, получим уравнение

Как видно из проведенных рассуждений, сила связана исключительно с трением среды о цилиндр. При этом составляющая силы, связанная с неравномерным распределением давления на цилиндре, считается в данных оценках пренебрежимо малой.

Перепишем полученное условие [1] устойчивости для уравнения (2.1) ${{h}_{1}} \geqslant \frac{n}{{{{p}_{1}}}}$ в размерных величинах

Найденные полуэмпирические оценки для силы [1], действующей на цилиндр со стороны вязкой жидкости, используются в более современных работах [2] для анализа способов повышения устойчивости таких систем. В настоящей работе сила получена из решения уравнений для вязкого ламинарного потока жидкости в приближении больших чисел Рейнольдса.

3. Решение в невязкой жидкости. Рассмотрим сначала невязкое течение несжимаемой жидкости между двумя цилиндрами. Возмущение поля скорости будем искать в виде разложения по малому смещению центра внутреннего цилиндра. В качестве среднего течения используем известное течение Куэтта с функцией тока ${{\Psi }_{0}}(r)$ = = $\Omega \frac{{{{R}_{1}}^{2}{{R}_{2}}^{2}}}{{{{R}_{2}}^{2} - {{R}_{1}}^{2}}}\left( { - \ln \frac{r}{{{{R}_{2}}}} + \frac{{{{r}^{2}}}}{{2{{R}_{2}}^{2}}}} \right)$, которое точно удовлетворяет как уравнениям Эйлера идеальной жидкости, так и уравнениям Навье–Стокса вязкой жидкости. В полярной системе координат $r,\varphi $ (рис. 1) радиальная ${{v}_{{0r}}}$ и трансверсальная ${{v}_{{0\varphi }}}$ компоненты скорости выражаются через функцию тока ${{\Psi }_{0}}$:

Это течение складывается из потенциального течения точечного вихря с угловой компонентой скорости

и течения с постоянным вихрем

Пусть внутренний цилиндр сдвинут вдоль оси Ox на величину ${{x}_{0}}$, и имеет вектор скорости $\left( {{{{\dot {x}}}_{0}},{{{\dot {y}}}_{0}}} \right)$ (см. рис. 2). Покажем, что функция тока

определяет поле скорости возмущенного течения ${\mathbf{v}} = {{{\mathbf{v}}}_{0}} + {{{\mathbf{v}}}_{1}}$. Здесь $r,\varphi $ сдвинутые полярные координаты, изображенные на рис. 2.

Действительно, поле возмущения скорости течения с функцией тока ${{\Psi }_{1}}\left( {r,\varphi } \right)$ потенциально и в согласии с теоремами о сохранении циркуляции и вихря [6] не изменяет циркуляцию $\Gamma $ и вихрь ${{\omega }_{0}}$.

Нормальная скорость на границе внутреннего смещенного цилиндра $r = {{R}_{1}}$ и внешнего цилиндра $r = {{R}_{2}} - {{x}_{0}}\cos \varphi $ + $O(x_{0}^{2})$ в линейном по ${{x}_{0}}$ приближении имеют вид

Таким образом, в линейном по величинам ${{x}_{0}},{{\dot {x}}_{0}},{{\dot {y}}_{0}}$ приближении поле скорости удовлетворяет условиям непротекания на границах цилиндров, что и требовалось показать.

При этом возмущение касательной скорости на границе внутреннего цилиндра равно

и условию прилипания не удовлетворяет (что не противоречит модели идеальной жидкости).

Сила, действующая на смещенный цилиндр, определяется [5] из уравнений Лагранжа всей системы

где $\Lambda $ – функция Лагранжа жидкости в слое между цилиндрами, которая может быть выражена через поле скоростей [7]. Уравнения Лагранжа можно записать в виде где компоненты силы выражаются через функцию Лагранжа жидкости $\Lambda $:

Функция $\Lambda $ была найдена в нелинейном приближении для произвольного течения Куэтта [5]. В линейном приближении она имеет вид

Подставляя выражения (3.2) и (3.3) в функцию Лагранжа течения, получим

Из уравнений (3.6) находим силу, выражение для которой в комплексной форме имеет вид:

Подставляя выражение для силы (3.7) в уравнение (1.2), получим

где параметр $\gamma = \frac{{\rho \pi R_{1}^{2}}}{M}$ – отношение плотности жидкости к плотности цилиндра. Получим уравнение для нахождения собственных частот колебаний, подставляя решение ${{z}_{0}}\left( t \right)\sim \exp \left( {\lambda t} \right)$ в уравнение (3.8)

Даже в отсутствии демпфирования (${{h}_{1}} = 0$) характеристическое уравнение имеет чисто мнимые корни, и собственные колебания оказываются нейтрально устойчивыми. Таким образом, движение вращающегося кругового цилиндра в кольцевом потоке идеальной жидкости с постоянной завихренностью устойчиво при ${{h}_{1}} \geqslant 0$. Это условие согласуется с результатами [4, 5]. Перейдем к исследованию задачи устойчивости в вязкой жидкости.

4. Уравнения движения вязкой жидкости. В вязкой жидкости функцию тока ищем в виде $\Psi = {{\Psi }_{{\operatorname{id} }}} + \Psi {\kern 1pt} '$, где ${{\Psi }_{{\operatorname{id} }}}$ определена выражениями (3.4). Вихрь течения вязкой жидкости ${{\omega }_{{\operatorname{ful} }}} = {{\omega }_{0}} + \omega {\kern 1pt} '$ складывается из вихрей ${{\omega }_{0}}$ и $\omega {\kern 1pt} '$ течений с функциями тока ${{\Psi }_{{\operatorname{id} }}}$ и $\Psi {\kern 1pt} '$. Постоянный вихрь ${{\omega }_{0}}$ определен выражением (3.3), а вязкое возмущение $\omega {\kern 1pt} '$ выражается через возмущение функции тока

и удовлетворяет уравнению переноса вихря

На границах цилиндров компоненты скорости должны удовлетворять условиям прилипания.

5. Приближение пограничного слоя. При малых смещениях цилиндра в приближении больших чисел Рейнольдса $\operatorname{Re} = \frac{{R_{1}^{2}\Omega }}{\nu } \gg 1$ течение разбивается на три области: область пограничного слоя около внутреннего цилиндра, область пограничного слоя около внешнего цилиндра и область между ними. Во внутренней области вязкими эффектами можно пренебречь, поле скоростей близко к течению в идеальной жидкости, изученному ранее [4, 5]. Вязкость следует учитывать только в пограничном слое внутреннего цилиндра.

В рассматриваемом приближении больших чисел Рейнольдса на границе внутреннего цилиндра образуется пограничный слой толщины порядка $\delta = \frac{{{{R}_{1}}}}{{\sqrt {\operatorname{Re} } }}$ = $\sqrt {\frac{\nu }{\Omega }} $. Проведем оценки величин и производных входящих в уравнения (4.1), (4.2): $\frac{\partial }{{\partial r}}\sim \frac{1}{\delta }$, $\frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}}\sim \frac{1}{{{{\delta }^{2}}}}$, $\Delta \sim \frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}}$, ${{v}_{r}}\frac{{\partial \omega {\kern 1pt} '}}{{\partial r}}$ ~ $\sqrt {\dot {x}_{0}^{2} + \dot {y}_{0}^{2}} \frac{{\omega {\kern 1pt} '}}{\delta }$, $\frac{{{{v}_{\varphi }}}}{r}\frac{{\partial \omega {\kern 1pt} '}}{{\partial \varphi }}$ ~ $\Omega \omega {\kern 1pt} '$. Вторым слагаемым в уравнении (4.2) можно пренебречь при условии $\frac{{\sqrt {\dot {x}_{0}^{2} + \dot {y}_{0}^{2}} }}{\delta } \ll \Omega $. Это условие дает следующее ограничение на скорость оси внутреннего цилиндра

В пограничном слое около внутреннего цилиндра возникает дополнительное вязкое течение с компонентами скорости $v_{\varphi }^{'}$, $v_{r}^{'}$. Компонента скорости $v_{\varphi }^{'}$ на границе внутреннего цилиндра удовлетворяет условию прилипания, которое в соответствии с (3.5) имеет вид

а вне пограничного слоя равна нулю. C учетом граничных условий (5.2) имеем оценку $\omega {\kern 1pt} '\sim \frac{{{{{\left. {{{{v}}_{{1\varphi }}}} \right|}}_{{r' = 0}}}}}{\delta }$ = $\frac{{\sqrt {\dot {x}_{0}^{2} + \dot {y}_{0}^{2}} }}{\delta }$, а ограничение (5.1) приводит к условию $\omega ' \ll \sqrt {\nu \Omega } {\text{/}}\delta $ = = $\sqrt {\nu \Omega } {\text{/}}\sqrt {\nu {\text{/}}\Omega } = \Omega $. Из проведенных оценок следует, что вязкость создает вихрь существенно меньший по сравнению с вихрем в течении Куэтта. Таким образом, при условии (5.1) уравнения пограничного слоя (4.1), (4.2) примут вид [9] где введена внутренняя переменная $r{\kern 1pt} ' = r - {{R}_{1}}$.

В отличие от традиционного уравнения Прандтля уравнение линейное.

В начальный момент возмущение завихренности положим равным нулю

Возмущения вне пограничного слоя так же отсутствуют

Запишем граничные условия прилипания на внутреннем цилиндре

где ${{\left. {{{{v}}_{{1\varphi }}}} \right|}_{{r' = 0}}}$ – тангенциальная компонента скорости на границе цилиндра в невязком приближении (3.5). Условие непротекания удовлетворяется невязким приближением.

Интегрируя второе уравнение в (5.3), получим $\frac{{\partial \Psi {\kern 1pt} '}}{{\partial r{\kern 1pt} '}} = \int_{r'}^\infty {\omega {\kern 1pt} 'dr{\kern 1pt} '} $. Подставляя полученное выражение в граничные условия (5.6), найдем, что

Уравнение (5.3), дополненное начальным условием (5.4) и граничными условиями (5.5) и (5.7), образует краевую задачу, решение которой будем искать в виде $\omega {\kern 1pt} ' = \operatorname{Re} [{{e}^{{ - i\left( {\varphi + \Omega t} \right)}}}W(t,r{\kern 1pt} ')]$. Тогда для функции $W\left( {t,r{\kern 1pt} '} \right)$ краевая задача перепишется в виде

где функция ${{W}_{0}}\left( t \right)$ может быть найдена из граничного условия (5.7). Решение задачи (5.8) можно выписать в виде

Преобразуем интеграл

Подставляя полученное выражение в граничное условие (5.7), получим для функции ${{W}_{0}}(t)$ интегральное уравнение Абеля

где ${{\dot {z}}_{0}} = {{\dot {x}}_{0}} + i{{\dot {y}}_{0}}$.

Решение интегрального уравнения (5.9) имеет вид [9]

6. Сила, действующая на внутренний цилиндр. Для того, чтобы проанализировать устойчивость положения цилиндра в циркуляционном потоке вязкой жидкости необходимо вычислить силу, действующую на него. Как известно [8], давление сохраняется в пограничном слое. Силу, действующую на цилиндр, разделим на две составляющие. Первая компонента, невязкая, связанная с интегралом давления по поверхности смещенного цилиндра, была рассмотрена ранее [4, 5]. Второй член, вязкий, связан с трением цилиндра об окружающую среду и может быть найден из решения (5.10).

Касательное напряжение на границе внутреннего цилиндра может быть записано как

Интегрируя касательное напряжение по поверхности внутреннего цилиндра, получим силу [9], действующую со стороны вязкой жидкости

Заметим, что в [9] знак “–” опущен.

Вязкая сила (6.1) является аналогом наследственной силы Бассе, действующей на сферу радиуса ${{R}_{1}}$ при ее неравномерном движении. Сила Бассе находится из приближения Стокса при малых числах Рейнольдса, тогда как сила (6.1) найдена в приближении большого числа Рейнольдса.

7. Решение задачи устойчивости в вязкой жидкости. Как было сказано ранее, для решения задачи устойчивости в вязкой жидкости необходимо в уравнениях динамики (1.1) поставить в правую часть сумму вязкой (6.1) и невязкой (3.7) сил.

На внутренний цилиндр действует суммарная сила F_id + F_ν, где ${{F}_{{\operatorname{id} }}}$ определена формулой (3.7), а ${{F}_{\nu }}$ – формулой (6.1).

Запишем уравнение движения цилиндра (1.1) в виде

где $h = \frac{H}{M}{{\left( {1 + \gamma \frac{{R_{1}^{2} + R_{2}^{2}}}{{R_{2}^{2} - R_{1}^{2}}}} \right)}^{{ - 1}}}$, ${{p}^{2}} = \frac{K}{M}{{\left( {1 + \gamma \frac{{R_{1}^{2} + R_{2}^{2}}}{{R_{2}^{2} - R_{1}^{2}}}} \right)}^{{ - 1}}}$, $a = \frac{1}{{\sqrt \pi }}\frac{{2\gamma {{{\left( \Omega \right)}}^{{1/2}}}\left( {R_{2}^{2} + R_{1}^{2}} \right)}}{{\left( {R_{2}^{2} - R_{1}^{2}} \right) + \gamma \left( {R_{2}^{2} + R_{1}^{2}} \right)}}$, $b = \frac{{\gamma \,\Omega R_{2}^{2}}}{{\left( {R_{2}^{2} - R_{1}^{2}} \right) + \gamma \left( {R_{2}^{2} + R_{1}^{2}} \right)}}$, $\gamma = \frac{{\rho \pi R_{1}^{2}}}{M}$ и $\varepsilon = {{\operatorname{Re} }^{{ - 1/2}}} \ll 1$.

Уравнение (7.1) может быть решено аналитически с помощью преобразования Лапласа. Интеграл в правой части имеет вид свертки, и в образах Лапласа интегро-дифференциальное уравнение (7.1) становится алгебраическим. Использование аналитических методов позволяет явно выделить область устойчивости системы и провести сравнение с имеющимися результатами для невязкого течения [4, 5] и результатами, полученными П.Л. Капицей [1].

Примем обозначение $Z\left( s \right) = L\left[ {z\left( t \right)} \right]$ = $\int_0^\infty {Z\left( t \right)\exp \left( { - st} \right)dt} $, тогда уравнение (7.1) в образах Лапласа примет вид

а его решение запишется как

Для анализа устойчивости необходимо найти обратное преобразование Лапласа $z\left( t \right) = \frac{1}{{2\pi i}}\int_{{{\sigma }_{1}} - i\infty }^{{{\sigma }_{1}} + i\infty } {Z\left( s \right){{e}^{{st}}}ds} $, где ${{\sigma }_{1}}$ выбрана таким образом, что все особенности (7.2) лежат левее контура интегрирования. Вывод об устойчивости или неустойчивости системы можно сделать, рассмотрев асимптотику решения на больших временах.

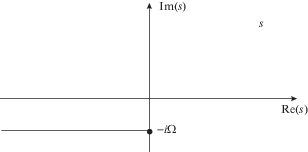
Решение в пространстве Лапласа (7.2) является многозначной функцией с точкой ветвления $s = - i\Omega $. Проведем разрез параллельно действительной оси (рис. 3) и выберем ветвь функции $\sqrt {s + i\Omega } $ так, что $\sqrt {s + i\Omega } > 0$ при действительном и положительном значении подкоренного выражения.

Теперь определим полюса решения (7.2) в приближении малых демпфирующих сил $h = \varepsilon \tilde {h}$

Будем искать решение уравнения (7.3) в виде разложения в ряд $s = {{s}_{0}} + \varepsilon {{s}_{1}} + ...$. В нулевом приближении оба полюса являются чисто мнимыми ${{s}_{0}} = ib \pm i\sqrt {{{b}^{2}} + {{p}^{2}}} $, и устойчивость решения определяется следующим приближением. В первом приближении (7.3) получим

Устойчивость системы будет определяться знаком действительной части выражений (7.4) и (7.5). Условия устойчивости запишутся так

Из них следуют два неравенства

Без ограничения общности будем считать, $\Omega > 0$. Тогда из двух неравенств следует оставить второе.

Таким образом, условие устойчивости всей системы можно записать в виде

В случае, если условие (7.6) не выполняется система неустойчива.

В уравнении (7.6) можно перейти к физически значимым переменным. Учитывая, что для газа параметр $\gamma $, определяющему отношение плотности жидкости к плотности цилиндра, очень мал, то можно учесть главный член разложения по этому параметру. Тогда условие примет вид

8. Сравнение условий устойчивости. Представляет интерес сравнение условия устойчивости П.Л. Капицы (2.2), условия устойчивости (7.7), полученного в настоящей работе и условия устойчивости в невязкой жидкости. Сравнение необходимого для устойчивости системы коэффициента демпфирования $H$ будет происходить с учетом оценок $\gamma \ll 1$.

Условие устойчивости можно записать в виде $H > H{\text{*}}$, где $H{\text{*}}$ – некоторое критическое значение, величина которого зависит от выбора модели течения

$H_{{\operatorname{id} }}^{*} = 0$ – идеальная жидкость;

$H_{K}^{*} = \frac{\kappa }{2}\pi \rho R_{1}^{2}\frac{{{{R}_{1}}}}{{{{R}_{2}} - {{R}_{1}}}}\frac{{{{\Omega }^{2}}}}{{{{\Omega }_{0}}}}$ – полуэмпирическое выражение [1];

$H_{\nu }^{*} = - \sqrt {2\pi \nu } \frac{{R_{1}^{2} + R_{2}^{2}}}{{R_{2}^{2} - R_{1}^{2}}}\rho {{R}_{1}}\sqrt {\left| {\Omega - {{\Omega }_{0}}} \right|} $ – вязкая жидкость (выражение (7.7) где $\kappa $ – эмпирический безразмерный коэффициент, ${{\Omega }_{0}} = \sqrt {\frac{K}{M}} $ – собственная частота колебаний ротора.

В невязкой жидкости система нейтрально устойчива ($H_{{\operatorname{id} }}^{*} = 0$). Исходя из оценок [1], вязкость приводит к появлению неустойчивости в системе ($H_{K}^{*} > 0$). В настоящей работе показано, что учет вязкости в выбранном приближении приводит к затуханию колебаний системы ($H_{\nu }^{*} < 0$). Такое расхождение может быть объяснено как разными моделями трения, так и разницей исходных предположений: [1] – сильно турбулентный поток, настоящая работа ламинарное среднее течение между цилиндрами при $\operatorname{Re} \gg 1$.

Работа выполнена по теме государственного задания (№ госрегистрации АААА-А20-120011690138-6).