Прикладная математика и механика, 2020, T. 84, № 5, стр. 554-569

Введение. При описании плоских потенциальных течений идеальной несжимаемой жидкости удобно пользоваться методом граничных элементов. Одним из преимуществ этого метода является уменьшение размерности задачи за счет сведения расчетов к (одномерной) границе области течения жидкости. Данная работа посвящена численному моделированию движения свободной границы в трех типах задач: деформации цилиндрических полостей в неограниченном объеме жидкости, деформации свободной границы цилиндров жидкости под действием заданного поля скоростей и обрушения капиллярно-гравитационных периодических волн. При определенных начальных условиях в каждой из этих задач на свободной поверхности жидкости могут образовываться тонкие кумулятивные струи. Сложность проведения таких расчетов обычно связана с потерей устойчивости численной схемы и стремительным ростом кривизны кумулятивной струи, требующей большого измельчения сетки в ее окрестности. Использование аппроксимаций специального вида, разработанных одним из авторов [1], позволяет преодолеть указанные трудности. Для обоснования достоверности расчетов по предложенной численной схеме авторами было сделано следующее:

• Проведены расчеты для задачи восстановления кривой по заданному распределению нормальной скорости и сравнение расчета с точным решением

• Приведены четыре закона сохранения, по которым ведется контроль точности расчетов

• Проведено сравнение численных расчетов с известными полуаналитическими решениями

• Проведен анализ уменьшения погрешности при удвоении элементов сетки.

1. Математическая постановка задачи. Конечной целью предлагаемого численного алгоритма будет являться нахождение формы движущейся свободной границы, которая может быть определена кинематически по значениям нормальной компоненты скорости жидкости $V$ на границе. Для определения $V$ достаточно знать значение функции тока $\Psi $ на границе, поскольку $V = \partial \Psi {\text{/}}\partial s$. Покажем, что для отыскания значений $\Psi $ и описания ее движения в задачах деформации цилиндрических полостей, движения цилиндров жидкости, а также движения периодических волн могут использоваться интегро-дифференциальные уравнения одного и того же типа.

Начнем с задачи деформации цилиндрической полости в неограниченном объеме идеальной несжимаемой жидкости, движение которой плоскопараллельно и потенциально. Пусть ось цилиндра направлена перпендикулярно плоскости течения. Будем рассматривать задачу в плоскости, параллельной течению. На этой плоскости внутренности полости соответствует некоторая ограниченная область $S$ с замкнутой гладкой свободной границей $\partial S$. Областью течения жидкости является внешность полости ${{\mathbb{R}}^{2}}{\backslash }S$, и в ней функция тока $\Psi $ удовлетворяет уравнению Лапласа. При условии, что жидкость покоится на бесконечности, из него можно вывести интегральное уравнение, связывающее значения $\Psi $ на границе $\partial S$ с вещественной функцией потенциала $\Phi $. Для этого введем два интегральных оператора $A$ и $B$. Пусть $F$ – произвольная гладкая функция, заданная на $\partial S$. Действие $A$ и $B$ на $F$ в точке $M \in \partial S$ определим по следующим формулам:

где $G(M,M{\kern 1pt} ')$ обозначает функцию Грина и для пары точек $M(x,y)$ и $M{\kern 1pt} '(x{\kern 1pt} ',y{\kern 1pt} ')$ вычисляется по формуле

При этом направление нормали на свободной границе выбрано внешним по отношению к полости $S$. Для $\Psi $ справедливо следующее уравнение:

которое и будет использоваться для построения численного алгоритма.

Постановка задачи о движении цилиндра жидкости со свободной границей может быть получена из постановки задачи о деформации цилиндрической полости. Для этого достаточно поменять местами полость $S$ и область течения жидкости ${{\mathbb{R}}^{2}}{\backslash }S$. Интегральное уравнение для $\Psi $ в этом случае также определено на $\partial S$, использует те же интегральные операторы $A$ и $B$, и ту же самую функцию Грина (1.3) и имеет следующий вид:

т.е. отличается от (1.4) лишь левой частью уравнения.

Для задания уравнения, определяющего значения $\Psi $ в задаче о движении периодической волны в жидкости постоянной глубины, требуется внести в (1.4) более существенные изменения. Сформулируем постановку задачи. Введем декартову систему координат $Oxy$, где ось $y$ направлена вертикально вверх. Пусть уровень дна задается уравнением $y = - h$, где $h > 0$ обозначает глубину жидкости. Для простоты будем считать, что длина волны $\lambda = 2\pi $. Область жидкости, заключенную между двумя вертикальными прямыми $x = 0$ и $x = 2\pi $ обозначим через ${{S}_{w}}$. Граница области ${{S}_{w}}$ является кусочно-гладкой и состоит из четырех частей: отрезка дна, пары вертикальных отрезков и криволинейного участка свободной границы, который мы обозначим через $L$.

При движении периодических волн в дополнение к уравнению Лапласа $\Psi $ удовлетворяет также условию периодичности

На дне задается условие непротекания. В этом случае прямая $y = - h$ (дно) совпадает с линией тока жидкости:

Без ограничения общности можно считать, что ${{\Psi }_{h}} = 0$. Следствием этих условий является интегральное уравнение

Здесь интегральные операторы $\tilde {A}$, $\tilde {B}$ определяются аналогично операторам $A$, $B$ из (1.1), (1.2), но вместо $\partial S$ интегрирование ведется по (незамкнутому) участку свободной границы $L$, а в качестве функции Грина используется

где $E = {{e}^{{ - 2h - y - y'}}}$. Направление нормали внешнее по отношению к области ${{S}_{w}}$. Вывод всех этих интегральных уравнений представлен в [2].

Таким образом, уравнения (1.4), (1.5) и (1.8) позволяют по известным значениям $\Phi $ на свободной границе определять значения $\Psi $ и $V = \partial \Psi {\text{/}}\partial s$ во всех трех типах задач. Касательная скорость точек границы $U$ на геометрическую форму не влияет, но от ее выбора существенно зависит устойчивость численной схемы. Ниже будет описан способ вычисления $U$, повышающий устойчивость численного алгоритма.

Наконец, чтобы получить полную систему уравнений, достаточную для построения численного алгоритма, необходимо указать способ вычисления потенциала $\Phi $. Будем использовать для этого интеграл Коши–Лагранжа. Дополнительно потребуем, чтобы давление $p$ на свободной поверхности во всех трех случаях равнялось нулю. Интеграл может быть записан в следующем виде:

где плотность жидкости $\rho $ полагается равной единице, $g$ характеризует силу тяжести, $\sigma $ – коэффициент поверхностного натяжения, $k$ – кривизна, а $F(t)$ – некоторая функция времени. Так как потенциал определен с точностью до произвольной функции времени, можно положить $F(t) = 0$. В зависимости от рассматриваемой задачи $g$ и $\sigma $ могут также оказаться равными нулю. Отметим, что для использования интеграла (1.10) на подвижной свободной границе необходимо отказаться от эйлеровых координат и выразить соответствующие слагаемые через координаты на границе.

2. Численный алгоритм. Предлагаемый численный алгоритм является обобщением алгоритма [3], предложенного для решения задачи деформации цилиндрических полостей. Численные эксперименты показали, что предложенный алгоритм [3] сохраняет устойчивость при расчете тонких кумулятивных струй жидкости, возникающих при деформации полостей. Поскольку кумулятивные струи могут возникать в каждом из трех рассматриваемых случаев, это служит мотивацией для выбора метода решения.

Рассмотрим более подробно аппроксимацию интегральных уравнений (1.4), (1.5) и (1.8). При этом достаточно рассмотреть аппроксимацию только операторов $A$ и $B$, поскольку аппроксимации $\tilde {A}$ и $\tilde {B}$ могут быть получены аналогичным образом: необходимо лишь учесть изменение вида функции Грина, а также незамкнутость $L$.

Заменим интегралы в $A$ и $B$ квадратурными формулами, порядок аппроксимации которых неограниченно возрастает с ростом количества точек сетки. Для этого введем гладкую параметризацию свободной границы $\partial S$ при помощи вспомогательного параметра $\zeta \in [0,1]$ (критерии выбора параметризации будут сформулированы ниже), зададим равномерную сетку ${{\zeta }_{i}} = i{\text{/}}N$, где $i = 1,2,...,N$, и применим квадратурные формулы [1]. Получим следующую аппроксимацию оператора $A$:

где

Для функции Грина (1.3) имеем

Соответствующие коэффициенты для функции Грина (1.9) имеют вид

Аппроксимация оператора $B$ приобретает вид

где

Формулы (2.1) и (2.2) оперируют значениями $\partial x{\text{/}}\partial \zeta $, $\partial y{\text{/}}\partial \zeta $ и $\partial \Phi {\text{/}}\partial \zeta $ в точках сетки. Для их вычисления можно, например, использовать аппроксимацию в виде кубического сплайна или аппроксимацию производной по 4 точкам. Пусть $F(\zeta )$ обозначает произвольную гладкую периодическую функцию, заданную на отрезке $\zeta \in [0,1]$. Продолжим функцию по периоду за пределы отрезка. Аппроксимация ее производной по 4 точкам имеет следующий вид:

Таким образом, уравнения (1.4), (1.5) и (1.8) сводятся к системе линейных уравнений относительно значений ${{\Psi }_{i}}$ в точках сетки. Они, в свою очередь, определяют ${{V}_{i}} = (\partial \Psi {\text{/}}\partial \zeta {{)}_{i}}$.

Определение касательных скоростей точек сетки ${{U}_{i}}(t): = U({{\zeta }_{i}},t)$ тесно связано со способом ее параметризации. Зададим параметризацию $\partial S$ (и аналогично $L$) при помощи вспомогательной положительной функции $f(\zeta )$ по формуле

где $l(t)$ – длина $\partial S$ (или одного периода волны $L$) в момент времени $t$. Функция $f(\zeta )$ здесь является известной заданной положительной функцией и позволяет управлять распределением точек на границе. Принципиальным является то, что $f$ не зависит от $t$, т.е. заданное в начальный момент распределение точек обязано сохраняться с течением времени. Такой подход позволяет за счет выбора $f(\zeta )$ вручную задать высокую плотность точек сетки на тех участках, где из-за высокой кривизны требуется более высокая точность, а также предотвратить возможность разрежения в процессе вычислений там, где точки сетки изначально были размещены близко друг к другу.

Сформулированное требование определяет значения ${{U}_{i}}$. Численно оно выражается в виде системы уравнений:

где $\Delta {{\tilde {s}}_{i}}$ – расстояние между точками сетки с индексами $i$ и $i - 1$ в момент $t + \Delta t$. Для получения системы уравнений относительно ${{U}_{i}}$ достаточно выразить $\Delta {{\tilde {s}}_{i}}$ через значения координат ${{x}_{i}}$, ${{y}_{i}}$ и скоростей ${{U}_{i}}$, ${{V}_{i}}$ на текущем шаге по времени $t$. Для решения (2.4) используется итерационный процесс по параметру $l(t + \Delta t)$.

3. Тестирование алгоритма вычисления касательной скорости. Для тестирования алгоритма вычисления ${{U}_{i}}$ рассмотрим численное решение задачи о восстановлении эволюции контура, изменяющего свою форму, по заданному распределению нормальной скорости на границе.

Сформулируем математическую постановку задачи. Пусть на отрезке $x \in [ - \pi ,\pi ]$ задан контур, эволюция которого с течением времени известна и определяется по следующему закону:

Уравнение кривой (3.1) имеет особенность в точке $(t,x) = (1,0)$, в которой координата $y$ обращается в $ + \infty $. При меньших значениях $t$ контур имитирует растяжение вдоль вертикали с неограниченным ростом кривизны в точке $x = 0$. Будем считать, что скорости точек, из которых состоит контур, в каждый момент времени направлены по нормали к контуру, т.е. $U = 0$. Необходимо численно восстановить форму профиля во все моменты времени по его начальной форме и известной (нормальной) компоненте скорости.

Вычислим нормальную компоненту вектора скорости. Пусть направление обхода контура задано от точки $x = \pi $ к точке $x = - \pi $, а вектор нормали получается из касательного вектора поворотом на угол $\pi {\text{/}}2$ по часовой стрелке (т.е. нормаль направлена “вверх”). Вектор нормали в осях $x,y$ имеет компоненты $(\partial y{\text{/}}\partial s, - \partial x{\text{/}}\partial s)$. Нормальная компонента скорости точек профиля точно определяется как

В начальный момент $t = 0$ контур имеет форму отрезка прямой. Будем использовать для его аппроксимации $N$ точек, распределенных равномерно в начальный момент времени. Приращения пространственных координат этих точек ${{x}_{i}}$ и ${{y}_{i}}$ будем определять на основе метода Эйлера при помощи нормальной скорости (3.2) и касательной скорости ${{U}_{i}}$, которую определим одним из двух способов:

• ${{U}_{i}} = 0$;

• Значения ${{U}_{i}}$ вычисляются из условия сохранения пропорций расстояний между узлами сетки.

В численном эксперименте будем использовать $N = 32$ точек сетки и постоянный шаг по времени $\Delta t{{ = 10}^{{ - 4}}}$. В первом случае результаты удается получить лишь для $t \leqslant 0.72$. Возникающее к этому моменту разрежение точек сетки в окрестности $x = 0$ вызывает дестабилизацию алгоритма, не позволяя продолжить вычисления из-за быстро растущей погрешности аппроксимации. Значение кривизны в точке $x = 0$ в последний момент составляет примерно $k \approx 9.18$. Во втором случае расчет удается продлить вплоть до момента времени ${{t}_{e}} = 0.92$, после чего погрешность от использования метода Эйлера уже становится слишком большой, чтобы можно было считать численное решение близким к аналитическому. Тем не менее значение кривизны в точке $x = 0$ в последний момент времени достигает величины $k \approx 143.75$, что наглядно демонстрирует влияние способа задания ${{U}_{i}}$ на устойчивость расчетов.

4. Законы сохранения. Одним из способов контроля точности в численном алгоритме могут служить законы сохранения. Например, для движения цилиндра жидкости со свободной границей при отсутствии массовых сил выполнены следующие законы сохранения импульса $({{I}_{x}},{{I}_{y}})$, энергии $E$ и момента количества движения $M$:

Ранее [4] на примере $({{I}_{x}},{{I}_{y}})$ было доказано, что указанные интегралы (4.1) сохраняются в том числе и при деформации полостей под действием течений с ненулевой циркуляцией $\Gamma $, хотя и не являются при этом импульсом, энергией и моментом количества движения, т.к. прямое вычисление их невозможно из-за расходимости соответствующих интегралов.

В дополнение к законам сохранения (4.1) в задаче о деформации границы цилиндрической полости сохраняется площадь поперечного сечения полости. Для ее вычисления справедлива следующая аналитическая формула:

Ее сеточный аналог имеет вид

где при помощи верхнего индекса $j$ обозначены значения соответствующих величин на $j$-м шаге по времени. Стоит отметить, что формула (5.3) учитывает гладкость подынтегральных функций. Если $x$ и $y$ являются бесконечно гладкими, то порядок аппроксимации величины (5.2) формулой (5.3) неограниченно возрастает вместе с увеличением количества точек сетки.

Уменьшение погрешности в (4.3) имеет важное значение для устойчивости численного алгоритма. Покажем, что величину погрешности можно оценить аналитически. Для простоты положим, что шаг алгоритма по времени $\Delta t$ фиксирован, аппроксимация координат ${{x}_{i}}$, ${{y}_{i}}$ при помощи ${{V}_{i}}$ и ${{U}_{i}}$ на каждом следующем шаге по времени выполняется по методу Эйлера первого порядка точности, а для аппроксимации производных используется формула (3.3).

Оценим величину приращения при переходе от ${{M}^{j}}$ к ${{M}^{{j + 1}}}$. При использовании метода Эйлера в численном алгоритме справедливы следующие формулы для вычисления приращений пространственных координат:

Аппроксимации (2.3) обладают свойством линейности, поэтому

Заметим, что для аппроксимаций (2.3) выполнен сеточный аналог формулы интегрирования по частям:

где ${{f}_{i}}$ и ${{g}_{i}}$ – две произвольные периодические сеточные функции. С учетом соотношений (4.5) формула для приращения приобретает следующий вид:

Поскольку коэффициенты при производных $\Psi $ по построению численного алгоритма в точности являются длинами единичных векторов нормали, полученное выражение удается упростить:

Если отдельно рассмотреть слагаемое при $\Delta t$ и подставить в него аппроксимацию (2.3), то получим

Таким образом, ${{M}^{{j + 1}}}$ и ${{M}^{j}}$ отличаются не более, чем на величину $O(\Delta {{t}^{2}})$ на любом шаге $j$ алгоритма по времени, следовательно, на любом фиксированном временном интервале $[0,T]$ сеточный аналог закона сохранения площади выполнен с точностью до погрешности порядка $O(\Delta t)$, т.е. определяется погрешностью метода Эйлера.

Фактически полученная оценка показывает, что использование в численном алгоритме интегрального уравнения (1.4) для $\Psi $, а также аппроксимации (2.3) позволяет исключить влияние шага сетки по пространственной координате $\zeta $ на погрешность в (4.3). Кроме того, несовпадение касательных скоростей точек сетки ${{U}_{i}}$ с касательными скоростями жидкости ${{(\partial \Phi {\text{/}}\partial s)}_{i}}$ также не влияет (в первом порядке) на погрешность в (4.3).

Еще раз отметим, что для упрощения рассуждений здесь использовался метод Эйлера при интегрировании по времени. В численных экспериментах использовались схемы с более высокими порядками аппроксимации, например, метод Рунге–Кутты четвертого порядка точности.

6. Численные результаты. Различным способам моделирования деформации свободной границы в задачах движения цилиндрических полостей в жидкости, а также жидких цилиндров посвящено много работ. Например, предложено полуаналитическое решение для задачи деформации полости [5], которая до этого решалась (численно) [6]. Рассмотрено [7] применение полуаналитического метода решения к задаче растекания цилиндра жидкости под действием заданного поля скоростей. Эти задачи использовались для тестирования численного алгоритма из настоящей работы. Рассчитанная по представленной схеме деформация формы полости при начальных условиях [6] изображена на рис. 1а, а модификация этой задачи с добавлением циркуляции – на рис. 1б. Добавление циркуляции нарушает симметрию задачи, делая проверку законов сохранения менее тривиальной. Рис. 2 соответствует задаче растекания цилиндра жидкости из [7].

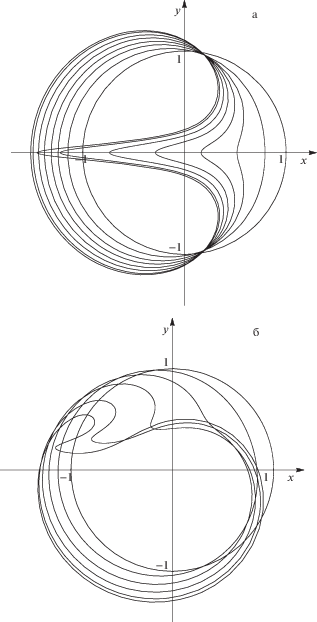
В каждом из случаев свободная граница в начальный момент имела форму единичной окружности с центром в начале координат. В первом случае потенциал течения в начальный момент задавался по формуле

Заметим, что особенность функции соответствует точке внутри полости. Во втором случае к потенциалу добавлялось дополнительное слагаемое, делающее его многозначной функцией:

В третьем случае для дополнительного подтверждения работоспособности алгоритма была рассмотрена задача [7], где решение строилось при помощи полуаналитических методов. Начальное поле скоростей цилиндра в этом случае задавалось по формуле

Силы тяжести и поверхностного натяжения во всех трех задачах отсутствовали. Каждой кривой на рисунках соответствует положение свободной границы в один из моментов времени. В совокупности они демонстрируют возникновение и развитие кумулятивных струй. При этом для получения рис. 1а, б использовалось всего 128 точек сетки, а для рис. 2 – 192 точки. Можно заметить, что точки распределялись на границе неравномерно и были размещены ближе друг к другу там, где возникали струи.

Для проверки точности вычислений использовались законы сохранения (4.1). Ошибка в них не превышала по абсолютной величине $3 \times {{10}^{{ - 4}}}$.

Исследованию процесса обрушения волн также посвящено большое количество работ (см., например, обзор [8]). Для сравнения будем использовать результаты [9], где также был построен численный алгоритм решения задачи.

В качестве начальной формы для численных экспериментов с обрушением использовалась прогрессивная волна для жидкости бесконечной глубины ($h = - \infty $, $\sigma = 0$). Форма прогрессивной волны рассчитывалась по итерационному алгоритму [10]. Суть метода сводилась к поиску экстремума функционала ${{E}_{c}} - {{E}_{g}} - {{E}_{\sigma }}$, где ${{E}_{c}}$, ${{E}_{g}}$ и ${{E}_{\sigma }}$ определялись по формулам

Здесь $c$ обозначает скорость волны, а потенциалом поля скоростей является функция $c\bar {\Phi }$.

Обрушение прогрессивной волны вызывалось внешним давлением, приложенным к свободной поверхности жидкости. Зависимость давления от времени задавалась по формуле вида [9]

Главный недостаток алгоритма [9] – его неустойчивость: свободная поверхность в процессе расчетов приобретает пилообразную форму. Для подавления неустойчивости авторы [9] прибегали к сглаживанию границы по формуле

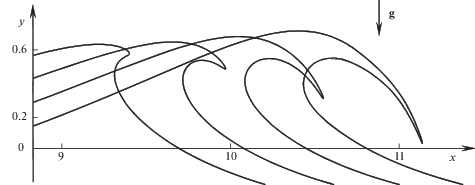
Использование сглаживания позволяло продлить расчет, однако также вносило погрешность в алгоритм. Частое применение формулы (5.1) искусственно понижало кривизну границы, из-за чего [9] удалось рассчитать лишь начальную стадию обрушения до момента времени $t = {\text{4}}.{\text{928}}$ (началом обрушения приблизительно можно считать момент времени $t = {\text{4}}.{\text{6}}$).

Предложенный в данной статье алгоритм также был применен к решению задачи [9]. Рассматривалась прогрессивная волна с амплитудой $a = 0.{\text{4}}0{\text{6}}$, что составляет приблизительно 90% от предельной амплитуды прогрессивной волны, а ${{p}_{0}} = 0.{\text{146}}$. Сравнение с результатами [9] при одинаковом количестве точек сетки показало, что новый алгоритм значительно устойчивее и позволяет продолжить расчет до полного обрушения волны. Радиус кривизны в вершине волны на конечной стадии более чем в 1000 раз меньше длины волны. Преимущества нового алгоритма наглядно демонстрирует рис. 3. Четырем контурам гребня волны соответствуют моменты времени t = 4.8; 5.1; 5.4; 5.7. Для получения первых двух контуров использовалось $N = 60$ точек сетки. Именно такое количество точек использовалось при аппроксимации границы [9]. Точки сгущались в окрестности формирующейся кумулятивной струи, что позволило рассчитать форму свободной границы вплоть до момента $t = {\text{5}}.{\text{1}}$ без потери гладкости. Для дальнейших расчетов 60 точек оказалось недостаточно, поэтому при $t > {\text{5}}.{\text{1}}$ их количество было увеличено до значения $N = 192$. Основные трудности при расчете последней стадии обрушения были связаны с удержанием наибольшей плотности точек сетки в вершине кумулятивной струи при помощи явного задания касательной скорости ${{U}_{0}}$. Для упрощения расчетов форма струи при $t = {\text{5}}.{\text{7}}$ была получена с использованием сглаживания в окрестности вершины по формуле (5.1).

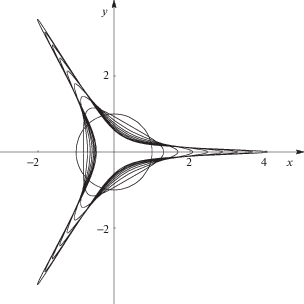
Перейдем к рассмотрению капиллярных волн ($g = 0$). Разработанный численный алгоритм применялся для расчета неустойчивости возмущенной волны Крэппера. Параметрическое уравнение волны Крэппера имеет следующий вид:

где $\lambda $ – длина волны, а $b$ – вещественный параметр, связанный с амплитудой волны $a$ соотношением

Как и в случае прогрессивной волны в тяжелой жидкости, профиль волны Крэппера не изменяется в процессе движения, а безразмерная скорость волны $c$ постоянна. Значение $c$ и скорость распространения волны определяются как

Сохранение формы профиля было экспериментально проверено в численном алгоритме в качестве теста. Рассматривалась волна Крэппера, заданная значением параметра b = 0.3. Ее достаточно сложная форма изображена на первом рис. 4. Для аппроксимации границы использовалось $N = 32$ точек сетки, распределенных равномерно по параметру $\alpha $. Для расчетов использовался фиксированный шаг по времени $\Delta t = 0.0{\text{1}}$. Сравнивались значения пространственных координат с интервалом $T = 100$. Невязка определялась в виде

где ${{x}_{i}}$, ${{y}_{i}}$ обозначают пространственные координаты точек сетки в начальный момент времени, ${{\tilde {x}}_{i}}$, ${{\tilde {y}}_{i}}$ – координаты в конечный момент времени. Было получено, что $r \leqslant 5.2 \times {{10}^{{ - 3}}}$. Эта проверка показывает, что в численном методе отсутствуют схемное поверхностное натяжение и схемная вязкость, которые обычно появляются в разностных схемах.

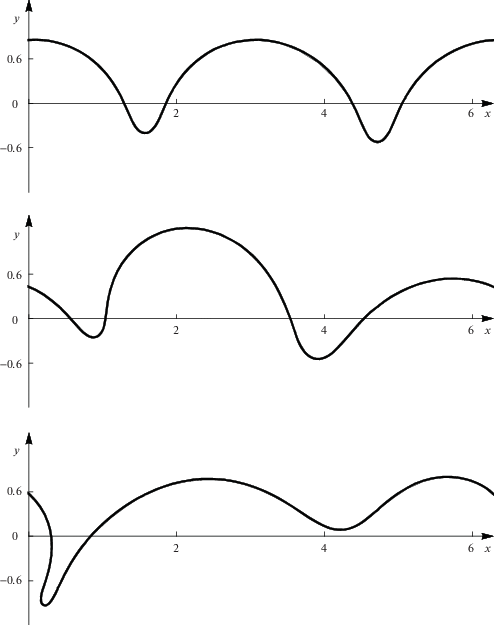
Ранее [11] была доказана устойчивость по Ляпунову точного решения Крэппера относительно возмущений с периодом, равным длине волны. Тем не менее, доказательство не распространяется на возмущения с периодом, превышающим длину волны, – устойчивость в этом случае не обязана сохраняться. В численных экспериментах использовались возмущения вида $\delta y = \varepsilon sinx$ при длине волны Крэппера $\lambda = \pi $. Расчеты показали, что подобные возмущения даже при малых значениях параметра $\varepsilon $ способны вызывать значительные по амплитуде колебания свободной поверхности, а при достаточно больших значениях параметра $b$ – приводить к разрушению волны. На рис. 4 изображена эволюция формы одного периода возмущенной волны при b = 0.3 и ε = 0.03. Для аппроксимации границы использовалось $N = 192$ точек сетки. Как и в предыдущем расчете, сгущение точек сетки проводилось в окрестности участков границы, имеющих наибольшую кривизну. Как видно из рис. 4, таких участков два; они соответствуют локальным минимумам функции $y$.

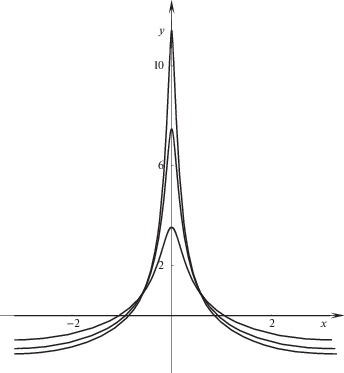
Наконец, перейдем к рассмотрению аналога опыта Покровского как простейшей демонстрации формирования кумулятивной струи на свободной поверхности жидкости. В оригинальном эксперименте, описанном в монографии [12] (с. 253–254), струя образуется при ударе падающей стеклянной пробирки с водой о твердую неподвижную поверхность. Измерения показывают, что при падении с 10 см кумулятивная струя достигает более метра в высоту.

Согласно [12] при ударе свободная поверхность жидкости получает такой импульс, что центральная часть поверхности приобретает конечную скорость, направленную вверх, а ее края вблизи стенок пробирки – скорость, направленную вниз.

При проведении численного эксперимента для простоты предполагалось, что в начальный момент времени жидкость заполняет полуполосу $ - \pi < x < \pi $, $y < 0$; нормальная скорость на границе $y = 0$ задавалась по формуле ${{v}_{y}} = cosx$. Данная скорость соответствует начальному потенциалу скорости жидкости $\Phi = {{e}^{y}}cosx$. Сила тяжести полагалась равной нулю, что позволяло струе неограниченно вытягиваться. Благодаря этому предположению удалось оценить возможности численного алгоритма, так как расчет можно вести до тех пор, пока схема не потеряет устойчивость. Результаты вычислений на сетке из $N = 128$ точек изображены на рис. 5. Приведены формы кумулятивной струи в моменты времени t = 2.05; 4.1 и 6.15. В момент времени 6.15 кривизна в вершине струи достигает значения 1143.5.

Дополнительно для данной задачи был проведен анализ уменьшения погрешности при удвоении элементов (с сохранением прежнего распределения точек на контуре, определяемого функцией $f(\zeta )$). Невязка определялась при помощи следующей формулы:

где $x_{i}^{j}$ и $y_{i}^{j}$ – пространственные координаты точек сетки в момент времени $t = j\Delta t$ для сетки из $N$ точек, а $\tilde {x}_{i}^{j}$ и $\tilde {y}_{i}^{j}$ – соответствующие координаты для сетки из $2N$ точек.

Было проведено сравнение результатов для 64 и 128 точек, а также для 128 и 256 точек в моменты времени 2.05 и 4.1. Эти результаты приведены в табл. 1. Отметим, что значение максимума достигалось на участках границы с наибольшим расстоянием между точками сетки.

Выводы. Приведенные примеры показали, что кривизна вершины струи может увеличиваться до очень больших значений без потери гладкости свободной границы. К этому же выводу пришли и авторы работ [5, 7], в которых построены полуаналитические решения для описания формирования кумулятивных струй. Предложенный в настоящей работе численный алгоритм позволяет за счет учета аналитичности свободных границ значительно сократить время расчетов тонких кумулятивных струй, сохраняя при этом высокую точность и устойчивость. Достоверность расчетов обоснована путем контроля точности на специально выведенных законах сохранения, сравнения расчетов с полуаналитическими решениями и другими специально построенными точными решениями.