1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 84, № 5, 2020

Прикладная математика и механика, 2020, T. 84, № 5, стр. 650-662

Модели критического состояния в механике безкогезионных сред (обзор)

С. В. Кузнецов 1, 2, 3, *

1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

2 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

3 Московский государственный строительный университет
Москва, Россия

* E-mail: kuzn-sergey@yandex.ru

Поступила в редакцию 03.02.2020
После доработки 14.05.2020
Принята к публикации 08.06.2020

Полный текст (PDF)

Аннотация

Анализируются основные уравнения и допущения, принимаемые при конструировании моделей критического состояния, применяемых в механике безкогезионных сред. Отмечается связь модифицированной кэм–клей модели с родственными моделями теории пластичности с изотропным упрочнением, описываемыми замкнутыми поверхностями пластичности. Дается анализ уравнений состояния модифицированных кэм–клей моделей в упругой зоне; отмечены работы, в которых упругое состояние описывается уравнениями гиперупругости с экспоненциальным потенциалом. Рассмотрены обобщения модифицированных кэм–клей моделей на случай конечных деформаций. Отмечено, что необходимы дополнительные исследования по кинематическим комбинированным нагружениям в шаровой и девиаторной области.

Ключевые слова: упругопластическая среда, модель критического состояния, кэм–клей модель, конечные деформации

Введение. Модель кэм–клей, также как и ее модификация, применяются для моделирования поведения безкогезионных или слабо когезионных грунтов при их упруго-пластическом деформировании [10, 11]. Впервые эта модель с логарифмической поверхностью пластичности в докритической зоне построена [28, 29]. Позже [27] предложено логарифмическую поверхность пластичности заменить эллипсоидальной (рис. 1). Такая модель именуется модифицированной кэм–клей моделью. Как кэм–клей, так и модифицированная кэм–клей модель относятся к упругопластическим моделям с изотропным упрочнением.

Рис. 1.

Поверхность пластичности и критический конус для модифицированной кэм–клей модели: штриховая линия отвечает пересечению эллипсоидальной поверхности текучести с критическим конусом [27].

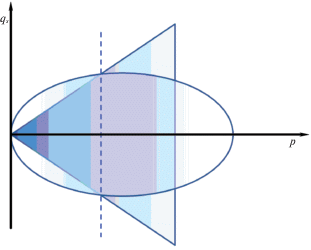
Имеется значительное число работ по применению как кэм–клей модели, так и ее модификации для исследования поведения различных гранулированных материалов с малой когезией в условиях как монотонных нагружений [3, 5, 8–12, 15, 17–19], так и при циклических воздействиях [2, 4, 14, 22, 23, 26, 30, 32, 35, 36, 38, 39]. Большая часть рассматриваемых исследований посвящена либо одноосному [30, 35], либо трехосному силовому нагружению [2, 4, 14, 23, 26, 36, 38].

Предложен [2, 23, 38] аналог модифицированной кэм–клей модели с кинематическим упрочнением, что позволяет учитывать в расчетах эффект Баушингера. В некоторых моделях вводят дополнительные параметры, учитывающие частоту циклических нагружений, а также деградацию материала [14, 24, 33, 39].

Ниже рассматривается модифицированная кэм–клей модель в условиях циклического кинематического нагружения при линейной связи между напряжениями и деформациями в упругой области и отсутствием упрочнения при объемном нагружении.

1. Основные уравнения. В этом разделе вводятся основные уравнения модифицированной кэм–клей модели для инфинитезимальных деформаций.

1.1. Основные обозначения. Для дальнейшего потребуется представление произвольного симметрического разложимого тензора второго ранга вида

(1.1)
${\mathbf{S}} = {\mathbf{a}} \otimes {\mathbf{b}} + {\mathbf{b}} \otimes {\mathbf{a}},\quad {\mathbf{a}},{\mathbf{b}} \in {{R}^{3}}$
на шаровую и девиаторную части
(1.2)
${\mathbf{V}} = \tfrac{1}{3}{\mathbf{I}} \otimes \left( {{\mathbf{I}} \cdot \cdot {\mathbf{S}}} \right),\quad {\mathbf{D}} = {\mathbf{S}} - {\mathbf{V}},$
где ${\mathbf{I}} \in {{R}^{3}} \otimes {{R}^{3}}$ – единичный тензор второго ранга.

Ниже вводятся тензорные инварианты тензора ${\mathbf{S}}$

(1.3)
${{I}_{{\mathbf{S}}}} \equiv \sum\limits_{k = 1}^3 {{{S}_{{kk}}}} ,\quad I{{I}_{{\mathbf{S}}}} \equiv {{\left\| {\mathbf{S}} \right\|}^{2}},\quad II{{I}_{{\mathbf{S}}}} \equiv \det ({\mathbf{S}}),$
где $\left\| {\mathbf{S}} \right\|$ – норма Шура тензора ${\mathbf{S}}$:

(1.4)
$\left\| {\mathbf{S}} \right\| = \sqrt {\sum\limits_{k,j} {S_{{kj}}^{2}} } $

Объединение (1.2), (1.3) дает

(1.5)
$I{{I}_{{\mathbf{D}}}} \equiv {{\left\| {\mathbf{S}} \right\|}^{2}} - \tfrac{1}{3}I_{{\mathbf{S}}}^{2}$

Декомпозиция (1.2) для тензора напряжений $\sigma $ и инфинитезимального тензора деформаций $\varepsilon $ обычно записывается в несколько измененном виде

(1.6)
${{\sigma }_{{ij}}} = - p{{\delta }_{{ij}}} + {{d}_{{ij}}},\quad {{\varepsilon }_{{ij}}} = - \tfrac{1}{3}\theta {{\delta }_{{ij}}} + {{e}_{{ij}}},\quad i,j = 1,2,3,$
где обозначено
(1.7)
$p = - \tfrac{1}{3}\sum\limits_{k = 1}^3 {{{\sigma }_{{kk}}}} ,\quad \theta = - \sum\limits_{k = 1}^3 {{{\varepsilon }_{{kk}}}} ,\quad {{d}_{{ij}}} = {{\sigma }_{{ij}}} + p{{\delta }_{{ij}}},\quad {{e}_{{ij}}} = {{\varepsilon }_{{ij}}} + \frac{1}{3}\theta {{\delta }_{{ij}}}$
в разложении (1.6)

(1.8)
${{\delta }_{{ij}}} = \left\{ {\begin{array}{*{20}{c}} {1,\quad i = j} \\ {0,\quad i \ne j} \end{array}} \right.$

Замечание 1. При решении задач динамики грунтовых сред знак объемной деформации обычно принимается таким же, как знак соответствующего первого инварианта тензора деформаций, однако, в кэм–клей модели (и некоторых других моделях критического состояния) знак объемной деформации берется противоположным знаку первого инварианта, по аналогии со знаком давления, см. соотношения (1.7).

В соответствии с определениями (1.3)–(1.7) удобно ввести следующую норму для девиаторов напряжений и деформаций

(1.9)
${{N}_{{\mathbf{s}}}} = \sqrt {I{{I}_{{\mathbf{s}}}}} ,\quad {{N}_{{\mathbf{e}}}} = \sqrt {I{{I}_{{\mathbf{e}}}}} $

Наряду с девиаторными нормами (1.9) для дальнейшего потребуются следующие параметры, основанные на нормах (1.9), см. [25]

(1.10)
$N_{{\mathbf{s}}}^{ \pm } = \frac{{f(\sigma )}}{{\left| {f(\sigma )} \right|}}\sqrt {I{{I}_{{\mathbf{s}}}}} ,\quad N_{{\mathbf{e}}}^{ \pm } = \frac{{f(\sigma )}}{{\left| {f(\sigma )} \right|}}\sqrt {I{{I}_{{\mathbf{e}}}}} ,$
где $f(\centerdot )$ – функция от соответствующих тензорных инвариантов. В большинстве приложений функция $f(\centerdot )$ выбирается совпадающей с первым инвариантом [25], таким образом (1.10) принимают вид

(1.11)
$N_{{\mathbf{s}}}^{ \pm } = - \frac{p}{{\left| p \right|}}\sqrt {I{{I}_{{\mathbf{s}}}}} ,\quad N_{{\mathbf{e}}}^{ \pm } = - \frac{\theta }{{\left| \theta \right|}}\sqrt {I{{I}_{{\mathbf{e}}}}} $

Вместо норм (1.9), в теориях пластичности могут использоваться девиаторные нормы, известные как напряжения и деформации Треска

(1.12)
${{\sigma }_{{\operatorname{Tresca} }}} = {{\sigma }_{1}} - {{\sigma }_{3}},\quad {{\varepsilon }_{{\operatorname{Tresca} }}} = {{\varepsilon }_{1}} - {{\varepsilon }_{3}},$
где ${{\sigma }_{k}}$, ${{\varepsilon }_{k}}$, $k = 1,2,3$ – главные компоненты соответствующих тензоров, ранжированные по убыванию. По аналогии с (1.10) могут быть введены параметры $N_{{\mathbf{s}}}^{ \pm }$ и $N_{\varepsilon }^{ \pm }$, основанные на нормах Треска.

1.2. Упругое состояние. Тензор деформаций может быть разбит на тензоры упругой и пластической деформаций

(1.13)
$\varepsilon = {{\varepsilon }^{p}} + {{\varepsilon }^{e}}$

В случае упругих деформаций, закон состояния в кэм–клей моделях формулируется либо в виде

(A) линейной связи между напряжениями и деформациями

(1.14)
$\sigma = {{\lambda }_{e}}{{\theta }^{e}}{\mathbf{I}} + 2{{\mu }_{e}}{{\varepsilon }^{e}},$
где ${{\lambda }_{e}}$ и ${{\mu }_{e}}$ упругие модули (константы Ламе);

(Б) гипоупругих соотношений, записываемых в виде [8, 27]

(1.15)
$\left\{ \begin{gathered} \frac{{{{p}_{0}} - {{p}_{t}}}}{{p - {{p}_{t}}}}\dot {p} = {{K}_{e}}{{{\dot {\theta }}}^{e}} \hfill \\ \dot {\sigma } + \frac{1}{3}\dot {p}{\mathbf{I}} = 2{{\mu }_{e}}{{{{\mathbf{\dot {e}}}}}^{e}} \hfill \\ \end{gathered} \right.,$
где ${{p}_{t}} \leqslant 0$ нижняя граница давлений, – параметр, позволяющий избежать сингулярности в первом уравнении (1.15) при малых $p$; ${{p}_{0}}$ начальное давление при ${{\theta }^{e}} = 0$; либо в виде

(В) гиперупругого потенциала [10, 11]

(1.16)
$W = {{p}_{0}}{{e}^{{\theta *}}}\left( {k + \alpha I{{I}_{\varepsilon }}} \right),$
где $\theta {\kern 1pt} *$ имеет вид

(1.17)
$\theta {\kern 1pt} * = {{\left( {\gamma k} \right)}^{{ - 1}}}\theta ,\quad \gamma = \frac{{3(1 - 2\nu )}}{{2(1 + \nu )}}$

Безразмерные константы $k,\alpha $ соответствуют объемному и сдвиговому модулям.

Замечание 2. a) Гипоупругие соотношения (1.15) могут быть записаны в терминах инкрементов $dp$, $d{{\theta }^{e}}$ или соответствующих скоростей:

(1.18)
$\dot {p} = K_{e}^{*}(p){{\dot {\theta }}^{e}},$
где $K_{e}^{*}(p) = (p - {{p}_{t}}){{K}_{e}}$.

б) В гипоупругих соотношениях (1.15) сдвиговой модуль обычно считают либо постоянным [14], либо определяют из (1.15) в предположении постоянного коэффициента Пуассона [9], в этом случае

(1.19)
${{\mu }_{e}} = \gamma K_{e}^{*}(p)$

Надо отметить, что случай постоянного коэффициента Пуассона и формула для модуля сдвига (1.19) представляются более реалистичными, чем условие постоянного модуля сдвига [9].

1.3. Поверхность пластичности. В модифицированных кэм–клей моделях поверхность пластичности описывается следующим уравнением [8, 27]

(1.20)
$f(p,{{q}_{{\mathbf{s}}}},{{p}_{c}}) \equiv \frac{1}{\beta }\left( {\frac{{{{p}^{2}}}}{{{{a}^{2}}}} - 2\frac{p}{a} + 1} \right) + \frac{{q_{{{{{\mathbf{D}}}_{\varepsilon }}}}^{2}}}{{{{{\left( {Ma} \right)}}^{2}}}} = 1,$
где $\beta $ – безразмерный параметр, определяющий форму эллипсоида: в докритической зоне (левая часть эллипсоида) $\beta = 1$, в закритической зоне (правая часть) $\beta \leqslant 1$; безразмерный параметр $M$, определяемый углом раствора критического конуса, определяет размер эллипсоида по оси ${{q}_{{\mathbf{s}}}}$; $q_{{{{{\mathbf{D}}}_{\varepsilon }}}}^{{}}$ – одна из эквивалентных норм девиатора деформаций, часто в качестве $q_{{{{{\mathbf{D}}}_{\varepsilon }}}}^{{}}$ используют норму Шура:

(1.21)
$q_{{{{{\mathbf{D}}}_{\varepsilon }}}}^{{}} = \sqrt {{{{\mathbf{D}}}_{\varepsilon }} \cdot \cdot {{{\mathbf{D}}}_{\varepsilon }}} $

Причем девиатор соответствует упругим деформациям. В уравнении (1.20) $a$ – параметр, определяющий собой размер эллипсоида по оси $p$:

(1.22)
$a = \frac{{{{p}_{c}}}}{{1 + \beta }},$
где ${{p}_{c}}$ текущее значение пластических давлений.

1.4. Объемное упрочнение. В соответствии с [8, 11], объемное упрочнение может быть задано в виде (i) кусочно-линейного продолжения соотношений (1.14); или (ii) с помощью соотношений гипоупругости (1.15), или (iii) с помощью гиперупругого потенциала (1.16). Надо отметить, что в моделях кэм–клей задается только объемное упрочнение.

(i) Объемное упрочнение, задаваемое в терминах кусочно-линейного продолжения уравнений (1.10), записывается в виде соответствующих скоростей

(1.23)
$\dot {p} = K(p)\dot {\theta }$

Обычно для объемного модуля принимают ступенчатую зависимость от $p$

(1.24)
$K(p) = \left\{ \begin{gathered} {{K}_{e}},\quad 0 < p < {{p}_{{c0}}} \hfill \\ {{K}_{p}},\quad p > {{p}_{{c0}}} \hfill \\ \end{gathered} \right.,$
где ${{K}_{p}}$ – модуль упрочнения (${{K}_{p}} < {{K}_{e}}$), а ${{p}_{{c0}}}$ – начальное значение давления, отвечающего началу пластического течения. Интегрирование уравнений (1.23) дает
(1.25)
$p = \left\{ \begin{gathered} {{K}_{e}}\theta ,\quad 0 < p < {{p}_{{c0}}} \hfill \\ {{p}_{{c0}}} + {{K}_{p}}{{\theta }_{p}},\quad p > {{p}_{{c0}}}, \hfill \\ \end{gathered} \right.$
где ${{\theta }_{p}}$ = $\theta - {{\theta }_{{c0}}}$ и ${{\theta }_{{c0}}} = {{p}_{{c0}}}{\text{/}}{{K}_{e}}$. При разгрузке $K(p)$ совпадает с ${{K}_{e}}$.

(ii) Продолжение уравнений (1.15) для учета пластичности осуществляется, фактически, теми же уравнениями: первое уравнение (1.15) можно переписать в терминах двух модулей, по аналогии с (1.23) [20, 31]

(1.26)
$\frac{{{{p}_{0}} - {{p}_{t}}}}{{p - {{p}_{t}}}}\dot {p} = \left\{ \begin{gathered} {{K}_{e}}{{{\dot {\theta }}}_{e}},\quad 0 < p < {{p}_{{c0}}} \hfill \\ {{K}_{p}}{{{\dot {\theta }}}_{p}},\quad p > {{p}_{{c0}}} \hfill \\ \end{gathered} \right.$

Замечание 3. Аналогично уравнению (1.18), второе уравнение (1.26) можно записать в терминах касательного модуля:

(1.27)
$\dot {p} = K_{p}^{*}(p){{\dot {\theta }}_{p}},$
где $K_{p}^{*}(p) = (p - {{p}_{t}}){{K}_{p}}$.

(iii) Продолжение гиперупругого потенциала (1.16) в зону пластичности осуществляется с помощью введения зависимостей параметров $\alpha $ и $k$ от давления при $p > {{p}_{{c0}}}$:

(1.28)
$W = {{p}_{0}}{{e}^{{\theta {\kern 1pt} *}}}\left( {k(p) + \alpha (p)I{{I}_{\varepsilon }}} \right)$

Наиболее простые зависимости $\alpha (p),\,\,k(p)$ получаются в случае билинейных функций:

(1.29)
$k(p) = \left\{ \begin{gathered} {{k}_{e}}\quad 0 < p < {{p}_{{c0}}} \hfill \\ {{k}_{p}},\quad p > {{p}_{{c0}}} \hfill \\ \end{gathered} \right.,\quad \alpha (p) = \left\{ \begin{gathered} {{\alpha }_{e}}\quad 0 < p < {{p}_{{c0}}} \hfill \\ {{\alpha }_{p}},\quad p > {{p}_{{c0}}} \hfill \\ \end{gathered} \right.$

1.5. Закон пластического течения. Для описания пластического течения, уравнение (1.20) должно быть дополнено уравнением, описывающим пластическое течение. В большинстве работ по кэм–клей пластичности [9, 27–29] принимается ассоциированный закон пластического течения. Это означает совпадение потенциалов течения и уравнения, определяющего поверхность пластичности (1.20), в каждой точке поверхности $f(p,{{q}_{{\mathbf{s}}}},{{p}_{c}}) = 0$:

(1.30)
${{\dot {\varepsilon }}_{p}} = \dot {\gamma }{{\nabla }_{\sigma }}f,$
где $\dot {\gamma }$ – параметр, определяющий скорость пластического течения. Уравнение (1.30) можно представить в виде двух уравнений в терминах шаровых и девиаторных тензоров

(1.31)
${{{\mathbf{\dot {e}}}}_{p}} \equiv \dot {\gamma }{{\nabla }_{{\mathbf{s}}}}f(p,{{q}_{{\mathbf{s}}}},{{p}_{c}}),\quad {{\dot {\theta }}_{p}} = 3\dot {\gamma }{{\partial }_{p}}f(p,{{q}_{{\mathbf{s}}}},{{p}_{c}})$

Выполняя дифференцирование в (1.31), получаем

(1.32)
${{{\mathbf{\dot {e}}}}_{p}} = \dot {\gamma }\frac{{2{\mathbf{s}}}}{{{{{(Ma)}}^{2}}}},\quad {{\dot {\theta }}_{p}} = \dot {\gamma }\frac{6}{{\beta a}}\left( {\frac{p}{a} - 1} \right)$

Учитывая (1.22), второе уравнение в (1.32) принимает вид

(1.33)
${{\dot {\theta }}_{p}} = \dot {\gamma }\frac{{6(1 + \beta )}}{{\beta {{p}_{c}}}}\left( {\frac{{p(1 + \beta )}}{{{{p}_{c}}}} - 1} \right)$

В предположении $p = {{p}_{c}}$ и, следовательно ${\mathbf{s}} = 0$, уравнение (1.33) дает

(1.34)
${{\dot {\theta }}_{p}} = \dot {\gamma }\frac{{6(1 + \beta )}}{{{{p}_{c}}}}$

Поскольку в точке $({{p}_{c}},\,0)$ выполняется одно из условий упрочнения (1.23)–(1.29), уравнение (1.34) может быть записано в терминах скорости ${{\dot {p}}_{c}}$

(1.35)
${{\dot {p}}_{c}} = \dot {\gamma }\frac{{6(1 + \beta )}}{{{{p}_{c}}}}g({{p}_{c}}),$
где функция $g({{p}_{c}})$ определена соответствующим уравнением, описывающим упрочнение. Например, для уравнения упрочнения (1.25)

(1.36)
$g({{p}_{c}}) = {{K}_{p}}$

Ввиду (1.35) скорость $\dot {\gamma }$ может быть определена из условия совместности Прагера:

(1.37)
${{\nabla }_{\sigma }}f \cdot \cdot \dot {\sigma } + {{\partial }_{{{{p}_{c}}}}}f\,{{\dot {p}}_{c}} = 0$

Подстановка в уравнение (1.37) представления для ${{\dot {p}}_{c}}$ из уравнения (1.35) дает искомое уравнение для скорости $\dot {\gamma }$

(1.38)
$\dot {\gamma } = - \frac{{{{\nabla }_{\sigma }}f \cdot \cdot \dot {\sigma }}}{{{{\partial }_{{{{p}_{c}}}}}f}} \times \frac{{{{p}_{c}}}}{{6(1 + \beta )g({{p}_{c}})}}$

Уравнение (1.38) является дополняющим уравнением для уравнения пластического течения (1.32).

1.6. Обобщение на случай конечных деформаций. Модификация кэм–клей моделей для учета конечных деформаций предложена в [11, 13, 34, 41, 42]. В рамках теории конечных деформаций рассматривалась [34] линейная зависимость $v - \ln p$ и принималось предположение о постоянном модуле сдвига, а построена [11, 13] аналогичная модель для постоянного коэффициента Пуассона.

Для обобщения кэм–клей модели на случай конечных деформаций, необходимо ввести безразмерный параметр ${v}$ (относительный объем)

(1.39)
$v = \frac{V}{{{{V}_{{\operatorname{solid} }}}}}$
где $V$ – текущий объем, содержащий поры, а ${{V}_{{\operatorname{solid} }}}$ – объем твердой фракции. В терминах относительного объема, может быть определена (конечная) объемная деформация
(1.40)
$\theta = \det {\mathbf{F}} - \det {\mathbf{I}} = \frac{{V - {{V}_{0}}}}{{{{V}_{0}}}},$
где ${\mathbf{F}}$ – градиент смещений, а ${{V}_{0}}$ – начальный объем. Как правило [34] в теориях, учитывающих конечные деформации гранулированных сред, объемным деформированием твердой фракции пренебрегают, это позволяет представить объемную деформацию в виде

(1.41)
$\theta = \frac{{{v} - {{{v}}_{0}}}}{{{{{v}}_{0}}}}$

Следуя [34, 42], закон состояния в упругой зоне удобно представить в виде

(1.42)
${\mathbf{\dot {s}}} = 2\mu (p,\left\| {\mathbf{e}} \right\|)\left( {{{I}_{{6 \times 6}}} - \frac{1}{3}{\mathbf{I}} \otimes {\mathbf{I}}} \right){\mathbf{\dot {e}}},$
где ${\mathbf{\dot {s}}}$ – инкремент девиатора напряжений, ${{I}_{{6 \times 6}}}$ – единичный тензор, действующий в шестимерном пространстве ${{R}^{6}}$, ${\mathbf{\dot {e}}}$ – инкремент девиатора упругих деформаций, $\mu (p,\left\| {\mathbf{e}} \right\|)$ – модуль сдвиговых деформаций, зависящий от текущего объема и какой-либо нормы текущего девиатора упругих деформаций. Наиболее часто [34, 42] в качестве нормы используется шуровская норма:

(1.43)
$\left\| {\mathbf{e}} \right\| = \sqrt {{\mathbf{e}} \cdot \cdot {\mathbf{e}}} $

Заметим, что в законе гипоупругости (1.42) соответствующие инкременты предполагаются малыми, – это позволяет использовать линейные инкрементальные соотношения.

Для описания закона состояния при объемном упругом деформировании применяют следующий линейный в полулогарифмических координатах закон состояния [20, 34]

(1.44)
$\ln \left( {\frac{p}{{{{p}_{0}}}}} \right) = - {{K}_{0}}{{\theta }_{e}}$
где ${{\theta }_{e}}$ – упругая часть объемной деформации, ${{K}_{0}}$ – постоянный (в полулогарифмических координатах) объемный модуль, ${{p}_{0}}$ – начальное давление. Закон состояния (1.44) позволяет записать соответствующее уравнение состояния в терминах инкрементов

(1.45)
$\,\frac{{\dot {p}}}{p} = - {{K}_{0}}{{\dot {\theta }}_{e}}$

Именно в инкрементальной форме (1.45) уравнения гипоупругости применяются для описания объемного упругого деформирования.

Объединяя (1.42) и (1.45), уравнение состояния рассматриваемой гранулированной среды представимо в виде тензорного уравнения для гипоупругой среды

(1.46)
$\dot {\sigma } = K(p){{\dot {\theta }}_{e}}{\mathbf{I}} \otimes {\mathbf{I}} + 2\mu (p,\left\| {\mathbf{e}} \right\|)\left( {{{I}_{{6 \times 6}}} - \frac{1}{3}{\mathbf{I}} \otimes {\mathbf{I}}} \right){\mathbf{\dot {e}}},\quad K(p) = {{K}_{0}}\frac{1}{p}$

В пластической стадии при учете больших деформаций используют уравнения (1.23)–(1.29), применявшиеся для описания пластичности с объемным упрочнением и отсутствием упрочнения в девиаторной плоскости, таким предполагается, что при больших деформациях инкременты девиаторных компонент напряжений отсутствуют [20, 34], а объемная пластическая деформация описывается следующим соотношением (1.27). Заметим, что поверхность пластичности обычно [34] описывается уравнением (1.20). С учетом уравнений состояния (1.46), удается решить задачу о деформировании гранулированной среды в условиях больших деформаций.

1.7. Дальнейшее развитие модифицированных кэм–клей моделей. Одна из модификаций [37] возникает при замене эллипсоидальной поверхности пластичности на яйцеобразную.

Еще одно развитие кэм–клей моделей связано с введением концепции ограничивающей поверхности (BS) [16]. Введение BS-поверхности позволяет охватить все допустимые в процессе нагружения поверхности пластичности. Модуль объемного упрочнения в этой теории задается как функция расстояния между текущей поверхностью пластичности и BS-поверхностью. Дальнейшее обобщение этой теории известно, как теория общей пластичности (General Plasticity, GP). Эта теория [6, 7], позволяет рассматривать несколько BS-поверхностей. Как BS, так и GP модели обеспечивают задание гладкого перехода от упругого к пластическому состоянию.

В последнее время рассмотрены [41–44] приложения модифицированных кэм–клей моделей для описания поведения гранулированных сред в условиях циклических квазистатических [41–44] нагружений, причем, как показано [42, 43], в закритической области циклическое деформирование в девиаторной плоскости необходимо приводит к размягчению в плоскости, определяемой параметрами $\theta - p$; см. рис. 2 [42]; в то же время в докритической области, при циклическом деформировании в девиаторной плоскости наблюдается упрочнение в плоскости $\theta - p$.

Рис. 2.

Сверхкритическая зона: изменение девиаторных компонент напряжений и давления от времени: штриховая линия – девиаторные компоненты напряжений Треска; сплошная линия – гидростатическое давление; напряжения, МПа, [42].

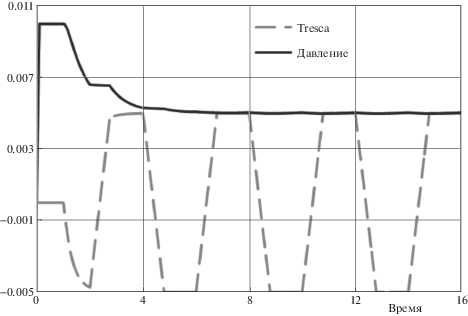
Некоторые задачи нестационарной сейсмодинамики, описываемые модифицированными кэм–клей моделями, рассмотрены в [45–48]. В недавних исследованиях [49–53] рассмотрены обобщения кэм–клей моделей на случай (трансверсальной) анизотропии как в упругой, так и в пластической зонах, причем [53] наряду с трансверсальной анизотропией рассмотрен несколько более общий случай кубической сингонии.

2. Заключительные замечания. Рассмотренные модели критического состояния и, в том числе кэм–клей модели, применяемые для анализа безкогезионных или слабо когезионных сред, можно рассматривать, как частный случай моделей с изотропным упрочнением и замкнутой поверхностью пластичности [38]. В этой связи кэм–клей модели наследуют свойства таких моделей и им присущи те же ограничения, что и другим моделям кэп-пластичности: это, прежде всего, выраженная область упругих деформаций, ограниченная поверхностью текучести и, принимаемый в большинстве исследований ассоциированный закон пластического течения.

Надо отметить, что известны также подходы, в которых рассматриваются модели с распределенной поверхностью пластичности (по терминологии [38] это модели с микропластичностью). Эти модели позволяют достичь эффектов, аналогичным эффектам, реализуемым в моделях критического состояния, в частности, в моделях микропластичности удается реализовать эффект разупрочнения, реализуемый в моделях критического состояния. Рассматривались [40] некоторые приложения моделей критического состояния к задачам волновой динамики.

Работа выполнена за счет гранта № 20-49-08002 Российского научного фонда.

Список литературы

  1. Aboim C., Roth W. Bounding surface plasticity theory applied to cyclic loading of sand // in: Intern. Symp. Num. Models Geomech. 1982. P. 65–72.

  2. Al Tabbaa A., Wood D.M. An experimentally based bubble model for clay // In: Proc. 3rd Intern. Symp. Num. Models Geomech. (NUMOG III), 1989. P. 90–99.

  3. Alawaji H., Runesson K., Sture S., Axelsson K. Implicit integration in soil plasticity under mixed control for drained and undrained response // Intern. J. Numer. Anal. Methods Geomech. 1992. V. 13. P. 737–756.

  4. Andersen K.H. Bearing capacity under cyclic loading – offshore, along the coast, and on land // Can. Geotech J. 2009. V. 46. P. 513–535.

  5. Armero F., Pérez-Foguet A. On the formulation of closest-point projection algorithms in elastoplasticity – Part I: The variational structure // Intern. J. Numer. Methods Eng. 2002. V. 53. P. 297–329.

  6. Auricchio F., Taylor R. A return-map algorithm for general associative isotropic elasto-plastic materials in large deformation regimes // Intern. J. Plasticity. 1999. V. 15. P. 1359–1378.

  7. Auricchio F., Taylor R.L., Lubliner J. Application of a return map algorithm to plasticity models // in: Computational Plasticity / Ed. by Owen D.R.J. et al. Barcelona: CIMNE, 1992. P. 2229–2248.

  8. Bigoni D., Hueckel T. Uniqueness and localization associative and non-associative elasto–plasticity // Intern. J. Solids Struct. 1991. V. 28. P. 197–213.

  9. Borja R.I., Lee S.R. Cam–Clay plasticity. Part I: Implicit integration of elasto-plastic constitutive relations // Comput. Methods Appl. Mech. Eng. 1990. V. 78. P. 49–72.

  10. Borja R., Sama K., Sanz P. On the numerical integration of three-invariant elastoplastic constitutive models // Comput. Methods Appl. Mech. Eng. 2003. V. 192. P. 1227–1258.

  11. Borja R., Tamagnini C. Cam–Clay plasticity, Part III: Extension of the infinitesimal model to include finite strains // Comput. Methods Appl. Mech. Eng. 1998. V. 155. P. 73–95.

  12. Buscarnera G., Dattola G., di Prisco C. Controllability, uniqueness and existence of the incremental response: A mathematical criterion for elastoplastic constitutive laws // Intern. J. Solids Struct. 2011. V. 48. P. 1867–1878.

  13. Callari C., Auricchio F., Sacco E. A finite-strain cam–clay model in the framework of multiplicative elasto-plasticity // Intern. J. Plasticity. 1998. V. 14. P. 1155–1187.

  14. Carter J.P., Booker J.R., Wroth C.P. Acritical state soil model for cyclic loading // in: Soil Mechanics–Transient and Cyclic Loading / Ed. by Pande G.N., Zienkiewicz O.C. Chichester: Wiley, 1982. P. 219–252.

  15. Conti R., Tamagnini C., De Simone A. Critical softening in Cam–Clay plasticity: Adaptive viscous regularization, dilated time and numerical integration across stress–strain jump discontinuities // Comput. Methods Appl. Mech. Eng. 2013. V. 258. P. 118–133.

  16. Dafalias Y.F., Herrmann L.R. A bounding surface soil plasticity model // in: Proc. Intern. Symp. Soils Cyclic Trans. Load. Swansea, 1980. P. 335–345.

  17. Dal Maso G., De Simone A. Quasistatic evolution for cam–clay plasticity: Examples of spatially homogeneous solutions // Math. Models Methods Appl. Sci. 2009. V. 19. P. 1643–1711.

  18. Dal Maso G., De Simone A., Solombrino F. Quasistatic evolution for cam–clay plasticity: A weak formulation via viscoplastic regularization and time rescaling // Calc. Var. 2011. V. 40. P. 125–181.

  19. Dal Maso G., Solombrino F. Quasistatic evolution for Cam–Clay plasticity: The spatially homogeneous case // Netw. Heter. Media. 2010. V. 5. P. 97–132.

  20. Hashiguchi K. On the linear relations of V–ln p and ln v–ln p for isotropic consolidation of soils // Intern. J. Num. Anal. Methods Geomech. 1995. V. 19. P. 367–376.

  21. Hirai H. An elastoplastic constitutive model for cyclic behaviour of sands // Intern. J. Num. Anal. Methods Geomech. 1987. V. 11. P. 503–520.

  22. Liu J., Xiao J. Experimental study on the stability of railroad silt subgrade with increasing train speed // J. Geotech. Geoenviron. Eng. 2010. V. 10. P. 833–841.

  23. Mroz Z. On the description of anisotropic work hardening // J. Mech. Phys. Solids. 1967. V. 15. P. 163–175.

  24. Ni J., Indraratna B., Geng X., Carter J., Chen Y. Model of soft soils under cyclic loading // Intern. J. Geomech. Eng. 2014. V. 10.1061. P. 1–10.

  25. Papuga J. A survey on evaluating the fatigue limit under multiaxial loading // Intern. J. Fatigue. 2011. V. 33. P. 153–165.

  26. Puppala A.J., Mohammad L.N., Allen A. Permanent deformation characterization of subgrade soils from RLT test // J. Mater. Civil Eng. 1999. V. 11. P. 274–282.

  27. Roscoe K.H., Burland J.B. On the generalized stress-strain behavior of wet clay // in: Engineering Plasticity / Ed. by Heyman J., Leckie F.A. Cambridge: Univ. Press, 1968. P. 535–609.

  28. Roscoe K.H., Schofield A.N., Wroth C.P. On the yielding of soils // Geotechnique. 1958. V. 8. P. 22–53.

  29. Roscoe K.H., Schofield A.N. Mechanical behavior of an idealized wet clay // in: Proc. 2nd European Conf. Soil Mechanics and Foundation Engineering, Wiesbaden. V. I. 1963. P. 47–54.

  30. Sangrey D.A. Cyclic loading of sands, silts and clays. Earthquake engineering and soil dynamics // Proc. ASCE Geot. Eng. Div. Conf. 1978. P. 836–851.

  31. Schofield A.N., Wroth C.P. Critical State Soil Mechanics. London: McGraw-Hill, 1968. 310 p.

  32. Selig E.T. Soil failure modes in undrained cyclic loading // J. Geot. Eng. Div. V. 107. 1981. P. 539–551.

  33. Shahin M.A., Loh R.B.H., Nikraz H.R. Some observations on the behaviour of soft clay under undrained cyclic loading // J. Geo Engng. 2011. V. 6. P. 109–112.

  34. Simo J.C., Meschke G. A new class of algorithms for classical plasticity extended to finite strains. Application to geomaterials // Comput. Mech. 1993. V. 11. P. 253–278.

  35. Takahashi M., Hight D.W., Vaughan P.R. Effective stress changes observed during undrained cyclic triaxial tests on clay // in: Proc. Intern. Symp. on Soils under Cyclic and Transient Loading / Ed. by Pande G.N., Zienkiewicz O.C. Rotterdam: Balkema, 1980. P. 201–209.

  36. Uzan J. Characterization of granular materials // Transp. Res. Rec. 1022, TRB. Washington DC: National Research Council, 1985. P. 52–59.

  37. Van Eekelen S.J., Van den Berg P. The delft egg model, a constitutive model for clay // in: DIANA Comput. Mech.’94. Springer. 1994. P. 103–116.

  38. Wood D.M. Soil Behaviour and Critical State Soil Mechanics. Cambridge: Univ. Press, 1990.

  39. Zhou J., Gong X. Strain degradation of saturated clay under cyclic loading // Can. Geotech. J. 2001. V. 38. P. 208–212.

  40. Zienkiewicz O., Mroz Z. Generalized plasticity formulation and applications to geomechanics // in: Mech. Eng. Mater. Chicheste: Wiley, 1984. P. 655–679.

  41. Гольдштейн Р.В., Кузнецов С.В. Модифицированная Кэм–клэй модель. Основы теории и численный анализ // Вычисл. мех. сплошных сред. 2016. № 2. С. 162–172.

  42. Goldstein R.V., Dudchenko A.V., Kuznetsov S.V. The modified Cam–Clay (MCC) model: cyclic kinematic deviatoric loading // Arch. Appl. Mech. 2016. V. 86. P. 2021–2031.

  43. Dudchenko A.V., Kuznetsov S.V. The modified Mohr–Coulomb and Drucker–Prager models. influence of eccentricity on hysteresis loop and energy loss // Intern. J. Comp. Civil Struct. Eng. 2017. V. 13. P. 35–44.

  44. Ilyashenko A.V., Kuznetsov S.V. Cam–clay models in mechanics of granular materials // Mech. Mech. Eng. 2017. V. 21. P. 813–821.

  45. Гольдштейн Р.В., Ильяшенко А.В., Кузнецов С.В. Волны Лэмба в анизотропных средах: шестимерный формализм Коши // Матеем. модел. 2017. № 10. С. 86–94.

  46. Sijia L., Brun M., Djeran-Maigre I., Kuznetsov S. Hybrid asynchronous absorbing layers based on Kosloff damping for seismic wave propagation in unbounded domains // Comput.&Geotechn. 2019. V. 109. P. 69–81.

  47. Kuznetsov S.V., Maigre H. Granular metamaterials for seismic protection. Hyperelastic and hypoelastic models // IOP Conf. Ser. 2020. V. 1425. P. 012184.

  48. Pham H.V., Dias D., Dudchenko A.V. 3D modeling of geosynthetic-reinforced pile-supported embankment under cyclic loading // Geosynthetics Intern., 2020. V. 27. P. 157–169.

  49. Coombs W.M. Continuously unique anisotropic critical state hyperplasticity // Intern. J. Numer. Anal. Methods Geomech. 2017. V. 41. P. 578–601.

  50. Sivasithamparam N., Castro J. An anisotropic elastoplastic model for soft clays based on logarithmic contractancy // Intern. J. Numer. Anal. Methods Geomech. 2016. V. 40. P. 596–621.

  51. Mo P.Q., Yu H.S. Undrained cavity contraction analysis for prediction of soil behavior around tunnels // Intern. J. Geomech. 2017. V. 17. Paper # 04016121.

  52. Liu K., Chen S.L. Theoretical analysis on drained cylindrical cavity expansion in anisotropic modified cam clay // in: GeoShanghai Intern. Conf. 2018, Shanghai, China, May 27–30, Paper # A0555.

  53. Chen S.L., Liu K. Undrained cylindrical cavity expansion in anisotropic critical state soils // Geotechn. 2019. V. 69. P. 189–202.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал