Прикладная математика и механика, 2020, T. 84, № 5, стр. 590-611

Введение. Центробежные аппараты широко используются во многих отраслях народного хозяйства. Вопросы проектирования новых моделей и совершенствование существующих конструкций тесно связаны с анализом процессов, происходящих в этих аппаратах. Гидродинамическая картина течения, реализуемая в таких устройствах, оказывает существенное влияние на весь технологический процесс. Очень часто в пневматических аппаратах в качестве рабочей среды используют воздух, а сами конструкции имеют сложную геометрическую форму. При этом режимы течения всегда являются турбулентными. Физическое моделирование таких процессов связано с большими затратами средств и времени. Методы математического моделирования можно рассматривать как один из перспективных способов успешного решения задачи о нахождении поля скорости, при этом получение аналитических решений практически невозможно или связано с низкой степенью достоверности. Следовательно, единственным способом решения поставленных задач можно считать метод численного моделирования [1].

В настоящее время для решения задач турбулентности используются метод прямого численного моделирования (Direct Numerical Simulation, DNS) [2, 3], метод моделирования крупных вихрей (Large Eddy Simulation, LES) [4] и методы, направленные на замыкание уравнений Навье–Стокса осредненные по Рейнольдсу (Reynolds-Averaged Navier–Stokes Equations, RANS). Современные возможности метода DNS с определением всех составляющих движения ограничены расчетами при относительно невысоких числах Рейнольдса, не превышающих величину порядка 10³. Метод LES по сравнению с DNS может применяться для расчетов течений с существенно большими числами Рейнольдса. Однако использование метода LES для расчета течений вблизи стенки требует применения сеток, приближающихся по своим характеристикам к сеткам метода DNS [5]. Поэтому для технических приложений более применимым является метод, базирующийся на решении осредненных уравнений Навье–Стокса по Рейнольдсу.

Таким образом, для инженерных расчетов требуются модели турбулентности, достаточно точно описывающие усредненные поля и крупномасштабные пульсации закрученных течений. Получившие широкое распространение в инженерных расчетах многие модели турбулентности плохо описывают такие течения. Чтобы улучшить адекватность моделирования турбулентных закрученных течений пытаются модифицировать существующие RANS модели турбулентности. Такими моделями являются широко известные модели SARC [6] и k-ω SST-RC [7], где введены специальные поправки на вращение потока в моделях SA [8] и k-ω SST [9] соответственно. В то же время отмечается [10], что в определенных задачах с сильным вращением потока эти модели могут дать не совсем адекватные результаты. Это объясняется тем, что в основе этих моделей лежит гипотеза Буссинеска, которая справедлива для изотропных турбулентных течений, а в течениях с сильной закруткой возникает анизотропная турбулентность. Поэтому для течений с анизотропной турбулентностью разработаны модели без привлечения гипотезы Буссинеска. Их представителями являются модели Рейнольдсовых напряжений. Недостаток моделей Рейнольдсовых напряжений в том, что необходимо решать много дифференциальных уравнений, не менее семи уравнений для турбулентности, что требует много вычислительных ресурсов. Кроме того, необходимо использовать специальные средства для улучшения устойчивости и сходимости, нет строгих физических оснований при постановке граничных условий на свободных границах для напряжений.

Необходимо упомянуть, что еще одним подходом к решению проблемы турбулентности, который на сегодняшний день можно считать почти забытым, является двухжидкостной подход Сполдинга [11]. Суть данного подхода заключается в том, что турбулентный поток делится на две жидкости по некоторым отличительным признакам потока. Например, для описания перемежаемости поток делится на ламинарный и турбулентный, в задачах горения на сгоревший и не сгоревший газ и т.д. Сложнее обстоит дело с простым турбулентным потоком, где отсутствуют явные отличительные черты потока, по которым можно было бы разделить поток на две жидкости. Поэтому в следующей работе Сполдинга [12] предложено умозрительно разделить поток на “быструю” и “медленную” жидкости. С помощью этой модели были получены результаты предсказавшие довольно точно турбулентные характеристики потока. Однако двухжидкостный подход [12] не получил дальнейшего развития. Причина этого явления заключается в том, что для замыкания систем уравнений, как в моделях RANS привлекались еще дополнительные уравнения на основе различных гипотез. В результате число решаемых уравнений удваивалось по сравнению с RANS-моделями, что увеличивало вычислительное время.

Новое развитие двухжидкостного подхода после более 30 летнего перерыва получено в недавно опубликованной работе одного из авторов [13] настоящей статьи. В указанной работе продемонстрировано, что новая двухжидкостная модель является низкорейнольдсовой и хорошо описывает сильно закрученные турбулентные течения. Поэтому целью настоящей работы является сравнение различных подходов к турбулентности для моделирования двухмерного осесимметричного турбулентного течения в воздушном центробежном сепараторе, который используется в процессах сепарации и классификации частиц, получении порошков требуемого качества. Для этого использованы хорошо апробированные и имеющие хорошую точность модели RANS с привлечением гипотезы Буссинеска SARC и SST-RC, один из вариантов метода Рейнольдсовых напряжений SSG/LRR-RSM-w2012, а также упомянутая новая двухжидкостная модель. Численные результаты этих моделей сравниваются не только между собой, но и с экспериментальными данными для дисперсного состава отсепарированного порошка.

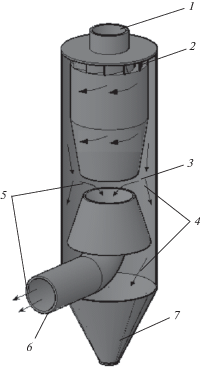
1. Физическая и математическая постановки задачи. Принципиальная схема центробежного сепаратора показана на рис. 1. Центробежный воздушный сепаратор работает следующим образом. Исходный материал подается через патрубок 1 в верхнюю часть сепаратора. Управляемыми лопатами 2 потоку воздуха придается вращательное движение. Под действием центробежной силы инерции частицы движутся к внутренней цилиндрической стенке корпуса сепаратора и попадают в зону классификации 3, расположенную между усеченными конусами и стенкой корпуса сепаратора. Крупные частицы – линии 4, вследствие своей большей массы под действием центробежной силы накапливаются около внутренней стенки корпуса сепаратора и по инерции попадают в бункер сепаратора 7. А мелкие частицы – линии 5, увлекаются воздухом и выносятся из сепаратора через выходной патрубок 6, который соединен с всасывающим вентилятором. Таким образом, исходный материал разделяется на две фракции.

Несложно понять, что эффективность такого сепаратора сильно зависит от его геометрии. Поэтому для поиска оптимальных геометрических параметров возникает задача моделирования кинематики частиц внутри установки. Ясно, что кинематика частиц зависит от динамики потока воздуха. Поэтому здесь возникают две задачи: 1) исследовать динамику воздушного потока; 2) на основе полученных гидродинамических параметров воздушного потока исследовать траектории сепарируемых частиц.

На практике объемная плотность пыли в сепараторах может достигать 50 г/м³. Данное значение существенно меньше, чем плотность несжимаемого воздуха (1.29 г/м³). Поэтому во многих работах влиянием твердой фазы на динамику воздуха пренебрегается. Однако около стенки, где скапливаются частицы пыли под действием центробежной силы, концентрация твердой фазы может достигать больших значений. В таком случае влиянием твердой фазы на динамику газовой фазы пренебрегать нельзя. Поэтому в настоящей работе проводится численное исследование турбулентного потока с учетом влияния твердой фазы на динамику воздушного потока внутри центробежной установки.

Для численного исследования поставленной задачи используется система уравнений Навье–Стокса, осредненная по Рейнольдсу с учетом взаимодействия между фазами [14]. При моделировании двухфазного потока не будут учитываться силы, действующие на частицы, обусловленные эффектами турбулентной миграции, Сефмена, Магнуса (подъемная сила) и Кориолиса, поскольку они существенно меньше, чем центробежная сила. Таким образом, для математического моделирования процессов переноса частиц порошка в сепараторе является достаточным учет центробежной и Стоксовой силы взаимодействия между фазами. По теории пограничного слоя Прандтля можно пренебречь и членами в диффузионных членах с производными в продольном и тангенциальном направлениях. Сепаратор имеет осевую симметрию, поэтому удобной системой является цилиндрическая система координат. Используя метод осреднения Рейнольдса для двухфазного потока можно получить систему уравнений

здесь $\bar {U}$, $\bar {V}$, $\bar {W}$ – соответственно аксиальная, радиальная и тангенциальная составляющие скорости воздушного потока; ${{\bar {U}}_{{pi}}}$, ${{\bar {V}}_{{pi}}}$, ${{\bar {W}}_{{pi}}}$ – аналогичные составляющие скорости для i-й фракции пыли; $\bar {p}$ – гидростатическое давление; $\rho $ – плотность газа; $\nu $ – его молекулярная вязкость; $\overline {{v}{\kern 1pt} 'u{\kern 1pt} '} $, $\overline {v{\kern 1pt} 'v{\kern 1pt} '} $, $\overline {v{\kern 1pt} 'w{\kern 1pt} '} $, $\overline {w{\kern 1pt} 'w{\kern 1pt} '} $ – компоненты тензора Рейнольдсовых напряжений; ${{\rho }_{i}}$ – массовая плотность пыли; k_i – коэффициент взаимодействия между воздухом и i-й фракции пыли; N – число фракций пыли. В работе рассмотрено число фракций N = 5.

Коэффициент взаимодействия между фазами определялся через параметр Стокса:

В данном выражении ${{\rho }_{\rho }}$ – плотность материала частиц пыли, ${{\delta }_{i}}$ – “эффективный” диаметр частиц. Система уравнений (1.1) является незамкнутой, т.к. возникающие Рейнольдсовые члены являются неизвестными. Следовательно, задача RANS-моделей турбулентности заключается в замыкании этой системы на основе различных гипотез и математических приемов. RANS-модели в основном разработаны для однофазного потока. Поэтому при использовании этих моделей для двухфазного потока необходимо учесть влияние твердой фракции на флуктуирующие характеристики турбулентного потока. Данная задача требует дополнительных исследований. В настоящей работе это влияние в первом приближении предполагается малым при небольших концентрациях и в моделировании не учитывается. Данное предположение можно оправдать тем, что концентрация частиц высока около стенки сепаратора, где находится вязкий подслой потока, где турбулентные пульсации имеют не большие значения. Таким образом, далее обратное влияние твердой фазы на течения газовой фазы в системе (1.1) учтено только через уравнения движения газовой фазы.

Для замыкания системы уравнений (1.1) в моделях, где используется гипотеза Буссинеска, использованы соотношения

Здесь ${{{v}}_{t}}$ – турбулентная вязкость, ${{\operatorname{Sc} }_{t}}$ – турбулентное число Шмидта. Следовательно, задача сводится к поиску неизвестной турбулентной вязкости. Что касается методов Рейнольдсовых напряжений, то дополнительные уравнения получаются из осредненных уравнений Рейнольдса и Навье–Стокса. Ниже используются модели SARC, SST-RC и SSG/LRR-RSM-w2012. Эти модели являются широко известными и методика их реализации представлена во многих ранее выполненных исследованиях, поэтому в данной работе они не приводятся. Больший интерес представляет реализация новой двухжидкостной модели для поставленной задачи. Особенность этой модели в том, что для ее вывода использован иной подход к проблеме турбулентности. По этой причине ниже приводится суть этого подхода и основные моменты вывода математической модели турбулентности на основе этого подхода.

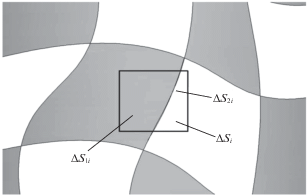
2. Новая двухжидкостная модель турбулентности. Рассмотрим течение двух жидкостей составляющие гетерогенную смесь, где эти жидкости состоят из отдельных объемов. На рис. 2 показано течение такой смеси в плоскости перпендикулярной к направлению i. Здесь темным цветом обозначена I жидкость и светлым цветом II жидкость. Обозначим через ${{V}_{1}}$, ${{V}_{2}}$ их скорости. Будем считать их плотности одинаковыми и равными $\rho $. Пусть $\Delta {{S}_{i}}$ неподвижная элементарная площадь, а $\Delta {{S}_{{1i}}}$ – площадь занимаемая жидкостью I и $\Delta {{S}_{{2i}}}$ – жидкостью II. Очевидно, что

Определим суммарную массу жидкостей проходящих через элементарную площадку $\Delta {{S}_{i}}$ за время $\Delta t$

С другой стороны данную массу через скорость смеси ${{V}_{i}}$ запишем в виде

Приравнивая правые части (2.2) и (2.3), а также учитывая (2.1) найдем скорость гетерогенной смеси двух жидкостей

Очевидно, что

Жидкости состоят из отдельных объемов. Поэтому элементарная площадь $\Delta {{S}_{i}}$ может быть полностью внутри I или II жидкости в промежутке времени $\tau \approx l{\text{/}}\left| {\vec {V}} \right|$, где $l$ – характерный размер объемов жидкостей. Если данный размер существенно меньше, чем характерный размер течения, т.е. $l \ll L$, то и время $\tau $ тоже будет существенно меньше, чем характерное время течения. Следовательно, параметр ${{\alpha }_{i}} = \Delta {{S}_{{1i}}}{\text{/}}\Delta {{S}_{i}}$ имеет флуктуирующий характер. Параметр ${{\alpha }_{i}}$ можно интерпретировать как поверхностную долю первой жидкости в элементарной площадке. Следовательно, соотношение (2.4) можно представить в виде

Рассмотрим теперь турбулентный поток для несжимаемой жидкости. Тогда флуктуациями плотности можно пренебречь. Следуя гипотезе Рейнольдса, скорость турбулентного потока представим в виде суммы осредненной ${{\bar {V}}_{i}}$ и флуктуирующей $v_{i}^{'}$ скоростей

Осреднение скорости здесь проводится по способу Рейнольдса

Здесь $T$ период интегрирования. Введем непульсирующую скорость ${{{v}}_{i}}$, для которой выполняется условие ${\text{|}}{{{v}}_{i}}{\text{|}} = {\text{|}}v_{i}^{'}{\kern 1pt} {{{\text{|}}}_{{\max }}}$ в промежутке времени $t - T{\text{/}}2 < \tau < t + T{\text{/}}2$. Флуктуирующую скорость представим в виде

где, ${{\varphi }_{i}} = \frac{{v_{i}^{'}}}{{{{{v}}_{i}}}}$ флуктуирующая безразмерная функция, которая меняется во времени в пределах $ - 1 < {{\varphi }_{i}} < 1$. Таким образом, скорость ${\text{|}}{{{v}}_{i}}{\text{|}}$ можно интерпретировать как амплитуду флуктуирующей скорости. Введем еще один параметр ${{\gamma }_{i}} = ({{\varphi }_{i}} + 1){\text{/}}2$. Тогда (2.9) можно записать в виде

Осредненное по времени значение флуктуирующей скорости должно быть равно нулю, т.е.

Отсюда следует, что ${{\bar {\gamma }}_{i}} = 0.5$. Таким образом, выражение (2.7) можно представить в виде

Опытные наблюдения показывают, что в турбулентном потоке жидкость распадается на отдельные объемы – моли. Эти моли совершают относительное движение. Следовательно, турбулентный поток можно представить, как гетерогенную смесь. Поэтому сравнивая выражения (2.12) и (2.6) можем заключить, что турбулентный поток можно представить в виде гетерогенной смеси из двух жидкостей со скоростями

и поверхностной доли первой жидкости

Следовательно

Из соотношений (2.13) следует, что первая жидкость соответствует более “быстрой”, а вторая жидкость более “медленной” жидкостям, а скорость ${{{v}}_{i}}$ можно рассматривать как относительную скорость жидкостей. Таким образом, флуктуирующий характер скорости в турбулентном потоке вызван относительным движением двух жидкостей и случайными изменениями их поверхностных долей во времени. Следовательно, в турбулентном потоке флуктуирующим параметром являются их поверхностные доли, а не скорости жидкостей, поскольку не существует такой силы, под действием которой объемы жидкостей (моли) могут иметь флуктуирующие скорости.

Для дальнейшего исследования введем объемную долю первой жидкости

Здесь $\Delta \Omega $ – элементарный объем, $\Delta {{\Omega }_{1}}$ – объем занимаемый первой жидкостью.

Теперь определим массовую плотность первой жидкости в элементарном объеме

Масса первой жидкости, пересекаемая через элементарную площадь $\Delta {{S}_{i}}$ за время T, определяется интегралом

С другой стороны, данная масса определяется интегралом

Сопоставляя правые части выражений (2.18) и (2.19) получим

Таким образом, представляя турбулентное течение, как смесь двух потоков, уравнения неразрывности для каждой жидкости запишем в виде

Здесь $J$ интенсивность массообмена между жидкостями. После подстановки в данное уравнение скорости из соотношения (2.13) и осреднения по времени получим уравнения

При этом учтена несжимаемость потока, а также, что $\overline \beta = {{\bar {\alpha }}_{j}} = 0.5$. Из систем уравнений (2.22) можно получить

Аналогично запишем для каждой жидкости уравнение движения [14]

Согласно гипотезе Рейнольдса давление жидкости представим в виде суммы осредненного и пульсационного давлений $p = \bar {p} + p{\kern 1pt} '$. Поэтому после осреднения по времени получим

В этих выражениях

Здесь μ – коэффициент динамической вязкости жидкости.

Подставим скорости молей из (2.13) в (2.25), затем сложим эти уравнения. В итоге получим уравнение импульса для осредненного потока

В данном уравнении

Теперь, если в системе (2.25) вычесть из первого уравнения второе, получим уравнение для относительной скорости

Таким образом, систему уравнений для осредненных величин турбулентного потока можно записать

Система (2.29) представляет собой основные уравнения нового двухжидкостного подхода к математическому описанию турбулентности. Как видно из (2.29) уравнение движения для осредненного потока имеет очень похожий вид, что и в осредненном уравнении Рейнольдса. Однако в уравнениях Рейнольдса турбулентные напряжения являются неизвестными. Следовательно, уравнения Рейнольдса незамкнуты, и для замыкания необходимо привлечь различные гипотезы. Что касается нового двухжидкостного подхода, то он дает замкнутую систему уравнений (2.29). Принципиальная разница двух подходов в том, что они основываются на различных концепциях. Подход Рейнольдса базируется на двух гипотезах: 1) скорость турбулентного потока состоит из осредненной и флуктуирующей скоростей; 2) турбулентный поток описывается уравнением Навье–Стокса. Приведенных условий оказывается недостаточным для описания турбулентности, поскольку на основе первой гипотезы вводятся две неизвестные скорости, а используется только одно уравнение. Первую гипотезу Рейнольдса на сегодняшний день можно считать экспериментально подтвержденной. Что касается второй гипотезы, то она не совсем очевидная, в силу того, что уравнение Навье–Стокса представляет собой “точную” модель ламинарного потока.

Для двухжидкостного подхода основными условиями являются первая гипотеза Рейнольдса и то, что в турбулентном потоке жидкость разбивается на отдельные объемы (моли), которые совершают относительное движение. В работе на основе этих условий математически показано, что турбулентный поток можно представить, как гетерогенную смесь двух жидкостей. Следовательно, для двух неизвестных можно записать два уравнения движения – для первой и второй жидкостей, что приводит к замкнутой системе уравнений. Еще одной особенностью двухжидкостной модели является то, что многие параметры турбулентности с большой достоверностью определяются через относительные скорости.

В упомянутой работе одного из авторов [13] подробно приводятся методики определения сил взаимодействия между жидкостями ${{\bar {f}}_{i}}$. Поэтому здесь приведем окончательный их вид

Здесь $2{{\bar {V}}_{i}}\bar {J}$ – сила вызванная массообменом между жидкостями, ${{F}_{{si}}}$ – поперечная сила Сефмена обусловленная сдвиговым полем скорости, ${{F}_{{fi}}}$ – сила трения, ${{F}_{{mi}}}$ – сила возникающая в результате относительного молярного движения жидкостей, $\operatorname{def} (\overline {{\mathbf{V}})} = \sqrt {2{{S}_{{ij}}}} {{S}_{{ij}}}$, ${{S}_{{ij}}} = \frac{1}{2}\left( {\frac{{\partial {{{\bar {V}}}_{i}}}}{{\partial {{x}_{j}}}} + \frac{{\partial {{{\bar {V}}}_{j}}}}{{\partial {{x}_{i}}}}} \right)$ – скорость деформации. Подставляя выражения (2.30) в систему уравнений (2.29) получим следующую систему уравнений для турбулентного потока в новом двухжидкостном подходе

Здесь ${{K}_{f}}$ – коэффициент трения

В данном выражении $d$ – ближайшее расстояние до твердой стенки, ${{\lambda }_{{\max }}}$ – наибольший корень характеристического уравнения

где $A$ матрица и ${\mathbf{\zeta }} = \operatorname{rot} {\mathbf{V}}$.

В тестовых задачах показано, что удовлетворительные результаты получаются при ${{C}_{1}} = 0.7825$, ${{C}_{2}} = 0.306$, ${{C}_{s}} = 0.2$.

Необходимо отметить, что при моделировании движения твердой фазы, как было отмечено выше, силой Сеффмена пренебрегается, поскольку плотность материала твердых включений намного больше, чем плотность газовой фазы. Поэтому твердые частицы в силу своей инертности не чувствительны к этой силе. А для движения газовой или жидкой фазы сила Сеффмена [15] играет решающую роль для возникновения турбулентного перемешивания. Например, при обтекании плоской пластины поперечное движение жидкостей обусловлено именно этой силой. О существовании такой силы упоминал еще Сполдинг в своей двухжидкостной модели. Эта сила достаточно хорошо изучена как в теоретическом, так и в экспериментальном плане.

3. Математическое моделирование двухфазного потока на основе новой двухжидкостной модели турбулентности. Для описания двухфазного потока в центробежном сепараторе систему уравнений новой двухжидкостной модели (2.31) запишем в цилиндрических координатах. Тогда полная система уравнений двухфазного потока (1.1) будет иметь вид

Для определения коэффициента трения ${{K}_{f}}$ составим матрицу $A$

Решением характеристического уравнения (2.33) для составленной матрицы будет

Из полученных решений находим наибольший вещественный корень

Еще одним неизвестным и очень важным параметром в системе (3.1) является коэффициент турбулентной диффузии частиц ${{D}_{p}}$. Согласно кинетической теории данный коэффициент определяется по формуле

Здесь ${{V}_{{отн}}}$ относительная скорость твердой фракции, ${{l}_{p}}$ – длина пути перемешивания концентрации частиц. В рамках двухжидкостной модели турбулентности твердые фракции содержатся как в первой, так и во второй жидкостях, а, так как эти жидкости имеют относительную скорость, то и твердые частицы, содержащихся в них, также совершают относительное движение. В первом приближении, для не очень крупных частиц, их относительные скорости можно считать равными относительным скоростям жидкости

В классической теории турбулентности делается гипотеза о пропорциональности длины пути перемешивания концентрации ${{l}_{p}}$ и длины пути перемешивания импульса $l$

Здесь ${{\operatorname{Sc} }_{t}} = 0.8$ – турбулентное число Шмидта. Т.к. относительные скорости частиц и жидкости одинаковые, то будут одинаковыми и их длины пути перемешивания импульсов. Ранее [13] на основе теории пути перемешивания Прандтля предложено соотношение

Подставляя полученные результаты в (3.2) найдем коэффициент диффузии

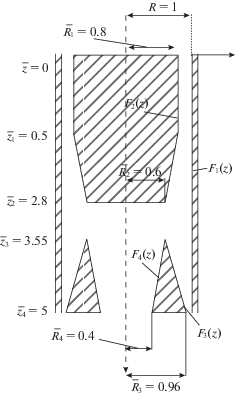
Для исследования стационарного решения динамики двухфазного потока применен метод установления, т.е. решаются нестационарные уравнения, и стационарное решение достигается при достаточно большом количестве итерации по времени. Для всех рассматриваемых моделей турбулентности в качестве начального условия задавалось решение уравнений Эйлера для однофазного потока. На твердых поверхностях ставились условия прилипания, на входе в сепаратор параметры потока задавались, а на выходе воздуха и в бункере использовалась экстраполяция второго порядка точности. Численное решение представленных систем уравнений проводилось в физических переменных скорость–давление [16]. Для конвективных членов использовался метод контрольного объема. Коррекция давления на скорости потока проводилась процедурой SIMPLEC. Для конечно-разностной аппроксимации исходных уравнений использована двухшаговая неявная схема Писмена–Ракфорда [17]. Для численного исследования течения двухфазного потока в сепараторе, область течения была разделена на 4 участка. Безразмерная схема расчетной области сепаратора показана на рис. 3.

Для численной реализации уравнений расчетная область приведена к прямоугольным областям. Для этого произведена замена переменных (z, r) на (ξ, η), где ξ = z, а вторая переменная определялась из соотношений

Как было сказано выше при обезразмеривании все длины были соотнесены к радиусу корпуса сепаратора, который в экспериментальной установке был равен $R = 125$ мм. Опыты проводились при следующих значениях параметров потока на входе в коаксиальный канал: ${{U}_{{\operatorname{ref} }}} = 5.5$ м/с, $V = 0$, ${{W}_{0}} = 4.7$ м/с, ${{\rho }^{0}} = 7000$ кг/м³. Здесь ${{U}_{{\operatorname{ref} }}}$ – средняя продольная скорость на входе, ${{W}_{0}}$ – средняя тангенциальная скорость, ${{\rho }^{0}}$ – плотность материала твердой фазы. В новой двухжидкостной модели относительные скорости жидкостей имели значения $u = 0.01$, $v = 0$, $w = 0$. Численные расчеты показали, что результаты слабо зависят от входных условий для относительных скоростей. Суммарная плотность твердой фазы на входе была равна ${{\rho }_{m}} = 18$ г/м³ и распределена по сечению однородно.

Несложно определить, что число Рейнольдса на входе по отношению к радиусу корпуса сепаратора имеет небольшое значение Re = 3820. Следовательно, толщина вязкого подслоя турбулентного потока имеет значительный размер и можно использовать довольно грубую расчетную сетку без сгущения около стенок. Поэтому в работе вязкий слой рассчитывался напрямую без использования пристеночных функций, т.к. все тестируемые в работе модели являются низкорейнольдсовыми. Численные результаты получены для расчетной сетки 100 × 100. Численные эксперименты показали, что сгущение расчетных ячеек в два раза приводило к изменениям не более 2%, но зато значительно увеличивало время расчета.

Лабораторный эксперимент был проведен для порошка цинка. Массовый состав частиц цинка по размерам приведен в таблице 1, который разделен на пять фракций.

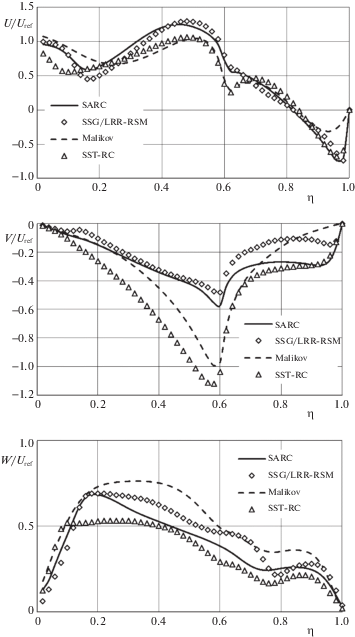
4. Обсуждение результатов. На рис. 4 иллюстрируются профили скоростей воздуха в сечении $z = 2$. Здесь $U{\text{/}}{{U}_{{\operatorname{ref} }}}$, $V{\text{/}}{{U}_{{\operatorname{ref} }}}$, $W{\text{/}}{{U}_{{\operatorname{ref} }}}$ безразмерные скорости. Данное сечение соответствует течению в расширяющемся коаксиальном канале.

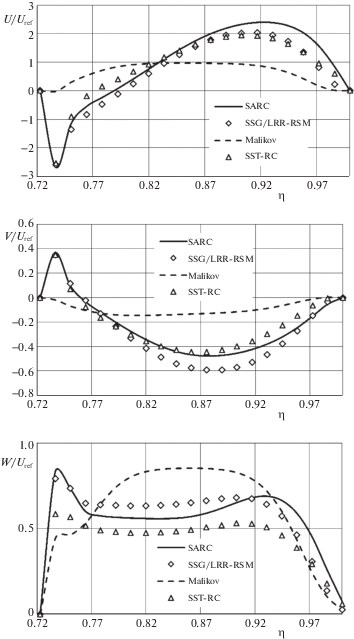
Рис. 4 показывает довольно заметное отличие результатов различных моделей. Особенно сильно различаются результаты RANS-моделей с результатами двухжидкостной модели. Данные различия авторы объясняют тем, что число Рейнольдса в пересчете на ширину коаксиального канала достаточно мало и соответствует переходному режиму от ламинарного к турбулентному. Известно, что для многих моделей турбулентности для расчета переходного режима требуются специальные поправки.

На рис. 5 показаны профили скоростей потока воздуха в сечении $z = 3.5$. Из рисунка видно, что в этом сечении результаты различных моделей качественно совпадают. Это происходит потому, что по всей видимости данное сечение соответствует зоне с наибольшей турбулентностью, что адекватно описывается всеми моделями.

На рис. 6 показаны линии тока осредненных скоростей для всех моделей. По этим линиям тока видно, что модель SSG/LRR-RSM дает большую длину зон рециркуляции как на оси, так и за уступом, по сравнению с расчетом по SARC, SST-RC и двухжидкостной модели.

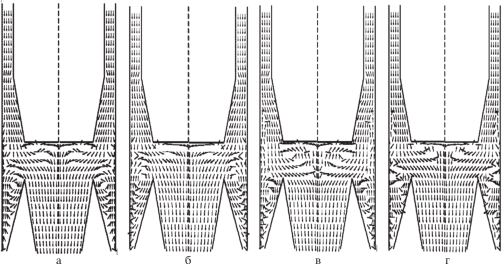
Еще одним отличием в этих картинах течений является циркуляция потока на входе в бункер. Можно заметить, что во всех RANS-моделях эта циркуляция в правой части бункера происходит против, а по результатам двухжидкостной модели по часовой стрелке. Данная циркуляция потока играет большую роль для эффективности сепаратора.

Для оперделения эффективности, а также для оптимизации параметров сепаратора большую информацию дает отслеживание траекторий частиц внутри установки [18–22]. Поэтому в работе кроме систем уравнений (1.1) и (3.1) дополнительно была исследована кинематика твердых частиц. Известно, что для отслеживания траекторий частиц удобным является подход Лагранжа. В лагранжевом подходе уравнения движения для частиц запишем в виде

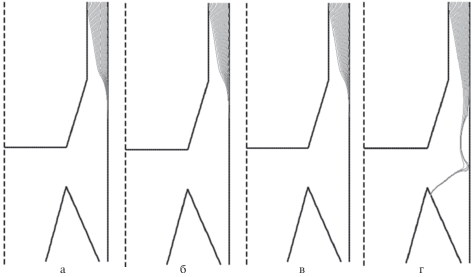
В данной системе уравнений производная в левых частях уравнений является субстанциональной производной. Как видно из этой системы зная поле скоростей несущей газовой фазы можно определить скорости частиц, а по ним и траектории для каждой фракции. Для численной реализации приведенной системы уравнений была использована неявная схема Эйлера с пересчетом. На рис. 7 приведены траектории частиц размером 10 мкм, рассчитанные различными моделями. Из рисунка видно, что все модели предсказывают улавливание частиц размером 10 мкм. Однако по результатам двухжидкостной модели за счет циркуляции потока по часовой стрелке, эти частицы отбрасываются в сторону выхода воздуха.

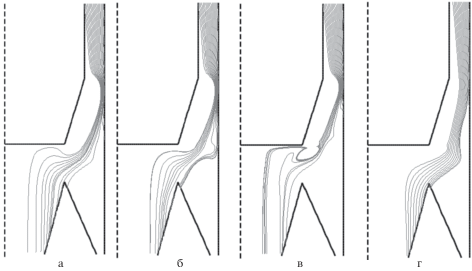
Аналогичная картина траекторий для частиц размером 8 мкм представлена на рис. 8, из которого видно, что по модели SSG/LRR-RSM частицы имеют более сложную траекторию, чем в других моделях.

Как видно из приведенных рисунков путем отслеживания траекторий для каждой фракции твердой фазы можно определить эффективность сепаратора. Поэтому на рис. 9 приведены расчетные графики различных моделей для дисперсного распределения частиц цинка, осевшие в сепараторе. Для сравнения приведено также дисперсное распределение частиц, полученное лазерным анализатором. Анализ проводился для уловленной пыли сепаратором. Видно, что наиболее близкие результаты к опытным данным имеет двухжидкостная модель турбулентности.

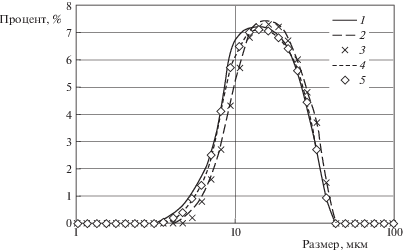
Выводы. Сопоставление численных результатов принципиально различных моделей турбулентности показывает, что они количественно дают разные результаты для параметров газового потока. Однако примерно одинаково предсказывают эффективность центробежного сепаратора. Численная реализация моделей показала, что эти модели имеют различные степени сложности в эксплуатации и требуют различные вычислительные ресурсы. Практически все модели турбулентности, кроме двухжидкостной модели, для устойчивости требовали очень малые шаги интегрирования по времени, что сильно увеличивало вычислительный ресурс. Например, модели SARC и SST-RC интегрировались безразмерным шагом по времени Δt = 10^–4, модель SSG/LRR-RSM шагом Δt = 5 × 10^–5. При незначительном увеличении шагов интегрирования эти модели давали неустойчивые решения. Что касается новой двухжидкостной модели, то она дала хорошие результаты при интегрировании шагом Δt = 10^–3. Кроме того, новая модель достаточно проста в реализации и дала наиболее близкие результаты к экспериментальным данным. Например, по сравнению с громоздкой моделью SSG/LRR-RSM, которая рекомендуется для расчетов течений с сильной закруткой потока, новая двухжидкостная модель оказалась существенно проще. Таким образом, представленный опыт, а также опыт из статьи [13] позволяют предположить, что новая двухжидкостная модель может оказаться эффективной при моделировании и других течений с анизотропной турбулентностью.