Прикладная математика и механика, 2020, T. 84, № 5, стр. 612-624

1. Постановка задачи. Акустический волновод $\Xi \subset {{\mathbb{R}}^{d}}$, $d \geqslant 2$, образован полубесконечными цилиндрами (рукавами)

и центральным ядром $\Theta $ (резонатором) – областью с липшицевой границей $\partial \Theta $ и компактным замыканием $\overline \Theta = \Theta \cup \partial \Theta $ (рис. 1). Система декартовых координат $x = ({{x}_{1}}, \ldots ,{{x}_{d}})$ соотнесена со всем сочленением $\Omega $, а в рукавах (1.1) применяются локальные координаты ${{y}^{n}}$ и ${{z}_{n}}$, поперечные и продольная. Поверхности $\partial {{\varpi }_{n}}$, ограничивающие сечения ${{\varpi }_{n}} \subset {{\mathbb{R}}^{{d - 1}}}$ цилиндров (1.1), также являются компактными и липшицевыми. Масштабированием характерный размер резонатора $\Theta $ сведен к единице, и тем самым декартовы координаты и геометрические параметры сделаны безразмерными.

При частоте $\omega > 0$ гармонических во времени колебаний акустической среды давление $u$ удовлетворяет краевой задаче Неймана для оператора Гельмгольца

Здесь $\nabla = \operatorname{grad} $, $\Delta = \nabla \cdot \nabla $ – оператор Лапласа и ${{\partial }_{\nu }}$ – производная вдоль внешней нормали, определенная почти всюду на поверхности $\partial \Xi $, липшицевой по предположению. Обобщенная формулировка задачи (1.2), (1.3) сводится к интегральному тождеству [1]

При этом ${{({\kern 1pt} ,)}_{\Xi }}$ – натуральное скалярное произведение в пространстве Лебега ${{L}^{2}}(\Xi )$, а пробные функции ${v} \in C_{c}^{\infty }(\overline \Xi )$ считаются бесконечно дифференцируемыми и имеющими компактные носители потому, что далее изучаются решения, не затухающие на бесконечности, т.е. не попадающие в пространство Соболева ${{H}^{1}}(\Xi )$. Из-за возможных особенностей решений в иррегулярных точках границы $\partial \Xi $ всюду под решениями краевых задач в неограниченной области $\Xi $ понимаем именно функции, удовлетворяющие соответствующим интегральным тождествам вида (1.4).

Проверено [2], что непрерывный спектр оператора задачи (1.4) (или краевой задачи (1.2), (1.3) в случае гладкой границы $\partial \Xi $) занимает замкнутую положительную полуось $\overline {{{\mathbb{R}}_{ + }}} = [0, + \infty )$. Таким образом, при любой частоте $\omega > 0$ в рукавах (1.1) возникают поршневые моды

Нормирующий множитель $a_{n}^{\omega }$, включающий ($d - 1$)-мерный объем ${\text{|}}{{\varpi }_{n}}{\text{|}}$ сечения ${{\varpi }_{n}}$, нужен для придания полезных свойств используемых далее объектам. Согласно классическому принципу излучения Зоммерфельда [2, 3] волна $w_{n}^{{\omega - }}$ приходящая в рукаве ${{\Pi }_{n}}$, а волна $w_{n}^{{\omega + }}$ уходящая на бесконечность.

Основная цель настоящей работы – изучение дифракционных характеристик сочленения $\Xi $ акустических волноводов ${{\Pi }_{1}}, \ldots ,{{\Pi }_{N}}$ на малых частотах, т.е. при $\omega \ll 1$. Далее решение задачи (1.4) или (1.2), (1.3) удобно обозначать ${{u}^{\omega }}$. Полученные асимптотические формулы показывают, что в главном структура матрицы рассеяния в волноводе $\Xi $ зависит только от количества $N$ рукавов и ($d - 1$)-мерного объема (площади при $d = 3$) сечений ${{\varpi }_{n}}$. Какие-либо странности в процессе рассеяния волн происходят только в случаях $N = 1$, $N = 2$ и при одинаковых объемах сечений

2. Матрица рассеяния и главный член ее асимптотики. Акустическое поле, инициированное приходящей в рукаве ${{\Pi }_{m}}$ волной, допускает представление

При этом $\tilde {\zeta }_{m}^{{{\kern 1pt} \omega }}$ – экспоненциально затухающий на бесконечности остаток, а ${{\chi }_{n}}$ – гладкая срезающая функция, служащая для локализации волн в рукаве ${{\Pi }_{n}}$

Коэффициенты $S_{{mn}}^{\omega }$ разложений (2.1) образуют ($N \times N$)-матрицу ${{S}^{\omega }}$, называемую матрицей рассеяния и в силу выбора нормирующих множителей (1.6) являющуюся унитарной и симметричной, но не обязательно эрмитовой (простая проверка этих свойств представлена, например, в статье [4]).

Определим главный член асимптотики матрицы рассеяния

Здесь и далее многоточие заменяет младшие асимптотические члены, не существенные для предпринимаемого формального анализа. Оценки асимптотических остатков будут приведены в разд. 5.

Метод сращиваемых асимптотических разложений [5, 6], ([7], Гл. 2) был приспособлен [4, 8] к исследованию бесконечных волноводов. Применим формулу Тейлора к волнам (1.5)

В итоге внешние разложения решения (2.1) в рукавах (1.1) принимают вид

Множители при ${{\omega }^{{p - 1/2}}}$ предписывают поведение на бесконечности членов внутреннего разложения, пригодного для описания поля $\zeta _{m}^{\omega }$ вблизи резонатора $\Theta $

Ввиду “излишней малости” спектрального параметра ${{\omega }^{2}}$ правой частью уравнения Гельмгольца (1.2) можно пренебречь, и поэтому первые два члена разложения (2.6) суть решения однородных задач Неймана для оператора Лапласа

однако уравнение в задаче для $Z_{m}^{{''}}$ становится неоднородным

При учете слагаемых порядка ${{\omega }^{{ - 1/2}}}$ в соотношении (2.5) получим для решения задачи (2.7) условия на бесконечности

В итоге гармоническая функция $Z_{m}^{0}$ ограничена и, следовательно, равна какой-то постоянной $c_{m}^{0}$, причем в силу формул (2.10) и (1.6) имеем

Выделив в разложении (2.5) члены $O({{\omega }^{{1/2}}})$, видим, что решение $Z_{m}^{'}$ задачи (2.8) нужно подчинить условию

Из-за линейного роста при ${{z}_{n}} \to + \infty $ такая гармоническая функция, обладающая нулевой нормальной производной на поверхности $\partial \Xi $, существует в том и только в том случае, если суммарный поток на бесконечность обращается в нуль, а именно

Иными словами, соотношение (2.13) служит условием существования решения (2.12) задачи (2.9).

В силу формулы (1.6) равенства (2.11) и (2.13) позволяют вычислить постоянную

Следовательно

Для того чтобы описать простейшие свойства матрицы ${{S}^{0}}$ с элементами (2.16) введем ортогональный проектор $P$ и диагональную матрицу $B$

Здесь $I$ и $E$ – матрицы размером $N \times N$, соответственно единичная и составленная из ${{N}^{2}}$ единиц, а след $\operatorname{tr} {{B}^{2}}$ матрицы ${{B}^{2}} = \operatorname{diag} {\kern 1pt} {\text{\{ }}\left| {{{\varpi }_{1}}} \right|, \ldots ,\left| {{{\varpi }_{N}}} \right|{\text{\} }}$ совпадает с величиной (2.15). Итак, матрица ${{S}^{0}}$ приобретает вид

и является ортогональной (вещественной унитарной), так как $E{{B}^{2}}E = E\operatorname{tr} {{B}^{2}}$ и

При этом $({{S}^{0}}){\kern 1pt} *$ – сопряженная для ${{S}^{0}}$ матрица, совпадающая с транспонированной ${{({{S}^{0}})}^{{\rm T}}}$ ввиду вещественности ${{S}^{0}}$, т.е. ${\rm T}$ – знак транспонирования.

Матрица (2.18) имеет собственные числа –1 и 1, причем первое простое и ему отвечает собственный вектор

Кратность второго собственного числа равна $N - 1$ и $P{{\mathbb{R}}^{N}}$ – соответствующее собственное подпространство.

3. Матрица поляризации и поправочный член асимптотики. Задача Неймана для уравнения Лапласа

помимо постоянного решения ${{Y}_{0}}(x) = 1$ обладает решениями ${{Y}_{1}}, \ldots ,{{Y}_{N}}$ с линейным ростом на бесконечности и остатками ${{\tilde {Y}}_{m}}$, экспоненциально затухающими при ${\text{|}}x{\text{|}} \to \infty $. У каждого из решений (3.2) суммарный поток на бесконечность обращается в нуль (ср. выкладку (2.13)). Таким образом, правая часть уравнения Пуассона в задаче Неймана для остатка ${{\tilde {Y}}_{m}}$ имеет компактный носитель ${{\Upsilon }_{m}}$ и нулевое среднее по множеству ${{\Upsilon }_{m}}$, а значит, гармонические функции ${{Y}_{m}}$ действительно существуют и их поведение при ${{z}_{n}} \to \infty $ выясняется при помощи метода Фурье.

Решения (3.2) ищем в виде

Правая часть

уравнения Пуассона в задаче Неймана для слагаемого ${{\hat {Y}}_{m}}$ суммы (3.3) имеет компактный носитель и нулевое среднее по $\Xi $

Следовательно, существует решение задачи (3.3) с конечным интегралом Дирихле, которое согласно методу Фурье ограничено и стабилизируется в рукавах ${{\Pi }_{n}}$ к некоторым постоянным ${{M}_{{mn}}}$. Поскольку решение ${{\hat {Y}}_{m}}$ определено с точностью до постоянного слагаемого, можно соблюсти равенства

Итак, матрица $M = ({{M}_{{mn}}})$ размером $N \times N$, составленная из коэффициентов в разложениях (3.2) и называемая матрицей поляризации, удовлетворяет соотношению

Функции (3.2) линейно зависимы. В самом деле, сумма ${{Y}_{1}} + \ldots + {{Y}_{N}}$ ограничена в $\Xi $, т.е. является постоянной, причем равенства (3.4) обеспечивают тождество

Введем ортогональный проектор

и заметим, что матрица поляризации осуществляет взаимно однозначное отображение

При этом

Кроме того, матрица поляризации симметрична, так как в силу формулы Грина и соотношений (3.4) имеем

Из решений (3.2) и ${{Y}_{0}}(x) = 1$ задачи (3.1) соорудим решение $Z_{m}^{'}(x)$ задачи (2.8), (2.12). С этой целью удобно использовать запись

и интерпретировать ее как разложение столбца функций ${\mathbf{G}} = ({{G}_{1}}, \ldots ,{{G}_{N}}{{)}^{{\rm T}}}$

Здесь $T = ({{T}^{1}}, \ldots ,{{T}^{N}})$ – числовая ($N \times N$)-матрица со столбцами ${{T}^{n}} \in {{\mathbb{C}}^{N}}$, $g = ({{g}_{1}}, \ldots ,{{g}_{N}}{{)}^{{\rm T}}}$ – столбец функций переменных ${{z}_{n}}$, а ${\mathbf{\tilde {G}}}$ – столбец экспоненциально затухающих остатков. В результате формулы (2.12) и (3.2) принимают вид

Введены обозначения ${\mathbf{z}} = ({{z}_{1}}, \ldots ,{{z}_{N}}{{)}^{{\rm T}}}$ и ${\mathbf{1}} = (1, \ldots {{,1)}^{{\rm T}}}$.

Сравнивая разложения (3.8) и (3.9), находим, что

Здесь $C{\kern 1pt} ' = \operatorname{diag} {\kern 1pt} \{ C_{1}^{'}, \ldots ,C_{N}^{'}\} $ – неизвестная числовая диагональная матрица. В силу соотношения (3.5) при любом $x \in \Xi $ справедливо включение ${\mathbf{Y}}(x) \in Q{{\mathbb{R}}^{N}}$. Следовательно, выражение ${{Q}^{{ - 1}}}{\mathbf{Y}}$ определено корректно и, кроме того, множитель ${{Q}^{{ - 1}}}$ можно не писать, так как сужение проектора $Q$ на подпространство $Q{{\mathbb{R}}^{N}}$ – тождественное отображение. Наконец, ${{Q}^{{ - 1}}}M = M$ согласно формуле (3.7).

Итак, соотношения (3.8)–(3.10) дают равенство

Для определения последнего слагаемого нужно было бы построить следующий член ${{\omega }^{2}}S{\kern 1pt} ''$ разложения (2.3). Точно так же для вычисления главного члена (2.18) потребовалась первичная информация о коэффициентах представления (2.12) асимптотических поправок $Z_{m}^{'}$ в разложениях (2.6).

4. Упрощенная постановка: второй поправочный член. В предыдущих разделах был построен главный член асимптотики (2.3) матрицы рассеяния, достаточный для целей данной работы. Закончим построение поправочного члена (3.11) в предположении (1.7), которое упомянуто в разд. 1 и будет принято в разд. 6 при обсуждении аномалий рассеяния. В этом случае формулы (3.6), (2.17) и (2.14), (2.18) принимают вид

Соотношения (1.7) и (3.7) обеспечивают равенство

Таким образом, в формуле (3.11) для поправочного члена $\omega S{\kern 1pt} '$ нужно найти лишь диагональную матрицу $C{\kern 1pt} '$.

В отличие от гармонических функций $Z_{m}^{0}$ и $Z_{m}^{'}$ третий член $Z_{m}^{{''}}$ разложения (2.6) – решение неоднородной задачи Неймана (2.9). Ищем его в виде

Остаток $\ddot {Y}_{m}^{{''}}(x)$ исчезает на бесконечности с экспоненциальной скоростью, ${{c}^{0}}$ – величина (4.2), ${{Y}_{1}}, \ldots ,{{Y}_{N}}$ и ${{Y}_{0}} = 1$ – введенные в разд. 3 решения задачи (3.1), а ${{\chi }_{n}}$ – срезающие функции (2.2). Присутствие в сумме (4.5) слагаемых ${{Y}_{m}}$ с разложениями (3.2) и произвол в выборе коэффициентов ${{K}_{1}}, \ldots ,{{K}_{N}}$, образующих матрицу $K = \operatorname{diag} \{ {{K}_{1}}, \ldots ,{{K}_{N}}\} $, позволили ввести одинаковый множитель (4.2) при ${{z}_{n}}$ в асимптотике (4.6) на каждом из рукавов ${{\Pi }_{1}}, \ldots ,{{\Pi }_{N}}$.

Постоянные слагаемые $M_{{mn}}^{{''}} \in \mathbb{R}$ далее не понадобятся, а множитель $c_{m}^{{''}}$ в линейных членах вычисляется при помощи формулы Грина

При этом

Следовательно, при учете формулы (2.14) получим

Согласно разложениям (2.5) и (2.6) решениям $Z_{m}^{{''}}$ задачи (2.9) предписано такое поведение на бесконечности:

Сравнивая соотношения (4.5), (3.3), (4.6) и (4.8), находим

Теперь при учете формул (3.11), (4.1), (4.4), (4.6) и (4.7) получим

Соотношение (4.9) позволяет вычислить и коэффициенты ${{K}_{1}}, \ldots ,{{K}_{N}}$ представления (4.5), однако явное выражение для них не понадобится.

5. Полные асимптотические ряды и обоснование асимптотики. Построение асимптотики матрицы рассеяния можно продолжить и вычислить коэффициенты формального ряда

В рамках метода сращиваемых разложений (см. [5, 6] и др.) скорость полиномиального роста решений предельной задачи (3.1) неограниченно возрастает от шага к шагу итерационного процесса, что делает сопутствующие рассуждения и выкладки излишне сложными и громоздкими. Поэтому более удобно применить метод составных разложений (см. [7, 9] и др.) и искать представление решения (2.1) в виде суммы формальных рядов

Алгоритм определения членов $\tilde {Z}_{m}^{{{\kern 1pt} (j)}}$ и $S_{{mn}}^{{(j)}}$ весьма прост: волны (1.5) раскладываются в ряды Тейлора (ср. формулы (2.4) и (2.5)), а функции $\tilde {Z}_{m}^{{{\kern 1pt} (j)}}$ служат для компенсации невязок, возникающих вследствие умножения названных волн на срезки (2.2), и приобретают экспоненциальное затухание при ${\text{|}}x{\text{|}} \to + \infty $ в результате подбора коэффициентов $S_{{mn}}^{{(j)}}$. При этом условия существования решения ${{u}^{0}} \in {{H}^{1}}(\Xi )$ неоднородной задачи (3.1)

принимают вид

В силу соотношения (3.5) условия ортогональности (5.4) с индексами $q = 1, \ldots ,N$ линейно зависимы, и поэтому формулы (5.4) фиксируют только $N$ связей и позволяют поочередно вычислить коэффициенты $S_{{mn}}^{{(j)}}$.

Обоснование асимптотических разложений проводится при помощи техники весовых пространств с отделенной асимптотикой [4, 8]. Обозначим $W_{\beta }^{1}(\Xi )$ пространство Кондратьева [10], полученное пополнением линейного множества $C_{c}^{\infty }(\overline \Xi )$ (бесконечно дифференцируемые функции с компактными носителями) по весовой соболевской норме

Пространство $W_{{\beta ,\omega }}^{1}(\Xi )$ составлено из функций

и снабжено гильбертовой нормой

Коэффициент ${{\omega }^{{1/2}}}$ при $\left\| {{{{\ddot {u}}}^{\omega }};W_{\beta }^{1}(\Xi )} \right\|$ учитывает наличие большого множителя $a_{n}^{\omega } = O({{\omega }^{{ - 1/2}}})$ в волнах (1.5) и тем самым уравнивает вклады слагаемых суммы (5.5) в составную норму (5.6).

Поскольку разложение (5.5) поля ${{u}^{\omega }} \in W_{{\beta ,\omega }}^{1}(\Xi )$ включает только уходящие в рукавах ${{\Pi }_{n}}$ волны $w_{n}^{{\omega + }}$ и исчезающий на бесконечности c экспоненциальной скоростью остаток ${{\ddot {u}}^{{{\kern 1pt} \omega }}}$, интегральное тождество

отвечает постановке условий излучения Зоммерфельда в задаче (5.3). При этом $F$ – линейный непрерывный функционал на пространстве $W_{{ - \beta }}^{1}(\Xi )$, принадлежащий сопряженному пространству $W_{{ - \beta }}^{1}(\Xi ){\kern 1pt} *$, например

Проверено [11, Гл. 5], [4, 8], что существует зависящее от области $\Xi $ число ${{\beta }_{\Xi }} > 0$, для которого при $\beta \in (0,{{\beta }_{\Xi }})$ оператор задачи (5.7)

осуществляет изоморфизм, причем его норма и норма обратного не превосходят $c{\kern 1pt} {{\omega }^{{ - 1/2}}}$.

Обоснование асимптотики (5.1) матрицы рассеяния ${{S}^{\omega }}$ проводится по стандартной схеме [4, 8]. Зафиксируем натуральное число $J$ и в качестве приближения $\zeta _{m}^{{\omega as}}$ к функции $\zeta _{m}^{\omega }$ возьмем частичные суммы рядов (5.2) (ограничиваем суммирование по $j = 0,1, \ldots ,J$). По построению функция $\zeta _{m}^{{\omega as}}$ оставляет малую невязку порядка ${{\omega }^{{J - 1/2}}}$ в задаче (1.2), (1.3), так что правая часть ${{F}^{{(j)}}}$ интегрального тождества вида (5.7) для разности $\zeta _{m}^{\omega } - \zeta _{m}^{{\omega as}}$, освободившейся от приходящей волны $w_{m}^{{\omega - }}$, удовлетворяющей условиям излучения Зоммерфельда и потому принадлежащей пространству $W_{{\beta ,\omega }}^{1}(\Xi )$, выполнено соотношение

В результате упомянутая оценка нормы обратного оператора ${{A}_{\beta }}{{(\omega )}^{{ - 1}}}$ дает неравенство

Норма (5.6) включает модули коэффициентов рассеяния, а значит, неравенство (5.8) влечет за собой искомую оценку

Понижение степени малого параметра $\omega $ на единицу в мажоранте (5.9) означает, что в сумме присутствует “лишний” член ${{\omega }^{J}}{{S}^{{(J)}}}$, который следует присоединить к остатку. Точно так же в разд. 2 для вычисления главного члена (2.18) асимптотики матрицы рассеяния потребовалось обследовать основную поправку $\omega S{\kern 1pt} ' = \omega {{S}^{{(1)}}}$.

6. Аномалии Вайнштейна. Явные формулы [12] для акустического поля в полубесконечной цилиндрической круговой трубе, открытой в пространство ${{\mathbb{R}}^{3}}$, указывают на эффект “почти полного” отражения волны, приходящей с бесконечности в трубе. Такое необычное поведение волн на околопороговых частотах можно смоделировать слабопроницаемой мягкой стенкой Неймана (третье краевое условие с большим множителем $O({{\omega }^{{ - 1}}})$ при производной ${{\partial }_{z}}$).

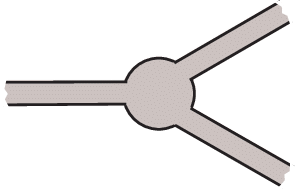
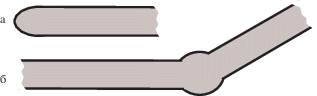
Похожие, но несколько другие эффекты обнаружены [13, 14] в цилиндрическом волноводе с резонатором и одним или двумя рукавами (рис. 2, а и б). Формулы (2.11) для главных членов асимптотики матрицы рассеяния позволяют сделать выводы о рассеянии волн в волноводах с разным количеством рукавов (рис. 1). Для упрощения дальнейших формул предположим, что все сечения одинаковы ${{\varpi }_{1}} = \ldots = {{\varpi }_{N}}$ и, следовательно, верны формулы (1.7) и (4.1)–(4.3).

1°. В случае $N = 1$ имеем

Разумеется, в акустическом волноводе с одним рукавом, ограниченном жесткими стенками, реализуется полное отражение приходящей с бесконечности волны – в конце волновода располагается жесткая стенка (краевое условие Неймана). Формула (6.1) означает, что коэффициент отражения $S_{{11}}^{\omega } = {{e}^{{i{{\psi }_{\omega }}}}}$ имеет фазу ${{\psi }_{\omega }} = 2\omega {{\left| \varpi \right|}^{{ - 1}}}\left| \Theta \right| + O(\omega 2)$, найденную при учете представлений (4.3) и (4.10), так как $M = {{M}_{{11}}} = 0 \in \mathbb{R}$.

2°. В случае $N = 2$ волновод $\Xi $, прямой или изломанный (рис. 2, а), характеризуется ($2 \times 2$)-матрицей рассеяния, которая согласно соотношениям (5.9) и (4.1) принимает вид

Итак, в рассматриваемом волноводе происходит почти “полное прохождение” волн. Этот эффект следует связать с инвертированной аномалией Вайнштейна. Если отказаться от требования (1.7), то согласно формуле (2.16) матрица рассеяния принимает вид

и эффект почти полного прохождения волны исчезает.

3°. При $N = 3$ для волновода $\Xi $ (рис. 1) выполнено соотношение

Таким образом, волна проникает во все рукава сочленения $\Xi $ в значительной мере. Такой же вывод получается при большем количестве рукавов.

4°. Гипотетический случай $N = \infty $ с большой натяжкой можно ассоциировать с упомянутой задачей Вайнштейна [12] о полубесконечной трубе, которая открыта в пространство, образованное бесконечным количеством цилиндрических волноводов. При этом формула (2.11) с $m = 1$ показывает, что $S_{{11}}^{\omega } = - 1$, т.е. реализуется прямая аномалия Вайнштейна, а выделенный рукав ${{\Pi }_{1}}$ у основания $\{ x:{{y}^{1}} \in {{\varpi }_{1}}$, ${{z}_{1}} = 0\} $ перекрыт малопроницаемой мягкой стенкой. Эти выводы конечно же условны.

Формулы (4.3) и (4.10) с повышенной точностью $O({{\omega }^{2}})$ описывают почти одинаковую картину рассеяния волны $w_{m}^{{\omega - }}$, приходящей с бесконечности в разных рукавах ${{\Pi }_{m}}$ волновода $\Xi $. Рассеяние волны можно условно разбить на два процесса. В первом волна $w_{m}^{{\omega - }}$ отражается от ядра $\Theta $ как от мягкой стенки, т.е. с сохранением фазы и изменением знака амплитуды на противоположный. Во втором в каждом из рукавов ${{\Pi }_{n}}$, $n = 1, \ldots ,N$, возникает уходящая волна с уменьшенной в $N{\text{/}}2$ раз амплитудой и слабым искажением фазы

Суммарные амплитуды волн определяются в главном лишь количеством рукавов у волновода, но фазы – также другими характеристиками, в частности, матрицей поляризации $M$, введенной в разд. 3. Только при ограничении (1.7) и в частных случаях $N = 1$ или $N = 2$ рассеяние волн трактуется как аномалия Вайнштейна, связанная с почти полными отражением или прохождением волны.

5°. На физическом уровне строгости приближенные формулы (6.2) и (6.3) могут быть получены при помощи простейшей одномерной модели. Сделаем замену координат $x \mapsto \xi = {{\omega }^{{ - 1/2}}}x$, т.е. превратим рукава (1.1) в тонкие, с сечениями диаметром $O({{\omega }^{{ - 1/2}}})$, цилиндры, сочленение $\Xi $ в область ${{\Xi }^{\omega }} = \{ \xi :{{\omega }^{{1/2}}}\xi \in \Xi \} $ и тем самым исключим малый параметр $\omega $ из уравнения Гельмгольца (1.2). Акустическое поле ${{u}^{\omega }}(x)$, записанное в координатах $\xi $, обозначим ${{u}^{\omega }}(\xi )$, и получим для него задачу

Первичный асимптотический анализ ([7], Гл. 5) задачи (6.4) на сочленении тонких областей предоставляет совокупность обыкновенных дифференциальных уравнений

с классическими условиями Кирхгофа

При выполнении соотношений

функции служат решениями одномерной задачи (6.5), (6.6) и одновременно дают главные члены асимптотики решения (2.1) многомерной задачи (1.2), (1.3). Коэффициенты $S_{{mn}}^{0}$, найденные из алгебраической системы (6.7), суть главные члены матриц рассеяния при любом $N$ (ср. формулы (6.1)–(6.3) при $N = 1,2,3$).

Полученные тем или иным образом первые члены асимптотики (2.3) матрицы ${{S}^{\omega }}$ показывают, что на малых частотах в главном матрица рассеяния не зависит от глобальной геометрии сочленения цилиндрических волноводов, но только от площадей их сечений ${{\varpi }_{n}}$. В то же время найденные поправочные члены (4.9) в анзаце (2.3) включают и другие характеристики: объем ${\text{|}}\Theta {\text{|}}$ ядра $\Theta $ сочленения $\Xi $ и, что особенно важно, матрицу поляризации $M$. Именно последняя зависит не только от скалярных величин $\left| \Theta \right|$ и $\left| {{{\omega }_{1}}} \right|, \ldots ,\left| {{{\omega }_{N}}} \right|$, но и от общей формы волновода $\Xi $.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 17-11-01003).