Прикладная математика и механика, 2020, T. 84, № 6, стр. 709-720
О численном моделировании фильтрации воды при околокритических условиях
1 Научно-исследовательский институт механики МГУ им. М.В. Ломоносова
Москва, Россия
* E-mail: afanasyev@imec.msu.ru
Поступила в редакцию 15.04.2020
После доработки 21.09.2020
Принята к публикации 25.09.2020
Аннотация
Рассмотрена проблема численного моделирования неизотермических течений воды и пара в пористой среде при околокритических термодинамических условиях. Показано, что уравнения однофазной и двухфазной фильтрации вырождаются в критической точке воды. Обсуждаются недостатки методов расчета течений, позволяющих исключить вырождение с помощью выбора давления и энтальпии в качестве независимых переменных модели. Предложен новый метод расчета при околокритических термодинамических условиях в стандартных переменных давление–температура. В основе метода лежит приближенное описание фазовой диаграммы жидкости линейными сплайнами, которое позволяет исключить вырождение законов сохранения в критической точке и использовать уравнения состояния, задающие свойства жидкости в зависимости от давления и температуры.
1. Введение. Течения в геологических пористых средах часто сопровождаются усложненными термодинамическими равновесиями насыщающих жидкостей и газов [1, 2]. Например, при фильтрации воды (H2O) в геотермальных системах могут достигаться критические давление (${{P}_{с}} = 220.9$ бар) и температура (${{T}_{с}} = 647$ K), при которых плотность, энтальпия и другие параметры жидкости и пара быстро изменяются в зависимости от $P$ и $T$. Причем, в пределе $P \to {{P}_{c}}$, $T \to {{T}_{c}}$ выполняются условия [3]
(1.1)
${{\left. {\frac{{\partial \rho }}{{\partial P}}} \right|}_{T}} \to \infty ,\quad {{\left. {\frac{{\partial h}}{{\partial T}}} \right|}_{P}} \to \infty ,$Рис. 1.
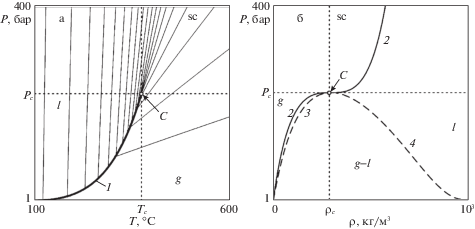
Фазовая диаграмма H2O. Кривая 1 – линия термодинамического равновесия пар–жидкость. Линии уровня – изохоры с шагом 50 кг/м3 (а). Кривые 2–4 – плотность H2O при $T = {{T}_{c}}$, а также плотности пара и воды в термодинамическом равновесии, соответственно (б). Символами $\operatorname{g} $, $l$, $\operatorname{sc} $ и ${\text{g}}{\kern 1pt} - {\kern 1pt} l$ обозначены области пара, воды, сверхкритической жидкости и двухфазных состояний пар–вода.
Учитывая накопленный в прикладных термодинамических расчетах опыт создания уравнений состояния в переменных ${\mathbf{X}}$ (например, уравнения состояния типа Ван-дер-Ваальса [3]), актуально развитие методов расчета фильтрации при околокритических параметрах именно в этих переменных. Для создания таких методов необходимо решить отмеченную проблему вырождения уравнений модели, что позволит использовать существующие отлаженные подходы для расчета теплофизических свойств смесей при заданных $P$ и $T$ и, следовательно, расширить область приложения моделей фильтрации.
В настоящей работе на примере однокомпонентных течений H2O дан обзор проблем расчета фильтрации в переменных ${\mathbf{X}}$ и недостатки их решения с помощью переформулирования модели в переменных ${\mathbf{Y}}$. Кратко описывается с чем именно связано вырождение уравнений фильтрации при ${\mathbf{X}} \to {{{\mathbf{X}}}_{c}}$, где ${{{\mathbf{X}}}_{c}} = \left\{ {{{P}_{c}},{{T}_{c}}} \right\}$. Предложена идея нового метода расчета фильтрации в переменных ${\mathbf{X}}$, позволяющего обойти вырождение и, следовательно, использовать существующие уравнения состояния.
2. Основные уравнения. Неизотермическая фильтрация H2O описывается следующей системой уравнений [4–6]:
(2.1)
${{\partial }_{t}}{{R}_{j}} + \nabla \cdot \left( {{{{\mathbf{Q}}}_{j}} + {{{\mathbf{\Psi }}}_{j}}} \right) = 0,\quad j = m,e$(2.2)
$\begin{gathered} {{R}_{m}} = \phi \sum {{{\rho }_{i}}{{s}_{i}}} ,\quad {{R}_{e}} = \phi \sum {{{\rho }_{i}}{{e}_{i}}{{s}_{i}}} + (1 - \phi ){{\rho }_{r}}{{e}_{r}} \\ {{{\mathbf{Q}}}_{m}} = \sum {{{\rho }_{i}}{{{\mathbf{w}}}_{i}}} ,\quad {{{\mathbf{Q}}}_{e}} = \sum {{{\rho }_{i}}{{h}_{i}}{{{\mathbf{w}}}_{i}}} \\ \end{gathered} $(2.3)
${{{\mathbf{w}}}_{i}} = - K\frac{{{{K}_{{ri}}}}}{{{{\mu }_{i}}}}\left( {\nabla P - {{\rho }_{i}}{\mathbf{g}}} \right),\quad i = 1,2,$Насыщенности фаз удовлетворяют следующему соотношению
Тогда, обозначив $s \equiv {{s}_{1}}$, имеем ${{s}_{2}} = 1 - s$.
Число фаз $p$ не превосходит 2. При $p = 1$ H2O находится в однофазном состоянии пара, воды или сверхкритической жидкости (области $g$, $l$ и $sc$ на рис. 1а), а параметры фазы $i = 2$ (${{\rho }_{2}}$, ${{e}_{2}}$, ${{h}_{2}}$, ${{\mu }_{2}}$) не определены. Они сокращаются в уравнениях (2.1)–(2.3), так как ${{s}_{2}} = 0$. При $p = 2$ H2O находится в двухфазном термодинамическом равновесии пар–вода ($g - l$). В этом случае $P$ и $T$ связаны соотношением [5, 6]
где ${{T}_{f}}$ – температура кипения воды при давлении $P$. Для определенности предполагается, что в двухфазных равновесиях индекс $i = 1$ в уравнениях (2.1)–(2.4) соответствует пару, а $i = 2$ – воде.На плоскости $\left\{ {P,T} \right\}$ уравнение (2.5) задает кривую термодинамического равновесия между паром и водой (рис. 1а, кривая 1). Правее этой кривой, при низких $P$ и высоких $T$, H2O находится в однофазном состоянии пара ($g$), а левее – при высоких $P$ и низких $T$ – в однофазном состоянии жидкости ($l$). Двухфазные состояния ($g - l$) возможны только при $P$ и $T$, принадлежащих линии (2.5). При возрастании $P$ и $T$ кривая (2.5) обрывается в критической точке $C$ при $P = {{P}_{c}}$, $T = {{T}_{c}}$ (${{T}_{c}} = {{T}_{f}}({{P}_{c}})$). При $P > {{P}_{c}}$ и $T > {{T}_{c}}$ H2O находится в однофазном состоянии сверхкритической жидкости ($\operatorname{sc} $).
Теплофизические параметры H2O задаются следующими тремя функциями давления и температуры:
для которых кривая (2.5) является линией разреза. На линии (2.5) при $P < {{P}_{c}}$ и $T < {{T}_{c}}$ функции (2.6) принимают два значения, первое из которых соответствует пару ($i = 1$), а второе – воде ($i = 2$). При $p = 2$ оба этих значения используются для замыкания уравнений переноса (2.1)–(2.3). При любых $P$ и $T$, не принадлежащих кривой (2.5), единственное значение каждой из функций (2.6) используется для замыкания уравнений переноса (2.1)–(2.3) при $p = 1$. Значения функций (2.6) могут рассчитываться, например, с помощью кубического уравнения состояния [3] или многокоэффициентных корреляций [7]. Удельная внутренняя энергия при данных $P$ и $T$ определяется из (2.6) с помощью соотношения $e = h - {P \mathord{\left/ {\vphantom {P \rho }} \right. \kern-0em} \rho }$.Для определенности предполагается, что скелет пористой среды – несжимаемая среда, внутренняя энергия которой есть линейная функция температуры:
где ${{c}_{r}} = {\text{const}}$ – теплоемкость скелета пористой среды.Функции относительной фазовой проницаемости задаются в виде соотношений
удовлетворяющих следующему условию в точке $C$:(2.9)
${\mathbf{X}} \to {{{\mathbf{X}}}_{c}}{\kern 1pt} :\;\;{{K}_{{ri}}}({{s}_{i}},T) \to {{s}_{i}}$В соотношении (2.8) зависимость ${{K}_{{ri}}}$ от $T$ характеризует изменение поверхностного натяжения между водой и паром при увеличении $T$. Данная зависимость становится существенной при приближении к критической точке $C$, в которой, согласно условию (2.9), относительные фазовые проницаемости должны быть равны соответствующим насыщенностям ${{s}_{i}}$ [4, 8].
Подставляя (2.2)–(2.8) в уравнения (2.1) получим замкнутую систему двух уравнений относительно переменных ${\mathbf{X}} = \left\{ {P,T} \right\}$ при $p = 1$ и ${\mathbf{X}} = \left\{ {P,s} \right\}$ при $p = 2$. Здесь ${\mathbf{X}}$ обозначает независимые переменные, т.е. минимальный набор параметров, распределение которых позволяет восстановить все другие параметры течения. При изменении числа фаз $p$ независимые переменные “переключаются” между $\left\{ {P,T} \right\}$ и $\left\{ {P,s} \right\}$ [5, 6].
2. О конечно-разностной схеме. При численном моделировании фильтрации часто используются полностью неявные конечно-разностные схемы, построенные методом конечных объемов [9]. Для описания проблем, возникающих при моделировании течений при околокритических условиях, рассмотрим расчет на сетке, содержащей всего 2 связанные ячейки $a$ и $b$. Считается, что параметры в ячейке $b$ (${{{\mathbf{X}}}^{b}} = {\text{const}}$) зафиксированы, а изменяются только параметры в ячейке $a$ (${\mathbf{X}}$) из-за перетоков между $a$ и $b$. Подобную постановку расчета можно интерпретировать следующим образом: ячейка $a$ принадлежит расчетной области $\Omega $, граница которой $\partial \Omega $ совпадает с гранью между $a$ и $b$, а ячейка $b$ используется для задания условий Дирихле (фиксированных переменных ${{{\mathbf{X}}}^{b}}$) на $\partial \Omega $. Здесь и далее параметры в ячейке $b$ обозначены верхним индексом $b$, а параметры в ячейке $a$ не имеют верхнего индекса.
Конечно-разностные аналоги законов сохранения (2.1) для ячейки $a$ записываются в виде
где введено обозначение(3.2)
${{B}_{j}} = \left( {{{R}_{j}} - {{R}_{{j,0}}}} \right)V + \left( {Q_{j}^{{ab}} + \Psi _{j}^{{ab}}} \right){{S}^{{ab}}}\tau $Здесь $V$ – объем ячейки, $Q_{j}^{{ab}}({\mathbf{X}},{{{\mathbf{X}}}^{b}})$ и $\Psi _{j}^{{ab}}({\mathbf{X}},{{{\mathbf{X}}}^{b}})$ – конечно-разностные аппроксимации потоков ${\mathbf{Q}}$ и ${\mathbf{\Psi }}$ из $a$ в $b$, вид которых несущественен для дальнейших рассуждений, ${{S}^{{ab}}}$ – площадь грани между ячейками $a$ и $b$, а $\tau $ – шаг по времени. Величины с нижним индексом 0 – параметры с явного ($t = {{t}_{0}}$), а без индекса – с неявного слоя по времени ($t = {{t}_{0}} + \tau $).
По постановке расчета предполагается, что ${\mathbf{X}}_{0}^{{}}$ и ${{{\mathbf{X}}}^{b}}$ заданы, а ${\mathbf{X}}$ – неизвестно. Для определения параметров ${\mathbf{X}}$ необходимо решить систему нелинейных уравнений (3.1). При численном моделировании фильтрации это решение часто ищется итерационным методом Ньютона (методом касательных), основывающемся на линеаризации (3.1) [10]. Учитывая (3.2), линеаризованные уравнения (3.1) запишутся в виде
где введен вектор ${\mathbf{B}} = {{\left\{ {{{B}_{m}},{{B}_{e}}} \right\}}^{T}}$, верхний индекс $T$ обозначает операцию транспонирования, а коэффициенты матрицы ${\mathbf{A}}$, имеющей размерность $2 \times 2$, даются соотношениями(3.4)
$\begin{gathered} {\mathbf{A}} = \frac{{\partial {\mathbf{B}}}}{{\partial {\mathbf{X}}}} = {{{\mathbf{A}}}_{R}}V + {{{\mathbf{A}}}_{Q}}\tau ,\quad {{{\mathbf{A}}}_{R}} = \frac{{\partial {\mathbf{R}}}}{{\partial {\mathbf{X}}}},\quad {{{\mathbf{A}}}_{Q}} = \left( {\frac{{\partial {{{\mathbf{Q}}}^{{ab}}}}}{{\partial {\mathbf{X}}}} + \frac{{\partial {{{\mathbf{\Psi }}}^{{ab}}}}}{{\partial {\mathbf{X}}}}} \right){{S}^{{ab}}} \\ {\mathbf{R}} = {{\left\{ {{{R}_{m}},{{R}_{e}}} \right\}}^{T}},\quad {{{\mathbf{Q}}}^{{ab}}} = {{\left\{ {Q_{m}^{{ab}},Q_{e}^{{ab}}} \right\}}^{T}},\quad {{{\mathbf{\Psi }}}^{{ab}}} = {{\left\{ {\Psi _{m}^{{ab}},\Psi _{e}^{{ab}}} \right\}}^{T}} \\ \end{gathered} $Для решения уравнений (3.1) относительно ${\mathbf{X}}$, на каждой итерации метода Ньютона они линеаризуются и полученная система (3.3) используется для определения нового приближения ${{{\mathbf{X}}}^{T}} = - {{{\mathbf{A}}}^{{ - 1}}}{\mathbf{B}}$ [10]. Итерационный процесс повторяется пока не будет достигнута требуемая точность $\varepsilon $ ($\left\| {\mathbf{B}} \right\| < \varepsilon $). В системе линейных уравнений (3.3) ${\mathbf{A}}$ и ${\mathbf{B}}$ – постоянные, вычисленные при текущем приближении ${\mathbf{X}}$. Для надежной работы алгоритма необходимо, чтобы матрица ${\mathbf{A}}$ удовлетворяла следующим условиям при любых ${\mathbf{X}}$ (т.е. при любых параметрах фильтрационного течения), в том числе при ${{{\mathbf{X}}}_{c}}$:
(3.5)
${{A}_{{\max }}}{\mathbf{X}}{{{\mathbf{X}}}^{T}} \geqslant {\mathbf{XA}}{{{\mathbf{X}}}^{T}} \geqslant {{A}_{{\min }}}{\mathbf{X}}{{{\mathbf{X}}}^{T}} > 0$Здесь ${\mathbf{X}}$ – произвольный вектор переменных, а ${{A}_{{\min }}}$ и ${{A}_{{\max }}}$ – некоторые положительные константы. Неравенства (3.5) означают, что матрица ${\mathbf{A}}$ положительно определена и ее коэффициенты ограничены [11].
Согласно соотношениям (3.4), ${\mathbf{A}}$ есть сумма двух матриц ${{{\mathbf{A}}}_{R}}V$ и ${{{\mathbf{A}}}_{Q}}\tau $, соответствующих членам с операторами ${{\partial }_{t}}$ и $\nabla $ в законах сохранения (2.1). При $\tau \to 0$ выполняется условие ${\mathbf{A}} \to {{{\mathbf{A}}}_{R}}V$, а при $\tau \to \infty $ – условие ${\mathbf{A}} \to {{{\mathbf{A}}}_{Q}}\tau $. Следовательно, в этих асимптотических случаях выполнение неравенств (3.5) зависит только от коэффициентов матрицы ${{{\mathbf{A}}}_{R}}$ или ${{{\mathbf{A}}}_{Q}}$, соответственно. При численном моделировании фильтрации конечно-разностные аппроксимации ${{{\mathbf{Q}}}^{{ab}}}$ и ${{{\mathbf{\Psi }}}^{{ab}}}$ часто не приводят к знакоопределенным матрицам ${{{\mathbf{A}}}_{Q}}$. В результате, условия (3.5) при ${\mathbf{A}} \to {{{\mathbf{A}}}_{Q}}\tau $ нарушаются, а расчет с большим шагом по времени $\tau $ часто невозможен из-за отсутствия сходимости метода Ньютона. Для продолжения расчета приходится уменьшать шаг $\tau $. Для гарантированной возможности расчета течения необходимо потребовать выполнение (3.5) при малых $\tau $, когда ${\mathbf{A}} \to {{{\mathbf{A}}}_{R}}V$. Тогда, даже если при больших $\tau $ сходимость отсутствует, то при уменьшении $\tau $ неравенства (3.5) выполняются, а расчет продолжается. Ниже проверяется выполнение условий (3.5) в асимптотическом случае $\tau \to 0$.
4. Вырождение в критической точке. Рассмотрим проблемы численного моделирования фильтрации, к которым приводят неограниченные производные (1.1) и совпадение параметров пара и воды (${{\rho }_{1}} \to {{\rho }_{2}}$, ${{h}_{1}} \to {{h}_{2}}$) при ${\mathbf{X}} \to {{{\mathbf{X}}}_{c}}$. Как отмечено в разделе 2, при $p = 1$ уравнения (2.1) образуют замкнутую систему уравнений относительно переменных ${\mathbf{X}} = \left\{ {P,T} \right\}$. В соответствии с (3.2) и (3.4), вычисляя для этого случая матрицу ${{{\mathbf{A}}}_{R}}$, получим:
(4.1)
$p = 1{\kern 1pt} :\quad {{{\mathbf{A}}}_{R}} = \left( {\begin{array}{*{20}{c}} {\phi {{{\left. {\frac{{\partial \rho }}{{\partial P}}} \right|}}_{T}}}&{\phi {{{\left. {\frac{{\partial \rho }}{{\partial T}}} \right|}}_{P}}} \\ {\phi {{{\left. {\frac{{\partial \rho e}}{{\partial P}}} \right|}}_{T}}}&{\phi {{{\left. {\frac{{\partial \rho e}}{{\partial T}}} \right|}}_{P}} + (1 - \phi ){{\rho }_{r}}{{c}_{r}}} \end{array}} \right)$(4.2)
${\mathbf{X}} \to {{{\mathbf{X}}}_{c}}{\kern 1pt} :\quad \det {{{\mathbf{A}}}_{R}} \to {{\phi }^{2}}\frac{{\partial \rho }}{{\partial P}}\left( {\rho \frac{{\partial h}}{{\partial T}} - 1} \right) \to \infty $При моделировании двухфазных течений ($p = 2$) в переменных ${\mathbf{X}} = \left\{ {P,s} \right\}$ матрица ${{{\mathbf{A}}}_{R}}$ удовлетворяет следующим соотношениям:
(4.3)
$p = 2{\kern 1pt} :\quad {{{\mathbf{A}}}_{R}} = \left( {\begin{array}{*{20}{c}} {{{{\left. {\frac{{\partial {{R}_{m}}}}{{\partial P}}} \right|}}_{s}}}&{\phi \left( {{{\rho }_{1}} - {{\rho }_{2}}} \right)} \\ {{{{\left. {\frac{{\partial {{R}_{e}}}}{{\partial P}}} \right|}}_{s}}}&{\phi \left( {{{\rho }_{1}}{{h}_{1}} - {{\rho }_{2}}{{h}_{2}}} \right)} \end{array}} \right)$При 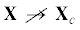 расчет параметров (2.6) в соответствии с непротиворечивой термодинамической моделью
жидкости (например, основывающейся на уравнении состояния) гарантирует выполнение
условий (3.5) для матриц (4.1) и (4.3) и, следовательно, сходимость алгоритмов расчета
фильтрации. При ${\mathbf{X}} \to {{{\mathbf{X}}}_{c}}$, согласно соотношению (4.2), коэффициенты матрицы ${{{\mathbf{A}}}_{R}}$ неограниченны при $p = 1$ (${{A}_{{\max }}} \to \infty $), а, согласно соотношению (4.4) и критерию Сильвестра [11], ${{{\mathbf{A}}}_{R}}$ не знакоопределена при $p = 2$ (${{A}_{{\min }}} \to 0$). В результате, ${{{\mathbf{A}}}_{R}}$ нельзя обратить, а линеаризованная система (3.3) не имеет решения при $\tau \to 0$ или ее решение неединственно. Применение метода Ньютона в случаях (4.2) и (4.4) приводит
к значительному в пределе ${\mathbf{X}} \to {\mathbf{X}}_{c}^{{}}$ стремящемуся к бесконечности изменению ${\mathbf{X}}$ за одну итерацию, а численное решение не сходится при любом сколь угодно малом шаге
по времени $\tau $.
расчет параметров (2.6) в соответствии с непротиворечивой термодинамической моделью
жидкости (например, основывающейся на уравнении состояния) гарантирует выполнение
условий (3.5) для матриц (4.1) и (4.3) и, следовательно, сходимость алгоритмов расчета
фильтрации. При ${\mathbf{X}} \to {{{\mathbf{X}}}_{c}}$, согласно соотношению (4.2), коэффициенты матрицы ${{{\mathbf{A}}}_{R}}$ неограниченны при $p = 1$ (${{A}_{{\max }}} \to \infty $), а, согласно соотношению (4.4) и критерию Сильвестра [11], ${{{\mathbf{A}}}_{R}}$ не знакоопределена при $p = 2$ (${{A}_{{\min }}} \to 0$). В результате, ${{{\mathbf{A}}}_{R}}$ нельзя обратить, а линеаризованная система (3.3) не имеет решения при $\tau \to 0$ или ее решение неединственно. Применение метода Ньютона в случаях (4.2) и (4.4) приводит
к значительному в пределе ${\mathbf{X}} \to {\mathbf{X}}_{c}^{{}}$ стремящемуся к бесконечности изменению ${\mathbf{X}}$ за одну итерацию, а численное решение не сходится при любом сколь угодно малом шаге
по времени $\tau $.
Общепринятый подход для исключения вырождения в точке $C$ заключается в переходе от ${\mathbf{X}}$ к другим независимым переменным. Часто используются переменные ${\mathbf{Y}} = \left\{ {P,\bar {h}} \right\}$ [4] или $\left\{ {\bar {\rho },T} \right\}$ [1], где $\bar {h}$ и $\bar {\rho }$ – полные, т.е. просуммированные по фазам, удельная энтальпия и плотность:
(4.5)
$\bar {h} = {{\sum {{{\rho }_{i}}{{h}_{i}}{{s}_{i}}} } \mathord{\left/ {\vphantom {{\sum {{{\rho }_{i}}{{h}_{i}}{{s}_{i}}} } {\bar {\rho }}}} \right. \kern-0em} {\bar {\rho }}},\quad \bar {\rho } = \sum {{{\rho }_{i}}{{s}_{i}}} $Согласно определению (4.5), $\bar {h} = {{h}_{1}}$ и $\bar {\rho } = {{\rho }_{1}}$ при $p = 1$. Предполагается, что в случае переменных ${\mathbf{Y}}$, уравнения состояния H2O задаются вместо уравнений (2.6) в виде
а насыщенности фаз вычисляются по $\bar {h}$ из уравнений (4.5). Преимущество ${\mathbf{Y}}$ перед ${\mathbf{X}}$ заключается в том, что частные производные функций (4.6) остаются ограниченными при любых осуществимых термобарических параметрах, в том числе в критической точке $C$ (при ${\mathbf{Y}} = {{{\mathbf{Y}}}_{c}} = \left\{ {{{P}_{c}},{{{\bar {h}}}_{c}}} \right\}$). В работе [4] показано, что это гарантирует выполнение (3.5) при любых параметрах однофазных и двухфазных течений.5. Проблемы использования переменных ${\mathbf{Y}} = \left\{ {P,\bar {h}} \right\}$. Применение нестандартных переменных, в частности ${\mathbf{Y}}$, требует определения и быстрого расчета функций (4.6). Это может представлять значительную вычислительную проблему, так как большинство уравнений состояния жидкостей и газов формулируются в переменных ${\mathbf{X}} = \left\{ {P,T} \right\}$, как, например, уравнение состояния Ван-дер-Ваальса [3]. Для решения этой проблемы требуется либо создавать новые уравнения состояния в переменных ${\mathbf{Y}}$, либо в существующих уравнениях состояния переходить от ${\mathbf{X}}$ к ${\mathbf{Y}}$. Подобная замена переменных используется в [2, 4, 12] для одно- и двухкомпонентных жидкостей, в которых по уравнению состояния Ван-дер-Ваальса рассчитывается термодинамический потенциал жидкости в ${\mathbf{Y}}$. Потенциал сохраняется в виде коэффициентов полиномиального сплайна, а расчет термодинамического равновесия сводится к поиску экстремума потенциала. Такой подход сталкивается со значительными техническими проблемами, связанными с необходимостью хранения функций (4.6) в виде усложненных многокоэффициентных сплайнов и неустойчивой сходимостью алгоритмов поиска экстремальных значений потенциала. В этой связи актуально создание метода расчета фильтрации в переменных ${\mathbf{X}}$, который позволит с одной стороны использовать существующие уравнения состояния, а с другой стороны исключить вырождение (2.1) при критических термодинамических параметрах. В данной работе для демонстрации основной идеи метода рассмотрим его на примере однокомпонентной жидкости (H2O).
6. Новый метод расчета фильтрации в переменных ${\mathbf{X}}$. Разобьем пространство $\left\{ {P,T} \right\}$ прямоугольной сеткой
(6.1)
$P = {{P}_{k}},\quad k = 1, \ldots ,{{N}_{P}};\quad T = {{T}_{n}},\quad n = 1, \ldots ,{{N}_{T}}$Рис. 2.
Триангуляция пространства $\left\{ {P,T} \right\}$. Разрывная кривая 1 – линия термодинамического равновесия.
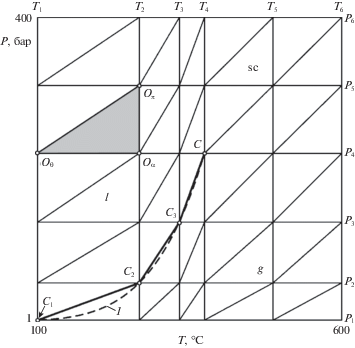
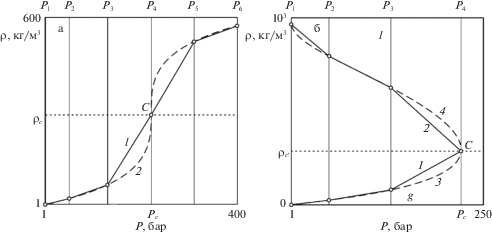
Рис. 3.
Плотность H2O в зависимости от $P$ при $T = {{T}_{c}}$ (а) и на кривой термодинамического равновесия (б). Разрывными линиями показаны зависимости (2.6), а сплошными – их интерполяции сплайнами (6.2).
На построенной триангуляции элементы вектора ${\mathbf{\Phi }}$ аппроксимируются кусочно-линейными функциями. Для этого в каждом узле сетки (6.1) вычисляются значения (2.6) при соответствующих ${{P}_{k}}$ и ${{T}_{n}}$. Причем, в вершинах ${{C}_{1}}$, ${{C}_{2}}$, ${{C}_{3}}$ и т.д. вычисляется два значения ${\mathbf{\Phi }}$, одно из которых соответствует воде $\left\{ {{{\rho }_{1}},{{h}_{1}},{{\mu }_{1}}} \right\}$, а другое – пару $\left\{ {{{\rho }_{2}},{{h}_{2}},{{\mu }_{2}}} \right\}$. Параметры H2O (2.6) внутри каждого треугольника аппроксимируются линейными функциями от $P$ и $T$:
(6.2)
${\mathbf{\Phi }} = {{{\mathbf{D}}}_{{\alpha l}}} + {{{\mathbf{D}}}_{{\pi l}}}P + {{{\mathbf{D}}}_{{\theta l}}}T,\quad {\mathbf{\Phi }},{\mathbf{D}} = \left\{ {\rho ,h,\mu } \right\},\quad l = 1, \ldots ,L$Здесь $L = 2\left( {{{N}_{P}} - 1} \right)\left( {{{N}_{T}} - 1} \right)$ – число симплексов, а ${{{\mathbf{D}}}_{{\alpha l}}}$, ${{{\mathbf{D}}}_{{\pi l}}}$ и ${{{\mathbf{D}}}_{{\theta l}}}$ – коэффициенты сплайна, однозначно определяющиеся значениями (2.6) в вершинах соответствующего симплекса. Например, рассмотрим произвольный треугольник ${{O}_{\alpha }}{{O}_{\pi }}{{O}_{\theta }}$ из построенного разбиения, параметры в вершинах которого обозначим индексами $\alpha $, $\pi $ и $\theta $. Для определенности положим, что ${{P}_{\alpha }} = {{P}_{\theta }} < {{P}_{\pi }}$ и ${{T}_{\alpha }} = {{T}_{\pi }} > {{T}_{\theta }}$ (рис. 2). Тогда коэффициенты сплайна (6.2) выражаются в виде
(6.3)
$\begin{gathered} {{{\mathbf{D}}}_{{\alpha l}}} = {{{\mathbf{\Phi }}}_{\alpha }} - {{{\mathbf{D}}}_{{\pi l}}}{{{\mathbf{\Phi }}}_{\pi }} - {{{\mathbf{D}}}_{{\theta l}}}{{{\mathbf{\Phi }}}_{\theta }} \\ {{{\mathbf{D}}}_{{\pi l}}} = \frac{{{{{\mathbf{\Phi }}}_{\pi }} - {{{\mathbf{\Phi }}}_{\alpha }}}}{{{{P}_{\pi }} - {{P}_{\alpha }}}},\quad {{{\mathbf{D}}}_{{\theta l}}} = \frac{{{{{\mathbf{\Phi }}}_{\theta }} - {{{\mathbf{\Phi }}}_{\alpha }}}}{{{{T}_{\theta }} - {{T}_{\alpha }}}} \\ \end{gathered} $Здесь ${{{\mathbf{\Phi }}}_{\alpha }}$, ${{{\mathbf{\Phi }}}_{\pi }}$ и ${{{\mathbf{\Phi }}}_{\theta }}$ – значения функций (2.6) в ${{O}_{\alpha }}$, ${{O}_{\pi }}$ и ${{O}_{\theta }}$, соответственно. Таким образом, на множестве треугольников строятся непрерывные сплайны для (2.6), а ломанная ${{C}_{1}}{{C}_{2}} \ldots С$, интерполирующая линию термодинамического равновесия (2.5) между водой и паром, является линией их разреза. Точность такого приближенного описания соотношений (2.5) и (2.6) сплайнами повышается при использовании более плотной сетки (6.1).
Построенные сплайны обладают двумя важными свойствами. Во-первых, они сохраняют монотонность функций (2.6) вдоль осей $P$ и $T$ и, если сетка (6.1) достаточно плотная, знак определенности матрицы ${{{\mathbf{A}}}_{R}}$. В частности, как интерполируемые функции (2.6), так и интерполирующие их сплайны удовлетворяют неравенствам
(6.4)
${{\left. {\frac{{\partial \rho }}{{\partial P}}} \right|}_{T}} > 0,\quad {{\left. {\frac{{\partial \rho }}{{\partial T}}} \right|}_{P}} < 0,\quad {{\left. {\frac{{\partial h}}{{\partial T}}} \right|}_{P}} > 0$Условия (6.4) гарантируют положительный знак коэффициентов сжимаемости и теплового расширения и теплоемкости H2O при постоянном давлении. Действительно, так как ${{\left. {{{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } {\partial P}}} \right. \kern-0em} {\partial P}}} \right|}_{T}} > 0$, то ${{\rho }_{\pi }} > {{\rho }_{\alpha }}$ и соответствующий коэффициент сплайна ${{\rho }_{{\pi l}}}$ = = ${{({{\rho }_{\pi }} - {{\rho }_{\alpha }})} \mathord{\left/ {\vphantom {{({{\rho }_{\pi }} - {{\rho }_{\alpha }})} {({{P}_{\pi }} - {{P}_{\alpha }})}}} \right. \kern-0em} {({{P}_{\pi }} - {{P}_{\alpha }})}}$ > 0 положительный. Следовательно, неравенство ${{\left. {{{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } {\partial P}}} \right. \kern-0em} {\partial P}}} \right|}_{T}}$ = ${{\rho }_{{\pi l}}} > 0$ выполняется для сплайна (6.2). Аналогично проверяется выполнение остальных неравенств (6.4).
Известно, что для двухпараметрической среды достаточно задать только одну из функций $\rho (P,T)$ или $h(P,T)$, например, достаточно задать только термическое уравнение состояния $\rho (P,T)$. Используя термодинамические соотношения, другие параметры среды можно выразить через заданную функцию, например, $h(P,T)$ можно выразить из $\rho (P,T)$ [3, 12]. При этом гарантируется выполнение термодинамических неравенств (6.4). Применение сплайна (6.2) предполагает независимое задание $\rho (P,T)$ и $h(P,T)$. В этом смысле термодинамическая модель (6.2), (6.3) является несогласованной. Однако, как показано выше, термодинамические неравенства (6.4), обеспечивающие диссипативность модели фильтрации, для (6.2) выполняются. Этого свойства модели (6.2), (6.3) достаточно для проведения устойчивых расчетов фильтрации.
Если свойства H2O задаются в форме (6.2) и (6.3), то, согласно (3.2) и (3.4), ${{{\mathbf{A}}}_{R}}$ имеет вид:
(6.5)
${{{\mathbf{A}}}_{R}} = \left( {\begin{array}{*{20}{c}} {\frac{{{{R}_{{m,\pi }}} - {{R}_{{m,\alpha }}}}}{{{{P}_{\pi }} - {{P}_{\alpha }}}}}&{\frac{{{{R}_{{m,\theta }}} - {{R}_{{m,\alpha }}}}}{{{{T}_{\theta }} - {{T}_{\alpha }}}}} \\ {\frac{{{{R}_{{e,\pi }}} - {{R}_{{e,\alpha }}}}}{{{{P}_{\pi }} - {{P}_{\alpha }}}}}&{\frac{{{{R}_{{e,\theta }}} - {{R}_{{e,\alpha }}}}}{{{{T}_{\theta }} - {{T}_{\alpha }}}}} \end{array}} \right)$Если 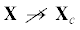 , то при измельчении сетки (6.1), т.е. при ${{N}_{P}}$, ${{N}_{T}} \to \infty $, матрица (6.5) стремится к знакоопределенной матрице (4.1) при $p = 1$ или (4.3) при $p = 2$. Следовательно, матрица (6.5) также знакоопределена при достаточно больших ${{N}_{P}}$ и ${{N}_{T}}$. Таким образом, построенная триангуляция, использующая выравнивание ребер симплексов
вдоль осей $P$ и $T$, гарантирует выполнение неравенств (3.5) и (6.4) при
, то при измельчении сетки (6.1), т.е. при ${{N}_{P}}$, ${{N}_{T}} \to \infty $, матрица (6.5) стремится к знакоопределенной матрице (4.1) при $p = 1$ или (4.3) при $p = 2$. Следовательно, матрица (6.5) также знакоопределена при достаточно больших ${{N}_{P}}$ и ${{N}_{T}}$. Таким образом, построенная триангуляция, использующая выравнивание ребер симплексов
вдоль осей $P$ и $T$, гарантирует выполнение неравенств (3.5) и (6.4) при 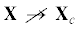 . Линейная интерполяция на произвольной триангуляции пространства $\left\{ {P,T} \right\}$, отличной от построенной выше, может не удовлетворять условиям (3.5) и (6.4).
. Линейная интерполяция на произвольной триангуляции пространства $\left\{ {P,T} \right\}$, отличной от построенной выше, может не удовлетворять условиям (3.5) и (6.4).
Второе важное свойство сплайнов (6.2) заключается в том, что их коэффициенты ${{{\mathbf{D}}}_{{\alpha l}}}$, ${{{\mathbf{D}}}_{{\pi l}}}$ и ${{{\mathbf{D}}}_{{\theta l}}}$ – ограничены, а значит ограничены и производные (6.4) интерполирующих функций в том числе в критической точке $C$. Действительно, на рис. 3а построены графики $\rho (P,{{T}_{c}})$ (кривые 1 и 2, соответственно), а на рис. 3б плотности пара ${{\rho }_{1}}$ (кривые 1 и 2) и воды ${{\rho }_{2}}$ (кривые 3 и 4) для (2.6) и сплайна (6.2), соответственно. В отличие от зависимостей (2.6), производные от сплайнов конечные, что обеспечивает выполнение неравенств (3.5) при $p = 1$ и, следовательно, устойчивую сходимость расчета однофазных течений H2O при околокритических условиях.
Так как при ${\mathbf{X}} \to {{{\mathbf{X}}}_{c}}$ плотности и энтальпии пара и воды, интерполируемые сплайнами (6.2), совпадают (${{\rho }_{1}} \to {{\rho }_{2}}$, ${{h}_{1}} \to {{h}_{2}}$), то, согласно (4.4), расчет двухфазной фильтрации в переменных ${\mathbf{X}} = \left\{ {P,s} \right\}$ при околокритических условиях невозможен. Это связано с тем, что матрица ${{{\mathbf{A}}}_{R}}$ дается соотношением (4.3), а неравенства (3.5) не выполняются (${{A}_{{\min }}} \to 0$). Покажем, что вырождение можно исключить, выбрав в качестве независимых переменных ${\mathbf{X}} = \left\{ {P,\bar {\rho }} \right\}$, где полная плотность $\bar {\rho }$ дается (4.5). В этом случае ${{{\mathbf{A}}}_{R}}$ дается соотношением
(6.6)
${{{\mathbf{A}}}_{R}} = \left( {\begin{array}{*{20}{c}} {{{{\left. {\frac{{\partial {{R}_{m}}}}{{\partial P}}} \right|}}_{{\bar {\rho }}}}}&\phi \\ {{{{\left. {\frac{{\partial {{R}_{e}}}}{{\partial P}}} \right|}}_{{\bar {\rho }}}}}&{\phi \frac{{{{\rho }_{1}}{{h}_{1}} - {{\rho }_{2}}{{h}_{2}}}}{{{{\rho }_{1}} - {{\rho }_{2}}}}} \end{array}} \right)$Коэффициенты в правом столбце (6.6) ограничены при любом ${\mathbf{X}}$, в том числе при ${{{\mathbf{X}}}_{c}}$, а условия (3.5) выполняются. Это обеспечивает устойчивую сходимость расчета двухфазных течений H2O при околокритических условиях.
Таким образом, применение кусочно-линейных сплайнов позволяет исключить вырождение уравнений фильтрации при ${\mathbf{X}} \to {{{\mathbf{X}}}_{c}}$. При этом, однофазные течения необходимо рассчитывать в переменных ${\mathbf{X}} = \left\{ {P,T} \right\}$, а двухфазные – в ${\mathbf{X}} = \left\{ {P,\bar {\rho }} \right\}$. Вырождение удается исключить за счет приближенного описания теплофизических свойств линейными функциями, причем погрешность этого описания увеличивается при ${\mathbf{X}} \to {{{\mathbf{X}}}_{c}}$ (рис. 3). Сплайны (6.2) описывают (2.5) и (2.6) точнее на более подробных сетках (6.1). Однако, при ${{N}_{P}}$, ${{N}_{T}} \to \infty $ константа ${{A}_{{\min }}}$ в условии (3.5) уменьшается, имея предел ${{A}_{{\min }}} \to 0$. Следовательно, более точная аппроксимация (2.5) и (2.6) сплайнами, приводит к ухудшению сходимости алгоритма расчета фильтрации (методом Ньютона) при ${\mathbf{X}} \to {{{\mathbf{X}}}_{c}}$. Применение сплайнов (6.2) в численном моделировании требует соблюдения баланса между точностью расчета свойств H2O и сходимостью алгоритмов. Важно, что область околокритических параметров, где необходимо приближенное описание, мала по сравнению с гораздо более широким диапазоном $P$ и $T$, при которых происходят течения в геотермальных системах. Следовательно, задав неравномерную сетку (6.1), более грубую в окрестности $C$, можно обеспечить удовлетворительную точность расчета свойств при всех параметрах за исключением околокритических значений и, таким образом, обеспечить достаточную точность расчета течений.
Исследование выполнено за счет гранта Российского научного фонда (проект № 19-71-10051).
Список литературы
Croucher A., O’Sullivan M. Application of the computer code TOUGH2 to the simulation of supercritical condition in geothermal system // Geothermics, 2008. V. 37. № 6. P. 622–634.
Afanasyev A., Costa A., Chiodini G. Investigation of hydrothermal activity at Campi Flegrei caldera using 3D numerical simulations: extension to high temperature processes// J. Volcanol. Geothermal Res. 2015. V. 299. P. 68–77.
Брусиловский А.И. Фазовые превращения при разработке месторождений нефти и газа. М.: Грааль, 2002. 575 с.
Афанасьев А.А., Мельник О.Э. О математическом моделировании многофазной фильтрации при околокритических условиях // Вестн. Моск. ун-та. Сер. 1, Математика. Механика. 2013. Т. 68. № 3. С. 68–72.
Бармин А.А., Цыпкин Г.Г. Математическая модель инжекции воды в геотермальный пласт, насыщенный паром // Изв. РАН. МЖГ. 1996. № 6. С. 92–98.
Афанасьев А.А., Бармин А.А. Нестационарные одномерные фильтрационные течения воды и пара с учетом фазовых переходов // Изв. РАН. МЖГ. 2007. № 4. С. 134–143.
Wagner W., Pruss A. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use // J. Phys. Chem. Ref. Data 2002. V. 31. № 2. P. 387–535.
Schechter D., Haynes J. Relative permeabilities of a near critical binary fluid // Transport Porous Med. 1992. V. 9. № 3. P. 241–260.
Aziz K., Settari A. Petroleum reservoir simulation. London: Appl. Sci. Publ., 1979. 476 p.
Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). М.: Наука, 1975. 632 с.
Гантмахер Ф.Р. Теория матриц (2-е изд.). М.: Наука, 1966. 576 с.
Афанасьев А.А. Моделирование свойств бинарной смеси углекислый газ-вода при до- и закритических условиях // Теплофизика высоких температур. 2012. Т. 50. № 3. С. 363–370.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика


