Прикладная математика и механика, 2020, T. 84, № 6, стр. 721-732

Введение. Показано, что при отсутствии вращения магнитного поля и вдува (отсоса) среды и удалении неподвижной стенки на бесконечность, решение переходит в известное решение задачи о нестационарном движении жидкости, ограниченной перемещающейся плоской стенкой [1]. Кроме того, при отсутствии магнитного поля и удалении неподвижной стенки на бесконечность решение совпадает с результатами [2], а при отсутствии магнитного поля и вдува (отсоса) среды решение переходит в решение [3].

В настоящей работе представлено обобщение исследования [4], в котором рассматривается нестационарный поток вязкой электропроводной несжимаемой жидкости во вращающейся щели при наличии внешнего однородного магнитного поля. Неустановившийся поток индуцирован продольными колебаниями одной из стенок. Далее изучается динамика неустановившегося течения вязкой электропроводной жидкости между вращающимися параллельными стенками при наличии поперечного потока и внешнего магнитного поля. Задача в такой постановке, насколько известно автору, поставлена впервые. В одном из последних исследований [5] рассматривалось течение электропроводной жидкости внутри вращающейся щели, но жидкость предполагалась идеальной и течение стационарным.

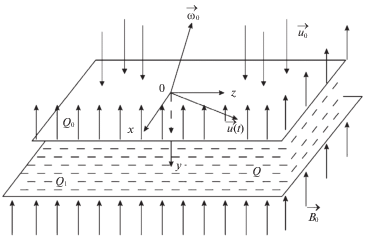
1. Аналитическое решение уравнений магнитной гидродинамики. Задача рассматривается в следующей постановке. Щель шириной $l$, образованная двумя бесконечными параллельно пористыми стенками ${{Q}_{0}}$ и ${{Q}_{1}}$ с изолирующими свойствами, заполнена вязкой электропроводной несжимаемой жидкостью. Жидкость находится в поле массовых сил с потенциалом $U$. Щель вместе с жидкостью вращается как одно целое с постоянной угловой скоростью ${{\vec {w}}_{0}} = {\text{const}}$, причем вектор ${{\vec {w}}_{0}}$ образует с этими плоскостями постоянный угол $\beta \left( {0 < \beta \leqslant \frac{\pi }{2}} \right)$. Частный случай в отсутствии магнитного поля и вдува (отсоса) среды $\left( {\beta = \frac{\pi }{2}} \right)$ был исследован ранее [6].

Свяжем с плоскостью ${{Q}_{0}}$ декартову систему координат ${{Q}_{{xyz}}}$ с ортами ${{\vec {e}}_{x}}$, ${{\vec {e}}_{y}}$, ${{\vec {e}}_{z}}$ так, что плоскость ${{Q}_{{xz}}}$ совпадает с плоскостью ${{Q}_{0}}$, а ось $y$ направлена по нормали к ней вглубь жидкости. В этой системе координат стенки и жидкость покоятся. В момент $t \geqslant 0$ стенка ${{Q}_{0}}$ начинает двигаться в продольном направлении со скоростью $u\left( t \right)$ В тот же момент времени вносится внешнее однородное магнитное поле с индукцией ${{B}_{0}} = {\text{const}}$ направленной по нормали к стенкам, и через верхнюю пластину ${{Q}_{0}}$ осуществляется вдув (отсос) жидкости со скоростью u(t) по нормали к поверхности пластины. Схематично геометрия задачи представлена на рис. 1.

Далее исследуется распространение возмущений в однородной проводящей среде под действием однородного магнитного поля, продольных колебаний стенки и вдува (отсоса) среды.

Движение жидкости в системе ${{O}_{{xyz}}}$, вращающейся с угловой скоростью ${{\vec {w}}_{0}}$, в магнитогидродинамическом приближении (бесконечно проводящая жидкость) описывается уравнением магнитной гидродинамики, а также граничными и начальными условиями, которые в обычных обозначениях имеют вид

Здесь $\vec {r}$ – радиус-вектор относительно полюса $O$, $\vec {V}$ – скорость жидкости, $P$ – давление, $\rho $ – плотность, $\nu $ – кинематическая вязкость, $U$ – потенциал внешних массовых сил, $\vec {B}$ – магнитная индукция, $\mu $ – магнитная проницаемость, $Q$ – объем жидкости.

Решение системы уравнений (1.1) ищется в виде

где ${{w}_{{0x}}} = {{\vec {w}}_{0}} \cdot {{\vec {e}}_{x}}$; ${{w}_{{0z}}} = {{\vec {w}}_{0}}{{\vec {e}}_{z}}$, а $q(y,t)$ – неизвестная функция давления.

Для определения поля скоростей $\vec {V}$ и индукции $\vec {B}$ получаем следующую систему уравнений

с граничными и начальными условиями вида

Введем комплексную структуру

Тогда система уравнений (1.4), граничные и начальные условия примут вид

Исключая магнитную индукция из уравнений (1.5), получаем

С использованием интеграла Дюамеля представим решение уравнения (1.7) в виде

здесь ${{\hat {V}}_{1}}(y,t)$ – решение краевой задачи

Рассмотрим случай ${{u}_{0}}(t) = {{u}_{0}} = \operatorname{const} $.

Введем образ Лапласа

В пространстве изображений задача (1.9) принимает вид

где $a\left( p \right) = \nu p + B_{0}^{2}{\text{/}}\mu \rho $.

Характеристическое уравнение (1.10) и его корни имеют вид

где $\sigma = \frac{{{{u}_{0}}p}}{{2\nu a}};$ ${{\omega }^{2}} = \frac{{u_{0}^{2}{{p}^{2}}}}{{4{{a}^{2}}}} + \frac{{{{p}^{2}} - i2\Omega p}}{a}$.

Решение уравнения (1.10) записывается в форме

Определяя постоянные интегрирования из граничных условий, получаем

где $F(y,p) = \frac{1}{p}{{e}^{{\sigma y}}},$ $G(y,p) = \frac{{\operatorname{sh} (l - y)\omega }}{{\operatorname{sh} \omega l}}$.

Разложим функцию $G(y,p) = \frac{{\operatorname{sh} (l - y)\omega }}{{\operatorname{sh} \omega l}}$ на простые дроби [7]:

где ${{\lambda }_{n}} = \pi n{\text{/}}l$.

Согласно известным формулам операционного исчисления [8] найдем оригиналы функций $F(y,p)$, $G(y,p)$

где $\alpha = B_{0}^{2}{\text{/}}\mu \rho \nu $, ${{J}_{0}}(x)$ – функция Бесселя нулевого порядка. где ${{p}_{{1n..3n}}}$ – корни кубического уравнения и введены обозначения: $s = \alpha - i2\Omega + \frac{{u_{0}^{2}}}{{4\nu }}$, ${{a}_{n}} = 2 - i2\Omega + \frac{{u_{0}^{2}}}{{4\nu }} + \nu \lambda _{n}^{2}$, ${{b}_{n}} = 2\nu \alpha \lambda _{n}^{2} - i2\alpha \Omega $, ${{c}_{n}} = \nu {{\alpha }^{2}}\lambda _{n}^{2}$, $d = - i2\Omega \alpha $.

Тогда выражение для ${{\hat {V}}_{1}}$ дается сверткой функций $f(y,t)$ и $g(y,t)$

или, проведя дифференцирование

Таким образом, решение задачи (1.7) определяется формулами (1.8) и (1.17)

Векторы касательных направлений, действующие со стороны жидкости на верхнюю и нижнюю стенки щели, находятся по формулам

и

Вектор магнитной индукции находится из соотношения

где ${{\hat {V}}_{1}}(y,r)$ определяется формулой (1.17).

2. Поле скоростей потока, индуцированное движением одной из стенок. Пусть одна из плоскостей ${{Q}_{0}}$, составляющих границы щели, движется в продольном направлении со скоростью $\vec {u}(t) = u(0){{e}^{{\lambda t}}}$, $\lambda = - \alpha + i\omega $.

Рассмотрим “нормальные” колебания вязкой электропроводной жидкости во вращающейся щели, т.е. будем изучать класс движений, в которых все временные факторы зависят от времени, посредством множителя ${{e}^{{\lambda t}}}$. Тогда система уравнений (1.5), граничные и начальные условия принимают вид

Исключая из системы (2.1) магнитную индукцию для функции $\hat {v}(y)$, получаем обыкновенное дифференциальное уравнение

и граничные условия где $\beta = B_{0}^{2}{\text{/}}\mu \rho \lambda $.

Корни характеристического уравнения имеют вид

Введем обозначения

Тогда ${{\chi }_{{1,2}}} = \sigma \pm q$. Общее решение уравнения (2.2) имеет вид

где ${{c}_{1}}$ и ${{c}_{2}}$ произвольные постоянные. Определяя постоянные интегрирования из граничных условий (2.3), получаем “нормальные” колебания вязкой электропроводной жидкости во вращающейся щели в постоянном магнитном поле при наличии поперечного потока

С помощью решений (2.5) находим векторы касательных напряжений, действующие со стороны жидкости на верхнюю и нижнюю стенки щели

Из выражений (2.5)–(2.7) видно, что поле скоростей жидкости и силы трения существенно зависят от комплексного параметра $q$, связывающего параметры гармонических колебаний пластин и вращения щели.

3. Структура пограничных слоев. Исследуем подробнее выражение для поля скоростей (2.5). Выражение для комплексных декрементов затухания можно записать в виде

где

Тогда, после некоторых преобразований поле скоростей жидкости можно представить в виде двух бегущих волн

где а показатель экспоненты определяется множителем где $A = {{\left( {\frac{{\sqrt {{{C}^{2}} + {{D}^{2}}} + C}}{2}} \right)}^{{\frac{1}{2}}}}$, $B = {{\left( {\frac{{\sqrt {{{C}^{2}} + {{D}^{2}}} - C}}{2}} \right)}^{{\frac{1}{2}}}}$,

При этом волновые числа имеют вид

Эти волны распространяются по оси навстречу друг другу с разными фазовыми скоростями, т.к. волновые числа ${{k}_{1}}$, ${{k}_{2}}$ различны. Кроме того, скорости зависят от частоты. Это означает, что поток вязкой электропроводной жидкости представляет собой дисперсионную среду.

Групповые скорости этих волн ${{v}_{{гр}}} = \frac{{d\omega }}{{dk}}$ также различны. Они зависят от коэффициентов затухания и вращения системы, магнитной индукции и параметров жидкости. Амплитуды этих волн зависят от глубины щели, величины проекции угловой скорости на ось $y$, параметров движения стенки, магнитной индукции и параметров жидкости. Отметим, что каждая из этих волн затухает на глубине ${{\delta }_{1}}$, ${{\delta }_{2}}$ соответственно.

Выберем индукцию $B_{0}^{2} = 2\nu \alpha \mu \rho $ и введем безразмерную переменную $Y = \omega {\text{/}}\alpha $. Тогда выражения для составляющих $\sigma $ и определяющие величину комплексных амплитуд волн (3.1) функции $C$ и $D$ примут вид

где $s = 2\Omega {\text{/}}\alpha $ и $\gamma = \frac{\alpha }{\nu }{\text{/}}{{\left( {\frac{{{{u}_{0}}}}{{2\nu }}} \right)}^{2}}$.

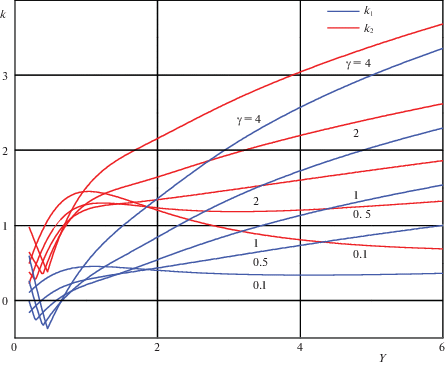
На рис. 2 представлены графики зависимости волновых чисел ${{k}_{1}} = B - {{\sigma }_{2}}$; ${{k}_{2}} = B + {{\sigma }_{2}}$; от $Y$ (частота $\omega $) при фиксированном $s = 2$ и скорости вдува жидкости ${{u}_{0}} = \sqrt {4\alpha \nu {\text{/}}\gamma } $ для различных значений $\gamma $.

В рассматриваемом случае $k(\omega )$ – волновое число, вообще говоря, комплексное. Его действительная часть характеризует зависимость фазовой скорости волны от частоты, а мнимая часть – зависимость коэффициента затухания амплитуды волны от частоты. Дисперсия, как правило, связана с внутренними свойствами материальной среды, обычно выделяются частотная (временная) дисперсия, когда поляризация в диспергирующей среде зависит от значений поля в предшествующие моменты времени (память), и пространственная дисперсия, когда поляризация в данной точке зависит от значений поля в некоторой области (нелокальность). Из графиков видно, что при малых скоростях вдува (большие значения параметра $\gamma $) волновые числа монотонно возрастают с увеличением частоты колебаний стенки. При больших скоростях вдува ($\gamma $ мало) волновое число ${{k}_{1}}$, слабо меняясь, выходит на константу, в то время как волновое число ${{k}_{2}}$ имеет ярко выраженный максимум при $Y = 1$ и с увеличением частоты колебаний стенки остается постоянной.

Анализ зависимостей волновых чисел ${{\delta }_{1}} = {{\left( {A - {{\sigma }_{1}}} \right)}^{{ - 1}}};$ ${{\delta }_{2}} = {{\left( {A + {{\sigma }_{1}}} \right)}^{{ - 1}}}$ от $Y$ (частоты $\omega $) при фиксированных $s$ ($s = 2$) и скорости вдува жидкости ${{u}_{0}} = \sqrt {4\alpha \nu {\text{/}}\gamma } $ для различных значений $\gamma $ показал, что существуют особые точки нестационарной задачи, в которых ${{\delta }_{1}}$ обращается в бесконечность, а производная $d{{\delta }_{2}}{\text{/}}dY$ терпит разрыв первого рода, поэтому вопрос распространения волновых пакетов в данной среде нуждается в дополнительном исследовании. Для волны, излучаемой колеблющейся стенкой, особыми точками являются $Y = 1$, $Y = 4$ и ряд точек из промежутка $1 < Y < 2$ в окрестности которых волновое число ${{\delta }_{1}}$ терпит разрыв. В то же время скорость волнового пакета ${{V}_{{g1}}}$ терпит разрыв только в точке $Y = 1$.

Для неподвижной стенки особой точкой является $Y = 1$, в которой волновое число ${{\delta }_{2}}$ имеет конечный скачок и с ростом частоты стремится к нулю, причем независимо от скорости вдува.

Анализ зависимости скоростей волновых пакетов от $Y$ (частоты $\omega $) при фиксированном $s$ ($s = 2$) и скоростях вдува жидкости ${{u}_{0}} = \sqrt {4\alpha \nu {\text{/}}\gamma } $ для различных значений $\gamma $ показал, что групповая скорость ${{V}_{{g1}}}$ терпит разрыв второго рода при $Y = 1$, а при дальнейшем росте частоты стремится к некоторой константе. Характер волнового пакета, излучаемого неподвижной стенкой, носит сложный характер. В особой точке $Y = 1$ кривая ${{V}_{{g2}}}$ распадается на серии кривых, которые зависят от скорости вдува среды.

Полагая скорость пограничного потока ${{u}_{0}} = 0$ получаем

что совпадает с ранее полученным результатом [4].

При $\alpha = 0$ волновые числа ${{k}_{1}}$ и ${{\delta }_{1}}$ обращаются в нуль, при этом ${{k}_{2}} = \nu {\text{/}}{{u}_{0}}$ и ${{\delta }_{2}} = {{u}_{0}}{\text{/}}\nu $, т.е. волна, бегущая вдоль оси $Oy$ от плоскости ${{Q}_{0}}$ к плоскости ${{Q}_{1}}$ отсутствует, а присутствует волна, бегущая от стенки ${{Q}_{1}}$ к стенке ${{Q}_{0}}$, которая затухает на расстоянии ${{\delta }_{2}}$.

Заключение. Проведен анализ нестационарного течения вязкой электропроводной несжимаемой жидкости в плоско-параллельной конфигурации при наличии поперечного потока. Найдены аналитические решения трехмерных нестационарных уравнений магнитной гидродинамики. При этом никаких ограничений на характер движения пластины не накладывается. Определены поле скоростей в потоке и векторы касательных напряжений, действующие из жидкости на стенки щели. Для случая “нормальных” колебаний одной из стенок рассмотрен случай резонанса, и исследована структура пограничных слоев, прилегающих к пластинам. Математическая процедура интегрирования системы дифференциальных уравнений рассматриваемой задачи может быть использована при исследовании более сложных задач. Кроме того, полученные результаты могут быть использованы для учета силовых воздействий при движении жидкости в каналах различной формы, а также при моделировании различных физических явлений в движущейся жидкости.