Прикладная математика и механика, 2020, T. 84, № 6, стр. 687-693

1. В монографии [1] описан волновой твердотельный гироскоп, физической основой которого является твердотельный резонатор, изготовленный из высококачественного кварца. В резонаторе возбуждаются незатухающие стоячие волны, которые и позволяют превратить этот резонатор в гироскоп. Подробное изложение принципа действия приведено также и в ряде других публикаций [2–4]. Волновые гироскопы широко используются в технике [5, 6]. Анализ свойств таких колебательных систем, вопросы определения их устойчивости и управления параметрами активно исследуются в настоящее время [7–10]. Для того чтобы гироскоп мог функционировать достаточно продолжительное время, колебания резонатора должны поддерживаться все время эксплуатации с постоянной амплитудой и частотой. Ранее [11] подробно рассмотрен автоколебательный режим резонатора. Имеются два детально изученных дифференциальных уравнения, описывающих возникновение и существование установившихся колебаний постоянной амплитуды и периода.

Уравнение Ван дер Поля [12]

Здесь $u$ и $\dot {u}$ – смещение и скорость осциллятора, $\varepsilon $ – создаваемый специальным устройством коэффициент обратной связи, обеспечивающий подачу энергии от внешнего постоянного источника.

Уравнение Рэлея [13]

где $u$, $\dot {u}$ и $\varepsilon $ – имеют тот же смысл, как и в уравнении Ван дер Поля.

Основные математические результаты, относящиеся к уравнениям Ван дер Поля и Рэлея, состоят в том, что тривиальное решение $u = \dot {u} = 0$ неустойчиво, однако существует периодическое решение с постоянной амплитудой и периодом $T\left( \varepsilon \right)$. Это периодическое решение асимптотически устойчиво, однако оно не оказывается одночастотным. Для улучшения гироскопических свойств резонатора необходимо, чтобы колебания описывались устойчивыми одночастотными периодическими решениями. Академик В.Ф. Журавлев предложил объединить уравнения (1.1) и (1.2) следующим образом

Действительно, полагая $u = A\cos t$, при $A = 1$ получаем точное решение уравнения (1.3) с периодом $T = 2\pi $.

Для осциллятора, описываемого уравнением

которое имеет интеграл энергии для систем с обратной связью (диссипацией) уравнение (1.3) может быть в случае потенциальной энергии $\Pi $ обобщено в виде где $\varepsilon $ – коэффициент обратной связи, ${{E}_{0}}$ – постоянная, которая показывает, до каких пор может расти энергия $E$ осциллятора, чтобы отрицательное сопротивление уменьшилось до нуля.

Дифференцируя энергию (1.5), найдем

Уравнение (1.7) показывает, что если в начальный момент времени

то энергия осциллятора с течением времени не меняется. Уравнение (1.7) можно переписать в интегральной форме где $v = \dot {u}$, $H$ – постоянная интегрирования. Если в начальный момент времени условие (1.8) не выполняется, то из уравнения (1.9) следует, что при $E\left( 0 \right) > {{E}_{0}}$ ($H > 0$) энергия будет невозрастающей функцией времени; а при $E\left( 0 \right) < {{E}_{0}}$ ($H < 0$) и $E$ – неубывающей. Если условие (1.8) рассматривать как функцию на фазовой плоскости $\left( {u,v} \right)$, график которой образует замкнутую кривую (набор замкнутых кривых – многосвязная область), то такая область будет предельным циклом уравнения (1.7). Запишем уравнение предельного цикла в явном виде

Если положить $v = 0$, то величина амплитуды определяется уравнением

Здесь по умолчанию предполагается, что при заданном значении ${{E}_{0}}$ существуют два конечных корня уравнения (1.10). Для определения периода колебаний воспользуемся уравнением (1.5), полагая $E = {{E}_{0}}$. Имеем

Величина периода и другие свойства колебаний будут очевидно определяться значением энергетического параметра ${{E}_{0}}$ и видом функции $f\left( u \right)$, с точностью до знака совпадающей с силовой функцией

2. Примеры.

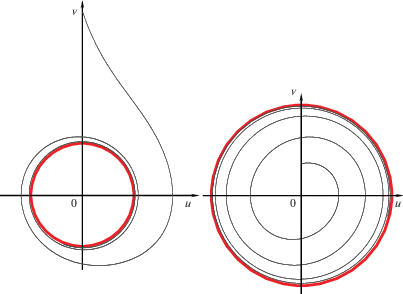
1. Фазовая картина автоколебательной системы гармонического осциллятора ($f\left( u \right) = - u$) приведена на рис. 1.

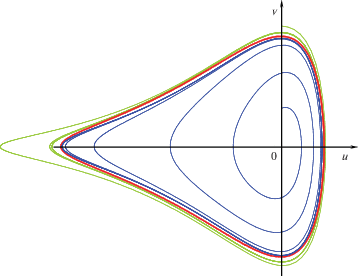
2. Пример автоколебательной системы с асимметричной силовой функцией вида

приведен на рис. 2.

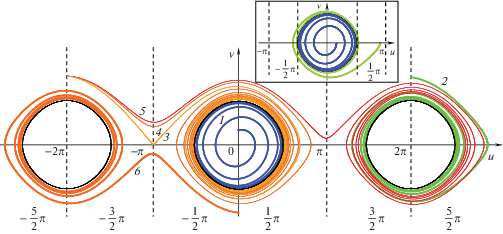
3. В качестве примера многосвязного предельного цикла рассмотрим автоколебательную систему, состоящую из маятника и электромеханического устройства, обеспечивающего обратную связь между постоянным источником питания и маятником. Такая автоколебательная система при произвольных углах отклонения маятника от вертикального положения описывается уравнением (далее используются безразмерные переменные)

Здесь $E = \frac{{{{v}^{2}}}}{2} + \left( {1 - \cos u} \right)$, $f = - \sin u$, далее принимается ${{E}_{0}} = 1$ – коэффициент, ограничивающий рост отрицательного сопротивления.

Фазовые траектории задач с начальными данными $u\left( 0 \right) = {{u}_{0}}$, $v\left( 0 \right) = 0$ приведены в верхнем правом углу рис. 3. В этом случае фазовые траектории будут притягиваться к ближайшей к начальным данным замкнутой кривой многосвязного предельного цикла. В случае начальных данных вида $u\left( 0 \right) = 0$, $v\left( 0 \right) = {{v}_{0}}$ поведение траекторий более сложное. Если начальные данные таковы, что выполняется условие $E < {{E}_{0}}$, то траектории будут наматываться на центральный предельный цикл (рис. 3, кривая 1). При больших значениях коэффициента обратной связи (диссипации) $\varepsilon $ и выполнении условия $E > {{E}_{0}}$ (рис. 3, кривая 2) траектории будут наматываться на ближайшую замкнутую область предельного цикла, причем их абсцисса не будет превышать некоторого предельного значения (для центральной области $\left| u \right| < \pi $). С уменьшением параметра $\varepsilon $ траектории будут приближаться к вертикальной сепаратрисе между областями предельного цикла так, что вторая производная ${{d}^{2}}v{\text{/}}d{{u}^{2}}$ будет обращаться в нуль. При достижении параметром $\varepsilon $ критического значения траектория достигнет сепаратрисы (для центральной области в точке $\left( {0,\pi } \right)$), а в производной $dv{\text{/}}du$ возникнет разрыв первого рода. При дальнейшем уменьшении $\varepsilon $ областью притяжения станет следующая справа от начальной замкнутая область предельного цикла (рис. 3, кривые 3, 4). Такой сценарий будет повторяться и далее при уменьшении $\varepsilon $ области притяжения траекторий будут сменяться на все более удаленные замкнутые области многосвязного предельного цикла (рис. 3, кривая 5). Можно показать, что поведение фазовых кривых для отрицательных значений начальных данных $u\left( 0 \right) = 0$, $v\left( 0 \right) = - {{v}_{0}}$ будут описываться траекториями антисимметричными по отношению к рассмотренным (рис. 3, кривая 6).

Заключение. Приведенные примеры показывают, что выделенный класс автоколебательных систем позволяет находить предельные циклы с помощью простых аналитических вычислений. При этом определяются амплитуды колебаний и их периоды. Если создать такие электромеханические устройства, которые обеспечивают обратную связь, описываемую нелинейным сопротивлением $2\varepsilon \left( {E - {{E}_{0}}} \right)\dot {u}$, то можно, например, сконструировать на основе примера 3 высокоточный маятниковый гравиметр.

Работа выполнена в рамках госзаданий АААА-А20-120011690138-6 и АААА-А20-120011690132-4.