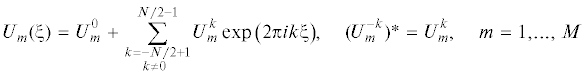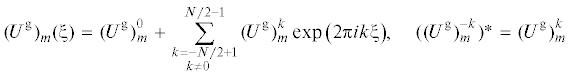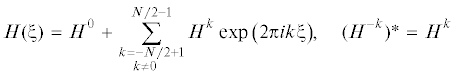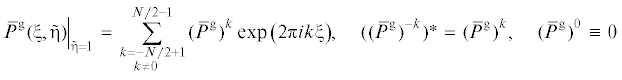Прикладная математика и механика, 2020, T. 84, № 6, стр. 694-708
Расчет линейной и нелинейной устойчивости двухслойного течения Куэтта
1 Институт теплофизики им. С.С. Кутателадзе СО РАН
Новосибирск, Россия
* E-mail: trifonov@itp.nsc.ru
Поступила в редакцию 03.07.2020
После доработки 30.09.2020
Принята к публикации 01.10.2020
Аннотация
Рассмотрена линейная и нелинейная устойчивость двухслойного течения Куэтта в горизонтальном канале. На первом этапе были линеаризованы уравнения Навье–Стокса в обеих фазах. Затем решалась спектральная задача и исследовалась динамика периодических возмущений в широком диапазоне изменений объемного содержания жидкостей и скорости верхней пластины. Рассчитаны нейтральные и наиболее быстро растущие возмущения неустойчивой моды. На втором этапе, для полных уравнений Навье–Стокса для обеих жидкостей рассчитавались нелинейные стационарно-бегущие волновые режимы для течения Куэтта в горизонтальном канале. Проведено сопоставление с имеющимися в литературе экспериментальными данными.
1. Введение и постановка задачи. В рамках первоначальной постановки задачи анализа линейной устойчивости расслоенного течения Куэтта–Пуазейля в плоском горизонтальном канале [1] (рис. 1) задавались отношение объемных содержаний двух жидкостей ${{h}_{1}}{\text{/}}{{h}_{2}}$ и число Рейнольдса построенное по скорости межфазной поверхности. Использовались асимптотические методы и рассматривались только длинноволновые возмущения. Анализ был ограничен жидкостями одинаковой плотности. Было показано, что достаточно разницы вязкостей верхней и нижней жидкости (${{\mu }_{1}}{\text{/}}{{\mu }_{2}} \ne 1$) для возниковения неустойчивых возмущений при любых числах Рейнольдса. С использованием численных методов для решения задачи Орра–Зоммерфельда, авторами [2, 3] было исследовано поведение как длинных, так и коротких возмущений для течения Пуазейля. Задача многопараметрическая и для получения качественных выводов варьировался параметр ${{h}_{1}}{\text{/}}{{h}_{2}}$ при различных постоянных значениях других параметров. Например, рассматривались жидкости одинаковой плотности ${{\rho }_{1}}{\text{/}}{{\rho }_{2}} = 1$ и нулевые значения поверхностного натяжения и силы тяжести. Для нескольких значений отношения вязкостей ${{\mu }_{1}}{\text{/}}{{\mu }_{2}}$, на плоскости параметров $\left( {\alpha ,{{h}_{1}}{\text{/}}{{h}_{2}}} \right)$ строились нейтральные кривые, α – волновое число возмущения. Затем, например, “включались” сила тяжести или сила поверхностного натяжения. Продемонстрировано существование нескольких областей неустойчивых возмущений, и некоторые из них являются замкнутыми. При больших числах Рейнольдса показано одновременное существование двух мод неустойчивости – “поверхностной” и “сдвиговой” (мода Толмина–Шлихтинга, ведущая к переходу к турбулентности).
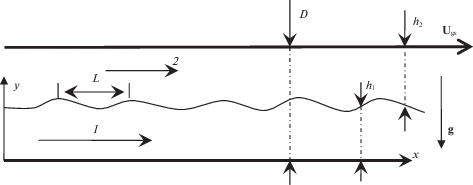
Рис. 1.
Расслоенное течение двух жидкостей в горизонтальном канале. Жидкость 1 (нижняя) – вода или водно-глицериновый раствор; жидкость 2 (верхняя) – воздух или минеральное масло. Верхняя плоскость двигается и приводит в движение обе жидкости – течение Куэтта.
Задача Орра–Зоммерфельда для течения Куэтта решалась с использованием аналитических и численных методов. Для случая жидкостей с близкими плотностями, найдены неустойчивые длинноволновые (в сравнении с толщиной жидкого слоя) и коротковолновые возмущения поверхностной моды. Хорошо известно [7, 8], что плоское однослойное течение Куэтта устойчиво относительно линейных периодических возмущений при любых значениях числа Рейнольдса. В случае двухслойного течения Куэтта, сдвиговая мода Толмина–Шлихтинга, ведущая к переходу к турбулентности, также не найдена. Рассматривалось [9–13] поведение возмущений на нелинейной стадии развития. С использованием асимптотического разложения, авторы получили эволюционное уравнение Курамото–Сивашинского для описания динамики малых длинноволновых возмущений поверхности раздела с интегралом для учета воздействия верхней жидкости. Были рассчитаны волновые режимы в малой окрестности кривой нейтральной устойчивости. Исследованию нелинейной стадии развития неустойчивых возмущений в рамках полных уравнений Навье–Стокса посвящено большое число исследовний (см., например, обзоры [13, 14]). Сравнительно недавно [15–17], получен существенный прогресс в этом направлении и рассчитано двухслойное волновое течение в наклонном канале. В частности, рассматривались [15] две “модельные” системы жидкостей с низким и высоким значением отношения ρ1/ρ2. Исследовалось [16, 17] течение Пуазейля для воды и воздуха. Обобщение подходов [16, 17] на случай горизонтального двухслойного течения Куэтта является одной из целей настоящей работы. Уравнения [16, 17], и использованная в них система безразмерных величин, не пригодны для горизонтального случая. Расчеты на основе полных уравнений Навье–Стокса особенно актуальны для дальнейшего развития и аппробации упрощенных моделей к описанию волнового двухслойного течения в горизонтальных и наклонных каналах. Единственным экспериментальным исследованием по устойчивости двухслойного течения Куэтта остается в настоящее время [18]. Исследовалось течение в горизонтальном канале глубиной 20 мм и шириной 40 мм. Этот канал замкнут в круг со средним диаметром 400 мм. Верхней жидкостью, увлекаемой в движение вращающейся пластиной, являлось минеральное масло. Нижней жидкостью являлась смесь воды и глицерина в различных пропорциях (четыре варианта). Изучалась динамика границы раздела при различных значениях отношения ${{h}_{1}}{\text{/}}{{h}_{2}}$ и при изменениях скорости вращения верхней пластины. Расчет динамики линейных и нелинейных возмущений для двухслойного течения жидкостей [18] также одна из основных целей нашей работы. В экспериментах [18] течение Куэтта трехмерное, глубина канала сопоставима с его шириной и присутствовали центробежные силы. В данной статье рассматривается плоский случай. Количественного соответствия с экспериментом ожидать не следует, и сравнение будет носить качественный характер. Будут проанализированы нейтральные кривые и наиболее опасные линейные возмущения, затем рассчитываются стационарно-бегущие волны конечной амплитуды. Рассматривается также течение Куэтта для воды и воздуха, что актуально для задач охлаждения электронных плат и других многочисленных приложений двухслойных течений (см., например, обзоры [19, 20]).
Таким образом, в части задачи о линейной устойчивости, в отличие от предшествующих исследований [1–6], рассмотрены реальные жидкости, использованные в экспериментах [18, 20]. Использование полных уравнений Навье–Стокса для обеих жидкостей является принципиальным отличием от предшествующих исследований [9–13] по описанию нелинейной динамики периодических возмущений в горизонтальном канале. В отличие от [15–17], исследовано течение Куэтта в горизонтальном канале для реальных жидкостей с сопоставимыми значениями вязкости и плотности.
2. Основные уравнения. Совместное волновое течение двух несмешивающихся жидкостей в горизонтальном канале (течение Куэтта, рис. 1) описывается системой уравнений Навье–Стокса с соответствующими граничными условиями:
(2.1)
$\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} = - \frac{{\partial{ \bar {P}}}}{{\partial x}} + \frac{1}{{\varepsilon \operatorname{Re} }}\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}} + {{\varepsilon }^{2}}\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}}} \right)$(2.2)
${{\varepsilon }^{2}}\left( {\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}}} \right) = - \frac{{\partial{ \bar {P}}}}{{\partial y}} - \frac{{3(1 - {{\varepsilon }_{\rho }})\varepsilon _{2}^{3}\operatorname{R} }}{{{{{\operatorname{Re} }}^{2}}}} + \frac{\varepsilon }{{\operatorname{Re} }}\left( {\frac{{{{\partial }^{2}}v}}{{\partial {{y}^{2}}}} + {{\varepsilon }^{2}}\frac{{{{\partial }^{2}}v}}{{\partial {{x}^{2}}}}} \right)$(2.6)
$\begin{gathered} \left( {\sigma _{{ik}}^{\operatorname{g} } - {{\sigma }_{{ik}}}} \right){{n}_{k}}{{\tau }_{i}} = 0 \Rightarrow {{\varepsilon }_{\mu }}n\left( {\frac{{\partial {{u}^{\operatorname{g} }}}}{{\partial y}} + {{\varepsilon }^{2}}\frac{{\partial {{v}^{\operatorname{g} }}}}{{\partial x}} + 4{{\varepsilon }^{2}}\frac{{\partial {{v}^{\operatorname{g} }}}}{{\partial y}}\frac{{\partial H}}{{\partial x}}\frac{1}{{1 - {{\varepsilon }^{2}}{{{\left( {\frac{{\partial H}}{{\partial x}}} \right)}}^{2}}}}} \right) - \\ - \;\frac{{\partial u}}{{\partial y}} - {{\varepsilon }^{2}}\frac{{\partial v}}{{\partial x}} - 4{{\varepsilon }^{2}}\frac{{\partial v}}{{\partial y}}\frac{{\partial H}}{{\partial x}}\frac{1}{{1 - {{\varepsilon }^{2}}{{{\left( {\frac{{\partial H}}{{\partial x}}} \right)}}^{2}}}} = 0, \\ y = H(x,t) \\ \end{gathered} $(2.7)
$\begin{gathered} \left( {\sigma _{{ik}}^{\operatorname{g} } - {{\sigma }_{{ik}}}} \right){{n}_{k}}{{n}_{i}} - \frac{\sigma }{{\hat {R}}} = 0 \Rightarrow - {{\varepsilon }_{\rho }}{{n}^{2}}{{{\bar {P}}}^{\operatorname{g} }} + \bar {P} - \\ - \;\frac{{2\varepsilon }}{{\operatorname{Re} }}\left( {\frac{{\partial v}}{{\partial y}} - {{\varepsilon }_{\mu }}n\frac{{\partial {{v}^{\operatorname{g} }}}}{{\partial y}}} \right)\frac{{1 + {{\varepsilon }^{2}}{{{\left( {\frac{{\partial H}}{{\partial x}}} \right)}}^{2}}}}{{1 - {{\varepsilon }^{2}}{{{\left( {\frac{{\partial H}}{{\partial x}}} \right)}}^{2}}}} + \frac{{\operatorname{We} {{\varepsilon }_{2}}{{\varepsilon }^{2}}\frac{{{{\partial }^{2}}H}}{{\partial {{x}^{2}}}}}}{{{{{\operatorname{Re} }}^{2}}{{{\left[ {1 + {{\varepsilon }^{2}}{{{\left( {\frac{{\partial H}}{{\partial x}}} \right)}}^{2}}} \right]}}^{{3/2}}}}} = 0, \\ y = H(x,t) \\ \end{gathered} $(2.9)
$\frac{1}{n}\frac{{\partial {{u}^{\operatorname{g} }}}}{{\partial t}} + {{u}^{\operatorname{g} }}\frac{{\partial {{u}^{\operatorname{g} }}}}{{\partial x}} + {{v}^{\operatorname{g} }}\frac{{\partial {{u}^{\operatorname{g} }}}}{{\partial y}} = - \frac{{\partial {{{\bar {P}}}^{\operatorname{g} }}}}{{\partial x}} + \frac{1}{{\varepsilon {{\varepsilon }_{2}}{{{\operatorname{Re} }}^{\operatorname{g} }}}}\left( {\frac{{{{\partial }^{2}}{{u}^{\operatorname{g} }}}}{{\partial {{y}^{2}}}} + {{\varepsilon }^{2}}\frac{{{{\partial }^{2}}{{u}^{\operatorname{g} }}}}{{\partial {{x}^{2}}}}} \right)$(2.10)
${{\varepsilon }^{2}}\left( {\frac{1}{n}\frac{{\partial {{v}^{\operatorname{g} }}}}{{\partial t}} + {{u}^{\operatorname{g} }}\frac{{\partial {{v}^{\operatorname{g} }}}}{{\partial x}} + {{v}^{\operatorname{g} }}\frac{{\partial {{v}^{\operatorname{g} }}}}{{\partial y}}} \right) = - \frac{{\partial {{{\bar {P}}}^{\operatorname{g} }}}}{{\partial y}} + \frac{\varepsilon }{{{{\varepsilon }_{2}}{{{\operatorname{Re} }}^{\operatorname{g} }}}}\left( {\frac{{{{\partial }^{2}}{{v}^{\operatorname{g} }}}}{{\partial {{y}^{2}}}} + {{\varepsilon }^{2}}\frac{{{{\partial }^{2}}{{v}^{\operatorname{g} }}}}{{\partial {{x}^{2}}}}} \right)$(2.11)
$\frac{{\partial {{u}^{\operatorname{g} }}}}{{\partial x}} + \frac{{\partial {{v}^{\operatorname{g} }}}}{{\partial y}} = 0$(2.12)
${{u}^{\operatorname{g} }} = {{U}_{{\operatorname{gs} }}},\quad {{v}^{\operatorname{g} }} = 0,\quad y = \frac{1}{{{{\varepsilon }_{2}}}}$Здесь $u$, $v$ – компоненты вектора скорости нижней жидкости (далее жидкость 1) вдоль осей $x$ и $y$ соответственно; ${{u}^{\operatorname{g} }}$, ${{v}^{\operatorname{g} }}$ – компоненты вектора скорости верхней жидкости (далее жидкость 2 или “газовая” фаза) вдоль осей $x$ и $y$ соответственно; $P$ и ${{P}^{\operatorname{g} }}$ – давление в жидкости и газе; ${{\sigma }_{{ik}}}$ и $\sigma _{{ik}}^{\operatorname{g} }$ – компоненты тензора напряжений в жидкой и газовой фазах; nk и τi – компоненты нормального и касательного векторов к волновой границе раздела $H(x,t)$; $\hat {R}$ – радиус кривизны.
Уравнения (2.1)–(2.4) представляют собой законы сохранения импульса и массы для жидкости, а также кинематическое условие на границе раздела, уравнение (2.5) – условие прилипания на стенке, уравнения (2.6)–(2.7) – условия равенства касательных и нормальных сил на поверхности раздела, уравнение (2.8) – условие прилипания на поверхности раздела. Уравнения (2.9), (2.10) представляют собой закон сохранения импульса для газовой фазы, уравнение (2.11) – закон сохранения массы и уравнение (2.12) является условием прилипания на верхней стенке канала для газовой фазы в случае плоского течения Куэтта для двух несмешивающихся жидкостей.
Уравнения (2.1)–(2.12) записаны в безразмерном виде. Безразмерные величины связаны с соответствующими размерными величинами (символы со звездочками) следующим образом:
Здесь ν, μ – кинематическая и динамическая вязкости жидкости; $\rho $ – плотность жидкости; $\sigma $ – поверхностное натяжение; D – высота канала; аналогично для газовой фазы ${{\nu }_{\operatorname{g} }}$, ${{\mu }_{\operatorname{g} }}$ – кинематическая и динамическая вязкости; ${{\rho }_{\operatorname{g} }}$ – плотность; ${{\operatorname{Re} }^{\operatorname{g} }}$ число Рейнольдса для газа. В качестве масштаба скорости $u_{0}^{\operatorname{g} }$ и $u_{0}^{{}}$ будем использовать скорость верхней пластины ${{U}_{{\operatorname{gs} }}}$ (значение n в этом случае равно единице). В качестве масштаба вдоль оси x используется длина волны рассматриваемых возмущений L. В качестве масштаба H0 вдоль оси y выбираем высоту нижнего слоя жидкости в канале, ${{H}_{0}} = {{h}_{1}}$. Отметим, что исходные давления в уравнениях (2.1)–(2.12) преобразованы и исключена гравитация в уравнениях для газовой фазы:
Для дальнейших расчетов делается преобразование координат $\eta = y{\text{/}}H(x,t)$ для уравнений в жидкой фазе и $\tilde {\eta }$ = $(1 - {{\varepsilon }_{2}}y){\text{/}}(1$ – ${{\varepsilon }_{2}}H(x,t))$ для уравнений в газовой фазе. Область течения в новых переменных становится известной: $\eta \in [0,1]$, $\tilde {\eta } \in [0,1]$. В целях экономии места уравнения (2.1)–(2.12) в переменных $(\eta ,\tilde {\eta })$ здесь не приводятся. Детали этого преобразования можно найти в [17].
В данной работе рассматриваются линейная и нелинейная устойчивость стационарных решений $[{{u}_{b}}(\eta )$, ${{{\bar {P}}}_{b}}(\eta )$, $u_{b}^{\operatorname{g} }(\tilde {\eta })$, ${\bar {P}}_{b}^{\operatorname{g} }(\tilde {\eta })$, ${{H}_{b}}]$ системы уравнений (2.1)–(2.12), соответствующих безволновому течению жидкости и газа (в этом случае значение ε = 1):
(2.13)
$\begin{gathered} {{u}_{b}}(x,\eta ) = {{\beta }_{1}}\eta ,\quad {{v}_{b}}(x,\eta ) = 0,\quad {{H}_{b}} = 1,\quad {{{\bar {P}}}_{b}}(\eta ) = - \frac{{3(1 - {{\varepsilon }_{\rho }})R\varepsilon _{2}^{3}(\eta - 1)}}{{{{{\operatorname{Re} }}^{2}}}} \\ \bar {P}_{b}^{\operatorname{g} }(\tilde {\eta }) = 0,\quad u_{b}^{\operatorname{g} }(x,\tilde {\eta }) = {{C}_{1}}\tilde {\eta } + 1,\quad v_{b}^{\operatorname{g} }(x,\tilde {\eta }) = 0 \\ {{\beta }_{1}} = {{\varepsilon }_{\mu }}{{\varepsilon }_{2}}{\text{/}}(1 - {{\varepsilon }_{2}}(1 - {{\varepsilon }_{\mu }})),\quad {{C}_{1}} = {{\beta }_{1}} - 1 \\ \end{gathered} $После подстановки
В результате задача сводится к обобщенной задаче на собственные значения для комплексных матриц общего вида:
(2.14)
$A\hat {x} = \lambda B\hat {x},\quad \hat {x} = {{\left( {\hat {H},{{{\left. {{{{\hat {P}}}^{\operatorname{g} }}} \right|}}_{{\tilde {\eta } = 1}}},{{{\hat {U}}}_{m}},{{{\hat {V}}}_{m}},{{{({{{\hat {U}}}^{\operatorname{g} }})}}_{m}},{{{({{{\hat {V}}}^{\operatorname{g} }})}}_{m}}} \right)}^{{\text{T}}}}$Матрицы $A$ и $B$ имеют размерность $2(M + {{M}^{\operatorname{g} }} + 1)$, их элементы определяются численно путем перебора единичных векторов возмущений [17].
Для получения ответа на вопрос об устойчивости стационарного решения $[{{u}_{b}}(\eta )$, ${{\bar {P}}_{b}}(\eta )$, $u_{b}^{\operatorname{g} }(\tilde {\eta })$, $\bar {P}_{b}^{\operatorname{g} }(\tilde {\eta })$, ${{H}_{b}}]$ необходимо проанализировать $2(M + {{M}^{\operatorname{g} }} + 1)$ собственных чисел задачи (2.14), варьируя волновое число возмущений $\alpha = 2\pi \varepsilon $. Решение устойчиво, если вещественные части всех собственных значений больше или равны нулю при всех положительных значениях волнового числа. Возмущение является нейтральным, если вещественная часть соответствующего ему собственного значения равна нулю – $\operatorname{Re} (\lambda ) = 0$. В этом случае фазовая скорость возмущения ${{c}_{{\operatorname{neut} }}} \equiv {\text{Im}}(\lambda ){\text{/}}\alpha $.
В задаче (2.14) имеется семь независимых параметров. Четыре параметра $\varepsilon $, ${{h}_{2}}{\text{/}}{{h}_{1}}$, ${{\varepsilon }_{\mu }}$, ${{\varepsilon }_{\rho }}$, R, We, ${{\operatorname{Re} }^{\operatorname{g} }}$, R, We, ${{\varepsilon }_{\mu }}$, ${{\varepsilon }_{\rho }}$ зависят только от физических свойств газа и жидкости и от размера канала. Отметим, что в случае $\sigma \ne 0$ и $g \ne {\text{0}}$, вместо параметров R и We можно использовать число Капицы $\operatorname{Fi} \equiv {{(\sigma {\text{/}}\rho )}^{3}}{\text{/}}(g{{\nu }^{4}})$ и отношение капиллярной постоянной к высоте канала, как это делалось ранее [17] – ${\text{R}} \equiv (1{\text{/}}3){{\operatorname{Fi} }^{{1/2}}}{{\left( {D{\text{/}}\sqrt {\sigma /(\rho g)} } \right)}^{3}}$, We ≡ ${{\operatorname{Fi} }^{{1/2}}}\left( {D{\text{/}}\sqrt {\sigma {\text{/}}(\rho g)} } \right)$.
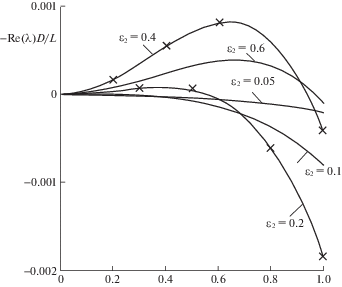
Для тестирования алгоритма решения задачи (2.14), были воспроизведены полученные ранее [4] зависимости инкремента роста линейных возмущений от волнового числа при различных толщинах нижнего слоя жидкости ε2 = h1/D, h2/h1 = (1 – ε2)/ε2. Рис. 2 демонстрирует сравнение наших расчетов (сплошные линии) и результатов [4] (символы) для одних и тех же параметров, пересчет которых друг в друга показан в подписи к рисунку 2. Ранее [4] использовались параметры $\alpha {\text{ }}$, ${{l}_{1}} = {{\varepsilon }_{2}}$, r0, $m$, ${{\operatorname{Re} }_{1}} = {{U}_{{\operatorname{gs} }}}D{\text{/}}{{\nu }_{1}}$; ${{\operatorname{F} }^{2}} = U_{{\operatorname{gs} }}^{2}{\text{/}}(gD)$ и $\operatorname{T} = \sigma {\text{/}}({{\mu }_{2}}{{U}_{{\operatorname{gs} }}})$.
Рис. 2.
Инкремент роста линейных возмущений (сплошные линии) в зависимости от длины волны при различных толщинах нижнего слоя ε2 = h1/D = l1. Сопоставление c расчетам работы [4] (обозначены ×). Здесь ερ = 1/ρ, εμ = 1/m, R = (Re1)2/(3F2), We = T Re1/m и значения параметров l1, r = 0.95, m = 100, Re1 = 10, F2 = 0.1, T = 0.1 соответствуют [4].
Расчет нелинейных стационарно-бегущих режимов $[u(\xi ,\eta )$, $\bar {P}(\xi ,\eta )$, ${{u}^{\operatorname{g} }}(\xi ,\tilde {\eta })$, ${{\bar {P}}^{\operatorname{g} }}(\xi ,\tilde {\eta })$, $H(\xi )]$ уравнений (2.1)–(2.12) аналогичен алгоритму [17]. Здесь $\xi = x - ct$, с – фазовая скорость. Ограничимся изложением основных моментов этого расчета. Для аппроксимации периодических по координате ξ решений использовались полиномы Чебышёва и разложение в ряд Фурье:
Здесь “звездочка” обозначает комплексное сопряжение. Численный алгоритм стартует с задания начального приближения для гармоник $U_{m}^{k}$, ${{H}^{k}}$, ${\text{(}}{{U}^{\operatorname{g} }})_{m}^{k}$, ${{{\text{(}}{{\bar {P}}^{\operatorname{g} }})}^{k}}$ и для величины c. В выборе начала отсчета координты x имеется произвол. Как следствие, фазу одной из гармоник можно считать заранее известной (например, Re(H1) = 0). Это дает уравнение для определения фазовой скорости c. При заданных $(M + {{M}^{\operatorname{g} }} + 2)(N - 1)$ значениях гармоник $U_{m}^{k}$, $({{U}^{\operatorname{g} }})_{m}^{k}$, ${{{\text{(}}{{\bar {P}}^{\operatorname{g} }})}^{k}}$, $c$, ${{H}^{k}}$, поля скоростей $v(\xi ,\eta )$, ${{v}^{\operatorname{g} }}(\xi ,\tilde {\eta })$ и давлений $\bar {P}(\xi ,\eta )$, ${{\bar {P}}^{\operatorname{g} }}(\xi ,\tilde {\eta })$ однозначно определяются из уравнений (2.1–2.12). Далее рассчитывается невязка уравнений. Для улучшения начального приближения неизвестных $(U_{m}^{k}$, ${{H}^{k}}$, ${\text{(}}{{U}^{\operatorname{g} }})_{m}^{k}$, ${{{\text{(}}{{\bar {P}}^{\operatorname{g} }})}^{k}}$, $c)$ далее используется итерационный метод Ньютона.
3. Результаты расчетов. Задача является многопараметрической, и расчеты проведены для жидкостей, физические свойства которых приведены в таблице 1. Рассмотрены два значения высоты канала D = 20 и 5 мм. В расчетах варьировались скорость верхней пластины, длина волны возмущений и значение отношения ${{h}_{2}}{\text{/}}{{h}_{1}}$. В качестве верхней жидкости выступало минеральное масло (жидкость 2 в таблице 1) или воздух (жидкость 2а в таблице 1). Минеральное масло увлекало собой водоглицериновый раствор (жидкости 1а–1г в таблице 1), а воздух – воду (жидкость 1д в таблице 1). На первом этапе, при различных значениях скорости 0 < ${{U}_{{\operatorname{gs} }}}$ < 10 м/с и для значений ${{h}_{2}}{\text{/}}{{h}_{1}} \in [0.1,10]$, рассчитывается общее количество неустойчивых мод в задаче (2.14). Длина волны возмущений менялась с малым шагом в широком диапазоне $2\pi D{\text{/}}L \in [0.005,100]$, и рассчитывался спектр собственных значений задачи (2.14). На втором этапе рассчитываются нейтральные кривые и анализировали наиболее опасные возмущения. Затем были рассчитаны нелинейные волны с длиной волны соответствующей длине волны наиболее опасных линейных возмущений. Результаты представлены на рисунках 3–7.
Таблица 1.
Физические свойства жидкостей, использованные в расчетах
| Жидкость | Обзнч. | μ (Па с) | ν (м2/с) × 105 | ρ (кг/м3) | σ (Па м) | εμ = μ2/μ1 | ερ = ρ2/ρ1 |
|---|---|---|---|---|---|---|---|
| Минеральное масло | 2 | 0.0297 | 3.51 | 846 | – | – | – |
| Вода + Глицерин 15% + 85% | 1а | 0.111 | 9.2 | 1214 | 0.030 | 0.268 | 0.697 |
| Вода + Глицерин 32% + 68% | 1б | 0.0191 | 1.63 | 1169 | 0.030 | 1.55 | 0.724 |
| Вода + Глицерин 37% + 63% | 1в | 0.0121 | 1.05 | 1155 | 0.030 | 2.45 | 0.732 |
| Вода + Глицерин 42% + 58% | 1г | 0.0108 | 0.95 | 1142 | 0.030 | 2.76 | 0.741 |
| Воздух | 2а | 1.82 × 10–5 | 1.52 | 1.2 | – | – | – |
| Вода | 1д | 0.001 | 0.10 | 1000 | 0.075 | 0.0182 | 0.0012 |
Рис. 3.
Bолновые числа нейтральных возмущений в зависимости от скорости верхней пластины. Совместное течение (2а–1в) минерального масла и водно-глицеринового раствора (37% и 63%) в канале D = 20 мм. Линии 1, 2 и 2' ограничивают области неустойчивых возмущений.
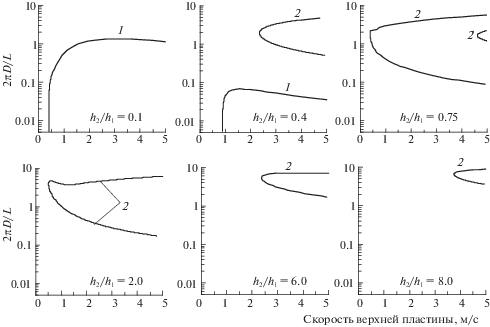
Рис. 4.
Bолновые числа нейтральных возмущений в зависимости от скорости верхней пластины. Совместное течение (2а–1а) минерального масла и водно-глицеринового раствора (15% и 85%) в канале D = 20 мм. Линии 1 и 2 ограничивают области неустойчивых возмущений.
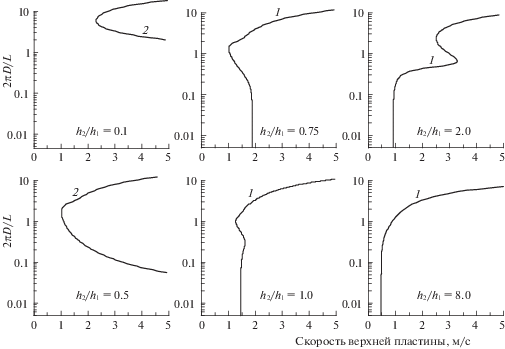
Рис. 5.
Bолновые числа нейтральных возмущений в зависимости от скорости верхней пластины. Совместное течение (2а–1д) воздуха и воды в канале D = 20 мм (верхние рисунки) и D = 5 мм (нижние рисунки). Линии 1 ограничивают области неустойчивых возмущений.
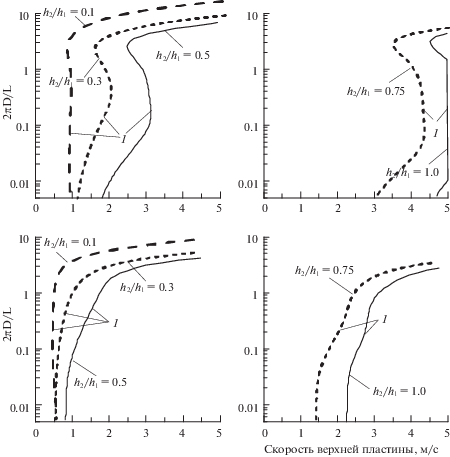
Рис. 6.
Ветвление нелинейных режимов от различных линий нейтральной устойчивости при Ugs = 2.0 м/с (см. рис. 3). Совместное течение (2а–1в) минерального масла и водно-глицеринового раствора (37% и 63%) в канале D = 20 мм. Здесь $H_{{\max }}^{*}$ – размерная максимальная толщина волнового профиля границы раздела. Рисунок 6(а) соответствует ветвлению от границы области неустойчивых длинноволновых возмущений при ${{h}_{2}}{\text{/}}{{h}_{1}} = 0.1$; рис. 6 б и в – от верхней и нижней границ области неустойчивых “коротковолновых” возмущений, соответственно, при ${{h}_{2}}{\text{/}}{{h}_{1}} = 0.75$.
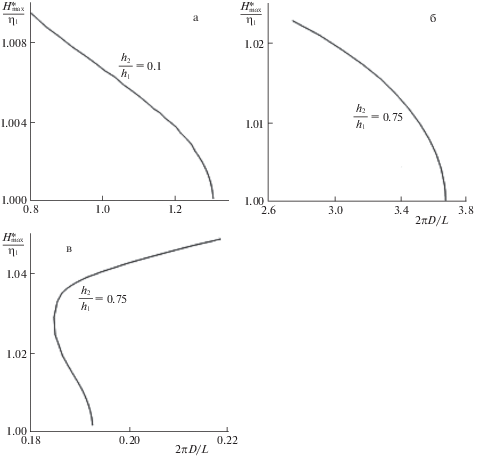
Рис. 7.
Зависимость максимальной толщины и частоты для нелинейных волн в зависимости от отношения толщины верхнего и нижнего слоев ${{h}_{2}}{\text{/}}{{h}_{1}}$. Совместное течение (2а–1в) минерального масла и водно-глицеринового раствора (37% и 63%) в канале D = 20 мм. Длина волны нелинейных режимов соответствует длине волны линейных возмущений максимального роста. Рис. 7а, б –“коротковолновая” область. Рис. 7в, г – длинноволновая область. Линии 1–3 соответствуют различным значениям скорости верхней пластины: 1 – Ugs = 5.0; 2 – 2.5; 3 – 0.5 (рис. 7а, б) и 1.0 (рис. 7в, г), м/с.
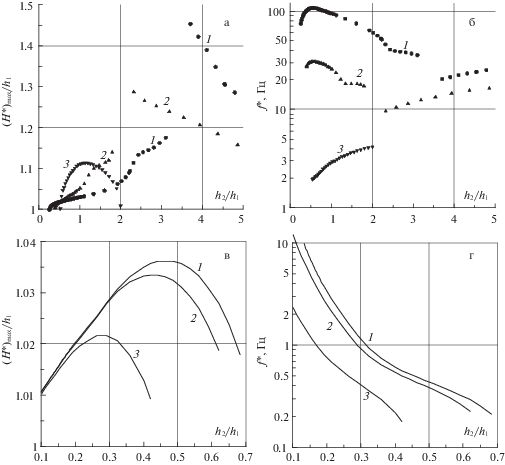
Для всех рассмотренных нами комбинаций жидкостей в исследованном диапазоне параметров найдена только одна неустойчивая мода – “поверхностная”. В спектре собственных значений задачи (2.14), для любого фиксированного набора параметров $(\varepsilon ,{{U}_{{\operatorname{gs} }}}{\text{,}}{{h}_{2}}{\text{/}}{{h}_{1}})$ из исследованного диапазона, присутствует только одно отрицательное собственное значение, либо ни одного. На рис. 3, для течения жидкостей (2 и 1в) из таблицы 1, представлены рассчитанные нейтральные кривые $\alpha ({{U}_{{\operatorname{gs} }}})$ при различных значениях параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$. Здесь $\alpha = 2\pi D{\text{/}}L$ – безразмерное волновое число. При малых значениях параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$, существует только одна область неустойчивых возмущений (см., например, рис. 3 при ${{h}_{2}}{\text{/}}{{h}_{1}} = 0.1$). Длинноволновые возмущения неустойчивы при таких значениях ${{h}_{2}}{\text{/}}{{h}_{1}}$, начиная с небольших скоростей верхней пластины. С увеличением параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$, эта область неустойчивости уменьшается и смещается в сторону еще более длинных возмущений. Например, длина волны нейтрального возмущения в этой зоне более чем в семьдесят раз превышает размер канала D при ${{h}_{2}}{\text{/}}{{h}_{1}} = 0.4$ на рис. 3. При дальнейшем увеличении параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$ область длинноволновых неустойчивых возмущений исчезает. Начиная с определенных значений параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$, появляется вторая область неустойчивости, ограниченная линией 2 или линиями 2 и 2' на рис. 3. На верхней границе второй области, длина волны нейтрального возмущения сопоставима с высотой канала и, условно, далее будем называть эту область неустойчивых возмущений коротковолновой. При дальнейшем увеличении параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$, область коротковолновых неустойчивых возмущений расширяется в зоне больших значений скорости верхней пластины (см. рис. 3). “Носик” коротковолновой области неустойчивых возмущений смещается в сторону меньших значений скорости верхней пластины. Для значений ${{h}_{2}}{\text{/}}{{h}_{1}} \geqslant 2$ область коротковолновых неустойчивых возмущений начинает уменьшаться и исчезает при ${{h}_{2}}{\text{/}}{{h}_{1}} \approx 10$ для течения жидкостей (2 и 1в) из таблицы 1.
Были рассчитаны, также, нейтральные кривые для течения жидкостей (2 и 1б) и (2 и 1г) из таблицы 1. При значениях $0.1 \leqslant {{h}_{2}}{\text{/}}{{h}_{1}} < ({{h}_{2}}{\text{/}}{{h}_{1}}){\kern 1pt} *$ имеется область длинноволновых неустойчивых возмущений. При значениях ${{({{h}_{2}}{\text{/}}{{h}_{1}})}_{*}}$ ≤ ${{h}_{2}}{\text{/}}{{h}_{1}}$ < ${{({{h}_{2}}{\text{/}}{{h}_{1}})}_{{*{\kern 1pt} *}}}$ < 10, имеется область “коротковолновых” неустойчивых возмущений. Качественно, эти зоны неустойчивых возмущений трансформируются аналогично рис. 3 и соответствующие фигуры здесь не представлены. Количественно, критические значения $({{h}_{2}}{\text{/}}{{h}_{1}}){\kern 1pt} *$, ${{({{h}_{2}}{\text{/}}{{h}_{1}})}_{*}}$, ${{({{h}_{2}}{\text{/}}{{h}_{1}})}_{{*{\kern 1pt} *}}}$ зависят от свойств жидкости. Можно отметить, что для рассмотренных нами трех комбинаций жидкостей, эти критические значения подчинялись следующей последовательности: ${{({{h}_{2}}{\text{/}}{{h}_{1}})}_{*}}$ < $({{h}_{2}}{\text{/}}{{h}_{1}}){\kern 1pt} *$ < ${{({{h}_{2}}{\text{/}}{{h}_{1}})}_{{*{\kern 1pt} *}}}$.
Для течения жидкостей (2 и 1а) из таблицы 1, нейтральные кривые, рассчитанные при различных значениях параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$, представлены на рис. 4. Видно ряд качественных отличий от результатов для течения жидкостей (2, 1б), (2, 1в) и (2, 1г) (см. рис. 3). При малых значениях параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$ неустойчивыми являются “коротковолновые возмущения”. С ростом параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$, эта область трансформируется и при значениях ${{h}_{2}}{\text{/}}{{h}_{1}} \geqslant 1$ (см. рис. 4) как коротковолновые, так и длинноволновые возмущения становятся неустойчивыми. Из таблицы 1 следует, что эта качественная особенность связана с величиной параметра ${{\varepsilon }_{\mu }}$. В отличие от течения жидкостей (2, 1б), (2, 1в) и (2, 1г), значение этого параметра меньше единицы для жидкостей (2, 1а) и верхняя жидкость является менее вязкой. На рис. 5 представлены нейтральные кривые для течения жидкостей (2а, 1д) – воздух и вода. Здесь величина параметра ${{\varepsilon }_{\mu }}$ много меньше единицы и верхняя жидкость значительно менее вязкая, чем нижняя жидкость. Далее представлены расчеты для двух значений высоты канала D = 20 и 5 мм. Область неустойчивых возмущений существенно сужается с ростом параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$ и смещается в область больших значений скорости верхней пластины ${{U}_{{\operatorname{gs} }}}$. Отметим, что с уменьшением высоты канала, при одинаковых значениях параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$, неустойчивость наступает при меньших значениях скорости верхней пластины.
В области неустойчивости, зависимость инкремента Re(–λ) от волнового числа демонстрирует экстремум. Существуют наиболее быстро растущие возмущения, и они являются наиболее “опасными”.
Характер ветвления нелинейных режимов вдоль различных линий нейтральной устойчивости показан на рис. 6. Области неустойчивых линейных возмущений для этого течения показаны на рис. 3. Ветвление от нейтральной кривой длинноволновой (рис. 6а) и от верхней границы коротковолновой (рис. 6б) областей неустойчивости носит мягкий характер. Рис. 6в соответствует ветвлению от нижней границы области неустойчивых “коротковолновых” возмущений и имеет жесткий характер.
На рис. 7 приведены зависимости максимальной толщины и частоты нелинейных волн в зависимости от отношения ${{h}_{2}}{\text{/}}{{h}_{1}}$ для трех значений скорости верхней пластины. Длина волны нелинейных режимов соответствует длине волны линейных возмущений максимального роста. Как в коротковолновой, так и в длинноволновой области неустойчивых возмущений (см. рис. 3) существует своя линейная волна максимального роста. Рис. 7а, б соответствуют нелинейным волнам в “коротковолновой” области; рис. 7в, г – нелинейным волнам в длинноволновой области. Отметим, что в коротковолновой области обнаружен разрыв в зависимостях основных характеристик нелинейных волн (см. линии 2, 3 рис. 7а, б), что свидетельствует о неединственности решений в этой области параметров.
Заключение. Исследована устойчивость двухслойного течения Куэтта в горизонтальном канале. Рассмотрено течение минерального масла и водно-глицеринового раствора (четыре комбинации), а также течение воздуха с водой. В исследованном диапазоне параметров найдена только одна неустойчивая мода – “поверхностная”. Проанализированы нейтральные кривые и наиболее опасные линейные возмущения этой моды. Показано, что при малых скоростях верхней пластины Ugs течение устойчиво для всех рассмотренных жидкостей и значений параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$. При увеличении скорости верхней пластины, появляются области неустойчивых возмущений. Трансформация этих областей с изменением Ugs определяется величиной отношения ${{h}_{2}}{\text{/}}{{h}_{1}}$, которая по данным расчетов качественно различна для течений с εμ > 1 и εμ < 1. В согласие с экспериментами [18], для жидкостей с εμ > 1 первыми проявляют себя длинноволновые возмущения (см. рис. 3). Их длина волны в области возникновения намного превосходит размер канала. Амплитуда и частота этих волн, показанные на рис. 7в, г, неплохо согласуются с измеренными [18] характеристиками волн – низкая частота 0.1–0.3 Гц и амплитуда в несколько десятых миллиметра. В экспериментах [18] найден, также, второй тип волн – коротковолновые режимы. В области их возникновения (малые значения Ugs), длина волны примерно равна 40 мм и сопоставима с высотой канала. Измеренная частота равнялась 7 Гц. Эти режимы хорошо соответствуют расчетным решениям в окрестности носика коротковолновой области неустойчивости (см. рис. 3 и 7а, б). В расчетах (см. рис. 6), ветвление нелинейных режимов происходит как в мягком, так и в жестком режимах, что хорошо согласуется с экспериментами [18].
Для жидкостей с εμ < 1, первыми проявляют себя “коротковолновые” возмущения (см. рис. 4). С увеличением параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$, область неустойчивости существенно расширяется и захватывает длинноволновую часть спектра возмущений.
Для системы воздух–вода (${{\varepsilon }_{\mu }} \ll 1$), начиная с самых малых значений параметра ${{h}_{2}}{\text{/}}{{h}_{1}}$, область неустойчивых возмущений простирается в широком диапазоне по длинам волн.
Работа выполнена при поддержки гранта РНФ_16-19-10449.
Список литературы
Yih C.S. Instability due to viscosity stratification // J. Fluid Mech. 1967. V. 27. P. 337–352.
Yiantsios S.G., Higgins B.G. Numerical solution of eigenvalue problems using the compound matrix method // J. Comput.Phys. Phys. 1988. V. 74. P. 25–40.
Yiantsios S.G., Higgins B.G. Linear stability of plane Poiseuille flow of two superposed fluids // Phys. Fluids. 1988. V. 31. P. 3225–3238.
Renardy Yu. Instability at the interface between two shearing fluids in a channel // Phys. Fluids. 1985. V. 28. № 12. P. 3441–3443.
Renardy Y.Y. The thin layer effect and interfacial stability in a two-layer Couette flow with similar liquids // Phys. Fluids. 1987. V. 30. P. 1627.
Hooper A.P. The stability of two superposed viscous fluids in a channel // Phys. Fluids. 1989. V. 28. P. 1613.
Штерн В.Н. Устойчивость плоского течения Куэтта // ПМТФ. 1969. № 5. С. 117–119.
Романов В.А. Устойчивость плоскопараллельного течения Куэтта // Функц. анализ и его прил. 1973. Т. 7. Вып. 2. С. 62–73.
Shlang T., Sivashinski G.I., Babchin A.J., Frankel A.L. Irregular wavy flow due to viscous stratification // J . Phys. Paris. 1985. V. 46. P. 863.
Hooper A.P., Grimshaw R. Nonlinear instability at the interface between two viscous fluids // Phys. Fluids. 1985. V. 28. P. 37.
Papageorgiou D.T., Maldarelli C., Rumschitzki D.S. Nonlinear interfacial stability of core-annular flows // Phys. Fluids A. 1990. V. 2. P. 340.
Цвелодуб О.Ю., Архипов Д.Г. Моделирование нелинейных волн на поверхности тонкой пленки жидкости, движущейся под действием турбулентного потока газа // ПМТФ. 2017. Т. 58. № 4. С. 56–67.
Хабахпашев Г.А. Моделирование нелинейной динамики поверхностных и внутренних волн в однородных и двухслойных жидкостях // Дисс. на соискание уч. ст. доктора физ.-мат. наук, Институт теплофизики им. С.С. Кутателадзе, Новосибирск, 2006.
Schmid P.J., Henningson D.S. Stability and Transition in Shear Flows. Applied Mathematical Sciences. Vol. 142. New York: Springer, 2001.
Schmidt P., O’Naraigh L., Lucquiaud M., Valluri P. Linear and nonlinear instability in vertical counter-current laminar gas-liquid flows // Phys. Fluids. 2016. V. 28. P. 042102.
Trifonov Y.Y. Instabilities of a gas-liquid flow between two inclined plates analyzed using the Navier–Stokes equations // Int. J. Multiphase Flow. 2017. V. 95. P. 144–154.
Trifonov Y.Y. Linear and nonlinear instabilities of a co-current gas-liquid flow between two inclined plates analyzed using the Navier–Stokes equations // Int. J. Multiphase Flow. 2020. V. 122. P. 103159.
Barthelet P., Charru F., Fabre J. Experimental study of interfacial long waves in a two-layer shear flow// J. Fluid Mech. 1995. V. 303. P. 23–53.
Weinstein S.J., Ruschak K. J. Coating flows // Annu. Rev. Fluid Mech. 2004. V. 36. P. 29–53.
Чиннов Е.А., Кабов О.А. Двухфазные течения в трубах и капиллярных каналах // Теплофизика высоких температур. 2006. Т. 44. Вып. 5. С. 777–795.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика