1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 85, № 1, 2021

Прикладная математика и механика, 2021, T. 85, № 1, стр. 121-134

Приближенный анализ экструзии пористого материала типа Грина

Г. М. Севастьянов 1, *, А. М. Севастьянов 2, **

1 Институт машиноведения и металлургии ХФИЦ ДВО РАН
Комсомольск-на-Амуре, Россия

2 Амурский гуманитарно-педагогический государственный университет
Комсомольск-на-Амуре, Россия

* E-mail: akela.86@mail.ru
** E-mail: mamiia20@mail.ru

Поступила в редакцию 17.03.2020
После доработки 29.07.2020
Принята к публикации 25.09.2020

Полный текст (PDF)

Аннотация

Рассмотрено стационарное движение идеально-пластического сжимаемого материала в сходящемся коническом канале. Полагается выполнение условия текучести Грина и ассоциированного с ним закона пластического течения. На поверхности контакта материала со стенкой канала считается выполненным закон максимального трения. Тензор напряжений Коши как функция локальной плотности среды определяется решением обыкновенного нелинейного дифференциального уравнения первого порядка, а установление пространственного распределения плотности сводится к отысканию определенного интеграла. Для произвольного вида функциональных коэффициентов модели Грина получены аналитические зависимости, которые задают двустороннюю оценку плотности и давления в канале. Проведено сравнение аналитических результатов с имеющимися экспериментальными данными.

Ключевые слова: жестко-пластический анализ, пористые материалы, условие пластичности Грина, экструзия, пластическая сжимаемость

Введение. Установившиеся течения пластических сред в сходящихся плоских или осесимметричных каналах исследуются с помощью математической теории пластичности уже почти столетие. Эти задачи моделируют широко распространенную технологическую операцию – прямую экструзию. Таким способом могут быть обработаны полимеры, металлы, различные материалы органического происхождения. Цели такой обработки могут быть различными: получение длинномерного изделия с сечением, отличным по площади от сечения заготовки; упрочнение заготовки (в т.ч. поверхностное); компактификация пористых материалов. Во многих практических приложениях разгрузка материала после экструзии не является предметом первостепенного интереса, и для оценки наиболее важных параметров процесса (необходимое давление и приобретенная деформация) используется жестко-пластический анализ. Первая известная работа, посвященная этой теме – исследование Надая [1]. В этой работе было найдено напряженное состояние пластического материала при течении в плоском щелевом канале с сужением при условии текучести Мизеса. Соответствующее этому напряженному состоянию поле скорости позже получил Хилл [2]. Первое решение для осесимметричного канала было получено Соколовским [3]. Для общего случая поверхности текучести, не зависящей от среднего напряжения, Шилд [4] получил систему обыкновенных дифференциальных уравнений, задающих решение осесимметричной задачи экструзии идеально-пластического материала. В этой же работе приведено и полное решение в рамках гипотезы Хаара–Кармана (для напряженного состояния, соответствующего одному из ребер призмы Треска). Среди других работ, посвященных течению несжимаемой среды, отметим также [5–8].

Аналогичные задачи для сжимаемых сред в целом сложнее. Поверхности текучести для пластически сжимаемых сред в наиболее простом виде задаются функциями, которые включают среднее напряжение и содержат две материальные константы. Среди них широко известны пирамида Мора–Кулона, поверхности Мизеса–Шлейхера, Друкера–Прагера, а также поверхность, соответствующая эллиптическому условию текучести Грина [9] с постоянными коэффициентами. Известно, что указанные выше классические двухконстантные условия текучести в ассоциированной формулировке пластического течения приводят к результатам, плохо согласующимся с экспериментальными данными в части предсказанного изменения объема. Тем не менее, именно для этих условий известны замкнутые решения в сферической геометрии (пригодные, среди прочего, для описания движения материала в осесимметричном сужающемся абсолютно гладком канале). Здесь укажем работы [10] (условие Мизеса–Шлейхера), [11] (условия Мора–Кулона и Друкера–Прагера), а также [12]. В последней работе использовано условие Грина с постоянными коэффициентами, которое приводит к статической определимости задачи о радиальной деформации полой сферы.

В более сложных моделях неизохорной пластичности используются функциональные коэффициенты при инвариантах тензора напряжений в уравнении поверхности текучести (пластические модули), явно зависящие от безразмерной относительной плотности пористого материала. К числу таких относятся модель Гурсона [13], а также ряд моделей типа Грина [14–19], нашедших применение для описания прессования порошков и деформирования различных пористых тел. Из указанных моделей наиболее часто используются эмпирическая модель [15] и полученная вариационными методами модель [18]. Для модели Гурсона известно приближенное аналитическое решение (первого порядка аппроксимации по пористости) о движении среды в коническом канале без трения [20]. Для модели Грина задача о движении среды в коническом канале сведена [21] к интегрированию связанной системы из двух дифференциальных уравнений первого порядка, получены численные результаты. В этой работе было рассмотрено течение в канале с шероховатыми стенками (сухое трение по закону Кулона–Амонтона), использована приближенная постановка задачи по методу Хилла. Известно также полное аналитическое решение задачи в той же постановке, но с использованием обобщения критерия Треска на некомпактные материалы [22]. Другие варианты подобного обобщения есть в работе [23].

Условия текучести в модели Грина и в модели Гурсона при нулевой пористости переходят в условие Мизеса, и в этом смысле являются его обобщением для некомпактных материалов. Возникает естественный вопрос – может ли пластическое течение, описываемое этими моделями, перейти в течение несжимаемого материала Мизеса при некоторой конечной степени редукции канала? Этот вопрос не исследовался ни в одной из указанных работ. Тем не менее, несложно сделать вывод, что решение [20] не допускает перехода к полному уплотнению пористого материала, а решение [22] допускает переход материала в состояние несжимаемости, в котором пластические свойства материала описываются моделью Треска, однако только при определенном условии на пластические модули. В настоящей работе получены в аналитическом виде такие условия для модели Грина.

В большинстве указанных выше работ рассматривались либо течения несжимаемой среды в каналах с шероховатыми стенками, либо течения сжимаемых сред в гладких каналах. Из известных аналитических результатов единственный раз [22] рассмотрено течение сжимаемой среды при наличии кулоновского трения, при этом использовано кусочно-линейное условие текучести, приводящее к статически определимой задаче. В настоящей работе рассматривается стационарное пластическое течение сжимаемой среды с гладким условием текучести в условиях максимального трения на контактной поверхности. Получены приближенные аналитические решения проблемы, которые представляют собой двустороннюю оценку решения.

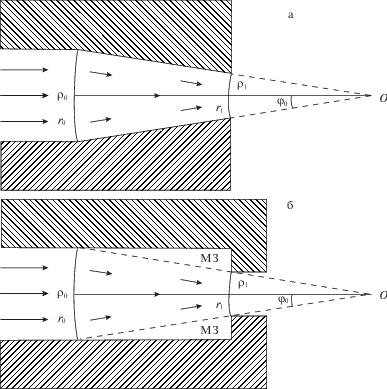
1. Постановка задачи и математическая модель процесса. Рассмотрим медленное стационарное движение пористого материала через конический канал с углом развертки $2{{\varphi }_{0}}$ (рис. 1, а). Задача об экструзии через цилиндрический канал (рис. 1, б) также может быть рассмотрена в указанной постановке, если предположить, что границей мертвой зоны материала является коническая поверхность [24]. В последнем случае угол развертки этой поверхности неизвестен и может быть установлен либо экспериментально, либо аналитически из условия минимума рассеянной энергии деформации. Будем пренебрегать обратимыми деформациями среды, считая, что пористый материал деформируется пластически только в сужающейся части канала, где полагается выполненным условие текучести Грина

(1.1)
$\Phi = {{\left( {{\sigma \mathord{\left/ {\vphantom {\sigma {{{\sigma }_{s}}}}} \right. \kern-0em} {{{\sigma }_{s}}}}} \right)}^{2}} + {{\left( {{\tau \mathord{\left/ {\vphantom {\tau {{{\tau }_{s}}}}} \right. \kern-0em} {{{\tau }_{s}}}}} \right)}^{2}} - 1 = 0,$
и ассоциированный закон течения
(1.2)
${\mathbf{\varepsilon }} = \Lambda \frac{{\partial \Phi }}{{\partial {\mathbf{\sigma }}}},$
где функции безразмерной относительной плотности среды ${{\tau }_{s}}(\rho )$ и ${{\sigma }_{s}}(\rho )$ есть сдвиговой и объемный пластические модули; ${\mathbf{\sigma }}$ – тензор напряжений Коши, $\sigma = {{\operatorname{tr} {\mathbf{\sigma }}} \mathord{\left/ {\vphantom {{\operatorname{tr} {\mathbf{\sigma }}} 3}} \right. \kern-0em} 3}$ – среднее напряжение, $\tau $ – интенсивность касательных напряжений, ${{\tau }^{2}}$ = ${{(\operatorname{tr} {{{\mathbf{\sigma }}}^{2}})} \mathord{\left/ {\vphantom {{(\operatorname{tr} {{{\mathbf{\sigma }}}^{2}})} 2}} \right. \kern-0em} 2}$ – ${{({{{\operatorname{tr} }}^{2}}{\mathbf{\sigma }})} \mathord{\left/ {\vphantom {{({{{\operatorname{tr} }}^{2}}{\mathbf{\sigma }})} 6}} \right. \kern-0em} 6}$; $\Lambda $ – скалярный пластический множитель; ${\mathbf{\varepsilon }}$ – тензор скорости деформации, $2{\mathbf{\varepsilon }}$ = ${{\left( {\nabla \otimes {\mathbf{v}}} \right)}^{T}}$ + $\left( {\nabla \otimes {\mathbf{v}}} \right)$, ${\mathbf{v}}$ – скорость точек среды, $\nabla $ – оператор Гамильтона.

Рис. 1.

Схема процесса экструзии через конический (а) и цилиндрический (б) канал; МЗ – мертвая зона материала.

Ассоциированный с поверхностью текучести (1.1) закон (1.2) позволяет, после необходимых преобразований [25], получить связь тензоров ${\mathbf{\sigma }}$ и ${\mathbf{\varepsilon }}$:

(1.3)
$\frac{{\sqrt 2 }}{2}\frac{{\mathbf{\sigma }}}{{{{\tau }_{s}}}} = \frac{{{\mathbf{\varepsilon }} + \vartheta {\mathbf{1}}\operatorname{tr} {\mathbf{\varepsilon }}}}{{\sqrt {\operatorname{tr} {{{\mathbf{\varepsilon }}}^{2}} + \vartheta {{{\operatorname{tr} }}^{2}}{\mathbf{\varepsilon }}} }},$
где ${\mathbf{1}}$ – единичный тензор, $\vartheta = {{{{{\left( {{{{{\sigma }_{s}}} \mathord{\left/ {\vphantom {{{{\sigma }_{s}}} {{{\tau }_{s}}}}} \right. \kern-0em} {{{\tau }_{s}}}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {{{{{\sigma }_{s}}} \mathord{\left/ {\vphantom {{{{\sigma }_{s}}} {{{\tau }_{s}}}}} \right. \kern-0em} {{{\tau }_{s}}}}} \right)}}^{2}}} 2}} \right. \kern-0em} 2} - {\text{1/3}}$.

Безразмерная плотность среды связана со скоростью материальных точек уравнением неразрывности, которое в стационарном случае имеет вид

(1.4)
$\nabla \cdot \left( {\rho {\mathbf{v}}} \right) = 0$

Введем сферическую систему координат $\left( {{{{\mathbf{e}}}_{{\mathbf{r}}}},{{{\mathbf{e}}}_{{\mathbf{\varphi }}}},{{{\mathbf{e}}}_{{\mathbf{\theta }}}}} \right)$ с центром в вершине $O$ конической поверхности $S$ (рис. 1). Сферическая поверхность $r = {{r}_{0}}$ соответствует входу в канал, $r = {{r}_{1}}$ – выходу из канала. Будем предполагать, что движение материала радиальное в сферической системе координат, что соответствует данным экспериментов, например, [26].

Компоненты тензора скорости деформации ${\mathbf{\varepsilon }}$ имеют вид

(1.5)
${{\varepsilon }_{{rr}}} = {{d{{v}_{r}}} \mathord{\left/ {\vphantom {{d{{v}_{r}}} {dr}}} \right. \kern-0em} {dr}},\quad {{\varepsilon }_{{\varphi \varphi }}} = {{\varepsilon }_{{\theta \theta }}} = {{{{v}_{r}}} \mathord{\left/ {\vphantom {{{{v}_{r}}} r}} \right. \kern-0em} r}$

Согласно соотношениям (1.3) и (1.5) тензор напряжений Коши диагональный с компонентами ${{\sigma }_{{rr}}}$, ${{\sigma }_{{\varphi \varphi }}} = {{\sigma }_{{\theta \theta }}}$.

Используем приближенное уравнение равновесия [22]

(1.6)
$r\frac{{d{{\sigma }_{{rr}}}}}{{dr}} + 2\left( {{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}} \right) + \gamma \cot \left( {\frac{{{{\varphi }_{0}}}}{2}} \right)\tau = 0.$

Здесь $\gamma = 0$ соответствует гладкому каналу, $\gamma = 1$ – шероховатому; $\tau $ – максимальное касательное напряжение, допустимое условием пластичности (1.1). Полагается, что влияние силы трения в шероховатом канале ограничивается слоем малой толщины вблизи контактной поверхности. В этой пристеночной зоне происходит интенсивное сдвиговое деформирование, касательное напряжение в этой области близко к своему максимально возможному значению и быстро убывает с удалением от стенок канала.

2. Двусторонняя оценка решения. Обозначим ${{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}} = \Delta \geqslant 0$. С учетом связи (1.3) и ${{\varepsilon }_{{rr}}} - {{\varepsilon }_{{\varphi \varphi }}} \geqslant 0$ имеет место соотношение

(2.1)
${{\Delta }^{2}} = \frac{{3\tau _{s}^{2}}}{{1 + {{\Re }^{2}}}},\quad \Re = - \frac{{\sqrt 3 }}{2}\frac{{{{\sigma }_{s}}}}{{{{\tau }_{s}}}}\frac{{{{\varepsilon }_{{rr}}} + 2{{\varepsilon }_{{\varphi \varphi }}}}}{{{{\varepsilon }_{{rr}}} - {{\varepsilon }_{{\varphi \varphi }}}}} \geqslant 0.$

В области пластического течения выполняется условие (1.1), следовательно, учитывая $\Delta = \sqrt 3 \tau $ и $\sigma = {{\sigma }_{{rr}}} - 2{\Delta \mathord{\left/ {\vphantom {\Delta 3}} \right. \kern-0em} 3} < 0$, имеем

(2.2)
${{\sigma }_{{rr}}} = \tfrac{2}{3}\Delta - {{\sigma }_{s}}{{\left( {1 - {{{\left( {\tfrac{\Delta }{{\sqrt 3 {{\tau }_{s}}}}} \right)}}^{2}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \left( {\tfrac{2}{{\sqrt 3 }}{{\tau }_{s}} - {{\sigma }_{s}}\Re } \right){{\left( {1 + {{\Re }^{2}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},$
давление $\left| {{{\sigma }_{{rr}}}} \right|$ ограничено сверху величиной ${{\sigma }_{s}}$, максимальное значение реализуется при $\Re \to + \infty $, чему соответствует состояние гидростатического сжатия.

Уравнение (1.4) позволяет получить соотношение ${{v}_{r}}\rho {{r}^{2}} = \operatorname{const} $. Тогда

(2.3)
$\frac{{{{\varepsilon }_{{rr}}} + 2{{\varepsilon }_{{\varphi \varphi }}}}}{{{{\varepsilon }_{{rr}}} - {{\varepsilon }_{{\varphi \varphi }}}}} = \frac{r}{\rho }\frac{{d\rho }}{{dr}}{{\left( {3 + \frac{r}{\rho }\frac{{d\rho }}{{dr}}} \right)}^{{ - 1}}}$

Уравнение (1.6) с учетом соотношений (2.1), (2.2) и (2.3) замыкается относительно плотности и принимает вид:

(2.4)
$\begin{gathered} \rho \frac{{d\Re }}{{d\rho }} = - \left( {1 + {{\Re }^{2}}} \right)\left[ {\frac{\alpha }{\Re } + \left( {\Re \rho \frac{{d{{\sigma }_{s}}}}{{d\rho }} - \rho \frac{2}{{\sqrt 3 }}\frac{{d{{\tau }_{s}}}}{{d\rho }}} \right){{{\left( {{{\sigma }_{s}} + \frac{2}{{\sqrt 3 }}{{\tau }_{s}}\Re } \right)}}^{{ - 1}}}} \right] \\ \alpha = 1 + \frac{\gamma }{{2\sqrt 3 }}\operatorname{ctg} \frac{{{{\varphi }_{0}}}}{2} \\ \end{gathered} $

Пространственное распределение плотности с учетом соотношений (2.1) и (2.3) определяется уравнением вида:

(2.5)
$\int\limits_{\rho \left( {{{r}_{{BC}}}} \right)}^\rho {\left( {1 + \frac{{\sqrt 3 }}{2}\frac{{{{\sigma }_{s}}}}{{{{\tau }_{s}}}}\frac{1}{\Re }} \right)\frac{{d\rho }}{\rho }} = - 3\ln \frac{r}{{{{r}_{{BC}}}}}$

Краевое условие для уравнения (2.5) заключается в задании локальной плотности на сферической поверхности $r = {{r}_{{BC}}}$. Краевое условие для замыкания (2.4) может быть получено из соотношения (2.2) по значению давления на входе или выходе канала. Наиболее простым является случай, когда давление и плотность заданы на одной и той же сферической поверхности.

Имеет место следующая двусторонняя оценка правой части уравнения (2.4):

$\begin{gathered} 0 \geqslant - \left( {1 + {{\Re }^{2}}} \right)\frac{\alpha }{\Re } \geqslant - \left( {1 + {{\Re }^{2}}} \right)\left[ {\frac{\alpha }{\Re } + \left( {\Re \rho \frac{{d{{\sigma }_{s}}}}{{d\rho }} - \rho \frac{2}{{\sqrt 3 }}\frac{{d{{\tau }_{s}}}}{{d\rho }}} \right){{{\left( {{{\sigma }_{s}} + \frac{2}{{\sqrt 3 }}{{\tau }_{s}}\Re } \right)}}^{{ - 1}}}} \right] \geqslant \\ \geqslant - \left( {1 + {{\Re }^{2}}} \right)\left( {\frac{\alpha }{\Re } + \Re \frac{\rho }{{{{\sigma }_{s}}}}\frac{{d{{\sigma }_{s}}}}{{d\rho }}} \right) \\ \end{gathered} $

Дифференциальное уравнение с разделяющимися переменными

(2.6)
$\rho \frac{{d\Re }}{{d\rho }} = - \left( {1 + {{\Re }^{2}}} \right)\frac{\alpha }{\Re }$
соответствует модели Грина с постоянными коэффициентами ${{\sigma }_{s}} = \operatorname{const} $, ${{\tau }_{s}} = \operatorname{const} $. Таким образом, известное решение [12] является предельным для общего условия Грина с коэффициентами модели, зависящими от плотности, в том смысле, что оно составляет одну из границ двусторонней оценки, которая представлена в настоящей работе. Уравнение (2.6) имеет решение

(2.7)
$\Re = {{\left( {C{{\rho }^{{ - 2\alpha }}} - 1} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$

Нелинейное дифференциальное уравнение

$\rho \frac{{d\Re }}{{d\rho }} = - \left( {1 + {{\Re }^{2}}} \right)\left( {\frac{\alpha }{\Re } + \Re \frac{\rho }{{{{\sigma }_{s}}}}\frac{{d{{\sigma }_{s}}}}{{d\rho }}} \right)$
линеаризуется заменой зависимой переменной ${{\sigma _{s}^{2}} \mathord{\left/ {\vphantom {{\sigma _{s}^{2}} {(1 + {{\Re }^{2}})}}} \right. \kern-0em} {(1 + {{\Re }^{2}})}}$ и имеет решение

(2.8)
$\Re = {{\left( {{{{\left( {1 + 2\alpha \sigma _{s}^{{ - 2}}{{\rho }^{{2\alpha }}}\int\limits_C^\rho {\sigma _{s}^{2}{{\rho }^{{ - \left( {2\alpha + 1} \right)}}}d\rho } } \right)}}^{{ - 1}}} - 1} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$

В выражениях (2.7), (2.8) $C$ – константы интегрирования.

3. Достаточные условия уплотнения до заданной плотности. Далее мы будем рассматривать следующий вариант постановки задачи: на выходе из канала задано целевое значение плотности, при этом противодавление в канале отсутствует: $\rho \left( {{{r}_{1}}} \right) = {{\rho }_{1}}$, ${{\sigma }_{{rr}}}\left( {{{\rho }_{1}}} \right) = 0$. Отсюда, согласно соотношению (2.2)

(3.1)
${{\Re }_{1}} = \Re \left( {{{\rho }_{1}}} \right) = \frac{2}{{\sqrt 3 }}\frac{{{{\tau }_{s}}\left( {{{\rho }_{1}}} \right)}}{{{{\sigma }_{s}}\left( {{{\rho }_{1}}} \right)}}$

На рис. 2 приведен график численного решения уравнения (2.4), а также графики аналитических оценок (2.7) и (2.8) при краевом условии (3.1). Использованы функциональные коэффициенты [18] модели Грина

${{\left( {\frac{{{{\sigma }_{s}}}}{\kappa }} \right)}^{2}} = \frac{4}{3}\frac{{{{\rho }^{2}}}}{{1 - \rho }},\quad {{\left( {\frac{{{{\tau }_{s}}}}{\kappa }} \right)}^{2}} = \frac{{3{{\rho }^{2}}}}{{5 - 2\rho }},$
где $\kappa $ – предел текучести на сдвиг материала каркаса.

Рис. 2.

Функция $\Re \left( \rho \right)$: $\blacktriangle $ – по (2.8), $\blacktriangledown $ – по (2.7), сплошная линия – численное интегрирование (2.4). Использована модель [17] и параметры ${{\rho }_{1}} = 0.98$, $\gamma = 1$ (закон максимального трения), ${{\varphi }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}$.

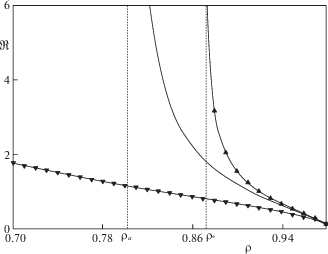
У верхней оценки (2.8) скорости изменения $\Re \left( \rho \right)$ присутствует качественная особенность, которая характерна и для решения исходного уравнения (2.4), а именно – наличие вертикальной асимптоты $\rho = {{\rho }_{*}}$, где ${{\rho }_{*}}$ есть корень уравнения

$\Re _{1}^{2}{{\left( {1 + \Re _{1}^{2}} \right)}^{{ - 1}}}\rho _{1}^{{ - 2\alpha }}\sigma _{s}^{2}\left( {{{\rho }_{1}}} \right) + 2\alpha \int\limits_{{{\rho }_{*}}}^{{{\rho }_{1}}} {\sigma _{s}^{2}{{\rho }^{{ - \left( {2\alpha + 1} \right)}}}d\rho } = \rho _{*}^{{ - 2\alpha }}\sigma _{s}^{2}({{\rho }_{*}})$

Поскольку точная асимптота $\rho = {{\rho }_{a}}$ решения (2.4), соответствующая ${{\sigma }_{{rr}}} = - {{\sigma }_{s}}$, неизвестна, то значение ${{\rho }_{*}}$ может быть использовано как верхняя оценка ${{\rho }_{a}}$. Пористый материал с начальной плотностью $\rho \geqslant {{\rho }_{*}}\left( {\alpha ,{{\rho }_{1}}} \right)$ гарантированно можно подвергнуть обработке прямой экструзией в канале с заданной характеристикой $\alpha $ до заданной плотности ${{\rho }_{1}}$. При этом для определения достаточной степени редукции канала ${{x}_{*}} = \ln \left( {{{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {{{r}_{1}}}}} \right. \kern-0em} {{{r}_{1}}}}} \right)$, ${{x}_{*}} = {{x}_{*}}\left( {\alpha ,{{\rho }_{1}}} \right)$ следует воспользоваться уравнением (2.5) с функцией $\Re \left( \rho \right)$ в виде (2.7) с учетом краевого условия (3.1):

${{x}_{*}} = \frac{1}{3}\int\limits_{{{\rho }_{*}}}^{{{\rho }_{1}}} {\left( {1 + \frac{{\sqrt 3 }}{2}\frac{{{{\sigma }_{s}}}}{{{{\tau }_{s}}}}{{{\left( {\left( {\Re _{1}^{2} + 1} \right){{{\left( {\frac{{{{\rho }_{1}}}}{\rho }} \right)}}^{{2\alpha }}} - 1} \right)}}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}} \right)\frac{{d\rho }}{\rho }} $

На рис. 3, а и б приведены изолинии ${{\rho }_{*}}\left( {{{\varphi }_{0}},{{\rho }_{1}}} \right)$. На рис. 4, а и б приведены изолинии ${{x}_{*}}\left( {{{\varphi }_{0}},{{\rho }_{1}}} \right)$. Пористые материалы с низкой начальной плотностью могут быть обработаны в шероховатом канале с большим углом развертки (в предельном случае – в абсолютно гладком канале с произвольным углом развертки, чему соответствует $\alpha = 1$) при достаточно высоких значениях степени редукции.

Рис. 3.

Изолинии ${{\rho }_{*}}\left( {{{\varphi }_{0}},{{\rho }_{1}}} \right)$ – плотность материала на входе в шероховатый канал с полным углом развертки $2{{\varphi }_{0}}$, достаточная для его уплотнения до заданной величины плотности ${{\rho }_{1}}$ на выходе из канала.

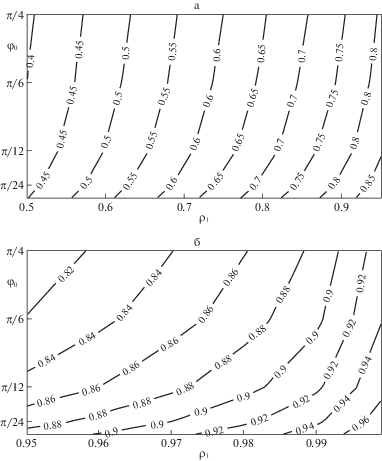
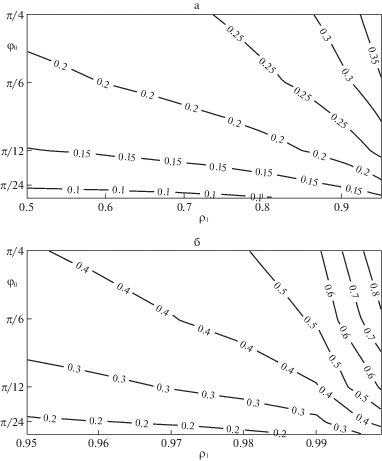
Рис. 4.

Изолинии ${{x}_{*}}\left( {{{\varphi }_{0}},{{\rho }_{1}}} \right)$ – степень редукции $\ln \left( {{{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {{{r}_{1}}}}} \right. \kern-0em} {{{r}_{1}}}}} \right)$ шероховатого канала с полным углом развертки $2{{\varphi }_{0}}$, достаточная для уплотнения пористого материала, который на входе в канал имеет плотность ${{\rho }_{*}}\left( {{{\varphi }_{0}},{{\rho }_{1}}} \right)$, до заданной величины плотности ${{\rho }_{1}}$ на выходе из канала.

Замечание (возможность полного уплотнения). Так как $\mathop {\lim }\limits_{\rho \to 1} {{\sigma }_{s}} = + \infty $, то на сферической поверхности, на которой произошло полное уплотнение материала, при конечном противодавлении согласно соотношению (2.2) должно выполняться $\Re = 0$. При этом выражение ${{\sigma }_{s}}\Re {{(1 + {{\Re }^{2}})}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ должно быть конечным. Тогда используя верхнюю оценку (2.8), имеем

$0 < \mathop {\lim }\limits_{\rho \to 1} 2\alpha {{\rho }^{{2\alpha }}}\int\limits_C^\rho {\sigma _{s}^{2}{{\rho }^{{ - \left( {2\alpha + 1} \right)}}}d\rho } < \mathop {\lim }\limits_{\rho \to 1} \sigma _{s}^{2}{{\Re }^{2}}{{\left( {1 + {{\Re }^{2}}} \right)}^{{ - 1}}} < + \infty $

Последнее соотношение по признаку Абеля требует

$0 < \int\limits_C^1 {\sigma _{s}^{2}d\rho } < + \infty ,\quad \forall C \in \left( {0,1} \right]$

Из известных моделей типа Грина этому условию удовлетворяют только модели [9, 19], где объемный пластический модуль имеет вид ${{\left( {{{{{\sigma }_{s}}} \mathord{\left/ {\vphantom {{{{\sigma }_{s}}} \kappa }} \right. \kern-0em} \kappa }} \right)}^{2}} = {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}{{\ln }^{2}}\left( {1 - \rho } \right)$.

4. Сравнение с экспериментальными данными. Известны [24] экспериментальные данные о процессе экструзии заготовки из спеченного порошка меди через канал, схематично представленный на рис. 1, б. В серии экспериментов для трех различных значений изменения площади поперечного сечения заготовки зафиксированы угол мертвой зоны материала и значение относительной плотности на выходе из канала, а также давление экструзии (см. табл. 1). Начальная относительная плотность материала в эксперименте ${{\rho }_{0}} = 0.9$.

Таблица 1
$1 - {{\left( {{{{{r}_{1}}} \mathord{\left/ {\vphantom {{{{r}_{1}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}} \right)}^{2}}$ ${{\varphi }_{0}}$ ${{\rho }_{1}}$ ${{\left. { - \left( {{{{{\sigma }_{{rr}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{rr}}}} \kappa }} \right. \kern-0em} \kappa }} \right)} \right|}_{{\rho = {{\rho }_{0}}}}}$
0.19 30° 0.936 0.68–0.72
0.36 48° 0.958 1.05–1.13
0.51 58° 0.977 1.42–1.58

На рис. 5 и 6 приведено сравнение указанных экспериментальных данных с численным решением (2.4), а также с аналитическими оценками (2.7) и (2.8). В расчетах в качестве исходных данных использованы экспериментальные значения ${{\varphi }_{0}}$, ${{\rho }_{0}}$ и ${{\rho }_{1}}$; расчетное значение $1 - {{\left( {{{{{r}_{1}}} \mathord{\left/ {\vphantom {{{{r}_{1}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}} \right)}^{2}}$ получено по (2.5), расчетное значение ${{\left. { - \left( {{{{{\sigma }_{{rr}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{rr}}}} \kappa }} \right. \kern-0em} \kappa }} \right)} \right|}_{{\rho = {{\rho }_{0}}}}}$ получено по формуле (2.2).

Рис. 5.

Изменение площади поперечного сечения заготовки: $ \bullet $ – экспериментальные данные [24], * – численный расчет, $\nabla $ – с использованием аналитической оценки (2.7), $\Delta $ – с использованием аналитической оценки (2.8).

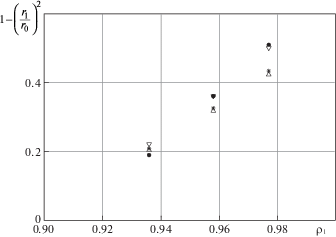
Рис. 6.

Давление экструзии: $\bracevert $ – экспериментальные данные [24], * – численный расчет, $\nabla $ – с использованием аналитической оценки (2.7), $\Delta $ – с использованием аналитической оценки (2.8).

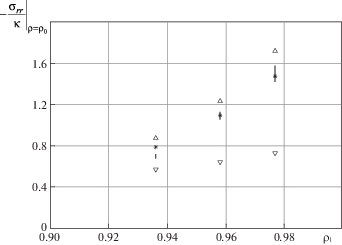
Численное решение достаточно точно соответствует экспериментальным данным, при этом аналитическая оценка (2.8) хорошо аппроксимирует численное решение. Аналитическая оценка (2.7) дает близкие результаты для изменения площади поперечного сечения заготовки, однако, по всей видимости, не может быть использована для оценки давления экструзии с достаточной точностью.

Заключение. Рассмотрено стационарное течение сжимаемой среды с условием пластичности Грина в коническом канале с шероховатыми (с выполнением на контактной поверхности законом максимального трения) или гладкими стенками. Полученные результаты также остаются справедливы для экструзии через цилиндрический канал с резко меняющимся сечением.

Исходная задача сведена к интегрированию одного нелинейного ОДУ и вычислению определенного интеграла. Получены двусторонние оценки решения этой системы уравнений и проведено их сравнение с экспериментальными результатами для величины давления экструзии и изменения площади поперечного сечения заготовки при заданной начальной и конечной пористости заготовки. Нижняя оценка давления, соответствующая постоянным пластическим модулям модели Грина, плохо согласуется с экспериментальными данными, в то время как верхняя оценка приемлемо описывает эксперимент.

Аналитические результаты могут быть использованы для оценки угла мертвой зоны материала в цилиндрическом канале посредством минимизации рассеянной мощности деформирования.

Полученная в работе аналитическая оценка подвижной особой точки системы уравнений процесса позволяет указать для произвольной модели типа Грина, какой выбор начального значения пористости материала и степени редукции канала гарантировано должен обеспечить уплотнение материала до заданной остаточной пористости. Проведенный анализ показывает, в частности, что полное уплотнение материала в коническом канале может быть реализовано только в рамках моделей с логарифмическим ростом объемного пластического модуля.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-31-00189.

Список литературы

  1. Nadai A. Über die Gleit- und Verzweigungsflächen einiger Gleichgewichtszustände bildsamer Massen und die Nachspannungen bleibend verzerrter Körper // Zeitschrift für Physik. 1924. V. 30. P. 106–138. https://doi.org/10.1007/BF01331828

  2. Hill R. Mathematical Theory of Plasticity. Oxford: The Clarendon Press, 1950.

  3. Соколовский В.В. Плоское и осесимметричное равновесие пластической массы между жесткими стенками // ПММ. 1950. Т. 14. Вып. 1. С. 75–92.

  4. Shield R.T. Plastic flow in a converging conical channel // J. Mech.&Phys. Solids. 1955. V. 3. P. 246–258. https://doi.org/10.1016/0022-5096(55)90035-1

  5. Ivlev D.D., Romanov A.V. On the generalization of Prandtl’s solution in spherical coordinates // JAMM. 1982. V. 46. № 5. P. 697–699. https://doi.org/10.1016/0021-8928(82)90021-1

  6. Alexandrov S., Barlat F. Modeling axisymmetric flow through a converging channel with an arbitrary yield condition // Acta Mechanica. 1999. V. 133. P. 57–68. https://doi.org/10.1007/BF01179010

  7. Bonitskaya O.V., Krasavin R.V., Markin A.A. The steady axisymmetric flow of ideally plastic materials in a conical channel // JAMM. 2010. V. 74. № 4. P. 494–500. https://doi.org/10.1016/j.jappmathmech.2010.09.016

  8. Georgiyevskii D.V. Extrusion of a plastic material from a circular sector with a small apex angle and a sink at the vertex // JAMM. 2013. V. 77. № 1. P. 109–114. https://doi.org/10.1016/j.jappmathmech.2013.04.014

  9. Green R.J. A plasticity theory for porous solids // Int. J. Mech. Sci. 1972. V. 14. P. 215–224. https://doi.org/10.1016/0020-7403(72)90063-X

  10. Monchiet V., Kondo D. Exact solution of a plastic hollow sphere with a Mises – Schleicher matrix // Int. J. Engng. Sci. 2012. V. 51. P. 168–178. https://doi.org/10.1016/j.ijengsci.2011.10.007

  11. Thore P., Pastor F., Pastor J., Kondo D. Closed-form solutions for the hollow sphere model with Coulomb and Drucker – Prager materials under isotropic loadings // Comptes Rendus Mecanique. 2009. V. 337. P. 260–267. https://doi.org/10.1016/j.crme.2009.06.030

  12. Shen W.Q., Shao J.F., Dormieux L., Kondo D. Approximate criteria for ductile porous materials having a Green type matrix: Application to double porous media // Comput. Mater. Sci. 2012. V. 62. P. 189–194. https://doi.org/10.1016/j.commatsci.2012.05.021

  13. Gurson A.L. Continuum theory of ductile rupture by void nucleation and growth: Part I – Yield criteria and flow rules for porous ductile media // Trans. ASME. J. Engng. Mater.&Technol. 1977. V. 99. P. 2–15. https://doi.org/10.1115/1.3443401

  14. Kuhn H.A., Downey C.L. Deformation characteristics and plasticity theory of sintered powder materials // Int. J. Powder Metallurgy. 1971. V. 7. № 1. P. 15–25.

  15. Shima S., Oyane M. Plasticity theory for porous metals // Int. J. Mech. Sci. 1976. V. 18. P. 285–291. https://doi.org/10.1016/0020-7403(76)90030-8

  16. Corapcioglu Y., Uz T. Constitutive equations for plastic deformation of porous materials // Powder Technol. 1978. V. 21. № 2. P. 269–274. https://doi.org/10.1016/0032-5910(78)80095-3

  17. Skorokhod V.V., Tuchinskii L.I. Condition of plasticity of porous bodies // Soviet Powder Metallurgy and Metal Ceramics. 1978. V. 17. № 11. P. 880–883. https://doi.org/10.1007/BF00792461

  18. Ponte Castaneda P. The effective mechanical properties of nonlinear isotropic composites // J. Mech.&Phys. Solids. 1991. V. 39. № 1. P. 45–71. https://doi.org/10.1016/0022-5096(91)90030-R

  19. Michel J.C., Suquet P. The constitutive law of nonlinear viscous and porous materials // J. Mech.&Phys. Solids. 1992. V. 40. № 4. P. 783–812. https://doi.org/10.1016/0022-5096(92)90004-L

  20. Durban D., Mear M.E. Asymptotic solution for extrusion of sintered powder metals // Trans. ASME. J. Appl. Mech. 1991. V. 58. P. 582–584. https://doi.org/10.1115/1.2897226

  21. Alexandrov S., Chesnikova O., Pirumov A. An approximate solution for axisymmetric extrusion of porous material // J. Technol. Plasticity. 2007. V. 32. № 1–2. P. 13–27.

  22. Alexandrov S.E., Druyanov B.A. Investigating the process of the steady extrusion of a compacted material // J. Appl. Mech.&Techn. Phys. 1990. V. 31. № 4. P. 645–649. https://doi.org/10.1007/BF00851344

  23. Revil-Baudard B., Cazacu O. Role of the plastic flow of the matrix on yielding and void evolution of porous solids: Comparison between the theoretical response of porous solids with Tresca and von Mises matrices // Mech. Res. Commun. 2014. V. 56. P. 69–75. https://doi.org/10.1016/j.mechrescom.2013.11.008

  24. Oh H.-K., Phark J.-W. A study of the axi-symmetric forward extrusion of porous metal through a square die // J. Mech. Working Technol. 1987. V. 15. P. 119–130. https://doi.org/10.1016/0378-3804(87)90029-5

  25. Itskov M. Tensor Algebra and Tensor Analysis for Engineers. With Applications to Continuum Mechanics. Cham: Springer, 2015.

  26. Crosta G.B., Powers P.S., Savage W.Z. A study of flow development in mass movements of granular materials // Dept. of the Interior, U.S. Geological Survey. Open file report 91–383. 1991.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал