Прикладная математика и механика, 2021, T. 85, № 1, стр. 3-20

Введение. Двухроторная электромеханическая система (далее TRMS – от англ. Twin Rotor MIMO System) состоит из двух перпендикулярных винтов с исполнительными устройствами на каждом из них и имеет две регулируемые координаты – углы тангажа и рысканья. В качестве задач управления рассматриваются слежение за заданными угловыми положениями либо стабилизация угловых положений на определенных уровнях. При построении алгоритмов управления TRMS возникают сложности, связанные с существенной нелинейностью математической модели объекта управления, наличием в ней перекрестных связей между винтами, а также параметрических и внешних возмущений. TRMS предназначена для апробации авторских алгоритмов управления, учитывающих указанные особенности математической модели, с дальнейшим применением их в реальном техническом устройстве – вертолете, динамика которого во многом схожа с динамикой TRMS. И для вертолета, и для TRMS характерно наличие перекрестных связей между винтами. Отличие TRMS от вертолета состоит в том, данная система закрепляется на неподвижной опоре, ее положение регулируется изменением угловых скоростей винтов. В вертолете угловые скорости вращения винтов практически постоянны, а его положение регулируется изменением углов атаки лопастей.

Для синтеза обратной связи в TRMS широко используются нелинейные законы с попыткой обеспечить глобальную стабилизацию. Одним из распространенных подходов является линеаризация системы статической обратной связью, в частности с использованием ПИД-регуляторов [1–3]. Подход основан на компенсации составляющих модели, для его реализации требуется параметрическая определенность модели объекта, либо идентификация параметров в реальном времени, что на практике может быть затруднительно. Отдельная проблема связана с настройкой параметров ПИД-регуляторов, поэтому используются модификации данного метода [4–7], обеспечивающие большую робастность. Альтернативным подходом является метод обратного хода [8–10], который опирается на свойства пассивности систем и также способен обеспечить робастность. Эффективным подходом при наличии параметрических неопределенностей и неизвестных согласованных возмущений является разрывное управление с организацией скользящего режима. Следует отметить, что законы разрывного управления приобретают эвристический характер при их применении в механических системах в качестве управляющих моментов [11, 12]. Кроме того, их использование в механических системах с учетом динамики электрических исполнительных устройств не даст ожидаемого эффекта, так как возмущения, действующие на механическую систему, не могут быть непосредственно подавлены.

Для многих механических систем, в том числе для TRMS, характерно наличие сил сухого трения, препятствующих желаемому движению объекта. Описание моделей сухого трения представлено в [13]. Возможным подходом к управлению при наличии сухого трения является его компенсация посредством ввода динамических моделей трения и наблюдателей состояния [14–16]. Однако его реализация требует параметрической определенности модели объекта управления, наличия всех необходимых измерений и адекватного построения моделей сил трения. Другим подходом выступают силовые методы, основанные на подавлении сил сухого трения за счет выбора ресурсов управления, превышающих предельно возможные коэффициенты трения [17–19]. Этот подход будет далее использован в работе. Его реализация не требует параметрической определенности, необходимо лишь знание границ изменения параметров. В качестве недостатка использования такого подхода можно отметить излишний расход ресурсов управления, когда фактические значения параметров оказываются существенно меньше заложенных в расчетах наихудших значений.

В данной работе для TRMS рассматривается задача отслеживания выходными переменными заданных сигналов при воздействии параметрических и внешних возмущений в условиях неполных измерений и при наличии проектных ограничений на переменные состояния и управления. Задача учета проектных ограничений представляется особенно актуальной, поскольку они следуют из технических требований и соображений безопасности. Поставленная задача решается с помощью метода декомпозиции [20] в рамках блочного подхода: в механической подсистеме последовательно назначаются стабилизирующие локальные связи, которые обеспечиваются разрывными управлениями в электрической подсистеме. В стандартном блочном подходе стабилизирующие фиктивные управления выбираются в виде неограниченных линейных функций с большими коэффициентами усиления, необходимыми для подавления возмущений [21, 22]. Однако использование линейных глубоких обратных связей на практике зачастую приводит к большой величине перерегулирования в начале переходных процессов. Предлагается принять стабилизирующие фиктивные управления в виде нелинейных S-образных сигма-функций [23–25]. Как гладкий аналог функции знака, сигма-функция позволяет обеспечить инвариантность по отношению к возмущениям с заданной точностью, а также обеспечить выполнение проектных ограничений ввиду своей ограниченности.

На практике для TRMS обычно не сложно организовать измерения угловых положений и токов якорей приводов постоянного тока, которые пересчитываются в моменты исполнительных устройств, но для реализации базового закона управления также необходимо знание угловых скоростей. В связи с этим возникает задача их оценивания, которая традиционно решается с помощью наблюдателя Луенбергера [8], а при наличии шумов в измерениях – с помощью расширенного фильтра Калмана [11, 26] и его модификаций [27]. Однако реализация данных наблюдателей требует точного знания параметров модели объекта, либо их идентификации с достаточной точностью. Кроме того, необходимо расширить пространство состояний за счет автономных динамических моделей, порождающих производные задающих сигналов и имитирующих внешние возмущения. Далее полагается, что задающие сигналы поступают в реальном времени, а их производные трактуются как неизвестные возмущения. Для оценивания угловых скоростей строится наблюдатель состояния пониженного порядка с сигмоидальными корректирующими воздействиями [23–25, 28], реализация которого не требует параметрической определенности и ввода дополнительной динамической модели внешних возмущений. Угловые скорости трактуются в виртуальной системе, записанной относительно ошибок наблюдения, как внешние ограниченные возмущения, а их оценку предоставляют сигмоидальные корректирующие воздействия.

Работа имеет следующую структуру. В разделе 1 описывается модель TRMS, формализуется постановка задачи слежения. В разделе 2 представлен основной результат. В рамках блочного подхода разработан базовый закон разрывного управления, приведена процедура выбора параметров сигмоидальных локальных связей, обеспечивающих выполнение проектных ограничений. В разделе 3 представлен синтез динамического наблюдателя угловых скоростей с сигмоидальными корректирующими воздействиями. В разд. 4 представлены результаты численного моделирования разработанных алгоритмов.

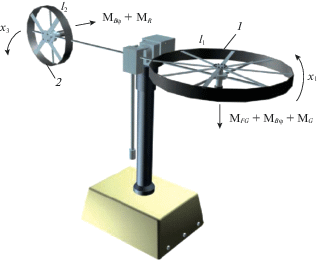
1. Описание объекта управления. Постановка задачи. На рис. 1 приведена схема TRMS. Механизм состоит из основного винта 1, к которому приложены гравитационный момент ${{M}_{{FG}}}$, момент сил трения ${{M}_{{B\psi }}}$ и гироскопический момент ${{M}_{G}}$. К хвостовому винту 2 приложен момент сил трения ${{M}_{{B\varphi }}}$ и момент ${{M}_{R}}$, возникающий за счет перекрестных связей между винтами. Математическая модель, соответствующая приведенной схеме, имеет вид [29]:

где ${{x}_{1}} = \psi $ – угол тангажа, ${{x}_{3}} = \varphi $ – угол рысканья (выходные, регулируемые переменные), $ - \pi {\text{/}}2 < {{x}_{1}}(t) < \pi {\text{/}}2$, $0 \leqslant {{x}_{3}}(t) \leqslant 2\pi $ – допустимые области изменения угловых положений, ${{x}_{2}}$, ${{x}_{4}}$ – угловые скорости, ${{I}_{1}}$, ${{I}_{2}}$ – моменты инерции основного и хвостового винтов, ${{K}_{{gy}}}$ – параметр гироскопического момента, $0 < {{K}_{{gy}}} < 1{\text{/}}(2\pi )$ ⇒ $1 - {{K}_{{gy}}}{{x}_{3}}\cos {{x}_{1}} > 0$, ${{f}_{1}} = {{M}_{{FG}}} + {{M}_{{B\psi }}} + {{\eta }_{1}}$ – сумма моментов, приложенных к основному винту, ${{M}_{{FG}}} = {{M}_{g}}\sin {{x}_{1}}$, ${{M}_{{B\psi }}} = {{B}_{{1\psi }}}x{}_{2}$ + ${{B}_{{2\psi }}}\operatorname{sign} x{}_{2}$, ${{M}_{g}}$ – параметр гравитационного момента, ${{B}_{{1\psi }}}$ и ${{B}_{{2\psi }}}$ – параметры момента силы трения, ${{f}_{2}} = {{M}_{{B\varphi }}} + {{\eta }_{2}}$ – сумма моментов, приложенных к хвостовому винту, ${{M}_{{B\varphi }}} = {{B}_{{1\varphi }}}{{x}_{4}} + {{B}_{{2\varphi }}}{\text{sign}}{{x}_{4}}$, ${{B}_{{1\varphi }}}$ и ${{B}_{{2\varphi }}}$ – параметры момента силы трения, ${{\eta }_{i}}$ – часть обобщенных моментов (в том числе аэродинамических моментов и моментов, возникающих за счет перекрестных связей), трактуемых как неизвестные ограниченные возмущения, ${\text{|}}{{\eta }_{i}}(t){\text{|}} \leqslant {{N}_{i}}$, $t \geqslant 0$, ${{\tilde {\tau }}_{i}} = {{a}_{i}}\tau _{i}^{2} + {{b}_{i}}{{\tau }_{i}}$ – моменты, создаваемые приводами на основном и хвостовом винтах соответственно, ${{a}_{i}}$, ${{b}_{i}}$ – коэффициенты передачи, $i = 1,2$.

Учитываемая динамика электрических исполнительных устройств (приводов постоянного тока) описывается следующими уравнениями [29]:

где ${{\tau }_{i}}$ – моменты сил на валу основного и хвостового двигателей; ${{T}_{{i0}}}$, ${{T}_{{i1}}}$, ${{k}_{i}}$ – параметры исполнительных устройств, ${{u}_{i}}$ – разрывные управления (напряжения якорей приводов), $i = 1,2$. В уравнениях (1.1)–(1.2) все конструктивные коэффициенты положительные.

Для объекта управления (1.1)–(1.2) ставится задача синтеза закона разрывного управления в форме обратной связи, обеспечивающего отслеживание выходными переменными ${{x}_{1}}(t)$ и ${{x}_{3}}(t)$ заданных сигналов ${{g}_{1}}(t)$ и ${{g}_{2}}(t)$ с некоторой точностью

где ${{e}_{{11}}}(t) = {{x}_{1}}(t) - {{g}_{1}}(t)$, ${{e}_{{12}}}(t) = {{x}_{3}}(t) - {{g}_{2}}(t)$ – ошибки слежения, с учетом проектных ограничений на угловые скорости, моменты, развиваемые исполнительными устройствами, и управления выполнение которых надо обеспечить в замкнутой системе.

Ограничения (1.4), обусловленные мощностью комплектных исполнительных устройств, определяют возможные рабочие режимы и точность отслеживания в установившемся режиме при действии неконтролируемых возмущений. В разделе 2 будут получены допустимые соотношения между границами проектных ограничений (1.4), а также оценки предельной достижимой точности ${{\Delta }_{{1i}}}$ с учетом (1.4). Проблема обеспечения заданного времени сходимости ${{t}_{{1i}}}$ или получения его оценки в работе не рассматривается.

В рамках поставленной задачи выдвигаются следующие предположения:

1) измерениям доступны угловые положения ${{x}_{1}}(t)$, ${{x}_{3}}(t)$, задающие воздействия ${{g}_{1}}(t)$, ${{g}_{2}}(t)$ и токи якорей приводов, по которым восстанавливаются текущие значения моментов сил, создаваемых приводами ${{\tilde {\tau }}_{1}}(t)$, ${{\tilde {\tau }}_{2}}(t)$, шумы в измерениях отсутствуют;

2) генератор задающих воздействий отсутствует, их производные трактуются как ограниченные возмущения

3) значения коэффициентов передачи ${{a}_{i}}$, ${{b}_{i}}$, $i = 1,\,2$ известны, остальные конструктивные коэффициенты точно не известны, имеются только диапазоны их изменения 0 < ${{ * }_{{\min }}}$ ≤ $ * (t)$ ≤ ${{ * }_{{\max }}}$, $t \geqslant 0$ (здесь под символом $*(t)$ понимаются неопределенные параметры системы (1.1)–(1.2), которые могут изменяться в процессе эксплуатации), в частности 0 < ${{\xi }_{{\min }}} \leqslant \xi \leqslant {{\xi }_{{\max }}}$, $\xi = 1 - {{K}_{{gy}}}{{x}_{3}}\cos {{x}_{1}}$;

4) тот факт, что в замкнутой системе целенаправленно будет обеспечиваться выполнение ограничений (1.4), позволяет принять для целей анализа следующие оценки суммарных моментов

и трактовать их как неизвестные ограниченные возмущения;

5) система (1.1)–(1.2) является управляемой, т.е. $d{{\tilde {\tau }}_{i}}{\text{/}}d{{\tau }_{i}} \ne 0$ [21], более конкретно:

Приведенное условие означает, что в подсистеме

коэффициенты при истинных управлениях ${{u}_{i}}$ не обращаются в нуль, следовательно, выбором ${{u}_{i}}$ можно обеспечить желаемое поведение ${{\tilde {\tau }}_{i}}$, $i = 1,\,2$.

2. Базовый закон управления. Электромеханическая система (1.1)–(1.2) имеет структуру блочной формы управляемости [21, 22], поэтому целесообразно разбить задачу синтеза управления системой 6-го порядка на 6 элементарных подзадач, которые решаются последовательным выбором стабилизирующих фиктивных, а потом и истинных управлений в каждом из уравнений. Фиктивными управлениями в уравнениях (1.1) полагаются переменные ${{x}_{2}}$, ${{\tilde {\tau }}_{1}}$, ${{x}_{4}}$ и ${{\tilde {\tau }}_{2}}$ соответственно. С целью выполнения проектных ограничений (1.4) на стадии синтеза фиктивные управления предлагается выбирать в виде всюду ограниченных сигма-функций [23–25]:

где $\sigma ({{k}_{{ji}}}{{e}_{{ji}}}) = \frac{2}{{1 + \exp ( - {{k}_{{ji}}}{{e}_{{ji}}})}} - 1$ – сигма-функция.

Для системы (1.1)–(1.2) сформируем новый координатный базис относительно невязок между переменными ${{x}_{2}}$, ${{\tilde {\tau }}_{1}}$, ${{x}_{4}}$, ${{\tilde {\tau }}_{2}}$ и выбранными стабилизирующими фиктивными сигмоидальными управлениями (2.1):

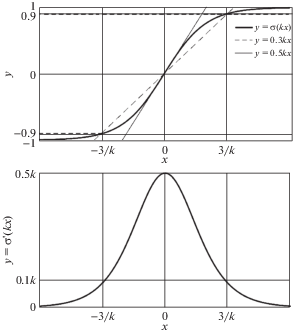
В отличие от линейных фиктивных управлений с большими коэффициентами, которые классически используются в блочном подходе [21, 22], сигмоидальные фиктивные управления имеют по два настраиваемых параметра: ${{m}_{{ji}}} > 0$ – амплитуды, определяющие скорость сходимости регулируемых переменных, и ${{k}_{{ji}}} > 0$ – коэффициенты наклона, играющие роль больших коэффициентов и отвечающие за точность стабилизации, $j = 1,2$, $i = 1,2$. Производные сигма-функции, которые появятся при дифференцировании невязок (2.2), имеют рекурсивный вид $\sigma {\kern 1pt} '({{k}_{{ji}}}{{e}_{{ji}}})$ = ${{k}_{{ji}}}(1 - {{{\sigma }}^{2}}({{k}_{{ji}}}{{e}_{{ji}}})){\text{/}}2$. Графики сигма-функции с ее производной представлены на рис. 2.

Как видно из рис. 2, сигма-функция $\sigma ({{k}_{{ji}}}{{e}_{{ji}}})$ может быть условно разделена на следующие части: при ${\text{|}}{{e}_{{ji}}}{\text{|}} \leqslant 3{\text{/}}{{k}_{{ji}}}$ она близка к линейной функции, при ${\text{|}}{{e}_{{ji}}}{\text{|}} > 3{\text{/}}{{k}_{{ji}}}$ она близка к постоянной. В точках области определения ${{e}_{{ji}}} = \pm 3{\text{/}}{{k}_{{ji}}}$, принятых в качестве границ разбиения, кривизна сигма-функции достигает максимума, а функция и ее производная принимают значения

В “линейной” зоне сигма-функция ограничена снизу секущей:

В пределе при ${{k}_{{ji}}} \to + \infty $ сигма-функция стремится к функции знака. Этот факт позволяет с помощью непрерывных сигмоидальных обратных связей обеспечить в замкнутой системе свойства, близкие к свойствам систем с разрывными управлениями, функционирующих в скользящем режиме. В том числе: декомпозицию общего движения на разнотемповые составляющие; инвариантность с заданной точностью по отношению к параметрическим и внешним согласованным возмущениям, которые обеспечиваются с помощью ограниченного управления [23–25].

Относительно ошибок слежения и невязок (2.2) приходим к следующей системе с локальными сигмоидальными связями:

где ${{\varsigma }_{1}} = \xi ({{x}_{1}},{{x}_{3}})$, ${{\varsigma }_{2}} = 1$; в правых частях нижних подсистем для компактности записи фигурируют производные верхних подсистем, вместо которых следует подставить соответствующие выражения.

В системе (2.5) сформируем разрывной закон управления, характерный для электрических исполнительных устройств, работающих в ключевом режиме:

Параметры фиктивных (2.1) и истинных управлений (2.6) необходимо выбрать так, чтобы обеспечить стабилизацию системы (2.5) и выполнение цели управления (1.3). Согласно идеологии блочного подхода, выбором амплитуд истинных управлений ${{m}_{{3i}}} > 0$ следует обеспечить возникновение скользящих режимов на поверхностях ${{e}_{{3i}}} = 0$, $i = 1,\,2$, а выбором амплитуд сигмоидальных фиктивных управлений ${{m}_{{ji}}} > 0$, $j = 1,\,2$ – последовательное (снизу вверх) попадание невязок в некоторые окрестности нуля – “линейные” зоны сигмоидальных управлений:

Еще раз подчеркнем, что в данной работе проблема оценивания времени сходимости не рассматривается, указанные неравенства для моментов времени отражают последовательность сходимости невязок, соответствующую принципу разделения движений, реализуемого в данном подходе [21, 22].

Границы “линейных” зон, от которых зависит точность стабилизации невязок, определяются выбором коэффициентов наклона:

Для настройки амплитуд, обеспечивающих (2.7), используем второй метод Ляпунова. В качестве кандидата на функцию Ляпунова замкнутой системы (2.5)–(2.6) рассмотрим квадратичную форму в виде суммы квадратичных форм: $V = \sum\nolimits_{j = 1}^3 {\sum\nolimits_{i = 1}^2 {{{V}_{{ji}}}} } $, ${{V}_{{ji}}} = \frac{1}{2}e_{{ji}}^{2}$. Вне областей (2.8) сигма-функция близка к постоянной и находится в пределах $0.9 < \left| {\sigma ({{k}_{{ji}}}{{e}_{{ji}}})} \right| < 1$ (2.3), что позволяет в целях анализа вместо ${{m}_{{ji}}}\sigma ({{k}_{{ji}}}{{e}_{{ji}}})$ рассматривать ее нижнюю границу $0.9{{m}_{{ji}}}\operatorname{sign} {{e}_{{ji}}}$, $j,\,i = 1,\,2$.

С учетом (1.4)–(1.6) и обратных соотношений (2.2), а именно,

на основе (2.5) можно дать следующие оценки для производных невязок:

Полученные оценки достаточно консервативные, что позволяет не учитывать при синтезе возможные небольшие нарушения ограничений по угловым скоростям в начале переходных процессов и опираться на заданные значения $\left| {{{x}_{2}}(t)} \right| \leqslant {{X}_{{21}}}$, $\left| {{{x}_{4}}(t)} \right| \leqslant {{X}_{{22}}}$.

Тогда вне областей (2.8), но с учетом иерархии сходимости переменных (2.7) и оценок (2.9), (2.10), для производных квадратичной формы справедливы следующие оценки, определяющие выбор амплитуд:

где ${{F}_{3}} = \frac{1}{{{{I}_{{1,\min }}}}}({{\xi }_{{\max }}}{{\tilde {T}}_{1}} + {{F}_{1}})$, ${{F}_{4}} = \frac{1}{{{{I}_{{2,\min }}}}}({{\tilde {T}}_{2}} + {{F}_{2}})$.

При выборе коэффициентов наклона согласно (2.8) и амплитуд управлений согласно (2.11)–(2.13), обеспечивается желаемое поведение (2.7) замкнутой системы (2.5)–(2.6).

Фиктивные сигмоидальные управления (2.1) можно трактовать как фиктивные задающие воздействия для соответствующих переменных, на которые накладываются ограничения, для учета которых необходимо дополнительно ограничить амплитуды управлений сверху заданными константами (1.4).

Формализуем процедуру выбора параметров, обеспечивающих сходимость невязок (2.6) с учетом проектных ограничений (1.4). Используя (2.11)–(2.13) и (1.4), приходим к двойным неравенствам на выбор амплитуд:

где ${{c}_{{1i}}} = \frac{{{{T}_{{i0,\max }}}{{T}_{i}}}}{{{{k}_{{i,\min }}}}}$, ${{c}_{{2i}}} = \frac{{0.5{{T}_{{i1,\max }}}{{F}_{{2 + i}}}}}{{({{b}_{i}} - 2{{a}_{i}}{{T}_{i}}){{k}_{{i,\min }}}}}$, ${{c}_{{3i}}} = \frac{{0.25{{T}_{{i1,\max }}}{{{\bar {X}}}_{{2i}}}}}{{({{b}_{i}} - 2{{a}_{i}}{{T}_{i}}){{k}_{{i,\min }}}}}$, ${{c}_{{4i}}} = 1.12\frac{{{{F}_{i}}}}{{{{\varsigma }_{{i,\min }}}}}$, c_5i = = $0.55\frac{{{{I}_{{i,\max }}}{{{\bar {X}}}_{{2i}}}}}{{{{\varsigma }_{{i,\min }}}}}$; $i = 1,2.$

Из третьего выражения (2.14) следует неравенство

Из второго и первого выражений (2.14) приходим к неравенствам

Для возможности выполнения ограничений границы в (2.15) и (2.16) должны быть положительными, следовательно, с учетом (2.14) имеем:

Чтобы расширить верхнюю границу выбора ${{k}_{{1i}}}$ во втором неравенстве (2.16) и, как следствие, повысить предельную достижимую точность (1.4), целесообразно принять максимальное допустимое значение ${{m}_{{3i}}}$:

Из (2.15) и (2.19) с учетом (2.20) имеем диапазон для выбора ${{k}_{{2i}}}$:

В (2.21) правая граница должна превышать левую. Отсюда получим:

Для выполнения данного неравенства потребуем:

Таким образом, приходим к следующим ограничениям на ${{m}_{{1i}}}$ вместо (2.17):

Отметим, что из (2.19), (2.18) и (2.23) следуют допустимые соотношения между верхними границами проектных ограничений (1.5), которые должны быть обеспечены априори:

При их выполнении формализуем процедуру настройки параметров обратной связи следящей системы:

1) фиксация $m_{{3i}}^{*}$ согласно (2.20) и последовательный выбор амплитуд $m_{{2i}}^{*}$ из (2.18) и $m_{{1i}}^{*}$ из (2.23), $i = 1,2$;

2) выбор больших коэффициентов $k_{{2i}}^{*}$, близких к нижним границам (2.21), что расширяет верхнюю границу для ${{k}_{{1i}}}$ (2.16) в целях увеличения предельной точности стабилизации ошибок слежения ${{e}_{{1i}}}(t)$. При выбранных $k_{{2i}}^{*}$ обеспечивается точность стабилизации невязок $\left| {{{e}_{{2i}}}(t)} \right| \leqslant 3{\text{/}}k_{{2i}}^{*} \leqslant \Delta _{{2i}}^{*}$, ${\text{ }}t > {{t}_{{2i}}}$, $i = 1,2$;

3) выбор больших коэффициентов $k_{{1i}}^{*}$ с учетом (2.16) из диапазонов

верхние границы которых определяют предельную точность стабилизации ошибок слежения ${\text{|}}{{e}_{{1i}}}(t){\text{|}} < \Delta _{{1i}}^{{}}$, ${\text{ }}t > {{t}_{{1i}}}$: $0 < \Delta _{{1i}}^{{}} < 3{\text{/}}\overline {{{k}_{{1i}}}} $. Заданная точность $\Delta _{{1i}}^{*}$ может быть достигнута выбором $k_{{1i}}^{*} = 3{\text{/}}\Delta _{{1i}}^{*}$, если $\Delta _{{1i}}^{*} \leqslant 3{\text{/}}\overline {{{k}_{{1i}}}} $. В противном случае может быть достигнута лишь указанная предельная точность.

Обратим внимание на тот факт, что возможность выполнения проектных ограничений (1.4) на стадии синтеза с помощью описанной процедуры связана с тем, что за счет стабилизации невязок (2.2) фиктивные управления ${{x}_{2}}(t)$, ${{x}_{4}}(t)$, ${{\tilde {\tau }}_{1}}(t)$, ${{\tilde {\tau }}_{2}}(t)$ отслеживают ограниченные всюду сигмоидальные сигналы (2.1), амплитуда которых не превосходит верхних границ в проектных ограничениях. Однако при выбранных на основе указанной процедуры параметрах регулятора в замкнутой системе гарантируется тотальное выполнение проектных ограничений при $t \geqslant 0$ только на управления ${{u}_{i}}(t)$, $i = 1,2$ в силу постоянных амплитуд (2.6) и на моменты ${{\tilde {\tau }}_{i}}(t)$, $i = 1,2$, поскольку для невязок ${{e}_{{3i}}}(t)$ с помощью разрывного управления обеспечиваются апериодические переходные процессы. Однако для невязок ${{e}_{{2i}}}(t)$ апериодические переходные процессы в рамках данной процедуры не гарантированы, поэтому по угловым скоростям ${{x}_{2}}(t)$, $x{}_{4}(t)$, в общем случае, вначале переходного процесса возможно незначительное нарушение заданных диапазонов (что требует, по возможности, снижения амплитуд ${{m}_{{11}}}$, ${{m}_{{12}}}$ на этапе синтеза). Но, как будет показано в разделе 4, величина перерегулирования будет заведомо меньше всплесков, характерных для замкнутых систем с линейными локальными связями, функционирующих в условиях неопределенности.

3. Наблюдатель угловых скоростей. Обратная связь (2.6) осуществляется по невязкам ${{e}_{{3i}}}$, $i = 1,2$. В данном случае нельзя воспользоваться наблюдателем для непосредственного оценивания сигналов ${{e}_{{3i}}}(t)$ [30], так как преобразованная система (2.5) ненаблюдаема относительно выхода из-за наличия в первых двух уравнениях внешних возмущений. Поэтому переменные ${{e}_{{3i}}}$, $i = 1,2$, которые являются функциями от ошибок слежения, угловых скоростей и моментов (2.2), будем вычислять в реальном времени по имеющимся измерениям ${{x}_{1}}(t)$, ${{x}_{3}}(t)$, ${{\tilde {\tau }}_{i}}(t)$ и ${{g}_{i}}(t)$, $i = 1,2$. Кроме того, нам потребуются текущие значения угловых скоростей ${{x}_{2}}(t)$, ${{x}_{4}}(t)$. Операций реального дифференцирования сигналов, которые приводят к возбуждению помех и появлению запаздывания, стараются избегать на практике. Для оценивания угловых скоростей по измерениям угловых положений предлагается использовать динамический дифференциатор, который был апробирован авторами для различных мехатронных объектов [23–25]. В данной работе дополнительно представлена оценка времени, за которое обеспечивается заданная точность оценивания. Данный дифференциатор представляет собой наблюдатель пониженного порядка, построенный как реплика кинематических соотношений механической подсистемы (1.1)

в виде где ${{z}_{i}}$ – переменные состояния наблюдателя, ${{\nu }_{i}} = {{p}_{i}}\sigma ({{l}_{i}}{{\varepsilon }_{i}})$ – сигмоидальные корректирующие воздействия, ${{p}_{i}} > 0$, ${{l}_{i}} > 0$, ${{\varepsilon }_{1}} = {{x}_{1}} - {{z}_{1}}$, ${{\varepsilon }_{2}} = {{x}_{3}} - {{z}_{2}}$ – ошибки наблюдения, $i = 1,2$. Задача наблюдения сводится к задаче стабилизации ошибок наблюдения вместе с их производными. Для анализа устойчивости составим вспомогательную виртуальную систему в которой неизмеряемые сигналы трактуются как внешние ограниченные возмущения (1.4) с ограниченными производными

Зададимся точностью стабилизации ошибок наблюдения и их производных:

При выполнении (3.3) искомые оценки ${{x}_{2}}$(t) и ${{x}_{4}}$(t) предоставят корректирующие воздействия ${{\nu }_{i}}$(t): ${\text{|}}{{x}_{2}}(t) - {{\nu }_{1}}(t){\text{|}} \leqslant \delta $, ${\text{|}}{{x}_{4}}(t) - {{\nu }_{2}}(t){\text{|}} \leqslant \delta $, $t > {{t}_{{0i}}}$, $0 \leqslant {{t}_{{0i}}} < {{t}_{{3i}}}$, $i = 1,2$. Заданная точность (3.3) достигается за счет выбора параметров ${{p}_{i}}$ и ${{l}_{i}}$, $i = 1,2$ корректирующих воздействий.

С учетом измерений установим в наблюдателе (3.1) следующие начальные условия: ${{z}_{1}}(0) = {{x}_{1}}(0)$, ${{z}_{2}}(0) = {{x}_{3}}(0) \Rightarrow {{\varepsilon }_{i}}(0) = 0$, $i = \overline {1,2} $. Тогда выбор амплитуд ${{p}_{i}}$ из достаточных условий, аналогичных (2.11)–(2.13), а именно

обеспечит нахождение ошибок наблюдения в малой окрестности нуля ${\text{|}}{{\varepsilon }_{i}}(t){\text{|}} \leqslant 3{\text{/}}{{l}_{i}}$, $i = 1,2$ при $t \geqslant 0$. Нижние оценки для выборов больших коэффициентов ${{l}_{i}}$, $i = 1,2$ определим с помощью достаточных условий устойчивости. С учетом (2.3), (2.4) условия (3.3) будут выполнены, если откуда следует

С учетом (2.3) и оценок начальных условий $\left| {{{{\dot {\varepsilon }}}_{i}}(0)} \right| \leqslant {{X}_{{2i}}} + {{p}_{i}}$, на интервале $[0,{{t}_{{0i}}}]$ справедлива следующая оценка решений двух последних уравнений в (3.2):

Отсюда приходим к оценке времени сходимости производных ${{\dot {\varepsilon }}_{i}}(t)$ в заданную окрестность $\delta $ (3.3) при выбранных значениях ${{p}_{i}}$ и ${{l}_{i}}$:

Как видим, с ростом ${{l}_{i}}$ сокращается не только ошибка оценивания (3.5), но и время оценивания, оно может быть обеспечено сколь угодно малым. Это позволяет пренебречь динамикой наблюдателя при анализе замкнутой системы с динамической обратной связью. Существенно, что рост параметров ${{l}_{i}}$ в сигмоидальных корректирующих воздействиях не приводит к всплескам оценочных сигналов, характерным для наблюдателей с глубокими линейными обратными связями [30].

Таким образом, текущие значения невязок (2.2) вычисляются на основе измеряемых и восстановленных сигналов:

При этом базовый закон управления (2.6) реализуется в виде

что с учетом (3.3) порождает реальный скользящий режим в малом пограничном слое поверхностей переключения.

4. Результаты моделирования. С целью верификации разработанного метода синтеза динамической обратной связи было проведено численное моделирование в среде MATLAB-Simulink. В электромеханической системе (1.1)–(1.2) были приняты следующие значения параметров [29]:

Внешние возмущения описывались следующими периодическими функциями с главным периодом 4 c:

где момент ${{M}_{R}}$, возникающий за счет перекрестных связей между винтами, моделировался согласно [29].

Требовалось обеспечить отслеживание угловыми координатами ${{x}_{1}}$ и ${{x}_{3}}$ заданных сигналов

с заданной точностью ${{\Delta }_{{11}}} = {{\Delta }_{{12}}} = 0.05$ в установившемся режиме при наличии следующих проектных ограничений:

На основе неравенств (2.15)–(2.19) были выбраны параметры фиктивных и истинных управлений:

а на основе неравенств (3.4), (3.5) и заданной точности оценки угловых скоростей $\delta = 0.01$ – следующие параметры наблюдателя состояния (3.1): ${{l}_{i}} = 60$, ${{p}_{i}} = 11$, $i = 1,2$.

Численное моделирование проводилось для замкнутой системы (1.1)–(1.2), (3.1), (3.6)–(3.7) с ограниченными сигмоидальными фиктивными управлениями (2.1). Также в целях сравнения было проведено моделирование для замкнутой системы с законом управления (3.7), но с классически используемыми неограниченными линейными фиктивными управлениями [21, 22]. При этом невязки между реальными и принятыми линейными фиктивными управлениями, аналогичные (3.6), имеют вид

где большие коэффициенты ${{\kappa }_{{ji}}}$, $j = 1,2$, $i = 1,2$ были определены из достаточных условий так, чтобы обеспечить такую же точность, что и при выбранных параметрах сигмоидальных фиктивных управлений:

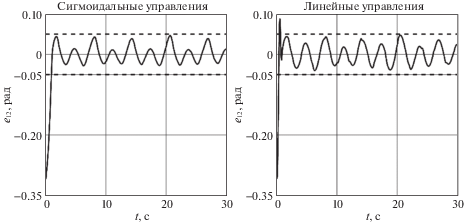
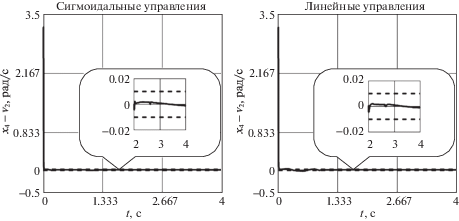
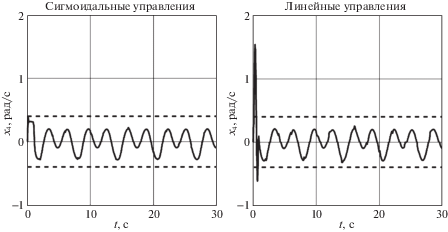
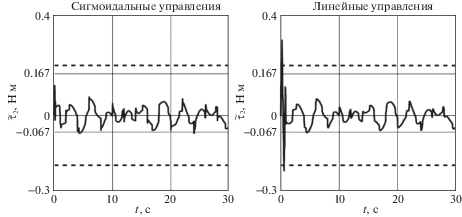
Результаты моделирования представлены для угла рыскания ${{x}_{3}}(t)$ (для угла тангажа ${{x}_{1}}(t)$ – схожие результаты). На рис. 3 приведены графики ошибки слежения ${{e}_{{12}}}(t)$ (пунктирными линиями обозначены границы заданных ошибок). На рис. 4 приведены графики ошибки оценивания угловой скорости ${{x}_{4}}(t)$ с помощью динамического дифференциатора (3.1). На рис. 5–6 представлены графики переменных состояния ${{x}_{4}}(t)$ и ${{\tilde {\tau }}_{2}}(t)$, на которые накладывались проектные ограничения (4.1), пунктирными линиями обозначены границы проектных ограничений.

В целях сравнительного анализа в таблице 1 представлены следующие показатели качества замкнутых систем с различными фиктивными управлениями: время переходного процесса ${{t}_{p}}$ – момент времени, начиная с которого достигается желаемая точность 0.05 рад, величина перерегулирования по ${{e}_{{12}}}$: ${{\Delta }_{{{{e}_{{12}}}}}} = \max {\text{|}}{{e}_{{12}}}(t){\text{|}}$, достигнутая точность ${{\Delta }_{{12}}}$ в установившемся режиме для ${{e}_{{12}}}$, а также величины перерегулирования по переменным ${{x}_{4}}(t)$, ${{\tilde {\tau }}_{2}}(t)$.

Таким образом, из рис. 3 и табл. 1 видно, что заданная точность слежения достигается, и она примерно одинакова для алгоритмов с разными фиктивными управлениями. Из графиков рис. 4 видно, что ошибка оценивания угловой скорости с помощью корректирующего воздействия наблюдателя сходится в заданную окрестность менее чем за 0.1 с. Стоит отметить, что для алгоритма с сигмоидальными фиктивными управлениями удается выполнить заданные ограничения на переменные состояния (4.1) благодаря выбору параметров фиктивных и истинных управлений, в то время как для алгоритма с линейными фиктивными управлениями ограничения не выполняются (см. рис. 5–6). Из табл. 1 следует, что для системы с линейными фиктивными управлениями время регулирования оказывается в 1.5 раза меньше, однако величина перерегулирования по контрольным переменным в 2.5–4 раза больше по сравнению с системой с сигмоидальными фиктивными управлениями. Последний факт позволит на практике использовать приводы меньшей мощности.

Заключение. Цель исследований состояла в синтезе системы слежения для TRMS при действии параметрических и внешних возмущений, наличии проектных ограничений на переменные состояния и управления и неполных измерениях. Поставленная цель была достигнута за счет использования блочного подхода с формированием сигмоидальных фиктивных управлений, обеспечивающих инвариантность по отношению к возмущениям с заданной точностью и выполнение проектных ограничений. Недостающие оценки угловых скоростей были получены с помощью наблюдателя пониженного порядка, не требующего параметрической определенности объекта управления и ввода динамической модели внешних возмущений. На основе результатов моделирования показано, что по сравнению с системой с линейными фиктивными управлениями, при использовании сигмоидальных управлений удается снизить величину перерегулирования в 2.5–4 раза. Однако в рамках разработанной процедуры, в общем случае, не гарантируется тотальное выполнение ограничений по угловым скоростям вначале переходных процессов. Для их обеспечения потребуется уточнение процедуры настройки параметров регулятора с учетом области допустимых начальных условий и оценкой времени переходных процессов, что составит предмет дальнейших исследований авторов.

Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований (проект 20-01-00363А).