1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 85, № 1, 2021

Прикладная математика и механика, 2021, T. 85, № 1, стр. 89-105

Послойный анализ напряженно-деформированного состояния нерегулярных трехслойных оболочек вращения ненулевой гауссовой кривизны

В. Н. Бакулин *

Институт прикладной механики РАН
Москва, Россия

* E-mail: vbak@yandex.ru

Поступила в редакцию 27.02.2020
После доработки 17.08.2020
Принята к публикации 17.10.2020

Полный текст (PDF)

Аннотация

Рассматривается построение оболочечной модели для послойного анализа напряженно-деформированного состояния трехслойных нерегулярных оболочек вращения двойной кривизны. Построение модели проводится на основе блочного конечно-элементного подхода. При этом рассматривается два типа оболочечных конечных элементов (КЭ) двойной кривизны – двумерный КЭ несущих слоев и трехмерный КЭ заполнителя. Проводится сравнительный анализ результатов расчета по приведенным алгоритмам с применением конечных элементов несущих слоев с аналитическим и конечно-элементным решениями, полученными с использованием программного комплекса ANSYS на задаче деформирования однослойной сферической оболочки под действием самоуравновешенных сил. В качестве примера решена задача об исследовании влияния сквозных и несквозных прямоугольных в плане вырезов на напряженно-деформированное состояние трехслойной оболочки вращения двойной кривизны.

Ключевые слова: послойный анализ, напряженно-деформированное состояние, трехслойные нерегулярные оболочки, двойная кривизна, модели, конечные элементы, блок, сквозные и несквозные вырезы

1. Введение. Краткий обзор конечно-элементных моделей. Слоисто-неоднородные, в том числе трехслойные оболочки находят растущее применение в конструкциях летательных аппаратов (ЛА) и др. современной техники [1–3]. Оболочки вращения двойной кривизны сферической, оживальной и др. форм используются в качестве элементов конструкций корпусов двигателей ЛА, головных частей и других агрегатов.

Анализ большого числа публикаций, посвященных моделям для расчета слоисто-неоднородных, в том числе трехслойных оболочек, проведен в ряде обзоров, некоторые из последних обзоров приведены в работах [4–7].

Провести расчет большинства реальных конструкций аналитическими методами, как правило, не удается из-за математических трудностей, что приводит к необходимости разрабатывать и применять модели на основе численных методов и особенно метода конечных элементов (МКЭ) [8, 9], позволяющего с необходимой степенью детализации проводить расчетные исследования.

Некоторые конечно-элементные модели (КЭМ) слоистых, в том числе трехслойных нерегулярных оболочек, рассматривались в монографиях [10–14] и других работах. В ряде этих и других работ модели построены на гипотезах, применяемых к пакету слоев. Наиболее распространенной из таких моделей является модель Тимошенко [11, 15, 16].

Построение конечно-элементных моделей для анализа НДС трехслойных нерегулярных оболочек на основе гипотезы ломаной линии рассматривалось в [10, 17] и многих других работах.

Для расчета многослойных оболочек вращения при произвольном нагружении использован объемный шестигранный конечный элемент с узловыми неизвестными в виде перемещений и их производных с разработкой соотношений между векторами узловых величин на границе раздела слоев материалов [18].

Цикл работ [19–22] посвящен векторной интерполяции полей перемещений в конечно-элементных расчетах оболочек и решению проблемы учета смещений конечного элемента как жесткого целого с помощью этого подхода. В монографиях [19, 20] обобщен материал этих научных исследований и рассмотрено использование метода конечных элементов в расчетах композиционных инженерных конструкций, а также изучена формулировка метода перемещений в расчетах тонких оболочек при учете физической и геометрической нелинейностей.

Излагается [21] алгоритм конечно-элементного расчета напряженно-деформированного состояния оболочек вращения с учетом деформаций поперечного сдвига на основе четырехугольного элемента при различных вариантах отсчета угла наклона нормали в процессе деформирования.

Проведено [22] сравнение эффективности использования конечных элементов различной мерности при анализе напряженно-деформированного состояния тонких оболочек. Представлены результаты при использовании двумерного элемента дискретизации в форме четырехугольного фрагмента срединной поверхности и трехмерного элемента в виде восьмиузлового шестигранника. В качестве узловых варьируемых параметров выбирались компоненты вектора перемещения и их первые производные. Функции формы для обоих типов элементов дискретизации были представлены произведениями полиномов Эрмита третьей степени. На примере расчета защемленной по торцам цилиндрической оболочки показано, что двумерная постановка в расчетах тонких оболочек является адекватной и позволяет получать приемлемые результаты при оптимальных затратах машинного времени.

Рассмотрен [23] метод решения задач теории упругости для толстых и тонких оболочек в пространственной постановке. Метод основан на концепции отсчетных поверхностей внутри оболочки. Согласно этому методу в теле оболочки вводятся N отсчетных поверхностей, параллельных срединной поверхности и расположенных в узлах многочлена Чебышёва, для того чтобы выбрать векторы перемещений этих поверхностей u1, u2, …, uN в качестве искомых функций. Такой выбор искомых функций позволяет представить разрешающие уравнения предложенной теории оболочек высокого порядка в достаточно компактной форме и получить деформационные соотношения, которые корректно описывают перемещения оболочки как жесткого тела [23].

Предложен [24] эффективный гибридно-смешанный четырехузловой оболочечный элемент. Рассматривалась [25] модель послойного анализа трехслойных нерегулярных конических оболочек.

Разработке и применению многосеточных конечных элементов (МнКЭ) посвящены работы [26–28]. Многосеточные КЭ проектируются в локальных декартовых системах координат на основе мелких (базовых) разбиений оболочек, которые учитывают их неоднородную и микронеоднородную структуру, сложную форму, сложный характер нагружений и закреплений. Напряженно-деформированное состояние в многосеточных конечных элементах описывается уравнениями трехмерной задачи теории упругости без введения дополнительных кинематических и статических гипотез, что позволяет использовать МнКЭ для расчета оболочек любой толщины.

Показана [26, 27] техника построения в криволинейных системах координат лагранжевых полиномов, которые эффективны при проектировании многосеточных конечных элементов оболочечного типа. Перемещения в конечных элементах, формирующих МнКЭ, аппроксимируются степенными и лагранжевыми полиномами различных порядков. Расчет напряженно-деформированного состояния с помощью предлагаемых многосеточных конечных элементов порождает сходящиеся последовательности приближенных решений и приводит к снижению порядка системы алгебраических уравнений метода конечных элементов, что обеспечивает существенную экономию ресурсов ЭВМ при небольших временных затратах. Приведен пример расчета трехслойной подкрепленной цилиндрической оболочки с применением трехсеточного конечного элемента оболочечного типа, который значительно уменьшает объем используемой памяти ЭВМ в сравнении с базовой конечно-элементной моделью. Это позволяет проводить расчеты композитных цилиндрических оболочечных конструкций больших размеров. Приведено сравнение полученных результатов с решением данной задачи в программном комплексе ANSYS [26, 27].

Отмечено [28], что основные достоинства многосеточных конечных элементов состоят в том, что они образуют дискретные модели, размерность которых в 102–106 раз меньше размерности базовых моделей, и порождают решения с малой погрешностью. Представлены примеры расчетов четырех- и трехслойных овальных оболочек различной толщины и формы при равномерном и локальном нагружениях с применением 3-сеточных КЭ. Сравнительный анализ полученных решений с решениями, построенными с помощью программного комплекса ANSYS, показывает высокую эффективность предлагаемых многосеточных конечных элементов в расчетах многослойных овальных оболочек.

Рассматривается [29] конечный элемент несущих слоев для построения модели послойного анализа напряженно-деформированного состояния трехслойных цилиндрических нерегулярных оболочек вращения. Проводится сравнение с конечными элементами других авторов.

При построении моделей конечных элементов важным является получение или выбор аппроксимаций искомых функций (перемещений, деформаций, напряжений). Это особенно актуально при послойном анализе [30, 31] напряженно-деформированного состояния слоисто-неоднородных, в том числе трехслойных нерегулярных оболочек.

Отмечалась актуальность проблемы построения эффективных конечно-элементных моделей [10, 11, 26, 27, 32, 33].

Наиболее эффективными при построении моделей конечных элементов являются аппроксимации искомых функций, построенные на основе аналитических решений [34–38]. Но получить аппроксимации перемещений с помощью аналитических решений удалось только для осесимметричных трехслойных цилиндрических оболочек и слоистых круговых стержней [34–38].

Эффективными также являются аппроксимации функций обобщенных деформаций [39–45]. Сложность и особенность оболочечных конечных элементов, построенных на основе аппроксимации функций обобщенных деформаций, заключается в необходимости удовлетворения этих функций уравнениям неразрывности (совместности) деформаций [46]. Получить такие аппроксимации и построить эффективные конечно-элементные модели удалось для незамкнутых круговых трехслойных цилиндрических оболочек в работах [40, 41, 43–45, 47].

Для повышения скорости сходимости численных результатов важным требованием к аппроксимациям функций перемещений оболочечных конечных элементов является учет b как твердых тел [10, 11, 17, 19, 25, 29, 43–45, 47–51].

2. Постановка задачи. В представленной статье рассматривается построение оболочечной модели для послойного анализа напряженно-деформированного состояния трехслойных нерегулярных оболочек вращения ненулевой гауссовой кривизны на основе блочного конечно-элементного подхода [52]. При этом блоки будут строиться из двух типов конечных элементов (КЭ) двойной кривизны, которые точно моделируют геометрию рассматриваемых оболочек [53]. Для моделирования напряженно-деформированного состояния в несущих слоях будем использовать двумерный КЭ, построенный на основе моментной теории тонких оболочек, к которым применимы гипотезы Кирхгофа–Лява. Напряженно-деформированное состояние в слое заполнителя будем моделировать необходимым для достижения требуемой точности и степени детализации числом трехмерных конечных элементов толстостенной оболочки вращения ненулевой гауссовой кривизны.

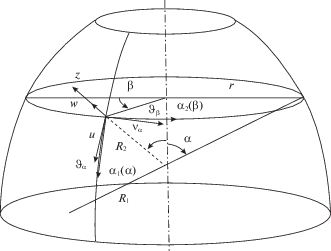
3. Модель для исследования напряженно-деформированного состояния в несущих слоях. Будем считать справедливыми для несущих слоев гипотезы Кирхгофа–Лява, тогда для моделирования напряженно-деформированного состояния в несущих слоях будем использовать двумерный конечный элемент естественной кривизны, построенный на основе моментной теории тонких оболочек вращения ненулевой гауссовой кривизны (рис. 1). На рис. 1 R1, R2 (R2 показан пуктиром) – главные радиусы кривизны срединной поверхности несущего слоя трехслойных оболочек вращения двойной кривизны.

Рис. 1.

Конечный элемент несущих слоев образован сечением оболочки двумя плоскостями, перпендикулярными оси вращения, и двумя плоскостями, проходящими через ось оболочки. Узловыми параметрами являются три перемещения точек срединной поверхности и углы поворота нормали к срединной поверхности относительно осей α1 (α) и α2 (β) (рис. 1) в четырех угловых точках конечного элемента.

Компоненты линейной составляющей вектора обобщенных деформаций (далее деформаций) несущего слоя

${\mathbf{\varepsilon }}_{i}^{с} = {{\left\{ {{{\varepsilon }_{1}},{{\varepsilon }_{2}},\gamma ,{{{\unicode{230} }}_{1}},{{{\unicode{230} }}_{2}},\chi } \right\}}^{Т}}$
связаны с компонентами вектора перемещений точек срединной поверхности
$\delta _{i}^{с} = {{\{ u,{v},w\} }^{T}}$
соотношениями [54]
(3.1)
$\begin{gathered} \varepsilon _{i}^{с} = {\mathbf{B}}_{i}^{с}\delta _{i}^{с} \\ {\mathbf{B}}_{i}^{с} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{{R}_{1}}}}\frac{\partial }{{\partial \alpha }}}&0&{\frac{1}{{{{R}_{1}}}}} \\ {\frac{{\cos \alpha }}{r}}&{\frac{1}{r}\frac{\partial }{{\partial \beta }}}&{\frac{{\sin \alpha }}{r}} \\ {\frac{1}{r}\frac{\partial }{{\partial \beta }}}&{\frac{1}{{{{R}_{1}}}}\frac{\partial }{{\partial \alpha }} - \frac{{\cos \alpha }}{r}}&0 \\ {\frac{1}{{R_{1}^{2}}}\frac{\partial }{{\partial \alpha }}}&0&{ - \frac{1}{{R_{1}^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{\alpha }^{2}}}}} \\ {\frac{{\cos \alpha }}{{{{R}_{1}}r}}}&{\frac{{\sin \alpha }}{{{{r}^{2}}}}\frac{1}{r}\frac{\partial }{{\partial \beta }}}&{ - \frac{1}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{\beta }^{2}}}} - \frac{{\cos \alpha }}{{{{R}_{1}}r}}\frac{\partial }{{\partial \alpha }}} \\ {\frac{1}{{{{R}_{1}}r}}\frac{\partial }{{\partial \beta }}}&{\frac{{\sin \alpha }}{{{{R}_{1}}r}}\frac{\partial }{{\partial \alpha }} - \frac{{\cos \alpha \sin \alpha }}{{{{r}^{2}}}}}&{ - \frac{1}{{{{R}_{1}}r}}\frac{{{{\partial }^{2}}}}{{\partial \alpha \partial \beta }} + \frac{{\cos \alpha }}{{{{r}^{2}}}}\frac{\partial }{{\partial \beta }}} \end{array}} \right], \\ \end{gathered} $
где i = 1, 2, 3 номер слоя, начиная с внутренней поверхности оболочки, индекс “c” означает, что слой – несущий. Для внутреннего несущего слоя i = 1, для внешнего несущего слоя i = 3. Система координат находится на срединной поверхности конечного элемента.

Запишем вектор перемещений КЭ несущих слоев

(3.2)
$\delta _{i}^{с} = \delta _{{\text{c}}}^{{\text{0}}} + \delta _{{\text{c}}}^{{\text{d}}},$
где i = 1, i = 3, $\delta _{\operatorname{c} }^{0}$ – вектор перемещений конечного элемента как твердого тела, компоненты которого находятся интегрированием соотношений (3.1) при нулевых значениях деформаций [17, 25, 29, 39, 40, 47, 49, 50, 52] и записываются с помощью шести неопределенных коэффициентов α1, …, α6, являющихся константами интегрирования; $\delta _{\operatorname{c} }^{\operatorname{d} }$ – вектор перемещений, вызванных деформированием конечного элемента. Компоненты вектора ${\mathbf{\delta }}_{\operatorname{c} }^{\operatorname{d} }$ записываются с помощью оставшихся после учета перемещений КЭ как твердого тела четырнадцати неопределенных коэффициентов α7, …, α20 .

Таким образом будем иметь

(3.3)
$\delta _{i}^{с} = {\mathbf{T}}_{i}^{с}\alpha _{i}^{с},$
где ${\mathbf{T}}_{i}^{с}$ (3 × 20) – матрица аппроксимирующих функций перемещений конечного элемента несущих слоев (табл. 1), $\alpha _{i}^{c}$ – вектор неопределенных коэффициентов α1, …, α20.

Таблица 1.

Матрица ${{({\mathbf{T}}_{i}^{с})}^{{\text{т}}}}$ аппроксимирующих функций перемещений конечного элемента несущих слоев, записанная с помощью вектора неопределенных коэффициентов

n 1 2 3
m
1 ${{c}_{1}}c$ $ - {{s}_{1}}$ $s{{c}_{1}}$
2 ${{s}_{1}}c$ ${{c}_{1}}$ $s{{s}_{1}}$
3 ${{c}_{1}}{{k}_{1}}$ $ - s{{c}_{1}}R_{1}^{0}$ $ - c{{c}_{1}}{{k}_{0}}$
4 ${{s}_{1}}{{k}_{1}}$ $c{{c}_{1}}R_{1}^{0}$ $ - c{{s}_{1}}{{k}_{0}}$
5 s 0 $ - c$
6 0 k 0
7 α 0 0
8 β 0 0
9 αβ 0 0
10 0 β 0
11 0 αβ 0
12 0 0 αβ
13 0 0 ${{\alpha }^{2}}$
14 0 0 ${{\beta }^{2}}$
15 0 0 ${{\alpha }^{2}}\beta $
16 0 0 $\alpha {{\beta }^{2}}$
17 0 0 ${{\alpha }^{3}}$
18 0 0 ${{\beta }^{3}}$
19 0 0 ${{\alpha }^{3}}\beta $
20 0 0 $\alpha {{\beta }^{3}}$

Здесь $c = \cos \alpha $, $s = \sin \alpha $, ${{c}_{1}} = \cos \beta $, ${{s}_{1}} = \sin \beta $, $R_{1}^{0}$ – радиус кривизны ${{R}_{1}}$ в начале местной системы координат конечного элемента несущих слоев, ${{k}_{0}} = {{r}_{0}} - R_{1}^{0}\sin {{\alpha }_{0}}$, ${{r}_{0}}$ – радиус окружности в плоскости перпендикулярной оси оболочки и проходящей через начало местной системы координат КЭ несущих слоев, ${{\alpha }_{0}}$ – угловая координата начала местной системы координат КЭ несущих слоев.

Если подставить координаты узлов конечного элемента в (3.3) и в формулы для углов поворота нормали к срединной поверхности вокруг координатных осей α1 (α) и α2 (β) (рис. 1) ${{\vartheta }_{\alpha }} = \frac{{\partial w}}{{r\partial \beta }} - \frac{{v}}{r}\sin \alpha $; ${{\vartheta }_{\beta }} = - \frac{{\partial w}}{{{{R}_{1}}\partial \alpha }} + \frac{u}{{{{R}_{1}}}}$, записанные с помощью (3.3) через α1, …, α20, будем иметь следующие зависимости для конечных элементов несущих слоев трехслойной в общем случае нерегулярной оболочки вращения двойной кривизны

(3.4)
$\begin{gathered} {\mathbf{q}}_{i}^{с} = {\mathbf{C}}_{i}^{с}{\mathbf{\alpha }}_{i}^{с} \\ \alpha _{i}^{с} = {{({\mathbf{C}}_{i}^{с})}^{{ - 1}}}{\mathbf{q}}_{i}^{с} \\ \end{gathered} $

Тогда (3.3) с учетом (3.4) будет иметь вид

(3.5)
${\mathbf{\delta }}_{i}^{c} = {\mathbf{F}}_{i}^{с}{\mathbf{q}}_{i}^{с},$
где ${\mathbf{F}}_{i}^{с} = {\mathbf{T}}_{i}^{с}{{({\mathbf{C}}_{i}^{с})}^{{ - 1}}}$ – матрица функций формы конечного элемента несущих слоев.

С учетом (3.1), (3.5) запишем вектор $\varepsilon _{i}^{c}$ через $\alpha _{i}^{c}$ и, используя физические соотношения (закон Гука) для несущих слоев, получим зависимости для усилий и моментов по алгоритмам, аналогичным приведенным в работе [38]. Матрицы жесткости конечных элементов несущих слоев трехслойной в общем случае нерегулярной оболочки вращения двойной кривизны определяются подобно [38].

4. Модель для исследования напряженно-деформированного состояния в слое заполнителя. Как уже отмечалось выше, слой заполнителя может моделироваться по толщине необходимым числом конечных элементов. Это позволяет учесть изменение геометрических характеристик, физико-механических свойств и параметров напряженно-деформированного состояния не только по меридиональной и окружной координатам, но и по толщине слоя заполнителя.

Рассмотренные аппроксимирующие функции перемещений конечного элемента несущих слоев применим для построения КЭ слоя заполнителя трехслойных нерегулярных оболочек вращения двойной кривизны.

Для этого аппроксимирующие функции перемещений КЭ несущих слоев приводятся к соответствующей поверхности стыковки с заполнителем аналогично [11, 55].

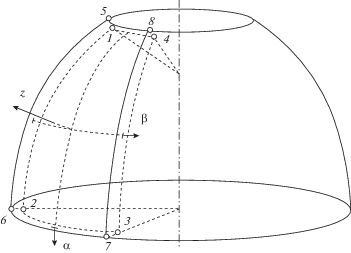
В качестве узловых выберем обе криволинейные поверхности трехмерного конечного элемента слоя заполнителя (рис. 2) (внутренняя поверхность с узлами 1–4 и внешняя криволинейная поверхность с узлами 5–8).

Рис. 2.

На поверхностях стыковки КЭ несущих слоев и заполнителя у конечных элементов слоя заполнителя на криволинейных поверхностях выбирается столько же узлов, сколько их у конечных элементов несущих слоев, и в качестве узловых параметров и аппроксимирующих функций используются те же обобщенные перемещения и аппроксимирующие функции, что и у КЭ несущих слоев трехслойных нерегулярных оболочек вращения двойной кривизны. Такой подход позволил избежать разрыва перемещений на поверхностях контакта конечных элементов несущих слоев и заполнителя трехслойной нерегулярной оболочки вращения.

Так как изменение геометрических, физико-механических характеристик и параметров напряженно-деформированного состояния по толщине слоя заполнителя учитывается моделированием требуемым числом конечных элементов, то в этих КЭ можно применить линейную аппроксимацию перемещений по толщине.

Выполнив все указанное в этом разделе 4, получим выражение вектора перемещений для конечного элемента слоя заполнителя $\delta _{{ij}}^{f} = {{\{ u,{v},w\} }^{T}}$ (у КЭ слоя заполнителя i = 2) через вектор неопределенных коэффициентов ${\mathbf{\alpha }}_{{ij}}^{f}$.

Рассматривая слой заполнителя как толстостенную оболочку вращения двойной кривизны и используя соотношения для трехмерного тела в криволинейных координатах [56], запишем

(4.1)
$\varepsilon _{{ij}}^{f} = {\mathbf{B}}_{{ij}}^{f}\delta _{{ij}}^{f},$
где ${\mathbf{\varepsilon }}_{{ij}}^{f} = {{\left\{ {{{\varepsilon }_{{11}}},{{\varepsilon }_{{22}}},{{\varepsilon }_{{33}}},{{\gamma }_{{11}}},{{\gamma }_{{22}}},{{\gamma }_{{33}}}} \right\}}^{T}}$ – вектор деформаций,
${\mathbf{B}}_{{ij}}^{f} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{{R}_{1}}}}\frac{\partial }{{\partial \alpha }}}&0&{\frac{1}{{{{R}_{1}}}}} \\ {\frac{{\cos \alpha }}{r}}&{\frac{\partial }{{r\partial \beta }}}&{\frac{{\sin \alpha }}{r}} \\ 0&0&{\frac{\partial }{{\partial z}}} \\ {\frac{1}{r}\frac{\partial }{{\partial \beta }}}&{\frac{1}{{{{R}_{1}}}}\frac{\partial }{{\partial \alpha }} - \frac{{\cos \alpha }}{r}}&0 \\ 0&{\frac{\partial }{{\partial z}} - \frac{{\sin \alpha }}{r}}&{\frac{1}{r}\frac{\partial }{{\partial \beta }}} \\ {\frac{\partial }{{\partial z}} - \frac{1}{{{{R}_{1}}}}}&0&{\frac{1}{{{{R}_{1}}}}\frac{\partial }{{\partial \alpha }}} \end{array}} \right],$
где индекс f  говорит о том, что рассматривается слой заполнителя,  j – номер КЭ в слое заполнителя по толщине, считая от внутренней поверхности заполнителя, r = R2$\sin \alpha $, R1, R2– главные радиусы кривизны срединной поверхности конечного элемента слоя заполнителя.

С помощью выражений (4.1), записанных через вектор неопределенных коэффициентов, и соотношений физического закона, получаются зависимости для напряжений в конечных элементах слоя заполнителя, записанные также через вектор неопределенных коэффициентов подобно работе [57]. Затем определяется матрица жесткости КЭ слоя заполнителя также, как это сделано в работе [38] для конечных элементов несущих слоев трехслойной цилиндрической оболочки.

На основе вычисленных коэффициентов матриц жесткости конечных элементов моментных несущих слоев и трехмерных конечных элементов заполнителя с помощью вычислительных программ проводится построение общей матрицы жесткости блока [52], состоящего из указанных КЭ, для трехслойной в общем случае нерегулярной оболочки вращения двойной кривизны.

5. Тестовая задача. Проводится сравнительный анализ результатов расчета по приведенным алгоритмам с аналитическим и конечно-элементным решениями, представленными в работе [58] для задачи деформирования сферической оболочки с параметром ${R \mathord{\left/ {\vphantom {R h}} \right. \kern-0em} h} = 100$ (R, h – радиус и толщина оболочки) под действием распределенных по дугам окружности самоуравновешенных сил q с равнодействующей Р [58]. Результаты конечно-элементного решения [58] с использованием программного комплекса ANSYS с помощью конечного элемента типа упругая оболочка для сетки КЭ, которая последовательно сгущалась до получения установившихся значений внутренних силовых факторов [58].

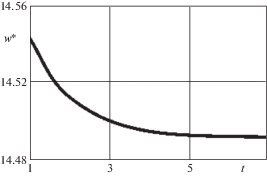
На основе проведенного расчета с помощью рассмотренного конечного элемента несущих слоев на рис. 3 представлен график сходимости прогиба. w* = Ehw/qR (Е – модуль упругости) в центре дуги приложения сил в зависимости от значения плотности конечно-элементной сетки t в меридиональном направлении при угловом размере КЭ в окружном направлении, равном 1 градусу.

Рис. 3.

Плотность конечно-элементной сетки t определяется по методике, изложенной в работе [59]. При этом t = 5 соответствует угловому размеру КЭ, равному ~0.8 градуса, а t = 8 – угловому размеру КЭ, равному 0.5 градуса.

Как показали полученные результаты расчета с помощью конечного элемента несущих слоев и представленные данные [58], наибольшими являются значения меридиональных напряжений, которые определяются преимущественно величиной изгибающего момента М1.

В таблице 2 сопоставлены результаты конечно-элементного расчета при плотности сетки в меридиональном направлении, соответствующей угловому размеру КЭ равному 0.5 градуса, при угловом размере КЭ в окружном направлении равном 1 градусу с аналитическим решением (АР) [58], а также полученным с использованием программного комплекса ANSYS в наиболее напряженной точке в центре дуги приложения сил (90°; 0) для двух значений параметра γ (угол полудуги в градусах). Здесь и в работе [58] ${{q}_{0}} = P{\text{/}}\pi R$.

Таблица 2.

Сравнительный анализ результатов расчета с аналитическим и конечно-элементным решениями, представленными в работе [58] для задачи деформирования сферической оболочки

γ, ° M1/(q0h)
МКЭ АР δ,% МКЭ
автор [58] автор [58]
20 6.9 6.6 6.8 1.45 2.9
10 15.88 15.3 15.7 1.1 2.5

Видно, что результаты получены с достаточным уровнем точности. Решение с помощью рассмотренного КЭ с уровнем точности, аналогичным полученному в работе [58], достигается на вдвое более крупной сетке, а погрешность δ% при этом, как видно из таблицы, в два раза меньше, чем в [58].

6. Численный пример. Исследование напряженно-деформированного состояния трехслойной оживальной оболочки, ослабленной сквозными и несквозными вырезами. Как уже отмечалось выше, при послойном анализе рассматриваемый подход позволяет моделировать напряженно-деформированное состояние трехслойных в общем случае нерегулярных оболочек вращения, в том числе ослабленных сквозными и несквозными (когда сплошность нарушена не во всех слоях) вырезами.

Рассмотрим задачу исследования влияния сквозных и несквозных прямоугольных в плане противоположно расположенных вырезов (углы раствора αВ = 10° и βВ = 40°), находящихся на расстоянии 30 см от большего основания, на напряженно-деформированное состояние трехслойной оживальной оболочки с шарнирно опертыми стеклопластиковыми несущими слоями (на торце меньшего диаметра разрешено осевое перемещение) и заполнителем из пенопласта при равномерном внутреннем давлении р = 1 кг/см2.

Параметры трехслойной оживальной оболочки:

${{R}_{1}} = 1.7\;{\text{м}},\quad {{R}_{2}} = 1\;{\text{м}},\quad L = 1.7\;{\text{м}},\quad {{h}_{1}} = {{h}_{3}} = 0.1\;{\text{см}},\quad {{h}_{f}} = 4.9\;{\text{см}},$
где R1 – главный радиус кривизны срединной поверхности внешнего несущего слоя, R2 – наружный радиус большего (нижнего) основания.

Физико-механически характеристики слоев трехслойной оживальной оболочки:

$E_{1}^{1} = E_{1}^{3} = 2.1 \times {{10}^{4}}\;{\text{МПа}},\quad E_{2}^{1} = E_{2}^{3} = 1.9 \times {{10}^{4}}\;МПа;\quad G_{{12}}^{1} = G_{{12}}^{3} = 0.36 \times {{10}^{4}}\;МПа;$
$\mu _{2}^{1} = \mu _{2}^{3} = 0.1;\quad E_{{11}}^{f} = E_{{22}}^{f} = E_{{33}}^{f} = 24\;МПа;\quad G_{{13}}^{f} = G_{{23}}^{f} = G_{{12}}^{f} = 10\;МПа.$

Индекс вверху означает: 1, 3 – внутренний и внешний несущие слои соответствен-но,  f – заполнитель.

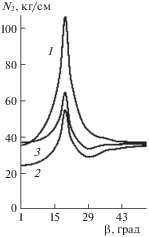
На рис. 4 приведены графики изменения мембранных усилий в окружном направлении N2 во внутреннем несущем слое вблизи края выреза с меньшим диаметром в сечении В-В (плоскость В-В перпендикулярна оси оболочки и проходит на расстоянии половины длины конечного элемента от края выреза с меньшим диаметром).

Рис. 4.

На графиках сквозные вырезы обозначены цифрой 1, цифрами 2 и 3 – несквозные вырезы. При этом цифра 2 соответствует варианту, когда вырез находится только во внутреннем несущем слое, а цифра 3 – во внутреннем несущем слое и заполнителе.

Отсчет β происходит от плоскости симметрии, которая делит вырез пополам. Наблюдаемый краевой эффект у выреза быстро затухает при удалении от него.

Наибольшими являются мембранные усилия в окружном направлении N2 во внутреннем несущем слое в окрестности угловых точек сквозных вырезов (рис. 4). Они на 15% больше, чем эти усилия во внешнем слое.

При несквозных вырезах усилия N2 в слоях значительно уменьшаются. Такая же закономерность наблюдается и для мембранных усилий в меридиональном направлении N1 – они ~ в 1.3 раза меньше N2. Мембранные напряжения в несущих слоях более, чем в 2.5 раза превышают моментные напряжения.

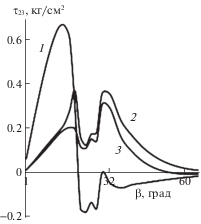
Для сквозных вырезов наибольшими в заполнителе являются напряжения поперечного сдвига τ23 в районе угловых точек вырезов (рис. 5), которые более, чем в 2 раза превышают напряжения поперечного сдвига τ13 и почти в 2.7 раза поперечные нормальные напряжения σ33. Наибольшие значения напряжений σ33 наблюдаются в районе середины края выреза с меньшим диаметром.

Рис. 5.

Для несквозных вырезов наибольшими являются напряжения в районе середины края выреза с меньшим диаметром для варианта 3. При этом τ13 незначительно превышают σ33 и более, чем в 2 раза τ23.

Приведенные результаты могут быть использованы при проектировании трехслойных отсеков оживальной формы со сквозными и несквозными прямоугольными в плане вырезами.

Заключение. Рассмотрена модель для уточненного послойного анализа напряженно-деформированного состояния (НДС) трехслойных нерегулярных оболочек вращения двойной кривизны, позволяющая учесть изменение геометрических характеристик, физико-механических свойств и параметров НДС не только по меридиональной и окружной координатам, но и по толщине оболочки и слоя заполнителя. Построение модели проводится на основе блочного конечно-элементного подхода. Рассмотрен алгоритм построения конечного элемента заполнителя. Проведен сравнительный анализ результатов расчета по приведенным алгоритмам с применением конечных элементов несущих слоев с аналитическим и конечно-элементным решением с использованием программного комплекса ANSYS на задаче деформирования однослойной сферической оболочки под действием самоуравновешенных сил.

В качестве примера решена задача об исследовании влияния сквозных и несквозных прямоугольных в плане вырезов на напряженно-деформированное состояние трехслойной оживальной оболочки со стеклопластиковыми несущими слоями и заполнителем из пенопласта.

Автор выражает благодарность В.В. Репинскому за помощь в проведении расчетов.

Работа выполнена в рамках государственного задания, номер государственной регистрации темы АААА-А19-119012290177-0.

Список литературы

  1. Бакулин В.Н., Образцов И.Ф., Потопахин В.А. Динамические задачи нелинейной теории многослойных оболочек: Действие интенсивных термосиловых нагрузок, концентрированных потоков энергии. М.: Наука. Физматлит, 1998. 464 с.

  2. Бакулин В.Н., Острик А.В. Комплексное действие излучений и частиц на тонкостенные конструкции с гетерогенными покрытиями. М.: Физматлит, 2015. 280 с.

  3. Bakulin V.N. Investigation of the Influence of the Cutout Dimensions on the Stress-strain State of Three-layer Shells with Load-bearing Layers of Composite Materials // J. Phys. Conf. Ser.: Materials Sci.&Engng. 2020. V. 714. P. 012002.

  4. Аннин Б.Д., Волчков Ю.М. Неклассические модели теории пластин и оболочек // ПМТФ. 2016. Т. 57. № 5. С. 5–14.

  5. Григолюк Э.И., Куликов Г.М. Пути развития теории упругих многослойных пластин и оболочек // Вестн. Тамбовского гос. тех. унив. 2005. Т. 11. № 2. С. 439–448.

  6. Григоренко Я.М., Григоренко A.Я. Статические и динамические задачи для анизотропных неоднородных оболочек с переменными параметрами и их числовым решением (обзор) // Прикл. мех. 2013. Т. 49. № 2. С. 3–70.

  7. Паймушин В.Н. Теория среднего изгиба подкрепленных на контуре трехслойных оболочек с трансверсально-мягким заполнителем // Мех. композ. матер. 2017. Т. 53. № 1. С. 3–26.

  8. Образцов И.Ф., Савельев Л.М., Хазанов Х.С. Метод конечных элементов в задачах строительной механики летательных аппаратов. М.: Высшая школа, 1985. 392 с.

  9. Бате К.-Ю. Методы конечных элементов. М.: Физматлит, 2010. 1024 с.

  10. Бакулин В.Н. Метод конечных элементов для исследования напряженно-деформированного состояния трехслойных цилиндрических оболочек. М.: ЦНИИ информации, 1985. 140 с.

  11. Бакулин В.Н., Рассоха А.А. Метод конечных элементов и голографическая интерферометрия в механике композитов. М.: Машиностроение, 1987. 312 с.

  12. Алфутов Н.А., Зиновьев П.А., Попов Б.Г. Расчет многослойных пластин и оболочек из композиционных материалов. М.: Машиностроение, 1984. 263 с.

  13. Пискунов В.Г., Вериженко В.Е., Присяжнюк В.К. и др. Расчет неоднородных пологих оболочек и пластин методом конечных элементов. Киев: Вища школа, 1987. 200 с.

  14. Рикардс Р.Б. Метод конечных элементов в теории оболочек и пластин. Рига: Зинатне, 1988. 284 с.

  15. Голованов А.И., Тюленева О.Н., Шигабутдинов А.Ф. Метод конечных элементов в статике и динамике тонкостенных конструкций. М.: Физматлит, 2006. 392 с.

  16. Каледин В.О., Аульченко С.М., Миткевич А.Б. и др. Моделирование статики и динамики оболочечных конструкций из композиционных материалов. М.: Физматлит, 2014. 196 с.

  17. Бакулин В.Н., Репинский В.В. Конечно-элементные модели деформации однослойных и трехслойных конических оболочек // Матем. модел. 2001. Т. 13. № 6. С. 39–46.

  18. Киселев А.П., Гуреева Н.А., Киселева Р.З. Расчет многослойной оболочки с использованием объемного конечного элемента // Изв. ВолгГТУ. Волгоград. 2010. № 4. С. 125–128.

  19. Николаев А.П., Клочков Ю.В., Киселев А.П., Гуреева Н.А. Векторная интерполяция полей перемещений в конечно-элементных расчетах оболочек. Волгоград: ФГБОУ ВПО Волгоградский ГАУ “Нива”, 2012. 264 с.

  20. Николаев А.П., Киселев А.П., Гуреева Н.А., Киселева Р.З. Расчет композиционных инженерных конструкций на основе метода конечных элементов. Волгоград: Нива, 2016. 128 с.

  21. Клочков Ю.В., Николаев А.П., Ищанов Т.Р. Конечно-элементный анализ НДС оболочек вращения с учетом деформаций поперечного сдвига // Строит. мех. инж. констр. и сооруж. 2016. № 5. С. 48–56.

  22. Клочков Ю.В., Николаев А.П., Соболевская Т.А., Клочков М.Ю. Сравнительный анализ эффективности использования конечных элементов различной мерности при анализе НДС тонких оболочек // Строит. мех. инж. констр. и сооруж. 2018. Т. 14. № 6. С. 459–466.

  23. Куликов Г.М., Плотникова С.В. Решение трехмерных задач для толстых упругих оболочек на основе метода отсчетных поверхностей // Изв. РАН. МТТ. 2014. № 4. С. 54–64.

  24. Kulikov G.M. Finite element modeling of laminated and functionally graded shells // Виртуальное моделирование, прототипирование и промышленный дизайн. Матер. II Междунар. научно-практической конференции. 2016. С. 395–397.

  25. Бакулин В.Н. Уточненная модель послойного анализа трехслойных нерегулярных конических оболочек // Докл. РАН. 2017. Т. 472. № 3. С. 272–277.

  26. Матвеев А.Д., Гришанов А.Н. Трехмерные композитные многосеточные конечные элементы оболочечного типа // Изв. АлтГУ. 2017. № 4. С. 120–125.

  27. Левин В.Е., Олегин И.П., Гришанов А.Н. Расчет подкрепленных композитных цилиндрических оболочек с применением многосеточных конечных элементов // Научн. вестн. НГТУ. 2018. Т. 71. № 2. С. 85–100.

  28. Pustovoi N.V., Grishanov A.N., Matveev A.D. Multi-grid finite elements in calculations of multilayer oval cylindrical shells // Sib. J. Sci.&Technol. 2019. V. 20. № 2. P. 174–182.

  29. Бакулин В.Н. Эффективная модель несущих слоев для послойного анализа напряженно-деформированного состояния трехслойных цилиндрических нерегулярных оболочек вращения // Изв. РАН. МТТ. 2020. № 3. С. 69–79.

  30. Бакулин В.Н. Модель для уточненного расчета напряжённо-деформированного состояния трехслойных конических нерегулярных оболочек вращения // ПММ. 2019. Т. 83. Вып. 2. С. 315–327.

  31. Бакулин В.Н. Блочная конечно-элементная модель для послойного анализа напряженно- деформированного состояния трехслойных оболочек с нерегулярной структурой // Изв. РАН. МТТ. 2018. № 4. С. 66–73.

  32. Бакулин В.Н. Неклассические уточненные модели в механике трехслойных оболочек // Вестн. Нижегородского унив. им. Н.И. Лобачевского. 2011. № 4. Ч. 5. С. 1989–1991.

  33. Образцов И.Ф. О некоторых перспективных прикладных проблемах механики, имеющих народнохозяйственное значение // Изв. АН СССР. МТТ. 1982. № 4. С. 3–9.

  34. Бакулин В.Н., Каледин В.О. Конечный элемент круговой арки с конечной сдвиговой жесткостью // Мех. композ. матер. 1988. № 5. С. 915–919.

  35. Образцов И.Ф., Бакулин В.Н. Уточненные модели для исследования напряженно-деформированного состояния трехслойных цилиндрических оболочек // Докл. РАН. 2006. Т. 407. № 1. С. 36–39.

  36. Каледин Вл.О., Шпиталь С.В. Выбор расчетной схемы при исследовании осесимметричного краевого эффекта в трехслойных цилиндрических оболочках с легким заполнителем // Мех. композ. матер. 1993. № 5. С. 657–665.

  37. Бакулин В.Н. Аппроксимации для моделирования напряженно-деформированного состояния слоистых цилиндрических оболочек // Матем. модел. 2004. Т. 16. № 6. С. 101–105.

  38. Бакулин В.Н. Конечно-элементная модель для анализа напряженно-деформированного состояния трехслойных оболочек // Матем. модел. 2006. Т. 18. № 1. С. 3–9.

  39. Ashwell D.G., Sabir A.B. A new cylindrical shell finite element, based on simple independent strain functions // Intern. J. Mech. Sci. 1972. V. 14. № 3. P. 171–183.

  40. Бакулин В.Н., Демидов В.И. Трехслойный конечный элемент естественной кривизны // Изв. вузов. Машиностроение. 1978. № 5. С. 5–10.

  41. Бакулин В.Н. Построение аппроксимаций для моделирования напряженно-деформированного состояния несущих слоев и слоев заполнителя трехслойных неосесимметричных цилиндрических оболочек // Матем. модел. 2006. Т. 18. № 8. С. 101–110.

  42. Sabir A.B. Strain-based finite elements for the analysis of cylinders with holes and normally intersecting cylinders // Nucl. Engng.&Design. 1983. V. 76. № 2. P. 111–120.

  43. Бакулин В.Н. Эффективные модели для уточненного анализа деформированного состояния трехслойных не осесимметричных цилиндрических оболочек // Докл. РАН. 2007. Т. 414. № 5. С. 613–617.

  44. Бакулин В.Н. Построение аппроксимаций и моделей для исследования напряженно-деформированного состояния трехслойных неосесимметричных цилиндрических оболочек // Матем. модел. 2007. Т. 19. № 12. С. 118–128.

  45. Бакулин В.Н. Тестирование конечно-элементной модели, предназначенной для исследования напряженно-деформированного состояния слоистых нерегулярных оболочек // Матем. модел. 2009. Т. 21. № 8. С. 121–128.

  46. Балабух Л.И., Колесников К.С., Зарубин В.С. и др. Основы строительной механики ракет. М.: Высшая школа, 1969. 494 с.

  47. Бакулин В.Н. Эффективная модель послойного анализа трехслойных нерегулярных оболочек вращения цилиндрической формы // Докл. РАН. 2018. Т. 478. № 2. С. 148–152.

  48. Кантин Г. Смещение криволинейных элементов как жесткого целого // Ракетная техника и космонавтика. 1970. № 7. С. 84–88.

  49. Железнов Л.П., Кабанов В.В. Функции перемещений конечных элементов оболочки вращения как твердых тел // Изв. РАН. МТТ. 1990. № 1. С. 131–136.

  50. Репинский В.В. Эффективные конечные элементы для расчета устойчивости тонких анизотропных оболочек вращения // Вопр. оборон. техн. Сер. 15. Вып. 1 (117). 1997. С. 3–7.

  51. Клочков Ю.В. Учет жестких смещений конечного элемента в неявном виде на основе использования векторной интерполяции перемещений // Вест. РУДН. 2002. С. 123–127.

  52. Bakulin V.N. Block finite-element approach to building refined models of layer-by-layer analysis of the stress-strain state of three-layer irregular shells // J. Phys. Conf. Ser. 2019. V. 1392. P. 012065.

  53. Бакулин В.Н. Блочная конечно-элементная модель послойного анализа трехслойных в общем случае нерегулярных оболочек вращения двойной кривизны // Докл. РАН. 2019. Т. 484. № 1. С. 35–40.

  54. Новожилов В.В. Теория тонких оболочек. Л.: Судпромгиз, 1951. 344 с.

  55. Бакулин В.Н., Каледин В.О., Рассоха А.А. Анализ термоупругих напряжений в слоистых оболочках двоякой кривизны // Мех. композ. матер. 1987. № 6. С. 1028–1033.

  56. Васильев В.В. Механика конструкций из композиционных материалов. М.: Машиностроение, 1988. 272 с.

  57. Бакулин В.Н. Послойный анализ напряженно-деформированного состояния трехслойных оболочек с вырезами // Изв. РАН. МТТ. 2019. № 2. С. 131–145.

  58. Виноградов Ю.И., Константинов М.В. Расчет сферического бака при локальном воздействии // Изв. РАН. МТТ. 2016. № 2. С. 109–120.

  59. Бакулин В.Н., Инфлянскас В.В. Оценка локальных параметров сетки в конечно-элементных задачах // Вычисл. мех. сплошн. сред. 2013. Т. 6. № 1. С. 70–77.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал