Прикладная математика и механика, 2021, T. 85, № 1, стр. 66-88
Длительная прочность стержней, растягиваемых в агрессивной среде, при различных двухсвязных формах их поперечных сечений
А. М. Локощенко 1, *, Л. В. Фомин 1, 3, Н. С. Ларин 1, 2
1 НИИ институт механики МГУ им. М.В. Ломоносова
Москва, Россия
2 МГУ имени М.В. Ломоносова
Москва, Россия
3 Самарский государственный технический университет
Самара, Россия
* E-mail: loko@imec.msu.ru
Поступила в редакцию 11.11.2019
После доработки 30.07.2020
Принята к публикации 17.10.2020
Аннотация
Исследуется длительная прочность стержней двухсвязного поперечного сечения, растягиваемых в агрессивной среде. Рассматриваются поперечные сечения стержней, в которых формы внешнего и внутреннего контуров подобны, кроме того, площади полой (внутренней) части составляют 25% от площадей окаймляющей внешней, нагруженной части. Площади нагруженных частей сечений с различными формами совпадают. Для оценки влияния агрессивной среды на длительную прочность используется кинетическая теория Ю.Н. Работнова с двумя структурными параметрами (поврежденность материала и концентрация элементов окружающей среды в материале стержня). Для определения уровня агрессивной среды в стержнях используются приближенные решения уравнений диффузии, основанные на учете движения диффузионных фронтов от наружной и внутренней поверхностей стержней.
Введение. Высокие требования к качеству и надежности конструкций, длительное время находящихся под нагрузками при высокой температуре, приводят к необходимости проводить прогнозирование долговечности их работы с учетом различных специфических особенностей, которые могут возникать в реальной действительности. Одним из важных факторов, существенно влияющих на характеристики ползучести и длительной прочности металлов, является рабочая среда, в которой находятся исследуемые конструкции или их отдельные элементы. Результаты испытаний, как правило, показывают значительное ухудшение эксплуатационных характеристик металлов вследствие воздействия таких сред. Известные исследования влияния агрессивной окружающей среды на ползучесть и длительную прочность металлов показывают, что это влияние в основном характеризуется протекающими в металле диффузионными и коррозионными процессами [1].
Приведен [2] подробный анализ особенностей механического поведения металлов при длительном высокотемпературном нагруженном состоянии в агрессивных средах и основных феноменологических подходов, используемых при моделировании влияния окружающей среды на ползучесть и длительную прочность.
Рассматривались [3] стержни с такими односвязными поперечными сечениями, у которых минимальные размеры совпадали. При этом исследовалось влияние формы поперечного сечения стержня на концентрацию агрессивной среды в нем и на время до разрушения при одном и том же значении растягивающего напряжения. Изучались [4] стержни различной формы односвязного поперечного сечения (круг, квадрат и прямоугольники с различным соотношением сторон) при условии равенства площадей этих сечений. В отличие от [3, 4], в данной статье рассматриваются двухсвязные поперечные сечения стержней, в которых площадь полой (внутренней) части составляет 25% от площади окаймляющей внешней, нагруженной части. Также отметим, что формы внешнего и внутреннего контуров поперечных сечений подобны. Площади нагруженных частей сечений с различными формами совпадают.
1. Обзор современных работ по влиянию агрессивной среды на деформационно-прочностные характеристики материалов и элементов конструкций и их длительное разрушение. Исследование влияния агрессивной среды, вступающей как в физическое, так и в химическое взаимодействие с материалом с учетом фазовых превращений, получены авторами [5–7]. Рассматривалось развитие механико-математических моделей для описания влияния механических напряжений на кинетику химических реакций в деформируемых телах. При этом учитывается физико-химическое обоснование описываемых подходов, в частности, используются уравнения химических реакций, которые происходят на границах раздела твердых фаз (металл, оксид) и газообразных веществ. Модели учитывают влияние как внешних, так и порождаемых химическими реакциями внутренних напряжений. Исследуется влияние вида напряженного состояния, величин и знаков напряжений на протекание химических реакций. Исследуется устойчивость распространения фронта химической реакции в напряженном теле. Рассматриваются кинетика фронта реакции в окрестности концентраторов напряжений и взаимосвязи химических реакций с процессами разрушения. С учетом химической реакции, локализованной на фронте реакции в системе “деформируемое тело–газообразная компонента”, записывается баланс массы, импульса и энергии, после чего выводится выражение для производства энтропии, позволяющее естественным образом получить формулу для тензора химического сродства, с помощью которого определяются как химическое равновесие, так и кинетика фронта превращения.
Отдельный интерес представляет исследование влияния ионизирующего излучения на деформационно-прочностные характеристики материалов и элементов конструкций. Ионизирующее излучение также можно считать агрессивной средой, влияющей на физико-механические характеристики материала, подвергнутого ее влиянию. Это влияние заключается в появлении радиационных дефектов кристаллической решетки металлов и распухании металла (увеличение объема металла при воздействии на него ионизирующего излучения). Рассматриваются [8] особенности методологии построения моделей деформирования и разрушения материалов в условиях радиационного облучения с использованием теории кинетических параметров [9], а также моделей, описывающих радиационные деформации (распухание) материала [10]. Анализируются результаты экспериментов по влиянию типа и вида напряженного состояния на радиационное распухание и ползучесть материалов.
В обзоре [11] показано, что в зависимости от вида материалов радиационные среды приводят к различному изменению кратковременных и длительных механических характеристик материалов, а также к радиационному распуханию. Приводятся и анализируются экспериментальные данные о влиянии радиационного облучения на механические свойства сталей и сплавов (диаграмму деформирования, модуль упругости, предел текучести, предел прочности, ползучесть и длительную прочность). Особо обращается внимание на наличие радиационного распухания и влияние вида напряженного состояния на ползучесть и длительную прочность материалов в условиях радиационного облучения.
Рекомендуется учитывать указанные эффекты при построении моделей деформирования и разрушения материалов и конструкций в условиях радиационного облучения [10]. Авторы отмечают, что радиационное воздействие приводит к необходимости учитывать его влияние на прочностные, пластические характеристики и особенно ползучесть.
Ранее установлено [12, 13], что нейтронное облучение, кроме всего прочего, приводит к увеличению скорости ползучести, снижению длительной прочности и пластичности материала. На основе анализа экспериментальных данных предложена модель межзеренного разрушения аустенитных сталей, учитывающая влияние нейтронного облучения на длительную прочность и пластичность. Разработанные подходы применимы для прогнозирования кинетики развития трещин во времени при различных интенсивностях потока нейтронов и с учетом накопленного флюенса.
Большой вклад в развитие экспериментально-теоретического исследования влияния ионизирующего излучения на напряженно-деформированное состояния и процессы разрушения внесли ученые из Нижнего Новгорода (академик Ф.М. Митенков, профессор Ю.Г. Коротких и др.). На базе современных достижений механики поврежденной среды и механики разрушения разработаны [14] математические модели, алгоритмы и программы для расчета процессов неизотермического упругопластического деформирования и накопления усталостных повреждений в материале опасных зон оборудования и систем ядерных энергетических установок. Разработанные модели позволяют учитывать влияние на скорость процессов накопления повреждений многоосности напряженного состояния, поворота главных площадок тензоров напряжений и деформаций, учитывать нелинейное суммирование повреждений при изменении режимов нагружения.
Методика прогнозирования в исследовании [15] в основном опирается на работы С.А. Шестерикова. Постоянные, входящие в базовые уравнения, определены по результатам испытаний на ползучесть при трех уровнях напряжений. Приведены экспериментальные данные, полученные при испытаниях стали 08Х16Н11М3-ПД на ползучесть и длительную прочность при 600°C и 650°C. На основе этих данных вычислены средние теоретические значения предела кратковременной прочности и другие коэффициенты базовых уравнений. В указанном интервале температур для прогнозирования длительной прочности стали с учетом ее радиационного облучения использовано предположение о равенстве отношения деформации разрушения по диаграмме растяжения к деформации разрушения при ползучести для близких по составу сталей AISI 316 и 08Х16Н11М3-ПД. Выявлено, что радиационное облучение приводит к существенному снижению предела длительной прочности.
В завершение теоретической части обзора отметим, что различные аспекты влияния агрессивной среды на характеристики деформирования и разрушения современных металлов и сплавов рассматриваются в большом количестве монографий (среди них, например, [16–18]).
Так, например, в монографии [16] рассмотрено деформирование и разрушение металла оборудования ядерных реакторов при радиационных и термических воздействиях. Сопоставлены данные по термической и радиационной ползучести, обсуждены изменение механических свойств и распухание материала при нейтронном облучении. Рассмотрено влияние охлаждающей среды на коррозионную усталость и стресс-коррозию аустенитной стали. Проанализированы особенности циклического деформирования в условиях нейтронного облучения. Рассмотрен коррозионный рост трещин при постоянных и циклических нагрузках. Даны критерии разрушения для различных условий работы металла. Автором приведено феноменологическое описание опытных данных при термической и радиационной ползучести. Предложены кинетические уравнения для сложного нагружения, а также методика расчета нестационарных задач термопластичности. Даны рекомендации по практическому использованию полученных результатов.
В монографии [17] рассматриваются вопросы моделирования поведения железобетонных элементов конструкций в условиях воздействия хлоридосодержащих сред, а в монографии [18] исследуется работоспособность конструкций в условиях высокотемпературной водородной коррозии.
Приведем вниманию читателей статьи некоторые экспериментальные работы, среди которых отметим ряд исследований, которые проведены в ЦНИИ “Прометей” (Санкт-Петербург) [19, 20]. Экспериментально были исследованы ползучесть и длительная прочность материалов и элементов конструкций оборудования атомных электростанций, находящихся в контакте с жидкометаллической агрессивной средой.
Изучены [19] вопросы длительной прочности конструкционных материалов, работающих в реакторной установке с жидкометаллическим свинцовым теплоносителем. Рабочая температура жидкометаллического теплоносителя на основе свинца превышает 500°С, т.е. находится в диапазоне температур, при которых в сталях могут интенсивно протекать процессы ползучести. Отмечается, что недостатком теплоносителей на основе свинца является их агрессивность по отношению к конструкционным материалам, мерой борьбы с этой агрессивностью является поддержание определенной концентрации кислорода в жидком теплоносителе. В результате на поверхности стали образуется оксидная пленка, предотвращающая контакт материала с жидкометаллическим теплоносителем. Приведены экспериментальные данные, полученные при длительных испытаниях образцов двух марок сталей 10X15Н9С3Б и 10Х9НСМФБ, а именно, приводятся данные по длительной прочности образцов этих марок стали на воздухе и в потоке жидкого свинца. В результате показано, что длительная прочность образцов, испытанных в потоке жидкого свинца, ниже длительной прочности образцов, испытанных на воздухе. Причины снижения длительной прочности в жидком свинце были выявлены в ходе металлографического анализа, который показал, что при высоком уровне напряжений на образцах имеются следы фронтальной жидкометаллической коррозии. При уменьшении уровня напряжений на образцах наблюдается плотная оксидная пленка, сплошность которой нарушается тем сильнее, чем ближе она к месту разрушения образца. Эта пленка защищает образец от агрессивного воздействия окружающей среды, причем ее толщина зависит от уровня напряжений и длительности контакта с жидким металлом.
Исследовано [20] влияние жидкометаллического свинцового теплоносителя на ползучесть хромистой мартенситной стали марки 10Х9НСМФБ. При проведении испытаний на длительную прочность отмечена повышенная скорость ползучести стали в контакте с жидким свинцом при температуре 550°С по сравнению со скоростью ползучести на воздухе. В статье приводятся результаты экспериментов и их обсуждение, в рамках которого дано объяснение различного поведения кривых ползучести образцов, испытанных в контакте с жидким свинцом и на воздухе при уровне напряжений 98 МПа и 68.6 МПа. Утверждается, что данные металлографического анализа образцов, разрушенных в потоке жидкого свинца, свидетельствуют о наличии двух принципиально различных механизмов разрушения образцов в контакте со свинцовым теплоносителем. Это явление, обнаруженное в работе [19], связано с влиянием уровня напряжений на устойчивость оксидных пленок. В заключение авторы отмечают, что для повышения надежности реакторной установки с жидкометаллическим теплоносителем на основе свинца при расчете максимально допустимых напряжений в конструкциях, работающих в контакте с жидким свинцом, рекомендуется учитывать пределы ползучести конструкционных материалов, вводя ограничения по допустимой деформации на выбранной временной базе.
Помимо исследований, описывающих влияние жидкометаллической среды на длительные свойства сталей, сотрудниками ЦНИИ “Прометей” проведены исследования о влиянии этой среды на циклическую долговечность материалов.
Далее отметим работы по теме влияния агрессивной среды. Экспериментально определялось сопротивление стали стресс-коррозии в коррозионной среде (солевые пары) при медленном растяжении [21]. В обзоре [22] рассматривается влияние нейтронного облучения на величину механического напряжения, вызывающего коррозионное растрескивание. Опубликованные результаты исследований указывают на то, что увеличение дозы нейтронного облучения приводит к непрерывному понижению сопротивления стали стресс-коррозионному разрушению. Однако показано, что у предела текучести наблюдается определенное насыщение его роста с увеличением дозы облучения. Таким образом, предел коррозионного растрескивания не коррелирует с величиной предела текучести после облучения.
Отмечается [23] влияние облучения на вязкость разрушения, которое проявляется в смещении кривой вязкости разрушения после облучения в область более высоких температур. Исследуется [24] радиационное распухание 2-х марок аустенитной хромоникелевой стали. Показана и определена зависимость распухания сталей от интенсивности накопленных повреждений.
Изучается [25] низкотемпературная ползучесть под действием нейтронного облучения.
Рассматривается [26] свеллинг (распухание) аустенитной стали. Температура максимального свеллинга и скорость распухания зависят от интенсивности радиационных повреждений. Распухание проявляется после накопления определенного порога радиационных повреждений. Это пороговое значение зависит от действующего напряжения, температуры и скорости набора повреждений. Изучаются [27] растяжение и малоцикловая усталость стали при нейтронном облучении.
Оценивается [28] влияние облучения ионами Fe при 450°C для изучения подверженности растрескиванию аустенитной нержавеющей стали 304L. После облучения Fe с энергией 10 МэВ до 5 dpa (dpa – displacements per atom) было охарактеризовано и количественно определено вызванное облучением повреждение в микроструктуре наряду с измерениями нанотвердости. Облученный ионами Fe материал, напряженный до 4% в среде легкой воды в водо-водяном ядерном реакторе (PWR), обнаруживал участки зарождения трещин, которые были аналогичны тем, которые встречаются в облученных нейтронами и протонами материалах. В сравнении, облученный ионами Fe материал, подвергнутый 4%-ной пластической деформации в инертной среде аргона, не обнаружил какого-либо растрескивания, что свидетельствует о том, что локализованная деформация сама по себе недостаточна для инициирования растрескивания для условий облучения, использованных в этом исследовании.
Рассматривается [29] влияние механической обработки на инициирование коррозионного растрескивания под напряжением отожженной нержавеющей аустенитной стали типа 316L в первичной воде реактора с водой под давлением. Данный факт был исследован путем ускоренных испытаний в высокотемпературной гидрогенизированной воде. Было отмечено, что трещины от коррозии под напряжением возникают только на обработанных поверхностях с насечками обработки, перпендикулярными направлению нагрузки, и пористый внутренний оксидный слой был идентифицирован как важный фактор, способствующий возникновению трещин. Кроме того, большинство трещин заканчивались внутри приповерхностного ультрамелкозернистого слоя, вызванного механической обработкой, и вызванные механической обработкой остаточные напряжения, по-видимому, не оказали существенного влияния на возникновение трещины. Выявлена и обсуждена корреляция между зарождением трещины и поверхностными-приповерхностными элементами.
Исследование [30] посвящено окислительному поведению оболочки топлива Zry-4 в смешанных паровоздушных атмосферах. Испытания на окисление Zry-4 проводились при температурах 1373 и 1573 К. Измерение прироста веса после испытания, а также металлографическое исследование проводились для отдельного изучения кинетики области, где образуются нитриды, и области, свободной от нитридов. Результаты испытаний на окисление при 1273 и 1473 К, опубликованные ранее теми же авторами, также рассматриваются в обсуждении. Прибавку массы из области, свободной от нитридов, оценивали с использованием одномерной модели конечной разности диффузии кислорода и измеряли толщину металлической части окисленного образца, столбчатого оксида и стабилизированного кислородом α-Zr(O), а также доля столбчатого оксида на границе раздела оксид–металл. Результаты показывают, что нитриды образуются под защитным столбчатым оксидным слоем и что большая часть прироста массы, связанная с образованием пористых смешанных областей ZrN–ZrO2, была связана с образованием ZrO2 из α-Zr (O).
Прослеживается [31] эволюция микроструктуры после ползучести при облучении в нескольких аустенитных сталях, облученных до 120 dpa при температуре 320°C. Трубки под давлением с напряжениями 127–220 МПа облучали в БОР-60 до 120 dpa при 320°C. Поведение ползучести зависело как от химического состава, так и от металлургического состояния сталей. Исследовались различные стали, облученные и без нагрузки. Без механического напряжения облучение приводило к высокой плотности дислокационных линий и петель Франка и, в зависимости от типа стали происходило выделение фазы. Механическое напряжение вызывало увеличение среднего размера и плотности выпавшей фазы и, для некоторых марок сталей, увеличение среднего размера петли и уменьшение их плотности. Анизотропия плотности петли Франка или размера, вызванного механическим напряжением, не наблюдалась систематически. Микроструктура линии дислокации, по-видимому, не отличается между напряженными и ненапряженными образцами. Полостей в этих образцах не было обнаружено. В сравнении с данными этой работы, обсуждаются основные модели ползучести облучения.
Определялся [32] характер ползучести при облучении тяжелыми ионами отожженных пленок Cu толщиной 200 нм и 500 нм, характеризуется использованием на кристалле одноосных микрорастягивающихся тестовых структур. Испытания проводились при комнатной температуре с приложенным напряжением от 100 до 250 МПа и скоростью накопления повреждений 5 × 10–4 и 6.3 × 10–4 dpa с–1. Преимущество метода заключается в том, что он позволяет одновременно измерять несколько десятков образцов, полностью облученных по всей их толщине. Было установлено, что механизмы пластичности являются заметно более однородными во время ползучести с учетом облучения, чем при только статической нагрузке. Закон степенной ползучести включает в себя показатель напряжения, равный 5, слабо зависящий от микроструктуры пленок. Микроструктурные наблюдения позволяют предположить, что механизм ползучести является результатом скольжения дислокаций при помощи их переползания, что объясняется простой моделью замкнутой формы.
Краткий обзор представленных исследований свидетельствует о важности учета влияния агрессивной среды на длительную прочность материалов и элементов конструкций.
2. Постановка задачи. В данной статье рассматриваются три формы поперечного сечения растягиваемых стержней: полый прямоугольник, у которого длины одной пары сторон во много раз меньше длин другой пары стороны, полый прямоугольник, длины сторон которого имеют один порядок, и кольцо. Для исследования диффузионного процесса в таких стержнях используются различные варианты уравнений диффузии: одномерное уравнение в первом случае, двумерное уравнение во втором случае и осесимметричное уравнение в третьем случае. Во всех трех случаях принимаются нулевые начальные условия и постоянные значения концентрации агрессивной среды на контурах поперечных сечений. Точные решения уравнения диффузии могут быть представлены только в виде бесконечных рядов. В данной статье рассмотрены приближенные уравнения, при этом начальное и граничные условия выполняются точно, а само уравнение удовлетворяется интегрально.
Для анализа зависимости процесса диффузии агрессивной окружающей среды от контура поперечного сечения стержня используется приближенный метод решения уравнения диффузии, основанный на введении диффузионного фронта, распространяющегося от поверхности стержня [33–35]. Такой подход позволяет разделить весь материал поперечного сечения стержня на возмущенную область (в которой среда уже проникла в материал) и невозмущенную область (в которой еще нет проникновения среды) и затем отслеживать движение границы между этими областями во времени.
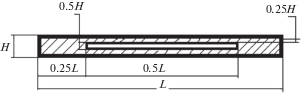
3. Одномерное уравнение диффузии в декартовых координатах. Рассмотрим длинный стержень с поперечным сечением в виде тонкого прямоугольника со сторонами $L$ и $H$ ($L \gg H$) (рис. 1).
Выделим из средней части этого прямоугольника отверстие в виде прямоугольника со сторонами $L{\text{/}}2$ и $H{\text{/}}2$, т.е. площадь отверстия составляет 25% от площади внешнего прямоугольника. В результате поперечное сечение исходного прямоугольника состоит из двух прямоугольников со сторонами $L{\text{/}}4$ и $H$ (рис. 1) и двух прямоугольников со сторонами $L{\text{/}}2$ и $H{\text{/}}4$ (рис. 1). Так как длины всех рассматриваемых прямоугольников значительно превышают их высоты, то во всех этих прямоугольниках можно рассматривать диффузионный процесс внедрения элементов окружающей среды в материал стержня как одномерный (влиянием агрессивной среды в стержень с коротких сторон его сечения можно пренебречь).
Рассмотрим диффузионный процесс в каждом из этих прямоугольников. Для концентрации $c$ среды в материале стержня примем нулевое начальное значение, в качестве граничных условий на поверхностях широких сторон сечения стержня используется равенство концентрации $c$ постоянному значению ${{c}_{0}}$.
Введем безразмерные переменные
(3.1)
$\frac{{\partial{ \bar {c}}}}{{\partial{ \bar {t}}}} = \frac{1}{{12}}\frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{{\bar {y}}}^{2}}}},\quad 0 \leqslant \bar {t} < \infty ,\quad 0 < \bar {y} < 1$Начальное и граничные условия, вследствие симметрии диффузионного процесса относительно середины стержня, записываются как:
Используем приближенный метод решения уравнения диффузии (3.1), основанный на введении диффузионного фронта [35].
Зависимость концентрации $\bar {c}$ от координаты $\bar {y}$ в данной работе принимается в виде квадратного полинома, удовлетворяющего граничным и начальному условиям. При этом рассматриваются два этапа процесса диффузии: этап проникновения фронта и этап насыщения, которые разделены моментом времени ${{\bar {t}}_{0}}$ [33, 35].
(3.2)
$\begin{gathered} \bar {c}\left( {\bar {y},\bar {t}} \right) = \left\{ \begin{gathered} 0\quad при\quad 0 \leqslant \bar {y} \leqslant \bar {l}\left( {\bar {t}} \right) \hfill \\ {{\left\{ {1 - \left[ {{{\left( {1 - \bar {y}} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \bar {y}} \right)} {\left( {1 - \bar {l}} \right)}}} \right. \kern-0em} {\left( {1 - \bar {l}} \right)}}} \right]} \right\}}^{2}}\quad при\quad \bar {l}\left( {\bar {t}} \right) < \bar {y} \leqslant 1 \hfill \\ \end{gathered} \right\}\quad при\quad 0 < \bar {t} \leqslant {{{\bar {t}}}_{0}} \\ \bar {c}\left( {\bar {y},\bar {t}} \right) = B + \left[ {1 - B} \right]{{\left( {\bar {y}} \right)}^{2}}\quad при\quad \bar {t} > {{{\bar {t}}}_{0}}, \\ \end{gathered} $Неизвестные зависимости $\bar {l}\left( {\bar {t}} \right)$ и $B\left( {\bar {t}} \right)$ определяются из интегрального удовлетворения параболической функции $\bar {c}\left( {\bar {y},\,\bar {t}} \right)$ по (3.2) уравнению диффузии (3.1)
(3.3)
$\int\limits_0^1 {\left| {\frac{{\partial{ \bar {c}}}}{{\partial{ \bar {t}}}} - \frac{1}{{12}}\frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{{\bar {y}}}^{2}}}}} \right|} {\kern 1pt} d{\kern 1pt} \bar {y} = 0$Показано [35], что если в (3.3) исключить знак модуля подынтегрального выражения, то отличие полученного приближенного решения уравнения диффузии от точного решения составляет всего единицы процентов, поэтому далее при использовании уравнения (3.3) знак модуля опустим.
Подставляя (3.2) в (3.3), получим координату диффузионного фронта $\bar {l}\left( {\bar {t}} \right)$ и концентрацию $B\left( {\bar {t}} \right)$ в следующем виде
(3.4)
$\bar {l} = 1 - \sqrt {\bar {t}} ,\quad B = 1 - \exp \left( { - \tfrac{{\bar {t} - {{{\bar {t}}}_{0}}}}{4}} \right)$Диффузионный фронт достигает срединной линии поперечного сечения стержня в момент времени ${{\bar {t}}_{0}}$, при этом $\bar {l} = 0$. На основе данного граничного условия получаем значение времени ${{\bar {t}}_{0}} = 1$.
Используя соотношения для концентрации (3.2) и соотношения (3.4), получим выражения для $\bar {c}\left( {\bar {y},\,\bar {t}} \right)$ в следующем виде
В дальнейшем для анализа влияния агрессивной среды на время до разрушения стержня будет использована интегрально средняя концентрация ${{\bar {c}}_{m}}\left( {\bar {t}} \right)$, которая имеет вид
(3.5)
${{\bar {c}}_{m}}\left( {\bar {t}} \right) = \int\limits_0^1 {\bar {c}\left( {\bar {y},\bar {t}} \right)dz} = \left\{ \begin{gathered} \tfrac{1}{3}\sqrt {\bar {t}} \quad при\quad 0 < \bar {t} \leqslant 1 \hfill \\ 1 - \tfrac{2}{3}\exp \left[ { - \tfrac{1}{4}\left( {\bar {t} - 1} \right)} \right]\quad при\quad \bar {t} > 1 \hfill \\ \end{gathered} \right.$Здесь в выражении (3.5) учитываются две стадии диффузионного процесса. На первой стадии при $0 \leqslant \bar {t} \leqslant 1$ происходит проникновение внешней среды в материал, которое характеризуется движением диффузионного фронта. На второй стадии при $\bar {t} \geqslant 1$ во всех точках рассматриваемого поперечного сечения концентрация отлична от нуля и происходит ее рост до полного насыщения.
Отсюда в случае прямоугольника со сторонами $H$ и $L{\text{/4}}$ получаем:
(3.6)
${{\bar {c}}_{{m1}}}\left( t \right) = \left\{ \begin{gathered} {{G}_{1}}\left( t \right) = \frac{1}{3}\frac{{\sqrt {48D} }}{H}\sqrt t \quad при\quad 0 \leqslant t \leqslant \frac{{{{H}^{2}}}}{{768D}} \hfill \\ {{G}_{2}}\left( t \right) = \frac{1}{3}\frac{{\sqrt {48D} }}{H}\sqrt t \quad при\quad \frac{{{{H}^{2}}}}{{768D}} \leqslant t \leqslant \frac{{{{H}^{2}}}}{{48D}} \hfill \\ {{G}_{3}}\left( t \right) = 1 - \frac{2}{3}\exp \left[ { - \frac{1}{4}\left( {\frac{{48D}}{{{{H}^{2}}}}t - 1} \right)} \right]\quad при\quad t > \frac{{{{H}^{2}}}}{{48D}} \hfill \\ \end{gathered} \right.$Аналогично в случае длинного прямоугольника со сторонами $L{\text{/}}2$ и $H{\text{/}}4$ $\left( {\bar {t} = \frac{{768D}}{{{{H}^{2}}}}t} \right)$ имеем
(3.7)
${{\bar {c}}_{{m2}}}\left( t \right) = \left\{ \begin{gathered} {{G}_{4}}\left( t \right) = \frac{1}{3}\frac{{\sqrt {768D} }}{H}\sqrt t \quad при\quad 0 \leqslant t \leqslant \frac{{{{H}^{2}}}}{{768D}} \hfill \\ {{G}_{5}}\left( t \right) = 1 - \frac{2}{3}\exp \left[ { - \frac{1}{4}\left( {\frac{{768D}}{{{{H}^{2}}}}t - 1} \right)} \right]\quad при\quad t > \frac{{{{H}^{2}}}}{{768D}} \hfill \\ \end{gathered} \right.$Зависимость интегрально среднего уровня концентрации агрессивной среды во всем сечении исходного прямоугольника с отверстием имеет вид
(3.8)
${{\bar {c}}_{m}}\left( t \right) = \frac{2}{3}{{\bar {c}}_{{m1}}}\left( t \right) + \frac{1}{3}{{\bar {c}}_{{m2}}}\left( t \right),$Таким образом, выражение для интегрально средней концентрации рассматриваемого поперечного сечения имеет вид:
(3.9)
${{\bar {c}}_{m}}\left( t \right) = \left\{ \begin{gathered} \frac{2}{3}{{G}_{1}}\left( t \right) + \frac{1}{3}{{G}_{4}}\left( t \right)\quad при\quad 0 \leqslant t \leqslant \frac{{{{H}^{2}}}}{{768D}} \hfill \\ \frac{2}{3}{{G}_{2}}\left( t \right) + \frac{1}{3}{{G}_{5}}\left( t \right)\quad при\quad \frac{{{{H}^{2}}}}{{768D}} \leqslant t \leqslant \frac{{{{H}^{2}}}}{{48D}} \hfill \\ \frac{2}{3}{{G}_{3}}\left( t \right) + \frac{1}{3}{{G}_{5}}\left( t \right)\quad при\quad t > \frac{{{{H}^{2}}}}{{48D}} \hfill \\ \end{gathered} \right.$Поскольку площадь реального сечения ${{F}_{{\operatorname{real} }}}$ (площадь сечения без отверстия) составляет ${{F}_{{\operatorname{real} }}} = \tfrac{3}{4}F$, то с учетом соотношений $F = HL$ и $\beta = H{\text{/}}L$ получаем ${{H}^{2}} = \beta F$ = = $\frac{4}{3}\beta {{F}_{{\operatorname{real} }}}$. Выражение (3.9) примет следующий вид:
(3.10)
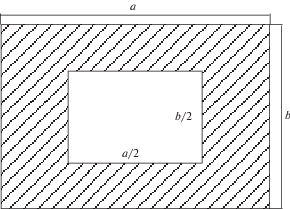
${{\bar {c}}_{m}}\left( t \right) = \left\{ \begin{gathered} \frac{2}{3}{{G}_{1}}\left( t \right) + \frac{1}{3}{{G}_{4}}\left( t \right)\quad при\quad 0 \leqslant t \leqslant \frac{{\beta {{F}_{{\operatorname{real} }}}}}{{576D}} \hfill \\ \frac{2}{3}{{G}_{2}}\left( t \right) + \frac{1}{3}{{G}_{5}}\left( t \right)\quad при\quad \frac{{\beta {{F}_{{\operatorname{real} }}}}}{{576D}} \leqslant t \leqslant \frac{{\beta {{F}_{{\operatorname{real} }}}}}{{36D}} \hfill \\ \frac{2}{3}{{G}_{3}}\left( t \right) + \frac{1}{3}{{G}_{5}}\left( t \right)\quad при\quad t > \frac{{\beta {{F}_{{\operatorname{real} }}}}}{{36D}} \hfill \\ \end{gathered} \right.$4. Двумерное уравнение диффузии в декартовых координатах. Рассмотрим поперечное сечение длинного стержня в виде прямоугольника со сторонами $a$ и $b$ ($b{\text{/}}a = \alpha $), из которого удалена внутренняя часть со сторонами $a{\text{/}}2$ и $b{\text{/}}2$. Из условия симметрии на рис. 2 представлена четверть рассматриваемого сечения: $0 \leqslant x \leqslant a{\text{/}}2$, $0 \leqslant y \leqslant b{\text{/}}2$, кроме точек, координаты которых удовлетворяют одновременно двум неравенствам: $a \leqslant 4x \leqslant 2a$ и $b \leqslant 4y \leqslant 2b$. Таким образом, площадь отверстия внутри сечения стержня составляет 25% от площади полного сечения. Рассматриваемое двухсвязное сечение находится в агрессивной окружающей среде.
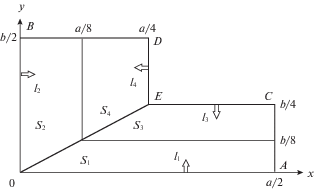
В площади поперечного сечения $S$ ($S$ – площадь рассматриваемой четверти сечения двухсвязного прямоугольника с прямоугольным отверстием) выделим четыре составляющих (рис. 3):
(4.1)
$\begin{gathered} S = {{S}_{1}} + {{S}_{2}} + {{S}_{3}} + {{S}_{4}} \\ {{S}_{1}}:\,\,\,\,\quad 0 \leqslant y \leqslant {{l}_{1}}\left( t \right),\quad 2\frac{y}{\alpha } \leqslant 2x \leqslant a \\ {{S}_{2}}:\,\,\,\quad 0 \leqslant x \leqslant {{l}_{2}}\left( t \right),\quad 2\alpha x \leqslant 2y \leqslant b \\ {{S}_{3}}:\,\quad 4{{l}_{3}}\left( t \right) \leqslant 4y \leqslant b,\quad 2\frac{y}{\alpha } \leqslant 2x \leqslant a \\ {{S}_{4}}:\quad 4{{l}_{4}}\left( t \right) \leqslant 4x \leqslant a,\quad 2\alpha x \leqslant 2y \leqslant b \\ \end{gathered} $Области $\left( {{{S}_{1}} + {{S}_{3}}} \right)$ и $\left( {{{S}_{2}} + {{S}_{4}}} \right)$ разделяются отрезком $OE$.
Для определения концентрации агрессивной среды $c(x,y,t)$ в рассматриваемом сечении воспользуемся общеизвестным уравнением диффузии в декартовых координатах:
(4.2)
$\frac{{\partial c}}{{\partial t}} - D\left( {\frac{{{{\partial }^{2}}c}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}c}}{{\partial {{y}^{2}}}}} \right) = 0$В качестве начального значения концентрации в рассматриваемом сечении двухсвязного прямоугольника с прямоугольным отверстием (многоугольник $OACEDBO$) примем нулевое значение
В качестве граничных значений примем
(4.4)
$\begin{gathered} {{\left. c \right|}_{{OA}}} = {{\left. c \right|}_{{OB}}} = {{\left. c \right|}_{{EC}}} = {{\left. c \right|}_{{ED}}} = {{c}_{0}} \\ {{\left. {\frac{{\partial c}}{{\partial x}}} \right|}_{{AC}}} = {{\left. {\frac{{\partial c}}{{\partial y}}} \right|}_{{BD}}} = 0 \\ \end{gathered} $Аналогично [38] рассмотрим вывод приближенного решения уравнения диффузии (4.2) в области $S$ с начальным (4.3) и граничными (4.4) условиями в виде полинома второй степени по пространственным координатам с коэффициентами, зависящими от времени. При получении этого решения начальное (4.3) и граничные (4.4) условия удовлетворяются точно, а само дифференциальное уравнение (4.2) – интегрально в области $S$. По аналогии с разд. 3 рассматриваются две стадии диффузионного процесса. На первой стадии принимается, что в областях ${{S}_{1}}$ и ${{S}_{3}}$ перпендикулярно оси $Ox$ от границ $OA$ и $EC$ внутрь поперечного сечения движутся диффузионные фронты ${{l}_{1}}(t)$ и ${{l}_{3}}(t)$ соответственно, разделяющие область $\left( {{{S}_{1}} + {{S}_{3}}} \right)$ на невозмущенную и возмущенную части. При $t = {{t}_{{01}}}$ фронты ${{l}_{1}}(t)$ и ${{l}_{3}}(t)$ соединяются: ${{l}_{1}}({{t}_{{01}}}) + {{l}_{3}}({{t}_{{01}}}) = b{\text{/}}4$. Аналогично областям ${{S}_{1}}$ и ${{S}_{3}}$ в областях ${{S}_{2}}$ и ${{S}_{4}}$ на первой стадии перпендикулярно оси $Oy$ от границ $OB$ и $ED$ внутрь поперечного сечения движутся диффузионные фронты ${{l}_{2}}(t)$ и ${{l}_{4}}(t)$ соответственно, разделяющие область $\left( {{{S}_{2}} + {{S}_{4}}} \right)$ на невозмущенную и возмущенную части. В области $\left( {{{S}_{2}} + {{S}_{4}}} \right)$ при $t = {{t}_{{02}}}$ выполняется равенство ${{l}_{2}}\left( {{{t}_{{02}}}} \right) + {{l}_{4}}\left( {{{t}_{{02}}}} \right) = a{\text{/}}4$. Можно показать, что ${{t}_{{01}}} = {{t}_{{02}}} = {{t}_{0}}$. Под ${{l}_{1}}, \ldots ,{{l}_{4}}$ всюду далее понимаются координаты соответствующих фронтов в осях $Ox$ и $Oy$. При $t > {{t}_{0}}$ в многоугольнике $OACEDBO$ реализуется вторая стадия диффузионного процесса.
4.1. Первая стадия диффузионного процесса. Решение дифференциального уравнения (4.2) рассмотрим в таком виде:
(4.5)
$c = \left\{ \begin{gathered} {{c}_{1}}(y,t)\quad \,{\text{в}}\quad {{S}_{1}} \hfill \\ {{c}_{2}}(x,t)\quad {\kern 1pt} {\text{в}}\quad {{S}_{2}} \hfill \\ {{c}_{3}}(y,t)\quad \,{\text{в}}\quad {{S}_{3}} \hfill \\ {{c}_{4}}(x,t)\quad {\kern 1pt} {\text{в}}\quad {{S}_{4}} \hfill \\ 0\quad {\text{в}}\quad \left( {{{S}_{2}} + {{S}_{4}}} \right)\quad {\text{при}}\quad {{l}_{2}}\left( t \right) \leqslant x \leqslant \frac{a}{4} - {{l}_{4}}\left( t \right) \hfill \\ 0\quad в\quad \left( {{{S}_{1}} + {{S}_{3}}} \right)\quad {\kern 1pt} {\kern 1pt} {\text{при}}\quad {{l}_{1}}\left( t \right) \leqslant y \leqslant \frac{b}{4} - {{l}_{3}}\left( t \right) \hfill \\ \end{gathered} \right.$Легко показать, что предложенный вариант (4.5) приближенного решения уравнения (4.2) удовлетворяет условиям (4.3) и (4.4). Для упрощения вычислений введем две гипотезы. Во-первых, предположим, что в $\left( {{{S}_{1}} + {{S}_{3}}} \right)$ скорости движения фронтов ${{l}_{1}}(t)$ и ${{l}_{3}}(t)$ по абсолютной величине равны, т.е. ${{l}_{1}}(t) + {{l}_{3}}(t) = b{\text{/}}4$, аналогично ${{l}_{2}}(t) + {{l}_{4}}(t) = a{\text{/}}4$. Во-вторых, допустим, что скорости движения фронтов от внешней поверхности поперечного сечения пропорциональны длинам соответствующих сторон сечения, т.е.
В результате величины всех четырех рассматриваемых фронтов ${{l}_{1}}(t) - {{l}_{4}}(t)$ можно свести к одной определяемой функции ${{l}_{1}}(t)$:
(4.6)
${{l}_{1}}(t) = \alpha {{l}_{2}}(t),\quad {{l}_{3}}(t) = \frac{b}{4} - {{l}_{1}}(t),\quad {{l}_{4}}(t) = \frac{a}{4} - \alpha {{l}_{1}}(t)$.При подстановке соотношений (4.5) в (4.2) и при дополнительном учете (4.6) получаем (далее обозначение в формулах “…” означает, что промежуточные выкладки опускаем):
Подставляя полученные выражения в уравнение
(4.7)
${{\dot {l}}_{1}} = \frac{{9b\left( {1 + {{\alpha }^{2}}} \right)}}{{\left( {b - 4{{l}_{1}}} \right){{l}_{1}}}}D$Введем переменные: ${{\hat {l}}_{1}} = {{l}_{1}}{\text{/}}b,$ $\hat {D} = D{\text{/}}{{b}^{2}}$, тогда уравнение (4.7) для определения зависимости координаты диффузионного фронта от времени запишется в виде
(4.8)
$\left( {1 - 4{{{\hat {l}}}_{1}}} \right){{\hat {l}}_{1}}\frac{{d{{{\hat {l}}}_{1}}}}{{dt}} = 9\left( {1 + {{\alpha }^{2}}} \right)\hat {D}$Поскольку в начальный момент времени $t = 0,$ ${{\hat {l}}_{1}} = 0$, т.е. производная $d{{\hat {l}}_{1}}{\text{/}}dt$ бесконечна, перейдем в уравнении (4.8) к обратной функции и получим решение начальной задачи $t\left( {{{{\hat {l}}}_{1}} = 0} \right) = 0$ в виде
Из условия симметрии следует:
Далее вычислим интегрально среднюю концентрацию агрессивной среды в материале стержня в процессе первой стадии диффузионного процесса. Площадь четверти сечения двухсвязного прямоугольника с прямоугольным отверстием составляет $\frac{3}{{16}}ab$.
(4.10)
$\frac{3}{{16}}ab\,{{\bar {c}}_{m}}\left( t \right) = {{I}_{1}} + {{I}_{2}} + {{I}_{3}} + {{I}_{4}},$Подставляя ${{I}_{1}}{\kern 1pt} - {\kern 1pt} {{I}_{4}}$ в (4.10), получаем ${{\bar {c}}_{m}}\left( t \right) = \frac{8}{3}{{\hat {l}}_{1}}$. Тогда учитывая решение (4.9) для момента времени ${{t}_{0}} = t\left( {{{{\hat {l}}}_{1}} = {\text{1/8}}} \right)$ получаем
4.2. Вторая стадия диффузионного процесса. При $t > {{t}_{0}}$ начинается вторая стадия диффузионного процесса, в любой точке рассматриваемого сечения концентрация агрессивной среды $c(x,y,t)$ положительна, при этом она возрастает во времени. Граничные условия на границах сечения OA, OB, EC, ED по-прежнему характеризуются постоянным значением $c = {{c}_{0}}$, вдоль отрезка $AC$: $\frac{{\partial c}}{{\partial x}}\left( {a{\text{/}}2,y,t} \right) = 0$, вдоль отрезка $BD$: $\frac{{\partial c}}{{\partial y}}\left( {x,b{\text{/}}2,t} \right) = 0$, начальные значения в областях ${{S}_{1}} \ldots {{S}_{4}}$ совпадают с соответствующими функциями $c(x,y,{{t}_{0}})$ в конце первой стадии. Как и ранее, будем использовать безразмерную концентрацию $\bar {c} = c{\text{/}}{{c}_{0}}$. В конце первой стадии концентрация в областях $\left( {{{S}_{1}} + {{S}_{3}}} \right)$ представляет параболическую зависимость $\bar {c}$ от $y$
с нулевым значением $\bar {c} = 0$ вдоль отрезка $y = b{\text{/}}8$. Предположим, что в этих областях зависимость концентрации $\bar {c}$ от координаты $y$ по-прежнему описывается квадратичной параболой, в которой минимальное значение $\bar {c}$, равное ${{B}_{1}}\left( t \right)$, реализуется при $y = b{\text{/}}8$: $\bar {c}\left( {x,b{\text{/}}8,t} \right) = {{B}_{1}}\left( t \right)$.Представим выражение для концентрации $\bar {c}(x,y,{{t}_{0}})$ в областях $\left( {{{S}_{1}} + {{S}_{3}}} \right)$ в следующем виде
(4.11)
$\bar {c}(x,y,{{t}_{0}}) = 1 - 16\left( {1 - {{B}_{1}}} \right)\frac{y}{b} + 64{{\left( {1 - {{B}_{1}}} \right)}^{2}}{{\left( {\frac{y}{b}} \right)}^{2}}$Очевидно, что соотношение (4.11) удовлетворяет всем начальным и граничным условиям в точной постановке. Подставив (4.11) в уравнение диффузии (4.2), получим:
Запишем интегральное следствие уравнения диффузии в областях $\left( {{{S}_{1}} + {{S}_{4}}} \right)$:
(4.12)
$\int\limits_{\left( {{{S}_{2}} + {{S}_{4}}} \right)} {\left[ {\frac{{\partial{ \bar {c}}}}{{\partial t}} - D\left( {\frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{y}^{2}}}}} \right)} \right]dxdy} = \frac{{ab}}{{16}}{{\dot {B}}_{1}} - D\frac{{12a}}{b}\left( {1 - {{B}_{1}}} \right)$Представим аналогичную зависимость $\bar {c}(x,y,t)$ в области $\left( {{{S}_{2}} + {{S}_{4}}} \right)$ в виде:
Легко показать, что это выражение для $\bar {c}(x,y,{{t}_{0}})$ в области $\left( {{{S}_{2}} + {{S}_{4}}} \right)$ при $t = {{t}_{0}}$ удовлетворяет всем начальному и граничным условиям. Используемые производные принимают следующий вид:
(4.13)
$\int\limits_{\left( {{{S}_{2}} + {{S}_{4}}} \right)} {\left[ {\frac{{\partial{ \bar {c}}}}{{\partial t}} - D\left( {\frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\bar {c}}}{{\partial {{y}^{2}}}}} \right)} \right]dxdy} = \frac{{ab}}{{16}}{{\dot {B}}_{2}} - D\frac{{12b}}{a}\left( {1 - {{B}_{2}}} \right)$Можно показать, что ${{B}_{1}}\left( t \right) = {{B}_{2}}\left( t \right) = B\left( t \right)$. Складывая (4.12) и (4.13), получаем интегральное следствие уравнения диффузии в виде:
Его решение для начальных данных $B\left( {{{t}_{0}}} \right) = 0$ имеет вид:
Рассчитаем интегрально среднюю по материалу стержня концентрацию агрессивной среды во второй стадии диффузионного процесса. Имеем
Отсюда получаем среднее значение:
(4.14)
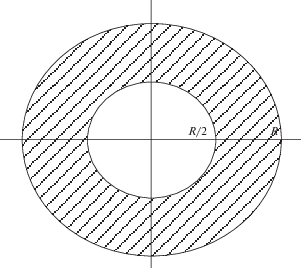
${{\bar {c}}_{m}}\left( t \right) = 1 - \frac{2}{3}\exp \left[ { - \frac{{96}}{{\alpha F}}\left( {{{\alpha }^{2}} + 1} \right)D\left( {t - {{t}_{0}}} \right)} \right]$5. Уравнение диффузии в осесимметричной постановке. В данном разделе рассматривается осесимметричная задача о диффузии элементов окружающей среды в полый стержень, поперечное сечение которого имеет форму кольца. Внешний радиус кольца $R$, а внутренний радиус составляет $R{\text{/}}2$, при этом площадь полого отверстия в поперечном сечении стержня составляет 25 процентов от полной площади поперечного сечения стержня (рис. 4).
По-прежнему рассмотрим для концентрации $c$ нулевое начальное условие, в качестве граничного условия на поверхностях стержня примем условие равенства концентрации с постоянному значению ${{c}_{0}}$. Введем безразмерные переменные
в которых уравнение диффузии принимает вид:Рассмотрим первую стадию диффузионного процесса. Зависимости концентрации от координаты и времени задаются в виде полиномов второй степени от координаты. В указанных зависимостях учтены зависящие от времени координаты двух диффузионных фронтов, движущихся от внутренней и внешней сторон поперечного сечения стержня в виде кольца.
(5.1)
$\bar {с}\left( {\tilde {r},\tilde {t}} \right) = \left\{ \begin{gathered} {{\left[ {\frac{{\tilde {r} - {{{\tilde {l}}}_{1}}}}{{1/2 - {{{\tilde {l}}}_{1}}}}} \right]}^{2}}\quad при\quad 1{\text{/}}2 \leqslant \tilde {r} \leqslant {{{\tilde {l}}}_{1}}\left( {\tilde {t}} \right),\quad 0 < \tilde {t} \leqslant {{{\tilde {t}}}_{0}} \hfill \\ 0,\quad \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\kern 1pt} {\kern 1pt} \,при\quad {{{\tilde {l}}}_{1}}\left( {\tilde {t}} \right) \leqslant \tilde {r} \leqslant {{{\tilde {l}}}_{2}}\left( {\tilde {t}} \right),\quad 0 < \tilde {t} \leqslant {{{\tilde {t}}}_{0}} \hfill \\ {{\left[ {\frac{{\tilde {r} - {{{\tilde {l}}}_{2}}}}{{1 - {{{\tilde {l}}}_{2}}}}} \right]}^{2}}\quad \,{\kern 1pt} \,\,\,\,при\quad 1 \leqslant \tilde {r} \leqslant {{{\tilde {l}}}_{2}}\left( {\tilde {t}} \right),\quad 0 < \tilde {t} \leqslant {{{\tilde {t}}}_{0}}, \hfill \\ \end{gathered} \right.$Определим функции ${{\tilde {l}}_{1}}\left( {\tilde {t}} \right)$, ${{\tilde {l}}_{2}}\left( {\tilde {t}} \right)$ из интегральных следствий уравнения диффузии и уравнения диффузии с весом $\tilde {r}$:
В результате получим систему дифференциальных уравнений
(5.2)
$\begin{gathered} \frac{{1 + {{{\tilde {l}}}_{1}}}}{{12}}{{{\dot {\tilde {l}}}}_{1}} - \frac{{1 + {{{\tilde {l}}}_{2}}}}{6}{{{\dot {\tilde {l}}}}_{2}} = \frac{{2{{{\tilde {l}}}_{1}} + 1}}{{2{{{\tilde {l}}}_{1}} - 1}} + \frac{{{{{\tilde {l}}}_{2}} + 1}}{{1 - {{{\tilde {l}}}_{2}}}} \\ \frac{{12{{{\tilde {l}}}_{1}}^{2} + 8{{{\tilde {l}}}_{1}} + 3}}{{12}}{{{\dot {\tilde {l}}}}_{1}} - \frac{{{{{\tilde {l}}}_{2}}^{2} + {{{\tilde {l}}}_{2}} + 4}}{{10}}{{{\dot {\tilde {l}}}}_{2}} = \frac{{2{{{\tilde {l}}}_{1}}^{2} + {{{\tilde {l}}}_{1}} + 2}}{{2{{{\tilde {l}}}_{1}} - 1}} + \frac{{\tilde {l}_{2}^{2} + {{{\tilde {l}}}_{2}} + 4}}{{1 - {{{\tilde {l}}}_{2}}}} \\ \end{gathered} $Зависимости ${{\tilde {l}}_{1}}\left( {\tilde {t}} \right)$, ${{\tilde {l}}_{2}}\left( {\tilde {t}} \right)$ находились из системы (5.2) численно. По ним, в свою очередь, определялась зависимость концентрации от координаты и времени $\bar {с}\left( {\tilde {r},\,\tilde {t}} \right)$.
В начале второй стадии диффузионного процесса концентрация во всем стержне отлична от нуля и определена в момент окончания первой стадии при смыкании двух диффузионных фронтов. Зависимость концентрации от времени задается в виде
(5.3)
$\bar {с}\left( {\tilde {r},\tilde {t}} \right) = \left\{ \begin{gathered} B + \left( {1 - B} \right){{\left[ {\frac{{\tilde {r} - \tilde {l}}}{{1/2 - \tilde {l}}}} \right]}^{2}}\quad при\quad 1{\text{/}}2 \leqslant \tilde {r} \leqslant \tilde {l}\left( {\tilde {t}} \right),\quad \tilde {t} > {{{\tilde {t}}}_{0}} \hfill \\ B + \left( {1 - B} \right){{\left[ {\frac{{\tilde {r} - \tilde {l}}}{{1 - \tilde {l}}}} \right]}^{2}}\quad \,\,\,\,{\kern 1pt} \,{\kern 1pt} при\quad \tilde {l}\left( {\tilde {t}} \right) \leqslant \tilde {r} \leqslant 1,\quad \tilde {t} > {{{\tilde {t}}}_{0}} \hfill \\ \end{gathered} \right.$Проводя рассуждения и выкладки, аналогичные проведенным на первой стадии, получим следующую систему дифференциальных уравнений.
(5.4)
$\begin{gathered} \frac{{\left( {4\tilde {l} + 9} \right)}}{{48}}\dot {B} + \left[ {\frac{{\dot {\tilde {l}}}}{{12}} - \frac{{2\tilde {l}}}{{\left( {\tilde {l} - 1} \right)\left( {2\tilde {l} - 1} \right)}}} \right]\left( {B - 1} \right) = 0 \\ \frac{{\left( {4{{{\tilde {l}}}^{2}} + 9\tilde {l} + 14} \right)}}{{40}}\dot {B} + \left[ {\frac{{\dot {\tilde {l}}\left( {8\tilde {l} + 9} \right)}}{{40}} + \frac{{2\left( {{{{\tilde {l}}}^{2}} + 3\tilde {l} - 1} \right)}}{{\left( {1 - 2\tilde {l}} \right)\left( {\tilde {l} - 1} \right)}}} \right]\left( {B - 1} \right) = 0 \\ \end{gathered} $Начальные условия системы (5.4) имеют следующий вид:
Величина правой части первого начального условия полагается равной значению решения системы (5.2) в момент времени ${{\tilde {t}}_{0}} = 0.002$ окончания первой стадии диффузионного процесса. Второе начальное условие означает, величину концентрации в точке смыкания фронтов в конце первой стадии диффузионного процесса в момент времени ${{\tilde {t}}_{0}}$. Как и для первой стадии зависимости $B\left( {\tilde {t}} \right)$, $\tilde {l}\left( {\tilde {t}} \right)$ определялись из численного решения системы (5.4).
Интегрально средняя концентрация определяется выражением:
6. Длительная прочность растягиваемых стержней в агрессивной среде. Рассмотрим кинетическое уравнение, в котором скорость накопления поврежденности зависит от растягивающего напряжения ${{\sigma }_{0}}$ (принимающего одно и то же значение во всех рассмотренных стержнях) и интегрально среднего уровня концентрации агрессивной среды ${{\bar {c}}_{m}}$ в следующем виде [9]:
(6.1)
$\frac{{d\omega }}{{dt}} = A{{\left( {\frac{{{{\sigma }_{0}}}}{{1 - \omega \left( t \right)}}} \right)}^{n}}f\left( {{{{\bar {c}}}_{m}}\left( t \right)} \right),\quad \omega \left( 0 \right) = 0,\quad \omega \left( {t{\kern 1pt} *} \right) = 1$(6.2)
$t_{0}^{*} = {{\left[ {\left( {n + 1} \right)A\sigma _{0}^{n}} \right]}^{{ - 1}}} = \int\limits_0^{t{\kern 1pt} *} {f\left( {{{{\bar {c}}}_{m}}\left( t \right)} \right)dt} $В случае зависимости $f\left( {{{{\bar {c}}}_{m}}} \right)$ с одной материальной константой можно рассматривать линейную функцию [39]:
Подставляя полученные ранее зависимости ${{\bar {c}}_{m}}\left( t \right)$ в (6.3), а затем в (6.2), получаем времена до разрушения стержней различной формы в агрессивной среде.
В качестве примера рассмотрим стержни с отверстиями при различных рассматриваемых ранее в статье формах поперечных сечений с неизменной величиной площади этих сечений $F = 100$ мм2. Эти стержни изготовлены из α-Fe и находятся в водородной среде при температуре 500°С, в этом случае коэффициент диффузии в материале стержня равен D = 1.02 мм2/мин. [40].
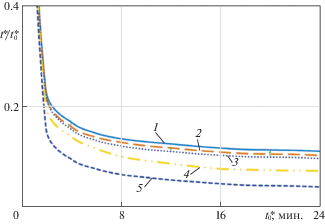
На рис. 5 приведены зависимости $t{\kern 1pt} *{\text{/}}t_{0}^{*}$ от $t_{0}^{*}$ (мин.) для рассматриваемых форм поперечного сечения. Из рис. 5 следует, что среди рассматриваемых форм поперечного сечения стержней минимальное время до разрушения соответствует стержню с двусвязным поперечным сечением в виде тонкого прямоугольника с отверстием.
Рис. 5.
Зависимость отношения времени до разрушения при наличии и отсутствии агрессивной среды $t{\text{*/}}t_{0}^{*}$ от времени до разрушения при ее отсутствии $t_{0}^{*}$ для стержней с отверстием при различной форме внешнего контура поперечного сечения: 1 – квадратное поперечное сечение, 2 – прямоугольное поперечное сечение $\alpha = 0.85$, 3 – прямоугольное поперечное сечение $\alpha = 0.7$, 4 – поперечное сечение в виде кольца, 5 – поперечное сечение в виде тонкого прямоугольника с отверстием.
В табл. 1 приведены значения времен $t{\kern 1pt} *$ и отношений $t{\kern 1pt} {\text{*/}}t_{0}^{*}$ для всех рассмотренных форм поперечного сечения при трех значениях $t_{0}^{*}$ (6, 16 и 26 мин.). Из табл. 1 следует, что в прямоугольниках независимо от величины $t_{0}^{*}$ большему значению длины контура поперечного сечения прямоугольника $M$ соответствует меньшее значение $t{\kern 1pt} *$. Это означает, что увеличение длины контура поперечного сечения прямоугольника M приводит к уменьшению времени до разрушения $t{\kern 1pt} *$ соответствующего стержня. Так, среди сечений в виде прямоугольников с различными комбинациями сторон время до разрушения стержней убывает при возрастании величины периметра поперечного сечения. Это верно, как для односвязных областей [4], так и для двухсвязных.
Таблица 1.
Значения времен $t{\kern 1pt} *$ и отношений времен $t{\kern 1pt} {\text{*/}}t_{0}^{*}$ для рассматриваемых двухсвязных форм поперечного сечения стержня
| № п/п | Форма поперечного сечения c отверстием | Размеры внешнего контура сечения мм | M, мм | $t{\text{*/}}t_{0}^{*}$, $t_{0}^{*}$ = 6 мин. | $t{\text{*/}}t_{0}^{*}$, $t_{0}^{*}$ = 16 мин. | $t{\text{*/}}t_{0}^{*}$, $t_{0}^{*}$ = 26 мин. |
|---|---|---|---|---|---|---|
| 1 | Кольцо | R = 15.642 | 53.179 | 0.696 | 1.208 | 1.817 |
| 0.116 | 0.075 | 0.070 | ||||
| 2 | Квадрат | a = 10 | 60.000 | 0.876 | 1.861 | 2.818 |
| a = 1 | b = 10 | 0.146 | 0.116 | 0.108 | ||
| 3 | Прямоугол. | a = 10.541 | 60.084 | 0.846 | 1.802 | 2.734 |
| α = 0.90 | b = 9.487 | 0.141 | 0.113 | 0.105 | ||
| 4 | α = 0.85 | a = 10.846 | 60.120 | 0.828 | 1.733 | 2.610 |
| b = 9.220 | 0.138 | 0.311 | 0.100 | |||
| 5 | α = 0.80 | a = 11.180 | 60.330 | 0.783 | 1.635 | 2.502 |
| b = 8.944 | 0.130 | 0.102 | 0.096 | |||
| 6 | α = 0.70 | a = 11.952 | 60.957 | 0.741 | 1.592 | 2.392 |
| b = 8.367 | 0.124 | 0.100 | 0.092 | |||
| 7 | α = 0.60 | a = 12.910 | 61.968 | 0.719 | 1.324 | 2.110 |
| b = 7.746 | 0.120 | 0.082 | 0.081 | |||
| 8 | α = 0.04 | a = 50.000 | 156 | 0.408 | 0.613 | 0.794 |
| b = 2.000 | 0.068 | 0.038 | 0.034 | |||
| 9 | α = 0.0225 | a = 66.667 | 202.400 | 0.386 | 0.601 | 0.732 |
| b = 1.500 | 0.064 | 0.038 | 0.028 | |||
| 10 | α = 0.01 | a = 100 | 303 | 0.354 | 0.583 | 0.699 |
| b = 1 | 0.059 | 0.036 | 0.027 | |||
| 11 | α = 0.0025 | a = 200 | 600.500 | 0.312 | 0.537 | 0.632 |
| b = 0.500 | 0.052 | 0.004 | 0.024 |
Заключение. С помощью приближенного решения уравнений диффузии определяются характеристики диффузионного процесса в стержнях при различных формах их двусвязных поперечных сечений (круг, квадрат и прямоугольники с различным соотношением сторон). Для определения влияния агрессивной среды на длительную прочность растягиваемых стержней используется вариант кинетической теории Ю.Н. Работнова. Вычисления показывают, что наименьшее время до разрушения реализуется в прямоугольных стержнях с минимальной толщиной $b$ (при $\alpha = {b \mathord{\left/ {\vphantom {b a}} \right. \kern-0em} a} = 0.0025$) среди рассмотренных. При принятом равенстве площадей рассматриваемых поперечных сечений и равенстве растягивающих напряжений стержень с прямоугольным поперечным сечением с минимальной толщиной является стержнем с поперечным сечением, имеющим максимальный периметр контура.
Показано, что среди сечений в виде полых прямоугольников с различными комбинациями сторон ($\alpha = 0.0025{\kern 1pt} - {\kern 1pt} 0.9$) время до разрушения стержней убывает с уменьшением $\alpha $ и, как следствие, с возрастанием величины периметра поперечного сечения $M$.
Приведенные выводы по зависимостям времен до разрушения от периметра для стержней с поперечными сечениями в виде полых прямоугольников естественны вследствие подобия наружного и внутреннего контуров сечений.
Полученные результаты времен до разрушения подобных друг другу полых поперечных сечений стержней не подтверждаются для сечений в виде полого квадрата и кольца, рассматриваемых в статье. Данный факт авторы статьи объясняют отсутствием подобия контуров этих сечений. При принятом равенстве площадей всех рассматриваемых в статье типов поперечных сечений и равенстве растягивающих напряжений время до разрушения стержня с поперечным сечением в виде полого квадрата ($\alpha = 1$) превышает время до разрушения кольца той же площади. Для рассматриваемых времен до разрушения в нейтральных условиях (6, 16 и 26 мин.) это превышение составляет от 25 до 55 процентов и увеличивается с ростом времени до разрушения. При этом длина периметра сечения в виде полого квадрата также превышает длину периметра кольца. Данный факт авторы статьи объясняют особенностями диффузионного процесса в углах сечения в виде полого квадрата.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 19-19-00062).
Список литературы
Локощенко А.М., Фомин Л.В. Моделирование поведения материалов и элементов конструкций, находящихся под воздействием агрессивных сред (обзор) // Пробл. прочн. пластичн. 2018. Т. 80. № 2. С. 145–179.
Локощенко А.М. Ползучесть и длительная прочность металлов в агрессивных средах (обзор) // Физ.-хим. мех. матер. 2001. № 4. С. 27–41.
Локощенко А.М., Фомин Л.В. Влияние формы поперечного сечения растягиваемых стержней на длительную прочность в присутствии агрессивной окружающей среды // ПМТФ. 2016. С. 35–44.
Ларин Н.С., Локощенко А.М., Фомин Л.В. Зависимость времени до разрушения стержней, растягиваемых при ползучести в присутствии агрессивной среды, от формы односвязного поперечного сечения // Изв. РАН. МТТ. 2019. № 5. С. 59–69.
Вильчевская Е.Н., Фрейдин А.Б., Морозов Н.Ф. Кинетика фронта химической реакции в центрально-симметричных задачах механохимии // Докл. РАН. 2015. Т. 461. № 5. С. 525–529.
Фрейдин А.Б. О тензоре химического сродства при химических реакциях в деформируемых материалах // Изв. РАН. МТТ. 2015. № 3. С. 35–69.
Фрейдин А.Б., Вильчевская Е.Н., Королев И.К. О фазовых превращениях в области неоднородности материала. Ч. 2. Взаимодействие трещины с включением, претерпевающим фазовое превращение // Изв. РАН. МТТ. 2011. № 5. С. 32–42.
Овчинников И.И., Овчинников И.Г., Богина М.Ю. Моделирование деформирования и разрушения материалов в условиях радиационного облучения с учетом влияния вида напряженного состояния. Сообщ. 1. Об учете влияния радиационного облучения при построении моделей деформирования в радиационных условиях с применением теории структурных параметров // Интернет-ж. Науковедение. 2013. № 2. http://publ.naukovedenie.ru
Работнов Ю.Н. Ползучесть элементов конструкций. М.: Наука, 1966. 752 с.
Овчинников И.Г., Овчинников И.И., Богина М.Ю., Матора А.В. Модели и методы, используемые при расчете и моделировании поведения конструкций, подвергающихся воздействию радиационных сред // Интернет-ж. Науковедение. 2013. № 2. http://publ.naukovedenie.ru
Овчинников И.Г., Богина М.Ю., Матора А.В. Влияние радиационных сред на механические характеристики материалов и поведение конструкций (обзор) // Интернет-ж. Науковедение. 2012. № 4. http://publ.naukovedenie.ru
Марголин Б.З., Гуленко А.Г., Курсевич И.П., Бучатский А.А. Прогнозирование длительной прочности аустенитных материалов при нейтронном облучении // Вопр. материал. 2005. № 2 (42). С. 163–186.
Марголин Б.З., Бучатский А.А., Гуленко А.Г. и др. Новый метод прогнозирования сопротивления циклическому нагружению при вязкоупругопластическом деформировании и нейтронном облучении // Пробл. проч. 2008. № 6. С. 5–24.
Митенков Ф.М., Большухин М.А., Козин А.В., Коротких Ю.Г., Панов В.А., Пахомов В.А., Пичков С.Н. Технология эксплуатационного мониторинга ресурса оборудования и систем ЯЭУ // Пробл. прочн. пластичн. 2012. Вып. 74. С. 68–77.
Демидов А.С., Кашелкин В.В., Каштанов А.Д., Яковлев В.А. Прогнозирование механических свойств реакторной стали 08Х16Н11МЗ-ПД в условиях ползучести без учета и с учетом радиационного облучения // Вестн. МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2015. № 2. С. 18–26.
Хажинский Г.М. Поведение металла ядерных реакторов. М.: Спутник+, 2018. 233 с.
Овчинников И.Г., Раткин В.В., Землянский А.А. Моделирование поведения железобетонных элементов конструкций в условиях воздействия хлоридосодержащих сред. СГТУ. Саратов. 2000. 232 с.
Овчинников И.Г., Хвалько Т.А. Работоспособность конструкций в условиях высокотемпературной водородной коррозии. Саратов: Сарат. гос. техн. ун-т, 2003. 176 с.
Кудрявцев А.С., Марков В.Г., Лаврухин В.С. Длительная прочность стали в жидкометаллическом теплоносителе на основе свинца // Вопр. материал. 2006. № 4(48). С. 89–94.
Кудрявцев А.С., Каштанов А.Д., Марков В.Г., Лаврухин В.С. Прочность хромистой мартенситной стали в теплоносителе на основе свинца // Вопр. материал. 2007. № 1(49). С. 78–82.
Chiang M.F., Hsu H.H., Young M.C., Huang J.Y. Mechanical degradation of cold-worked 304 stainless steel in salt spray environments // J. Nucl. Mater. 2012. V. 422. P. 58–68.
Chopra O.K., Rao A.S. A review of irradiation effects on LWR core internal materials – IASCC susceptibility and crack growth rates of austenitic stainless steels // J. Nucl. Mater. 2011. V. 409. P. 235–256.
Fukuya K. Current understanding of radiation-inducted creep of light water reactor structural materials // J. Nucl. Mater. 2013. V. 50. P. 213–254.
Garner F.A., Makenas B.J., Chastain S.A. Swelling and creep observed in AISI 304 fuel pin cladding from three MOX fuel assembles irradiated in ERB-II // J. Nucl. Mater. 2011. V. 413. P. 53–61.
Garnier J., Brechet Y., Delnondedieu M., Pokor C., Dubuissison P., Renault A., Averty X., Massoud J.P. Irradiating creep of SA 304L and CW 316 stainless steels: Mechanical behavior and microstructural aspects. Part I. Experimental results // J. Nucl. Mater. 2011. V. 413. P. 63–69.
Gurovich B.A., Kuleshova E.A., Frolov A.S., Maltsev D.A., Prikhodko K.E., Fedotova S.V., Margolin B.Z., Sorokin A.A. Investigation of high temperature annealing effective-ness for recovery of radiation-inducted structural changes and properties of 18Cr-10Ni-Ti austenitic stainless steels // J. Nucl. Mater. 2015. V. 465. P. 565–581.
Materna-Morris E., Möslang A., Schneider H.-C. Tensile and low cycle fatigue properties of EUROFER97-steel after 16.3 dpa neutron irradiation at 523, 623 and 723K // J. Nucl. Mater. 2013. V. 442. P. 562–566.
Gupta J., Hure J., Tanguy B., Laffont L., Lafont M.-C., Andrieu E. Evaluation of stress corrosion cracking of irradiated 304L stainless steel in PWR environment using heavy ion irradiation // J. Nucl. Mater. 2016. V. 476. P. 82–92.
Litao Chang M., Grace Burke, Fabio Scenini. Stress corrosion crack initiation in machined type 316L austenitic stainless steel in simulated pressurized water reactor primary water // Corrosion Sci. 2018. V. 138. P. 54–65.
Negyesi M., Masaki Amaya. The effect of nitride formation on the oxidation kinetics of Zry-4 fuel cladding under steam-air atmospheres at 1273–1573 K // J. Nucl. Mater. 2019. V. 524. P. 263–277.
Renault-Laborne A., Garnier J., Malaplate J., Gavoille P., Sefta F., Tanguy B. Evolution of microstructure after irradiation creep in several austenitic steels irradiated up to 120 dpa at 320°C // J. Nucl. Mater. 2016. V. 475. P. 209–226.
Lapouge P., Onimus F., Coulombier M., Raskin J.-P., Pardoen T., Bréchet. Y. Creep behavior of submicron copper films under irradiation // Acta Mater. 2017. V. 131. P. 77–87.
Локощенко А.М. Ползучесть и длительная прочность металлов в агрессивных средах. М.: МГУ, 2000. 178 с.
Локощенко А.М. Моделирование процесса ползучести и длительной прочности металлов. М.: Моск. гос. индустр. ун-т., 2007. 264 с.
Локощенко А.М. Ползучесть и длительная прочность металлов. М.: Физматлит, 2016. 504 с.
Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике. М.: ГИТТЛ, 1956. 684 с.
Смирнов М.М. Задачи по уравнениям математической физики. М.: Наука, 1968. 112 с.
Кулагин Д.А. Метод приближенного решения двумерного уравнения диффузии // Научн. тр. III Международного семинара “Современные проблемы прочности” (20–24.IX.1999. Старая Русса). НовГУ. Великий Новгород. 1999. Т. 2. С. 114–117.
Фомин Л.В. Описание длительной прочности растягиваемых стержней прямоугольного и круглого поперечных сечений в высокотемпературной воздушной среде // Вестн. Сам. гос. техн. ун-та. Сер. физ.-мат. науки. 2013. № 3(32). С. 87–97.
Гельд П.В., Рябов Р.А. Водород в металлах и сплавах. М.: Металлургия, 1974. 364 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика