Прикладная математика и механика, 2021, T. 85, № 1, стр. 44-65
Контакт с межмолекулярным взаимодействием для вязкоупругого слоя (самосогласованный подход): анализ особенностей процесса подвода/отвода индентора
1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: iasoldat@hotmail.com
Поступила в редакцию 25.05.2020
После доработки 11.09.2020
Принята к публикации 06.12.2020
Аннотация
Рассматривается контакт бесконечно протяженного плоского индентора и вязкоупругого слоя в рамках самосогласованного по Дерягину подхода с поверхностным (традиционная постановка) и объемным (уточненная постановка) приложением сил межмолекулярного взаимодействия. Получены уравнения, описывающие изменение контактного зазора во времени при таком контакте. Сформулировано условие, при котором возможно скачкообразное изменение контактного зазора во времени. Выполнены расчеты, свидетельствующие о немонотонном характере зависимостей контактного зазора и давления от времени в режимах подвода и отвода индентора. Показано, что традиционная и уточненная постановки задачи могут приводить к существенно различным результатам расчета характеристик контакта индентора и вязкоупругого слоя.
При изучении контакта деформируемых тел силы межмолекулярного взаимодействия впервые учитывались применительно к герцевскому контакту [1]. В дальнейшем был разработан ряд эффективных подходов к решению контактных задач такого типа, среди которых следует отметить подходы, использующие концепцию поверхностной энергии – модели JKR и DMT [2, 3]. Эти подходы также использовались для расчета адгезионного контакта слоистых [4–7] и вязкоупругих тел [8–11].
Строгая постановка контактной задачи, учитывающая межмолекулярное взаимодействие, предполагает существование некоторого зазора $r$ между контактирующими телами. Величина этого зазора должна обеспечивать баланс сил, обусловленных контактной деформацией тел и их межмолекулярным взаимодействием (самосогласованный подход по Дерягину [12]). При таком подходе возможны постановки задачи с поверхностным (традиционная постановка [13–15]) и объемным (уточненная постановка [16–19]) приложением сил межмолекулярного взаимодействия.
Одной из характерных особенностей адгезионного контакта является возможность скачкообразного изменения его параметров. Впервые подобное изменение было теоретически описано применительно к подпружиненному контакту твердых тел при наличии сил Лондона–Ван-дер-Ваальса [20]. В дальнейшем скачкообразное изменение параметров адгезионного контакта упругих тел рассматривалось во многих исследованиях, среди которых отметим работы [12–14, 21], использующие самосогласованный подход при постановке задачи.
В данной работе производится расчет контактного взаимодействия бесконечно протяженного плоского индентора с вязкоупругим слоем при наличии сил межмолекулярного взаимодействия (самосогласованный подход, традиционная и уточненная постановки задачи). Значительное внимание уделяется анализу скачкообразного изменения контактного зазора.
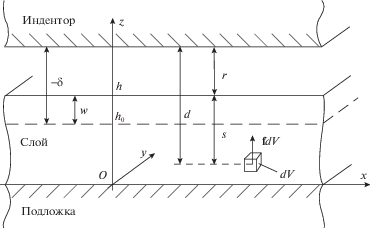
1. Постановка задачи. Рассмотрим контактное взаимодействие бесконечно протяженного плоского индентора и основания, состоящего из вязкоупругого слоя толщины $h$, связанного с подложкой (рис. 1), причем индентор и подложка являются абсолютно жесткими. Считается, что индентор и слой разделены контактным зазором $r$, обеспечивающим баланс сил вязкоупругого и межмолекулярного взаимодействий контактирующих тел (самосогласованный подход) [12]. Свяжем с основанием систему координат $Oxyz$, совместив ее плоскость $Oxy$ с границей раздела слоя и подложки. Контакт индентора и слоя считается плоскопараллельным, что обуславливает зависимость всех контактных характеристик только от координаты $z$ и времени $t$. Толщину слоя в недеформированном состоянии обозначим через ${{h}_{{{\kern 1pt} 0}}}$.
Рис. 1.
Контактное взаимодействие индентора с основанием, состоящим из вязкоупругого слоя, связанного с абсолютно жесткой подложкой.
Межмолекулярное взаимодействие индентора и основания определяется парными взаимодействиями их молекул (гипотеза Гамакера). Соответствующая сила $F$ зависит от свойств пары молекул и расстояния $l$ между ними. Существуют разные формы такой зависимости, и в дальнейшем будет использоваться известный закон Леннард–Джонса [22]:
где ${{a}_{1}},{{a}_{2}},m,n$ – параметры взаимодействия, причем обычно полагают $m = 7$, $n = 13$. Применительно к рассматриваемой задаче, обозначим через ${{a}_{{1c}}},{{a}_{{2c}}}$ параметры в законе (1.1), отвечающие взаимодействию молекул индентора и слоя, а через ${{a}_{{1b}}},{{a}_{{2b}}}$ – взаимодействию молекул индентора и подложки.При определенных допущениях [14], [23, с. 205–220] суммирование парных взаимодействий молекул позволяет для каждой точки слоя рассчитать объемную силу ${\mathbf{f}}$, обусловленную межмолекулярным взаимодействием. Эта сила направлена вдоль оси $z$ и зависит от расстояния $d = r + s = r + h - z$ между точкой ее приложения и индентором (рис. 1), причем толщину $h$ слоя здесь можно заменить постоянным значением ${{h}_{{{\kern 1pt} 0}}}$, что допустимо при малых деформациях. Таким образом, если обозначить через ${{f}_{i}}$, $i = 1,2,3$ компоненты объемной силы в системе координат $O{\kern 1pt} {{x}_{1}}{\kern 1pt} {{x}_{2}}{\kern 1pt} {{x}_{3}}$, то
Кроме того, суммирование парных взаимодействий молекул позволяет определить силу $p$ воздействия индентора на основание, приходящуюся на единицу площади его поверхности (верхней границы):
(1.3)
$p(t) = \Phi (r(t)),\;\;\;\;\Phi (r) = - \,\int\limits_0^\infty f (r + s){\mkern 1mu} {\kern 1pt} ds,$В случае закона Леннард–Джонса функции $f$ и $\Phi $ имеют вид [19]
(1.4)
$f(d) = \frac{{{{b}_{{1\# }}}}}{{{{d}^{{m - 3}}}}} - \frac{{{{b}_{{2\# }}}}}{{{{d}^{{n - 3}}}}} = \frac{{{{b}_{{1\# }}}}}{{d_{{e\# }}^{{m - 3}}}}\left[ {{{{\left( {\frac{{{{d}_{{e\# }}}}}{d}} \right)}}^{{m - 3}}} - {{{\left( {\frac{{{{d}_{{e\# }}}}}{d}} \right)}}^{{n - 3}}}} \right]$(1.5)
$\Phi (r) = - \frac{{{{A}_{{1c}}}}}{{r_{{ec}}^{k}}}\left\{ {\left[ {{{{\left( {\frac{{{{r}_{{ec}}}}}{r}} \right)}}^{k}} - {{{\left( {\frac{{{{r}_{{ec}}}}}{H}} \right)}}^{k}}} \right] - \left[ {{{{\left( {\frac{{{{r}_{{ec}}}}}{r}} \right)}}^{l}} - {{{\left( {\frac{{{{r}_{{ec}}}}}{H}} \right)}}^{l}}} \right]} \right\} - \frac{{{{A}_{{{\kern 1pt} 1b}}}}}{{r_{{eb}}^{k}}}\left[ {{{{\left( {\frac{{{{r}_{{eb}}}}}{H}} \right)}}^{k}} - {{{\left( {\frac{{{{r}_{{eb}}}}}{H}} \right)}}^{l}}} \right],$Традиционная постановка контактной задачи при наличии межмолекулярного взаимодействия подразумевает, что определяемое по формуле (1.3) контактное давление прикладывается к поверхности слоя, в результате чего он деформируется [12–15]. Ниже также рассматривается уточненная постановка, в которой естественным образом предполагается, что деформация слоя порождается объемными силами (1.2), распределенными по его глубине, тогда как поверхность слоя свободна от нагрузок [16–19]. В качестве параметра нагружения слоя в обеих постановках выступает зазор $r$, однозначно определяющий объемную силу ${{f}_{i}}$ по формуле (1.2) и контактное давление $p$ по формуле (1.3).
Отметим, что ввиду быстрого затухания объемные силы $f$ сконцентрированы в подповерхностной области нанометровой толщины ~${{d}_{{ec}}}$~${{d}_{{eb}}}$, причем, в силу соотношения (1.3), их равнодействующая, отнесенная к элементу поверхности слоя, с точностью до знака равна $p$. По принципу Сен-Венана, действие таких сил на расстояниях существенно превышающих ${{d}_{{ec}}}$ эквивалентно приложению контактного давления $p$ к поверхности слоя, что как раз отвечает традиционной постановке задачи. Таким образом, можно заключить (и это подтверждается расчетами [18, 19]), что использование уточненной постановки задачи актуально на наноуровне (масштаб ~${{d}_{{ec}}}$). На микро- или макроуровне (масштаб $ \gg {\kern 1pt} {{d}_{{ec}}}$) допустимо использование более простой традиционной постановки задачи.
В качестве контактной характеристики будем использовать внедрение $\delta $ индентора в слой, отсчитываемое от поверхности слоя в недеформированном состоянии, т.е. от уровня $z = {{h}_{{{\kern 1pt} 0}}}$ (рис. 1). Отметим, что внедрение $\delta $ может принимать как положительные, так и отрицательные значения, причем последний случай изображен на рис. 1. Имеет место условие контакта
связывающее внедрение $\delta $ с зазором $r$ и перемещением $w = h - {{h}_{{{\kern 1pt} 0}}}$ поверхности слоя вдоль оси $z$.Считается, что до момента времени $t = 0$ взаимодействие индентора с основанием является стационарным с постоянными во времени внедрением ${{\delta }^{s}}$ и зазором ${{r}^{s}}$, т.е.
(1.7)
$\begin{gathered} \delta (t) = {{\delta }^{s}},\quad r(t) = {{r}^{s}},\quad {{f}_{3}}(z,t) = {{f}^{s}}(z) = f({{r}^{s}} + {{h}_{{{\kern 1pt} 0}}} - z) \\ p(t) = {{p}^{s}} = \Phi ({{r}^{s}});\quad {\text{ }}t \leqslant 0 \\ \end{gathered} $В момент времени $t = 0$ внедрение $\delta $ начинает изменяться некоторым заданным образом, что приводит к изменению и зазора $r$. Согласно формулам (1.2) и (1.3), функция $r(t)$ полностью определяет эволюцию во времени объемной силы ${{f}_{3}}(z,t)$ и контактного давления $p(t)$.
Деформационные свойства слоя описываются линейным законом наследственного типа [24–26]
(1.8)
$\begin{gathered} {{\sigma }_{{ij}}}(z,t) = {{\delta }_{{ij}}}\lambda \theta (z,t) + 2\mu {{\varepsilon }_{{ij}}}(z,t) - \\ \, - {{\delta }_{{ij}}}\int\limits_{ - \infty }^t {\Lambda (t - \tau )\theta (z,\tau )d\tau - } 2\int\limits_{ - \infty }^t {{\rm M}(t - \tau ){{\varepsilon }_{{i{\kern 1pt} j}}}(z,\tau )d\tau } , \\ \end{gathered} $(1.9)
$\Lambda (t) = \lambda {{R}_{{{\kern 1pt} 2}}}(t) + \frac{2}{3}\mu ({\kern 1pt} {{R}_{{{\kern 1pt} 2}}}(t) - {{R}_{{{\kern 1pt} 1}}}(t)),\quad {\rm M}(t) = \mu {\kern 1pt} {{R}_{{{\kern 1pt} 1}}}(t)$Для построения полной системы уравнений НДС слоя соотношение (1.8) следует дополнить формулой Коши: ${{\varepsilon }_{{ij}}}(z,t) = ({{u}_{{i,{\kern 1pt} j}}}(z,t) + {{u}_{{j,{\kern 1pt} i}}}(z,t)){\text{/}}2$ и уравнением равновесия [24, 25]:
в котором объемная сила ${{f}_{i}}$ обусловлена межмолекулярным взаимодействием и определяется равенствами (1.2). Здесь и далее, ${{u}_{i}}$ – компоненты вектора перемещений, и для записи частной производной функции используется общепринятое обозначение с запятой.Располагая функцией $r(t)$ можно рассчитать эволюцию НДС слоя во времени [27]. В связи с этим ставится задача: при заданной зависимости внедрения $\delta $ от времени $t$ определить изменение во времени контактного зазора $r$.
Далее будет рассматриваться непрерывная зависимость $\delta (t)$, отвечающая переходу слоя из начального стационарного состояния (1.7) в другое стационарное состояние, характеризуемое конечным внедрением ${{\delta }_{m}}$ индентора, т.е.
(1.11)
$\delta (t) \in C( - \infty ,\infty );\quad \delta (t) = {{\delta }^{s}},\quad t \leqslant 0;\quad \delta (t) = {{\delta }_{m}},\quad t \geqslant {{t}_{m}},$Подобный характер изменения внедрения $\delta (t)$ позволяет допустить, что функция $r(t)$ ограничена снизу некоторой положительной величиной ${{r}_{{\min }}}$ и непрерывна, кроме, быть может, некоторой точки $\hat {t} > 0$, в которой она имеет разрыв первого рода (т.е. является кусочно-непрерывной):
(1.14)
$0 < {{r}_{{\min }}} \leqslant r(t),\quad t \in ( - \infty ,\infty );\quad r(t) \in C\left\{ {( - \infty ,\infty ){\backslash }\hat {t}} \right\}$Оговоренный разрыв функции $r(t)$ при непрерывном внедрении $\delta (t)$ учитывает возможность скачкообразного изменения параметров контакта при наличии межмолекулярного взаимодействия [12–14, 21].
Кроме того, последнее равенство (1.11) позволяет допустить, что
где ${{r}_{m}}$ – значение контактного зазора в стационарном состоянии с внедрением ${{\delta }_{m}}$. Вопрос определения величины ${{r}_{m}}$ по заданному внедрению ${{\delta }_{m}}$ индентора будет рассмотрен ниже.2. Основные уравнения. Для решения поставленной в предыдущем разделе задачи потребуется конкретизировать ядра интегральных операторов в соотношении (1.8). Не ограничивая общности рассмотрения, пренебрежем объемной ползучестью материала слоя и положим [26, с. 18]: ${{R}_{{{\kern 1pt} 1}}}(t) = {{R}_{{{\kern 1pt} 0}}}{{e}^{{ - \alpha {\kern 1pt} t}}}$, ${{R}_{{{\kern 1pt} 2}}}(t) \equiv 0$, где $\alpha = 1{\text{/}}{{t}_{r}}$, ${{t}_{r}}$ – время релаксации причем, из физических соображений: $0 < {{R}_{{{\kern 1pt} 0}}} < \alpha $. Тогда, с учетом соотношений (1.9):
(2.1)
$\left\{ \begin{gathered} \Lambda (t) \hfill \\ {\rm M}(t) \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} {{\Lambda }_{0}} \hfill \\ {{{\rm M}}_{0}} \hfill \\ \end{gathered} \right\}{{e}^{{ - \alpha {\kern 1pt} t}}},\quad {{\Lambda }_{0}} = - \frac{2}{3}\mu {\kern 1pt} {{R}_{{{\kern 1pt} 0}}},\quad {{{\rm M}}_{0}} = \mu {\kern 1pt} {{R}_{{{\kern 1pt} 0}}}$Как указывалось выше, для рассматриваемого случая плоскопараллельного контакта индентора со слоем компоненты ${{u}_{i}},{{\varepsilon }_{{ij}}},{{\sigma }_{{ij}}}$ НДС слоя зависят только от координаты $z$ и времени $t$, что приводит к равенству нулю всех этих компонент, кроме ${{u}_{3}},{{\varepsilon }_{{33}}}$, ${{\sigma }_{{11}}} = {{\sigma }_{{22}}},{{\sigma }_{{33}}}$. При помощи равенств (1.8) и (2.1) компоненты ${{\sigma }_{{11}}} = {{\sigma }_{{22}}},\;{{\sigma }_{{33}}}$ выражаются известным образом через поперечное (вдоль оси $z$) перемещение ${{u}_{3}}(z,t)$ слоя [27]. Подстановка таких выражений в уравнения равновесия (1.10) позволяет вывести уравнение для перемещения ${{u}_{3}}$, из которого следует, что [27]
(2.2)
${{u}_{3}}(z,t) = \frac{{B{{{\rm N}}_{0}}}}{\alpha }{{w}^{s}}(z){{e}^{{ - \beta t}}} - B\left[ {X(z,t) + B{{{\rm N}}_{0}}\int\limits_0^t {{{e}^{{ - \beta (t - \tau )}}}X(z,\tau )d\tau } } \right],\quad t \geqslant 0,$(2.3)
$\begin{gathered} B = \frac{1}{{\lambda + 2\mu }},\quad {{B}^{\infty }} = \frac{1}{{{{\lambda }^{\infty }} + 2{{\mu }^{\infty }}}} = \frac{\alpha }{\beta }B,\quad {{{\rm N}}_{0}} = \frac{4}{3}\mu {{R}_{{{\kern 1pt} 0}}},\quad \beta = \alpha - B{{{\rm N}}_{0}} > 0 \\ {{w}^{s}}(z) = - {{B}^{\infty }}{{X}^{s}}(z),\quad X(z,t) = \left( \begin{gathered} p(t)z \\ \mathcal{R}({{f}_{3}})(z,t) \\ \end{gathered} \right),\quad {{X}^{s}}(z) = \left( \begin{gathered} {{p}^{s}}z \\ \mathcal{R}({{f}^{s}})(z) \\ \end{gathered} \right), \\ \end{gathered} $(2.4)
$\mathcal{R}(g)(z) = \int\limits_0^z {\Omega (\xi )d\xi } - \Omega ({{h}_{{{\kern 1pt} 0}}})z,\quad \Omega (\xi ) = \int\limits_0^\xi {g(\eta )d\eta } $Отметим, что перемещение (2.2), как положено, удовлетворяет условию сцепления слоя с абсолютно жесткой подложкой: ${{u}_{3}}(0,t) = 0$. Соответствующее напряжение ${{\sigma }_{{33}}}$ при $z = {{h}_{{{\kern 1pt} 0}}}$ равно нулю для уточненной постановки задачи и совпадает с отрицательным значением контактного давления $p$ для традиционной постановки задачи. При $t = 0$ перемещение ${{u}_{3}}$ совпадает с функцией ${{w}^{s}}(z)$.
Введем в рассмотрение функцию $\Psi (r)$ такую, что
(2.5)
$\Psi (r(t)) = \frac{1}{{{{h}_{{{\kern 1pt} 0}}}}}\mathcal{R}({{f}_{3}})({{h}_{{{\kern 1pt} 0}}},t)$Причем неявная зависимость правой части равенства (2.5) от времени $t$ через функцию $r(t)$ обуславливается выражением (1.2) для компоненты ${{f}_{3}}$ объемной силы. Согласно равенствам (1.2), (2.4) и (2.5), вид функции $\Psi (r)$ зависит от формы закона парного взаимодействиями молекул. В случае закона Леннард–Джонса (1.1) [19]:
(2.6)
$\begin{gathered} \Psi (r) = - \frac{{{{A}_{{1c}}}}}{{r_{{ec}}^{k}}}\left\{ {{{{\left( {\frac{{{{r}_{{ec}}}}}{r}} \right)}}^{k}} - {{{\left( {\frac{{{{r}_{{ec}}}}}{r}} \right)}}^{l}} - \frac{{{{r}_{{ec}}}}}{{(k - 1){{h}_{{{\kern 1pt} 0}}}}}\left[ {{{{\left( {\frac{{{{r}_{{ec}}}}}{r}} \right)}}^{{k - 1}}} - {{{\left( {\frac{{{{r}_{{ec}}}}}{H}} \right)}}^{{k - 1}}}} \right]} \right. + \\ \left. { + \;\frac{{{{r}_{{ec}}}}}{{(l - 1)h_{0}^{{^{{}}}}}}\left[ {{{{\left( {\frac{{{{r}_{{ec}}}}}{r}} \right)}}^{{l - 1}}} - {{{\left( {\frac{{{{r}_{{ec}}}}}{H}} \right)}}^{{l - 1}}}} \right]} \right\} \\ \end{gathered} $Введем обозначение:
используя для него прежнее правило интерпретации верхнего и нижнего вариантов. Отметим следующие свойства функции $Z(r)$:(2.8)
$Z(r) \in {{C}^{\infty }}(0,\infty ),\quad Z(r(t)) \in C\left\{ {( - \infty ,\infty ){\backslash }\hat {t}} \right\}$(2.9)
$X({{h}_{{{\kern 1pt} 0}}},t) = {{h}_{{{\kern 1pt} 0}}}Z(r(t)),\quad {{X}^{s}}({{h}_{{{\kern 1pt} 0}}}) = {{h}_{{{\kern 1pt} 0}}}Z({{r}^{s}}) \equiv {{h}_{{{\kern 1pt} 0}}}{{Z}^{s}}$Используя равенства (2.9), положим в формуле (2.2) $z = {{h}_{{{\kern 1pt} 0}}}$ и получим выражение для граничного перемещения $w(t) = {{u}_{3}}({{h}_{{{\kern 1pt} 0}}},t)$. Подставив это выражение в условие контакта (1.6), придем к следующему интегральному уравнению относительно зазора $r(t)$:
в котором(2.12)
${{I}_{z}}(t) = B{{h}_{{{\kern 1pt} 0}}}\int\limits_0^t {{{e}^{{ - \beta (t - \tau )}}}Z(r(\tau ))d\tau } + \frac{{B{{h}_{{{\kern 1pt} 0}}}}}{\beta }{{Z}^{s}}{{e}^{{ - \beta t}}} \in C[0,\infty )$Указанная здесь непрерывность функции $\delta {\text{*}}(t)$ обеспечивается условием (1.11) и свойством (2.12) непрерывности функции ${{I}_{z}}(t)$, причем это свойство является следствием допущения (2.8) [28].
Отметим некоторые свойства производной ${{\dot {I}}_{z}}(t)$. Дифференцирование правой части выражения (2.12) по времени $t$ позволяет установить, что
(2.13)
${{\dot {I}}_{z}}(t) = B{{h}_{{{\kern 1pt} 0}}}Z(r(t)) - \beta {{I}_{z}}(t) = \frac{\beta }{{B{{{\rm N}}_{0}}}}\left[ {{{B}^{\infty }}{{h}_{{{\kern 1pt} 0}}}Z(r(t)) - r(t) - \delta (t)} \right] \in C\left\{ {[0,\infty ){\backslash }\hat {t}} \right\}$(2.14)
${{\dot {I}}_{z}}(t) = B{{h}_{{{\kern 1pt} 0}}}\int\limits_0^t {{{e}^{{ - \beta (t - \tau )}}}Z{\kern 1pt} '(r(\tau ))\dot {r}(\tau )d\tau } ,\quad \dot {r}(\tau ) \in C[0,t]$На основе интегрального уравнения (2.10) можно вывести следующее дифференциальное уравнение относительно зазора $r(t)$:
в котором(2.16)
${{F}_{z}}(t,r) = \frac{{\dot {\delta }{\kern 1pt} *(t)}}{{B{{h}_{{{\kern 1pt} 0}}}Z{\kern 1pt} '(r) - 1}} = \frac{{\dot {\delta }(t) - \beta \left[ {{{B}^{\infty }}{{h}_{{{\kern 1pt} 0}}}Z(r) - r - \delta (t)} \right]}}{{B{{h}_{{{\kern 1pt} 0}}}Z{\kern 1pt} '(r) - 1}}$Первое выражение (2.16) для функции ${{F}_{z}}(t,r)$ получается непосредственно из продифференцированного по времени $t$ уравнения (2.10), тогда как для вывода второго выражения следует дополнительно воспользоваться выражением (2.11), предварительно исключив из него производную ${{\dot {I}}_{z}}(t)$ с помощью второго равенства (2.13).
Решение дифференциального уравнения (2.15) ищется при начальном условии:
причем для построения решения в окрестности точки $\hat {t}$ разрыва используется специальная процедура, описанная ниже (раздел 4).Уравнение (2.10) также позволяет получить соотношение, связывающее начальный ${{r}^{s}}$ и конечный ${{r}_{m}}$ зазоры с соответствующими внедрениями ${{\delta }^{s}}$ и ${{\delta }_{m}}$ в оговоренных выше стационарных состояниях слоя. Рассмотрим для определенности второе состояние, формирование которого, согласно допущениям (1.11) и (1.15), обуславливается асимптотиками вида $\delta (t) \to {{\delta }_{m}}$, $r(t) \to {{r}_{m}}$ при $t \to \infty $. При таком поведении функции $r(t)$ интеграл в правой части равенства (2.12) также обладает асимптотикой, которая позволяет установить, что ${{I}_{z}}(t) \to {{\beta }^{{ - 1}}}B{{h}_{{{\kern 1pt} 0}}}Z({{r}_{m}})$ при $t \to \infty $. Осуществляя в уравнении (2.10) предельный переход $t \to \infty $ с учетом указанных асимптотик, придем к следующему равенству:
Аналогичное равенство имеет место для исходного стационарного состояния с внедрением ${{\delta }^{s}}$ и зазором ${{r}^{s}}$. Учитывая это, а также выражение (2.3) для параметра ${{B}^{\infty }}$, получим искомое соотношение:
(2.18)
${{D}^{\infty }}\left( {\left\{ \begin{gathered} {{r}^{s}} \hfill \\ {{r}_{m}} \hfill \\ \end{gathered} \right\}} \right) = \left\{ \begin{gathered} {{\delta }^{s}} \hfill \\ {{\delta }_{m}} \hfill \\ \end{gathered} \right\},$Интегральное уравнение (2.10) или эквивалентное ему дифференциальное уравнение (2.15) определяют изменение зазора $r$ в процессе контактного взаимодействия индентора с основанием. Располагая функцией $r(t)$, можно с помощью равенства (1.6) определить граничное перемещение $w$, а по формулам (1.8), (2.2) и (2.3) рассчитать НДС слоя в любой момент времени $t$ [27].
3. Общий анализ контактного взаимодействия индентора преследует своей целью выявление характерных особенностей функции $r(t)$ как решения интегрального (2.10) или дифференциального (2.15) уравнений. Эти особенности будут в дальнейшем (раздел 4) учитываться при построении численного решения дифференциального уравнения (2.15).
Укажем вначале некоторые:
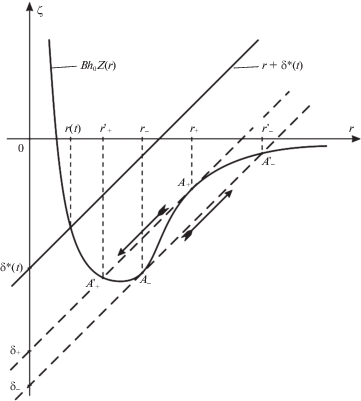
3.1. Особенности произведения $B{{h}_{{{\kern 1pt} 0}}}{\kern 1pt} Z(r)$, присутствующего в уравнениях (2.10) и (2.15), как функции переменной $r$. Для этого отметим, что определяемые по формулам (1.5) и (2.6) функции $\Phi (r)$ и $\Psi (r)$ строятся на основе закона Леннарда–Джонса (1.1) и сохраняют присущие ему характерные особенности [22, 23] – в окрестности нуля они неограниченно возрастают, а при увеличении аргумента $r$ проходят через локальный минимум и стремятся к нулю, оставаясь отрицательными. Очевидно, что аналогичным образом ведут себя и произведения $B{{h}_{{{\kern 1pt} 0}}}{\kern 1pt} \Phi (r)$ и $B{{h}_{{{\kern 1pt} 0}}}{\kern 1pt} \Psi (r)$. Функция $B{{h}_{{{\kern 1pt} 0}}}{\kern 1pt} Z(r)$, представляющая их на основе правила (2.7), схематично изображена на рис. 2.
Как будет показано ниже, поведение контактного зазора $r(t)$ в процессе взаимодействия индентора с основанием существенным образом зависит от того, какой из следующих случаев имеет место:
или (рис. 2)(3.2)
$B{{h}_{{{\kern 1pt} 0}}}Z{\kern 1pt} '(r) < 1,\quad r \in (0,{{r}_{ - }}) \cup ({{r}_{ + }},\infty );\quad B{{h}_{{{\kern 1pt} 0}}}Z{\kern 1pt} '(r) > 1,\quad r \in ({{r}_{ - }},{{r}_{ + }}),$Опишем некоторые геометрические свойства функции $B{{h}_{{{\kern 1pt} 0}}}{\kern 1pt} Z(r)$ в случае (3.2).
В силу равенства (3.3), кривая $\zeta = B{{h}_{{{\kern 1pt} 0}}}Z(r)$ в точке ${{A}_{ \pm }}$, имеющей координату ${{r}_{ \pm }}$, касается прямой $\zeta = r + {{\delta }_{ \pm }}$ (рис. 2), причем
Кроме того, каждой точке ${{A}_{ \pm }}$ кривой $\zeta = B{{h}_{{{\kern 1pt} 0}}}Z(r)$ соответствует точка $A_{ \pm }^{'}$ пересечения этой кривой с прямой $\zeta = r + {{\delta }_{ \pm }}$ (рис. 2). Координата $r_{ \pm }^{'}$ точки $A_{ \pm }^{'}$ удовлетворяет равенству
Принципиальное различие случаев (3.1) и (3.2) заключается в том, что в первом случае любая прямая $\zeta = r + \delta {\kern 1pt} *$ пересекает кривую $\zeta = B{{h}_{{{\kern 1pt} 0}}}Z(r)$ только в одной точке, тогда как во втором случае это имеет место только, если $\delta {\kern 1pt} * \in ( - \infty ,{{\delta }_{ - }}) \cup ({{\delta }_{ + }},\infty )$ (рис. 2). При остальных значениях $\delta {\kern 1pt} *$ число точек пересечения может достигать трех.
Указанные свойства функции $B{{h}_{{{\kern 1pt} 0}}}Z(r)$ остаются в силе и для функции ${{B}^{\infty }}{{h}_{{{\kern 1pt} 0}}}Z(r)$ при формальной замене $B$ на ${{B}^{\infty }}$. Соответствующие формулы ниже будут помечаться символом “$\infty $”. В частности, в случае (3.2)∞ по формулам (3.3)∞ и (3.4)∞ можно ввести в рассмотрение величины $r_{ \pm }^{\infty }$ и $\delta _{ \pm }^{\infty }$. После этого можно установить, что любая прямая $\zeta = r + \delta {\kern 1pt} *$ пересекает кривую $\zeta = {{B}^{\infty }}{{h}_{{{\kern 1pt} 0}}}Z(r)$ только в одной точке, если (рис. 2)
(3.6)
$\delta {\kern 1pt} * \in ( - \infty ,\delta _{ - }^{\infty }) \cup (\delta _{ + }^{\infty },\infty )$В случае (3.1)∞ указанные линии всегда пересекаются в одной точке.
Применительно к уравнению (2.18), решение которого совпадает с координатой точки пересечения кривой $\zeta = {{B}^{\infty }}{{h}_{{{\kern 1pt} 0}}}Z(r)$ и прямой $\zeta = r + \delta {\kern 1pt} *,$ $\delta {\kern 1pt} * = \left\{ \begin{gathered} {{\delta }^{s}} \hfill \\ {{\delta }_{m}} \hfill \\ \end{gathered} \right\}$, вышесказанное позволяет заключить, что в случае (3.1)∞ это уравнение однозначно разрешимо относительно величин ${{r}^{s}}$ и ${{r}_{m}}$ при любых значениях ${{\delta }^{s}}$ и ${{\delta }_{m}}$. В случае (3.2)∞ также можно обеспечить существование однозначного решения уравнения (2.18), если воспользоваться результатом (3.6) и наложить на значения ${{\delta }^{s}}$ и ${{\delta }_{m}}$ соответствующие ограничения, а именно:
(3.7)
$\begin{gathered} {{\delta }^{s}} < \delta _{ - }^{\infty },\quad \delta _{ + }^{\infty } < {{\delta }_{m}} - {\text{подвод индентора}} \\ \delta _{ + }^{\infty } < {{\delta }^{s}},\quad {{\delta }_{m}} < \delta _{ - }^{\infty } - {\text{отвод индентора}} \\ \end{gathered} $3.2. Анализ разрывов функции $r(t)$. Рассмотрим уравнение (2.10), и заметим, что значение его решения $r(t)$ в каждый момент времени совпадает с координатой точки пересечения кривой $\zeta = B{{h}_{{{\kern 1pt} 0}}}Z(r)$ и прямой $\zeta = r + \delta {\kern 1pt} *(t)$ (рис. 2). В случае (3.1) эта точка определяется однозначно, так что при непрерывном, согласно условию (2.11), изменении во времени величины $\delta {\kern 1pt} *(t)$ соответствующая величина $r(t)$ также изменяется непрерывно. Подобное поведение функции $r(t)$ согласуется с дифференциальным уравнением (2.15), правая часть которого не имеет особенностей при наличии неравенства (3.1). С точки зрения аналитического анализа, случай (3.1) представляется тривиальным и в данном разделе рассматриваться не будет.
Однако в случае (3.2) решение $r(t)$ уравнение (2.10) может иметь разрывы. Действительно, если величина $\delta {\kern 1pt} *(t)$, монотонно возрастая в некоторый момент времени ${{t}_{ + }}$ проходит значение ${{\delta }_{ + }}$, то в этот момент точка пересечения кривой $\zeta = B{{h}_{{{\kern 1pt} 0}}}Z(r)$ и прямой $\zeta = r + \delta {\kern 1pt} *(t)$ должна мгновенно поменяться с ${{A}_{ + }}$ на $A_{ + }^{'}$, а соответствующее значение $r(t)$ – с ${{r}_{ + }}$ на $r_{ + }^{'}$ (рис. 2). Аналогично, если величина $\delta {\kern 1pt} {\text{*}}(t)$, монотонно убывая в некоторый момент времени ${{t}_{ - }}$ проходит значение ${{\delta }_{ - }}$, то в этот момент точка пересечения кривой $\zeta = B{{h}_{{{\kern 1pt} 0}}}Z(r)$ и прямой $\zeta = r + \delta {\kern 1pt} *{\kern 1pt} (t)$ должна мгновенно поменяться с ${{A}_{ - }}$ на $A_{ - }^{'}$, а соответствующее значение $r(t)$ – с ${{r}_{ - }}$ на $r_{ - }^{'}$ (рис. 2).
Таким образом, в случае (3.2) возможно скачкообразное изменение зазора $r(t)$:
(3.8)
$r({{t}_{ + }} - 0) = {{r}_{ + }},\quad r({{t}_{ + }} + 0) = r_{ + }^{'} - {\text{скачок}}\quad {{r}_{ + }} \to r_{ + }^{'}$(3.9)
$r({{t}_{ - }} - 0) = {{r}_{ - }},\quad r({{t}_{ - }} + 0) = r_{ - }^{'} - {\text{скачок}}\quad {{r}_{ - }} \to r_{ - }^{'}$Момент времени ${{t}_{ \pm }}$ скачка удовлетворяет равенству $\delta {\kern 1pt} *{\kern 1pt} ({{t}_{ \pm }}) = {{\delta }_{ \pm }}$ и представляет собой точку $\hat {t}$ разрыва функции $r(t)$, оговоренную в условии (1.14). Здесь и далее используется общепринятая сокращенная запись пределов функции слева и справа:
Описанное выше поведение функции $r(t)$ согласуется с дифференциальным уравнением (2.15), правая часть которого, в силу первого неравенства (3.2) и равенства (3.3), имеет сингулярные особенности при $r(t) \to {{r}_{ \pm }} \pm 0$. Как будет показано ниже, скачок ${{r}_{ + }} \to r_{ + }^{'}$ реализуется при подводе индентора (условие (1.12)), тогда как скачок ${{r}_{ - }} \to r_{ - }^{'}$ – при его отводе (условие (1.13)).
Отметим, что значения ${{r}_{ \pm }}$ и $r_{ \pm }^{'}$ можно считать известными, т.к. они являются корнями алгебраических уравнений (3.4) и (3.5). Однако значение ${{t}_{ \pm }}$ заранее неизвестно и определяется в ходе решения уравнения (2.10) или (2.15) как момент достижения функцией $r(t)$ значения ${{r}_{ \pm }}$.
Аналогичное рис. 2 графическое представление скачкообразного изменения контактного зазора встречается в работе [29] применительно к подпружиненному адгезионному контакту твердых тел.
Наличие скачка (3.8) или (3.9) в случае (3.2), очевидно, зависит от возможности достижения зазором $r(t)$ значения ${{r}_{ \pm }}$ с течением времени. Кроме того, предполагаемый выше монотонный характер функции $\delta {\kern 1pt} *{\kern 1pt} (t)$ в окрестности ее значений ${{\delta }_{ \pm }}$, согласно равенствам (2.11) и (2.12), зависит от поведения функции $r(\tau )$ при $\tau \in [0,t]$. Таким образом, описанное выше скачкообразное изменение контактного зазора может быть установлено и проанализировано только путем построения соответствующей функции $r(t)$, как решения интегрального (2.10) или дифференциального (2.15) уравнения. Тем не менее, можно выявить ряд характерных особенностей скачкообразного изменения функции $r(t)$, исходя из некоторых общих допущений относительно ее свойств. Сделаем это, считая внедрение индентора гладким на отрезке $[0,{{t}_{m}}]$, т.е.
при условии, что $\dot {\delta }(0) = \dot {\delta }(0 + 0)$, $\dot {\delta }({{t}_{m}}) = \dot {\delta }({{t}_{m}} - 0)$.Предположим, что в режиме (1.12) подвода индентора функция $r(t)$ монотонно убывает, достигая значения ${{r}_{ + }}$ в момент времени ${{t}_{ + }}$, когда происходит скачок ${{r}_{ + }} \to r_{ + }^{'}$ (3.8). В этом случае, при $t \in [0,{{t}_{ + }})$: ${{r}_{ + }} < r(t)$ и, следовательно, в силу первого неравенства (3.2), $B{{h}_{{{\kern 1pt} 0}}}Z{\kern 1pt} '(r(t)) - 1 < 0$. Последнее неравенство и свойства (1.14), (3.10) позволяют на основе уравнения (2.15) установить непрерывность производной $\dot {r}(t)$ на промежутке $[0,{{t}_{ + }})$. Вышесказанное позволяет записать следующие соотношения:
В связи со сделанным предположением о монотонном убывании функции $r(t)$ заметим, что вначале процесса подвода индентора: $\dot {r}(t) < 0$, если дополнительно к условию (1.12) допустить неравенство $0 < \dot {\delta }(0 + 0)$. Этот результат непосредственно следует из уравнения (2.15) с учетом уравнения (2.18) для ${{r}^{s}}$ и первого неравенства (3.2) при $r = {{r}^{s}} > {{r}_{ + }}$.
Аналогичным образом, предполагая, что в режиме (1.13) отвода индентора функция $r(t)$ монотонно возрастает до скачка ${{r}_{ - }} \to r_{ - }^{'}$ (3.9), можно записать соотношения
Дальнейшие выкладки для краткости ограничим рассмотрением режима (1.12) подвода индентора, отметив, что они без труда переносятся на случай режима (1.13) отвода индентора.
Свойства (3.11) функции $r(t)$ позволяют использовать для производной ${{\dot {I}}_{z}}(t)$ на промежутке $[0,{{t}_{ + }})$ представление (2.14), подынтегральное выражение в котором принимает только отрицательные значения, т.к. $0 < Z{\kern 1pt} '(r)$ при ${{r}_{ + }} < r$ (рис. 2). Таким образом, оказывается, что
и, следовательно, с учетом выражения (2.11) и условия (1.12):Покажем, что неравенство (3.14) сохраняется некоторое время после скачка (3.8), т.е. имеет место предполагаемое монотонное возрастание функции $\delta {\kern 1pt} *{\kern 1pt} (t)$ в окрестности ее значения ${{\delta }_{ + }}$. Для этого воспользуемся выражением (2.13) и установим, что производная ${{\dot {I}}_{z}}(t)$ в точке $\hat {t} = {{t}_{ + }}$ имеет конечные пределы слева и справа:
(3.15)
${{\dot {I}}_{z}}({{t}_{ + }} - 0) = B{{h}_{{{\kern 1pt} 0}}}Z({{r}_{ + }}) - \beta {{I}_{z}}({{t}_{ + }}),\quad {{\dot {I}}_{z}}({{t}_{ + }} + 0) = B{{h}_{{{\kern 1pt} 0}}}Z(r_{ + }^{'}) - \beta {{I}_{z}}({{t}_{ + }})$При записи формул (3.15) учтены соответствующие пределы (3.8) функции $r(t)$ и принято во внимание свойство (2.12) непрерывности функции ${{I}_{z}}(t)$. Исключая из формул (3.15) величину ${{I}_{z}}({{t}_{ + }})$, можно получить равенство
(3.16)
$0 < \dot {\delta }{\kern 1pt} *{\kern 1pt} (t),\quad t \in ({{t}_{ + }},{{t}_{ + }} + \varepsilon )$Проведенные выкладки позволяют также установить существование положительных односторонних пределов функции $\dot {\delta }{\kern 1pt} *{\kern 1pt} (t)$ в точке ${{t}_{ + }}$:
Действительно, это непосредственно следует из равенства (2.11) при учете условия (3.10) и формул (3.15).
3.3. Характер поведения функции $r(t)$ в окрестности точки разрыва, т.е. при $t \to {{t}_{ + }} \pm 0$, можно определить с помощью дифференциального уравнения (2.15), используя в нем первое выражение (2.16) для функции ${{F}_{z}}(t,r)$. Осуществим в этом уравнении предельный переход $t \to {{t}_{ + }} + 0$, учитывая второй предел (3.8). В результате установим, что
(3.18)
$\dot {r}({{t}_{ + }} + 0) = \frac{{\dot {\delta }{\kern 1pt} *{\kern 1pt} ({{t}_{ + }} + 0)}}{{B{{h}_{0}}Z{\kern 1pt} '(r_{ + }^{'}) - 1}} < 0,$Однако получить аналогичное (3.18) выражение для $\dot {r}({{t}_{ + }} - 0)$ не удается, т.к., в силу первого предельного соотношения (3.8) и равенства (3.3), знаменатель в правой части уравнения (2.15) при $t \to {{t}_{ + }} - 0$ стремится к нулю слева, а сама правая часть, соответственно, к $ - \infty $. Данное обстоятельство требует более детального анализа поведения функции $r(t)$ при $t \to {{t}_{ + }} - 0$.
Приступая к такому анализу, примем во внимание существование конечного предела $\dot {\delta }{\kern 1pt} *{\kern 1pt} ({{t}_{ + }} - 0)$ и положим по непрерывности $\dot {\delta }{\kern 1pt} *{\kern 1pt} ({{t}_{ + }}) = \dot {\delta }{\kern 1pt} *{\kern 1pt} ({{t}_{ + }} - 0)$, так что
(3.19)
$\dot {\delta }{\kern 1pt} *{\kern 1pt} (t) \in C[0,{{t}_{ + }}];\quad 0 < \dot {\delta }{\kern 1pt} *{\kern 1pt} (t),\quad t \in [0,{{t}_{ + }}]$Указанная непрерывность функции $\dot {\delta }{\kern 1pt} *{\kern 1pt} (t)$ обуславливается свойствами (2.13) и (3.10) при наличии выражения (2.11), тогда как неравенство (3.19) является следствием неравенств (3.14) и (3.17).
Учитывая свойство (2.8) функции $Z(r)$, воспользуемся для ее производной формулой Тейлора [28]
(3.20)
$Z'(r) = Z{\kern 1pt} '({{r}_{ + }}) + Z{\kern 1pt} '{\kern 1pt} '(\rho (r))(r - {{r}_{ + }}),\quad r \in [{{r}_{ + }},\infty ),$(3.21)
$\rho ({{r}_{ + }}) = \rho ({{r}_{ + }} + 0) = {{r}_{ + }},\quad r({{t}_{ + }}) = r({{t}_{ + }} - 0) = {{r}_{ + }}$Отметим, что при втором допущении (3.21) и условии (1.14) функцию $r(t)$ можно считать непрерывной на отрезке $[0,{{t}_{ + }}]$.
Введем в рассмотрение функции ${{Z}_{1}}(r)$ и ${{Z}_{2}}(t)$ такие, что
(3.23)
${{Z}_{2}}({{t}_{ + }}) = {{Z}_{1}}({{r}_{ + }}) = Z{\kern 1pt} '{\kern 1pt} '\left( {\rho ({{r}_{ + }})} \right) = Z{\kern 1pt} '{\kern 1pt} '\left( {{{r}_{ + }}} \right) < 0,$Определяемая равенством (3.22) функция ${{Z}_{1}}(r)$ непрерывна на интервале $({{r}_{ + }},\infty )$ – это следует из формулы (3.20) при условии (2.8) непрерывности производной $Z{\kern 1pt} '(r)$. Кроме того, в силу равенств (3.21)–(3.23): ${{Z}_{1}}({{r}_{ + }} + 0) = {{Z}_{1}}({{r}_{ + }})$, т.е. функция ${{Z}_{1}}(r)$ непрерывна в точке ${{r}_{ + }}$ справа. Таким образом, оказывается, что ${{Z}_{1}}(r) \in C[{{r}_{ + }},\infty )$.
Установленные выше свойства непрерывности функций $r(t)$ и ${{Z}_{1}}(r)$ обеспечивают непрерывность сложной функции ${{Z}_{1}}(r(t))$ при $t \in [0,{{t}_{ + }}]$ [28], поэтому, на основе второго равенства (3.22):
Кроме того, согласно соотношениям (3.23): ${{Z}_{2}}({{t}_{ + }}) < 0$, так что, по известной теореме об устойчивости знака непрерывной функции [28]
где $\varepsilon $ – сколь угодно малая положительная величина.Использование функции ${{Z}_{2}}(t) \equiv Z{\kern 1pt} '{\kern 1pt} '\left( {\rho (r(t))} \right)$ и учет равенства (3.3) в формуле (3.20) позволяет записать выражение
(3.27)
$K(t) \equiv \frac{{ - \dot {\delta }{\kern 1pt} *{\kern 1pt} (t)}}{{B{{h}_{{{\kern 1pt} 0}}}{{Z}_{2}}(t)}} \in C[{{t}_{ + }} - \varepsilon ,{{t}_{ + }}];\quad 0 < K(t) < \infty ,\quad t \in [{{t}_{ + }} - \varepsilon ,{{t}_{ + }}]$Указанные свойства функции $K(t)$ обеспечиваются соотношениями (3.19), (3.24) и (3.25).
Интегрирование уравнения (3.26) позволяет установить, что
(3.28)
$0 = \frac{1}{2}{{[r(t) - {{r}_{ + }}]}^{2}} + \int\limits_{{{t}_{ + }}}^t {K(\xi )d\xi = } \frac{1}{2}{{[r(t) - {{r}_{ + }}]}^{2}} + K(\tau (t))(t - {{t}_{ + }}),$(3.29)
$r(t) = {{r}_{ + }} + \sqrt {2K(\tau (t))({{t}_{ + }} - t)} ,\quad t \in [{{t}_{ + }} - \varepsilon ,{{t}_{ + }}],$(3.30)
$\mathop {\lim }\limits_{t \to {{t}_{ + }} - 0} K(\tau (t)) = K({{t}_{ + }}) = \frac{{ - \dot {\delta }{\kern 1pt} *{\kern 1pt} ({{t}_{ + }} - 0)}}{{B{{h}_{{{\kern 1pt} 0}}}Z{\kern 1pt} '{\kern 1pt} '({{r}_{ + }})}}$Справедливость равенств (3.30) обеспечивается соотношениями (3.23), (3.27) и предельным соотношением $\tau ({{t}_{ + }} - 0) = {{t}_{ + }}$.
Поведение функции $r(t)$ в окрестности точки ${{t}_{ - }}$ в режиме (1.13) отвода индентора описывается аналогичными формулами:
(3.31)
$\dot {r}({{t}_{ - }} + 0) = \frac{{\dot {\delta }{\kern 1pt} *{\kern 1pt} ({{t}_{ - }} + 0)}}{{B{{h}_{{{\kern 1pt} 0}}}Z{\kern 1pt} '(r_{ - }^{'}) - 1}} > 0$(3.32)
$r(t) = {{r}_{ - }} - \sqrt {2K(\tau (t))({{t}_{ - }}{\kern 1pt} - t)} ,\quad t \in [{{t}_{ - }} - \varepsilon ,{{t}_{ - }}],$Таким образом, выражения (3.29) и (3.32) свидетельствуют о том, что перед скачком ${{r}_{ \pm }} \to r_{ \pm }^{'}$ зазор $r(t)$ изменяется по корневому закону. Соответствующая скорость $\dot {r}(t)$ изменения зазора стремится к $ \mp {\kern 1pt} {\kern 1pt} \infty $, что согласуется с описанным ранее поведением правой части дифференциального уравнения (2.15) при $t \to {{t}_{ \pm }} - 0$. После скачка ${{r}_{ \pm }} \to r_{ \pm }^{'}$, согласно выражениям (3.18) и (3.31), зазор $r(t)$ изменяется с конечной скоростью без каких-либо особенностей.
Выявленные особенности поведения функции $r(t)$ качественно сохраняются для объемной силы ${{f}_{3}}(z,t)$ и контактного давления $p(t)$, т.к. они определяются величиной зазора $r$ через гладкие функции $f(d)$ и $\Phi (r)$ согласно формулам (1.2) и (1.3). Некоторые из этих особенностей будут продемонстрированы в следующем разделе на примерах численного решения дифференциального уравнения (2.15).
Замечание 1. Реализация случая (3.2) и, соответственно, возможность скачкообразного изменения зазора $r(t)$, зависит только от коэффициента $B$ упругой податливости слоя, его толщины ${{h}_{{{\kern 1pt} 0}}}$ и физических параметров межмолекулярного взаимодействия, входящих в выражения (1.5), (2.6) для функции $\Phi (r),\Psi (r)$. Только от этих величин, согласно уравнениям (3.4) и (3.5), зависят начальное ${{r}_{ \pm }}$ и конечное $r_{ \pm }^{'}$ значения зазора $r$ при скачке (3.8) или (3.9). Вязкие свойства материала слоя (– параметры ядер релаксации в законе (1.8)) не оказывают влияния на возможность скачка зазора $r$ и на его параметры ${{r}_{ \pm }}$ и $r_{ \pm }^{'}$.
Замечание 2. Случай (3.1) имеет место при достаточно малых значениях коэффициента $B$ упругой податливости слоя, отвечающих, согласно выражению (2.3), высоким значениям модулей $\lambda ,\mu $ упругости. Напротив, случай (3.2), при котором возможны скачки (3.8) и (3.9), реализуется при достаточно малых значениях коэффициента $B$ и низких модулях $\lambda ,\mu $, т.е. для мягкого слоя. Такой вывод согласуется с известным результатом о появлении скачков в адгезионном контакте упругих тел при больших значениях параметра Тейбора, характеризующего степень упругой деформации, вызванной межмолекулярным взаимодействием [12, 14, 21].
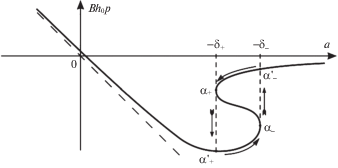
Замечание 3. При традиционной постановке задачи, используя уравнение (2.10), можно построить зависимость контактного давления $p$ от величины $a = - \delta {\kern 1pt} *$, которая для упругого слоя (т.е. при ${{{\rm N}}_{0}} = 0$) совпадает с отрицательным значением внедрения $\delta $ и характеризует сближение индентора со слоем (рис. 3). В случае (3.2) эта зависимость является неоднозначной (S-образной), причем в режиме подвода и отвода индентора скачку (3.8) или (3.9) отвечает скачок ${{\alpha }_{ + }}\alpha _{ + }^{'}$ или ${{\alpha }_{ - }}\alpha _{ - }^{'}$, показанный на рис. 3. Подобные зависимости контактной нагрузки от сближения тел встречается во многих исследованиях адгезионного контакта упругих тел, среди которых можно отметить работы [12, 14, 21].
4. Численный анализ контактного взаимодействия индентора с основанием выполнялся на основе решения дифференциального уравнения (2.15) относительно функции $r(t)$ с использованием численного метода Рунге–Кутты четвертого порядка точности [30]. В случае (3.1), когда правая часть уравнения (2.15) не имеет особенностей, применение этого метода не встречает затруднений. Однако в случае (3.2) при решении уравнения (2.15) возникают две проблемы, обусловленные наличием сингулярной особенности правой части этого уравнения в точке ${{t}_{ \pm }}$. Укажем эти проблемы и способы их устранения на примере режима подвода индентора.
Первая проблема связана с асимптотикой $\dot {r}(t) \to - \infty $ при $t \to {{t}_{ + }} - 0$ и $r(t) \to {{r}_{ + }} + 0$, которая имеет место согласно формуле (3.29). Подобное поведение функции $r(t)$, в частности, существенно осложняет расчет момента ${{t}_{ + }}$ скачка ${{r}_{ + }} \to r_{ + }^{'}$ (3.8) этой функции. Устранить эту проблему можно, если в окрестности ${{t}_{ + }} - 0$ вместо искомой функции $r(t)$ использовать обратную к ней функцию $t(r)$, что допустимо при условии (3.11) монотонности функции $r(t)$. Дифференциальное уравнение для функции $t(r)$ получается непосредственно из уравнения (2.15) и имеет вид
Правая часть уравнения (4.1) не имеет особенностей в окрестности ${{r}_{ + }} + 0$ значений переменной $r$ и само уравнение может быть решено методом Рунге–Кутты, например, на отрезке $[{{r}_{ + }},{{r}^{s}}]$ при начальном условии $t({{r}^{s}}) = 0$. Найденное решение $t(r)$ определяет функцию $r(t)$ на отрезке $[0,{{t}_{ + }}]$ и момент ${{t}_{ + }}$ как значение $t({{r}_{ + }})$.
Вторая проблема, возникающая при решении уравнения (2.15) в случае (3.2), связана с наличием скачка ${{r}_{ + }} \to r_{ + }^{'}$ (3.8) функции $r(t)$. Это не позволяет использовать единую процедуру численного решения уравнения (2.15) (или (4.1)) на всем промежутке времени $[0,\infty )$ с начальным условием (2.17). Устранить проблему такого типа можно, если организовать новую процедуру численного решения уравнения (2.15) на промежутке времени $[{{t}_{ + }},\infty )$, т.е. после скачка ${{r}_{ + }} \to r_{ + }^{'}$, с начальным условием
Отметим, что, согласно результатам предыдущего раздела, правая часть уравнения (2.15) не имеет особенностей в окрестности ${{t}_{ + }} + 0$, поэтому применение метода Рунге–Кутты для решения этого уравнения на промежутке $[{{t}_{ + }},\infty )$ при условии (4.2) не встречает затруднений.
Использование описанных выше процедур учета сингулярной особенности правой части дифференциального уравнения (2.15) позволяет применить к нему известную теорему существования и единственности решения [31].
Расчеты проводились при следующих значениях параметров задачи: $m = 7$, $n = 13$, ${{r}_{{ec}}} = 1$ нм, ${{r}_{{eb}}} = 0.5\,{{r}_{{ec}}}$, ${{R}_{{{\kern 1pt} 0}}} = 0.8$ с–1, ${{t}_{r}}$ = 1 с, ${{h}_{0}}$ = 2 нм (тонкий слой) или ${{h}_{0}}$ = 5 нм (толстый слой). Кроме того, полагалось, что ${{A}_{{{\kern 1pt} 1c}}} = {{(6\pi )}^{{ - 1}}}{{A}_{H}}$ [12] и ${{A}_{{{\kern 1pt} 1b}}} = 10{{A}_{{{\kern 1pt} 1c}}}$, где ${{A}_{H}}$ – постоянная Гамакера, ${{A}_{H}} = {{10}^{{ - 19}}}$ Дж. Были рассмотрены два варианта упругих свойств слоя: $\lambda = 1.0417$ МПа, $\mu = 1.5625$ МПа (мягкий слой) и $\lambda = 2.0833$ МПа, $\mu = 3.1250$ МПа (жесткий слой), которым отвечают значения $B = 0.24$ МПа–1 и $B = 0.12$ МПа–1 мгновенного коэффициента упругой податливости слоя.
Изменение внедрения индентора за время ${{t}_{m}}$ от начального ${{\delta }^{s}}$ до конечного ${{\delta }_{m}}$ значений считалось линейным:
(4.3)
$\delta (t) = \left\{ \begin{gathered} {{\delta }^{s}},\quad t \leqslant 0 \hfill \\ {{\delta }^{s}} + ({{\delta }_{m}} - {{\delta }^{s}})t{\text{/}}{{t}_{m}},\quad t \in (0,{{t}_{m}}) \hfill \\ {{\delta }_{m}},\quad t \geqslant {{t}_{m}} \hfill \\ \end{gathered} \right.,$(4.4)
$\begin{gathered} {{\delta }^{s}} = - 4{{r}_{{ec}}},\quad {{\delta }_{m}} = 0.1{{r}_{{ec}}} - {\text{подвод индентора}} \\ {{\delta }^{s}} = 0.1{{r}_{{ec}}},\quad {{\delta }_{m}} = - 4{{r}_{{ec}}} - {\text{отвод индентора}} \\ \end{gathered} $Выбор (4.4) значений ${{\delta }^{s}}$ и ${{\delta }_{m}}$ означает, что отвод индентора начинается из его конечного положения в режиме подвода, и за цикл “подвод–отвод” индентор возвращается в исходное положение. Кроме того, выбранные значения ${{\delta }^{s}}$ и ${{\delta }_{m}}$ удовлетворяют условию (3.7) существования однозначного решения уравнения (2.18), причем соответствующие значения ${{r}^{s}}$ и ${{r}_{m}}$ удовлетворяют неравенствам
которые обеспечивают наличие скачка (3.8) или (3.9) в случае (3.2) (рис. 2). Согласно уравнению (2.18), добиться выполнения этих неравенств можно, если использовать достаточно малые (большие) значения ${{\delta }^{s}}$ и достаточно большие (малые) значения ${{\delta }_{m}}$ при подводе (отводе) индентора.Зависимость контактного давления $p$ от времени $t$ рассчитывалась с помощью формулы (1.3) по найденному решению $r(t)$ уравнения (2.15). Отметим, что, как указывалось выше, при уточненной постановке задачи поверхность слоя свободна от нагрузок, поэтому контактное давление в классическом смысле отсутствует. Определяемая по формуле (1.3) величина $p$ в этом случае интерпретируется как контактное давление, т.к. представляет собой силу воздействия индентора на основание, приходящуюся на единицу площади его поверхности.
Для графического представления результатов расчетов ниже используются безразмерные величины $\tilde {t} = t{\text{/}}{{t}_{r}}$, $\tilde {r} = r{\text{/}}{{r}_{{ec}}},$ $\tilde {p} = p{\text{/}}{{E}_{*}},$ ${{E}_{*}} = 1$ МПа. Сплошные (штриховые) линии на графиках отвечают уточненной (традиционной) постановке задачи.
На рис. 4 и 5 показаны расчетные зависимости контактного зазора и давления от времени в режиме подвода (а) и отвода (б) индентора при $B = 0.24$ МПа–1, ${{h}_{{{\kern 1pt} 0}}} = 2$ нм (тонкий мягкий слой) и ${{t}_{m}} = 2{\kern 1pt} {\kern 1pt} {{t}_{r}}$ (быстрое перемещение индентора). При таких значениях параметров $B,{{h}_{0}}$ для уточненной постановки задачи выполняется неравенство (3.1), тогда как для традиционной постановки задачи имеет место случай (3.2), при котором возможны скачки (3.8) (или (3.9)) в режиме подвода (отвода) индентора. Этим объясняется показанный на рис. 4 и 5 непрерывный характер функций $r(t)$ и $p(t)$ при уточненной постановке задачи (сплошные линии) и наличие у этих функций скачков при традиционной постановке задачи (штриховые линии). Выполненные расчеты подтверждают предположение (3.11), (3.12) о монотонном характере изменения функции $r(t)$ на промежутке времени $[0,{{t}_{ \pm }})$.
Рис. 4.
Зависимости контактного зазора от времени в режиме подвода (а) и отвода (б) индентора (тонкий мягкий слой).
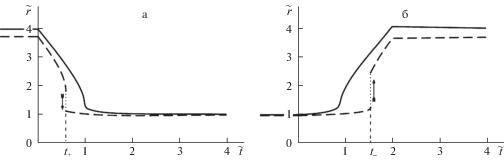
Рис. 5.
Зависимости контактного давления от времени в режиме подвода (а) и отвода (б) индентора (тонкий мягкий слой).
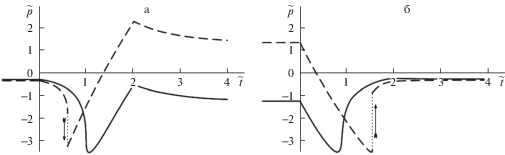
На рис. 6 показано поведение контактного давления при прежних значениях параметров $B,{{h}_{0}}$ (тонкий мягкий слой) и ${{t}_{m}} = 40{\kern 1pt} {\kern 1pt} {{t}_{r}}$ (медленное перемещение индентора). В данном случае, по причине медленного деформирования, слой ведет себя как упругое тело с длительными модулями ${{\lambda }^{\infty }},{{\mu }^{\infty }}$ [24], что объясняет отсутствие на рис. 6 заметной релаксации контактного давления при $t > {{t}_{m}}$.
Рис. 6.
Зависимости контактного давления от времени в режиме подвода (а) и отвода (б) индентора при медленном перемещении индентора (тонкий мягкий слой).
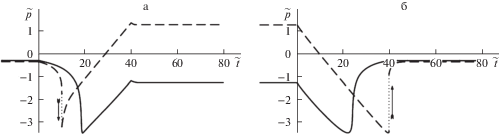
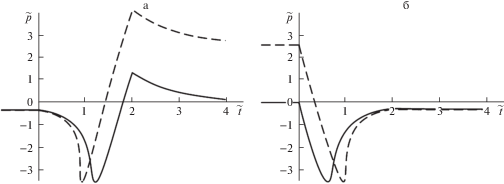
Если использовать слой той же толщины ${{h}_{{{\kern 1pt} 0}}} = 2$ нм, но с более низким коэффициентом упругой податливости $B = 0.12$ МПа–1 (тонкий жесткий слой), то для обеих постановок задачи выполняется неравенство (3.1). Соответствующие непрерывные зависимости контактного давления от времени в режимах подвода и отвода индентора при ${{t}_{m}} = 2{\kern 1pt} {\kern 1pt} {{t}_{r}}$ показаны на рис. 7 а и б.
Рис. 7.
Зависимости контактного давления от времени в режиме подвода (а) и отвода (б) индентора (тонкий жесткий слой).
Увеличение толщины слоя до значения ${{h}_{{{\kern 1pt} 0}}} = 5$ нм при прежнем коэффициенте упругой податливости $B = 0.12$ МПа–1 (толстый жесткий слой) приводит к нарушению неравенства (3.1) и реализации случая (3.2) как для уточненной, так и для традиционной постановок задачи. Соответствующие зависимости контактного давления от времени со скачком в режимах подвода (отвода) индентора при ${{t}_{m}} = 2{\kern 1pt} {\kern 1pt} {{t}_{r}}$ показаны на рис. 8 а и б.
Рис. 8.
Зависимости контактного давления от времени в режиме подвода (а) и отвода (б) индентора (толстый жесткий слой).
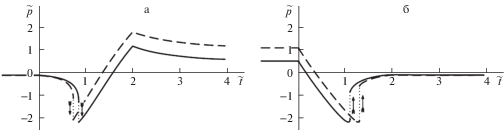
Как и следовало ожидать при сделанном выборе (4.4) параметров закона (4.3) внедрения, на рисунках 4–8 начальные (конечные) значения функций $r(t)$ и $p(t)$ в режиме подвода индентора совпадают с их конечными (начальными) значениями в режиме отвода индентора.
Рис. 4, 5, 7 и 8 иллюстрируют влияние параметров $B$ и ${{h}_{{{\kern 1pt} 0}}}$ на скачкообразное поведение контактного зазора и давления. В частности, оказывается, что появлением или отсутствием скачков этих величин можно управлять путем изменения толщины ${{h}_{{{\kern 1pt} 0}}}$ слоя.
Представленные результаты свидетельствуют о том, что реализация скачкообразного поведения контактного зазора и давления зависит от используемой постановки задачи. Так, в случае тонкого мягкого слоя (рис. 4 и 5), при уточненной постановке задачи скачок функций $r(t)$ и $p(t)$ отсутствует, а при традиционной постановке задачи – присутствует.
Выводы.
1. Рассмотрен контакт бесконечно протяженного плоского индентора и вязкоупругого слоя в рамках самосогласованного по Дерягину подхода с поверхностным (традиционная постановка) и объемным (уточненная постановка) приложением сил межмолекулярного взаимодействия. Получены эквивалентные друг другу интегральное (2.10) и дифференциальное (2.15) уравнения, описывающие изменение контактного зазора $r$ во времени при таком контакте.
2. Сформулировано условие в виде неравенств (3.2), при котором возможно скачкообразное изменение контактного зазора во времени. Реализация такого поведения зависит от используемой постановки задачи (уточненная или традиционная), упругих свойств слоя, его толщины, параметров межмолекулярного взаимодействия, и не зависит от вязких свойств материала слоя.
3. Выявлены особенности скачкообразного поведения контактного зазора во времени. В частности, установлено, что перед скачком скорость изменения контактного зазора в режиме подвода/отвода индентора неограниченно убывает/возрастает.
4. Предложен и реализован алгоритм построения разрывного решения дифференциального уравнения (2.15), учитывающий выявленные особенности скачкообразного поведения контактного зазора во времени.
5. Выполненные расчеты свидетельствуют о немонотонном характере зависимостей контактного зазора и давления от времени в режимах подвода и отвода индентора. Показано, что традиционная и уточненная постановки задачи могут приводить к существенно различным результатам расчета характеристик контакта индентора и вязкоупругого слоя.
Работа выполнена по теме государственного задания (№ госрегистрации АААА-А20-120011690132-4) и при финансовой поддержке РФФИ и БРФФИ в рамках научного проекта № 20-58-00007.
Список литературы
Derjaguin B. Untersuchungen über die Reibung und Adhäsion, IV. Theorie des Anhaftens kleiner Teilchen // Kolloid-Zeitschrift. 1934. Bd.69. H.2. S.155–164.
Johnson K.L., Kendall K., Roberts A.D. Surface energy and the contact of elastic solids // Proc. Roy. Soc. London. Ser. A. 1971. V. 324. № 1558. P. 301–313.
Derjaguin B.V., Muller V.M., Toporov Yu.P. Effect of contact deformations on the adhesion of particles // J. Coll. Interface Sci. 1975. V. 53. № 2. P. 314–326.
Sridhar I., Johnson K.L., Fleck N.A. Adhesion mechanics of the surface force apparatus // J. Phys. D. Appl. Phys. 1997. V. 30. № 12. P. 1710–1719.
Sergici A.O., Adams G.G., Müftü S. Adhesion in the contact of a spherical indenter with a layered elastic half-space // J. Mech. Phys. Solids. 2006. V. 54. № 9. P. 1843–1861.
Reedy E.D. Thin-coating contact mechanics with adhesion // J. Mater. Res. 2006. V. 21. № 10. P. 2660–2668.
Borodich F.M., Galanov B.A., Perepelkin N.V., Prikazchikov D.A. Adhesive contact problems for a thin elastic layer: Asymptotic analysis and the JKR theory // Math.&Mech. Solids. 2018. V. 24. № 5. P. 1405–1424.
Greenwood J.A., Johnson K.L. The mechanics of adhesion of viscoelastic solids // Phil. Mag. A. 1981. V. 43. № 3. P. 697–711.
Горячева И.Г., Губенко М.М., Маховская Ю.Ю. Скольжение сферического индентора по вязкоупругому основанию с учетом сил молекулярного притяжения // ПМТФ. 2014. Т. 55. № 1. С. 99–107.
Lin Y.Y., Hui C.Y. Mechanics of contact and adhesion between viscoelastic spheres: An analysis of hysteresis during loading and unloading // J. Polym. Sci. Part B: Polym. Phys. 2002. V. 40. P. 772–793.
Haiat G., Phan Huy M.C., Barthel E. The adhesive contact of viscoelastic spheres // J. Mech.&Phys. Solids. 2003. V. 51. № 1. P. 69–99.
Muller V.M., Yushchenko V.S., Derjaguin B.V. On the influence of molecular forces on the deformation of an elastic sphere and its sticking to a rigid plane // J. Coll. Interface Sci. 1980. V. 77. № 1. P. 91–101.
Attard P., Parker J.L. Deformation and adhesion of elastic bodies in contact // Phys. Rev. A. 1992. V. 46. № 12. P. 7959–7971.
Greenwood J.A. Adhesion of elastic spheres // Proc. R. Soc. Lond. A. 1997. V. 453. № 1961. P. 1277–1297.
Солдатенков И.А. Применение метода последовательных приближений к расчету упругого контакта при наличии молекулярной адгезии // ПММ. 2012. Т. 76. Вып. 5. С. 734–743.
McMeeking R.M. A Maxwell stress for material interactions // J. Coll. Interface Sci. 1998. V. 199. № 2. P. 187–196.
Sauer R.A., Li S. A contact mechanics model for quasi-continua // Int. J. Numer. Meth. Engng. 2007. V. 71. № 8. P. 931–962.
He L.H. Stress and deformation in soft elastic bodies due to intermolecular forces // J. Mech. Phys. Solids. 2013. V. 61. № 6. P. 1377–1390.
Солдатенков И.А. Контактная задача при объемном приложении сил межмолекулярного взаимодействия (уточненная постановка) // ПММ. 2013. Т. 77. Вып. 6. С. 877–893.
Overbeek J.T.G., Sparnaay M.J. Classical coagulation. London-van der Waals attraction between macroscopic objects // Discuss. Faraday Soc. 1954. V. 18. P. 12–24.
Wu J.-J. The jump-to-contact distance in atomic force microscopy measurement // J. Adhesion. 2010. V. 86. № 11. P. 1071–1085.
Kaplan I.G. Intermolecular Interactions: Physical Picture, Computational Methods and Model Potentials. Chichester: Wiley, 2006. xii + 367 p.
Israelachvili J.N. Intermolecular and Surface Forces. London: Academic, 2011. xxx + 674 p.
Кристенсен Р. Введение в теорию вязкоупругости. М.: Мир, 1974. 338 с.
Огибалов П.М., Ломакин В.А., Кишкин Б.П. Механика полимеров. М.: Изд-во Московского ун-та, 1975. 528 с.
Адамов А.А., Матвеенко В.П., Труфанов Н.А., Шардаков И.Н. Методы прикладной вязкоупругости. Екатеринбург: УрО РАН, 2003. 411 с.
Солдатенков И.А. Контакт с межмолекулярным взаимодействием для вязкоупругого слоя (самосогласованный подход): расчет НДС и диссипации энергии // ПММ. 2020. Т. 84. № 1. С. 102–121.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления (в 3-х тт.). М.: Физматлит, 2001. Т. 1. 616 с. Т. 2. 810 с.
Chen Y.L., Helm C.A., Israelachvili J.N. Molecular mechanisms associated with adhesion and contact angle hysteresis of monolayer surfaces // J. Phys. Chem. 1991. V. 95. № 26. P. 10736–10747.
Калиткин Н.Н. Численные методы. 2-е изд. СПб.: БХВ-Петербург, 2011. 586 с.
Степанов В.В. Курс дифференциальных уравнений. М: ГИФМЛ, 1959. 468 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика