Прикладная математика и механика, 2021, T. 85, № 2, стр. 239-256

Введение. Задача расчета напряженно деформированного состояния массива горных пород, вмещающего угольный пласт и пройденную по нему выработку, является важной и актуальной научной проблемой [1–6]. Предельно напряженные зоны, образующиеся в краевых частях пласта, существенно влияют на распределение поля напряжений и в угольном пласте, и в породах массива, окружающих горную выработку [7–9]. При определенных сочетаниях его компонентов оно может быть причиной ряда геодинамических явлений: горных ударов, обильного газовыделения в выработки, внезапных выбросов из забоев выработок горной массы, пучения почвы и значительных смещений их кровли [1, 10–15], и эти обстоятельства оказывают пагубное влияние на горные работы [10, 12].

Несмотря на то обстоятельство, что на угольных шахтах эти явления происходят довольно часто, существующие методы прогноза и борьбы с ними не всегда эффективны [1, 10, 12, 15] и, в первую очередь, из-за недостаточной изученности проблемы о напряженном состоянии краевой зоны пласта.

Современные понятия и представления о горных ударах и внезапных выбросах основаны на предположениях о том, что в большинстве случаев они происходят в предельно напряженных краевых зонах угольных пластов. К настоящему времени разработаны теории, описывающие эти виды геодинамических явлений [10, 12]. Однако в силу сложности математического описания физических процессов, сопутствующих этим явлениям, единой теории о горных ударах и выбросах не создано. Следует отметить, что все существующие теории едины в том, что для описания этих явлений необходимо знать характер распределения напряженного состояния массива в краевых зонах угольного пласта. В этой связи задача о геомеханическом состоянии пласта обычно сводится к определению параметров опорного давления, к которым относится эпюра вертикальной нормальной компоненты тензора напряжений в его краевой части и размер зоны неупругих деформаций (предельно напряженной зоны). Эти параметры могут быть определены экспериментально непосредственно в области ведения горных работ [1–3], а также теоретически в рамках ряда существующих моделей геомеханического состояния массива [4, 5, 7–10].

Модели, в рамках которых рассчитываются параметры опорного давления, можно условно классифицировать на несколько типов (категорий):

1. Модели напряженно-деформированного состояния пласта, разработанные на основе положений и методов теории упругости, в которых угольный пласт представляется включением, у которого упругие характеристики существенно отличаются от характеристик горных пород вмещающего массива [16].

2. Модели напряженного состояния краевой зоны пласта, построенные на базе методов теории упругости и пластичности, в которых состояние пласта в предельной зоне следует классическим критериям пластичности Треска–Сен-Венана или Губера–Мизеса [17, 18].

3. Модели напряженного состояния пласта, разработанные на базе методов предельного состояния горных пород, сыпучих сред. В этих моделях эпюра напряжений в предельно напряженной зоне описывается полуэмпирическими зависимостями, в которых часть параметров определяется по результатам экспериментов, проводимых в натурных условиях [1, 7–9].

4. Модели напряженного состояния пласта, разработанные на основе фундаментальных методов механики деформируемого твердого тела и сыпучих сред [19]. В этих моделях учитываются разные характеристики прочности пласта и на его контакте с окружающим массивом.

Сравнение моделей показывает, что третий и четвертый типы из приведенного списка наиболее близко отражают реальное состояние пласта и могут эффективно применяться к исследованию и напряженного состояния пласта, и геомеханического состояния углепородного массива. Однако результаты распределения напряжений в предельно напряженной зоне пласта, полученные в рамках этих моделей довольно значительно отличаются друг от друга, особенно вдали от его кромки.

Сравнение экспериментального и теоретического подходов к определению параметров опорного давления показывает, что применение моделей имеет ряд преимуществ по сравнению с экспериментами. Во-первых, они менее затратные, во-вторых, позволяют установить качественные и количественные закономерности в поведении массива и, следовательно, устанавливать некоторые прогнозные оценки о напряженном состоянии пласта и вмещающего массива.

Зачастую угольные пласты содержат прослойки угля или горной породы c довольно низкими характеристиками прочности по сравнению с характеристиками прочности самого пласта. В таких случаях формулирование задачи и ее решение связано с определенными трудностями, обусловленными более сложным механизмом формирования предельно напряженных зон по сравнению в задаче с однородным угольным пластом.

В моделях третьего типа влияние прослойка на напряженное состояние угольного пласта учитывается путем предварительного вычисления средневзвешенного предела прочности пласта и прослойка и дальнейшим использованием его в полуэмпирической формуле для получения эпюры опорного давления [1]. Однако такой подход не отражает действительную картину распределения опорного давления в предельно напряженной зоне, поскольку в расчетах учитывается тот же структурно однородный пласт, что и в отсутствии прослойка, но лишь с более низким пределом прочности пласта. В других же моделях прочностные характеристики прослойка вообще никак не учитываются.

В этой связи разработан подход к расчету краевой части пласта с прослойком и представлены результаты, полученные в рамках этого подхода. В его основе лежит разработанная автором модель напряженного состояния краевой части структурно однородного пласта, находящегося в предельно напряженном состоянии [19]. По вышеприведенной классификации она относится к моделям четвертого типа.

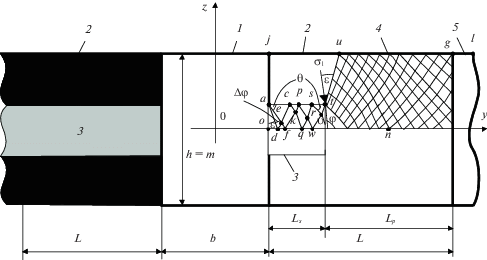
1. Постановка задачи о геомеханическом состоянии массива, вмещающего пластовую выработку, и построение его решения. Задача формулируется следующим образом. В массиве горных пород, моделируемом невесомой плоскостью, имеется (рис. 1) выработка 1 прямоугольного сечения размерами b × h, пройденная на глубине H по угольному пласту 2 на всю мощность. Характеристики прочности пласта: σ₀ – предел прочности на одноосное сжатие, K – коэффициент сцепления, ρ – угол внутреннего трения меньше, чем характеристики прочности пород вмещающего массива, но больше, чем характеристики (K′ – коэффициент сцепления, ρ' – угол внутреннего трения) по контактам пласта с остальным массивом. В средней части пласта имеется слой (пачка, прослоек) “слабого” низко прочного угля мощностью h_s. Предел прочности слоя σ_0s значительно ниже, чем σ₀, а угол внутреннего трения ρ_s близок к значению ρ. Массив нагружен гравитационным давлением сверху и снизу γH (γ – средневзвешенный объемный вес налегающих пород), а с боков – λγH (λ – коэффициент бокового давления). В краевых частях пласта образуются зоны неупругого деформирования 3, 4 шириной L = L_s + L_p (L_s – ширина зоны прослойка, L_p – ширина зоны пласта), а за ними вглубь массива находится область упругого деформирования пласта 5. Система координат y0z совпадает с центральными осями выработки.

На рис. 1 приведена схема линий скольжения в прослойке и пласте. Для упрощения линии показаны для частей пласта и прослойка, расположенных над осью y. Их описание приведено ниже. Вдоль линии jugl строятся графики напряжений (эпюры напряжений) в краевой части пласта.

В процессе решения задачи полагается:

1) длина выработки вдоль оси x значительно превосходит размеры поперечного сечения, поэтому породы в окрестности выработки находятся в условиях плоской деформации;

2) прочности прослойка выше, чем по контактам с породами вмещающего массива и угольным пластом, но ниже прочности самого пласта, чья прочность значительно ниже прочности вмещающих пород;

3) сжимающие нормальные напряжения положительны, а растягивающие отрицательны.

В ходе решения задачи рассматриваются условия перехода пласта в предельно напряженное (пластическое) состояние и определяются параметры опорного давления (размер предельно напряженной зоны L и максимальная величина вертикальной компоненты нормальных напряжений σ_z) для ряда значений предела прочности прослойка.

Особенность задачи о напряженном состоянии массива с пластовой выработкой заключается в том, что прочность окружающих горных пород, как правило, существенно выше прочности пласта, по которому пройдена выработка. Поэтому краевые части пласта переходят в предельно напряженное состояние, тогда как вмещающие породы деформируются упруго.

Механизм формирования предельно напряженных зон с образованием линий скольжения изложен в работах [20, 21]. В них показано, что предельно напряженные зоны структурно однородного пласта развиваются вглубь пласта, начиная с его обнажения (от его кромки), когда вертикальные главные напряжения σ₁ (главное напряжение σ₃ на обнажении равно нулю) достигают значения σ₀. При увеличении σ₁ зона неупругих деформаций в бортах выработки увеличивается. В этой зоне пласт деформируется не только по направлению его мощности, но и в плоскости с окружающими породами, где происходит его проскальзывание. В этой связи в нем будут одновременно существовать два предельных состояния равновесия: общее или обыкновенное (состояние самого пласта) и специальное (состояние по контакту пласта с окружающим массивом) [1, 22]. Эти два условия соответствуют критериям Кулона–Мора для прямолинейных огибающих кругов предельных состояний по пласту и по поверхности ослабления (контакту пласта с массивом).

Критерии Кулона–Мора совместно с дифференциальными уравнениями равновесия образуют систему уравнений напряженного состояния краевой зоны угольного пласта. В задаче с плоской деформацией путем перехода от компонентов тензора напряжений к приведенному напряжению σ и углу наклона φ между осью y и напряжением σ₁ система сводится к двум уравнениям, относящимся к уравнениям гиперболического типа.

Напряжение σ и угол φ связаны с компонентами тензора напряжений σ_y, σ_z, τ_yz и характеристиками прочности K, ρ, θ соотношениями, вытекающими из анализа круга Мора, построенного на напряжениях, соответствующих предельно напряженному состоянию пласта, при одновременном выполнении обоих критериев Кулона–Мора (общего и специального) [1, 18, 22]

где c и c' – временные сопротивления всестороннему равномерному растяжению самого пласта и на его контакте с массивом [1, 22]. Они определяются через коэффициенты сцепления K, K ' непосредственно из круга Мора следующими выражениями в которых параметры K и K ' связаны с σ₀ и $\sigma _{0}^{'}$ также известными соотношениями, вытекающими из круга напряжений [1, 22] а угол между главным напряжением σ₁ и линией скольжения определяется формулой, также вытекающей из круга напряжений [1, 22]

Уравнения гиперболического типа решаются методом характеристик (характеристических линий), в котором они совпадают с линиями скольжения материала [22]. На характеристиках уравнения упрощаются, но, несмотря на это, их интегрирование в замкнутом виде получается только на участках пласта, расположенных в непосредственной близости к его обнажению.

На остальных участках его предельно напряженной зоны решение можно получить только путем вычислительной процедуры, последовательно решая три краевые задачи механики предельного равновесия, используя при этом рекуррентные конечно-разностные соотношения [22].

После решения системы компоненты напряжений σ_y, σ_z, τ_yz, σ₁, σ₃ выражаются через напряжение σ и угол φ по формулам, также вытекающим из анализа напряжений с помощью круга Мора [22]

Разработанная на основе описанного выше подхода к оценке состояния краевой зоны пласта модель подробно изложена в работах [20, 21]. В них приведены также результаты решения задачи о предельно напряженной зоне пласта и даны сравнительные оценки с результатами расчетов, полученных в рамках других моделей. Основываясь на этих моделях в работе [19] построена компьютерная модель линий скольжения в предельно напряженной зоне, сформулирована и решена упругопластическая задача, по результатам которой получены значения параметров опорного давления в окрестности пластовой выработки.

Очевидно, что при наличии в угольном пласте прослойка предельное состояние наступает сначала в нем и, следовательно, зависимости (1.1)–(1.6) справедливы и для прослойка, но только в них следует вместо σ₀, с, ρ, K положить параметры для прослойка: σ_0s, с_s, ρ_s, K_s.

Схема характерных участков с линиями скольжения на их границах показана на рис. 1. Они имеют такой же вид, как и для структурно однородного пласта [19–21]. Так, например, на участке oad система линий скольжения представляет собой сетку изогональных линий. Напряжения в пределах участка постоянны, а напряжение σ₃ и на кромке прослойка, и во всех точках участка равны нулю. Приведенное напряжение σ определяется по формулам [20–22]

В соседнем треугольном участке ade, называемом зоной Прандтля, напряжения вдоль радиальных прямых линий постоянны, а в окружном направлении они меняются по экспоненциальному закону [1, 22]. Так, на линии напряжения вычисляются по следующей формуле [22]

где c_s – временное сопротивление всестороннему равномерному растяжению прослойка, угол Δφ, как следует из рис. 1, определяется по формуле

Во всех точках треугольной области ace линий скольжения представлены двумя системами изогональных наклонных линий, пересекающихся под углом 2ε.

Во всех других участках, расположенных в глубине пласта, распределение линий скольжения можно получить только в результате численного решения второй и третьей краевых задач на основе рекуррентных конечно-разностных соотношений.

Распределения напряжений и линий скольжения на участке def получаются из решения третьей краевой задачи. Граничными условиями в этой задаче являются условия по общей с участком ade границе de, а также по границе df, на которой заданы часть граничных условий: z = 0, φ = π/2 (ось y – ось симметрии и, поэтому, σ₁ вертикальна). В ходе численного решения задачи обе системы линий скольжения на этом участке получаются криволинейными.

Распределение линий скольжения внутри участка cefk следует из решения второй краевой задачи, в которой полный набор граничных условий задается по двум границам участка (области). В данном случае условия заданы по сторонам ce и ef, являющиеся общими границами участков def и ace, в которых решение уже получено. В ходе решения задачи одна система линий скольжения будет прямолинейной, а другая криволинейной.

Картины распределения напряжений и линий скольжения на участке ckp получаются из решения третьей краевой задачи. Сторона ck является общей границей с участком cefk, поэтому граничные условия на ней заданы полностью, а по стороне cp задана только часть граничных условий: z = h_s/2, а угол φ определяется из выражений (1.2). Обе системы линий скольжения также получаются криволинейными.

При решении краевых задач для участков, расположенных правее линии dec, можно поступить и по-другому. Так, например, линия cd является совокупностью двух линий: кривой линии de и прямой линии ce, которые являются границами участков, по которым распределение линий скольжения и напряжений уже построено. Следовательно, в каждой точке линии cd граничные условия заданы. Вдоль другой стороны dq участка decq число точек принимается таким же, как и по стороне cd, и в каждой из них известны ордината z = 0 и угол φ = π/2. Таким образом, граничные условия сформулированы для решения третьей краевой задачи. Поскольку граничная линия dc криволинейно-прямолинейная, то и линии скольжения представляют две системы сочетающих кривых и прямых линий. По результатам решения этой краевой задачи рассмотренный участок состоит из трех меньших участков, в пределах каждого из них система линий скольжения имеет характерные очертания. Так, в пределах участка def обе системы линий скольжения криволинейны, а в четырехугольнике сefk одна система линий скольжения прямолинейна, другая же криволинейная. В треугольнике fkq обе системы линий скольжения прямолинейны.

Далее решается третья краевая задача для участка ckqs. Здесь вдоль комбинированной линии ckq заданы все граничные условия, получающиеся из решения задачи для только что рассмотренного участка, а вдоль стороны cs с таким же количеством участков, что и по линии ckq, задана часть условий: ордината z = h_s/2 и угол φ, определяемый из выражений (1.2). В пределах этого участка система линий скольжения имеет свой характерный вид в пределах каждого их трех меньших участков, входящих в участок ckqs.

Для каждого последующего участка решается третья краевая задача, подобная той, что решалась для участков decq и ckqs.

По характеру распределения линий скольжения нетрудно установить и характер распределения напряжений в пределах каждого участка. Так, например, вдоль сторон fq, ps, принадлежащих треугольникам с прямолинейными границами, напряжения постоянны, а вдоль сторон cp и qw, принадлежащим треугольникам с криволинейными границами, напряжения нелинейны.

Таким образом, напряжения вдоль контакта прослойка, как и вдоль его оси эпюры нормальных напряжений, представляют собой графики в виде сменяющих друг друга участков с постоянными и нелинейно возрастающими линиями.

В дальнейших исследованиях напряженного состояния массива горных пород эти графики следует аппроксимировать аналитическими зависимостями, например, полиномами. Такая замена упрощает решение упругопластической задачи, позволяя ее свести к упругой и решить ее методом граничных интегральных уравнений. Коэффициенты полинома определяются из решения системы алгебраических уравнений, число которых совпадает с количеством выбранных участков в предельно напряженной зоне слоя. Правые части уравнений этой системы равны значениям найденных напряжений на границах этих участков [20].

Для расчета напряженного состояния пласта с низко прочным прослойком и оценки влияния этого прослойка на геомеханическое состояние основной части пласта также может быть использован подход, основанный на фундаментальном методе характеристик.

Из рис. 1 видно, что предельное состояние в пласте возникает лишь на некотором удалении от его кромки и при достижении приведенным напряжением в прослойке величины приведенного напряжения в пласте, которое соответствует одноосному напряженному состоянию. Из соображений непрерывности приведенных напряжений и отсутствия разрывов в линиях скольжения в пласте и слое условия перехода пласта в предельное состояние принимает следующий вид,

где σ_p – приведенное напряжение в пласте, σ_s – приведенное напряжение в прослойке, φ_p – угол наклона к горизонту напряжения σ₁ в пласте, φ_s – угол наклона σ₁ в прослойке на расстоянии L_s от обнажения пласта; σ_s – определяемое по формуле (1.7).

Очевидно, что часть пласта ajut (рис. 1) находится в упругом состоянии. Из условия ее равновесия следует, что касательная нагрузка, действующая вдоль линии ju, противоположна касательной нагрузке вдоль линии at.

После перехода пласта в предельное состояние и появление линии скольжения tu дальнейшее развитие его предельно напряженной зоны происходит совместно с прослойком. Поскольку на этой линии приведенное напряжение соответствует одноосному сжатию, то она является прямой линией. Во всех ее точках координаты, а также приведенное напряжение и угол φ определяются решениями краевой задачи для участка прослойка. Таким образом, вдоль линии скольжения $w{v}tu$ граничные условия известны.

Очевидно, что вдоль оси y, являющейся осью симметрии, угол φ = π/2, ордината произвольной точки отрезка любой длины равна нулю.

В этой связи линия скольжения $w{v}tu$ может рассматриваться одной границей следующего участка предельно напряженной зоны, охватывающей и прослойки. В качестве другой границы, на которой условия заданы лишь частично, может быть выбран отрезок с таким же количеством участков, что и на предыдущей границе (на рис. 1 это отрезок wn). Сформулированные таким образом граничные условия участка предельно напряженной зоны пласта являются условиями для третьей краевой задачи. После ее решения, приведенные напряжения σ, угол наклона φ и координаты точек y, z на границе un (рис. 1) выступают граничными условиями третьей краевой задачи для следующего участка ung. На другой границе ug этого участка в каждой точке известна ее ордината z = h/2, а угол φ определяется по формуле (1.2)

где i – номер произвольной точки участка.

После решения третьей краевой задачи для этого участка решается третья краевая задача для следующего участка аналогично тому, как это делалось для участка wun.

Представленных выше зависимостей, описывающих предельно напряженное состояние в прослойке и угольном пласте, недостаточно для решения задачи о построении поля напряжений в массиве около выработки, поскольку в этих зависимостях протяженность предельно напряженной зоны, а, следовательно, и граница раздела предельной зоны и упругой области не определены. Неизвестной величиной остается и значение максимального вертикального напряжения на границе раздела двух областей. Для их определения необходимо решить упругопластическую задачу, по результатам которой и находятся эти параметры, называемые параметрами опорного давления.

Упругопластическая задача путем замены предельно напряженных зон пласта реактивными усилиями, действующими на границе этих зон, может быть сведена ко второй внешней краевой задаче теории упругости [7] и представлена интегральным уравнением Фредгольма второго рода относительно плотности поверхностной (фиктивной) нагрузки, приложенной к контуру выработки [23, 24]. Уравнение решается численно – методом механических квадратур [24, 25].

После решения уравнения напряжения в любой точке массива определяются суперпозицией напряжений от действия найденной фиктивной нагрузки и напряжений в массиве до проведения выработки. Напряжения от действия фиктивной нагрузки находятся с помощью решения Кельвина о действии силы на упругое пространство [26].

Данный подход применялся к определению поля напряжений в массиве горных пород с прочностной анизотропией при построении зон нарушения сплошности массива вокруг горных выработок [27, 28].

В отличие от классической задачи граничные условия формулируются не только по контуру выработки, но и по контуру, включающему кровлю, почву выработки и контакт пласта с окружающим массивом на участке предельной зоны. В левой части этого уравнения они выражены через неизвестную фиктивную нагрузку, а в правой части эти условия представлены через усилия, обусловленные напряжениями исходного поля и реактивными усилиями, создаваемыми крепью выработки и напряжениями в предельно напряженной зоне на контакте пласта с массивом.

Область интегрирования в интегральном уравнении кроме размеров выработки включает и неизвестный размер предельно напряженной зоны L. Для его определения используется метод последовательных приближений: сначала задается размер предельно напряженной зоны, затем решается интегральное уравнение и после этого вычисляются напряжения вдоль контакта пласта с массивом. Далее, на границе упругой области и предельно напряженной зоны сравниваются полные напряжения p_y, p_z. Эти напряжения на горизонтальных участках равны соответственно напряжениям σ_z и τ_yz, поскольку нормаль к горизонтальной площадке составляет с ней угол π/2. Если результаты отличаются друг от друга, то решение интегрального уравнения производится при другом значении L. Процедура счета продолжается до тех пор, пока значения полных напряжений не совпадут или будут достаточно близки друг к другу.

Разработанная на основе описанного подхода модель геомеханического состояния углепородного массива в окрестности пластовой выработки, в которой учтены геометрические и механические параметры прослойка, отличные от параметров пласта, является новой и в этой статье излагается впервые. В работе [19] модель геомеханического состояния построена на условии однородной структуры пласта и в этом ее существенное отличие от модели состояния пласта с прослойком.

2. Анализ полученных результатов. В рамках рассматриваемой модели проведен вычислительный эксперимент, за исходные данные в котором приняты следующие параметры массива, выработки и пласта: H = 800 м, λ = 1, γ = 25 кН/м³, σ₀ = 10 МПа, ρ = = 20°, ρ_s = 20°, ρ' = 10°, K' = 0, b = 5 м, h = 3 м, h_s = 0.5 м. Другие параметры в ходе вычислений менялись.

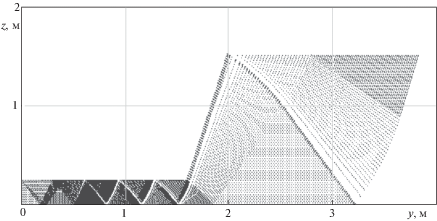
На рис. 2 представлена компьютерная модель сетки линий скольжения в предельно напряженной зоне для верхней части угольного пласта, вмещающего низко прочный прослоек. В качестве дополнительных исходных данных принято σ_0s = 2 МПа. Сетка построена по результатам численного решения трех краевых задач механики сыпучих сред для двенадцати характерных участков прослойка, соответствующих наступлению предельного состояния пласта, и двух участков для самого пласта. На рисунке отчетливо просматриваются участки с характерным распределением сетки линий скольжения, которая представлена своими узлами (точками пересечения линий скольжения).

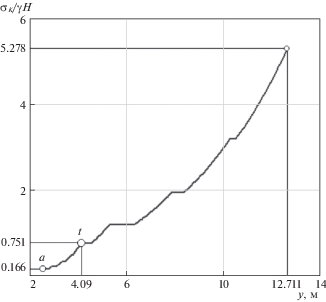
На рис. 3 построен график (эпюра) распределения приведенного напряжения вдоль кровли прослойка и пласта σ_K для двадцати характерных участков предельно напряженной зоны. Из них двенадцать участков принадлежат прослойку (σ_0s = 2 МПа) и восемь непосредственно пласту. На графике показаны две крайние точки a и t участка графика, соответствующего прослойку (рис. 1). Правее часть графика соответствует пласту вместе с прослойком. Из рисунка видно, что график на обоих участках, как это отмечено ранее, имеет вид попеременно сменяющих горизонтальных и нелинейно возрастающих участков. Из графика следует, что размер предельно напряженной зоны прослойка, соответствующего моменту перехода пласта в предельное состояние, равен 1.59 м (4.09 м – b/2), а величина приведенного напряжения при этом составляет 0.751/γH. Длина участка краевой предельно напряженной зоны пласта при двадцати участках равна 10.211 м (12.711 м – b/2), а приведенное напряжение достигает значения 5.278/γH.

После определения приведенных напряжений и угла φ компоненты тензора напряжений, вычисленные по формулам (1.5) или (1.6), могут быть представлены графически.

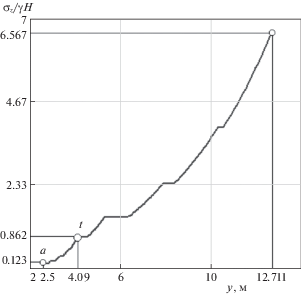
На рис. 4 построена эпюра вертикальных напряжений σ_z вдоль кровли предельно напряженной зоны пласта. Как и σ_K на рис. 3, она представляет собой совокупность участков с постоянными и переменными напряжениями. Часть графика на участке at также соответствует напряжениям в прослойке. Напряжение в конце двадцатого участка равно, 6.567/γH, а при переходе пласта в предельное состояние оно равно 0.862/γH.

При решении упругопластической задачи эпюры компоненты тензора напряжений σ_y, σ_z, τ_yz, как уже отмечено выше, следует аппроксимировать аналитическими функциями.

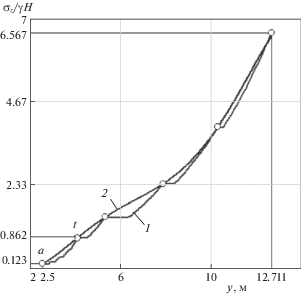
На рис. 5 построены два графика зависимости напряжения σ_z от координаты y. Кривая 1 – эпюра исходного напряжения, показанного на рис. 4, а кривая 2 аппроксимирующий полином пятой степени. Узловыми точками при определении коэффициентов полинома приняты границы горизонтальных и нелинейных участков на исходной эпюре напряжений.

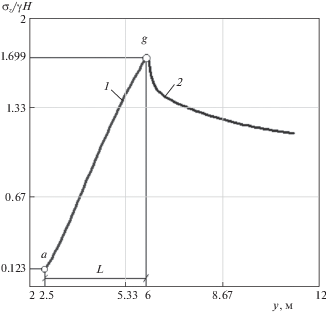
На рис. 6 представлены результаты решения упругопластической задачи в виде графика нормальных напряжений σ_z, построенного вдоль кровли пласта (вдоль линии jl на рис. 1). Кривая 1 – эпюра напряжений в предельно напряженной зоне пласта, а кривая 2 – эпюра напряжений в его упругой области. Их значения совпадают в точке g, соответствующей границе упругой и предельно напряженной зон.

Из рисунка следует, что максимальное нормальное напряжение σ_{z max} в краевой части пласта, являющееся одним из параметров опорного давления в окрестности выработки, действует на границе предельно напряженной зоны и упругой области пласта. Оно равно 1.699 γH. Другой параметр опорного давления – ширина предельно напряженной зоны L из графика равна 3.5 м (6 м – b/2). Для сравнения максимум опорного давления σ_{z max} в пласте без прослойка равен 1.582 γH, а ширина зоны L = 4.9 м [19].

Ниже определены параметры опорного давления в пласте с прослойком на основе подхода о средневзвешенной прочности пласта σ_c [1], в котором предел прочности вычисляется по следующей формуле

При исходных данных

а параметры опорного давления получаются равными: σ_z max = 1.592 γH, L = 5.65 м. Сравнение этих значений с параметрами опорного давления, полученными в рамках разработанного подхода, показывает, что результаты отличаются друг от друга не только количественно, но и качественно. Во-первых, максимум опорного давления, исходя из средневзвешенной прочности пласта, получается меньше, а размер предельно напряженной зоны существенно выше, чем на основе разработанного подхода.

Таким образом, оценка геомеханического состояния углепородного массива на основе подхода, в котором влияние прослойка учитывается лишь при подсчете по средневзвешенной прочности пласта, может оказаться весьма ошибочной.

При решении задачи о напряженном состоянии пласта с низко прочным прослойком важно установить протяженность предельно напряженной зоны этого прослойка, при которой начинается переход пласта в предельно напряженное состояние. Ее размер устанавливает положение линии скольжения, параметры которой являются начальными граничными условиями в задаче о развитии предельного состояния остальной части пласта.

В этой связи проведены исследования и представлены графические результаты, отражающие связь длины предельно напряженной зоны прослойка L_pR (рис. 1) с его характеристиками прочности, соответствующими переходу всей толщи пласта в предельное состояние.

На рис. 7 показан график изменения размера предельно напряженной зоны прослойка, соответствующего переходу пласта в предельное состояние, в зависимости от предела прочности прослойка. Ось абсцисс уменьшена в σ₀ раз.

Из рисунка следует, что график состоит из двух прямолинейных участков AB и BС с изломом в точке C. Абсцисса точки B равна 6.6 МПа, а ордината равна 0.425 м.

Важно отметить, что переход пласта в предельное состояние на самой его кромке начинается при σ_0s < σ₀. Действительно, предельное состояние в пласте по стороне ac, непосредственно примыкающей к кромке oa, на основании первого условия (1.10) наступит при равенстве значений напряжений, определяемых формулами (1.7) и (1.8). После подстановки правых частей этих выражений в условие (1.10) и учете в них выражений (1.3) и (1.4) легко получается зависимость между пределами прочности пласта и прослойка, при которых наступает предельное состояние пласта непосредственно у его кромки.

Если c' равно нулю, то эта зависимость выражается следующим образом

а из формул (1.2) и (1.9) следуют достаточно простые по виду выражения для углов θ и Δφ

В соответствии с исходными данными перечисленные параметры равны следующим величинам: θ = 45°, Δφ = 10°, σ_0s = 8.95 МПа. Следовательно, при данном значении предела прочности прослойка пласт переходит в предельное состояние в любом месте участка ac (рис. 1), начиная с его кромки.

В этой связи размер L_s (рис. 1) либо равен нулю, либо равен длине L_ac этого участка.

На рис. 8, 9 показаны результаты решения упруго пластической задачи о напряженном состоянии массива в окрестности пластовой выработки. Они представлены в виде графиков зависимости параметров опорного давления в краевой части пласта от предела прочности прослойка.

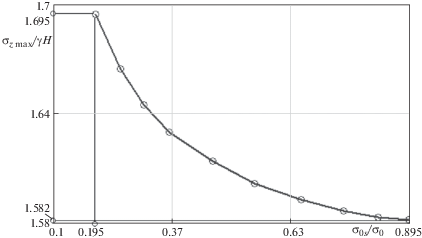
Так, на рис. 8 построен график опорного давления в краевой части пласта в зависимости от предела прочности прослойка. График имеет вид плавно убывающей вогнутой кривой. Из него следует, что меньшему значению прочности прослойка соответствует большее значение максимума опорного давления (при σ_0s = 1.95 МПа, σ_z max = = 1.695 γH), а при прочности прослойка σ_0s = 8.95 МПа максимум опорного давления равен максимуму опорного давления в пласте в отсутствии низко прочного прослойка и составляет 1.582 γH. Разница между этими значениями составляет 7.14%.

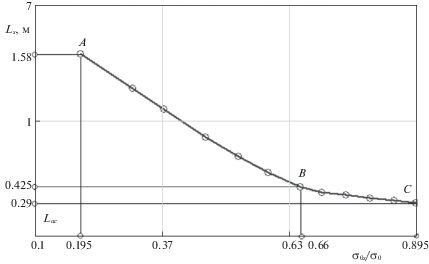
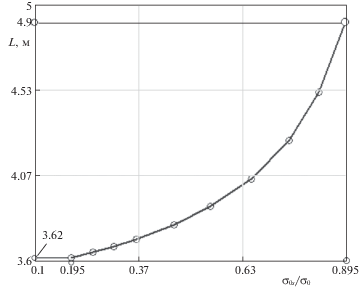
На рис. 9 построен график зависимости другого параметра опорного давления – размера предельно напряженной зоны пласта от предела прочности прослойка. Из рисунка видно, что график имеет вид плавной возрастающей кривой и с увеличением предела прочности прослойка также возрастает. Минимальный размер предельно напряженной зоны на принятом интервале изменения σ_0s равен 3.62 м, а при σ_0s = 8.95 МПа размер этой зоны соответствует размеру предельно напряженной зоны пласта, не имеющего прослойка, составляет 4.9 м. Разница между этими значениями равна 26.12%.

Заключение. 1. Наличие в угольном пласте прослойка из низко прочного материала, расположенного в центральной части пласта, приводит к появлению предельно напряженной зоны сначала в прослойке, начиная от самой его кромки. Эта зона распространяется вглубь пласта до тех пор, пока в самом пласте не наступит предельное состояние. Как только оно будет достигнуто, предельно напряженная зона распространяется и в самом пласте.

2. В предельно напряженной зоне реализуются два критерия предельного состояния Кулона–Мора: общий (по пласту) и специальный (по контакту пласта с окружающими породами). Распределение поля напряжений в предельно напряженной зоне и прослойка, и пласта производится путем решения трех краевых задач для дифференциальных уравнений гиперболического типа методом характеристик, представленных в конечноразностной канонической форме.

3. Задача о геомеханическом состоянии массива горных пород, вмещающего выработку, пройденную по угольному пласту, путем замены предельно напряженных зон пласта напряжениями, действующими по его контакту с окружающим массивом, сведена ко второй внешней краевой задаче теории упругости для интегрального сингулярного уравнения. Его решение получено методом механических квадратур и с помощью процедуры последовательных приближений, в ходе которой осуществляется проверка статических граничных условий на границе предельно напряженной зоны и упругой области пласта. Поле напряжений в массиве построено на основе фундаментальных решений Кельвина о действии единичной сосредоточенной силы в бесконечной среде.

4. Анализ полученных результатов показал:

а) эпюра напряжений вдоль контакта прослойка с пластом, а также контакта пласта с окружающим массивом представляет собой ломаную линию в виде комбинации поочередно сменяющих друг друга горизонтальных и нелинейно возрастающих участков. На горизонтальных участках реализуется специальный критерий Кулона–Мора, а на нелинейно возрастающих участках справедлив общий критерий Кулона–Мора;

б) с уменьшением прочности прослойка увеличивается расстояние от кромки пласта до того сечения, где начинается его переход в предельно состояние. Переход пласта в предельное состояние у самой кромки возможен при меньшем значении предела прочности прослойка, чем самого пласта, но, при этом, разность между ними не превышает одиннадцати процентов;

в) в пласте, имеющем прослоек, максимум опорного давления выше, а протяженность предельно напряженной зоны меньше по сравнению с параметрами опорного давления пласта в отсутствии прослойка. То есть наличие прослойка несколько увеличивает максимум опорного давления, но при этом значительнее смещает его в сторону кромки пласта (борта выработки). Подобного эффекта с параметрами опорного давления в пласте с прослойком, не обнаружить, если использовать подход, в котором прочность прослойка учитывается лишь при подсчете средневзвешенной прочности пласта.