1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 85, № 2, 2021

Прикладная математика и механика, 2021, T. 85, № 2, стр. 193-209

Динамическое поведение балки, лежащей на обобщенном упругом основании, с движущейся нагрузкой

В. И. Ерофеев 1, *, Е. Е. Лисенкова 1, **, И. С. Царев 1, ***

1 Институт проблем машиностроения РАН
Нижний Новгород, Россия

* E-mail: erof.vi@yandex.ru
** E-mail: eelissen@yandex.ru
*** E-mail: tsarev_ivan97@mail.ru

Поступила в редакцию 01.07.2020
После доработки 08.12.2020
Принята к публикации 26.12.2020

Полный текст (PDF)

Аннотация

Приводится анализ наиболее известных моделей упругого основания. Показано, что, несмотря на различие в названии, речь идет об одной обобщенной модели, характеризующейся двумя коэффициентами. Такая модель позволяет не только сохранить простоту математического аппарата, которая присуща винклеровой модели, но и получить более достоверные результаты. Рассматривается согласованное динамическое поведение балки, лежащей на обобщенном упругом основании, характеризующимся двумя коэффициентами постели (коэффициентом сжатия и коэффициентом сдвига), с движущейся нагрузкой. Изучаются особенности генерации изгибных волн движущейся нагрузкой и определены критические скорости ее движения. Получено выражение для давления волн (силы сопротивления движению). Исследуется зависимость постоянной составляющей этой силы от скорости движения объекта. Приводится сравнение с результатами, полученными при использовании классической модели упругого основания.

Ключевые слова: балка, обобщенная модель упругого основания, движущаяся нагрузка, критическая скорость, изгибные волны, сила сопротивления движению

Введение. Динамическому поведению упругих систем с движущимися нагрузками уделено достаточно внимания в литературе, что связано с широким практическим приложением [1–18]. Особый интерес представляют задачи о колебаниях балок на винклеровском основании, которые используются в качестве моделей, описывающих динамику железнодорожного полотна [8, 12]. В связи с развитием высокоскоростных магистралей повышаются требования к модели и точности расчетов [11, 12, 14–18]. Использование обобщенной модели упругого основания, которая характеризуется двумя коэффициентами постели (коэффициентом сжатия и коэффициентом сдвига) позволяет, с одной стороны, сохранить простоту математического аппарата присущую модели Винклера [19], а с другой, получить более достоверные результаты.

Известно [7, 12], что при движении высокоскоростных нагрузок по упругим направляющим в последних возникают колебания в виде волн деформаций, давление которых дает основной вклад в сопротивление движению. Кроме того, эффекты волнообразования являются причиной многих проблем эксплуатации рельсовых направляющих ракетного трека [20–24]. Ниже исследуются динамические процессы в балке, лежащей на обобщенном упругом основании, с движущимся объектом, являющимся носителем источника колебаний, которые, так или иначе, связаны с эффектами волнообразования.

1. Классическая и обобщенная модели упругого основания. Одним из основных понятий теории сооружений является упругое основание, под которым подразумевается механическая расчетная модель упругой среды, сопротивляющейся деформированию конструкции, взаимодействующей с ней. Такой средой в задачах строительной механики , как правило, выступает грунтовое основание. Исторически первая и самая распространенная модель упругого основания базируется на гипотезе Винклера (1867) [19], развитой Циммерманом (1888 г.) [25]. Эта гипотеза предполагает, что зависимость между давлением на грунт (q) и вызванной им осадкой точки (u) является прямо пропорциональной

(1.1)
$q = Ku$

Из (1.1) следует, что при давлении на поверхность грунта на какой-либо одной малой площадке грунт будет оседать только под ней. В действительности же грунт обладает распределительной способностью, т.е. он оседает не только под нагруженной областью, под фундаментом, но и вблизи него.

Учитывать влияние соседних нагрузок на упругую осадку грунта в данной точке под нагруженной поверхностью по убывающей показательной функции

(1.2)
$u\left( r \right) = A{{e}^{{ - \alpha r}}}$
предложил К. Вигхардт (1922 г.) [26].

М.М. Филоненко-Бородичем (1945 г.) [27] предложена модель упругого основания, в которой независимые “винклеровские” пружины дополняются по верху нерастяжимой нитью (“мембранная модель”) с постоянной горизонтальной проекцией натяжения T или балкой (“ламинарная модель”). В пространственном случае нити заменяются мембранами, а балка – плитой.

Дифференциальное уравнение, характеризующее работу основания по Филоненко-Бородичу в случае мембранной модели, имеет следующий вид:

(1.3)
$Ku - T\left( {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}}} \right) = q(x,y)$

Следует заметить, что дифференциальное уравнение поверхности мембраны, подкрепленной пружинами, ранее было получено Т. Карманом [28], и (1.3) полностью совпадает с этим уравнением.

В качестве модели грунта, с которым взаимодействуют конструкции, П.Л. Пастернак (1954 г.) предложил использовать “сплошное упругооседающее и упруговращающееся основание” [29], свойства которого описываются двумя независимыми коэффициентами постели: коэффициентом сжатия h1, имеющим размерность (кГ/см3), и коэффициентом сдвига h2 размерности кГ/см, учитывающим совместную работу соседних областей. Первый коэффициент аналогичен коэффициенту постели Винклера, а второй “дает возможность выразить интенсивность вертикальной силы сдвига (или изгибающего момента) в виде произведения h2 на производную осадки в соответствующем направлении” [29].

Схематическое изображение такого упругого основания приведено, например, в [30].

Упругое основание Пастернака описывается уравнением, совпадающим по виду с (1.3), $K = {{h}_{1}}$, $T = {{h}_{2}}$.

При разработке технической теории расчета конструкций на упругом основании в качестве основания использовалась [31, 32] однослойная или многослойная модели, описываемые двумя или большим количеством обобщенных упругих характеристик. При этом работа однослойного упругого основания Власова–Леонтьева описывалась уравнением вида (1.3).

В случае одномерной однородной задачи, соответствующей (1.3), получается уравнение

(1.4)
${{\alpha }^{2}}u - \frac{{{{d}^{2}}u}}{{d{{x}^{2}}}} = 0,$
где $\alpha = \sqrt {{K \mathord{\left/ {\vphantom {K T}} \right. \kern-0em} T}} $.

Уравнение (1.4) имеет “затухающее” решение в виде:

(1.5)
$u\left( x \right) = A{{e}^{{ - \alpha x}}}$

Заметим, что (1.5) совпадает с соотношением (1.2) (модель Вигхардта).

Сопоставление (1.2)–(1.4) и (1.5) показывает, что речь идет об одной обобщенной модели упругого основания. Кроме авторов работ [19, 25–29, 31, 32], подобную же модель рассматривали Э. Рейсснер [33], и М. Хетеньи [34]. Таким образом, обобщенную модель упругого основания справедливо называть моделью Вигхардта–Кармана–Филоненко-Бородича–Пастернака–Власова–Леонтьева–Рейсснера–Хетеньи.

Уравнение равновесия деформируемой поверхности, согласно модели (1.3), представляет собой классическое неоднородное уравнение Гельмгольца. Параметрам $K$ и $T$, входящим в уравнение (1.3), разные авторы дают различную механическую трактовку.

Обобщенную модель упругого основания называют двухкоэффициентной [29], двуххарактеристической [35, 36], двухпараметрической [37–40], но чаще всего – моделью Пастернака (см., например, [41–45]).

Модель упругого основания с двумя коэффициентами постели (на растяжение и на сдвиг) далее в этой работе будем называть обобщенной или моделью Пастернака, в отличие от классической модели упругого основания (модель Винклера).

Для моделирования деформируемого основания кроме методов, основанных на работе с системами дискретных упругих элементов, применяются и методы теории упругости. Еще в 1919 г. Г.Э. Проктор предложил моделировать основание однородной изотропной упругой средой [46–48]. К этому же направлению относится работа М.И. Горбунова-Посадова [49].

Однако гипотеза о деформируемом основании как об упругом пространстве наделяет среду преувеличенно высокими распределительными свойствами, т.е. приводит во многих случаях (особенно при плоской деформации) к существенному преувеличению расчетных величин – прогибов и изгибающих моментов.

Преодолеть это противоречие удается с помощью моделей упругого слоя с различными условиями на его границе [50–54]. Такие модели предполагают, что с нагруженным фундаментом (конструкцией) взаимодействует ограниченная по высоте область грунтового массива. Ниже этой области находится недеформируемая область, жесткость которой принимается бесконечно большой.

При уменьшении толщины слоя такие модели приближаются к винклеровской, а при увеличении толщины слоя – к модели упругого полупространства.

Показано [55, 56], что расчет по моделям (1.2)–(1.5), являющийся промежуточным между расчетами по модели Винклера и модели упругого полупространства, дает более быстрое затухание осадок поверхности грунта по мере удаления от края фундамента, чем теория упругости.

2. Постановка и решение задачи о действии подвижной нагрузки на балку, лежащую на обобщенном упругом основании. Рассмотрим систему, состоящую из направляющей, вдоль которой по неизвестному закону $x = l\left( t \right)$ движется объект, обладающий моментом инерции ${{I}_{0}}$ и массой $m$, на который действует переменная сила P(t). Динамическое поведение упругой направляющей и движущегося по ней объекта взаимообусловлены, т.е. характер колебаний направляющей зависит от закона движения объекта, а движение последнего происходит как под действием внешних сил, так и сил реакции со стороны направляющей.

Направляющую будем считать лежащей на упругом основании модели Пастернака [29] однородной балкой, колебания которой описываются в рамках гипотезы Бернулли–Эйлера [57].

Воспользуемся вариационным подходом для вывода уравнений движения и естественных краевых условий. С этой целью выпишем плотность функции Лагранжа $\lambda $ рассматриваемой направляющей и функцию Лагранжа $L$ движущегося объекта:

$\lambda = \frac{1}{2}\left( {\rho Fu_{t}^{2} - IEu_{{xx}}^{2} - {{h}_{1}}{{u}^{2}} - {{h}_{2}}u_{x}^{2}} \right),\quad L = \frac{1}{2}m\left( {\dot {u}_{0}^{2} + {{{\dot {\ell }}}^{2}}} \right) + \frac{1}{2}{{I}_{0}}\dot {w}_{0}^{2},$
где $u\left( {x,t} \right)$ – поперечное смещение срединной линии балки; $\rho F$ – погонная плотность; $I$ – момент инерции, E – модуль Юнга, ${{h}_{1}}$ и ${{h}_{2}}$ – коэффициент “постели” на сжатие и коэффициент “сдвига” основания балки, соответственно; ${{u}_{0}}\left( t \right)$ и ${{w}_{0}}(t)$ – поперечное смещение и угол поворота объекта.

Здесь и далее индексами t обозначаются частные производные по времени, индексами x – производные по координате, а точкой – обыкновенная производная по времени.

Используя методику постановок краевых задач на основе вариационного принципа Гамильтона–Остроградского [7, 58], получим, что взаимообусловленное динамическое поведение балки и движущегося по ней объекта (в предположении, что их параметры постоянны) описывается системой уравнений

(2.1)
${{u}_{{tt}}} + {{\alpha }^{2}}{{u}_{{xxxx}}} - c_{{II}}^{2}{{u}_{{xx}}} + \omega _{0}^{2}u = 0$
(2.2)
$\begin{gathered} u\left( {x = l(t) + 0,t} \right) = u\left( {x = l(t) - 0,t} \right) = u\left( {l(t),t} \right) = {{u}_{0}}(t) \\ {{u}_{x}}\left( {x = l(t) + 0,t} \right) = {{u}_{x}}\left( {x = l(t) - 0,t} \right) = {{u}_{x}}\left( {l(t),t} \right) = {{w}_{0}}(t) \\ \end{gathered} $
(2.3)
${{I}_{0}}{{\ddot {w}}_{0}} = IE\left[ {{{u}_{{xx}}}} \right]$
(2.4)
$m{{\ddot {u}}_{0}}(t) = - \rho F\left[ {{{\alpha }^{2}}{{u}_{{xxx}}} - c_{{II}}^{2}{{u}_{x}} - \dot {l}{{u}_{t}}} \right] + P\left( t \right)$
(2.5)
$m\ddot {l} = {{F}_{{pr}}} + Q,\quad {{F}_{{pr}}} = - \frac{1}{2}\rho F\left[ {u_{t}^{2} + {{\alpha }^{2}}u_{{xx}}^{2} + c_{{II}}^{2}u_{x}^{2} - \omega _{0}^{2}{{u}^{2}} - 2{{\alpha }^{2}}{{u}_{x}}{{u}_{{xxx}}} + 2\dot {l}{{u}_{x}}{{u}_{t}}} \right]$

Здесь квадратные скобки означают разность предельных значений стоящих в них величин справа и слева от движущейся границы $x = l\left( t \right)$, $\alpha = \sqrt {{{IE} \mathord{\left/ {\vphantom {{IE} {\rho F}}} \right. \kern-0em} {\rho F}}} $, ${{c}_{{II}}} = \sqrt {{{{{h}_{2}}} \mathord{\left/ {\vphantom {{{{h}_{2}}} {\rho F}}} \right. \kern-0em} {\rho F}}} $, ${{\omega }_{0}} = \sqrt {{{{{h}_{1}}} \mathord{\left/ {\vphantom {{{{h}_{1}}} {\rho F}}} \right. \kern-0em} {\rho F}}} $ – наинизшая частота возбуждаемых в балке волн, Fpr – давление волн, Q – внешняя сила. Для полноты постановки задачи следует задать начальные условия и ограниченности смещений $u\left( {x,t} \right)$ при $x \to \pm \infty $.

Предполагаем, что балка является бесконечной. Такая идеализация допустима, если на ее границах находятся оптимальные демпфирующие устройства, т.е. параметры граничного закрепления таковы, что падающие на него возмущения не будут отражаться. На основе точных решений модельных задач для упругих систем обосновано [58] существование согласованных концевых гасителей различных типов колебаний, не дающих отраженных возмущений в системе. Это позволяет рассматривать модель балки без учета граничных условий, а вибрации, распространяющиеся по балке, рассматривать как бегущие изгибные волны.

Полагая движение равномерным ($l\left( t \right) = Vt$, $V = \operatorname{const} $), и используя разработанный подход к исследованию подобного рода задач [7, 58], будем искать установившееся (стационарное) решение слева ($x < Vt$) и справа ($x > Vt$) от движущейся нагрузки в форме бегущей гармонической волны:

(2.6)
$A\exp \left[ {i\left( {\omega t - kx} \right)} \right],$
где $A$ – комплексная амплитуда, $\omega $ – круговая частота, k – волновое число.

Тогда задача определения частот, волновых чисел возбуждаемых волн и критических скоростей движения нагрузки, часто называемая задачей кинематики волн, сведется к решению дисперсионного уравнения

(2.7)
$ - {{\omega }^{2}} + {{\alpha }^{2}}{{k}^{4}} + c_{{II}}^{2}{{k}^{2}} + \omega _{0}^{2} = 0$
совместно с кинематическим инвариантом [7, 58]:
(2.8)
$\omega - Vk = \Omega ,$
выражающим равенство фаз излучаемых волн в точке, где находится движущийся источник возмущений частоты $\Omega $. Условие (2.8) определяет величину смещения частоты согласно эффекту Доплера [7]. В случае постоянной силы ($\Omega = 0$) кинематический инвариант запишется в виде $\omega - kV = 0$. Заметим, что для однозначного определения кинематических характеристик возбуждаемых волн необходимо воспользоваться условиями ограниченности прогибов направляющей на бесконечности и условиями излучения Мандельштама [7, 58].

Одним из основных вопросов при исследовании динамического поведения направляющих под действием движущихся нагрузок является вопрос о критических скоростях. Под критической скоростью (${{V}_{*}}$) движения нагрузки понимается такая скорость, при превышении которой качественно меняется картина волнообразования [7]. Необходимость в правильном расчете критических скоростей при проектировании скоростных наземных магистралей связана, прежде всего, с тем, что они являются предельно допустимыми (см. [11, 12] и литературу к ним).

Из условия вырождения корней системы уравнений (2.7), (2.8) получим, что критические скорости движения нагрузки определяются решением уравнения восьмого порядка, которое в безразмерных переменных имеет вид

(2.9)
$\begin{gathered} {{{\tilde {V}}}^{8}} - {{\beta }^{2}}\left( {4 - {{{\tilde {\Omega }}}^{2}}} \right){{{\tilde {V}}}^{6}} + \left[ { - 9{{{\tilde {\Omega }}}^{2}}\left( {4 - {{{\tilde {\Omega }}}^{2}}} \right) + 3{{\beta }^{4}}\left( {2 - {{{\tilde {\Omega }}}^{2}}} \right) - 8{{{\left( {1 - {{{\tilde {\Omega }}}^{2}}} \right)}}^{2}}} \right]{{{\tilde {V}}}^{4}} + \\ + \;{{\beta }^{2}}\left[ {36{{{\tilde {\Omega }}}^{2}}\left( {1 - {{{\tilde {\Omega }}}^{2}}} \right) - {{\beta }^{4}}\left( {4 - 3{{{\tilde {\Omega }}}^{2}}} \right) + 16{{{\left( {1 - {{{\tilde {\Omega }}}^{2}}} \right)}}^{2}}} \right]{{{\tilde {V}}}^{2}} + \\ + \;\left( {1 - {{{\tilde {\Omega }}}^{2}}} \right){{\left( {{{\beta }^{4}} - 4 + 4{{{\tilde {\Omega }}}^{2}}} \right)}^{2}} = 0, \\ \end{gathered} $
где $\tilde {V} = {V \mathord{\left/ {\vphantom {V {\sqrt {\alpha {{\omega }_{0}}} }}} \right. \kern-0em} {\sqrt {\alpha {{\omega }_{0}}} }}$, ${{\beta }^{2}} = {{c_{{II}}^{2}} \mathord{\left/ {\vphantom {{c_{{II}}^{2}} {\left( {\alpha {{\omega }_{0}}} \right)}}} \right. \kern-0em} {\left( {\alpha {{\omega }_{0}}} \right)}}$, $\tilde {\Omega } = {\Omega \mathord{\left/ {\vphantom {\Omega {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$.

В пренебрежении коэффициентом сдвига ($\beta \to 0$) из (2.9) получим известные выражения [58] для критических скоростей движения нагрузки вдоль балки Бернулли–Эйлера на винклеровском основании:

(2.10)
$\tilde {V}_{{1,2}}^{*} = \sqrt[4]{{\frac{1}{2}\left( {8 + 20{{{\tilde {\Omega }}}^{2}} - {{{\tilde {\Omega }}}^{4}} \mp \tilde {\Omega }{{{\left( {{{{\tilde {\Omega }}}^{2}} + 8} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right)}}$

Они определяют на плоскости параметров ($\tilde {\Omega }$, $\tilde {V}$) задачи две кривые, разбивающие ее на области с различным числом возбуждаемых волн (рис. 1).

Рис. 1.

Зависимость скорости движения объекта от частоты источника колебаний при $\beta = 0$ и $\beta = 2$.

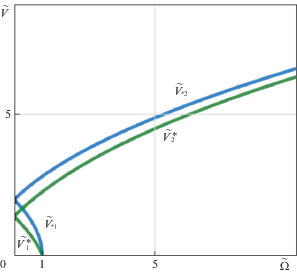
Учет коэффициента сдвига ($\beta \ne 0$) в основании не приводит к изменению числа критических скоростей (их, по-прежнему, две, если частота источника не превосходит ${{\omega }_{0}}$, либо одна – в противном случае) и качественной картины волнообразования (рис. 1). Так, при частоте источника меньше критической $\tilde {\Omega } < 1$ и скорости его движения меньше первой критической скорости $\tilde {V} < {{\tilde {V}}_{{*1}}}$ движущий источник создает локальное собственное поле, представляющее собой суперпозицию спадающих по экспоненте осцилляций. Если скорость движения объекта превышает первую критическую ${{\tilde {V}}_{{*1}}}$, но не превосходит вторую критическую ${{\tilde {V}}_{{*2}}}$ скорость (${{\tilde {V}}_{{*1}}} < \;\tilde {V} < {{\tilde {V}}_{{*2}}}$), то кроме собственного поля излучаются две волны, одна из которых с большей частотой распространяется перед объектом, а другая с меньшей частотой – позади (к этой ситуации относится и случай $\tilde {\Omega } > 1$, $\tilde {V} < {{\tilde {V}}_{{*2}}}$). При превышении второй критической скорости собственное поле отсутствует, но зато возбуждаются по две волны впереди и позади объекта. Направления распространения этих волн аналогичны [58].

Проведем расчет критических скоростей по формулам (2.9) и (2.10) в случае рельсовой направляющей ракетного трека [21] с параметрами: изгибная жесткость EI = 1.16 МНм2, погонная плотность $\rho F$ = 65 кг/м, жесткость упругого основания ${{h}_{1}} = 200$ МНм2, значение частоты воздействия на рельсовую направляющую Ω = 620 1/с. Положим ${{\beta }^{2}} \approx 3.28$, исходя из того, что для большинства грунтов отношение коэффициентов сдвига и сжатия меньше единицы [29]. В результате из (2.9) и (2.10) соответственно будем иметь

$V_{{*1}}^{{}} = 920\;{\text{м/с}},\quad V_{{*2}}^{{}} = 1258\;{\text{м/с}},\quad V_{1}^{*} = 505~\;{\text{м/с}},\quad V_{2}^{*} = 846\;{\text{м/с}}$

Наличие второго коэффициента в основании приводит к увеличению значений критических скоростей, которые сопоставимы с экспериментальными данными. Так, например, на ракетном треке ВНИИЭФ при скоростях разгона 1160–1450 м/с взаимодействие ступени ракетного поезда с направляющей в некоторых случаях приводило к появлению волнообразных остаточных деформаций и, в конечном итоге, разрушению рельсовой направляющей.

На основе решения задачи кинематики, колебания балки под действием равномерно движущейся нагрузки представимо в форме

(2.11)
$u\left( {x,t} \right) = \left\{ {\begin{array}{*{20}{c}} {{{u}_{1}}\left( {x,t} \right) = {{A}_{1}}{{e}^{{i\left( {{{\omega }_{1}}t - {{k}_{1}}x} \right)}}} + {{A}_{2}}{{e}^{{i\left( {{{\omega }_{2}}t - {{k}_{2}}x} \right)}}}\quad {\text{при}}\quad x \leqslant Vt} \\ {{{u}_{2}}\left( {x,t} \right) = {{A}_{3}}{{e}^{{i\left( {{{\omega }_{3}}t - {{k}_{3}}x} \right)}}} + {{A}_{4}}{{e}^{{i\left( {{{\omega }_{4}}t - {{k}_{4}}x} \right)}}}\quad {\text{при}}\quad x > Vt} \end{array}} \right.$

Комплексные амплитуды ${{A}_{j}}$ ($j = \overline {1,4} $) определяются из системы алгебраических уравнений, получающихся после подстановки (2.11) в (2.1)–(2.4), и имеют вид

${{A}_{1}} = {{\left[ { - {{k}_{{32}}}{{k}_{{42}}}IE + i{{I}_{0}}{{\Omega }^{2}}{{k}_{2}}} \right]{{P}_{0}}} \mathord{\left/ {\vphantom {{\left[ { - {{k}_{{32}}}{{k}_{{42}}}IE + i{{I}_{0}}{{\Omega }^{2}}{{k}_{2}}} \right]{{P}_{0}}} {{{k}_{{12}}}\Delta }}} \right. \kern-0em} {{{k}_{{12}}}\Delta }},\quad {{A}_{2}} = {{\left[ {{{k}_{{31}}}{{k}_{{41}}}IE - i{{I}_{0}}{{\Omega }^{2}}{{k}_{1}}} \right]{{P}_{0}}} \mathord{\left/ {\vphantom {{\left[ {{{k}_{{31}}}{{k}_{{41}}}IE - i{{I}_{0}}{{\Omega }^{2}}{{k}_{1}}} \right]{{P}_{0}}} {{{k}_{{12}}}\Delta }}} \right. \kern-0em} {{{k}_{{12}}}\Delta }}$
${{A}_{3}} = - {{\left[ {{{k}_{{42}}}{{k}_{{41}}}IE + i{{I}_{0}}{{\Omega }^{2}}{{k}_{4}}} \right]{{P}_{0}}} \mathord{\left/ {\vphantom {{\left[ {{{k}_{{42}}}{{k}_{{41}}}IE + i{{I}_{0}}{{\Omega }^{2}}{{k}_{4}}} \right]{{P}_{0}}} {{{k}_{{43}}}\Delta }}} \right. \kern-0em} {{{k}_{{43}}}\Delta }},\quad {{A}_{4}} = {{\left[ {{{k}_{{31}}}{{k}_{{32}}}IE + i{{I}_{0}}{{\Omega }^{2}}{{k}_{3}}} \right]{{P}_{0}}} \mathord{\left/ {\vphantom {{\left[ {{{k}_{{31}}}{{k}_{{32}}}IE + i{{I}_{0}}{{\Omega }^{2}}{{k}_{3}}} \right]{{P}_{0}}} {{{k}_{{43}}}\Delta }}} \right. \kern-0em} {{{k}_{{43}}}\Delta }}$
$\begin{gathered} \Delta = \left[ {{{k}_{{32}}}{{k}_{{42}}}{{k}_{{31}}}{{k}_{{41}}}{{I}^{2}}{{E}^{2}} + {{I}_{0}}m{{\Omega }^{4}}} \right]i + \\ + \;\left( {{{k}_{{31}}} + {{k}_{{42}}}} \right)IEm{{\Omega }^{2}} + \left[ {{{k}_{1}}{{k}_{2}}\left( {{{k}_{1}} + {{k}_{2}}} \right) - {{k}_{3}}{{k}_{4}}\left( {{{k}_{3}} + {{k}_{4}}} \right)} \right]IE{{I}_{0}}{{\Omega }^{2}}, \\ \end{gathered} $
где ${{P}_{0}}$ – амплитуда источника колебаний, ${{k}_{{nm}}} = {{k}_{n}} - {{k}_{m}}$.

При движении по направляющей тяжелой массы ($P = - mg$, ${{I}_{0}} = 0$) существует только одна критическая скорость, при переходе через которую возбуждаются бегущие волны. Выражение для нее находится из (2.9) в явном виде ${{V}_{{\text{*}}}} = \sqrt {2\alpha {{\omega }_{0}} + c_{{II}}^{2}} $. Следует отметить, что такое выражение для критической скорости, по-видимому, впервые было получено другим способом в работе [35]. Эта скорость совпадает с минимальной фазовой скоростью распространения волн для данной модели (рис. 2) и превышает аналогичную для балки модели Бернулли–Эйлера на винклеровском основании [7, 58].

Рис. 2.

Зависимости фазовой и групповой скоростей от волнового числа.

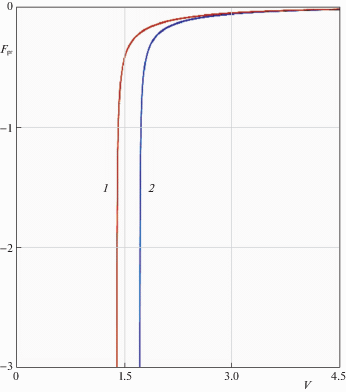
На рис. 2 представлены в безразмерном виде (${{{\tilde {v}}}_{{\operatorname{ph} }}}$ = ${{{{{v}}_{{\operatorname{ph} }}}} \mathord{\left/ {\vphantom {{{{{v}}_{{\operatorname{ph} }}}} {\sqrt {\alpha {{\omega }_{0}}} }}} \right. \kern-0em} {\sqrt {\alpha {{\omega }_{0}}} }}$, ${{{\tilde {v}}}_{{\operatorname{gr} }}}$ = ${{{{{v}}_{{\operatorname{gr} }}}} \mathord{\left/ {\vphantom {{{{{v}}_{{\operatorname{gr} }}}} {\sqrt {\alpha {{\omega }_{0}}} }}} \right. \kern-0em} {\sqrt {\alpha {{\omega }_{0}}} }}$, $\tilde {k} = k\sqrt {{\alpha \mathord{\left/ {\vphantom {\alpha {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}} $, ${{\beta }^{2}} = {{c_{{II}}^{2}} \mathord{\left/ {\vphantom {{c_{{II}}^{2}} {\left( {\alpha {{\omega }_{0}}} \right)}}} \right. \kern-0em} {\left( {\alpha {{\omega }_{0}}} \right)}}$) зависимости фазовой (${{{v}}_{{\operatorname{ph} }}} = {\omega \mathord{\left/ {\vphantom {\omega k}} \right. \kern-0em} k}$) и групповой скоростей (${{{v}}_{{\operatorname{gr} }}}$ = ${{d\omega } \mathord{\left/ {\vphantom {{d\omega } {dk}}} \right. \kern-0em} {dk}}$) от волнового числа k для различных параметров $\beta $ ($\beta $ = 0.1; 2; 10). При длине волны $2\pi \sqrt {\alpha {\text{/}}{{\omega }_{0}}} $ фазовая скорость по величине совпадает с групповой и достигает своего минимального значения равного $\sqrt {2\alpha {{\omega }_{0}} + c_{{II}}^{2}} $. Видно (рис. 2), что в диапазоне от 0 до 1 для безразмерных волновых чисел (от 0 до $\sqrt {\alpha {\text{/}}{{\omega }_{0}}} $ – в размерных переменных), значения фазовых скоростей волн превосходят значения их групповых скоростей, следовательно дисперсия является нормальной. Аномальная дисперсия наблюдается при превышении этого диапазона ($\tilde {k} > 1$). Если $c_{{II}}^{{}} = \sqrt {2\alpha {{\omega }_{0}}} $, то зависимость групповой скорости от волнового числа линейна (рис. 2б) как для балки модели Бернулли–Эйлера без учета упругого основания [59].

Учитывая, что на бесконечности прогибы балки ограничены, а бегущие волны отводят энергию от объекта, т.е.

$\left\{ {\begin{array}{*{20}{l}} {\operatorname{Im} k > 0} \\ {{{V}_{{\operatorname{gr} }}} < V} \end{array}} \right.\quad {\text{при}}\quad x < Vt,\quad \left\{ {\begin{array}{*{20}{l}} {\operatorname{Im} k < 0} \\ {{{V}_{{\operatorname{gr} }}} > V} \end{array}} \right.\quad {\text{при}}\quad x > Vt$
(${{V}_{{\operatorname{gr} }}} = {{d\omega } \mathord{\left/ {\vphantom {{d\omega } {dk}}} \right. \kern-0em} {dk}}$ – групповая скорость волн) из (2.7), (2.8) находим, что при $V < {{V}_{*}}$ слева от нагрузки ($x < Vt$)
${{k}_{{1,2}}} = \frac{1}{{2\alpha }}\left( { \pm \sqrt {2\alpha {{\omega }_{0}} - c_{{II}}^{2} + {{V}^{2}}} + i\sqrt {2\alpha {{\omega }_{0}} + c_{{II}}^{2} - {{V}^{2}}} } \right),$
а справа при $x > Vt$

(2.12)
${{k}_{{3,4}}} = \frac{1}{{2\alpha }}\left( { \pm \sqrt {2\alpha {{\omega }_{0}} - c_{{II}}^{2} + {{V}^{2}}} - i\sqrt {2\alpha {{\omega }_{0}} + c_{{II}}^{2} - {{V}^{2}}} } \right),\quad {{\omega }_{{1 - 4}}} = {{k}_{{1 - 4}}}V$

Следовательно, у неподвижной нагрузки или движущейся со скоростью, меньше критической, поле поперечных смещений локализовано около источника и представляет собой суперпозицию спадающих по экспоненте осцилляций. Полученные решения справедливы при $c_{{II}}^{2} < 2\alpha {{\omega }_{0}}$, что имеет место в большинстве практических случаев, а также при $V > \sqrt {c_{{II}}^{2} - 2\alpha {{\omega }_{0}}} $, если $c_{{II}}^{2} > 2\alpha {{\omega }_{0}}$. Заметим, что при движении нагрузки со скоростью $V < \sqrt {c_{{II}}^{2} - 2\alpha {{\omega }_{0}}} $, когда $c_{{II}}^{2} \geqslant 2\alpha {{\omega }_{0}}$ волновые числа будут чисто мнимыми. В этом случае осциллирующая часть отсутствует. Профиль прогиба под нагрузкой симметричен и экспоненциально спадает по мере удаления от нее.

Источник нулевой частоты, движущийся со скоростью $V > {{V}_{*}}$, собственного поля не создает, но зато излучает четыре волны, две из которых бегут впереди движущейся нагрузки, а две другие – ей вослед, отводя от нее энергию. Волновые числа и частоты волн определяются формулами

(2.13)
$\begin{gathered} {{k}_{{1,2}}} = \pm \tfrac{1}{{\sqrt 2 \alpha }}{{\left( {{{V}^{2}} - c_{{II}}^{2} - \sqrt {{{{\left( {{{V}^{2}} - c_{{II}}^{2}} \right)}}^{2}} - 4{{\alpha }^{2}}\omega _{0}^{2}} } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \\ {{k}_{{3,4}}} = \pm \tfrac{1}{{\sqrt 2 \alpha }}{{\left( {{{V}^{2}} - c_{{II}}^{2} + \sqrt {{{{\left( {{{V}^{2}} - c_{{II}}^{2}} \right)}}^{2}} - 4{{\alpha }^{2}}\omega _{0}^{2}} } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \\ {{\omega }_{{1 - 4}}} = {{k}_{{1 - 4}}}V \\ \end{gathered} $

Таким образом, зная конкретный вид частот и волновых чисел излучаемых волн, имеем решение (2.11) в параметрах задачи для каждого качественно-различного кинематического случая (2.12), (2.13):

при $V < {{V}_{*}}$

${{u}_{{1,2}}}\left( {x,t} \right) = - A{{e}^{{ \pm b\left( {x - Vt} \right)}}}\cos \left( { \mp \sqrt {2\alpha \omega _{0}^{{}} - c_{{II}}^{2} + {{V}^{2}}} {{{\left( {2\alpha } \right)}}^{{ - 1}}}\left( {x - Vt} \right) - \varphi } \right)$
$A = \frac{{\sqrt \alpha mg}}{{\rho F\sqrt {4{{\alpha }^{2}}\omega _{0}^{3} - {{\omega }_{0}}{{{\left( {{{V}^{2}} - c_{{II}}^{2}} \right)}}^{2}}} }},\quad b = \sqrt {2\alpha \omega _{0}^{{}} + c_{{II}}^{2} - {{V}^{2}}} {{\left( {2\alpha } \right)}^{{ - 1}}}$
$\varphi = 2\operatorname{arctg} \left( {\frac{{2\sqrt {\alpha {{\omega }_{0}}} - \sqrt {2\alpha {{\omega }_{0}} - c_{{II}}^{2} + {{V}^{2}}} }}{{\sqrt {2\alpha {{\omega }_{0}} + c_{{II}}^{2} - {{V}^{2}}} }}} \right)$

и при $V > {{V}_{*}}$

${{u}_{{1,2}}}\left( {x,t} \right) = \frac{{mg{{b}_{{2,1}}}\sin \left( {{{{{b}_{{1,2}}}\left( {x - Vt} \right)} \mathord{\left/ {\vphantom {{{{b}_{{1,2}}}\left( {x - Vt} \right)} \alpha }} \right. \kern-0em} \alpha }} \right)}}{{\rho F{{\omega }_{0}}\sqrt {{{{\left( {{{V}^{2}} - c_{{II}}^{2}} \right)}}^{2}} - 4{{\alpha }^{2}}\omega _{0}^{2}} }}$
${{b}_{{1,2}}} = \frac{1}{{\sqrt 2 }}\sqrt {{{V}^{2}} - c_{{II}}^{2} \mp \sqrt {{{{\left( {{{V}^{2}} - c_{{II}}^{2}} \right)}}^{2}} - 4{{\alpha }^{2}}\omega _{0}^{2}} } $

Амплитуды волн неограниченно возрастают при критической скорости движения нагрузки $V = {{V}_{*}}$, т.е. резонансные условия совпадают с условиями кратности корней задачи кинематики. На рис. 3 представлены графики поперечного смещения срединной линии балки в системе координат, связанной с движущейся нагрузкой $\xi $ = = $\left( {x - Vt} \right)\sqrt {{{{{\omega }_{0}}} \mathord{\left/ {\vphantom {{{{\omega }_{0}}} \alpha }} \right. \kern-0em} \alpha }} $ для различных безразмерных значений $\tilde {V}$ и $\beta $.

Рис. 3.

Изменение прогиба направляющей в системе координат, связанной с движущейся нагрузкой а) при докритических скоростях $\tilde {V} < {{\tilde {V}}_{*}}$ 1) $\beta = 0$, $\tilde {V} = 0$, 2) $\beta = 0$, $\tilde {V} \ne 0$, 3) $\beta \ne 0$, $\tilde {V} = 0$, 4) $\beta \ne 0$, $\tilde {V} \ne 0$, б) при закритических скоростях $\tilde {V} > {{\tilde {V}}_{*}}$, 1) $\beta = 0$, 2) $\beta \ne 0$ с учетом и в пренебрежении безразмерным коэффициентом сдвига упругого основания.

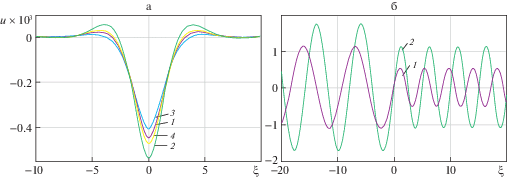
Расчеты проводились при ${{\beta }^{2}} = 0;0.4$; ${{\tilde {V}}^{2}} = 0;0.6;2.6$ и тех же параметрах направляющей ракетного трека, которые использовались выше и в работе [21]. Увеличение скорости приводит к более медленному затуханию прогибов с удалением от точки приложения движущегося источника, чем от статической нагрузки (рис. 3а). Коэффициент затухания нераспространяющейся волны для направляющей, лежащей на обобщенном упругом основании, превосходит аналогичный для балки на винклеровском основании, уменьшаясь с возрастанием скорости. При закритических скоростях движения прогиб в точке приложения силы равен нулю (рис. 3б) для обеих моделей. Источник, движущийся по балке на основании Пастернака, излучает бегущие волны с большими амплитудами, чем по балке на винклеровском основании (рис. 3б).

На основе общего решения задачи получим следующее выражение для давления волн (силы сопротивления движению [60, 61])

${{F}_{{{\text{pr}}}}} = \left\{ \begin{gathered} 0,\quad V < {{V}_{*}}, \hfill \\ - \frac{{{{{\left( {mg} \right)}}^{2}}}}{{2\rho F\sqrt {{{{\left( {{{V}^{2}} - c_{{II}}^{2}} \right)}}^{2}} - 4{{\alpha }^{2}}\omega _{0}^{2}} }},\quad V > {{V}_{*}} \hfill \\ \end{gathered} \right.$

Поскольку собственное поле не оказывает давление на нагрузку, то для $V < {{V}_{*}}$ имеем ${{F}_{{\operatorname{pr} }}} \equiv 0$ (рис. 4). Случай $V = {{V}_{*}}$ является “резонансным” значением скорости, сопровождающейся неограниченным ростом ${{F}_{{{\text{pr}}}}}$. На рис. 4 первая кривая построена для балки на винклеровском основании, вторая – на основании модели Пастернака. Начиная со скорости $V = {{V}_{{\text{*}}}}$ (как было сказано выше), в системе происходит излучение волн по две слева и справа от нагрузки, бегущих в +x направлении, подобно эффекту Вавилова–Черенкова [62], оказывая давление на нагрузку. Видно, что при $V > {{V}_{*}}$ сила давления волн ${{F}_{{{\text{pr}}}}}$ всегда направлена против движения (тормозящая).

Рис. 4.

Среднее значение силы давления волн в зависимости от скорости движения объекта.

Заключение. При малых скоростях движения объекта (рис. 3а) использование винклеровой модели упругого основания дает завышенное значение поперечного смещения направляющей под нагрузкой по сравнению с моделью Пастернака, а при закритических скоростях (рис. 3б) – заниженные динамические характеристики бегущих волн и силы давления волн в движущемся контакте (рис. 4). Если движение нагрузки происходит со скоростью $\sqrt {2\alpha {{\omega }_{0}}} $ < V < $\sqrt {2\alpha {{\omega }_{0}} + c_{{II}}^{2}} $, то в первом случае (винклерово основание) колебания направляющей носят волновой характер, в то время как при использовании основания с двумя коэффициентами постели, бегущие волны еще не излучаются. Расчет критических скоростей по формуле (2.9) показал сопоставимость с экспериментальными данными, полученными на ракетном треке ВНИИЭФ при высоких скоростях разгона.

Следует также отметить, что полученный вывод о безграничном возрастании амплитуд волн и силы сопротивления являются следствием пренебрежения затуханием. В действительности, если учесть, например, диссипативные потери в основании балки, то это приведет к ограничению резонансных максимумов, асимметрии прогиба направляющей впереди и позади от движущейся нагрузки и к наличию сопротивления движению при докритических скоростях [12, 58, 60] даже в отсутствие трения.

Ясно, что принятая в работе идеализация не учитывает многие особенности, присущие реальным техническим системам, так, например, в случае железнодорожного пути, это рельсовые скрепления и т.п., но удобна и чаще всего используется для решения инженерных задач, а, кроме того, позволяет получить точное решение рассматриваемой задачи.

Рассмотренная задача дополняет цикл исследований проблем волновой динамики и устойчивости движения высокоскоростных объектов по рельсовым направляющим ракетного трека [20–24]. Полученные результаты могут служить методическим и расчетным сопровождением при постановке экспериментов по высокоскоростному разгону полезной нагрузки.

Работа выполнена при поддержке Российского научного фонда (грант № 20-19-00613).

Список литературы

  1. Филиппов А.П. Колебания деформируемых систем. М.: Машиностроение, 1970. 734 с.

  2. Fryba L. Vibration of Solids and Structures under Moving Loads. Prague: Academia, 1972. 484 p.

  3. Филиппов А.П., Кохманюк С.С., Воробьев Ю.С. Воздействие динамических нагрузок на элементы конструкций. Киев: Наук. думка, 1974. 176 с.

  4. Кохманюк С.С., Янютин В.Г., Романенко Л.Г. Колебания деформируемых систем при импульсных и подвижных нагрузках. Киев: Наук. думка, 1980. 232 с.

  5. Бондарь Н.Г., Козьмин Ю.Г., Ройтбурд З.Г., Тарасенко В.П., Яковлев Г.Н. Взаимодействие железнодорожных мостов с подвижным составом. М.: Транспорт, 1984. 272 с.

  6. Вериго М.Ф., Коган А.Я. Взаимодействие пути и подвижного состава. М.: Транспорт, 1987. 560 с.

  7. Весницкий А.И. Волны в системах с движущимися границами и нагрузками. М.: Физматлит, 2001. 320 с.

  8. Veritchev S.N. Instability of a Vehicle Moving on an Elastic Structure. 2002. 190 p.

  9. Vostrukhov A.V. Three-Dimensional Dynamic Models of a Rail-Way Track for High-Speed Trains. Delft: Univ. Press, 2002. 184 p.

  10. Козин В.М., Жесткая В.Д., Погорелова А.В., Чижиумов С.Д., Джабраилов М.Р., Морозов В.С., Кустов А.Н. Прикладные задачи динамики ледяного покрова. М.: Изд-во Академии естествознания. 2008. https://www.monographies.ru/ru/book/view?id=14

  11. Иванченко И.И. Динамика транспортных сооружений: высокоскоростные подвижные, сейсмические и ударные нагрузки. М.: Наука, 2011. 574 с.

  12. Метрикин А.В., Веричев С.Н., Вострухов А.В. Фундаментальные задачи высокоскоростного наземного транспорта. Saarbrucken: Lambert Acad. Publ., 2015. 200 с.

  13. Оконечников А.С., Тарлаковский Д.В., Федотенков Г.В. Нестационарное движение нормальной сосредоточенной нагрузки вдоль границы упругой полуплоскости // Тр. МАИ. 2015. № 82. 20 с. www.mai.ru/science/trudy

  14. Савин А.В. Выбор конструкции пути для высокоскоростного движения // Транспорт РФ. 2017. № 1 (68). С. 18–21.

  15. Абдурашитов А.Ю., Локтев А.А., Сычева А.В., Сычев П.В. Расчет высокочастотных вибраций железнодорожного пути под подвижным составом при скоростях 200–250 км/ч // Вестн. трансп. Поволжья. 2018. № 6 (72). С. 22–28.

  16. Абдурашитов Ю.А., Сычев В.П., Абдурашитов А.Ю. Оценка влияния воздействия подвижного состава с различной нагрузкой на ось на железнодорожный путь с различной толщиной балластного слоя и элементами верхнего строения пути на основе моделирования // Внедр. совр. констр. и перед. технол. в путевое хоз-во. 2018. Т. 12. № 12 (12). С. 58–64.

  17. Абдурашитов А.Ю., Кузнецов С.В. О выборе профиля рельсов для кривых участков пути // Внедр. совр. констр. и перед. технол. в путевое хоз-во. 2020. Т. 16. № 16 (16). С. 20–25.

  18. Savin A., Suslov O., Korolev V., Loktev A., Shishkina I. Stability of the continuous welded rail on transition sections // Adv. in Intell. Syst.&Comput. 2020. V. 1115. AISC. P. 648–654

  19. Winkler E. Die Lehre von der Elastizität und Festigkeit. Prague, 1867.

  20. Бутова С.В., Герасимов С.И., Ерофеев В.И., Камчатный В.Г. Устойчивость движения высокоскоростных объектов по направляющим ракетного трека // Пробл. машиностр. и надежн. машин. 2015. № 1. С. 3–8.

  21. Герасимов С.И., Ерофеев В.И. Расчет изгибно-крутильных колебаний рельсовой направляющей ракетного трека // Пробл. машиностр. и надежн. машин. 2016. № 3. С. 25–27.

  22. Erofeev V., Lissenkova E., Malkhanov A. Wave resistance to the movement of objects along the rocket track guides // MATEC Web Conf. 2018. V. 224. Article ID 02016. P. 1–6.

  23. Герасимов С.И., Ерофеев В.И., Камчатный В.Г., Одзерихо И.А. Условие на скользящем контакте в анализе устойчивости движения ступени на ракетном треке // Пробл. машиностр. и надежн. машин. 2018. № 3. С. 21–27.

  24. Герасимов С.И., Ерофеев В.И., Одзерихо И.А., Смирнов Д.Ю. Оценка влияния волновых процессов в упругой направляющей на динамику ракетного трека // Вестн. научно-технич. развит. 2019. № 6 (142). С. 3–12.

  25. Zimmerman H. Die Berechnung des Eisenbahnoberbauee. Berlin, 1888.

  26. Wieghardt K. Uber den Ralken auf Nachgibiebiger Unterlage // Zeitschriff fur Angewandte Mathematik und Mechanik. 1922. Bd. 2. H. 3. S. 165–184.

  27. Филоненко-Бородич М.М. Простейшая модель упругого основания, способная распределять нагрузку // Тр. Моск. электромех. ин-та инж. трансп. 1945. № 53. С. 92–108.

  28. von Karman T. Festigkeitsproblem im maschinenbau // Encyk. D. Math. Wiss. IV. 1910. P. 311–385.

  29. Пастернак П.Л. Основы нового метода расчета фундаментов на упругом основании при помощи двух коэффициентов постели. М.: Госстройиздат, 1954. 56 с.

  30. Леонтьев Н.Н., Леонтьев А.Н., Анохин Н.Н., Соболев Д.Н. Основы теории балок и плит на деформируемом основании. М.: МИСИ, 1982. 120 с.

  31. Власов В.З., Леонтьев Н.Н. Техническая теория расчета фундаментов на упругом основании // Тр. МИСИ. 1956. Вып. 14 (154). С. 12–31.

  32. Власов В.З., Леонтьев Н.Н. Балки, плиты, оболочки на упругом основании. М.: Гос. изд. физ.-мат. лит., 1960. 492 с.

  33. Reissner E. Selected Works in Applied Mechanics and Mathematics. Sudbury (MA): Jones&Bartlett Pub., 1996.

  34. Hetenyi M. Beams on Elastic Foundations. Michigan: Univ. Press, 1946. 255 p.

  35. Дуплякин И.А. Движение экипажа с постоянной скоростью по балке бесконечной длины, лежащей на основании с двумя упругими характеристиками // ПММ. 1991. Т. 55. № 3. С. 461–471.

  36. Александров В.М., Дуплякин И.А. Динамика бесконечной балки Тимошенко, лежащей на основании с двумя упругими характеристиками, при движении деформируемого экипажа // Изв. РАН. МТТ. 1996. № 1. С. 180–197.

  37. Сливкер В.И. К вопросу о назначении характеристик двухпараметрового упругого основания // Строит. мех. и расчет сооруж. 1981. № 1. С. 36–39.

  38. Eisenberger M., Clastornik J. Beams on variable two-parameter elastic foundation // Comput.&Struct. 1986. V. 23. P. 351–356.

  39. Куреннов С.С. Модель двухпараметрического упругого основания в расчете напряженного состояния клеевого соединения // Электрон. ж. Труды МАИ. 2013. № 66. 7 c. http://www.mai.ru/science/trudy/

  40. Рао Ч.К., Рао Л.Б. Закритическое поведение тонкостенной свободно опертой балки с открытым профилем поперечного сечения, покоящейся на двухпараметрическом упругом основании, при ее кручении // ПМТФ. 2018. Т. 59. № 1 (347). С. 204–213.

  41. Wang T.M., Stephens J.E. Natural frequencies of Timoshenko beams on Pasternak foundations // J. Sound&Vibr. 1977. V. 51. № 2. P. 149–155.

  42. Wang T.M., Gagnon L.W. Vibrations of continuous Timoshenko beams on Winkler-Pasternak foundations // J. Sound&Vibr. 1978. V. 59. № 2. P. 211–220.

  43. Козел А.Г. Перемещения в круговой трехслойной пластине на двухпараметрическом основании // Механика. Исслед. и иннов. 2017. Вып. 10. С. 90–95.

  44. Козел А.Г., Старовойтов Э.И. Изгиб упругой трехслойной круговой пластины на основании Пастернака // Механика композ. матер. и констр. 2018. Т. 24. № 3. С. 392–406.

  45. Feng Q., Fu Sh., Wang Ch., Liu W.W. Analytical solution for fracture problem of slope roof based on Pasternak foundation model // Soil Mech.& Found. Engng. 2019. V. 56. № 2. P. 142–150.

  46. Проктор Г.Э. Заметка к вопросу о расчете балок, лежащих на упругом основании // Изв. Иваново-Вознес. Политехн. ин-та. 1923. Т. 7. С. 34–89.

  47. Проктор Г.Э. Механика изменяемого твердого тела (Сопротивление материалов). Иваново-Вознесенск: Студенч. изд-во Губбюро Пролетстуда, 1926. 476 с.

  48. Проктор Г.Э. Дополнительные главы по сопротивлению материалов. М.: МЭИ, 1936. 30 с.

  49. Горбунов-Посадов М.И. Расчет балок и плит на упругом полупространстве // ПММ. 1940. Т. 4. № 3. С. 61–80.

  50. Шехтер О.Я. О влиянии мощности слоя на распределение напряжений в фундаментной балке // Сб. тр. НИС треста глубин. работ. 1939. № 10. С. 15–25.

  51. Давыдов С.С. Расчет и проектирование подземных конструкций. М.: Стройиздат, 1960. 376 с.

  52. Егоров К.Е. К расчету деформаций оснований. Сб. статей. М.: ВНИИНТПИ, 1984. 400 с.

  53. Горбунов-Посадов М.И., Маликова Т.А., Соломин В.И. Расчет конструкций на упругом основании. М.: Стройиздат, 1984. 679 с.

  54. Высоковский Д.А., Русакова Е.Б. Устойчивость плиты Э. Рейсснера на упругом невинклеровском основании // Инж. вестн. Дона. 2017. № 2 (45). 10 с. http://ivdon.ru/ru/magazine/archive/n2y2017/4250

  55. Васильков Г.В., Рапопорт Г.А., Шпитюк Е.Н. Квазидвухмерные расчетные схемы при конечноэлементной реализации модели упругого сжимаемого слоя // Изв. вузов. Строительство. 1999. № 6. С. 21–25.

  56. Рапопорт Г.А. К расчету зданий и сооружений по комплексным расчетным схемам. Решение задачи В.З. Власова об упругом сжимаемом слое методом Л.В. Канторовича // В сб.: Коммунальное хозяйство городов. Киев: Техника, 2004. Вып. 55. С. 281–290.

  57. Вибрации в технике. Т. 1. Колебания линейных систем / Под ред. В.В. Болотина. М.: Машиностроение, 1999. 504 с.

  58. Весницкий А.И. Избранные труды по механике. Н. Новгород: ИД “Наш дом”, 2010. 248 с.

  59. Ерофеев В.И., Лисенкова Е.Е. Общие соотношения для волн в одномерных упругих системах // ПММ. 2013. Т. 77. № 2. С. 315–321.

  60. Быченков В.А., Крысов С.В., Холуев В.В. Волновое сопротивление движению нагрузок вдоль деформируемых систем // Машиноведение. 1988. № 3. С. 60–66.

  61. Андрианов В.Л. О сопротивлении движению нагрузок вдоль упругих направляющих, вызываемом излучением в них волн // ПММ. 1993. Т. 57. № 2. С. 156–160.

  62. Болотовский Б.М., Гинзбург В.Л. Эффект Вавилова–Черенкова и эффект Доплера при движении источников со скоростью больше скорости света в вакууме // УФН. 1972. Т. 106. № 4. С. 577–592.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал