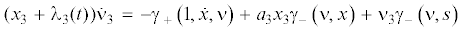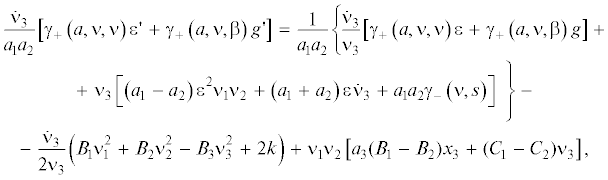1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 85, № 2, 2021

Прикладная математика и механика, 2021, T. 85, № 2, стр. 139-151

О решениях уравнений движения гиростата с переменным гиростатическим моментом

Г. В. Горр 1, *, Т. В. Белоконь 2, **

1 Институт прикладной математики и механики
Донецк, Украина

2 Донецкий национальный университет экономики и торговли им. М. Туган-Барановского
Донецк, Украина

* E-mail: gvgorr@gmail.com
** E-mail: B.Tatyana13@mail.ru

Поступила в редакцию 22.06.2020
После доработки 12.10.2020
Принята к публикации 20.10.2020

Полный текст (PDF)

Аннотация

Рассмотрена задача о движении гиростата с переменным гиростатическим моментом под действием потенциальных и гироскопических сил. Получено три новых решения уравнений движения, которые определяются тремя линейными инвариантными соотношениями (ИС) на компоненты вектора угловой скорости. Для случая тяжелого гиростата найдено решение, которое характеризуется обобщенными условиями класса Ковалевской и Горячева–Чаплыгина. Два следующих решения имеют место для уравнений класса Кирхгофа–Пуассона. Одно из них существует в случае динамически симметричных гиростатов, а в другом решении распределение масс произвольно.

Ключевые слова: гиростатический момент, инвариантные соотношения, потенциальные и гироскопические силы, обобщенные условия Ковалевской, Горячева–Чаплыгина

Введение. Задача о движении гиростата, имеющего неподвижную точку, является обобщением классической задачи, которая описывается уравнениями Эйлера–Пуассона. Постановка задачи о движении гиростата и первые результаты получены [1–4] и др. В динамике гиростата применяются различные определения и типы гиростатов, что связано с рассмотрением различных постановок. Первая постановка состоит в том, что изучается система твердых тел $S$, состоящая из тела-носителя $S_{0}^{{}}$ и несомых роторов $S_{1}^{{}},\; \ldots ,\;S_{n}^{{}}$, вращающихся вокруг своих осей симметрии. В частности, в этой постановке рассматриваются гиростаты [1]. В монографии [5] дается полное определение гиростата со ссылкой на статью [4]. Основное предположение в данном определении состоит в том, что распределение масс системы $S$ не изменяется с течением времени. Кроме этого, при изучении движения гиростатов [1] полагается, что они имеют постоянные относительные компоненты суммарного кинетического момента, вычисленные по отношению к телу-носителю. Рассматривается [6, 7] движение гиростата, которое является статически и динамически уравновешенным [6], или характеризуется свойством динамической симметрии роторов, вращающихся вокруг своих барицентрических осей [7]. Если гиростатический момент гиростата постоянен, то, например, уравнения движения тяжелого гиростата имеют три первых интеграла.

Вторая постановка задачи о движении гиростата (гиростаты Жуковского–Вольтерра) характеризуется тем, что в ней рассматриваются системы, образованные телом-носителем с внутренними полостями с циркулирующей в них жидкостью.

С прикладной точки зрения важным свойством движения гиростата служит учет переменности гиростатического момента [7, 8]. Данное обстоятельство учитывается при исследовании спутников-гиростатов [9–11]. Особое значение имеет математическое моделирование движения гиростата с неподвижной точкой под действием потенциальных и гироскопических сил, так как оно позволяет установить базовые свойства динамики гиростата с переменным гиростатическим моментом. В этом направлении опубликовано много исследований, среди которых отметим статьи [11, 12], а также монографию [13], в которой дан обзор результатов, полученных в динамике неавтономного гиростата. В последней монографии основное внимание уделено анализу результатов по исследованию прецессионных движений гиростата. Данная статья посвящена интегрированию уравнений движения гиростата с переменным гиростатическим моментом под действием потенциальных и гироскопических сил.

Для исследования условий существования решений уравнений движения гиростата применен метод инвариантных соотношений (ИС). Этот метод разработан в [5, 14] и обобщен в статье [15]. Метод ИС использован [16, 17] применительно к другим задачам динамики. Данный подход связан с тем, что в общем случае уравнения динамики твердого тела и гиростата неинтегрируемы в квадратурах по Якоби [18, 19]. В данной статье рассмотрена задача о движении гиростата под действием потенциальных и гироскопических сил на заданных ИС уравнений движения. Построены три новых решения в динамике неавтономного гиростата. Для случая тяжелого гиростата условия существования характеризуются следующими условиями на распределение масс гиростата: гиростат динамически симметричен, центр масс лежит в экваториальной плоскости (обобщенные условия Ковалевской и Горячева–Чаплыгина). Два следующих решения имеют место в задаче о движении гиростата под действием потенциальных и гироскопических сил; одно из них выполняется для тех же классов гиростатов, а другое соответствует случаю произвольного распределения масс гиростата.

1. Постановка задачи. Многие задачи динамики твердого тела и гиростата описываются системой дифференциальных уравнений, которая содержит уравнения Пуассона [20–25]

(1.1)
${\mathbf{\dot {\nu }}} = {\mathbf{\nu }} \times {\mathbf{\omega }},$
где ${\mathbf{\nu }} = ({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}})$ – вектор, характеризующий направление оси симметрии силового поля; ${\mathbf{\omega }} = ({{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}})$ – вектор угловой скорости тела-носителя гиростата; точка над переменной ${\mathbf{\nu }}$ обозначает относительную производную по времени $t$.

Был изучен [25] важный класс инвариантных соотношений (ИС), которые имеют вид [25, 26]

(1.2)
${{\omega }_{1}} = {{\nu }_{1}}\varepsilon + {{\beta }_{1}}g,\quad {{\omega }_{2}} = {{\nu }_{2}}\varepsilon + {{\beta }_{2}}g,\quad {{\omega }_{3}} = h,$
где ${{\beta }_{1}}$, ${{\beta }_{2}}$ – постоянные параметры, $\varepsilon = \varepsilon ({{\nu }_{3}})$, $g = g({{\nu }_{3}})$, $h = h({{\nu }_{3}})$ – дифференцируемые функции переменной ${{\nu }_{3}}$. Особенность ИС (1.2) состоит в том, что уравнение (1.1), которое в скалярной форме приводится к системе уравнений [25]
(1.3)
${{\dot {\nu }}_{1}} = {{\nu }_{2}}(h - {{\nu }_{3}}\varepsilon ) - {{\beta }_{2}}{{\nu }_{3}}g,\quad {{\dot {\nu }}_{2}} = {{\nu }_{1}}({{\nu }_{3}}\varepsilon - h) + {{\beta }_{1}}{{\nu }_{3}}g,\quad {{\dot {\nu }}_{3}} = ({{\beta }_{2}}{{\nu }_{1}} - {{\beta }_{1}}{{\nu }_{2}})g,$
допускает интегральное представление
(1.4)
${{\beta }_{1}}{{\nu }_{1}} + {{\beta }_{2}}{{\nu }_{2}} + \int {\frac{{[h - {{\nu }_{3}}\varepsilon ]d{{\nu }_{3}}}}{g} = {{c}_{0}}} ,$
где ${{c}_{0}}$ – произвольная постоянная. Наличие соотношения (1.4) позволило построить новые классы решений уравнений движения твердого тела, имеющего неподвижную точку, в потенциальном силовом поле [25, 26], которые изучены в [27]. Но в задаче о движении гиростата с переменным гиростатическим моментом ИС (1.2) не рассматривались.

Запишем уравнения движения гиростата под действием потенциальных и гироскопических сил [23–25, 28]. В качестве подвижной системы координат $Oxyz$ с единичными векторами ${\mathbf{i}}_{1}^{{}}$, ${\mathbf{i}}_{2}^{{}}$, ${\mathbf{i}}_{3}^{{}}$ выберем главную систему координат тела-носителя:

(1.5)
${\mathbf{\dot {x}}} + {\mathbf{\dot {\lambda }}} = ({\mathbf{x}} + {\mathbf{\lambda }}(t)) \times a{\mathbf{x}} + a{\mathbf{x}} \times B{\mathbf{\nu }} + {\mathbf{s}} \times {\mathbf{\nu }} + {\mathbf{\nu }} \times C{\mathbf{\nu }}$
(1.6)
${\mathbf{\dot {\nu }}} = {\mathbf{\nu }} \times a{\mathbf{x}},$
где $a$ – гирационный тензор: $a = {\text{diag(}}{{a}_{{\text{1}}}}{\text{,}}{{a}_{{\text{2}}}}{\text{,}}{{a}_{{\text{3}}}}{\text{)}}$, $B = {\text{diag(}}{{B}_{{\text{1}}}}{\text{,}}{{B}_{{\text{2}}}}{\text{,}}{{B}_{{\text{3}}}}{\text{)}}$, $C = {\text{diag(}}{{C}_{{\text{1}}}}{\text{,}}{{C}_{{\text{2}}}}{\text{,}}{{C}_{{\text{3}}}}{\text{)}}$; $s = ({{s}_{1}},{{s}_{2}},{{s}_{3}})$ – постоянный вектор. Запишем ИС (1.2) в компонентах вектора ${\mathbf{x}}$. Используя равенства ${{x}_{i}} = {{\omega }_{i}}{\text{/}}{{a}_{i}}$ ($i = \overline {1,3} $), из (1.2) получим [25]

(1.7)
${{x}_{1}} = \frac{1}{{{{a}_{1}}}}\left( {{{\nu }_{1}}\varepsilon + {{\beta }_{1}}g} \right),\quad {{x}_{2}} = \frac{1}{{{{a}_{2}}}}\left( {{{\nu }_{2}}\varepsilon + {{\beta }_{2}}g} \right),\quad {{x}_{3}} = \frac{1}{{{{a}_{3}}}}h$

Будем полагать, что вектор гиростатического момента имеет вид [7]

(1.8)
${\mathbf{\lambda }}(t) = \sum\limits_{i = 1}^3 {{{D}_{i}}(a{\mathbf{x}} \cdot {{{\mathbf{i}}}_{i}} + {{{\dot {\kappa }}}_{i}}){{{\mathbf{i}}}_{i}}} ,$
где ${{D}_{i}}$ – моменты инерции несомых тел ${{S}_{i}}$ относительно главных осей инерции; ${{\dot {\kappa }}_{i}}$ – угловые скорости вращения этих тел вокруг осей ${{l}_{i}}$, направленных по главным осям инерции. Общий момент количества движения гиростата ($S_{0}^{{}}$, $S_{1}^{{}}$, $S_{2}^{{}}$, $S_{3}^{{}}$) выражается по формуле [7]

(1.9)
${\mathbf{x}}* = {\mathbf{x}} + {\mathbf{\lambda }}(t)$

В равенстве (1.9) ${\mathbf{x}} = A{\mathbf{\omega }}$, где $A = a_{{}}^{{ - 1}}$ – тензор инерции, функция ${\mathbf{\lambda }}(t)$ определена равенством (1.8). Если уравнения (1.5), (1.6) проинтегрировать, то необходимо дополнительно рассмотреть уравнения

(1.10)
${{D}_{i}}\dot {p}_{i}^{{}}(t) = L_{i}^{{}}(t)\quad (i = \overline {1,3} ),$
в которых, в силу (1.8), $p_{i}^{{}}(t)$ имеют вид

(1.11)
${{p}_{i}} = a{\mathbf{x}} \cdot {{{\mathbf{i}}}_{i}} + {{\dot {\kappa }}_{i}}$

В уравнениях (1.10) правая часть ${{L}_{i}}(t)$ – проекция на ${{l}_{i}}$ внутренних сил, действующих со стороны тела-носителя на тела ${{S}_{i}}$.

Уравнения (1.5), (1.6) допускают два первых интеграла

(1.12)
${\mathbf{\nu }} \cdot {\mathbf{\nu }} = 1,\quad ({\mathbf{x}} + {\mathbf{\lambda }}(t)) \cdot {\mathbf{\nu }} - \frac{1}{2}(B{\mathbf{\nu }} \cdot {\mathbf{\nu }}) = k,$
где $k$ – произвольная постоянная.

2. Случай тяжелого гиростата. Положим в уравнениях (1.5), (1.12) $B = 0$, $C = 0$, $\lambda _{1}^{{}}(t) = 0$, $\lambda _{2}^{{}}(t) = 0$ и запишем (1.6) в скалярном виде:

(2.1)
${{a}_{2}}{{x}_{2}}{{\lambda }_{3}}(t) = - {{\dot {x}}_{1}} + ({{a}_{3}} - {{a}_{2}}){{x}_{2}}{{x}_{3}} + {{s}_{2}}{{\nu }_{3}} - {{s}_{3}}{{\nu }_{2}}$
(2.2)
${{a}_{1}}{{x}_{1}}{{\lambda }_{3}}(t) = {{\dot {x}}_{2}} - ({{a}_{1}} - {{a}_{3}}){{x}_{3}}{{x}_{1}} - {{s}_{3}}{{\nu }_{1}} + {{s}_{1}}{{\nu }_{3}}$
(2.3)
${{{\mathbf{\dot {\lambda }}}}_{3}}(t) = - {{\dot {x}}_{3}} + ({{a}_{2}} - {{a}_{1}}){{x}_{1}}{{x}_{2}} + {{s}_{1}}{{\nu }_{2}} - {{s}_{2}}{{\nu }_{1}}$
(2.4)
${{\dot {\nu }}_{1}} = {{a}_{3}}{{x}_{3}}{{\nu }_{2}} - {{a}_{2}}{{x}_{2}}{{\nu }_{3}},\quad {{\dot {\nu }}_{2}} = {{a}_{1}}{{x}_{1}}{{\nu }_{3}} - {{a}_{3}}{{x}_{3}}{{\nu }_{1}},\quad {{\dot {\nu }}_{3}} = {{a}_{2}}{{x}_{2}}{{\nu }_{1}} - {{a}_{1}}{{x}_{1}}{{\nu }_{2}}$
(2.5)
$\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2} = 1,\quad ({{x}_{1}} + {{\lambda }_{1}}(t)){{\nu }_{1}} + ({{x}_{2}}{{\nu }_{2}} + {{x}_{3}}{{\nu }_{3}}){{\nu }_{3}} = k$

Гиростатический момент ${\mathbf{\lambda }}(t)$ из (1.8) упрощается:

(2.6)
${\mathbf{\lambda }}(t) = {{\lambda }_{3}}(t){\mathbf{i}}_{3}^{{}},\quad {{\lambda }_{3}}(t) = D_{3}^{{}}{\text{[(}}a{\mathbf{x}} \cdot {\mathbf{i}}_{3}^{{}}) + \dot {\kappa }_{3}^{{}}{\text{]}}$

Рассмотрим систему уравнений (2.1)–(2.6). Исключим из уравнений (2.1), (2.2) переменную $\lambda _{3}^{{}}(t)$. Результат представим в виде

(2.7)
${{\left[ {\frac{1}{2}{{\gamma }_{ + }}\left( {a,x,x} \right) - {{s}_{3}}{{\nu }_{3}}} \right]}^{ \bullet }} + {{a}_{3}}({{a}_{2}} - {{a}_{1}}){{x}_{1}}{{x}_{2}}{{x}_{3}} + {{\nu }_{3}}{{\gamma }_{ - }}\left( {s,ax} \right) = 0,$
где точкой обозначена производная по времени от функции, входящей в квадратную скобку; ${{\gamma }_{ + }}\left( {a,x,y} \right)$ = ${{a}_{2}}{{x}_{1}}{{y}_{1}} + {{a}_{1}}{{x}_{2}}{{y}_{2}}$, ${{\gamma }_{ - }}\left( {x,y} \right)$ = ${{x}_{1}}{{y}_{2}} - {{x}_{2}}{{y}_{1}}$. Уравнение (2.7) рассматривалось [12] в случае, когда выполняются равенства

(2.8)
${{a}_{2}} = {{a}_{1}},\quad {{s}_{2}} = 0,\quad {{s}_{1}} = 0$

В силу условий (2.8) из уравнения (2.7) получим первый интеграл

(2.9)
$\frac{{{{a}_{1}}}}{2}\left( {x_{1}^{2} + x_{2}^{2}} \right) - {{s}_{3}}{{\nu }_{3}} = {{b}_{0}},$
где $b_{0}^{{}}$ – произвольная постоянная. Из уравнения (2.3) находится дополнительный интеграл [12]

(2.10)
${{x}_{3}} + {{\lambda }_{3}}(t) = {\text{const}}$

Условия (2.8) характеризуют обобщенный интеграл Лагранжа (2.10) задачи о движении тяжелого твердого тела. Если второе уравнение из (2.5) продифференцировать только в силу уравнений (2.3), (2.4), то опять получим уравнение (2.7).

В качестве второго разрешающего уравнения будем использовать комбинацию уравнений (2.1), (2.2), которая получается в результате исключения из этих уравнений параметра $s_{3}^{{}}$:

(2.11)

Подставим в уравнение (2.11) значение $x_{3}^{{}} + \lambda _{3}^{{}}$, найденное из второго уравнения (2.5), и воспользуемся третьим уравнением из системы (2.4):

(2.12)
$\frac{{k{{{\dot {\nu }}}_{3}}}}{{{{\nu }_{3}}}} = \frac{{{{{\dot {\nu }}}_{3}}}}{{{{\nu }_{3}}}}{{\gamma }_{ + }}\left( {1,x,\nu } \right) - {{\gamma }_{ + }}\left( {1,\dot {x},\nu } \right) + {{a}_{3}}{{x}_{3}}{{\gamma }_{ - }}\left( {\nu ,x} \right) + {{\nu }_{3}}{{\gamma }_{ - }}\left( {\nu ,s} \right)$

Таким образом, при рассмотрении условий существования ИС (1.7) необходимо изучать редуцированную систему, которая состоит из уравнений (2.4), (2.7), (2.12).

Рассмотрим уравнения (2.4), (2.7), (2.12) при наличии у них ИС (1.7). Вначале изучим систему уравнений (1.3) в случае, когда функции $h$ и $\varepsilon $ удовлетворяют равенству

(2.13)
$h = {{\nu }_{3}}\varepsilon $

Тогда из уравнения (1.3) и представления (1.4) имеем

(2.14)
${{\dot {\nu }}_{1}} = - {{\beta }_{2}}{{\nu }_{3}}g,\quad {{\dot {\nu }}_{2}} = {{\beta }_{1}}{{\nu }_{3}}g,\quad {{\dot {\nu }}_{3}} = {{\gamma }_{ - }}\left( {\nu ,\beta } \right)g$
(2.15)
${{\gamma }_{ + }}\left( {1,\beta ,\nu } \right) = {{c}_{0}}$

Было показано [25, 27], что компоненты ${{\nu }_{1}}$, ${{\nu }_{2}}$ вектора ${\mathbf{\nu }}$ в силу интеграла $\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2}$ = = 1 и ИС (2.15) являются функциями вспомогательной переменной ${{\nu }_{3}}$:

(2.16)
$\begin{gathered} {{\nu }_{1}} = \frac{1}{{\kappa _{0}^{2}}}\left( {{{c}_{0}}{{\beta }_{1}} + {{\beta }_{2}}\sqrt {D\left( {{{\nu }_{3}}} \right)} } \right),\quad {{\nu }_{2}} = \frac{1}{{\kappa _{0}^{2}}}\left( {{{c}_{0}}{{\beta }_{2}} - {{\beta }_{1}}\sqrt {D\left( {{{\nu }_{3}}} \right)} } \right) \\ D\left( {{{\nu }_{3}}} \right) = (\kappa _{0}^{2} - c_{0}^{2}) - \kappa _{0}^{2}\nu _{3}^{2}, \\ \end{gathered} $
а зависимость ${{\nu }_{3}}(t)$ находится путем обращения интеграла

(2.17)
$\int\limits_{\nu _{3}^{{(0)}}}^{{{\nu }_{3}}} {\frac{{d{{\nu }_{3}}}}{{g\sqrt {D\left( {{{\nu }_{3}}} \right)} }} = t - {{t}_{0}}} $

В формулах (2.16), (2.17) обозначено $\kappa _{0}^{2} = \beta _{1}^{2} + \beta _{2}^{2}$.

Распишем уравнения (2.7), (2.12) с учетом равенств (1.7), (2.13):

(2.18)
$\begin{gathered} {{{\dot {\nu }}}_{3}}\left\{ {\varepsilon {\kern 1pt} '\left[ {{{\gamma }_{ + }}\left( {a,\nu ,\nu } \right)\varepsilon + {{\gamma }_{ + }}\left( {a,\nu ,\beta } \right)g} \right] + g{\kern 1pt} '{\kern 1pt} \left[ {{{\gamma }_{ + }}\left( {a,\nu ,\beta } \right)\varepsilon + {{\gamma }_{ + }}\left( {a,\beta ,\beta } \right)g} \right]} \right\} = \\ = {{a}_{1}}{{a}_{2}}\left[ {{{s}_{3}}{{{\dot {\nu }}}_{3}} - {{\nu }_{3}}{{\gamma }_{ - }}\left( {s,\nu } \right)\varepsilon - {{\nu }_{3}}{{\gamma }_{ - }}\left( {s,\beta } \right)g} \right] - {{\nu }_{3}}{{\varepsilon }^{2}}\left[ {({{a}_{2}} - {{a}_{1}}){{\nu }_{1}}{{\nu }_{2}}\varepsilon + {{\gamma }_{ - }}(\beta ,a\nu )g} \right], \\ \end{gathered} $
(2.19)
$\begin{gathered} {{{\dot {\nu }}}_{3}}\left[ {{{\gamma }_{ + }}\left( {a,\nu ,\nu } \right)\varepsilon {\kern 1pt} '\; + {{\gamma }_{ + }}\left( {a,\nu ,\beta } \right)g{\kern 1pt} '} \right] = \frac{{{{{\dot {\nu }}}_{3}}}}{{{{\nu }_{3}}}}\left[ {{{\gamma }_{ + }}\left( {a,\nu ,\nu } \right)\varepsilon + {{\gamma }_{ + }}\left( {a,\nu ,\beta } \right)g} \right] + \\ + \;{{a}_{1}}{{a}_{2}}\left[ {{{\nu }_{3}}{{\gamma }_{ - }}\left( {\nu ,s} \right) - \frac{{k{{{\dot {\nu }}}_{3}}}}{{{{\nu }_{3}}}}} \right] + {{{\dot {\nu }}}_{3}}{{\nu }_{3}}({{a}_{1}} + {{a}_{2}})\varepsilon + ({{a}_{1}} - {{a}_{2}}){{\nu }_{1}}{{\nu }_{2}}{{\nu }_{3}}{{\varepsilon }^{2}} \\ \end{gathered} $

Для удобства использования уравнений (2.18), (2.19) в них не подставлено значение

(2.20)
${{\dot {\nu }}_{3}} = {{\gamma }_{ - }}\left( {\nu ,\beta } \right)g$

Таким образом, справедливо утверждение.

Утверждение 1. Задача интегрирования уравнений движения тяжелого гиростата (2.1)–(2.4) на ИС (1.7), в которых функция $h({{\nu }_{3}})$ имеет вид (2.13), сведена к интегрированию уравнений (2.18), (2.19) и нахождению функции ${{\nu }_{3}}(t)$ путем обращения интеграла (2.17).

Замечание 1. Из метода получения уравнения (2.18) и из вида уравнения (2.7) следует, что на рассматриваемых ИС при условиях

(2.21)
$g = {{g}_{0}},\quad \varepsilon = {{\varepsilon }_{0}},\quad {{a}_{2}} = {{a}_{1}},\quad {{s}_{3}} = 0,\quad {{s}_{1}} = {{\sigma }_{0}}{{\beta }_{1}},\quad {{s}_{2}} = {{\sigma }_{0}}{{\beta }_{2}},$
где ${{g}_{0}}$, ${{\varepsilon }_{0}}$, ${{\sigma }_{0}}$ – постоянные, уравнение (2.7) имеет первый интеграл

(2.22)
$\frac{{{{a}_{1}}}}{2}\left( {x_{1}^{2} + x_{2}^{2}} \right) - {{s}_{3}}{{\nu }_{3}} - \frac{{{{\varepsilon }_{0}}}}{{2{{g}_{0}}}}{{\sigma }_{0}}\nu _{3}^{2} = {{c}_{*}}$

Здесь ${{c}_{*}}$ – произвольная постоянная. На основании условий из (2.21) можно сделать заключение, что распределение масс гиростата определяется обобщенными условиями Ковалевской (${{a}_{3}} = 2{{a}_{1}}$) и Горячева–Чаплыгина (${{a}_{3}} = 4{{a}_{1}}$). В силу первых двух равенств системы (2.21) и равенства (2.13), ИС (1.2) являются линейными функциями переменных ${{\nu }_{i}}$ ($i = \overline {1.3} $).

Для дальнейшего рассмотрения уравнений (2.18), (2.19) представим их в следующем виде:

(2.23)
$\varepsilon {\kern 1pt} ' = H\left( {{{\nu }_{3}},\varepsilon ,g} \right),\quad g{\kern 1pt} ' = L\left( {{{\nu }_{3}},\varepsilon ,g} \right)$

Данная система представляет, по-видимому, только теоретический интерес. Поэтому рассмотрим пример интегрирования системы (2.18), (2.19). Положим, что функции $\varepsilon $ и $g$ принимают постоянные значения

(2.24)
$\varepsilon = {{\varepsilon }_{0}},\quad g = {{g}_{0}},$
которые являются частью условий (2.21) (остальные равенства не используем). Вместо переменной $\nu _{3}^{{}}$ введем новую переменную $\psi $ по формуле

(2.25)
${{\nu }_{3}} = \frac{{{{\mu }_{0}}}}{{{{\kappa }_{0}}}}\sin \psi ,\quad {{\mu }_{0}} = \sqrt {\kappa _{0}^{2} - c_{0}^{2}} $

Тогда из третьего уравнения системы (2.14), в силу (2.15), (2.25), получим

(2.26)
$\psi (t) = {{\kappa }_{0}}{{g}_{0}}t + {{\psi }_{0}}$

На основании (2.16), (2.25) запишем компоненты $\nu _{1}^{{}}$, $\nu _{2}^{{}}$:

(2.27)
${{\nu }_{i}}(\psi ) = \frac{1}{{\kappa _{0}^{2}}}\left( {{{c}_{0}}{{\beta }_{i}} - {{{\left( { - 1} \right)}}^{i}}{{\mu }_{0}}{{\beta }_{{3 - i}}}\cos \psi } \right),\quad i = 1,\;2$

Для исследования зависимости остальных переменных задачи от переменной $\psi $ обратимся к соотношениям (1.7). На основании формул (2.13), (2.24), (2.25), (2.27) найдем

(2.28)
$\begin{gathered} {{x}_{i}}(\psi ) = \frac{1}{{{{a}_{i}}\kappa _{0}^{2}}}\left[ {{{\beta }_{i}}({{c}_{0}}{{\varepsilon }_{0}} + {{g}_{0}}\kappa _{0}^{2}) - {{{\left( { - 1} \right)}}^{i}}{{\beta }_{{3 - i}}}{{\varepsilon }_{0}}{{\mu }_{0}}\cos \psi } \right],\quad i = 1,\;2 \\ {{x}_{3}}(\psi ) = \frac{{{{\varepsilon }_{0}}{{\mu }_{0}}}}{{{{a}_{3}}{{\kappa }_{0}}}}\sin \psi \\ \end{gathered} $

Используя равенства (2.25), (2.27), (2.28), потребуем, чтобы уравнения (2.18), (2.19) были тождествами по переменной $\psi $. Тогда получим следующие условия:

(2.29)
${{a}_{2}} = {{a}_{1}},\quad {{s}_{3}} = 0,\quad {{s}_{1}} = {{\sigma }_{0}}{{\beta }_{1}},\quad {{s}_{2}} = {{\sigma }_{0}}{{\beta }_{2}}$
(2.30)
$k = \frac{1}{{{{a}_{1}}}}\left( {{{c}_{0}}{{g}_{0}} + {{\varepsilon }_{0}}} \right),\quad {{\sigma }_{0}} = - \frac{{{{\varepsilon }_{0}}{{g}_{0}}}}{{{{a}_{1}}}}$

Условия (2.29) совпадают с условиями (2.21), при выполнении которых имеет место интеграл (2.22). Их характеристика дана выше. Отметим только, что в равенствах (2.29) параметр $\sigma _{0}^{{}}$ принимает конкретное значение из (2.30).

Для рассмотрения свойств сил, действующих на несомое тело со стороны тела-носителя, обратимся к третьему уравнению из (1.10) при условии $i = 3$. Используя третье уравнение из (1.11), в силу

(2.31)
${{p}_{3}}(t) = \frac{{{{\varepsilon }_{0}}{{\mu }_{0}}}}{{{{\kappa }_{0}}}}\sin ({{\kappa }_{0}}{{g}_{0}}t + {{\psi }_{0}}) + {{\dot {\kappa }}_{3}}(t),\quad {{\lambda }_{3}}(t) = \frac{{{{\varepsilon }_{0}}{{\mu }_{0}}}}{{{{\kappa }_{0}}}}\frac{{{{a}_{3}} - {{a}_{1}}}}{{{{a}_{1}}{{a}_{3}}}}\sin ({{\kappa }_{0}}{{g}_{0}}t + {{\psi }_{0}}),$
получим

(2.32)
${{L}_{3}}(t) = {{\varepsilon }_{0}}{{\mu }_{0}}{{g}_{0}}\frac{{{{a}_{3}} - {{a}_{1}}}}{{{{a}_{1}}{{a}_{3}}}}\cos ({{\kappa }_{0}}{{g}_{0}}t + {{\psi }_{0}})$

Следовательно, проекция внутренних сил на ось вращения ротора $S_{3}^{{}}$ равна значению (2.32).

Справедливо утверждение.

Утверждение 2. Необходимыми условиями существования у системы (2.18), (2.19) линейных инвариантных соотношений по основным переменным задачи (1.5), (1.6) являются равенства (2.29), (2.30), которые характеризуют динамически симметричный гиростат, распределение масс которого определяется обобщенными условиями Ковалевской и Горячева–Чаплыгина.

3. Случай движения гиростата под действием потенциальных и гироскопических сил. Запишем уравнение (1.5) в скалярной форме, положив $\lambda _{1}^{{}}(t) = 0$, $\lambda _{2}^{{}}(t) = 0$:

(3.1)
$\begin{gathered} {{a}_{2}}{{x}_{2}}{{\lambda }_{3}}(t) = - {{{\dot {x}}}_{1}} + ({{a}_{3}} - {{a}_{2}}){{x}_{2}}{{x}_{3}} + {{s}_{2}}{{\nu }_{3}} - {{s}_{3}}{{\nu }_{2}} + \\ + \;{{a}_{2}}{{B}_{3}}{{x}_{2}}{{\nu }_{3}} - {{a}_{3}}{{B}_{2}}{{\nu }_{2}}{{x}_{3}} + ({{C}_{3}} - {{C}_{2}}){{\nu }_{2}}{{\nu }_{3}}, \\ \end{gathered} $
(3.2)
$\begin{gathered} {{a}_{1}}{{x}_{1}}{{\lambda }_{3}}(t) = {{{\dot {x}}}_{2}} - ({{a}_{1}} - {{a}_{3}}){{x}_{3}}{{x}_{1}} - {{s}_{3}}{{\nu }_{1}} + {{s}_{1}}{{\nu }_{3}} - \\ - \;{{a}_{3}}{{B}_{1}}{{x}_{3}}{{\nu }_{1}} + {{a}_{1}}{{B}_{3}}{{\nu }_{3}}{{x}_{1}} - ({{C}_{1}} - {{C}_{3}}){{\nu }_{3}}{{\nu }_{1}}, \\ \end{gathered} $
(3.3)
$\begin{gathered} {{{\dot {\lambda }}}_{3}}(t) = - {{{\dot {x}}}_{3}} + ({{a}_{2}} - {{a}_{1}}){{x}_{1}}{{x}_{2}} + {{s}_{1}}{{\nu }_{2}} - {{s}_{2}}{{\nu }_{1}} + \\ + \;{{a}_{1}}{{B}_{2}}{{x}_{1}}{{\nu }_{2}} - {{a}_{2}}{{B}_{1}}{{\nu }_{1}}{{x}_{2}} + ({{C}_{2}} - {{C}_{1}}){{\nu }_{1}}{{\nu }_{2}} \\ \end{gathered} $

К уравнениям (3.1)–(3.3) следует добавить уравнения Пуассона (2.4) и первые интегралы (1.12):

(3.4)
$\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2} = 1,\quad {{x}_{1}}{{\nu }_{1}} + {{x}_{2}}{{\nu }_{2}} + ({{x}_{3}} + {{\lambda }_{3}}(t)){{\nu }_{3}} - \frac{1}{2}\left( {{{B}_{1}}\nu _{1}^{2} + {{B}_{2}}\nu _{2}^{2} + {{B}_{3}}\nu _{3}^{2}} \right) = k,$
так как в разд. 2 показано, что в этом частном случае можно провести полный анализ условий существования ИС (1.2). Используя подход, изложенный в п. 2, систему уравнений (3.1)–(3.3) редуцируем к системе уравнений

(3.5)
$\begin{gathered} {{\left[ {\frac{1}{2}{{\gamma }_{ + }}\left( {a,x,x} \right) - {{s}_{3}}{{\nu }_{3}}} \right]}^{ \bullet }} + {{a}_{3}}({{a}_{2}} - {{a}_{1}}){{x}_{1}}{{x}_{2}}{{x}_{3}} + {{\nu }_{3}}{{\gamma }_{ - }}\left( {s,ax} \right) + \\ + \;{{a}_{3}}{{x}_{3}}{{\gamma }_{ - }}\left( {ax,B\nu } \right) - {{\nu }_{3}}\left[ {{{\gamma }_{ - }}\left( {C\nu ,x} \right) - {{C}_{3}}{{\gamma }_{ - }}\left( {\nu ,ax} \right)} \right] = 0, \\ \end{gathered} $
(3.6)
$\begin{gathered} \frac{{{{{\dot {\nu }}}_{3}}k}}{{{{\nu }_{3}}}} = \frac{1}{{{{\nu }_{3}}}}{{\gamma }_{ + }}\left( {1,x,\nu } \right){{{\dot {\nu }}}_{3}} - {{\gamma }_{ + }}\left( {1,\dot {x},\nu } \right) + {{a}_{3}}{{x}_{3}}{{\gamma }_{ - }}\left( {\nu ,x} \right) + {{\nu }_{3}}{{\gamma }_{ - }}\left( {\nu ,s} \right) - \\ - \;\frac{{{{{\dot {\nu }}}_{3}}}}{{2{{\nu }_{3}}}}({{B}_{1}}\nu _{1}^{2} + {{B}_{2}}\nu _{2}^{2} - {{B}_{3}}\nu _{3}^{2}) + {{\nu }_{1}}{{\nu }_{2}}\left[ {{{a}_{3}}({{B}_{1}} - {{B}_{2}}){{x}_{3}} + ({{C}_{1}} - {{C}_{2}}){{\nu }_{3}}} \right] \\ \end{gathered} $

Для получения замкнутой системы уравнений необходимо рассматривать систему (3.5), (3.6) совместно с уравнениями Пуассона

(3.7)
${{\dot {\nu }}_{1}} = {{a}_{3}}{{x}_{3}}{{\nu }_{2}} - {{a}_{2}}{{x}_{2}}{{\nu }_{3}},\quad {{\dot {\nu }}_{2}} = {{a}_{1}}{{x}_{1}}{{\nu }_{3}} - {{a}_{3}}{{x}_{3}}{{\nu }_{1}},\quad {{\dot {\nu }}_{3}} = {{a}_{2}}{{x}_{2}}{{\nu }_{1}} - {{a}_{1}}{{x}_{1}}{{\nu }_{2}}$

После интегрирования системы (3.5)–(3.7) функцию $\lambda _{3}^{{}}(t)$ определяем из второго соотношения системы (3.4):

(3.8)
${{\lambda }_{3}}(t) = \frac{1}{{{{\nu }_{3}}}}\left[ {k - {{x}_{1}}{{\nu }_{1}} - {{x}_{2}}{{\nu }_{2}} - {{x}_{3}}{{\nu }_{3}} + \frac{1}{2}\left( {{{B}_{1}}\nu _{1}^{2} + {{B}_{2}}\nu _{2}^{2} + {{B}_{3}}\nu _{3}^{2}} \right)} \right]$

Как уже было отмечено выше, в предположении $B = 0$, $C = 0$ рассмотрен случай [12], который в обозначениях данного раздела соответствует величинам: $s_{1}^{{}} = 0$, $s_{2}^{{}} = 0$, $a_{2}^{{}} = a_{1}^{{}}$. Здесь рассмотрим более общий вариант, положив в (3.3), (3.5), (3.6) и (3.8)

(3.9)
${{s}_{1}} = 0,\quad {{s}_{2}} = 0,\quad {{a}_{2}} = {{a}_{1}},\quad {{B}_{2}} = {{B}_{1}},\quad {{C}_{2}} = {{C}_{1}}$

Тогда из (3.3) следует первый интеграл

(3.10)
$\lambda (t) + {{x}_{3}} + {{B}_{1}}{{\nu }_{3}} = {{b}_{1}},$
где ${{b}_{1}}$ – произвольная постоянная. При условиях (3.9) уравнение (3.5) принимает вид

(3.11)
${{\left[ {\frac{{{{a}_{1}}}}{2}(x_{1}^{2} + x_{2}^{2}) - {{s}_{3}}{{\nu }_{3}} + \frac{1}{2}({{C}_{3}} - {{C}_{1}})\nu _{3}^{2}} \right]}^{ \bullet }} = - {{B}_{1}}{{a}_{3}}{{x}_{3}}{{\dot {\nu }}_{3}}$

Если в (3.11) положить $B_{1}^{{}} = 0$, то получим дополнительный первый интеграл

(3.12)
$\frac{{a_{1}^{{}}}}{2}\left( {x_{1}^{2} + x_{2}^{2}} \right) - s_{3}^{{}}\nu _{3}^{{}} + \frac{1}{2}(C_{3}^{{}} - C_{1}^{{}})\nu _{3}^{2} = b_{2}^{{}},$
где $b_{2}^{{}}$ – произвольная постоянная.

Замечание 2. Наличие у системы шести уравнений (3.3), (3.5), (3.6) трех первых интегралов (3.10)–(3.12) не позволяет выполнить интегрирование данной системы в квадратурах. Аналогичная проблема имела место и в исследованиях статьи [12]. Поэтому в [12] дополнительно предполагалось, что в соотношениях (2.6) $\lambda _{3}^{{}} = {\text{const}}$. В изучаемом здесь случае данное предположение приводит, в силу соотношения (3.10), к решению [24], которое представляет собой обобщение решения Кирхгофа [22].

Данное замечание и итоги разд. 2 показывают, что целесообразно рассматривать уравнения (3.5)–(3.8) в случае существования у них инвариантных соотношений [25]

(3.13)
${{x}_{1}}({{\nu }_{3}}) = \frac{1}{{{{a}_{1}}}}\left( {{{\nu }_{1}}({{\nu }_{3}})\varepsilon + {{\beta }_{1}}g} \right),\quad {{x}_{2}}({{\nu }_{3}}) = \frac{1}{{{{a}_{2}}}}\left( {{{\nu }_{2}}({{\nu }_{3}})\varepsilon + {{\beta }_{2}}g} \right),\quad {{x}_{3}}({{\nu }_{3}}) = \frac{1}{{{{a}_{3}}}}{{\nu }_{3}}\varepsilon $

Подставим значения (3.13) в уравнения (3.5), (3.6) и воспользуемся уравнениями Пуассона (3.7):

(3.14)
$\begin{gathered} {{\gamma }_{ - }}\left( {\nu ,\beta } \right)\left\{ {\left[ {\varepsilon {{\gamma }_{ + }}\left( {a,\nu ,\nu } \right) + g{{\gamma }_{ + }}\left( {a,\nu ,\beta } \right)} \right]g\varepsilon {\kern 1pt} '\; + \left[ {\varepsilon {{\gamma }_{ + }}\left( {a,\nu ,\beta } \right) + g{{\gamma }_{ + }}\left( {a,\beta ,\beta } \right)} \right]gg{\kern 1pt} '} \right\} = \\ = - {{\nu }_{3}}\left\{ {({{a}_{2}} - {{a}_{1}}){{\nu }_{1}}{{\nu }_{2}}\varepsilon + \left[ {{{\gamma }_{ - }}\left( {\beta ,a\nu } \right)g + {{a}_{1}}{{a}_{2}}({{B}_{2}} - {{B}_{1}}){{\nu }_{1}}{{\nu }_{2}}} \right]} \right\}{{\varepsilon }^{2}} + \\ + \;{{a}_{1}}{{a}_{2}}\left\{ {{{\nu }_{3}}\left[ {({{C}_{1}} - {{C}_{2}}){{\nu }_{1}}{{\nu }_{2}} - {{\gamma }_{ - }}\left( {\beta ,B\nu } \right)g - {{\gamma }_{ - }}\left( {s,\nu } \right)} \right]\varepsilon + } \right. \\ \left. { + \;\left[ {{{s}_{3}}{{\gamma }_{ - }}\left( {\nu ,\beta } \right) - {{\nu }_{3}}{{\gamma }_{ - }}\left( {s,\beta } \right) + {{\beta }_{2}}({{C}_{1}} - {{C}_{3}}){{\nu }_{1}}{{\nu }_{3}} + {{\beta }_{1}}({{C}_{3}} - {{C}_{2}}){{\nu }_{2}}{{\nu }_{3}}} \right]g} \right\}, \\ \end{gathered} $
(3.15)
где $\dot {\nu }_{3}^{{}}$ имеет значение (2.20). Для удобства исследования уравнения (3.15) выражение $\dot {\nu }_{3}^{{}}$ не внесено в (3.15). В силу постановки задачи к уравнениям (3.14), (3.15) необходимо присоединить уравнения (2.14) и инвариантное соотношение (2.15). То есть в уравнениях (3.14), (3.15) функции $\nu _{1}^{{}}({{\nu }_{3}})$, $\nu _{2}^{{}}({{\nu }_{3}})$ имеют вид (2.16), а зависимость $\nu _{3}^{{}}(t)$ устанавливается из (2.17). Отметим, что ИС (2.15) описывают прецессионные движения [28, 29] – движения, при которых постоянен угол между вектором ${\mathbf{\beta }}(\beta _{1}^{{}},\beta _{2}^{{}},0)$ и вектором ${\mathbf{\nu }}$.

В общем случае задача интегрирования уравнений (3.14), (3.15) представляет весьма сложную проблему (см. п. 2 настоящей статьи). Поэтому рассмотрим вариант, когда ИС (3.13) являются линейными функциями, то есть компоненты вектора угловой скорости имеют вид

(3.16)
${{\omega }_{1}} = {{\varepsilon }_{0}}{{\nu }_{1}} + {{\beta }_{1}}{{g}_{0}},\quad {{\omega }_{2}} = {{\varepsilon }_{0}}{{\nu }_{2}} + {{\beta }_{2}}{{g}_{0}},\quad {{\omega }_{3}} = {{\varepsilon }_{0}}{{\nu }_{3}}$

В силу равенств (3.16) прецессия тела-носителя относится к классу регулярных прецессий [28, 29].

Подставим значения (3.13) (в которых $\varepsilon (\nu _{3}^{{}}) = \varepsilon _{0}^{{}}$, $g(\nu _{3}^{{}}) = g_{0}^{{}}$) и значения (2.25), (2.27) в уравнения (3.14), (3.15) и потребуем, чтобы полученные равенства были тождествами по $\psi $:

(3.17)
$(a_{2}^{{}} - {{a}_{1}})\left( {2c_{0}^{{}}\varepsilon _{0}^{{}} + g_{0}^{{}}\kappa _{0}^{2}} \right) + c_{0}^{{}}a_{1}^{{}}a_{2}^{{}}(B_{2}^{{}} - {{B}_{1}}) = 0$
(3.18)
${{\sigma }_{0}} = \frac{{{{g}_{0}}}}{{\kappa _{0}^{2}}}\left\{ { - \frac{{{{\varepsilon }_{0}}\left( {{{a}_{1}}\beta _{2}^{2} + {{a}_{2}}\beta _{1}^{2}} \right)}}{{{{a}_{1}}{{a}_{2}}}} + \frac{1}{2}\left[ {\beta _{1}^{2}({{B}_{3}} - {{B}_{2}}) + \beta _{2}^{2}({{B}_{3}} - {{B}_{1}})} \right]} \right\}$
(3.19)
$\varepsilon _{0}^{2}({{a}_{1}} - {{a}_{2}}) + {{a}_{1}}{{a}_{2}}\left[ {{{\varepsilon }_{0}}({{B}_{1}} - {{B}_{2}}) + ({{C}_{1}} - {{C}_{2}})} \right] = 0$
(3.20)
$s_{3}^{{}} = 0,\quad s_{1}^{{}} = \sigma _{0}^{{}}\beta _{1}^{{}},\quad s_{2}^{{}} = \sigma _{0}^{{}}\beta _{2}^{{}}$
(3.21)
$\begin{gathered} \varepsilon _{0}^{2}{{g}_{0}}\left( {{{a}_{2}}\beta _{1}^{2} + {{a}_{1}}\beta _{2}^{2}} \right) + {{a}_{1}}{{a}_{2}}\left\{ {{{\varepsilon }_{0}}\left[ {{{\sigma }_{0}}\kappa _{0}^{2} + {{g}_{0}}({{B}_{2}}\beta _{1}^{2} + {{B}_{1}}\beta _{2}^{2})} \right] + } \right. \\ \left. { + \;{{g}_{0}}\left[ {\beta _{1}^{2}({{C}_{3}} - {{C}_{2}}) + \beta _{2}^{2}({{C}_{3}} - {{C}_{1}})} \right]} \right\} = 0, \\ \end{gathered} $
где $\sigma _{0}^{{}}$ – параметр. Параметр $k$, входящий в равенство (3.8) при условиях (3.17)–(3.21), имеет значение

(3.22)
$\begin{gathered} k = \frac{1}{{2a_{1}^{{}}a_{2}^{{}}\kappa _{0}^{4}}}\left\{ {2\varepsilon _{0}^{{}}\left[ {\kappa _{0}^{4}(a_{1}^{{}} + {{a}_{2}}) - c_{0}^{2}\left( {a_{1}^{{}}\beta _{1}^{2} + a_{2}^{{}}\beta _{2}^{2}} \right)} \right]} \right. - \\ - \;\left. {a_{1}^{{}}a_{2}^{{}}\left[ {B_{3}^{{}}\kappa _{0}^{4} + c_{0}^{2}\left( {\beta _{1}^{2}(B_{1}^{{}} - {{B}_{3}}) + \beta _{2}^{2}(B_{2}^{{}} - {{B}_{3}})} \right)} \right]} \right\} \\ \end{gathered} $

Функцию $\lambda _{3}^{{}}(t)$ определим на основании равенств (2.25), (2.27), (3.16)–(3.21):

(3.23)
$\begin{gathered} \lambda _{3}^{{}}(t) = \frac{{\mu _{0}^{{}}}}{{2a_{1}^{{}}a_{2}^{{}}a_{3}^{{}}\kappa _{0}^{3}}}\left\{ {2\varepsilon _{0}^{{}}} \right.\left[ {a_{3}^{{}}\left( {a_{1}^{{}}\beta _{1}^{2} + a_{2}^{{}}\beta _{2}^{2}} \right) - \kappa _{0}^{2}a_{1}^{{}}a_{2}^{{}}} \right] - \\ - \;a_{1}^{{}}a_{2}^{{}}{{a}_{3}}\left. {\left[ {\beta _{1}^{2}(B_{2}^{{}} - {{B}_{3}}) + \beta _{2}^{2}(B_{1}^{{}} - {{B}_{3}})} \right]} \right\}\sin (\kappa _{0}^{{}}g_{0}^{{}}t + \psi _{0}^{{}}) \\ \end{gathered} $

Обсудим условия (3.17)–(3.23). Если в полученных условиях полагать, что ${{B}_{i}} = 0$, $C_{i}^{{}} = 0$ ($i = \overline {1,3} $), то получим условия (2.29)–(2.31).

Положим в (3.17)–(3.21) ${{a}_{2}} \ne {{a}_{1}}$. Тогда из (3.17) следует

$c_{0}^{{}} = \frac{{g_{0}^{{}}\kappa _{0}^{2}(a_{1}^{{}} - a_{2}^{{}})}}{{2\varepsilon _{0}^{{}}(a_{2}^{{}} - {{a}_{1}}) + a_{1}^{{}}a_{2}^{{}}(B_{2}^{{}} - {{B}_{1}})}}$

Из уравнения (3.19) можно определить параметр $\varepsilon _{0}^{{}}$, если выполняется условие

$a_{1}^{{}}a_{2}^{{}}(B_{1}^{{}} - {{B}_{2}})_{{}}^{2} + 4(a_{2}^{{}} - {{a}_{1}})(C_{1}^{{}} - {{C}_{2}}) \geqslant 0$

Равенство (3.21) можно рассматривать как условие на параметры $C_{i}^{{}}$ ($i = \overline {1,3} $).

Таким образом, доказано утверждение.

Утверждение 3. Построено новое решение (2.25)–(2.28) уравнений (3.5)–(3.7), которое описывает прецессионное движение тела-носителя в задаче о движении гиростата под действием потенциальных и гироскопических сил. Условиями существования данного решения являются равенства (3.17)–(3.22): в них, в отличие от случая (2.29), отсутствует требование динамической симметрии гиростата.

4. Линейные ИС уравнений движения неавтономного гиростата под действием потенциальных и гироскопических сил в случае непрецессионных движений. Ранее [25] было получено решение уравнений движения динамически симметричного твердого тела ($a_{2}^{{}} = a_{1}^{{}}$) в потенциальном поле сил:

(4.1)
$x_{1}^{{}} = \frac{1}{{{{a}_{1}}}}\left( { - \frac{{{{\mu }_{1}}}}{3}\nu _{1}^{{}} + \beta _{1}^{{}}\mu _{2}^{{}}} \right),\quad x_{2}^{{}} = \frac{1}{{{{a}_{1}}}}\left( { - \frac{{{{\mu }_{1}}}}{3}\nu _{2}^{{}} + \beta _{2}^{{}}\mu _{2}^{{}}} \right),\quad x_{3}^{{}} = \frac{{{{\mu }_{1}}}}{{{{a}_{3}}}}\nu _{3}^{{}}$
(4.2)
$\begin{gathered} \nu _{1}^{{}}(\nu _{3}^{{}}) = \frac{1}{{3\mu _{2}^{{}}\kappa _{0}^{2}}}\left( {\mu _{1}^{{}}\beta _{1}^{{}}(1 - 2\nu _{3}^{2}) - \beta _{2}^{{}}\sqrt {F({{\nu }_{3}})} } \right) \\ \nu _{2}^{{}}(\nu _{3}^{{}}) = \frac{1}{{3\mu _{2}^{{}}\kappa _{0}^{2}}}\left( {\mu _{1}^{{}}\beta _{2}^{{}}(1 - 2\nu _{3}^{2}) + \beta _{1}^{{}}\sqrt {F({{\nu }_{3}})} } \right), \\ \end{gathered} $
где

(4.3)
$F(\nu _{3}^{{}}) = - \varepsilon _{2}^{2}\nu _{3}^{4} + \varepsilon _{1}^{{}}\nu _{3}^{2} + \varepsilon _{0}^{{}},\quad \varepsilon _{0}^{{}} = 9\kappa _{0}^{2}\mu _{2}^{2} - \mu _{1}^{2},\quad \varepsilon _{1}^{{}} = 4\mu _{1}^{2} - 9\kappa _{0}^{2}\mu _{2}^{2},\quad \varepsilon _{2}^{{}} = 2\mu _{1}^{{}}$

Подчеркнем, что в равенствах (4.1), (4.2) свойство динамической симметрии гиростата

(4.4)
$a_{2}^{{}} = a_{1}^{{}}$
сохраняется. В формулах (4.1)–(4.3) $\mu _{1}^{{}}$, $\mu _{2}^{{}}$ – постоянные параметры, $\kappa _{0}^{2}$ – параметр, имеющий значение $\beta _{1}^{2} + \beta _{2}^{2}$. Зависимость $\nu _{3}^{{}}(t)$ находится путем обращения интеграла [27]:

(4.5)
$\int\limits_{\nu _{3}^{{(0)}}}^{{{\nu }_{3}}} {\frac{{d{{\nu }_{3}}}}{{\sqrt {F({{\nu }_{3}})} }}} = - \frac{1}{3}(t - t_{0}^{{}})$

Величины (4.2) получены из ИС

(4.6)
$\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2} = 1,\quad \beta _{1}^{{}}\nu _{1}^{{}} + \beta _{2}^{{}}\nu _{2}^{{}} = \frac{{{{\mu }_{1}}}}{{3{{\mu }_{2}}}}\left( {1 - 2\nu _{3}^{2}} \right),$
которые допускают уравнение Пуассона (1.1) на ИС (4.1). Так как второе ИС из (4.6) отличается от ИС (2.15), то движение гиростата не является прецессионным [28].

Дополнительно к условию (4.4) предположим, что имеют место равенства

(4.7)
$s_{1}^{{}} = \sigma _{0}^{{}}\beta _{1}^{{}},\quad s_{2}^{{}} = \sigma _{0}^{{}}\beta _{2}^{{}},$
т.е. рассмотрим условия существования ИС (4.1), (4.2), (4.6) уравнений (3.5), (3.6) при наличии ограничений на параметры (4.4), (4.7). Отличие ИС (4.6) от ИС п. 3 состоит в том, что второе ИС из (4.6) является нелинейным.

Для получения наглядных результатов будем считать, что выполняются равенства

(4.8)
$B_{2}^{{}} = B_{1}^{{}},\quad C_{2}^{{}} = C_{1}^{{}}\quad (i = \overline {1,\;3} )$

Подствим значения (4.1), (4.2) в уравнения (3.5), (3.6). Учитывая в редуцированных уравнениях ИС (4.6) равенства (4.7). (4.8), потребуем, чтобы они были тождествами по переменной $\nu _{3}^{{}}$. Тогда найдем условия

(4.9)
$s_{3}^{{}} = 0,\quad k = - \frac{1}{2}B_{{11}}^{{}},\quad \sigma _{0}^{{}} = - \frac{{\mu _{2}^{{}}}}{{6a_{1}^{{}}}}\left[ {2\mu _{1}^{{}} + 3a_{1}^{{}}(B_{1}^{{}} + {{B}_{3}})} \right]$
(4.10)
$4\mu _{1}^{2} - 3a_{1}^{{}}\mu _{1}^{{}}(B_{3}^{{}} + 7{{B}_{1}}) + 18a_{1}^{{}}(C_{1}^{{}} - {{C}_{3}}) = 0$

Из первого равенства системы (4.9) следует, что центр масс гиростата лежит в плоскости кругового сечения эллипсоида инерции гиростата. Третье условие из (4.9) служит для нахождения параметра $\sigma _{0}^{{}}$, из равенства (4.10) при выполнении неравенства $C_{3}^{{}} > C_{1}^{{}}$ можно получить значение параметра $\mu _{1}^{{}}$.

Функцию гиростатического момента ${{\lambda }_{3}}({{\nu }_{3}})$ в данном решении определим с помощью равенства (3.8):

(4.11)
$\lambda _{3}^{{}}(\nu _{3}^{{}}) = \frac{1}{{6{{a}_{1}}{{a}_{3}}}}\left[ {2\mu _{1}^{{}}(a_{3}^{{}} - 3{{a}_{1}}) + 3a_{1}^{{}}a_{3}^{{}}(B_{3}^{{}} - {{B}_{1}})} \right]\nu _{3}^{{}},$
где функция $\nu _{3}^{{}}(t)$ удовлетворяет интегральному соотношению (4.5), которое изучено ранее [27].

Приведем пример исследования интеграла (4.5). Следуя [27], положим, что параметры из (4.3) подчинены условию $\mu _{1}^{2}$ = $9\kappa _{0}^{2}\mu _{2}^{2}$. Тогда интеграл (4.5) принимает вид

(4.12)
$\int\limits_{\nu _{3}^{{(0)}}}^{{{\nu }_{3}}} {\frac{{d{{\nu }_{3}}}}{{{{\nu }_{3}}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} }}} = - \frac{{2{{\mu }_{1}}}}{3}(t - {{t}_{0}}),$
т.е. переменная $\nu _{3}^{{}}$ изменяется на отрезке
(4.13)
$ - \lambda _{0}^{{}} \leqslant \nu _{3}^{{}} \leqslant \lambda _{0}^{{}}\quad \left( {\lambda _{0}^{{}} = \frac{{\sqrt 3 }}{2}} \right),$
где $\nu _{3}^{{(0)}} \ne 0$. Интеграл (4.12) вычисляется в элементарных функциях

(4.14)
$\nu _{3}^{{}}(t) = \frac{{\sqrt 3 }}{{2\operatorname{ch} w(t)}},\quad w(t) = \frac{{\mu _{1}^{{}}(t - {{t}_{0}})}}{{\sqrt 3 }}$

В силу (4.1), (4.2), (4.13), (4.14), движение тела-носителя при $t \to \infty $ стремится к состоянию покоя [27]. Значение гиростатического момента ${{\lambda }_{3}}(t)$ находим из (4.11). Таким образом, справедливо утверждение.

Утверждение 4. Построен класс решений уравнений движения динамически симметричного гиростата под действием потенциальных и гироскопических сил, которое не является прецессионным. Для него движение тела-носителя обладает свойством асимптотичности к состоянию покоя. Центр масс гиростата лежит в плоскости равных главных моментов инерции.

Заключение. В статье построены новые решения уравнений движения гиростата с переменным гиростатическим моментом в двух задачах динамики: в задаче о движении тяжелого гиростата и в задаче о движении гиростата под действием потенциальных и гироскопических сил.

Список литературы

  1. Thomson W. On the motion of rigid solids in a liquid circulating irrotationally through perforations in them or in any fixed solid // Proc. Roy. Soc. Edinburgh. 1872. V. 7. P. 668–674.

  2. Volterra V. Sur la théorie des variations des latitudes // Acta. Math. 1899. V. 22. P. 201–358.

  3. Жуковский Н.Е. О движении твердого тела, имеющего полости, наполненные однородной капельной жидкостью // Собр. соч. Т. 1. М., 1949. С. 31–152.

  4. Gray A. A Treatise on Gyrostatics and Rotational Motion. Theory and Applications. New York: Dover Publ., 1959. 530 p.

  5. Леви-Чивита Т., Амальди У. Курс теоретической механики. Т. 2, ч. 2. М.: Изд-во иностр. лит., 1951. 555 с.

  6. Румянцев В.В. Об управлении ориентацией и о стабилизации спутника роторами // Вестн. Моск. ун-та. Сер. Математика, механика. 1970. № 2. С. 83–96.

  7. Харламов П.В. Об уравнениях движения системы твердых тел // Механика твердого тела. 1972. Вып. 4. С. 52–73.

  8. Виттенбург Й. Динамика систем твердых тел. М.: Мир, 1980. 292 с.

  9. Kane T.R., Fowler R.C. Equivalence of two gyrostatic stability problems // J. Appl. Mech. V. 37 (4). 1970. P. 1146–1147.

  10. Roberson R.E. The equivalence of two classical problems of free spinning gyrostats // J. Appl. Mech. V. 38 (3). 1971. P. 1146–1147.

  11. Асланов В.С., Дорошин А.В. Движение системы соосных тел переменной массы // ПММ. 2004. Т. 68. Вып. 6. С. 999–1009.

  12. Асланов В.С., Дорошин А.В. О двух случаях движения неуравновешенного гиростата // Изв. РАН. МТТ. № 4. 2006. С. 42–55.

  13. Горр Г.В., Мазнев А.В., Котов Г.А. Движение гиростата с переменным гиростатическим моментом. Донецк: Изд-е ГУ “Институт прикладной математики и механики”, 2017. 250 с.

  14. Харламов П.В. Об инвариантных соотношениях системы дифференциальных уравнений // Механика твердого тела. 1974. Вып. 6. С. 15–24.

  15. Ковалев А.М., Горр Г.В., Неспирный В.Н. Инвариантные соотношения неавтономных систем дифференциальных уравнений с приложением в механике // Механика твердого тела. 2013. Вып. 43. С. 3–19.

  16. Ольшанский В.Ю. Линейные инвариантные соотношения уравнений Пуанкаре–Жуковского // ПММ. 2014. Т. 78. Вып. 1. С. 29–45.

  17. Ольшанский В.Ю. Об одном новом линейном инвариантном соотношении уравнений Пуанкаре–Жуковского // ПММ. 2012. Т. 76. Вып. 6. С. 883–894.

  18. Зиглин С.Л. Расщепление сепаратрис, ветвление решений и несуществование интеграла в динамике твердого тела // Тр. Москов. мат. об-ва. 1980. Т. 41. С. 287–303.

  19. Козлов В.В., Онищенко Д.А. Неинтегрируемость уравнений Кирхгофа // Докл. АН СССР. 1982. Т. 266. № 6. С. 1298–1300.

  20. Горр Г.В., Кудряшова Л.В., Степанова Л.А. Классические задачи динамики твердого тела. Развитие и современное состояние. Киев: Наук. думка, 1978. 294 с.

  21. Борисов А.В., Мамаев И.С. Динамика твердого тела. Ижевск: Регулярная и хаотическая динамика, 2001. 384 с.

  22. Kirchhoff G.R. Über die Bewegung eines Rotationkörpers in einer Flüssigkeit // J. für die reine und angew. Math. 1870. Bd. 71. S. 237–262.

  23. Стеклов В.А. О движении твердого тела в жидкости. Харьков, 1893. 234 с.

  24. Харламов П.В. О движении в жидкости тела, ограниченного многосвязной поверхностью // ПМТФ. 1963. № 4. С. 17–29.

  25. Горр Г.В. О трех инвариантных соотношениях уравнений движения тела в потенциальном поле сил // ПММ. 2019. Т. 83. № 2. С. 202–214.

  26. Gorr G.V., Tkachenko D.N., Shchetinina E.K. Research on the motion of a body in a potential force field in the case of three invariant relations // Russ. J. Nonlin. Dyn. 2019. V. 15. № 3. P. 327–342.

  27. Горр Г.В., Мазнев А.В. Динамика гиростата, имеющего неподвижную точку. Донецк: ДонНУ, 2010. 364 с.

  28. Горр Г.В., Ковалев А.М. Движение гиростата. Киев: Наук. думка, 2013. 408 с.

  29. Grioli G. Questioni di dinamica del corpo rigido // Atti. Accad. Naz. Lincei, Rend. Cl. Sci. Fis. Mat. e Natur. 1963. V. 35. F. 1–2. P. 35–39.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал