Прикладная математика и механика, 2021, T. 85, № 2, стр. 257-272
Определение мест расположения контрольно-термических скважин при искусственном замораживании породного массива
М. А. Семин 1, *, Л. Ю. Левин 1, М. С. Желнин 2, О. А. Плехов 2
1 Горный институт УрО РАН
Пермь, Россия
2 Институт механики сплошных сред УрО РАН
Пермь, Россия
* E-mail: seminma@inbox.ru
Поступила в редакцию 08.07.2020
После доработки 29.09.2020
Принята к публикации 14.01.2021
Аннотация
В статье проведено исследование оптимальных мест расположения контрольно-термических скважин, исходя из критерия наиболее быстрой и достоверной калибровки теплофизической модели замораживаемого породного массива по измерениям температуры. Для этого исследована чувствительность решения прямой задачи Стефана к вариации теплофизических свойств породного массива. Определены зоны наибольшей чувствительности решения по отношению к вариациям теплопроводностей и влажности массива – в этих зонах наиболее целесообразно располагать контрольно-термические скважины. Далее получено численное решение обратной задачи Стефана в фазовой плоскости параметров калибровки математической модели. Подтверждены выводы о выборе мест расположения скважин, полученные при анализе чувствительности решения прямой задачи Стефана. В дополнение к этому, получено, что при комплексной калибровке множества теплофизических параметров массива оптимальное расположение контрольно-термической скважины может существенно не совпасть с ее расположениями при рассмотрении параметров калибровки по отдельности.
Введение. Математическое моделирование процесса искусственного замораживания породного массива является неотъемлемым этапом при мониторинге формирования ледопородных ограждений (завес) строящихся подземных сооружений [1, 2]. Достаточно актуальным на сегодня является вопрос адекватности и точности математических моделей, используемых для описания искусственного замораживания породного массива. В особенности это касается параметризации математических моделей. Так, например, отмечается [3, 4], что исходные значения теплофизических свойств породного массива (особенно теплопроводностей) могут иметь существенную погрешность, связанную как с несовершенством методов лабораторных испытаний образцов керна, так и с недостаточным количеством кернового материала, отбираемого в процессе геологических изысканий. В конечном счете, это проявляется в сильных расхождениях между рассчитанной и измеренной температурами в местах расположения контрольно-термических скважин. Как следствие, теплофизические модели породного массива, построенные по данным лабораторных испытаний образцов керна, не могут обеспечить достоверное прогнозирование процесса искусственного замораживания породного массива при строительстве подземных сооружений.
Для решения указанной проблемы предложены и применены на практике [1, 3, 4] методы калибровки теплофизических свойств замораживаемого породного массива по данным измерения температуры породного массива в контрольно-термических скважинах. Идея заключалась в подборе теплофизических свойств массива таким образом, чтобы обеспечить наилучшее соответствие между рассчитанной и измеренной температурами в местах расположения контрольно-термических скважин. Математически такой подбор теплофизических свойств массива производился путем решения обратной задачи теплопереноса с движущейся границей фазового перехода поровой воды (или обратной задачи Стефана) [5]. В зарубежной литературе данный подход к идентификации параметров модели на основе полевых измерений называется “обратный анализ” [6].
Возникает естественный вопрос о том, как выбирать места расположения контрольно-термических скважин. К настоящему времени имеется немногочисленное количество исследований, в которых рассматривался этот вопрос [7, 8]. Местоположения скважин определялись по таким принципам, как смыкание фронтов замерзания поровой воды, распространяющихся от отдельных замораживающих скважин, и достижение ледопородного ограждения требуемой толщины.
В настоящей статье делается попытка ответить на вопрос выбора мест расположения контрольно-термических скважин с использованием другого критерия – наиболее быстрой и достоверной калибровки теплофизических свойств замораживаемого породного массива по измеренным температурам в контрольно-термических скважинах. Для этого в соответствии с теорией оптимального планирования эксперимента проводится теоретическое исследование чувствительности решения прямой задачи Стефана к вариации теплофизических свойств породного массива. Исходя из определенных зон наибольшей чувствительности решения, делается заключение о выборе мест расположения контрольно-термических скважин. Полученные выводы подкрепляются данными численного решения обратной задачи Стефана для условий промплощадки рудника Петриковского горно-обогатительного комплекса.
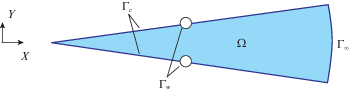
1. Математическая постановка задачи. Искусственное замораживание породного массива для строительства вертикального шахтного ствола осуществляется по следующей технологической схеме: вокруг проектируемой горной выработки бурится круговой контур замораживающих скважин, в которые монтируются колонки, далее колонки подключаются к рассольной сети, и организуется непрерывная циркуляция охлажденного до отрицательных температур рассола по системе замораживающих колонок. В результате окружающий породный массив постепенно охлаждается и замерзает. Следуя терминологии [7], где поровая вода полностью перешла в твердое состояние, будем называть зоной льда, а зону, где поровая вода находится в жидком состоянии – зоной охлаждения.
Сформулируем постановку прямой задачи Стефана в обобщенном виде [8] для горизонтального слоя влагонасыщенного породного массива в условиях искусственного замораживания. Для этого примем следующие упрощающие гипотезы:
1. Промерзающий влагонасыщенный породный массив представляет собой горизонтально-слоистую пористую среду, состоящую из сухого скелета и порового пространства, которое заполнено водой и льдом.
2. Теплофизические свойства каждого породного слоя являются однородными и изотропными в зонах льда и охлаждения.
3. Вертикальный тепловой поток отсутствует; распределение температуры считается однородным по всей толщине слоя.
4. Конвективный теплоперенос вследствие миграции поровой воды не учитывается.
5. Локальное тепловое равновесие между различными фазами (сухой скелет, вода, лед).
6. Отклонения положений замораживающих колонок от проектных значений не рассматриваются.
Введенные гипотезы позволяют перейти к двумерной постановке задачи и рассмотреть круговой сектор, заключенный между двумя главными плоскостями ледопородного ограждения (рис. 1).
Уравнение баланса энергии влагонасыщенного слоя породного массива без явного выделения границы фазового перехода в декартовых координатах может быть записано как [9]:
(1.1)
$\rho {{c}_{{\operatorname{eff} }}}\frac{{\partial T}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\lambda \frac{{\partial T}}{{\partial y}}} \right),\quad (x,y) \in \Omega ,\quad t \in [0,{{t}_{{\operatorname{end} }}}],$Теплофизические параметры влагонасыщенного породного слоя определяются согласно [10, 11]:
(1.2)
$\rho = \theta {{\rho }_{{\operatorname{sd} }}} + (1 - \theta ){{\rho }_{{\operatorname{lq} }}}$(1.3)
$\lambda = \theta {{\lambda }_{{\operatorname{sd} }}} + (1 - \theta ){{\lambda }_{{\operatorname{lq} }}}$(1.4)
${{c}_{{\operatorname{eff} }}} = \frac{1}{\rho }\left[ {\theta {{\rho }_{{\operatorname{lq} }}}{{c}_{{\operatorname{lq} }}} + (1 - \theta ){{\rho }_{{\operatorname{sd} }}}{{c}_{{\operatorname{sd} }}}} \right] + \frac{L}{2}\frac{d}{{dT}}\left[ {\frac{{(1 - \theta ){{\rho }_{{\operatorname{lq} }}} - \theta {{\rho }_{{\operatorname{sd} }}}}}{\rho }} \right],$Удельная теплота фазового перехода $L$ определяется в зависимости от массовой влажности w, кг/кг, [10, 12]
где ${{L}_{0}}$ – удельная теплота кристаллизации воды, Дж/кг. Отметим, что влажность породного массива $w$ здесь трактуется в смысле [13] – как масса влаги, в малом объеме породы, отнесенная на массу этого объема породы во влажном состоянии.Функция θ записывается в зависимости от температуры $T$ следующим образом:
(1.6)
$\theta (T) = \left\{ \begin{gathered} 1,\quad T \leqslant {{T}_{{\operatorname{sd} }}} \hfill \\ {{\left( {{{T}_{{\operatorname{lq} }}} - T} \right)}^{3}}{\text{/}}{{\left( {{{T}_{{\operatorname{lq} }}} - {{T}_{{\operatorname{sd} }}}} \right)}^{3}},\quad {{T}_{{\operatorname{sd} }}} < T \leqslant {{T}_{{\operatorname{lq} }}} \hfill \\ 0,\quad {{T}_{{\operatorname{lq} }}} < T \hfill \\ \end{gathered} \right.$Данная функция служит для сглаживания перехода между теплофизическими свойствами в зоне охлаждения и зоне льда в пределах интервала сглаживания $[{{T}_{{\operatorname{sd} }}},{{T}_{{\operatorname{lq} }}}]$.
Граничные и начальное условия задачи представлены ниже:
(1.7)
${{\left. T \right|}_{{{{\Gamma }_{w}}}}} = {{T}_{w}}(t),\quad {{\left. T \right|}_{{{{\Gamma }_{\infty }}}}} = {{T}_{0}},\quad {{\left. {\frac{{\partial T}}{{\partial {\mathbf{n}}}}} \right|}_{{{{\Gamma }_{C}}}}} = 0$В уравнении (1.1) вся информация о фазовом переходе поровой влаги заключена в эффективную удельную теплоемкость (1.4), что позволяет выполнить моделирование теплопереноса во влагонасыщенной пористой среде с учетом скрытой теплоты кристаллизации без явного выделения границы фазового перехода. Данный подход к моделированию фазовых переходов в средах называется подходом эффективных теплоемкостей [9, 14, 15].
2. Исследование чувствительности решения задачи к вариации свойств массива. Сформулированная выше прямая задача Стефана использовалась для исследования чувствительности поля температур в замораживаемом породном слое к вариации его теплофизических свойств. В качестве варьируемых параметров выбраны теплопроводности в зонах льда ${{\lambda }_{{\operatorname{sd} }}}$ и охлаждения ${{\lambda }_{{\operatorname{lq} }}}$, а также влажность пород $w$. В статье подробно рассмотрены результаты исследований для слоя мела в условиях строящихся стволов калийного рудника Петриковского горно-обогатительного комбината. Основные теплофизические свойства мела, определенные в ходе инженерно-геологических изысканий, сведены в табл. 1. Прочие параметры задачи представлены в табл. 2.
Таблица 1.
Теплофизические свойства слоя мела
| Свойство | Значение |
|---|---|
| ${{\lambda }_{{\operatorname{sd} }}}$, Вт/(м °С) | 2.18 |
| ${{\lambda }_{{\operatorname{lq} }}}$, Вт/(м °С) | 1.31 |
| ${{\rho }_{{\operatorname{sd} }}}$, кг/м3 | 1771 |
| ${{\rho }_{{\operatorname{lq} }}}$, кг/м3 | 1816 |
| ${{c}_{{\operatorname{sd} }}}$, Дж/(кг °С) | 1126 |
| ${{c}_{{\operatorname{lq} }}}$, Дж/(кг °С) | 1767 |
| $w$, кг/кг | 0.32 |
| ${{T}_{{\operatorname{sd} }}}$, °С | –1 |
| ${{T}_{{\operatorname{lq} }}}$, °С | 0 |
| ${{L}_{0}}$, Дж/кг | 33 0000 |
| ${{T}_{0}}$, °С | 6.5 |
Таблица 2.
Геометрические и физические параметры задачи
| Параметр | Значение |
|---|---|
| Радиус кругового сектора (расчетной области), м | 16.25 |
| Расстояния от центра кругового сектора до центра замораживающей колонки, м | 8.25 |
| Радиус замораживающей колонки, м | 0.073 |
| Угол между ограничивающими сектор радиусами, ° | 8.78 |
| ${{t}_{{\operatorname{end} }}}$, с | 3 × 107 |
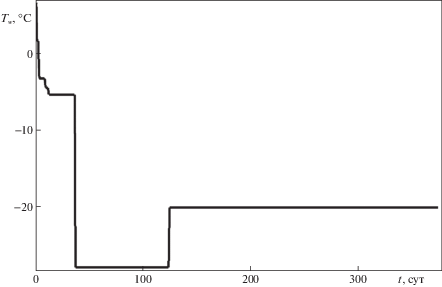
Температура на границах замораживающих колонок задается в виде временной функции, представленной на рис. 2. Данная функция соответствует реальной временной динамике температуры рассола, подаваемого в замораживающие колонки, при строительстве стволов калийного рудника Петриковского горно-обогатительного комплекса.
Прежде всего, исследовано относительное влияние вариаций теплофизических свойств породного массива на поле температуры на различном удалении от контура замораживания – 1, 3 и 5 м. На соответствующих удалениях от контура замораживания вдоль оси $X$ установлены модельные контрольно-термические скважины $K{{T}_{1}}$, $K{{T}_{2}}$ и $K{{T}_{3}}$. Рассмотрено два модельных времени:
– время окончания активного замораживания и достижения требуемой по проекту толщины ледопородного ограждения: ${{t}_{1}}$ = 110.4 сут. (9.54 × 106 с),
– время окончания пассивного замораживания: ${{t}_{2}}$ = 347.2 сут. (3 × 107 c).
Для оценки влияния рассчитывались усредненные по времени квадратичные отклонения температур породного слоя $E$ в контрольно-термических скважинах $K{{T}_{i}}$ в результате относительного увеличения каждого из трех исследуемых теплофизических параметров ${{p}_{k}}$ (${{p}_{1}} = {{\lambda }_{{\operatorname{sd} }}}$, ${{p}_{2}} = {{\lambda }_{{\operatorname{lq} }}}$, ${{p}_{3}} = \omega $) на 50%:
(2.1)
$\begin{gathered} E({{x}_{i}},{{y}_{i}},{{p}_{k}}) = \int\limits_{{{t}_{0}}}^{{{t}_{j}}} {{{{[T({{x}_{i}},{{y}_{i}},t;p_{k}^{'}) - T({{x}_{i}},{{y}_{i}},t;{{p}_{k}})]}}^{2}}dt} ,\quad p_{k}^{'} = 1.5{{p}_{k}} \\ (i,k = 1,\;2,\;3;\quad j = 1,2), \\ \end{gathered} $Функционал $E$ действует на множестве решений задачи (1.1)–(1.8) и ставит в соответствие решению $T = T(x,y,t;p_{k}^{'})$, полученного для возмущенного параметра $p_{k}^{'}$, его отклонение по времени в точке $({{x}_{i}},{{y}_{i}})$, соответствующей расположению контрольно-термической скважине $K{{T}_{i}}$, от решения $T = T(x,y,t;{{p}_{k}})$, найденного для параметра ${{p}_{k}}$, приведенного в табл. 1. Приращение параметров определялось, исходя из ограничений на значения теплофизических свойств породного массива, – например, максимальные и минимальные значения теплопроводностей, которые встречаются на практике для рассматриваемого слоя горных пород. Значения функционала $E$ для времен моделирования ${{t}_{j}}$ представлены в табл. 3, 4.
Таблица 3.
Значения E для времени моделирования 110.4 сут.
| Контрольно-термическая скважина | ${{\lambda }_{{\operatorname{sd} }}}$ | ${{\lambda }_{{\operatorname{lq} }}}$ | $w$ |
|---|---|---|---|
| $K{{T}_{1}}$ | 12 870.3 | 374.5 | 1218.0 |
| $K{{T}_{2}}$ | 50.5 | 623.7 | 13.4 |
| $K{{T}_{3}}$ | 0.8 | 122.2 | 0.3 |
Таблица 4.
Значения E для времени моделирования 347.2 сут.
| Контрольно-термическая скважина | ${{\lambda }_{{\operatorname{sd} }}}$ | ${{\lambda }_{{\operatorname{lq} }}}$ | $w$ |
|---|---|---|---|
| $K{{T}_{1}}$ | 43 917.9 | 710.6 | 37 384.6 |
| $K{{T}_{2}}$ | 3675.0 | 1578.3 | 1536.9 |
| $K{{T}_{3}}$ | 584.6 | 1328.3 | 219.6 |
В ближайшей к контуру замораживания скважине $K{{T}_{1}}$ теплопроводность ${{\lambda }_{{\operatorname{sd} }}}$ оказывает наиболее сильное влияние на поле температуры в массиве (об этом свидетельствует наибольшее значение функционала $E$), а теплопроводность ${{\lambda }_{{\operatorname{lq} }}}$ – наиболее слабое. Если в момент времени 110.4 сут. влияние влажности w на решение на порядок ниже, чем влияние теплопроводности ${{\lambda }_{{\operatorname{sd} }}}$, то в момент времени 347.2 сут. ситуация меняется и влажность начинает влиять на решение сопоставимо с теплопроводностью в зоне льда.
В более удаленных от контура скважинах $K{{T}_{2}}$ и $K{{T}_{3}}$ для времени 110.4 сут. влияние теплопроводности ${{\lambda }_{{\operatorname{lq} }}}$ существенно превосходит влияние остальных двух параметров. Для времени 347.2 сут. в средней скважине $K{{T}_{2}}$ доминирующее влияние на решение по-прежнему оказывает теплопроводность ${{\lambda }_{{\operatorname{sd} }}}$, но для более дальней скважины $K{{T}_{3}}$ влияние ${{\lambda }_{{\operatorname{sd} }}}$ на поле температур примерно в 2.5 раза ниже, чем для ${{\lambda }_{{\operatorname{lq} }}}$.
Возмущение влажности $w$ оказывает промежуточное влияние на поле температуры независимо от продолжительности наблюдений – значения функционала $E$ для вариации параметра $w$ меньше, чем соответствующие значения либо для вариации ${{\lambda }_{{\operatorname{sd} }}}$, либо для вариации ${{\lambda }_{{\operatorname{lq} }}}$. Характер изменения влияния возмущения влажности $w$ на поле температуры с увеличением расстояния скважины от контура замораживания и увеличением продолжительности наблюдений качественно совпадает с изменением влияния теплопроводности ${{\lambda }_{{\operatorname{sd} }}}$. По данной причине далее рассматривались вариации только двух теплофизических параметров породного массива – теплопроводностей ${{\lambda }_{{\operatorname{sd} }}}$ и ${{\lambda }_{{\operatorname{lq} }}}$.
На следующем этапе исследовались распределения чувствительности поля температуры при вариации каждого из рассматриваемых теплофизических свойств. В качестве меры чувствительности принимался следующий скалярный критерий:
(2.2)
$\Phi (x,y,{{t}_{{\operatorname{end} }}}) = - \ln \left[ {\frac{1}{{{{t}_{{\operatorname{end} }}} - {{t}_{0}}}}\int\limits_{{{t}_{0}}}^{{{t}_{{\operatorname{end} }}}} {{{{\left( {\frac{{\partial T(x,y,\tau )}}{{\partial {{p}_{i}}}}} \right)}}^{2}}{\text{d}}\tau } } \right],\quad i = 1,\;2,\;3$Критерий $\Phi $ по форме аналогичен известному в литературе D-критерию оптимальности экспериментального плана, широко применяемому в теории оптимального планирования экспериментов для оценки влияния условий проведения эксперимента на решение обратной задачи [16].
Оптимальные местоположения контрольно-термических скважин в расчетной области ищутся по критерию наибольшей чувствительности решения к вариации теплофизических свойств массива. Для этого решается задача поиска минимума критерия Φ с помощью метода сопряженных градиентов [17]. Расчет величин $\partial T{\text{/}}\partial {{p}_{i}}$ выполняется путем численного решения методом конечных элементов краевой задачи в приращениях температуры, записанной для задачи (1.1)–(1.8).
Численные расчеты для определения распределения критерия $\Phi $ при вариациях каждого из трех рассматриваемых теплофизических свойств выполнялись для ранее рассмотренного слоя мела. На рис. 3 представлены распределения критерия $\Phi $ в расчетной области $\Omega $ для теплопроводности в зоне охлаждения ${{\lambda }_{{\operatorname{lq} }}}$ при различных временах ${{t}_{{\operatorname{end} }}}$ моделирования. В качестве конечных времен ${{t}_{{\operatorname{end} }}}$ моделирования рассмотрены моменты времени:
Рис. 3.
Распределение критерия Φ для теплопроводности в зоне охлаждения ${{\lambda }_{{\operatorname{lq} }}}$ для различных времен моделирования а–г ${{t}_{{\operatorname{end} }}}$ = 25; 50; 110.4; 347.2 сут. зеленая линия обозначает фронт фазового перехода.
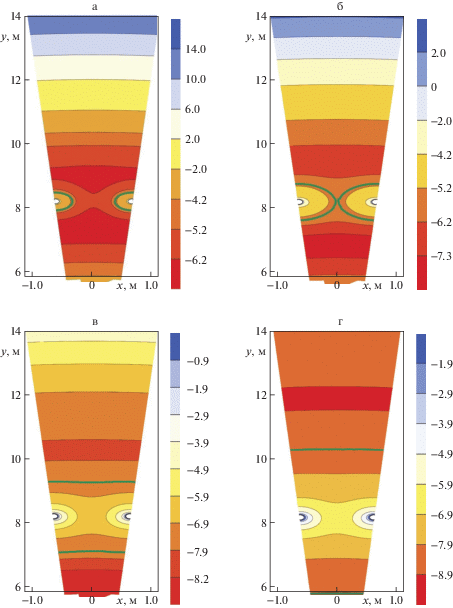
– до смыкания ледопородных цилиндров, соответствующих зонам льда вокруг замораживающих скважин, ${{t}_{{\operatorname{end} }}}$ = 25 сут.;
– смыкание ледопородных цилиндров и формирование сплошного ледопородного ограждения, ${{t}_{{\operatorname{end} }}}$ = 50 сут.;
– достижение проектной толщины ледопородного ограждения ${{t}_{{\operatorname{end} }}}$ = 110.4 сут.;
– окончание замораживания: ${{t}_{{\operatorname{end} }}}$ = 347.2 сут.
Из рис. 3 видно, что во всех рассмотренных случаях критерий Φ достигает своих максимальных значений в зоне охлаждения. Критерий Φ является гладкой функцией, без резких перепадов и скачков. Рассматривая значения критерия Φ на замковой плоскости ледопородного ограждения, можно сказать, что он имеет немонотонный характер распределения по расчетной области и два локальных минимума. Один минимум расположен внутри контура замораживания, а второй – вовне. При этом значение локального минимума, расположенного внутри контура замораживания меньше, чем расположенного вовне. До смыкания отдельных ледопородных цилиндров (25 сут.) локальные минимумы находятся вблизи контура замораживания на расстояниях соответственно 0.85 и 0.65 м от этого контура. С увеличением времени моделирования локальные минимумы смещаются вслед за границей фазового перехода, удаляясь от контура замораживания. Так при временах моделирования 50, 110.4 и 347.2 сут. внешний локальный минимум расположен на расстояниях от контура замораживания, равных соответственно 1.15, 1.95 и 3.65 м.
Таким образом, для решения коэффициентной обратной задачи Стефана относительно теплопроводности в зоне охлаждения ${{\lambda }_{{\operatorname{lq} }}}$ оптимальное положение контрольно-термической скважины зависит от длительности измерений температуры и конечного положения границы фазового перехода. В целом в этом случае оптимальное положение контрольно-термической скважины находится в зоне охлаждения, при этом нет принципиальной разницы в размещении контрольно-термической скважины в замковой или главной плоскостях ледопородного ограждения. Если в качестве наиболее значимого времени моделирования принять время достижения проектной толщины ледопородного ограждения, то на основании рис. 3в контрольно-термическую скважину следует размещать вовне контура замораживания на расстоянии 2–2.5 м от него.
На рис. 4 представлены распределения критерия Φ в расчетной области для теплопроводности в зоне льда ${{\lambda }_{{\operatorname{sd} }}}$ для различных времен моделирования ${{t}_{{\operatorname{end} }}}$. Из распределений видно, что критерий Φ достигает своих минимальных значений в зоне льда. Значения Φ изменяются от точки к точке сильнее по сравнению с более пологим распределением критерия Φ для теплопроводности в зоне охлаждения (рис. 3). При проведении наблюдений вплоть до момента смыкания отдельных ледопородных цилиндров (50 сут.), минимумы Φ расположены вблизи замораживающих скважин. На момент достижения проектной толщины ледопородного ограждения (110.2 сут.) критерий Φ имеет единственный минимум, расположенный примерно на пересечении контура замораживания с замковой плоскости ледопородного ограждения. При дальнейшем увеличении продолжительности наблюдений у критерия Φ возникают два локальных минимума, один вовне контура замораживания (на расстоянии 0.85 м от него) и один внутри контура замораживания (на расстоянии 1.1 м от него).
Рис. 4.
Распределение критерия Φ для теплопроводности в зоне льда ${{\lambda }_{{\operatorname{sd} }}}$ для различных времен моделирования а–г ${{t}_{{\operatorname{end} }}}$ = 25; 50; 110.4; 347.2 сут., зеленая линия обозначает фронт фазового перехода.
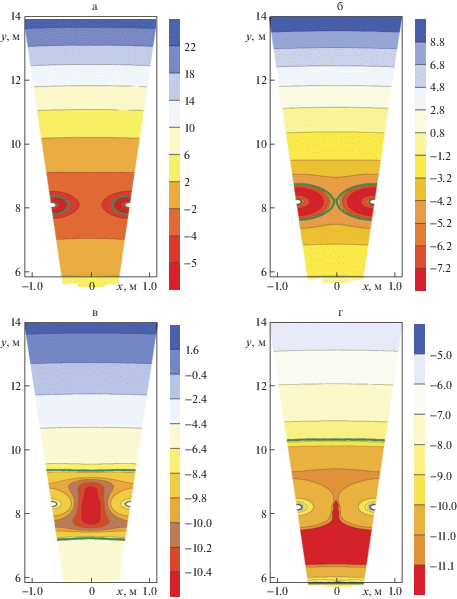
Для решения коэффициентной обратной задачи Стефана относительно теплопроводности в зоне льда ${{\lambda }_{{\operatorname{sd} }}}$ оптимальное расположение контрольно-термической скважины также зависит от продолжительности наблюдений, но находится в зоне льда. С учетом ограничений технического плана расстояния между двумя ближайшими скважинами не может быть меньше некоторой величины, зависящей от глубины бурения [7, 18]. Данная величина зачастую сопоставима или равна расстоянию между замораживающими колонками. С учетом этого ограничения и полученных расчетных данных (рис. 4) следует принять, что контрольно-термическую скважину следует размещать в замковой плоскости ледопородного ограждения на минимальном расстоянии от контура замораживания.
3. Исследование решения обратной задачи Стефана. Полученные выводы о чувствительности решения прямой задачи Стефана к вариации теплофизических свойств массива были апробированы посредством численного решения коэффициентной обратной задачи Стефана. Решения строились при различных местоположениях контрольно-термических скважин для возможности проведения сравнения результатов решений на предмет единственности и наискорейшей сходимости численной итерационной процедуры решения.
Постановка обратной задачи Стефана и численный алгоритм ее решения, основанный на методе градиентного спуска, описаны в ранее [3, 12]. Это не единственные методы решения обратных задач Стефана, так, для решения подобных задач используется метод дескриптивной регуляризации [19] и вариационно-итерационный метод [20].
Для формулировки обратной задачи необходимо переопределить прямую задачу (1.1)–(1.7) посредством введения заданных измеренных температур $T_{i}^{{(c)}}(t)$ в местах расположения $\left( {{{x}_{i}},{{y}_{i}}} \right)$ каждой контрольно-термической скважины номера i:
(3.1)
$T\left( {t,{{x}_{i}},{{y}_{i}}} \right) = T_{i}^{{(c)}}{\kern 1pt} \left( t \right),\quad i = 1,\; \ldots ,\;{{N}_{C}}$Здесь ${{N}_{C}}$ – количество контрольно-термических скважин.
Таким образом, решение обратной задачи Стефана в данном случае состоит в определении поля температур $T\left( {t,x,y} \right)$ и значений теплофизических свойств массива ${{p}_{j}}$ ($j = 1,\; \ldots ,\;{{N}_{P}}$), удовлетворяющих системе уравнений (1.1)–(1.8), (3.1). Здесь ${{N}_{P}}$ – количество калибруемых теплофизических свойств массива. В рассматриваемом нами случае имеется два калибруемых теплофизических свойства – теплопроводности в зонах льда ${{p}_{1}} = {{\lambda }_{{\operatorname{sd} }}}$ и охлаждения ${{p}_{2}} = {{\lambda }_{{\operatorname{lq} }}}$.
Численное решение поставленной коэффициентной обратной задачи осуществляется с помощью метода естественной регуляризации [5], в рамках которого жесткое условие (3.1) заменяется на условие минимума функционала $I = I\left( {{{\lambda }_{{\operatorname{sd} }}},{{\lambda }_{{\operatorname{lq} }}}} \right)$ рассогласований температур, имеющего вид:
(3.2)
$I = \sqrt {\frac{1}{{{{N}_{C}}{{N}_{m}}}}\frac{1}{{\Delta {{T}^{2}}}}\sum\limits_{k = 1}^{{{N}_{m}}} {\sum\limits_{i = 1}^{{{N}_{C}}} {{{{\left[ {{{T}_{i}}\left( {{{t}_{k}},{{x}_{i}},{{y}_{i}}} \right) - T_{i}^{{(c)}}\left( {{{t}_{k}}} \right)} \right]}}^{2}}} } } ,$Количество контрольно-термических скважин принято равным единице. Рассмотрено четыре варианта положений контрольно-термической скважины – на расстояниях 0.25, 1.25, 2.5 и 3.75 м от контура замораживания. Во всех случаях контрольно-термическая скважина располагалась на замковой плоскости ледопородного ограждения. Рассмотрено время моделирования ${{t}_{{\operatorname{end} }}}$, равное 110.4 сут (время окончания активного замораживания).
На рис. 5 представлены изолинии функционала рассогласований температур в фазовом пространстве параметров минимизации – теплопроводностей в зонах льда ${{\lambda }_{{\operatorname{sd} }}}$ и охлаждения ${{\lambda }_{{\operatorname{lq} }}}$. Четыре поля изолиний соответствуют четырем различным местам размещения контрольно-термических скважин. Также на рис. 5 а, б представлены кривые, соответствующие итерационной процедуре минимизации функционала (3.2) из двух разных начальных точек ${{H}_{1}}$ и ${{H}_{2}}$. На рис. 6 представлены зависимости функционала рассогласований температур от отдельных параметров минимизации, построенные вдоль штриховых линий, указанных на рис. 5.
Рис. 5.
Изолинии функционала рассогласований температур $I$ в фазовом пространстве параметров минимизации (${{\lambda }_{{\operatorname{sd} }}}$, ${{\lambda }_{{\operatorname{lq} }}}$) при различных расстояниях контрольно-термической скважины от контура замораживания: а) – 0.25 м, б) – 1.25 м, в) – 2.5 м, г) – 3.75 м.
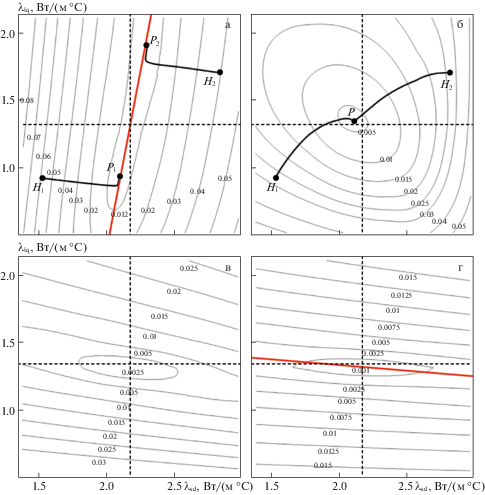
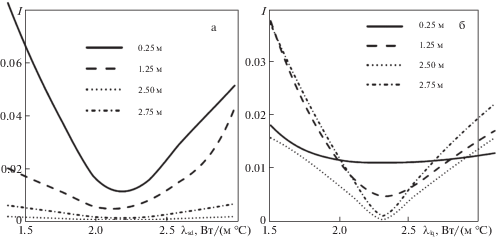
Рис. 6.
Зависимости функционала $I$ рассогласований температур от теплопроводности в зоне льда ${{\lambda }_{{\operatorname{sd} }}}$ (а) и теплопроводности в зоне охлаждения ${{\lambda }_{{\operatorname{lq} }}}$ (б).
Из рис. 5 следует, что форма функционала рассогласования в фазовом пространстве теплопроводностей сильно меняется с изменением положения контрольно-термической скважины, что согласуется с ранее полученными результатами [3]. Если для скважин вблизи контура замораживания изолинии расположены практически вдоль оси ординат, то при постепенном удалении скважины от контура замораживания изолинии функционала постепенно перестраиваются и вытягиваются вдоль оси абсцисс.
В целом случай а) слишком близкого расположения контрольно-термической скважины к контуру замораживания одинаково плох, как и случай г) слишком дальнего расположения контрольно-термической скважины к контуру замораживания – в обоих этих случаях на графиках можно выделить линию (см. рис. 5 а,г, красный цвет), вдоль которой значения функционала рассогласований меняются очень слабо. Это, по сути, означает, что при минимизации функционала $I$ есть риск оказаться в любой из точек на этих прямых – т.е. любая из этих точек окажется решением обратной задачи Стефана. Этот факт подтвержден при численном решении обратной задачи – при разных начальных значениях теплопроводностей массива на рис. 5а получаются различные решения обратной задачи – точки ${{P}_{1}}$ и ${{P}_{2}}$. При этом, на рис. 5б в аналогичной ситуации достигается единственное решение задачи – точка $P$.
При этом, если рассматривать обусловленность задачи минимизации функционала $I$ по каждой из теплопроводностей в отдельности (см. рис. 6), то видно, что функционал $I$ имеет наиболее характерный минимум по теплопроводности в зоне льда ${{\lambda }_{{\operatorname{sd} }}}$ при самом близком расположении контрольно-термической скважины к контуру замораживания 0.25 м (рис. 6а), а минимум по теплопроводности в зоне охлаждения ${{\lambda }_{{\operatorname{lq} }}}$ наблюдается при расположении контрольно-термической скважины в интервале расстояний 1.25 и 2.5 м от контура замораживания (рис. 6б). Судить о характерности минимумов можно исходя из степени наклона кривых на рис. 6 – чем больше средний угол наклона кривой, тем сильнее выражен ее минимум. Эти выводы находятся в полном соответствии с результатами, полученными в предыдущем разделе этой статьи.
Таким образом, наиболее благоприятные места расположения контрольно-термических скважин по фактору наиболее быстрого и однозначного решения задачи минимизации функционала (3.2) для отдельных параметров минимизации (теплопроводностей породного массива) могут не обеспечивать скорость и однозначность решения обратной задачи Стефана для этих параметров в совокупности. Это означает, что выбор оптимальных мест размещения контрольных скважин по фактору наилучшего решения обратной задачи Стефана, должен производиться из комплексного рассмотрения всех калибруемых параметров модели. Для рассмотренного случая калибровки теплопроводностей породного массива в зонах льда и охлаждения полученное оптимальное расположение скважины находится на расстоянии примерно 1.25 м от контура замораживания. В этом случае изолинии функционала $I$ близки к окружностям.
Заключение. В результате проведенных исследований сделаны следующие выводы относительно выбора мест расположения контрольно-термической скважины исходя из критерия наиболее быстрой и достоверной калибровки теплофизических свойств замораживаемого породного массива по измеренным температурам в контрольно-термических скважинах.
– Для наилучшей калибровки теплопроводности породного массива в зоне охлаждения контрольно-термическую скважину следует размещать вовне контура замораживания на расстоянии 2–2.5 м от него. Это обеспечит наиболее точное решение обратной задачи Стефана на момент достижения ледопородного ограждения проектной толщины.
– Для наилучшей калибровки теплопроводности породного массива в зоне льда, а также влажности породного массива контрольно-термическую скважину следует размещать в замковой плоскости ледопородного ограждения на минимальном расстоянии от контура замораживания.
– При этом, при рассмотрении комплексной задачи калибровки множества теплофизических параметров массива выбор положений контрольно-термических скважин должен производиться исходя из комплексного рассмотрения калибруемых теплофизических свойств породного массива. Полученное таким образом оптимальное расположение контрольно-термической скважины может существенно не совпасть с ее расположениями при рассмотрении параметров калибровки по отдельности.
– Неоптимальный выбор мест расположения контрольно-термических скважин может привести к существованию множества решений обратной задачи Стефана.
Исследование выполнено при поддержке Российского научного фонда в рамках проекта № 17-11-01204.
Список литературы
Vitel M., Rouabhi A., Tijani M. et al. Thermo-hydraulic modeling of artificial ground freezing: Application to an underground mine in fractured sandstone // Comput.&Geotechn. 2016. V. 75. P. 80–92.
Papakonstantinou S., Anagnostou G., Pimentel E. Evaluation of ground freezing data from the Naples subway // Proc. Inst. Civil Engineers: Geotechnical Engineering. 2013. V. 166. № 3. P. 280–298.
Левин Л.Ю., Семин М.А., Зайцев А.В. Калибровка теплофизических свойств породного массива при моделировании формирования ледопородного ограждения строящихся шахтных стволов // Физикотехн. пробл. разработ. полезн. ископ. 2019. № 1. С. 172–184.
Долгов О.А. Методика расчета процесса замораживания горных пород при проходке стволов шахт способом замораживания на большую глубину // в кн.: Замораживание горных пород при проходке стволов шахт. М.: Изд. АН СССР, 1961. С. 9–64.
Алифанов О.М. Обратные задачи теплообмена. М.: Машиностроение, 1988. 280 с.
Russo G. et al. Artificial ground freezing to excavate a tunnel in sandy soil. Measurements and back analysis // Tunnell.&Undergr. Space Technol. 2015. V. 50. P. 226–238.
Трупак Н.Г. Замораживание горных пород при проходке стволов. М.: Углетехиздат, 1954. 895 с.
Маньковский Г.И. Специальные способы сооружения стволов шахт. М.: Наука, 1965. 315 с.
Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача. М.: Едиториал УРСС, 2003. 784 с.
Желнин М.С., Плехов О.А., Левин Л.Ю. Оптимизация пассивного режима искусственного замораживания водонасыщенного породного массива // ИФЖ. 2020. Т. 93. № 3. С. 706–714.
Comsol v.5.4 Documentation. Heat Transfer Module User’s Guide. 2018, 784 p.
Левин Л.Ю., Семин М.А., Зайцев А.В. Решение обратной задачи Стефана при анализе замораживания грунтовых вод в породном массиве // ИФЖ. 2018. Т. 91. № 3. С. 655–663.
Янченко Г.А. О взаимосвязях между показателями суммарного содержания влаги в мерзлых горных породах и грунтах // Горные науки и технол. 2016. № 1. С. 25–32.
Хохолов Ю.А., Соловьев Д.Е. Методика совместного расчета температурного и вентиляционного режимов нестационарной сети горных выработок криолитозоны // Физ.-техн. пробл. разраб. Полезн. ископ. 2013. Т. 49. № 1. С. 138–145.
Самарский А.А., Моисеенко Б.Д. Экономичная схема сквозного счета для многомерной задачи Стефана // ЖВММФ. 1965. Т. 5. № 5. С. 816–827.
Ермаков С.М., Жиглявский А.А. Математическая теория оптимального эксперимента. М.: Наука, 1987. 320 с.
Желнин М.С., Плехов О.А., Семин М.А. и др. Численное решение обратной задачи определения объемной теплоемкости породного массива в процессе искусственного замораживания // Вестн. Пермского НИПУ. Механика. 2017. № 4. С. 56–75.
Мишедченко О.А. История развития способа искусственного замораживания пород // Горный информ.-аналит. бюлл. (научно-технич. ж.). 2010. № 2. С. 226–231.
Гольдман Н.Л. Обратные задачи Стефана. Теория и методы решения. М.: МГУ, 1999. 294 с.
Słota D. Direct and inverse one-phase Stefan problem solved by the variational iteration method // Comput. & Math. with Appl. 2007. V. 54. № 7–8. P. 1139–1146.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика