Прикладная математика и механика, 2021, T. 85, № 3, стр. 358-369
Оптимальное демпфирование колебаний при поступательном движении панели в потоке жидкости
Н. В. Баничук 1, *, С. Ю. Иванова 1, **
1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: banichuk@ipmnet.ru
** E-mail: syuivanova@yandex.ru
Поступила в редакцию 24.12.2020
После доработки 20.01.2021
Принята к публикации 02.02.2021
Аннотация
Рассматривается движение упругой панели в потоке идеальной жидкости. Предполагается, что панель совершает малые поперечные колебания и подвержена для их подавления внешним механическим воздействиям. Формулируется и решается задача оптимизации процесса демпфирования колебаний, оцениваемых квадратичным энергетическим критерием. Выведены необходимые условия оптимальности, применяемые для подавления гидроупругих колебаний на конечном интервале времени. Приводится итерационный алгоритм демпфирования колебаний, основанный на последовательном решении “прямых” задач взаимодействия движущихся жидкости и панели и сопряженных задач возвратного интегрирования однородного уравнения с последовательным определением соответствующего приближения для оптимального управления, подавляющего колебания. Развиваемый алгоритм оптимального демпфирования колебаний иллюстрируется на примере аналитического определения стабилизирующего воздействия.
Проблема подавления колебаний механических систем представляет значительный теоретический и прикладной интерес. Для распределенных систем колебания и динамическая устойчивость изучались как в рамках самосопряженных (консервативных), так и несамосопряженных (неконсервативных) задач. Возникающие в этом направлении вопросы рассматривались ранее [1–3]. Значительное внимание при этом уделялось проблемам колебаний деформируемых систем, взаимодействующих с жидкостью или газом (см., например, [4–8]). Отметим здесь представляющие интерес задачи о гидроупругих взаимодействиях, основанные на точных выражениях для реакции жидкости [9–14]. Исследовались [13–19] проблемы устойчивости и оптимизации движущихся упругих и вязкоупругих материалов. В результате определялись критические величины скоростей материала и потока жидкости, а также критические значения натяжения материала, приводящие к потере устойчивости.
В данной работе на основе точного аналитического решения связанной задачи гидроупругости и использования аппроксимации реакции жидкости выведено уравнение в частных производных, описывающее колебания панели, движущейся поступательно в потоке идеальной жидкости. Приведена формулировка и исследование задачи оптимального подавления колебаний в результате приложения к панели активных демпфирующих воздействий. Решение задачи оптимизации выполняется на основе выведенных в работе необходимых условий экстремума и конечно-элементной аппроксимации дифференциального уравнения вынужденных колебаний и сопряженного однородного дифференциального уравнения. Реализация метода Галёркина сводится к интегрированию двух систем обыкновенных дифференциальных уравнений, определяющих функцию прогибов и сопряженную переменную. Описывается эффективный итерационный алгоритм отыскания определяющих переменных и соответствующих демпфирующих воздействий. Приводится иллюстрирующий пример аналитического решения задачи оптимального подавления колебаний.
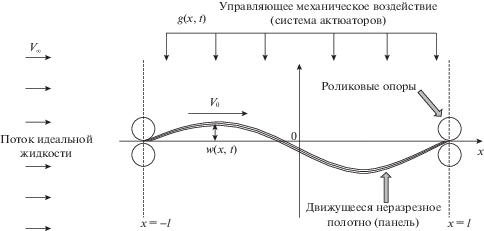
1. Основные соотношения. Рассматривается равномерное поступательное движение со скоростью ${{V}_{0}}$ упругой панели, погруженной в поток идеальной несжимаемой жидкости, движущейся со скоростью ${{{v}}_{\infty }}$ в направлении оси $x$ используемой лабораторной (Эйлеровой) системы координат $xOy$ (рис. 1). Уравнение малых поперечных колебаний движущейся панели записывается в виде [13]
(1.1)
$m\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} + 2m{{V}_{0}}\frac{{{{\partial }^{2}}w}}{{\partial x\partial t}} + \left( {mV_{0}^{2} - T} \right)\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + D\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} = {{q}_{f}} + {{g}_{p}},$(1.2)
${{\left( w \right)}_{{t = 0}}} = {{g}_{1}}\left( x \right),\quad {{\left( {\frac{{\partial w}}{{\partial t}}} \right)}_{{t = 0}}} = {{g}_{2}}\left( x \right);\quad x \in \left[ { - 1,\;1} \right]$(1.3)
${{\left( w \right)}_{{x = \pm 1}}} = 0,\quad {{\left( {\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}} \right)}_{{x = \pm 1}}} = 0;\quad t \in \left[ {0,{{t}_{f}}} \right],$Влияние воздействия потока жидкости на колебания движущейся упругой панели описывается, как показано в [11–13], при помощи сингулярного интеграла, усложняющего реализацию вычислительного процесса при использовании модели (1.1)–(1.3). Учитывая необходимость многократного использования в данной работе этой модели, применим в дальнейшем аппроксимацию реакции жидкости следующим дифференциальным выражением [14]
С использованием величины $C = \sqrt {T{\text{/}}m} $ определим основные используемые безразмерные параметры
(1.4)
$\begin{gathered} {\text{L}}\left( w \right) \equiv {{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right)\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} + 2\alpha \kappa \left( {1 + {{r}_{m}}{{r}_{{v}}}} \right)\frac{{{{\partial }^{2}}w}}{{\partial x\partial t}} + \\ + \;\left[ {{{\kappa }^{2}}\left( {1 + {{r}_{m}}r_{{v}}^{2}} \right) - 1} \right]\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + {{\beta }}\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} = g\left( {x,t} \right);\quad \left( {x,t} \right) \in \Omega \\ \end{gathered} $Заметим, что фигурирующая в правой части уравнения (1.4) безразмерная функция нагрузки $g = g\left( {x,t} \right)$ (функция безразмерных координат $x$, $t$) связана с исходной размерной величиной ${{g}_{p}}$ следующим соотношением:
Заметим также, что модели присоединенных масс часто используются для учета инерционных эффектов в задачах о взаимодействии элементов конструкций с жидкостью. В данной работе теория присоединенных масс применена для моделирования поведения гибких движущихся панелей. При этом предполагаются выполненными предположения о плавном обтекании движущейся панели жидкостью и о не превышении критических скоростей (${{V}_{0}} < {{\left( {{{V}_{0}}} \right)}_{{\operatorname{cr} }}}$, ${{{v}}_{\infty }} < {{\left( {{{{v}}_{\infty }}} \right)}_{{\operatorname{cr} }}}$), т.е. скоростей дивергенции и флаттера [13, 14]. При сделанных предположениях невозмущенное состояние движущейся панели является устойчивым. Точное аналитическое выражение для реакции жидкости в форме сингулярного интеграла [13, 14] аппроксимируется дифференциальным выражением, которое было получено строгим аналитическим методом и не накладывает дополнительных ограничений на параметры задачи и применимо при тех же условиях, что и исходная интегро-дифференциальная модель.
2. Задача оптимизации и условия оптимальности. Рассмотрим процесс подавления возникающих поперечных гидроупругих колебаний движущейся в потоке панели, осуществляющийся за счет прикладываемых к панели поперечных нагрузок $g = g\left( {x,t} \right)$ (управляющих воздействий). Качество процесса подавления колебаний оценивается значением функционала, зависящего от перемещений $w\left( {x,{{t}_{f}}} \right)$ и скоростей $\partial w\left( {x,{{t}_{f}}} \right){\text{/}}\partial t$ в конечный момент времени $t = {{t}_{f}}$, то есть
(2.1)
${{J}_{g}} = \int\limits_{ - 1}^1 {{{{\left[ {{{\alpha }_{1}}{{w}^{2}} + {{\alpha }_{2}}{{{\left( {\frac{{\partial w}}{{\partial t}}} \right)}}^{2}}} \right]}}_{{t = {{t}_{f}}}}}} dx$Здесь ${{\alpha }_{1}} \geqslant 0$ и ${{\alpha }_{2}} \geqslant 0$ – заданные параметры.
На управляющее демпфирующее воздействие $g\left( {x,t} \right)$ наложено энергетическое ограничение в виде следующего неравенства:
(2.2)
${{J}_{{{\mu }}}} = \int\limits_\Omega {{{g}^{2}}\left( {x,t} \right)d\Omega \leqslant {{M}_{0}}} ,$Рассматриваемая задача оптимизации процесса гашения колебаний движущейся в потоке жидкости упругой панели заключается в отыскании управляющего экстремального воздействия $g\left( {x,t} \right)$ ($\left( {x,t} \right) \in \Omega $), удовлетворяющего энергетическому неравенству (2.2) и минимизирующего квадратичный функционал качества (2.1).
Для реализации процесса минимизации рассматриваемого функционала выведем необходимые условия оптимальности. Для этого воспользуемся уравнением колебаний и начально-краевыми условиями в вариациях
(2.3)
$\begin{gathered} \delta {\text{L}}\left( w \right) = {\text{L}}\left( {\delta w} \right) = {{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right)\frac{{{{\partial }^{2}}\delta w}}{{\partial {{t}^{2}}}} + 2\alpha \kappa \left( {1 + {{r}_{m}}{{r}_{{v}}}} \right)\frac{{{{\partial }^{2}}\delta w}}{{\partial x\partial t}} + \\ + \;\left[ {{{\kappa }^{2}}\left( {1 + {{r}_{m}}r_{{v}}^{2}} \right) - 1} \right]\frac{{{{\partial }^{2}}\delta w}}{{\partial {{x}^{2}}}} + \beta \frac{{{{\partial }^{4}}\delta w}}{{\partial {{x}^{4}}}} - \delta g = 0;\quad \left( {x,t} \right) \in \Omega \\ \end{gathered} $(2.4)
${{\left( {\delta w} \right)}_{{t = 0}}} = 0,\quad {{\left( {\frac{{\partial \delta w}}{{\partial t}}} \right)}_{{t = 0}}} = 0;\quad x \in \left[ { - 1,\;1} \right]$(2.5)
${{\left( {\delta w} \right)}_{{x = \pm 1}}} = 0,\quad {{\left( {\frac{{{{\partial }^{2}}\delta w}}{{\partial {{x}^{2}}}}} \right)}_{{x = \pm 1}}} = 0;\quad t \in \left[ {0,{{t}_{f}}} \right],$Будем иметь
(2.7)
$\begin{gathered} \delta {{J}_{g}} = 2{{\int\limits_{ - 1}^1 {\left[ {{{\alpha }_{1}}w\delta w + {{\alpha }_{2}}\frac{{\partial w}}{{\partial t}}\delta \left( {\frac{{\partial w}}{{\partial t}}} \right)} \right]} }_{{t = {{t}_{f}}}}}dx \\ \delta \left( {{{J}_{\mu }} - {{M}_{0}} + {{\theta }^{2}}} \right) = 2\int\limits_\Omega {g\delta gd\Omega + 2\theta \delta \theta = 0} \\ \end{gathered} $Введем в рассмотрение сопряженную переменную ${v}\left( {x,t} \right)$, удовлетворяющую по определению граничным условиям
(2.8)
${{\left( {v} \right)}_{{x = \pm 1}}} = 0,\quad {{\left( {\frac{{{{\partial }^{2}}{v}}}{{\partial {{x}^{2}}}}} \right)}_{{x = \pm 1}}} = 0;\quad t \in \left[ {0,{{t}_{f}}} \right],$(2.9)
$\begin{gathered} \delta {{J}_{a}} = \int\limits_\Omega {{v}\left[ {{\text{L}}\left( {\delta w} \right) - \delta g} \right]d\Omega } = \int\limits_\Omega {\left\{ {\left[ {{\text{L}}\left( {v} \right)} \right]\delta w - {v}\delta g} \right\}} d\Omega + \\ + \;\int\limits_{ - 1}^1 {{{{\left\{ {{{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right)\left[ {{v}\delta \left( {\frac{{\partial w}}{{\partial t}}} \right) - \frac{{\partial {v}}}{{\partial t}}\delta w} \right] + 2\alpha \kappa \left( {1 + {{r}_{m}}{{r}_{{v}}}} \right)\frac{{\partial {v}}}{{\partial x}}\delta w} \right\}}}_{{t = {{t}_{f}}}}}} dx \\ \end{gathered} $Необходимое условие оптимальности процесса демпфирования колебаний сводится к равенству нулю вариации расширенного функционала Лагранжа, то есть
(2.10)
$\delta J = \delta {{J}_{g}} + \delta {{J}_{a}} + \mu \left( {2\int\limits_\Omega {g\delta gd\Omega + 2\theta \delta \theta } } \right) = 0,$(2.11)
$g\left( {x,t} \right) = \frac{1}{{2\mu }}{v}\left( {x,t} \right);\quad \left( {x,t} \right) \in \Omega ,$(2.12)
${{\mu }^{2}} = \frac{1}{{4{{M}_{0}}}}\int\limits_\Omega {{{{v}}^{2}}\left( {x,t} \right)d\Omega } $В случае строгого неравенства в (2.2) величина вспомогательной переменной $\theta $ в (2.6) отлична от нуля, а из необходимого условия экстремума ($\mu \theta = 0$), которое получается из (2.10), следует, что $\mu = 0$.
Из условия обращения в ноль полной вариации в (2.10) также получим однородное дифференциальное уравнение для сопряженной переменной
(2.13)
$\begin{gathered} {\text{L}}\left( {v} \right) \equiv {{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right)\frac{{{{\partial }^{2}}{v}}}{{\partial {{t}^{2}}}} + 2\alpha \kappa \left( {1 + {{r}_{m}}{{r}_{{v}}}} \right)\frac{{{{\partial }^{2}}{v}}}{{\partial x\partial t}} + \left[ {{{\kappa }^{2}}\left( {1 + {{r}_{m}}r_{{v}}^{2}} \right) - 1} \right]\frac{{{{\partial }^{2}}{v}}}{{\partial {{x}^{2}}}} + {{\beta }}\frac{{{{\partial }^{4}}{v}}}{{\partial {{x}^{4}}}} = 0; \\ \left( {x,t} \right) \in \Omega , \\ \end{gathered} $(2.14)
${{\left( {v} \right)}_{{t = {{t}_{f}}}}} = - \frac{{2{{\alpha }_{2}}}}{{{{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right)}}{{\left( {\frac{{\partial w}}{{\partial t}}} \right)}_{{t = {{t}_{f}}}}};\quad x \in \left[ { - 1,\;1} \right]$(2.15)
${{\left( {\frac{{\partial {v}}}{{\partial t}}} \right)}_{{t = {{t}_{f}}}}} = \frac{2}{{\alpha \left( {1 + {{r}_{m}}} \right)}}{{\left[ {\frac{{{{\alpha }_{1}}}}{\alpha }w + \kappa \left( {1 + {{r}_{m}}{{r}_{{v}}}} \right)\frac{{\partial {v}}}{{\partial x}}} \right]}_{{t = {{t}_{f}}}}};\quad x \in \left[ { - 1,\;1} \right]$При помощи исключения зависимости от $\partial {v}{\text{/}}\partial x$ в правой части условия (2.15) получим удобное для применения условие в конечный момент времени
(2.16)
${{\left( {\frac{{\partial {v}}}{{\partial t}}} \right)}_{{t = {{t}_{f}}}}} = \frac{2}{{{{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right)}}{{\left[ {{{\alpha }_{1}}w - \frac{{2{{\alpha }_{2}}\left( {1 + {{r}_{m}}{{r}_{{v}}}} \right)}}{{\alpha \left( {1 + {{r}_{m}}} \right)}}\frac{{{{\partial }^{2}}w}}{{\partial t\partial x}}} \right]}_{{t = {{t}_{f}}}}};\quad x \in \left[ { - 1,\;1} \right]$Отметим, что условие экстремума расширенного функционала
означает, что для неактивного ограничения (2.2), выполняющегося со знаком строгого неравенства, из (2.2) и (2.6) следует, что $\theta \ne 0$. Соответствующий множитель Лагранжа в этом случае должен полагаться равным нулю, как это следует из необходимого условия оптимальности (2.17). Тем самым, ограничение (2.2) в этом случае не учитывается при отыскании оптимального решения. Если же $\mu \ne 0$, то $\theta = 0$, и соответствующее ограничение является “активным”.Таким образом, рассматриваемая задача оптимизации сводится к решению связанных начально-краевой задачи (1.2)–(1.4) и краевой задачи (2.8), (2.13) с условиями (2.14), (2.15) или (2.14), (2.16) в конечный момент времени. При этом оптимальное демпфирующее воздействие $g\left( {x,t} \right)$ находится с применением условий экстремума.
3. Метод решения задачи оптимизации. Для отыскания способа оптимального гашения колебаний движущейся в потоке жидкости упругой панели предложен алгоритм определения управляющих воздействий, который основывается на применении выведенных условий экстремума и решении связанных терминальными условиями уравнений, определяющих распределения прогибов $w\left( {x,t} \right)$ и сопряженной переменной ${v}\left( {x,t} \right)$. Итерационный алгоритм решения задачи оптимизации заключается в последовательном выполнении описанных ниже итераций и шагов.
На первом шаге первой итерации решается “прямая” задача, состоящая в интегрировании уравнения динамики (1.4) с граничными условиями (1.3) при $x = \pm 1$ и начальными условиями (1.2) при $t = 0$, описывающими начальные распределения возмущений перемещений $w$ и скоростей $\partial w{\text{/}}\partial t$ при $t = 0$. На начальном этапе итерационного процесса при выполнении первого шага первой итерации в качестве демпфирующего воздействия задается некоторое неоптимальное управление $g\left( {x,t} \right)$ = = ${{g}^{1}}\left( {x,t} \right)$, удовлетворяющее неравенству (2.2). При выполнении последующих итераций алгоритма в качестве управляющего воздействия на первом шаге принимается воздействие, полученное из условий оптимальности на третьем шаге предыдущей итерации.
На втором шаге итерационного алгоритма с учетом найденного на первом шаге распределения $w\left( {x,{{t}_{f}}} \right)$ и соответствующих величин $\partial w\left( {x,{{t}_{f}}} \right){\text{/}}\partial t$ и ${{\partial }^{2}}w\left( {x,{{t}_{f}}} \right){\text{/}}\partial t\partial x$, входящих в терминальные условия (2.14), (2.16), решается задача возвратного интегрирования сопряженного уравнения (2.13) с граничными условиями (2.8) и условиями (2.14), (2.16) в конечный момент времени, рассматриваемыми в качестве начальных условий при отыскании ${v}\left( {x,t} \right)$.
На третьем шаге с применением найденного на втором шаге распределения сопряженной переменной ${v}\left( {x,t} \right)$ и использованием условий экстремума (2.2), (2.6), (2.11), (2.12) и (2.17) находится текущее приближение для оптимального воздействия $g\left( {x,t} \right)$, прикладываемого к панели в области $\Omega $ ($\left( {x,t} \right) \in \Omega $). Полученное на третьем шаге итерационного процесса демпфирующее управление рассматривается далее в качестве “начального” при переходе к первому шагу следующей итерации алгоритма.
Приведем некоторые детали нахождения оптимального управления, основанного на методе Галёркина [20]. Представим искомые распределения поперечных перемещений панели $w\left( {x,t} \right)$ и сопряженной переменной ${v}\left( {x,t} \right)$ в виде рядов
(3.1)
$w\left( {x,t} \right) = \sum\limits_{n = 1}^{{{n}_{0}}} {{{q}_{n}}\left( t \right){{\Psi }_{n}}} \left( x \right),\quad {v}\left( {x,t} \right) = \sum\limits_{n = 1}^{{{n}_{0}}} {{{s}_{n}}\left( t \right){{\Psi }_{n}}} \left( x \right),$(3.2)
${{\Psi }_{n}}\left( x \right) = \sin \left( {\frac{{n\pi }}{2}\left( {x + 1} \right)} \right);\quad x \in \left[ { - 1,\;1} \right]$и удовлетворяющие граничным условиям (1.3) для $w$ и (2.8) для ${v}$ при $x = \pm 1$. Для координатных функций метода Галёркина ${{q}_{n}}\left( t \right)$ и ${{s}_{n}}\left( t \right)$ получим обыкновенные дифференциальные уравнения, подставив выражения (3.1) в соответствующие динамические уравнения (1.4), (2.13), определяющие переменные $w\left( {x,t} \right)$ и ${v}\left( {x,t} \right)$, и умножив получающиеся соотношения на ${{\Psi }_{j}}\left( x \right)$ ($j = 1,\;2,\; \ldots $) с последующим интегрированием по $x \in \left[ { - 1,\;1} \right]$. Выполняя стандартные операции, характерные для метода Галёркина [20, 21], будем иметь две системы дифференциальных уравнений, служащих для определения величин ${{q}_{n}}\left( t \right)$ и ${{s}_{n}}\left( t \right)$
(3.3)
$\begin{gathered} \sum\limits_{n = 1}^{{{n}_{0}}} {\left\{ {{{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right){{A}_{{jn}}}\frac{{{{d}^{2}}{{q}_{n}}}}{{d{{t}^{2}}}} + 2\alpha \kappa \left( {1 + {{r}_{m}}{{r}_{{v}}}} \right){{B}_{{jn}}}\frac{{d{{q}_{n}}}}{{dt}} + } \right.} \\ \left. {^{{^{{^{{^{{}}}}}}}} + \;\left( {\left[ {{{\kappa }^{2}}\left( {1 + {{r}_{m}}r_{{v}}^{2}} \right) - 1} \right]{{C}_{{jn}}} + \beta {{D}_{{jn}}}} \right){{q}_{n}}} \right\} - {{G}_{j}}\left( t \right) = 0 \\ \end{gathered} $(3.4)
$\begin{gathered} \sum\limits_{n = 1}^{{{n}_{0}}} {\left\{ {{{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right){{A}_{{jn}}}\frac{{{{d}^{2}}{{s}_{n}}}}{{d{{t}^{2}}}} + 2\alpha \kappa \left( {1 + {{r}_{m}}{{r}_{v}}} \right){{B}_{{jn}}}\frac{{d{{s}_{n}}}}{{dt}} + } \right.} \\ \left. { + \;\left( {\left[ {{{\kappa }^{2}}\left( {1 + {{r}_{m}}r_{v}^{2}} \right) - 1} \right]{{C}_{{jn}}} + \beta {{D}_{{jn}}}} \right){{s}_{n}}} \right\} = 0 \\ \end{gathered} $Коэффициенты ${{A}_{{jn}}}$, ${{B}_{{jn}}}$, ${{C}_{{jn}}}$, ${{D}_{{jn}}}$ и функции ${{G}_{j}}\left( t \right)$ ($j = 1,\;2,\; \ldots $) определяются выражениями
(3.5)
${{C}_{{jn}}} = \int\limits_{ - 1}^1 {{{\Psi }_{j}}\frac{{{{d}^{2}}{{\Psi }_{n}}}}{{d{{x}^{2}}}}dx = - {{{\left( {\frac{{j\pi }}{2}} \right)}}^{2}}{{\delta }_{{jn}}}} $(3.6)
${{\left( {{{q}_{j}}} \right)}_{{t = 0}}} = \int\limits_{ - 1}^1 {{{\Psi }_{j}}{{g}_{1}}\left( x \right)dx} ,\quad {{\left( {\frac{{d{{q}_{j}}}}{{dt}}} \right)}_{{t = 0}}} = \int\limits_{ - 1}^1 {{{\Psi }_{j}}{{g}_{2}}\left( x \right)dx} $(3.7)
$\begin{gathered} {{\left( {{{s}_{j}}} \right)}_{{t = {{t}_{f}}}}} = - \frac{{2{{\alpha }_{2}}}}{{{{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right)}}{{\left( {\frac{{d{{q}_{j}}}}{{dt}}} \right)}_{{t = {{t}_{f}}}}} \\ {{\left( {\frac{{d{{s}_{j}}}}{{dt}}} \right)}_{{t = {{t}_{f}}}}} = \frac{2}{{{{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right)}}{{\left( {{{\alpha }_{1}}{{q}_{j}} - \frac{{2{{\alpha }_{2}}\kappa \left( {1 + {{r}_{m}}{{r}_{{v}}}} \right)}}{{\alpha \left( {1 + {{r}_{m}}} \right)}}\sum\limits_{n = 1}^{{{n}_{0}}} {{{B}_{{jn}}}\frac{{d{{q}_{n}}}}{{dt}}} } \right)}_{{t = {{t}_{f}}}}} \\ \end{gathered} $4. Пример оптимизации процесса демпфирования колебаний. Проиллюстрируем процесс определения оптимального демпфирования, полагая
(4.1)
$\begin{gathered} {{g}_{1}}\left( x \right) = \sin \left( {\frac{\pi }{2}\left( {x + 1} \right)} \right),\quad {{g}_{2}}\left( x \right) = 0;{\text{ }}x \in \left[ { - 1,\;1} \right] \\ {{\alpha }_{1}} = {{\alpha }_{0}} > 0,\quad {{\alpha }_{2}} = 0,\quad {{n}_{0}} = 1,\quad {{\Psi }_{1}}\left( x \right) = \sin \left( {\frac{\pi }{2}\left( {x + 1} \right)} \right) \\ \end{gathered} $(4.2)
$\frac{{{{d}^{2}}q_{1}^{{(1)}}}}{{d{{t}^{2}}}} + {{a}_{1}}q_{1}^{{(1)}} = 0,\quad {{a}_{1}} = \frac{{\left[ {{{\kappa }^{2}}\left( {1 + {{r}_{m}}r_{{v}}^{2}} \right) - 1} \right]{{C}_{{11}}} + \beta {{D}_{{11}}}}}{{{{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right){{A}_{{11}}}}}$(4.3)
${{\left( {q_{1}^{{(1)}}} \right)}_{{t = 0}}} = \int\limits_{ - 1}^1 {{{\Psi }_{1}}{{g}_{1}}\left( x \right)dx = 1} ,{\text{ }}{{\left( {\frac{{dq_{1}^{{(1)}}}}{{dt}}} \right)}_{{t = 0}}} = \int\limits_{ - 1}^1 {{{\Psi }_{2}}{{g}_{2}}\left( x \right)dx = 0} ,$(4.4)
$q_{1}^{{(1)}}\left( t \right) = \cos \left( {\sqrt {{{a}_{1}}} t} \right);\quad t \in \left[ {0,{{t}_{f}}} \right]$Используя это решение, на втором шаге первой итерации алгоритма при возвратном интегрировании сопряженного уравнения с условиями в момент времени $t = {{t}_{f}}$
(4.5)
$\begin{gathered} s_{1}^{{(1)}}\left( t \right) = \frac{Q}{{\sqrt {{{a}_{1}}} }}\sin \left( {\sqrt {{{a}_{1}}} \left( {t - {{t}_{f}}} \right)} \right) = {{Q}_{1}}\sin \left( {\sqrt {{{a}_{1}}} t} \right) + {{Q}_{2}}\cos \left( {\sqrt {{{a}_{1}}} t} \right) \\ Q = \frac{{2{{\alpha }_{1}}\cos \left( {\sqrt {{{a}_{1}}} {{t}_{f}}} \right)}}{{{{\alpha }^{2}}\left( {1 + {{r}_{m}}} \right)}},\quad {{Q}_{1}} = \frac{{Q\cos \left( {\sqrt {{{a}_{1}}} {{t}_{f}}} \right)}}{{\sqrt {{{a}_{1}}} }},\quad {{Q}_{2}} = - \frac{{Q\sin \left( {\sqrt {{{a}_{1}}} {{t}_{f}}} \right)}}{{\sqrt {{{a}_{1}}} }} \\ \end{gathered} $При этом получаемое на третьем шаге первой итерации алгоритма приближение для оптимального демпфирующего воздействия запишется в виде
(4.6)
${{g}^{{(2)}}} = \frac{1}{{2{{\mu }}}}{{{v}}^{{(1)}}}\left( {x,t} \right) = \frac{1}{{2{{\mu }}}}s_{1}^{{(1)}}\left( t \right){{\Psi }_{1}}\left( x \right) = {{\left( {\frac{{2{{M}_{0}}}}{{{{t}_{f}}}}} \right)}^{{1/2}}}\sin \left( {\sqrt {{{a}_{1}}} \left( {t - {{t}_{f}}} \right)} \right)\sin \left( {\frac{\pi }{2}\left( {x + 1} \right)} \right)$Применим найденное выражение (4.6) для ${{g}^{{(2)}}}\left( {x,t} \right)$ при интегрировании уравнения колебаний
(4.7)
$\begin{gathered} \frac{{{{d}^{2}}q_{1}^{{(2)}}}}{{d{{t}^{2}}}} + {{a}_{1}}q_{1}^{{(2)}} + {{a}_{2}} = 0,\quad G_{1}^{{(2)}}\left( t \right) = \int\limits_{ - 1}^1 {{{\Psi }_{1}}\left( x \right){{g}^{{(2)}}}\left( {x,t} \right)dx;\quad t \in \left[ {0,{{t}_{f}}} \right]} \\ {{a}_{2}}\left( t \right) = - \frac{{G_{1}^{{(2)}}\left( t \right)}}{{{{\alpha }^{2}}{{A}_{{11}}}\left( {1 + {{r}_{m}}} \right)}} = - \frac{{Q\sin \left( {\sqrt {{{a}_{1}}} \left( {t - {{t}_{f}}} \right)} \right)}}{{2\mu {{\alpha }^{2}}{{A}_{{11}}}\left( {1 + {{r}_{m}}} \right)}};\quad \mu = \frac{Q}{2}{{\left( {\frac{{{{t}_{f}}}}{{2{{M}_{0}}{{a}_{1}}}}} \right)}^{{1/2}}} \\ \end{gathered} $(4.8)
$\begin{gathered} q_{1}^{{(2)}}\left( t \right) = {{R}_{0}}\cos \left( {\sqrt {{{a}_{1}}} {{t}_{f}}} \right)\left[ {\sin \left( {\sqrt {{{a}_{1}}} \left( {t - {{t}_{f}}} \right)} \right) - t\sqrt {{{a}_{1}}} \cos } \right.\left( {\sqrt {{{a}_{1}}} \left( {t - {{t}_{f}}} \right)} \right) - \\ - \;\left. {\cos \left( {\sqrt {{{a}_{1}}} t} \right)\sin \left( {\sqrt {{{a}_{1}}} {{t}_{f}}} \right)} \right] \\ {{R}_{0}} = {{\alpha }_{1}}{{\left[ {2\mu {{\alpha }^{4}}a_{1}^{{3/2}}{{A}_{{11}}}{{{\left( {1 + {{r}_{m}}} \right)}}^{2}}} \right]}^{{ - 1}}} \\ \end{gathered} $Для величины, получаемой при минимизации функционала (2.1) на второй итерации, имеем
(4.9)
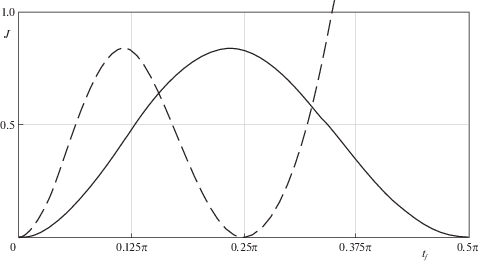
${{\left( {J_{g}^{{(2)}}} \right)}_{{t = {{t}_{f}}}}} = {{\alpha }_{1}}\left( {q_{1}^{{(2)}}} \right)_{{t = {{t}_{f}}}}^{2} = {{\alpha }_{1}}R_{0}^{2}{{\cos }^{2}}\left( {\sqrt {{{a}_{1}}} {{t}_{f}}} \right){{\left( {\sqrt {{{a}_{1}}} {{t}_{f}} + \frac{1}{2}\sin \left( {2\sqrt {{{a}_{1}}} {{t}_{f}}} \right)} \right)}^{2}}$При этом получаемая на второй итерации величина оптимизируемого функционала качества процесса демпфирования колебаний достигает минимального значения
при ${{t}_{f}} = \pi {\text{/}}\left( {2\sqrt {{{a}_{1}}} } \right)$. На рис. 2 представлены зависимости функционала $J\left( {{{t}_{f}}} \right)$ = ${{\left( {J_{g}^{{(2)}}} \right)}_{{t = {{t}_{f}}}}}$ от значения параметра ${{t}_{f}}$. При этом сплошная кривая соответствует значению величины ${{a}_{1}} = 1$, штриховая кривая – значению ${{a}_{1}} = 4$; параметры ${{\alpha }_{1}}$ и ${{R}_{0}}$ полагались равными единице. Еще один пример, иллюстрирующий применение представленного алгоритма подавления колебаний, приведен в работе [21] для других исходных данных задачи.5. Некоторые замечания и выводы. Проведенное исследование развивает гидроупругую модель взаимодействия продольно движущейся панели и потока идеальной жидкости с учетом возникающих поперечных колебаний панели. Влияние внешней жидкой среды на упругие деформации учитывается на основе присоединенных масс. Проблема эффективного подавления поперечных колебаний за счет приложения к пластине поперечных механических воздействий сформулирована и решена с применением современной теории оптимизации систем с распределенными параметрами. С этой целью наряду с исходной задачей о вынужденных гидроупругих колебаниях движущейся в потоке панели сформулирована сопряженная динамическая задача для сопряженной переменной и выведены необходимые условия оптимальности. Эти условия и сформулированные задачи для функции состояния и сопряженной переменной позволили развить эффективный итерационный алгоритм последовательной оптимизации. Приведенный пример аналитического решения задачи оптимизации процесса подавления поперечных колебаний иллюстрирует разработанный алгоритм.
Для подавления гидроупругих колебаний управляющее воздействие представлялось в виде $g = g\left( {x,t} \right)$ с неопределенными (в общем случае) независимыми переменными $x$ и $t$. Но в общем случае экстремальное управляющее воздействие может оказываться очень сложным, и его практическая реализация будет затруднительна. Принимая это во внимание, можно предложить разделенное представление $g\left( {x,t} \right)$ = ${{e}_{1}}\left( x \right){{e}_{2}}\left( t \right)$ с отдельными функциями положения $x$ и времени $t$. В этом подходе раздельно представлены конкретная геометрическая реализация (взаимное расположение актьюаторов в случае применения нескольких актьюаторов и типы актьюаторов: точечные, площадные, стационарные, подвижные и др.), определяемая ${{e}_{1}}\left( x \right)$, и вариации действия по времени ${{e}_{2}}\left( t \right)$. Такое разделение делает возможным исследование и сравнение эффективности различных способов приложения демпфирующих воздействий к панели и оценивание разнообразных программ функционирования во времени, таких как релейное управление, гармоническое, ударное и другие управляющие программы подавляющих воздействий.
Заметим также, что предложенный подход подавления гидроупругих колебаний движущейся панели естественным образом обобщается на движущиеся неразрезные панели из термоупругих материалов, подверженные термомеханическим воздействиям.
Работа выполнена по теме госзадания (номер госрегистрации АААА-А20-120011690132-4) и при частичной финансовой поддержке Российским фондом фундаментальных исследований (проект № 20-08-00082а).
Список литературы
Болотин В.В. Неконсервативные задачи теории упругой устойчивости. М.: Госиздат. Физматлит, 1961. 339 с.
Болотин В.В. Динамическая устойчивость упругих систем. М.: Гостехиздат, 1956. 600 с.
Баничук Н.В., Иванова С.Ю., Шаранюк А.В. Динамика конструкций. Анализ и оптимизация. М.: Наука, 1989. 262 с.
Frondelius T., Koivurova H., Pramila A. Interaction of an axially moving band and surrounding fluid by boundary layer theory // J. Fluids&Struct. 2006. V. 22. № 8. P. 1047–1056.
Ghayech M.H., Amabili M., Paidoussis M.P. Nonlinear dynamics of axially moving plates // J. Sound&Vibr. 2013. V. 332. № 2. P. 391–406.
Marynowski K., Kapitaniak T. Dynamics of axially moving continua // Int. J. Mech. Sci. 2014. V. 81. P. 26–41.
Damaren C.J. Hydroelastic analysis of the floating plate optimized for maximum radiation damping // Ocean Eng. February 2010. V. 37. № 2–3. P. 252–261.
Kulachenko A., Gradin P., Koivurova H. Modeling the dynamical behav-iour of a paper web. Part I // Comp.&Struct. 2007. V. 85. P. 131–147.
Баничук Н.В., Миронов А.А. Схема струйного обтекания для исследования равновесных форм упругих пластин в потоке жидкости и задачи оптимизации // ПММ. 1979. Т. 43. Вып. 1. С. 83–90.
Баничук Н.В. Оптимизация форм упругих тел. М.: Наука, 1980. 256 с.
Ashley H., Landahl M. Aerodynamics of Wings and Bodies. New York: Dover Pub., 1965. 304 p.
Lighthill J. An Informal Introduction to Theoretical Fluid Mechanics. Oxford: Sci. Pub., 1986. 260 p.
Banichuk N., Jeronen J., Neittaanmäki P. et al. Mechanics of Moving Materials. Cham: Springer, 2014. 253 p.
Banichuk N., Barsuk A., Jeronen J. et al. Stability of Axially Moving Materials. Cham: Springer, 2020. 642 p.
Chen L.-Q., Wang B. Stability of axially accelerating viscoelastic beams: asymptotic perturbation analysis and differential quadratic validation // Eur. J. Mech. A/Solids. 2009. V. 28. № 4. P. 786–791.
Banichuk N.V. Problems and Methods of Optimal Structural Design. New York: Plenum Press, 1983. 313 p.
Tang Y.-Q., Chen L.-Q. Stability analysis and numeral confirmation in parametric resonance of axially moving viscoelastic plates with time-dependent speed // Eur. J. Mech. A: Solids. 2013. V. 37. P. 106–121.
Marynowski K. Free vibration analysis of the axially moving Levi-type viscoelastic plate // Eur. J. Mech. A/Solids. 2010. V. 29. № 5. P. 879–886.
Saksa T., Jeronen J. Dynamic analysis for axially moving viscoelastic Poynting–Thomson beams // in: Mathematical Modeling and Optimization of Complex Structures. Computational Methods in Applied Sciences. V. 40 / Ed. by Neittaanmäki P. et al. Cham: Springer, 2016. P. 131–151.
Келдыш М.В. О методе Б.Г. Галёркина для решения краевых задач // Изв. АН СССР, сер. матем. 1942. Т. 6. № 6. С. 309–330.
Баничук Н.В., Иванова С.Ю. О подавлении поперечных колебаний упругой панели, продольно движущейся в потоке жидкости // Докл. РАН. 2020. Т. 492. С. 81–85.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика