Прикладная математика и механика, 2021, T. 85, № 3, стр. 383-395

1. Введение. В современной технике большое применение находят трехслойные оболочки [1, 2]. Работ по построению теорий расчета напряженно-деформированного состояния (НДС) неоднородных и трехслойных оболочек достаточно много. Значительно меньше моделей, позволяющих с необходимой точностью и степенью детализации провести расчет НДС трехслойных оболочек.

Одни из последних обзоров по анализу моделей для расчета слоисто-неоднородных, в том числе трехслойных оболочек приведены в работах [3, 4].

Проведенный обзор и анализ большого числа публикаций показал, что недостаточно изучено НДС в общем случае нерегулярных оболочек с учетом неоднородности оболочки, в том числе на уровне слоя заполнителя, моментного состояния несущих слоев, трехмерного напряженного состояния в слое заполнителя.

Распространенные модели часто не позволяют с необходимой точностью и степенью детализации провести расчет НДС трехслойных оболочек при учете указанных особенностей.

Поэтому построение адекватных моделей, позволяющих учесть эти и многие другие особенности является актуальной научной проблемой, имеющей важное прикладное значение.

Модели послойного анализа [5] позволяют решить многие важные задачи по расчету НДС трехслойных нерегулярных оболочек вращения. Послойный анализ заключается в том, что при необходимости стенка оболочки, в том числе заполнитель, разбивается по толщине на отдельные слои, которые затем стыкуются между собой.

Анализ многих работ показывает, что решение подобных задач с учетом указанных особенностей аналитическими методами сталкивается с большими трудностями математического характера. Для решения таких задач применяются численные методы и в первую очередь метод конечных элементов (МКЭ) [6].

Один из последних обзоров по анализу конечно-элементных моделей (КЭМ) для расчета оболочек, в том числе слоисто-неоднородной и трехслойной структуры, приведен в работе [7].

В [8] отмечается, что математические модели исследуемых систем должны обеспечивать выполнение заданных требований к информативности и точности исследований и одновременно являться “экономичными, способствуя, в частности, минимизации затрат машинного времени и памяти ЭВМ…”.

2. Постановка задачи. Модели послойного анализа [9–11] отличаются большой размерностью, зависящей от числа слоев и числа конечных элементов (КЭ), с помощью которых моделируются слои, в том числе по толщине, а также от числа степеней свободы КЭ и эффективности аппроксимирующих функций искомых параметров НДС внутри КЭ. Эффективными будем называть аппроксимации, позволяющие повысить скорость сходимости численных алгоритмов и получаемых результатов, а следовательно приводящие к уменьшению требуемого для решения задач числа КЭ, что особенно актуально при разработке и применении моделей послойного анализа оболочек слоисто-неоднородной структуры.

В представленной статье для уменьшения размерности моделей послойного анализа трехслойных нерегулярных оболочек вращения цилиндрической формы рассматривается применение в отличие от большинства работ по МКЭ, в которых аппроксимируются функции перемещений, эффективных аппроксимирующих функций обобщенных деформаций (далее будем называть АФД) для двумерных КЭ несущих слоев, построенных на основе моментной теории тонких оболочек. При этом АФД должны удовлетворять уравнениям неразрывности (совместности) деформаций [12, 13].

Для того, чтобы использовать хорошо разработанные алгоритмы метода перемещений МКЭ, интегрированием геометрических соотношений, связывающих выражения деформаций с перемещениями, при полученных АФД находим аппроксимирующие функции перемещений (АФП) КЭ несущих слоев.

Эти функции будем применять для построения АФП трехмерных КЭ слоя заполнителя. При построении модели КЭ слоя заполнителя трехслойных нерегулярных цилиндрических оболочек вращения используем соотношения для трехмерного тела в цилиндрических координатах. При этом алгоритм построения модели основывается на предложенном блочном конечно-элементном подходе [14, 15].

Следует отметить, что получение или выбор аппроксимаций искомых функций внутри КЭ, является важным этапом построения конечно-элементных моделей [16], так как от этого в конечном итоге зависит скорость сходимости численных процедур и получаемых результатов, а, следовательно, размерность КЭМ. При большой размерности задач растут погрешности вычислений, необходимые ресурсы ЭВМ, время расчета. Как отмечалось выше, особенно важен этот этап при уточненном послойном анализе, когда слой заполнителя моделируется и по толщине необходимым числом КЭ.

Очевидно, что наиболее эффективными будут аналитические решения, принятые в качестве аппроксимаций искомых функций внутри КЭ [17–21]. Но получить такие аппроксимации и построить на их основе модели удалось только для решения осесимметричных задач трехслойных цилиндрических оболочек и задач по расчету НДС слоистых круговых стержней.

3. Алгоритм построения конечно-элементной модели для анализа НДС несущих слоев. Как правило, на практике наиболее распространены трехслойные оболочки с тонкими и жесткими несущими слоями и толстым, но менее жестким заполнителем. Для исследования напряженно-деформированного состояния в тонких и жестких несущих слоях рассмотрим модель естественной кривизны, построенную на основе классической теории моментных оболочек вращения. В тех случаях, когда гипотезы Кирхгофа–Лява будут несправедливы, НДС в несущих слоях можно исследовать с помощью представленной в разделе 4 модели заполнителя, построенной с использованием соотношений для трехмерного тела в цилиндрических координатах.

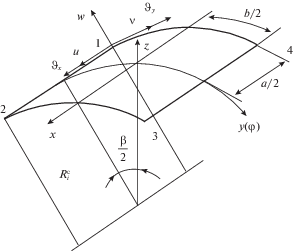
Считая справедливыми гипотезы Кирхгофа–Лява для тонких моментных несущих слоев, запишем вектор обобщенных деформаций (далее деформации) $\varepsilon _{i}^{c} = \{ {{\varepsilon }_{1}},{{\varepsilon }_{2}},\gamma ,{{\unicode{230} }_{1}},{{\unicode{230} }_{2}}$, χ}^T, который связан с вектором перемещений точек срединной поверхности несущих слоев $\delta _{i}^{\operatorname{c} } = {{\{ u,{v},w\} }^{T}}$ (рис. 1), соотношениями Коши [12] (индексы, соответствующие номеру слоя, у коэффициентов векторов и матриц указывать не будем)

где i = 1, 2, 3 номер слоя, считая от внутренней поверхности трехслойной цилиндрической оболочки, индекс “c” означает, что слой является несущим.

Тогда для внутреннего несущего слоя i = 1, для внешнего несущего слоя i = 3.

Если проинтегрировать соотношения (3.1) при нулевых значениях деформаций, то получим перемещения как твердого тела, записанные с помощью шести неопределенных коэффициентов α₁, …, α₆, являющихся константами интегрирования.

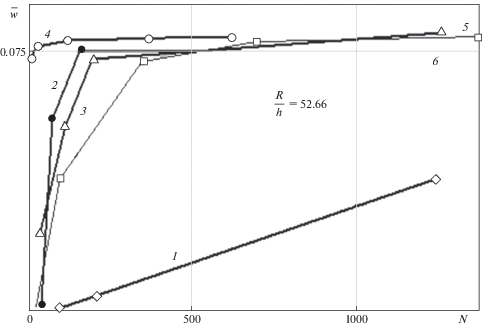
Учет перемещений как твердых тел (ПТТ) является важным требованием к аппроксимациям функций перемещений оболочечных конечных элементов [22–26]. Такой учет значительно повышает скорость сходимости получаемых численных решений. Покажем это на примере решения задачи С.П. Тимошенко [27] (рис. 2) о прогибе цилиндрической оболочки при действии самоуравновешенных диаметрально противоположных сосредоточенных радиальных сил Р, приложенных по середине длины оболочки и направленных к ее оси.

На рис. 2 приведены графики прогиба цилиндрической оболочки в точке приложения самоуравновешенных диаметрально противоположных радиальных сил Р в зависимости от числа решаемой системы уравнений N. При этом на КЭ разбивается одна восьмая симметричная часть оболочки. На рис. 2 принято следующее обозначение $\bar {w} = - wDl{\text{/}}P{{R}^{3}}{\text{ }}$, где w – прогиб; D, l, R, h – цилиндрическая жесткость, длина, радиус, толщина оболочки соответственно. Цифрами показаны решения наиболее распространенных КЭ с различными аппроксимациями [28]: 1 – АФП без учета перемещений как твердого тела (КЭ с 24 степенями свободы); 2 – АФП-КЭ с 48 степенями свободы; 3 – АФП с учетом перемещений как твердого тела (КЭ с 24 степенями свободы) [29]; 4 – рассматриваемые аппроксимации обобщенных деформаций и перемещений (КЭ с 20 степенями свободы); 5 – АФП-КЭ с 20 степенями свободы оболочки вращения нулевой кривизны [5, 10]; 6 – аналитическое решение С.П. Тимошенко [27].

Как видно из анализа графиков (рис. 2) не учет перемещений как твердого тела в АФП (кривая 1) приводит к очень низкой скорости сходимости численных результатов.

Для исследования НДС тонких моментных несущих слоев трехслойной в общем случае нерегулярной цилиндрической оболочки вращения рассмотрим двумерный КЭ (рис. 1). За узловые параметры в четырех угловых точках КЭ примем три линейных перемещения u, ${v}$, w точек срединной поверхности и два угла поворота нормали к срединной поверхности относительно осей координат в осевом и кольцевом направлениях. Таким образом, в каждом из четырех узлов будет по пять степеней свободы и КЭ несущих слоев будет иметь двадцать степеней свободы.

В дальнейшем функции, аппроксимирующие обобщенные деформации и перемещения, будем записывать через неопределенные коэффициенты $\alpha $. Число неопределенных коэффициентов равно числу степеней свободы КЭ.

Так как при записи перемещений как твердого тела задействованы шесть неопределенных коэффициентов α₁, …, α₆, то при получении АФД для рассматриваемого КЭ несущих слоев можно использовать оставшиеся четырнадцать неопределенных коэффициентов α₇, …, α₂₀.

В соответствии с рассматриваемым подходом проводится аппроксимация обобщенных деформаций полиномами, которые выбираются, исходя из предполагаемого характера изменения параметров НДС. То есть обобщенные деформации, соответствующие превалирующим видам предполагаемого НДС, например, изгиб в какой-либо плоскости, или растяжение, или др. виды НДС аппроксимируются полиномами более высоких порядков.

Распределим четырнадцать неопределенных коэффициентов α₇, …, α₂₀ между обобщенными деформациями при записи их с помощью полиномов и добавим функции для удовлетворения уравнениям неразрывности (совместности) деформаций [12]

После определения добавленных функций совместным интегрированием уравнений неразрывности деформаций (3.3) и проведения математических операций получим выражение для вектора деформаций

где $\Omega _{i}^{\operatorname{c} }$ – матрица (6 × 20) (табл. 1), $\alpha _{i}^{\operatorname{c} }$ – вектор неопределенных коэффициентов.

Так как аппроксимирующие функции деформаций КЭ несущих слоев записаны с помощью четырнадцати неопределенных коэффициентов α₇, …, α₂₀, то первые шесть столбцов матрицы ${\mathbf{\Omega }}_{i}^{\operatorname{c} }$ имеют нулевые коэффициенты аппроксимации и в табл. 1 они не показаны.

Аппроксимирующие функции перемещений, вызванные деформированием КЭ, определяются интегрированием соотношений (3.1) при заданных (полученных) выражениях аппроксимирующих функций деформаций (3.4).

Полные АФП складываются из перемещений как твердых тел и перемещений, вызванных деформированием элемента. Полученные таким образом полные функции, аппроксимирующие перемещения, будут выглядеть следующим образом

или в матричном виде где ${\mathbf{T}}_{i}^{\operatorname{c} }$ (3 × 20) – матрица аппроксимирующих функций перемещений КЭ несущих слоев трехслойной цилиндрической нерегулярной оболочки.

Получив зависимости для вектора обобщенных деформаций КЭ несущих слоев (3.4) и, зная физические соотношения (закон Гука) для несущих слоев, легко записать выражения для усилий и моментов через вектор неопределенных коэффициентов, а затем через вектор узловых перемещений.

Матрица жесткости КЭ несущих слоев определяется аналогично [18] из условия минимума полной потенциальной энергии (вариационный принцип Лагранжа) [12]. Дальнейшее решение задачи осуществляется с помощью процедур метода перемещений.

Исторически сложилось так, что на примере решения задачи С.П. Тимошенко [27] проводится сравнение скорости сходимости получаемых численных результатов и эффективности аппроксимаций КЭ круговых цилиндрических оболочек (рис. 2). Сопоставление скорости сходимости численных результатов (рис. 2), показало эффективность (высокую скорость сходимости полученных решений, что позволило уменьшить необходимое для расчета число КЭ) рассматриваемой модели (рис. 2, кривая 4) по сравнению с распространенными КЭ других авторов.

Рассмотренный подход хорош тем, что выбор аппроксимирующих функций деформаций является более наглядным, позволяет осознанно, исходя из предполагаемого характера изменения параметров НДС, задать порядок аппроксимирующих полиномов АФД и сохранить преимущества метода перемещений (универсальность, алгоритмичность и др.) без потери точности при вычислении напряжений. Кроме того, при аппроксимации деформаций проще удовлетворять требованиям, предъявляемым к АФП (учет перемещений как твердых тел, критерий постоянства деформаций).

Достоверность, сходимость и точность результатов, полученных с помощью рассмотренной модели, и эффективность КЭ несущих слоев подтверждена и другими исследованиями [28].

Рассмотренная модель хорошо зарекомендовала себя при исследовании напряженно-деформированного состояния ортотропных композитных цилиндрических оболочек с прямоугольными в плане вырезами, когда приходится применять мелкие сетки разбиений.

4. Алгоритм построения блочной модели для расчета НДС в слое заполнителя. Блочная модель для анализа НДС в слое заполнителя строится из трехмерных конечных элементов естественной кривизны.

Особенностью построения оболочечного трехмерного конечного элемента слоя заполнителя является выбор внутренней и внешней цилиндрических поверхностей этого КЭ в качестве узловых и применение рассмотренных аппроксимирующих функций перемещений конечного элемента несущих слоев для построения КЭ слоя заполнителя. Такой подход позволяет избежать разрыва перемещений на цилиндрических поверхностях контакта конечных элементов несущих слоев и заполнителя, который наблюдается при применении двумерных и трехмерных оболочечных КЭ для моделирования соответственно моментных несущих слоев и слоя заполнителя, если они построены с использованием различных аппроксимирующих функций перемещений.

Одним из требований при расчете оболочек и пластин МКЭ является требование, чтобы не было разрыва искомых параметров по линиям сопряжения конечных элементов, а в рассматриваемом случае при использовании различных аппроксимирующих функций перемещений будут разрывы по двум поверхностям контакта КЭ несущих слоев и заполнителя. Оценка погрешности решения при таком разрыве является отдельной сложной задачей.

Для избежания разрыва аппроксимирующих функций перемещений на указанных поверхностях контакта КЭ несущих слоев и заполнителя в соответствии с предложенным подходом у КЭ слоя заполнителя на цилиндрических поверхностях выбирается столько же узлов, сколько их у конечного элемента несущих слоев, и в качестве узловых параметров и аппроксимирующих функций используются те же обобщенные перемещения и аппроксимирующие функции, что и у КЭ несущих слоев трехслойных оболочек. То есть, у КЭ заполнителя (КЭЗ) будет восемь узлов, находящихся в угловых точках КЭ.

При этом аппроксимирующие функции перемещений КЭ несущих слоев приводятся к соответствующей цилиндрической поверхности стыковки с КЭ слоя заполнителя с помощью матриц перехода аналогично [22]. Векторы перемещений КЭ несущих слоев на поверхностях стыковки с КЭ слоя заполнителя будем обозначать чертой вверху – $\bar {\delta }_{i}^{c}$.

Рассмотрим алгоритм построения аппроксимирующих функций перемещений оболочечного конечного элемента слоя заполнителя. Местную систему координат оболочечного КЭ заполнителя расположим на срединной поверхности КЭ с началом координат, находящихся на пересечении линий, отстоящих на одинаковом расстоянии от продольных и торцевых граней этих конечных элементов.

Учет изменения свойств и параметров НДС по толщине слоя заполнителя осуществляется путем разбиения заполнителя на необходимое число КЭ, которые объединяются в блок, стыкуемый с КЭ несущих слоев. В соответствии с предложенным подходом построения трехмерного КЭ слоя заполнителя вектор перемещений $\delta _{{ij}}^{\operatorname{f} } = {{\{ u,v,w\} }^{T}}$ (для слоя заполнителя i = 2 и этот индекс в дальнейшем не указывается, j – номер КЭЗ по толщине слоя заполнителя, считая от его внутренней поверхности, f соответствует тому, что КЭ принадлежит заполнителю) запишем через векторы перемещений внутренней ${\mathbf{\delta }}_{j}^{1}$ и внешней $\delta _{j}^{2}$ цилиндрических поверхностей КЭЗ

где ${{\varphi }}_{j}^{1} = (1 - 2{{z}_{j}}{\text{/}}{{h}_{j}}){\text{/}}2$; ${{\varphi }}_{j}^{2} = 1 - {{\varphi }}_{j}^{1}$, $z_{j}^{\operatorname{f} }$ – нормальная к срединной поверхности конечного элемента заполнителя координата, $h_{j}^{\operatorname{f} }$ – толщина КЭЗ.

Запишем в векторной форме условия стыковки КЭЗ по толщине слоя заполнителя при построении блочной модели

Зная аппроксимирующие функции перемещений КЭ несущих слоев (3.5), с помощью зависимостей (4.1), (4.2), получим аппроксимирующие функции перемещений конечных элементов слоя заполнителя, выраженные через вектор неопределенных коэффициентов ${\mathbf{\alpha }}_{j}^{\operatorname{f} }$

где ${\mathbf{T}}_{j}^{\operatorname{f} }$ – матрица аппроксимирующих функций перемещений конечных элементов слоя заполнителя.

При построении модели КЭ слоя заполнителя используем соотношения для трехмерного тела в цилиндрических координатах. Подставляя выражения (4.3) в геометрические соотношения, связывающие деформации с перемещениями, получим зависимости для компонент вектора обобщенных деформаций КЭ слоя заполнителя

Получив эти зависимости для вектора обобщенных деформаций КЭ слоя заполнителя и зная для него физические соотношения (закон Гука), записываются выражения для напряжений в этих КЭЗ через вектор $\alpha _{j}^{\operatorname{f} }$. Матрица жесткости (МЖ) КЭ слоя заполнителя определяется аналогично [18] из условия минимума полной потенциальной энергии (вариационный принцип Лагранжа) [12].

Из полученных МЖ трехмерных КЭ слоя заполнителя с помощью вычислительных программ формируется общая матрица жесткости блока указанных КЭЗ, к которой затем добавляются МЖ двумерных КЭ моментных несущих слоев. Из этих блоков строится глобальная матрица жесткости трехслойной в общем случае нерегулярной цилиндрической оболочки вращения.

Рассмотренная модель хорошо зарекомендовала себя при исследовании НДС трехслойных цилиндрических ортотропных (композитных) оболочек с прямоугольными в плане вырезами.

5. Численный пример. Исследование изменения напряжений по толщине слоя заполнителя проиллюстрировано на трехслойной цилиндрической оболочке вращения с шарнирно опертыми ортотропными несущими слоями из конструкционного стеклопластика: $E_{1}^{\operatorname{c} } = 2.1 \times {{10}^{{10}}}$ Па; $E_{2}^{\operatorname{c} } = 2.2 \times {{10}^{{10}}}$ Па; $\mu _{1}^{\operatorname{c} } = 0.1$; $\mu _{2}^{\operatorname{c} } = 0.105$; $G_{{12}}^{\operatorname{c} } = 3.5 \times {{10}^{{10}}}$ Па; $h_{1}^{\operatorname{c} } = h_{3}^{\operatorname{c} } = 0.00375$ м; $L{\text{/}}{{R}_{{вн}}} = 0.223$; $p{\text{/}}G_{{13}}^{\operatorname{f} } = 0.2$; и заполнителем типа пенополиуретана $E_{{11}}^{\operatorname{f} } = E_{{22}}^{\operatorname{f} } = E_{{33}}^{\operatorname{f} }$ = $127.8 \times {{10}^{5}}$ Па; $G_{{12}}^{\operatorname{f} } = G_{{13}}^{\operatorname{f} } = G_{{23}}^{\operatorname{f} }$ = $50 \times {{10}^{5}}$ Па; ${{h}^{\operatorname{f} }} = 0.0425$ м.

На оболочку изнутри действует кольцевая радиальная равномерная поперечная нагрузка р, приложенная в середине пролета оболочки на участке c длиной площадки 0.07L.

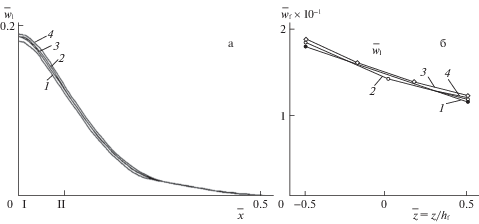
Изменение прогибов w₁/H (H – толщина пакета слоев) для внутреннего несущего слоя в осевом направлении показано на рис. 3а. Безразмерная продольная координата отсчитывается от середины оболочки. Максимальные прогибы отмечаются в районе приложения нагрузки на середине оболочки (на рисунках обозначено римской цифрой I, находящейся в начале системы координат на рис. 3а). По толщине заполнителя эти прогибы изменяются почти линейно (рис. 3б). Цифрами 1, 2, 3, 4 обозначено разбиение заполнителя по толщине на один, два, три рассмотренных КЭЗ и 10 осесимметричных КЭ [17, 18].

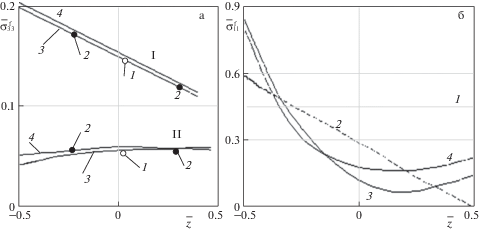
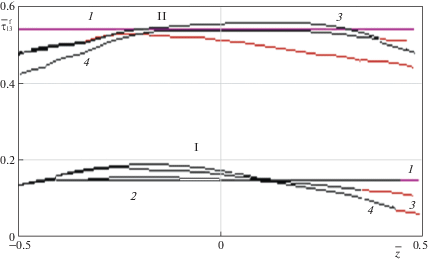
Наибольшими являются напряжения – $\sigma _{{33}}^{\operatorname{f} }$ в зоне I (место приложения нагрузки – на середине оболочки). По толщине заполнителя они изменяются почти линейно (рис. 4а). Эти напряжения почти на порядок выше других напряжений в заполнителе. Наибольшая нелинейность по толщине слоя заполнителя отмечена для напряжений $\bar {\sigma }_{{11}}^{f}$ в зоне II – на расстоянии ~L/10 от середины оболочки (зона максимальных $\tau _{{13}}^{{\max }}$) (рис. 4б). На рис. 5 приведено распределение поперечных сдвиговых напряжений по толщине заполнителя.

Исследуемые параметры приведены в безразмерном виде $\bar {w} = w{\text{/}}H$, ${\text{ }}\bar {\sigma } = \sigma {\text{/}}p$. На рис. 3б, 4, 5 показано изменение этих параметров по толщине заполнителя.

Заключение. Рассмотрено построение модели для послойного анализа напряженно-деформированного состояния (НДС) трехслойных нерегулярных цилиндрических оболочек вращения, при котором стенка оболочки, в том числе заполнитель моделируется по толщине конечными элементами, которые затем стыкуются между собой и объединяются в блоки. Модель позволяет учесть изменение свойств и параметров НДС как по меридиональной и окружной координатам, так и по толщине оболочки и слоя заполнителя, адекватно моделировать особенности слоисто-неоднородного строения, моментное состояние несущих слоев, трехмерное напряженно-деформированное состояние в заполнителе, а также учесть нарушение сплошности слоев, различные условия их закрепления и нагружения. Для уменьшения размерности модели блочно-послойного анализа применены эффективные функции аппроксимаций деформаций и перемещений.

Работа выполнена в рамках государственного задания ИПРИМ РАН.