1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 85, № 3, 2021

Прикладная математика и механика, 2021, T. 85, № 3, стр. 321-331

Колебания штампа на поверхности гетерогенного слоя при учете трения в области контакта

О. А. Беляк 1, *, Т. В. Суворова 1, **

1 Ростовский государственный университет путей сообщения
Ростов-на-Дону, Россия

* E-mail: o_bels@mail.ru
** E-mail: suvorova_tv111@mail.ru

Поступила в редакцию 30.01.2021
После доработки 25.02.2021
Принята к публикации 15.03.2021

Полный текст (PDF)

Аннотация

Рассматривается контактная задача о колебаниях штампа с плоским основанием на поверхности гетерогенного слоя при учете сил трения в области контакта. Микроструктура пористоупругого насыщенного флюидом слоя описывается уравнениями Био-Френкеля, в области контакта выполняется закон трения Кулона–Амонтона. Краевая задача сведена к разностному интегральному уравнению 1-го рода относительно контактных давлений. Построено приближенное решение интегрального уравнения с использованием метода граничных элементов. Исследовано влияние частоты вибрации, толщины слоя на контактные напряжения на примере маслосодержащего композита на основе фенилона, механические модули которого определены с помощью методов микромеханики и наноиндентирования.

Ключевые слова: динамическая контактная задача, трение в области контакта, гетерогенный слой

1. Введение. Контактным задачам теории упругости посвящены многочисленные исследования, отметим здесь монографии и статьи школы академика Бабешко В.А., где рассмотрены динамические контактные задачи для упругих слоистых оснований [1–4], для насыщенных пористоупругих сред такие задачи представлены в работах [5–9]. Особым интересом и актуальностью пользуются приложения контактных задач к трибологии. Решения широкого круга контактных задач в статической и квазистатической постановках для однородных упругих и вязкоупругих сред рассмотрены работах [10–12], для пористоупругих насыщенных сред, описываемых моделью Био-Френкеля рассмотрены в работах [13–15], в том числе в динамической постановке [7–9].

В настоящей работе рассматривается динамическая контактная задача для гетерогенного двухфазного слоя при учете трения в области контакта. Для описания микроструктуры основания, состоящего из изотропной вязкоупругой матрицы и вязкого флюида, использованы уравнения гетерогенной среды Био [16–18]. Практическое значение рассматриваемой задачи при конструировании новых наномодифицированных композиционных материалов [19–21] состоит в изучении влияния динамических эффектов, возникающих за счет вибрации, на трибологический процесс. С этой целью численные расчеты представлены для маслонаполненного композита с матрицей на основе фенилона и наноразмерных добавок, экспериментально определены модуль Юнга, в том числе, с помощью наноиндентирования, коэффициент Пуассона [21]. Изменение механических модулей многофазной среды при росте пористости получено с помощью дифференциальной схемы метода самосогласования и конечно-элементных моделей со стохастически распределенными сферическими порами [22].

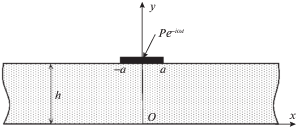
2. Постановка задачи. Рассматривается контактная задача о вибрации с частотой $\omega $ жесткого штампа с плоским основанием шириной $2a$ под действием приложенной к нему силы ${\mathbf{P}} = \{ {{P}_{1}}{{e}^{{ - i\omega t}}},{{P}_{2}}{{e}^{{ - i\omega t}}}\} $ изменяющейся по гармоническому закону, на верхней границе слоя $ - \infty < x < \infty $, $0 \leqslant y \leqslant h$, занятого гетерогенной средой, состоящей из двух фаз: вязкоупругой пористой матрицы-скелета и вязкого флюида (рис. 1).

Рис. 1.

Схема динамической контактной задачи.

Будем полагать, что амплитуда приложенной силы такова, что в процессе колебаний не происходит нарушение контакта или возникновение зон скольжения. В области контакта нормальные и касательные напряжения связаны законом Амонтона–Кулона, а внутренняя микроструктура основания описывается уравнениями Био-Френкеля [16–18]. Считаем, что штамп и границы слоя непроницаемы для жидкой фазы, а режим колебаний является установившимся. После отделения временного множителя уравнения Био-Френкеля имеют вид:

$\begin{gathered} N\Delta {\mathbf{u}} + \nabla \left( {(A + N)\nabla \cdot {\mathbf{u}} + Q\nabla \cdot {\mathbf{v}})} \right) + {{\omega }^{2}}({{\rho }_{{11}}}{\mathbf{u}} + {{\rho }_{{12}}}{\mathbf{v}}) + i\omega b\left( {{\mathbf{u}} - {\mathbf{v}}} \right) = 0 \\ \nabla \left( {Q\nabla \cdot {\mathbf{u}} + R\nabla \cdot {\mathbf{v}})} \right) + {{\omega }^{2}}({{\rho }_{{12}}}{\mathbf{u}} + {{\rho }_{{22}}}{\mathbf{v}}) - i\omega b\left( {{\mathbf{u}} - {\mathbf{v}}} \right) = 0 \\ \end{gathered} $
(2.1)
$\begin{gathered} \sigma _{{ij}}^{s} = Ae{{\delta }_{{ij}}} + 2N{{e}_{{ij}}} + Q\varepsilon {{\delta }_{{ij}}} \\ {{\sigma }^{f}} = Qe + R\varepsilon ;\quad i,j = 1,2 \\ \end{gathered} $
$\begin{gathered} {{e}_{{ij}}} = ({{u}_{{i,j}}} + {{u}_{{j,i}}}){\text{/}}2,\quad {{\varepsilon }_{{ij}}} = ({{{v}}_{{i,j}}} + {{{v}}_{{j,i}}}){\text{/}}2 \\ e = \nabla \cdot {\mathbf{u}},\quad \varepsilon = \nabla \cdot {\mathbf{v}},\quad {{\Gamma }_{{ij}}} = \sigma _{{ij}}^{s} + {{\delta }_{{ij}}}{{\sigma }^{f}}, \\ \end{gathered} $
где A, N, Q, R, ${{\rho }_{{11}}}$, ${{\rho }_{{12}}}$, ${{\rho }_{{22}}}$ – механические характеристики двухфазной среды, $e$ и $\varepsilon $ − тензоры деформации, соответствующие амплитудным значениям векторов перемещений твердой фазы ${\mathbf{u}}\{ {{u}_{1}},{{u}_{2}}\} $ и жидкой фазы ${\mathbf{v}}\{ {{{v}}_{1}},{{{v}}_{2}}\} $, ${{\sigma }^{s}}$ – тензор напряжений, действующий на вязкоупругий скелет, ${{\sigma }^{f}}$ – давления, действующие на флюид в порах, $b = {{m}^{2}}\eta k_{o}^{{ - 1}}$, где $\eta $, ${{k}_{o}}$ – динамическая вязкость флюида и проницаемость среды соответственно, $m$ – пористость среды.

Граничные условия в случае слоя, лежащего без трения на жестком основании, имеют вид:

(2.2)
$\begin{gathered} {{\Gamma }_{{21}}}(x,h) = \mu {{\Gamma }_{{22}}}(x,h);\quad \left| x \right| \leqslant a \\ {{\Gamma }_{{22}}}(x,h) = q(x),\quad {{u}_{2}}(x,h) = {{{v}}_{2}}(x,h) = \delta ;\quad \left| x \right| \leqslant a \\ {{\Gamma }_{{22}}}(x,h) = 0,\quad {{u}_{2}}(x,h) = {{{v}}_{2}}(x,h);\quad \left| x \right| > a \\ {{u}_{2}}(x,0) = {{{v}}_{2}}(x,0) = 0,\quad {{\Gamma }_{{21}}}(x,0) = 0, \\ \end{gathered} $
где $\delta $ – амплитуда перемещения штампа в вертикальном направлении, μ – коэффициент трения, $q(x)$ – неизвестные контактные давления.

Перейдем в соотношениях (2.1)–(2.2) к безразмерному виду:

$\begin{gathered} {{q}_{{11}}} = (A + 2N){\text{/}}N,\quad {{q}_{{12}}} = Q{\text{/}}N,\quad {{q}_{{22}}} = R{\text{/}}N \\ {{\gamma }_{{11}}} = ({{\rho }_{{11}}} + ib{\text{/}}\omega ){\text{/}}{{\rho }_{{11}}},\quad {{\gamma }_{{12}}} = ({{\rho }_{{12}}} - ib{\text{/}}\omega ){\text{/}}{{\rho }_{{11}}} \\ {{\gamma }_{{22}}} = ({{\rho }_{{22}}} + ib{\text{/}}\omega ){\text{/}}{{\rho }_{{11}}},\quad {{\vartheta }^{2}} = \rho {{\omega }^{2}}{{a}^{2}}{\text{/}}N,\quad {{\delta }_{0}} = \delta {\text{/}}a, \\ \end{gathered} $
линейные величины отнесены к полуширине штампа. Замыкают постановку краевой задачи (2.1)–(2.2) условие излучения волн на бесконечность, устанавливаемые аналогично случаю упругой среды [2]. Далее, будем разыскивать контактные давления $q(x)$ и горизонтальные смещения ${{u}_{1}}(x,0)$ под штампом.

3. Сведение краевой задачи к интегральному уравнению. Применим к уравнениям (2.1)–(2.2) интегральное преобразование Фурье [23] по переменной $x$. Представим перемещения в виде двух скалярных и векторного потенциалов [8]. В результате уравнения (2.1) расщепляются на три волновые уравнения, а потенциалы соответствуют трем типам волн: медленной и быстрой продольной, и поперечной волны, распространяющимся в гетерогенной среде со скоростями ${{V}_{i}}$, $i = 1,2,3$. В результате получим связь перемещений и напряжений для слоя:

(3.1)
$\begin{gathered} {\mathbf{u}}\left( {x,y} \right) = \frac{1}{{2\pi }}\int\limits_\Upsilon {{\mathbf{G}}\left( {\alpha ,y} \right){\mathbf{Q}}\left( \alpha \right){{e}^{{ - i\alpha x}}}d\alpha } \\ {\mathbf{v}}\left( {x,y} \right) = \frac{1}{{2\pi }}\int\limits_\Upsilon {{{{\mathbf{G}}}_{{v}}}\left( {\alpha ,y} \right){\mathbf{Q}}\left( \alpha \right){{e}^{{ - i\alpha x}}}d\alpha } \\ {\mathbf{Q}}\left( \alpha \right) = \int\limits_{ - \infty }^\infty {{\mathbf{q}}\left( x \right){{e}^{{i\alpha x}}}dx} ,\quad {\mathbf{q}} = \left\{ {{{\Gamma }_{{21}}}\left( x \right),{{\Gamma }_{{22}}}\left( x \right)} \right\} \\ \end{gathered} $

Контур $\Upsilon $ выбирается в соответствии с условиями излучения волн на бесконечность, $\alpha $ – параметр преобразования Фурье, ${\mathbf{G}}(\alpha ,y)$, ${{{\mathbf{G}}}_{{v}}}(\alpha ,y)$ – матрицы Грина для перемещений скелета и флюида соответственно.

${\mathbf{G}}(\alpha ,y) = {\mathbf{B}}(\alpha ){\mathbf{E}}(\alpha ,y){{\left( {{\mathbf{D}}(\alpha ,h)} \right)}^{{ - 1}}}$
${{{\mathbf{G}}}_{{v}}}(\alpha ,y) = {\mathbf{B}}(\alpha ){\mathbf{E}}_{{v}}^{{}}(\alpha ,y){{\left( {{\mathbf{D}}(\alpha ,h)} \right)}^{{ - 1}}}$
${\mathbf{B}}(\alpha ) = \left( {\begin{array}{*{20}{c}} { - i\alpha }&{ - i\alpha }&{\frac{\partial }{{\partial y}}} \\ {\frac{\partial }{{\partial y}}}&{\frac{\partial }{{\partial y}}}&{i\alpha } \end{array}} \right),$
где ${\mathbf{E}}(\alpha ,y) = \left( {{{E}_{{ii}}}(\alpha ,y)} \right)$, ${{{\mathbf{E}}}_{{v}}}(\alpha ,y) = \left( {{{E}_{{{v},ii}}}(\alpha ,y)} \right)$ – диагональные матрицы с элементами ${{E}_{{ii}}} = \operatorname{ch} {{s}_{i}}y$, ${{E}_{{{v},ii}}} = {{m}_{i}}\operatorname{ch} {{s}_{i}}y$, $i = 1,2,3$,
${\mathbf{D}}(\alpha ,y) = \left( {\begin{array}{*{20}{c}} { - 2i\alpha {{s}_{1}}\operatorname{sh} {{s}_{1}}y}&{ - 2i\alpha {{s}_{2}}\operatorname{sh} {{s}_{2}}y}&{({{\alpha }^{2}} + s_{3}^{2})\operatorname{sh} {{s}_{3}}y} \\ {{{g}_{{01}}}\operatorname{ch} {{s}_{1}}y}&{{{g}_{{02}}}\operatorname{ch} {{s}_{2}}y}&{2i\alpha {{s}_{3}}\operatorname{ch} {{s}_{3}}y} \\ {{{m}_{{01}}}{{s}_{1}}\operatorname{sh} {{s}_{1}}y}&{{{m}_{{02}}}{{s}_{2}}\operatorname{sh} {{s}_{2}}y}&{i\alpha {{\gamma }_{{13}}}\operatorname{sh} {{s}_{3}}y} \end{array}} \right)$
${{g}_{{0i}}} = 2{{\alpha }^{2}} - \theta _{i}^{2}({{q}_{{11}}} + {{q}_{{12}}} + ({{q}_{{12}}} + {{q}_{{22}}}){{m}_{i}})$
(3.2)
${{m}_{{0i}}} = 1 - {{m}_{i}},\quad i = 1,2,\quad {{\gamma }_{{13}}} = 1 + {{\gamma }_{{12}}}{\text{/}}{{\gamma }_{{22}}}$
${{s}_{k}} = \sqrt {{{\alpha }^{2}} - \theta _{k}^{2}} ;\quad k = 1,2,3$
$\varsigma _{3}^{{}} = ({{\gamma }_{{11}}}{{\gamma }_{{22}}} - {{\gamma }_{{12}}}^{2}){\text{/}}{{\gamma }_{{22}}},\quad \theta _{i}^{2} = {{\rho }_{s}}{{\omega }^{2}}{{a}^{2}}{{\varsigma }_{i}}{\text{/}}N,$
а ${{m}_{i}}$, ${{\varsigma }_{i}}$, $i = 1,2$ определяются соотношениями:

$\left| {\begin{array}{*{20}{c}} {{{q}_{{12}}}}&{{{q}_{{11}}}} \\ {{{q}_{{22}}}}&{{{q}_{{12}}}} \end{array}} \right|{{\varsigma }^{2}} + \left. {\left( {\left| {\begin{array}{*{20}{c}} {{{\gamma }_{{11}}}}&{{{\gamma }_{{12}}}} \\ {{{q}_{{12}}}}&{{{q}_{{22}}}} \end{array}} \right|} \right. + \left| {\begin{array}{*{20}{c}} {{{\gamma }_{{22}}}}&{{{\gamma }_{{12}}}} \\ {{{q}_{{12}}}}&{{{q}_{{11}}}} \end{array}} \right|} \right)\varsigma + \left| {\begin{array}{*{20}{c}} {{{\gamma }_{{12}}}}&{{{\gamma }_{{11}}}} \\ {{{\gamma }_{{22}}}}&{{{\gamma }_{{12}}}} \end{array}} \right| = 0$
${{m}_{i}} = \frac{{{{\gamma }_{{12}}} - {{\varsigma }_{i}}{{q}_{{12}}}}}{{{{\varsigma }_{i}}{{q}_{{22}}} - {{\gamma }_{{22}}}}}$

С целью оптимизации вычислительных процессов проведем ряд аналитических преобразований и раскрытий неопределенностей, в результате матрица Грина примет вид:

${\mathbf{G}}(\alpha ,y) = \frac{1}{{D(\alpha )}}\left( {{{G}_{{ij}}}(\alpha ,y)} \right);\quad i,j = 1,2$
$D(\alpha ) = 2{{\alpha }^{2}}(2{{g}_{0}}\operatorname{sh} {{s}_{1}}h\operatorname{sh} {{s}_{2}}h\operatorname{ch} {{s}_{3}}h + {{\gamma }_{{13}}}g_{4}^{{}}\operatorname{sh} {{s}_{3}}h) - ({{\alpha }^{2}} + s_{3}^{2})g_{5}^{{}}\operatorname{sh} {{s}_{3}}h$
${{g}_{0}} = ({{m}_{1}} - {{m}_{2}}){{s}_{1}}{{s}_{2}}{{s}_{3}}$
$G_{{11}}^{{}}(\alpha ,h) = {{s}_{3}}(g_{6}^{{}}{{\alpha }^{2}} + g_{5}^{{}})\operatorname{ch} {{s}_{3}}h + {{\gamma }_{{13}}}{{\alpha }^{2}}({{g}_{{01}}} - {{g}_{{02}}})\operatorname{ch} {{s}_{1}}h\operatorname{ch} {{s}_{2}}h\operatorname{sh} {{s}_{3}}h$
(3.3)
$G_{{12}}^{{}}(\alpha ,h) = - i\alpha (2{{g}_{0}}\operatorname{sh} {{s}_{1}}h\operatorname{sh} {{s}_{2}}h\operatorname{ch} {{s}_{3}}h + 2{{\alpha }^{2}}{{\gamma }_{{13}}}g_{7}^{{}}\operatorname{sh} {{s}_{3}}h - ({{\alpha }^{2}} + s_{3}^{2})g_{6}^{{}}\operatorname{sh} {{s}_{3}}h)$
$G_{{21}}^{{}}(\alpha ,h) = i\alpha \left( {{{g}_{0}}\operatorname{sh} {{s}_{1}}h\operatorname{sh} {{s}_{2}}h\operatorname{ch} {{s}_{3}}h - ({{\gamma }_{{13}}}g_{4}^{{}} - g_{5}^{{}})\operatorname{sh} {{s}_{3}}h} \right)$
$G_{{22}}^{{}}(\alpha ,h) = ({{m}_{1}} - {{m}_{2}}){{s}_{1}}{{s}_{2}}\theta _{3}^{2}\operatorname{sh} {{s}_{1}}h\operatorname{sh} {{s}_{2}}h\operatorname{sh} {{s}_{3}}h$
$g_{4}^{{}} = \left| {\begin{array}{*{20}{c}} {{{g}_{{01}}}\operatorname{ch} {{s}_{1}}h}&{{{g}_{{02}}}\operatorname{ch} {{s}_{2}}h} \\ {{{s}_{1}}\operatorname{sh} {{s}_{1}}h}&{{{s}_{2}}\operatorname{sh} {{s}_{2}}h} \end{array}} \right|,\quad g_{5}^{{}} = \left| {\begin{array}{*{20}{c}} {{{g}_{{01}}}\operatorname{ch} {{s}_{1}}h}&{{{g}_{{02}}}\operatorname{ch} {{s}_{2}}h} \\ {{{m}_{{01}}}{{s}_{1}}\operatorname{sh} {{s}_{1}}h}&{{{m}_{{02}}}{{s}_{2}}\operatorname{sh} {{s}_{2}}h} \end{array}} \right|$
$g_{6}^{{}} = \left| {\begin{array}{*{20}{c}} {\operatorname{ch} {{s}_{1}}h}&{\operatorname{ch} {{s}_{2}}h} \\ {{{m}_{{01}}}{{s}_{1}}\operatorname{sh} {{s}_{1}}h}&{{{m}_{{02}}}{{s}_{2}}\operatorname{sh} {{s}_{2}}h} \end{array}} \right|,\quad g_{7}^{{}} = \left| {\begin{array}{*{20}{c}} {\operatorname{ch} {{s}_{1}}h}&{\operatorname{ch} {{s}_{2}}h} \\ {{{s}_{1}}\operatorname{sh} {{s}_{1}}h}&{{{s}_{2}}\operatorname{sh} {{s}_{2}}h} \end{array}} \right|$

В случае толщины слоя $h \to \infty $ соотношения (3.3) принимают вид:

$D(\alpha ) = 2{{\alpha }^{2}}(2{{g}_{0}} + {{\gamma }_{{13}}}g_{4}^{{}}) - ({{\alpha }^{2}} + s_{3}^{2})g_{5}^{{}}$
$G_{{11}}^{{}}(\alpha ) = {{s}_{3}}(g_{6}^{{}}{{\alpha }^{2}} + g_{5}^{{}}) + {{\gamma }_{{13}}}{{\alpha }^{2}}({{g}_{{01}}} - {{g}_{{02}}})$
$G_{{12}}^{{}}(\alpha ) = - i\alpha (2{{g}_{0}} + 2{{\gamma }_{{13}}}g_{7}^{{}}{{\alpha }^{2}} - ({{\alpha }^{2}} + s_{3}^{2})g_{6}^{{}})$
$G_{{21}}^{{}}(\alpha ) = i\alpha \left( {{{g}_{0}} - ({{\gamma }_{{13}}}{{g}_{4}} - {{g}_{5}})} \right)$
$G_{{22}}^{{}}(\alpha ) = ({{m}_{1}} - {{m}_{2}}){{s}_{1}}{{s}_{2}}\theta _{3}^{2}$
$g_{4}^{{}} = {{g}_{{01}}}{{s}_{2}} - {{g}_{{02}}}{{s}_{1}},\quad g_{5}^{{}} = {{g}_{{01}}}{{m}_{{02}}}{{s}_{2}} - {{g}_{{02}}}{{m}_{{01}}}{{s}_{1}}$
$g_{6}^{{}} = {{m}_{2}} - {{m}_{1}},\quad g_{7}^{{}} = {{s}_{2}} - {{s}_{1}}$
и совпадают с ранее полученными соотношениями для компонент матрицы Грина в случае гетерогенной полуплоскости [8].

После удовлетворения граничных условий (2.2), приходим к интегральному уравнению 1-го рода с разностным ядром относительно неизвестного контактного давления:

(3.4)
$\int\limits_{ - 1}^1 {k(x - \xi )q(\xi )} d\xi = {{\delta }_{0}}$

Ядро интегрального уравнения (3.4) имеет вид:

(3.5)
$k(x - \xi ) = \frac{1}{{2\pi }}\int\limits_\Upsilon ^{} {\left( {\mu {{G}_{{21}}}(\alpha ,h) + {{G}_{{22}}}(\alpha ,h)} \right){\text{/}}D(\alpha ){{e}^{{i\alpha (x - \xi )}}}d\alpha } $

4. Построение решения интегрального уравнения. Элементы матрицы ${\mathbf{G}}(\alpha ,h)$ являются мероморфными функциями в комплексной плоскости, с общими комплексными полюсами, определяемыми соотношением $D(\alpha ) = 0$. Комплексные полюса определяют скорость и затухание поверхностных волн в гетерогенном слое. Проведен анализ поведения элементов матрицы ${\mathbf{G}}(\alpha ,h)\,$ при $\alpha \to 0$:

(4.1)
$\begin{gathered} \mathop {\lim }\limits_{\alpha \to \infty } {{G}_{{ii}}}(\alpha ){\text{/}}D(\alpha ) = \frac{{{{d}_{{ii}}}}}{{\left| \alpha \right|}} \\ \mathop {\lim }\limits_{\alpha \to \infty } {{G}_{{ij}}}(\alpha ){\text{/}}D(\alpha ) = \frac{{{{{( - 1)}}^{i}}{{d}_{{ij}}}}}{\alpha };\quad i \ne j,\quad i,j = 1,2 \\ \end{gathered} $

Аналитические методы регуляризации и решения уравнений с разностным ядром для упругих сред развиты в фундаментальных работах школы академика Бабешко В.А., например, в работах [1–4]. В настоящей работе для построения приближенного решения уравнения (3.4) применен метод граничных элементов, при этом в качестве регуляризатора уравнения использована функция ${{d}_{{ii}}}{\text{/}}\sqrt {{{\alpha }^{2}} + {{R}^{2}}} $, $i = 1,2$, не имеющая полюсов в комплексной плоскости и совпадающая по асимптотическому поведению с членом, несущим логарифмическую особенность. Для пористоупругого полупространства этот метод успешно апробирован и изложен в [7–9]. Выделим в (3.5) логарифмическую особенность:

(4.2)
$\begin{gathered} k(x - \xi ) = I(x - \xi ) + {{K}_{0}}(R\left| {x - \xi } \right|){\text{/}}\pi \\ I(x - \xi ) = \frac{1}{{2\pi }}\int\limits_\Upsilon ^{} {L(\alpha ){{e}^{{i\alpha (x - \xi )}}}d\alpha } \\ L(\alpha ) = \mu {{G}_{{21}}}(\alpha ) + {{G}_{{22}}}(\alpha ) - {{d}_{{22}}}{\text{/}}\sqrt {{{\alpha }^{2}} + {{R}^{2}}} , \\ \end{gathered} $
где ${{K}_{0}}(z)$ – функция Макдональда нулевого порядка [24]. Интеграл $I(x - \xi )$ в (4.2) является быстро сходящимся. Выбор $R \gg 1$ ускоряет сходимость при дальнейших вычислениях интегралов. Проведем дискретизацию области контакта для плоского штампа, выбрав точки коллокации ${{x}_{i}}$, ${{\xi }_{i}}$, равномерно распределенными, с шагом $h = 2{\text{/}}N$ на отрезке $[ - 1 + h{\text{/}}2,1 - h{\text{/}}2]$, ${{\xi }_{k}} = - 1 + h(k - 0.5)$; $k = 1,2,...,N$. При этом полагаем ${{\left. {q(x)} \right|}_{{{{x}_{i}} < x < {{x}_{{i + 1}}}}}} = q({{x}_{i}}) = {{q}_{i}}$; $i = 1,2,...,N$.

В результате решение интегрального уравнения (3.4) сводится к конечной системе линейных уравнений $N$ порядка, быстро сходящейся и обладающей квазидиагональной матрицей:

$\begin{gathered} \sum\limits_{m = 1}^N {{{r}_{{mn}}}} {{q}_{n}} = {{\delta }_{0}}{\text{/}}h;\quad n = 1,2,...,N \\ {{r}_{{mn}}} = I({{x}_{m}} - {{\xi }_{n}}) + {{c}_{1}}(\operatorname{erf} ({{z}_{2}}) - \operatorname{erf} ({{z}_{1}}));\quad m \ne n, \\ \end{gathered} $
(4.3)
${{d}_{0}} = {{d}_{{22}}}\operatorname{sign} ({{x}_{m}} - {{\xi }_{n}}){\text{/}}h$
$\begin{gathered} {{z}_{1}} = \sqrt {({{x}_{m}} - {{\xi }_{n}})R} ,\quad {{z}_{2}} = \sqrt {({{x}_{{m + 1}}} - {{\xi }_{n}})R} \\ {{r}_{{nn}}} = {{I}_{1}}({{x}_{n}} - {{\xi }_{n}}) + 2{{d}_{{22}}}\operatorname{erf} (\sqrt {hR{\text{/}}2} ){\text{/}}h, \\ \end{gathered} $
где $\operatorname{erf} (z)$ – интеграл вероятности [24].

Элементы матрицы системы (4.3) имеют максимальное значение на главной диагонали и быстро убывают по мере удаления от нее. Интеграл $I({{x}_{m}} - {{\xi }_{n}})$ вычисляется по контуру $\Upsilon $ в комплексной плоскости, который выбирается в соответствии с условиями излучения, так, чтобы перемещения поверхности гетерогенного слоя убывали при удалении от вибрирующего штампа. Этот выбор производится после нахождения полюсов подынтегральных функций в (3.5) и их анализа при стремлении внутреннего трения среды к нулю [2]. Отметим, что для анализа скорости сходимости процесса оценивались элементы невязки для количества разбиений N и 3N. Измельчение сетки производилось до относительного значения невязки, меньшего чем ${{10}^{{ - 4}}}$. Горизонтальные смещения под штампом определялись через контактные давления следующим образом:

(4.4)
${{u}_{1}}(x) = \frac{1}{{2\pi }}\sum\limits_{n = 1}^N {{{q}_{n}}} \int\limits_{{{\xi }_{n}}}^{{{\xi }_{{n + 1}}}} {\int\limits_\Upsilon ^{} {\left( {\mu {{G}_{{11}}}(\alpha ) + {{G}_{{12}}}(\alpha )} \right){{e}^{{i\alpha (x - \xi )}}}d\alpha d\xi } } $

Заметим, что при построении численного алгоритма в соотношениях (3.2)–(3.4) для функций $\operatorname{sh} {{s}_{i}}h$, $\operatorname{ch} {{s}_{i}}h$; $i = 1,2,3$, необходимо выносить растущие при больших аргументах экспоненты за рамки вычислительного процесса.

5. Результаты численного анализа. На примере гетерогенного слоя моделировалось покрытие из композиционного материала с матрицей на основе ароматического полиамида фенилона, модифицированного наноразмерной добавкой (алюмо-магниевая шпинель) и наполнителем в виде цилиндрового масла [21]. Модуль Юнга и коэффициент Пуассона композита определены экспериментально, в том числе, с помощью наноиндентирования [21]. Изменение этих модулей при различной пористости, а также модуля объемного сжатия дренированной среды получены с помощью конечно-элементного моделирования [22] и на основе дифференциальной схемы метода самосогласования. Коэффициенты уравнений (2.1) по известным модулям объемного сжатия вязкоупругой матрицы ${{K}_{s}}$, пористой среды с незаполненными порами ${{K}_{b}}$, флюида ${{K}_{f}}$, пористости $m$ вычислялись по формулам, приведенным в [16, 18]. Численный анализ проводился при следующих данных: ${{K}_{s}} = 5.2$ ГПа, ${{K}_{f}} = 2$ ГПа, $N = 1.85$ ГПа, ${{\rho }_{s}} = 1.2 \times {{10}^{3}}$ кг/м3, ${{\rho }_{f}} = 0.93 \times {{10}^{3}}$ кг/м3, ${{K}_{b}}(m = 5\% ) = 4.38$ ГПа, ${{K}_{b}}(m = 10\% )$ = = 3.58 ГПа, ${{K}_{b}}(m = 15\% ) = 2.78$ ГПа, ${{K}_{b}}(m = 20\% ) = 2.21$ ГПа.

Вязкость матрицы композита учитывалась в рамках модели частотно-независимого внутреннего трения, поскольку фенилон отличается малой склонностью к ползучести под действием напряжений [25], а использование нанодобавок с целью модификации матрицы композита позволяет подавлять релаксационные процессы [25]. Согласно такому подходу модуль сдвига имеет вид $N(1 + i{{\gamma }_{0}})$, где величина ${{\gamma }_{0}}$ пропорциональна тангенсу угла механических потерь вязкоупругого материала [26–29]. Вследствие этой зависимости присутствует малая комплексная составляющая в коэффициентах уравнения (2.1) N, A, Q, R [18, 27], ${{10}^{{ - 3}}} < {{\gamma }_{0}} < 0.5 \times {{10}^{{ - 1}}}$. Диапазон изменения параметра ${{\gamma }_{0}}$ был оценен на основании анализа влияния различных наноразмерных добавок на величину внутреннего трения композиционного материала с матрицей из фенилона [27]. Отметим, что на скорость сходимости процесса решения системы уравнений в соотношениях (4.3) параметр ${{\gamma }_{0}}$ влияние не оказывает, а изменение контактных давлений для приведенного диапазона изменения ${{\gamma }_{0}}$ при этом не превышает 2%. Коэффициент проницаемости гетерогенной среды изменялся в диапазоне ${{10}^{{ - 14}}} < {{k}_{o}} < {{10}^{{ - 10}}}$ м2 [30], а извилистость поровых каналов соответствовала случаю частиц сферической формы [31].

В рамках численного эксперимента исследовались нормальные и касательные контактные напряжения при вибрации на верхней границе слоя штампа с плоским основанием при заданной единичной осадке. На основании проведенных исследований установлен ряд общих закономерностей поведения контактных напряжений при учете трения в области контакта, как для гетерогенного полупространства, приведенные в работах [7–9], так и для слоя. При возрастании коэффициента трения значительно увеличивается несимметричность распределения напряжений под штампом, появляется выраженный экстремум. Зависимость нормальных и касательных контактных напряжений от пористости гетерогенного основания [7, 8], проницаемости композита, вязкости жидкой фракции, определяющей степень межфазной адгезии и взаимодействия фаз [9], носит нелинейный характер. Модули контактных напряжений уменьшаются при увеличении пористости и насыщенности флюидом [7, 8].

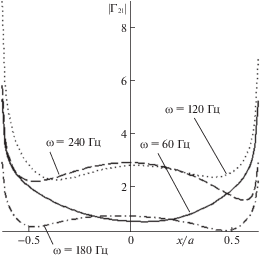
Наибольшее отличие от гетерогенного полупространства имеют зависимости контактных напряжений от частоты колебаний штампа, от толщины слоя. Рис. 2 иллюстрирует распределение под штампом модуля касательных контактных напряжений ${{\Gamma }_{{21}}}$ при разных частотах колебаний $\omega = 60$ Гц, $\omega = 120$ Гц, $\omega = 180$ Гц, $\omega = 240$ Гц, $\eta {\text{/}}{{k}_{o}} = 0.3 \times {{10}^{9}}$, $m = 0.2\,$, $\,\mu = 0.3$, $h{\text{/}}a = 1$. При увеличении частоты не наблюдается монотонное изменение контактных напряжений, имеется диапазон частот, где контактные напряжения имеют максимальное значение, этот диапазон зависит от всех параметров задачи.

Рис. 2.

Влияние частоты колебаний штампа на распределение модуля касательных контактных напряжений.

Среднее за период изменение количества энергии источника колебаний, отдаваемое в среду через область контакта, следуя [4], определяется соотношением:

${\rm E} = - \frac{\omega }{2}\operatorname{Im} \int\limits_{ - 1}^1 {\left( {{\mathbf{u}},{\mathbf{q}}} \right)} dx,$
где $\left( {{\mathbf{u}},{\mathbf{q}}} \right)$ – скалярное произведение векторов, с учетом соотношений (2.2), (3.1). На основании численного анализа контактных напряжений и горизонтальных перемещений можно оценить энергетическое воздействие за период колебаний, от которого, в том числе, зависит износостойкость композиционного материала, при этом изменение амплитуды силы трения за период колебаний играет ключевую роль. Эту закономерность иллюстрирует рис. 3, где показаны изменение нормальных контактных напряжений ${{\Gamma }_{{22}}}$ за период колебаний Т для двух значений частоты колебаний штампа $\omega = 60$ Гц (слева) и $\omega = 120$ (справа). Сплошная линия соответствует t = 0, пунктирная t = T/4, штриховая t = T/2, штрих-пунктирная t = 3T/4. Диапазон изменения нормальных контактных напряжений пропорционален энергетическому воздействию при колебаниях штампа, имеет максимальное значение при $\omega $ = 100–180 Гц для данной гетерогенной среды. При этом необходимо учитывать не только нормальные, но и горизонтальные перемещения в области контакта.

Рис. 3.

Изменение нормальных контактных напряжений за период колебаний Т.

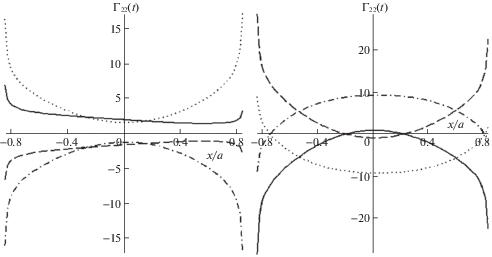
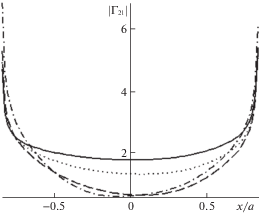
Если количество поверхностных волн остается неизменным, контактные давления меняются монотонно, прослеживается нелинейная зависимость их от толщины слоя. В случае двух распространяющихся поверхностных мод распределение касательных напряжений по области контакта при возрастании толщины слоя иллюстрирует рис. 4, где сплошная линия соответствует $h{\text{/}}a = 0.5$, пунктирная – $h{\text{/}}a = 0.75$, штриховая – $h{\text{/}}a = 1.0$, штрих-пунктирная – $h{\text{/}}a = 1.25$, $\omega $ = 60 Гц. Зависимость контактных напряжений от частоты колебаний, толщины покрытия, пористости, вязкости флюида в порах нелинейная.

Рис. 4.

Влияние толщины слоя на распределение модуля касательных напряжений под штампом.

Заключение. Построено аналитико-численное решение динамической контактной задачи для гетерогенного слоя в рамках модели Био при учете сил трения в области контакта. На основании проведенного численного анализа контактных напряжений показана необходимость учета не только механических характеристик гетерогенной среды, ее пористости, флюидонасыщенности среды, степени взаимодействия фаз, но и частоты колебаний и толщины слоя. Дана оценка энергетического воздействия в контактной области за период колебаний, которое играет ключевую роль в износостойкости конструированного гетерогенного композиционного материала. Проведенные исследования позволяют найти оптимальное соотношение механических свойств композитного материала, работающего в условиях динамического нагружения, управлять трибологическим процессом с помощью подбора толщины слоя и состава композита.

Работа выполнена при финансовой поддержке РФФИ, грант 20-08-00614-а.

Список литературы

  1. Бабешко В.А. Обобщенный метод факторизации в пространственных динамических смешанных задачах теории упругости. М.: Наука, 1984. 256 с.

  2. Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории упругости для неклассических областей. М.: Наука, 1979. 319 с.

  3. Бабешко В.А., Евдокимова О.В., Бабешко О.М. Блочные элементы в контактных задачах с переменным коэффициентом трения // Докл. РАН. 2018. Т. 480. № 5. С. 537–541.

  4. Бабешко В.А., Глушков Е.В., Зинченко Ж.Ф. Динамика неоднородных линейно-упругих сред. М.: Наука, 1989. 344 с.

  5. R. He, L. Wang, H.Y. Yu Time harmonic point load and dynamic contact problem of contacting fluid and poroelastic half-spaces // Soil Dyn.& Earthq. Engng. 2012. V. 36. P. 20–31.

  6. Ватульян А.О. Коэффициентные обратные задачи механики. М.: Физматлит, 2019. 272 с.

  7. Колесников В.И., Беляк О.А., Колесников И.В. и др. О математической модели для прогнозирования трибологических свойств маслонаполненных композитов при вибрации // Докл. РАН. 2020. Т. 491. С. 44–47.

  8. Kolesnikov V.I., Suvorova T.V., Belyak O.A. Modeling antifriction properties of composite based on dynamic contact problem for a heterogeneous foundation // Mater. Phys.&Mech. 2020. V. 46. № 1. P. 139–148.

  9. Беляк О.А., Суворова Т.В. О влиянии взаимодействия фаз гетерогенного основания на контактные напряжения при колебаниях штампа с трением // Эколог. вестн. научн. центров Черном. эконом. сотр. 2020. Т. 17. № 3. С. 29–36.

  10. Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука, 2001. 478 с.

  11. Горячева И.Г., Добычин М.Н. Контактные задачи в трибологии. М.: Машиностроение, 1988. 253 с.

  12. Chen W., Wang Q., Huan Z. et al. Semi analytical viscoelastic contact modeling of polymer based materials // J. Tribology. 2011. V. 133. № 4. P. 041404.

  13. Liu M., Huang H. Poroelastic response of spherical indentation into a half space with a drained surface via step displacement // Int. J. Solids&Struct. 2019. V. 165. P. 34–49.

  14. Суворова Т.В., Беляк О.А. Контактные задачи для пористоупругого композита при наличии сил трения // ПММ. 2020. Т. 84. № 4. С. 529–539.

  15. Беляк О.А., Суворова Т.В. Влияние микроструктуры основания на силы трения при движении плоского штампа // Эколог. вестн. научн. центров Черном. эконом. сотр. 2018. № 3. С. 25–31.

  16. Био М.А. Механика деформирования и распространения акустических волн в пористой среде // Сб. пер. иностр. статей. 1963. Вып. 6. № 82. С. 103–134.

  17. Ковтун А.А. Об уравнениях Био и их модификациях // Уч. зап. СПбГУ. 2011. Вып. 44. № 444. С. 3–26.

  18. Degrande G., Roeck G. De, Breck P. Van Den et al. Wave propagation in layered dry, saturated and unsaturated poroelastic media // Int. J. Solids&Struct. 1998. V. 35 (34-35). P. 4753–4778.

  19. Долгополов К.Н., Колесников И.В., Мельников Э.Л. Применение антифрикционных полимерных самосмазывающихся материалов класса “Масляниты” в узлах трения скольжения // Ремонт. Восстановление. Модернизация. 2018. № 4. С. 23–26.

  20. Sytar V.I., Kuzyayev I.M., Sukhyy K.M. et al. Influence of the nature and concentration of porogens on the structure and properties of phenylone // Voprosy khimii i khimicheskoi tekhnologii. 2019. № 6. P. 213–220.

  21. Иваночкин П.Г., Суворова Т.В., Данильченко С.А. и др. Комплексное исследование полимерных композитов с матрицей на основе фенилона С-2 // Вестн. РГУПС. 2018. В. 4. С. 18–25.

  22. Belyak O.A., Suvorova T.V. Modeling stress deformed state upon contact with the bodies of two phase microstructure // Solid State Phenom. 2020. V. 299. P. 124–129.

  23. Брычков Ю.А., Прудников А.П. Интегральные преобразования обобщенных функций. М.: Наука, 1977. 288 с.

  24. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Т. 2. М.: Наука, 1974. 296 с.

  25. Абакумова Н.М., Гудимов М.М., Финогенов Г.Н. и др. Физико-механические свойства ароматических полиамидов марки фенилон // Пластич. массы. 1973. № 9. С. 30–32.

  26. Афашагова З.Х., Буря А.И., Козлов Г.В. и др. Структура и свойства дисперсно-наполненных нанокомпозитов фенилон/аэросил // Механика композ. матер. 2007. Т. 13. № 4. С. 479–492.

  27. Иваночкин П.Г., Беляк О.А. Влияние наноразмерных наполнителей на вязкоупругие свойства композиционных материалов с матрицей на основе фенилона // Новые матер. и технол. в машиностр. 2020. № 32. С. 25–29.

  28. Guyer R.A., Kim H. Alicia, Derome D. et al. Hysteresis in modeling of poroelastic systems: Quasistatic equilibrium // Phys. Rev. E. 2011. № 83. P. 061408.

  29. Chandra R., Singh S.P., Gupta K. A study of damping in fiber-reinforced composites // J. Sound&Vibr. 2003. V. 262. № 3. P. 475–496.

  30. Chevillotte F., Jaouen L., Bécot F. On the modeling of visco-thermal dissipations in heterogeneous porous media // J. Acoust. Soc. Am. 2015. V. 138. № 6. P. 3922–3929.

  31. Wu A., Yang B., Xi Y. et al. Pore structure of ore granular media by computerized tomography image processing // J. Central South Univ. Technol. 2007. V. 14. № 2. P. 220–224.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал