Прикладная математика и механика, 2021, T. 85, № 3, стр. 296-308

1. Введение. Основной областью научных интересов Владимира Андреевича Бабешко, с начала научной работы под руководством И.И. Воровича в 1960-х годах и до наших дней, является решение динамических задач теории упругости. Академик Бабешко – один из основоположников интегрального подхода, базирующегося на выводе и использовании интегрального представления вектора смещений возбуждаемого волнового поля $u$ через матрицу Грина $k$ для рассматриваемой упругой слоистой структуры и вектор приложенной нагрузки ${\mathbf{q}}$ [1]:

Здесь $K = F[k]$ и ${\mathbf{Q}} = F[{\mathbf{q}}]$ – Фурье-символы (результат преобразования Фурье $F$ по горизонтальным координатам $x$ и $y$) матрицы-функции $k({\mathbf{x}})$ и вектор-функции ${\mathbf{q}}(x,y)$; ${\mathbf{x}}$ = $(x,y,z)$ = $({{x}_{1}},{{x}_{2}},{{x}_{3}})$. Такое представление позволяет разрабатывать эффективные полуаналитические методы как для решения динамических контактных задач (определение неизвестных контактных напряжений ${\mathbf{q}}$ и тем самым динамической реакции упругой среды), так и для исследования волновых процессов.

Контактные задачи сводятся к интегральным уравнениям, для решения которых В.А. Бабешко был разработан и реализован набор эффективных методов, таких как метод факторизации [1] и метод фиктивного поглощения [2]. Для исследования волновых процессов используются методы численного интегрирования (в ближней зоне) или выводятся асимптотики рассматриваемых интегралов (для дальней зоны) [3]. Важно, что интегральное представление (1.1) и полученные из него асимптотики справедливы для любой вертикально-неоднородной упругой среды, отличие только в конкретном виде матрицы $K$. Для классических однородных изотропных волноводов (слой, полупространство) ее элементы могут быть выписаны в явном виде, а для сред более сложного строения (многослойность, непрерывная зависимость упругих свойств от глубины и др.) для ее построения требуется разработка численно устойчивых алгоритмов [4–6]. При этом самостоятельный интерес представляют анизотропные волноводы, к которым, в частности, относятся пластины из многослойных композитных материалов [7].

Представление (1.1) остается справедливым и в этом случае, но задача усложняется как с точки зрения разработки эффективных алгоритмов построения матрицы $K$, так и вывода асимптотики бегущих волн, который уже не сводится к простому применению теоремы Коши о вычетах. Следует отметить, что для однородного ортотропного слоя А.О. Ватульяну удалось получить матрицу $K$ в явном виде [8]. Однако в общем случае произвольной анизотропии разработка алгоритмов построения матрицы $K$ потребовала значительной модификации по сравнению с изотропным случаем [9, 10].

Для моделирования распространения бегущих волн в упругих слоистых волноводах традиционно используется техника модального анализа. Они ищутся в виде плоских волн, волновой вектор которых указывает направление распространения, а их скорости и собственные формы определяются дисперсионными соотношениями, возникающими при подстановке искомого решения в однородные граничные условия. В анизотропном случае для многослойных волноводов разрабатываются специальные матричные алгоритмы вычисления волновых характеристик [11–14]. Причем некоторые из указанных подходов, например, метод дискретных слоев, базирующийся на конечно-элементной дискретизации по толщине [15], позволяет не только строить дисперсионные кривые, но и вычислять динамическую функцию Грина многослойного полупространства. Разработанные подходы к исследованию волн Лэмба в многослойных анизотропных пластинах (см., например обзор [16]) позволяют также исследовать такие интересные явления, как влияние сильной неоднородности материала на волновые эффекты [17] или строить их длинноволновые и коротковолновые асимптотики [18].

В отличие от изотропного случая, вектор групповой скорости ${\mathbf{c}}$, указывающий направление переноса энергии волновым пакетом, вообще говоря, не совпадает по направлению с волновым вектором ${\mathbf{k}}$, отклоняясь от него на некоторый угол $\vartheta $. Возникает дополнительная проблема определения такого направления $\gamma $ волнового вектора ${\mathbf{k}}$, которое дает требуемое направление $\varphi $ для вектора групповой скорости ${\mathbf{c}}$. Ее решение важно, например, для развития SHM-технологии неразрушающего ультразвукового контроля композитных материалов, используемых в аэрокосмических изделиях [19]. Асимптотика, полученная из интегрального представления (1.1), описывает цилиндрические бегущие волны, распространяющиеся от источника (области приложения нагрузки ${\mathbf{q}}$) [9, 10]. Ее замечательным свойством является то, что значение групповой скорости $c = \left| {\mathbf{c}} \right|$ определяется этой асимптотикой для любого требуемого направления $\varphi $ без необходимости находить направление волнового вектора ${\mathbf{k}}$ для эквивалентной плоской волны. Ниже это свойство подробно обсуждается в сопоставленнии с результатами модального анализа. Преимущества асимптотических представлений, полученных в рамках интегрального подхода, иллюстрируются практическими приложениями к задачам обнаружения повреждений и скрытых дефектов методами SHM, а также к обратным задачам определения эффективных упругих модулей армированных углепластиков и нанокомпозитов.

2. Цилиндрические бегущие волны. Рассматривается $M$-слойная упругая пластина с произвольной анизотропией слоев, к поверхности которой в области $\Omega $ приложена осциллирующая нагрузка ${\mathbf{q}}(x,y){{e}^{{ - i\omega t}}}$, генерирующая поле установившихся гармонических колебаний ${\mathbf{u}}({\mathbf{x}}){{e}^{{ - i\omega t}}}$; $\omega = 2\pi f$ – круговая частота, $f$ – частота (рис. 1). В частности, это может быть композитная пластина толщины $H$, изготовленная из волоконно-армированных трансверсально-изотропных слоев-препрегов [7], с приклеенным к поверхности круговым пьезоактуатором.

Вектор комплексной амплитуды смещений ${\mathbf{u}}$ удовлетворяет в каждом из слоев уравнениям эластодинамики

Здесь ${{C}_{{ijkl}}}$ – компоненты тензора упругих постоянных, $\rho $ – плотность. Слои жестко сцеплены между собой, т.е. поля перемещений ${\mathbf{u}}({\mathbf{x}})$ и напряжений ${\mathbf{\tau }}({\mathbf{x}})$ непрерывны во всем объеме пластины ${\text{|}}x{\text{|}} < \infty $, ${\text{|}}y{\text{|}} < \infty $, $ - H < z < 0$, в том числе и на внутренних границах раздела слоев $z = {{z}_{m}}$. Внешние границы $z = - H$ и $z = 0$ свободны от напряжений за исключением области приложения нагрузки. В случае пленочного пьзоактуатора нагрузка ${\mathbf{q}}$ – это радиальные контактные напряжения, концентрирующиеся на границе области контакта $\Omega $ [20, 21].

Решение данной краевой задачи представимо в виде (1.1). В полярных координатах

двукратный контурный интеграл сводится к однократному интегралу по контуру ${{\Gamma }_{ + }}$, идущему в комплексной плоскости $\alpha $ вдоль положительной вещественной полуоси, отклоняясь от нее при обходе вещественных полюсов подынтегральной функции ${{\zeta }_{n}}$, и внутреннему интегралу по угловой переменной $\gamma $:

Основной идеей, позволившей сформировать алгоритм построения матрицы $K$ в компактной матричной форме, является замена производных по пространственным координатам $\partial {\text{/}}\partial {{x}_{j}}$ на их Фурье-символы $ - i{{\alpha }_{j}}$, в том числе и для производной по поперечной координате $z = {{x}_{3}}$, по которой преобразование Фурье формально не применимо [22]. При кусочно-постоянной зависимости упругих свойств от $z$ общее решение уравнений (2.1) в области преобразования Фурье выписывается в каждом слое в явном виде с точностью до шести постоянных множителей ${{{\mathbf{t}}}_{m}} = (t_{m}^{{(1)}},t_{m}^{{(2)}},...,t_{m}^{{(6)}})$, $m = 1,2,...,M$. Вектор неизвестных коэффициентов ${\mathbf{t}} = ({{{\mathbf{t}}}_{1}},{{{\mathbf{t}}}_{2}},...,{{{\mathbf{t}}}_{M}})$ длиной $6M$ определяется из системы линейных алгебраических уравнений $A{\mathbf{t}} = {\mathbf{f}}$, возникающей при удовлетворении граничных условий. Поэтому по построению определитель матрицы этой систомы $\Delta = \det A$ входит в знаменатель коэффициентов ${{{\mathbf{t}}}_{m}}$, а тем самым и в общий знаменатель элементов матрицы $K:$ $K = \hat {K}({{\alpha }_{1}},{{\alpha }_{2}},z){\text{/}}\Delta ({{\alpha }_{1}},{{\alpha }_{2}})$. Корни $\alpha = {{\zeta }_{n}}$ характеристического уравнения

являются полюсами подынтегральной функции в представлении (2.2) (числитель $\hat {K}$, как и Фурье-символ нагрузки ${\mathbf{Q}}$, полюсов не имеет). В анизотропном случае они зависят не только от частоты $\omega $, но и от направления $\gamma $ в плоскости $({{\alpha }_{1}},{{\alpha }_{2}})$: $\alpha = {{\zeta }_{n}}(\omega ,\gamma )$.

Как в изотропном, так и в анизотропном случае разворот контура ${{\Gamma }_{ + }}$ и его замыкание в соответствии с леммой Жордана позволяет воспользоваться теоремой Коши, заменив интеграл по $\alpha $ суммой вычетов в полюсах ${{\zeta }_{n}}$, попадающих внутрь замкнутого контура (для обратной волны вычет берется в отрицательном полюсе $ - {{\zeta }_{n}}$). Вычеты в вещественных полюсах дают бегущие волны. В изотропном случае их асимптотика в дальней зоне представима в виде [3]

$N$ – число вещественных полюсов. Каждое слагаемое в разложении (2.4) описывает цилиндрическую бегущую волну, распространяющуюся от источника на бесконечность с фазовой скоростью ${{v}_{n}} = \omega {\text{/}}{{\zeta }_{n}}$ и групповой скоростью ${{c}_{n}} = d\omega {\text{/}}d{{\zeta }_{n}}$. При этом амплитудные множители ${{{\mathbf{a}}}_{n}}$ однозначно определяются свойствами волновода (через $\operatorname{res} K$) и параметрами источника (через ${\mathbf{Q}}$).

В анизотропном случае зависимость полюсов ${{\zeta }_{n}}$ от $\gamma $ не позволяет после взятия вычетов свести внутренние интегралы по $\gamma $ к цилиндрическим функциям Бесселя. Поэтому для дальней зоны ${{\zeta }_{n}}r \gg 1$ строится их асимптотика методом стационарной фазы [23]. После замены переменных $\gamma = \beta + \varphi + \pi {\text{/}}2$ фазовая функция в показателе осциллирующей экспоненты принимает вид [10]

Стационарные точки ${{\beta }_{{nm}}}$ определяются корнями уравнения

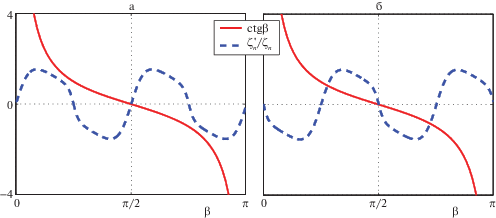
которое эквивалентно уравнению $\operatorname{ctg} \beta = - \zeta _{n}^{'}(\theta ){\text{/}}{{\zeta }_{n}}(\theta )$. В изотропном случае $\zeta _{n}^{'}(\theta ) = 0$, что приводит к фазовому уравнению $cos\beta = 0$, имеющему на отрезке $[0,\pi ]$ единственный корень $\beta = \pi {\text{/}}2$, дающий в конечном счете асимптотику (2.4).

В анизотропном случае $\zeta _{n}^{'}(\theta ) \ne 0$, что приводит, во-первых, к отклонению стационарной точки от $\pi {\text{/}}2$, а во-вторых, к возможности появления дополнительных стационарных точек – корней уравнения (2.6). В качестве иллюстрации на рис. 2, взятом из работы [10], показаны графики функций $\operatorname{ctg} \beta $ и $ - \zeta _{n}^{'}(\theta ){\text{/}}{{\zeta }_{n}}(\theta )$ для направления $\varphi $ вдоль армирующих волокон верхнего слоя (рис. 2, а) и под углом 45° к ним (рис. 2, б) для фундаментальной моды $S{{H}_{0}}$, воздуждаемой в композитной пластине, геометрические и упругие свойства которой приведены в указанной работе. Точки пересечения этих кривых дают корни уравнения (2.6). В первом случае, для главного направления вдоль волокон, корень $\beta = \pi {\text{/}}2$ такой же, как и в изотропном случае, а во втором случае наблюдается пересечение в трех точках. Это означает, что в асимптотике бегущих волн для этого направления $\varphi $ одному полюсу ${{\zeta }_{n}}$ соответствует три волны, распространяющиеся с различными скоростями. В общем случае асимптотика цилиндрических бегущих волн, возбуждаемых локализованной нагрузкой ${\mathbf{q}}$ принимает вид [9, 10]:

Здесь, как и в представлении (2.4), амплитудные множители ${{{\mathbf{a}}}_{{nm}}}$ выражаются через вычеты элементов матрицы $K$ в полюсах $\alpha = {{\zeta }_{n}}$ при $\gamma = {{\theta }_{{nm}}}$ и ${\mathbf{Q}}( - {{s}_{{nm}}},\varphi )$; ${{M}_{n}}$ – число стационарных точек (корней ${{\beta }_{{nm}}}$ уравнения (2.6)) для фиксированного направления $\varphi $, ${{s}_{{nm}}} = {{s}_{n}}({{\beta }_{{nm}}})$, $\zeta $ – характерное значение волнового числа.

Наряду с возможным существованием нескольких бегущих волн, соответствующих одному полюсу ${{\zeta }_{n}}$, качественное отличие разложения (2.7) от асимптотики (2.4) состоит в том, что сам по себе полюс уже не является волновым числом. Вместо него в показателе экспоненты при радиальной переменной $r$ стоят коэффициенты ${{s}_{{nm}}}$, отличающиеся от ${{\zeta }_{n}}$ сомножителем $sin{{\beta }_{{nm}}}$. Именно они и играют роль волнового числа. Соответственно, разложение (2.7) описывает набор бегущих волн, распространяющихся с фазовыми и групповыми скоростями

причем их число может меняться в зависимости от направления $\varphi $.

3. Модальный анализ. В рамках модального анализа распространяющиеся вдоль пластины бегущие волны описываются собственными решениями рассматриваемой краевой задачи, которые ищутся в виде плоских волн

Волновой вектор ${\mathbf{k}} = ({{k}_{x}},{{k}_{y}},0)$, ${{k}_{x}} = kcos\gamma $, ${{k}_{y}} = ksin\gamma $, $k = {\text{|}}{\mathbf{k}}{\text{|}}$, определяет ориентацию волнового фронта в плоскости $(x,y)$, указывая ортогональное к фронту направление $\gamma $ (традиционное обозначение волнового числа $k$ совпало с также ставшим традиционным обозначением матрицы Грина в представлении (1.1); это не должно приводить к путанице, т.к. они используются в различных контекстах). Подстановка представления (3.1) в уравнения (2.1) приводит к системе обыкновенных дифференциальных уравнений второго порядка относительно неизвестных компонент амплитудного вектора ${\mathbf{a}}(z)$. Как и при построении матрицы $K$, в каждом из слоев композита ее общее решение выписывается в явном виде с точностью до постоянных множителей ${{{\mathbf{t}}}_{m}}$, а общий вектор неизвестных ${\mathbf{t}}$ определяется из возникающей при удовлетворении граничных условий однородной системы $A{\mathbf{t}} = {\mathbf{0}}$ с той же матрицей $A$, но только с компонентами волнового вектора $({{k}_{x}},{{k}_{y}})$ вместо параметров преобразования Фурье $({{\alpha }_{1}},{{\alpha }_{2}})$. Поэтому условие $\det A = 0$, необходимое для существования ее ненулевого решения, дает такое же дисперсионное уравнение как и (2.3):

Соответственно, его корни выражаются через те же полюса ${{\zeta }_{n}}$:

В то время как векторы фазовой скорости ${{{\mathbf{k}}}_{n}}$ для мод бегущих волн, определяемых корнями дисперсионного уравнения, коллинеарны волновым векторам:

векторы групповой скорости ${{{\mathbf{c}}}_{n}}$ могут отклоняться от ${{{\mathbf{k}}}_{n}}$, т.е. быть не ортогональными к фронту волны.

Для определения ${{{\mathbf{c}}}_{n}}$ уравнение (3.2) разрешается относительно частоты $\omega $:

и используется представление [24, 25]

Чтобы не вычислять производные от искомых корней ${{\omega }_{n}}$, удобно также использовать представление

для вывода которого достаточно взять полные производные уравнения (3.2) по ${{k}_{x}}$ и ${{k}_{y}}$:

Отклонение ${{{\mathbf{c}}}_{n}}$ от ${{{\mathbf{k}}}_{n}}$ хорошо иллюстрируется следующими геометрическими построениями. Будучи градиентом к поверхности ${{\omega }_{n}}({\mathbf{k}})$, вектор ${{{\mathbf{c}}}_{n}}$ ортогонален к линии уровня ${{\omega }_{n}} = \operatorname{const} $, вычерчиваемой на плоскости $({{k}_{x}},{{k}_{y}})$ волновым вектором ${{{\mathbf{k}}}_{n}}(\gamma )$ при $0 \leqslant \gamma \leqslant 2\pi $ (рис. 3, а). В изотропном случае ${{\zeta }_{n}}$ не зависит от $\gamma $ и кривая, определяемая равенствами (3.3), является окружностью, у которой радиус-вектор ${{{\mathbf{k}}}_{n}}$ ортогонален к касательной, т.е. угол $\varphi $, определяющий направление вектора групповой скорости ${{{\mathbf{c}}}_{n}} = ({{c}_{{n,x}}},{{c}_{{n,y}}})$:

совпадает с углом $\gamma $ волнового вектора. Следует отметить, что свойство ортогональности ${{{\mathbf{c}}}_{n}}$ к кривой ${{{\mathbf{k}}}_{n}}(\gamma )$ взаимно обратно: волновой вектор ${{{\mathbf{k}}}_{n}}$ также ортогонален к кривой, вычерчиваемой вектором групповой скорости ${{{\mathbf{c}}}_{n}}(\varphi )$ (рис. 3, б).

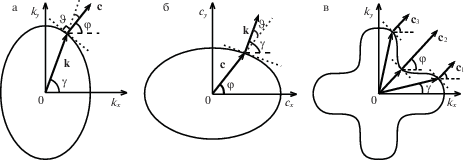
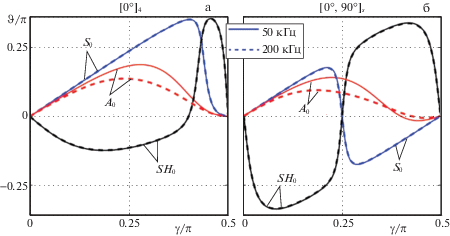
Зависимость полюсов ${{\zeta }_{n}}$ от $\gamma $ дает кривую, отличную от окружности, нормаль к которой в общем случае не совпадает с направлением радиус-вектора ${{{\mathbf{k}}}_{n}}(\gamma )$ (совпадает только для главных осей анизотропии). При этом угол отклонения $\vartheta = \varphi (\gamma ) - \gamma $ зависит не только от $\gamma $, но и от частоты $\omega $ и может достигать значительных величин, превышающих 45°. В качестве примера на рис. 4 показаны зависимости $\vartheta $ от $\gamma $ для фундаментальных мод ${{A}_{0}}$, ${{S}_{0}}$ и $S{{H}_{0}}$, возбуждаемых в однонаправленном (рис. 4, а) и перекрестно-армированном (рис. 4, б) композитах толщины $H = 1.1$ мм, составленных из слоев-препрегов плотности $\rho = 1482$ кг/м³. Препреги моделируются трансверсально-изотропными слоями с упругими модулями ${{C}_{{11}}} = 95.9$, ${{C}_{{12}}} = 3.6$, ${{C}_{{22}}} = 9.6$, ${{C}_{{44}}} = 3.0$, ${{C}_{{55}}} = 3.45$ (ГПа) (${{C}_{{ij}}}$ в нотации Фойгта [7]).

4. Сравнение характеристик цилиндрических и плоских волн. Как правило, вектор ${{{\mathbf{k}}}_{n}}(\gamma )$ вычерчивает выпуклую кривую. Но если ${{\zeta }_{n}}(\gamma )$ в диапазоне $0 \leqslant \gamma \leqslant \pi {\text{/}}2$ меняется немонотонно, то эта кривая становится невыпуклой. В этом случае несколько точек ${{\gamma }_{m}}$ могут давать одно и то же направление $\varphi $ для соответствующих векторов групповой скорости ${{{\mathbf{c}}}_{m}}$ (рис. 3, в), то есть в таком направлении $\varphi $ распространяется несколько волновых пакетов, переносимых плоскими волнами с разным направлением волновых векторов. Это полностью согласуется с возможностью существования в асимптотике (2.7) ${{M}_{n}}$ бегущих цилиндрических волн, соответствующих одному и тому же полюсу ${{\zeta }_{n}}$. Более того, значения ${{c}_{n}}(\varphi )$, получающиеся для плоских волн по формуле (3.4) или (3.5), совпадают со значениями групповой скорости цилиндрических волн ${{c}_{{nm}}}(\varphi )$, получаемых из (2.8).

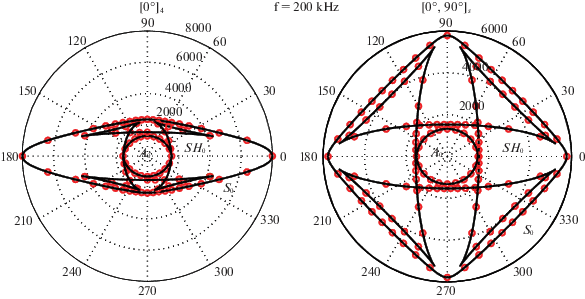
В качестве примера на рис. 5 показаны угловые диаграммы групповых скоростей плоских волн ${{c}_{n}}(\varphi )$ (сплошные линии) и цилиндрических волн ${{c}_{{nm}}}(\varphi )$ (маркеры) для фундаментальных мод, распространяющихся в тех же композитных пластинах, что и на рис. 4. Для каждого направления $\varphi $ их значения полностью совпадают, однако формулы (2.8) дают их сразу, в то время как углы $\gamma $ волновых векторов плоских волн, определяющих их групповую скорость в этом направлении, заранее неизвестны. Поэтому в практических приложениях на каждом шаге применения формул (3.4)–(3.5) необходим поиск требуемых углов ${{\gamma }_{m}}$.

Кроме того, разложение (2.7) дает однозначные величины амплитудных коэффициентов ${{{\mathbf{a}}}_{{nm}}}(\varphi ,z)$, тогда как собственные формы ${\mathbf{a}}(z)$ плоских волн (3.1) определяются с точностью до постоянного множителя, не учитывая параметры источника. Тем не менее, их нормированные зависимости от $z$ для одинаковых $\varphi $ совпадают: и те, и другие описывают одни и те же собственные формы нормальных мод.

В целом, полученная из интегрального представления асимптотика бегущих волн (2.7) дает те же волновые характеристики, что и классический модальный анализ (скорость, собственные формы), но вдобавок имеет два важных преимущества:

1) учет источника, позволяющий получать значение амплитуды возбуждаемых волн и тем самым анализировать амплитудно-частотные характеристики, определять оптимальные диапазоны возбуждения требуемых мод и т.п.

2) нет необходимости подбирать нужную ориентацию плоской волны для определения групповой скорости движения волнового пакета в требуемом направлении $\varphi $.

5. Практические приложения. Преимущества интегрального подхода позволяют решать задачи, которые сложно или даже невозможно решить, используя только модальный анализ. Из недавних примеров отметим реализацию метода обращения времени для анизотропных композитов [26] и определение эфффективных упругих модулей нанокомпозитов [27].

5.1. Метод обращения времени [28], известный в отечественной литературе как метод обращения волн [29], основан на инвариантности волнового оператора относительно замены времени $t$ на $ - t$ для сред без внутреннего трения. Это позволяет использовать сигналы ${{{v}}_{j}}(t)$, регистрируемые в различных точках ${{{\mathbf{x}}}_{j}}$ поверхности упругой пластины, например, сетью пьезосенсоров, в качестве обращенных по времени управляющих сигналов ${{q}_{j}}(t) = p{{{v}}_{j}}( - t)$ источников, расположенных в этих же точках; $p$ – размерный коэффициент. Эти источники генерируют волновые поля ${{{\mathbf{u}}}_{j}}({\mathbf{x}},t)$, и, если сигналы ${{{v}}_{j}}(t)$ были принесены волнами, рассеянными скрытым дефектом, то обращенные волны фокусируются на нем, обнаруживая его местоположение.

Для изотропных пластин местоположение рассеивателя может быть определено и более простыми средствами, например, с помощью триангуляции, зная время прихода сигналов и групповую скорость приносящих их волн. Однако для анизотропных композитных пластин зависимость вектора групповой скорости ${{{\mathbf{c}}}_{n}}$ от направления распространения и частоты не позволяет использовать простую триангуляцию или фокусировку обращенных плоских волн ${{{\mathbf{u}}}_{j}}$.

В то же время, использование полученных в рамках интегрального подхода асимптотик (2.7) для вычисления обращенных волн ${{{\mathbf{u}}}_{j}}$ по данным экспериментальных измерений сигналов ${{{v}}_{j}}(t)$ позволило реализовать метод обращения времени и для композитных образцов [26].

5.2. Определение эффективных упругих модулей композитной пластины по характеристикам возбуждаемых в ней бегущих волн базируется на минимизации фунционала невязки

в котором $C$, $\rho $ и $h$ – массивы упругих модулей, плотностей и толщин слоев образца, а $d_{j}^{m}$ и $d_{j}^{c}$ измеренные и расчетные волновые характеристики, например, групповые скорости или длины волн на определенных частотах. Алгоритмы минимизации функционала $F$ могут быть различными (покоординатный или градиентный спуск, метод сопряженных градиентов, генетический алгоритм и др.), но каждый их шаг требует пересчета волновых характеристик $d_{j}^{c}$ по новым значениям варьируемых (неизвестных) входных параметров. Использование асимптотики (2.7) и представлений (2.8) дает такое же преимущество по сравнению с модальным анализом, как и в методе обращения времени. Однако поиск корней дисперсионного уравнения (2.3) все еще требует сотни и тысячи вызовов процедуры вычисления матрицы $K$ на каждом шаге, определяя общий уровень вычислительных затрат. Тем не менее, реализация такого подхода позволила успешно определить свойства используемых в экспериментах образцов и провести на этой основе экспериментальную верификацию полученных интегральных и асимптотических представлений (2.2), (2.7) для анизотропных композитных пластин [30].

При использовании лазерно-оптической установки измерения дисперсионных характеристик бегущих волн на определенных фиксированных частотах методом TGM (transient grating method) [31] удалось избежать поиска корней ${{\zeta }_{n}}$, снизив этим вычислительные затраты на 2–3 порядка [27]. Идея заключается в том, что для полученных методом TGM пар $({{\lambda }_{j}},{{f}_{j}})$, $j = 1,2,...$ (длина волны – частота), дающих пиковые значения частотного спектра поверхностных акустических волн (ПАВ), целевую функцию можно сформировать в следующем виде

где ${{K}_{{33}}}$ элемент матрицы $K$, дающий вертикальную компоненту смещений при нормальном воздействии ${{q}_{3}}$, ${{\alpha }_{j}} = 2\pi {\text{/}}{{\lambda }_{j}}$, ${{\omega }_{j}} = 2\pi {{f}_{j}}$. Для ПАВ значения ${{\alpha }_{j}}$, ${{\omega }_{j}}$ должны совпадать с корнями дисперсионного уравнения (2.3). Обратная величина элементов маирицы $K$ при этом должна обращаться в ноль, что и позволяет использовать функционал (5.2) вместо (5.1). Минимизация этого функционала уже не требует затратного поиска корней дисперсионного уравнения, а только вычисления значений ${{K}_{{33}}}$ в нескольких точках $({{\alpha }_{j}},{{\omega }_{j}})$.

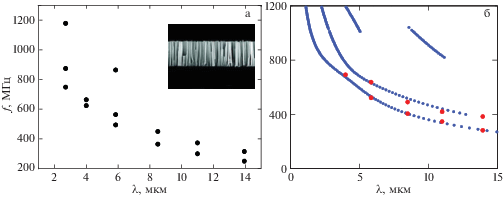
В качестве примера на рис. 6, а показано типичное распределение точек резонансного отклика в плоскости $(\lambda ,f)$, полученное для композитной пленки толщиной около 1 микрона с III-нитридными нанонитями GaN, запеченными в пластик HSQ [27]. Дисперсионные кривые, посчитанные для эффективных параметров композита, полученных при минимизации функционала (5.2), проходят через эти точки (рис. 6, б), т.е. дают наблюдаемые в эксперименте характеристики ПАВ.

Заключение. Рассмотрено приложение интегрального подхода к анализу бегущих волн в анизотропных композитных пластинах. Показаны преимущества полученных асимптотических представлений при решении задач неразрушающего ультразвукового контроля и определения эффективных упругих свойств композитных материалов.

Работа выполнена при поддержке Российского научного фонда (проект № 17-11-01191).