Прикладная математика и механика, 2021, T. 85, № 3, стр. 370-382

Некоторые решения теории упругости для прямоугольника

М. Д. Коваленко^1, *, И. В. Меньшова^2, 3, **, А. П. Кержаев^2, ***, Т. Д. Шуляковская^4, ****

¹ Институт прикладной механики РАН
Москва, Россия

² Институт теории прогноза землетрясений и математической геофизики РАН
Москва, Россия

³ Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

⁴ Институт физики Земли им. О.Ю. Шмидта РАН
Москва, Россия

^* E-mail: kov08@inbox.ru
^** E-mail: menshovairina@yandex.ru
^*** E-mail: alex_kerg@mail.ru
^**** E-mail: 5095739@mail.ru

Поступила в редакцию 19.11.2020
После доработки 01.02.2021
Принята к публикации 25.02.2021

DOI: 10.31857/S0032823521030073

Полный текст (PDF)

Аннотация

В статье приводятся готовые формулы, описывающие решения краевых задач теории упругости в прямоугольнике, у которого две противоположные стороны свободны, а на двух других заданы нормальные или касательные напряжения. Рассмотрены все случаи симметрии относительно центральных осей. Решения представляются рядами по собственным функциям Папковича–Фадля. Коэффициенты рядов определяются по простым замкнутым формулам как интегралы Фурье от заданных граничных функций. Приводится пример сравнения точного решения с решением, полученным на основе балочной теории, для достаточно узкого прямоугольника.

Ключевые слова: прямоугольник, собственные функции Папковича–Фадля, точные решения

1. Введение. Точные решения краевых задач теории упругости в прямоугольнике с различными граничными условиями на его сторонах – одна из наиболее известных проблем (обзоры [1, 2]). Это связано как с их практической значимостью, так и с различными вопросами теоретического характера (влияние концевых эффектов, поведение решений в окрестности сингулярных точек, оценка различных приближенных теорий и т.д. [3]).

Статья базируется на ранее полученных авторами точных решениях для полуполосы [4–8] благодаря несложному обобщению: экспоненциальные функции заменяются гиперболическими. По этой причине промежуточные выкладки опущены и сразу приводятся окончательные формулы.

Строгая постановка и решение краевых задач теории упругости в прямоугольнике в виде рядов по собственным функциям Папковича–Фадля возможны только в рамках модели с остаточными напряжениями [9] (что обусловлено базисными свойствами собственных функций). В этой модели стороны прямоугольника, непрямолинейные до деформации, становятся прямолинейными после. Поэтому граничные условия выполняются строго на прямолинейных сторонах области. Для перехода к (представленным в работе) решениям в традиционной постановке нужно в решениях, описывающих остаточные напряжения, определенным образом изменить знаки перед некоторыми формулами.

В противоположность этому, в классической модели Шермана [10] стороны прямоугольника, прямолинейные до деформации, остаются прямолинейными и после. Это достигается добавлением недостающего или удалением лишнего материала (создание “вкладок” [11]). Вкладками устраняются разрывы перемещений, поэтому в модели Шермана–Мусхелишвили (в отличие от модели с остаточными напряжениями) выполняются условия совместности деформаций, но при этом граничные условия ставятся на осях вкладок, совпадающих с первоначальными границами прямоугольника (эти вопросы подробно обсуждались в предыдущих статьях авторов, например, [4–8]).

Все формулы имеют одинаковую структуру (идентичную решениям Файлона–Рибьера [3]): вначале стоит коэффициент Лагранжа – аналог коэффициента Фурье в периодических решениях, затем зависящее только от переменной $y$ отношение какой-либо собственной функции Папковича–Фадля к отвечающему ей нормирующему множителю (в периодических решениях он обычно равен единице) и, наконец, зависящее только от переменной $x$ выражение, в которое входят гиперболические функции. Некоторая внешняя громоздкость формул обусловлена комплекснозначностью выражений.

2. Постановка задачи и общие формулы. Ниже приводятся формулы, описывающие решения краевых задач в полуполосе $\{ {{\Pi }^{ + }}{\kern 1pt} :\;x \geqslant 0,\;{\text{|}}y{\text{|}} \leqslant h\} $ и в прямоугольнике $\{ P{\kern 1pt} :\;{\text{|}}x{\text{|}} \leqslant d,\;{\text{|}}y{\text{|}} \leqslant h\} $ (их схемы показаны на рис. 1 и 2 ).

Рис. 1.

Рис. 2.

Горизонтальные стороны $y = \pm h$ полуполосы и прямоугольника свободны, т.е. здесь напряжения

(2.1)

${{\sigma }_{y}}(x, \pm h) = {{\tau }_{{xy}}}(x, \pm h) = 0$

На торце полуполосы

(2.2)

${{\sigma }_{x}}(0,y) = \sigma (y),\quad {{\tau }_{{xy}}}(0,y) = \tau (y),$

а на торцах прямоугольника

(2.3)

${{\sigma }_{x}}( - d,y) = \sigma (y),\quad {{\tau }_{{xy}}}( - d,y) = \tau (y);\quad {{\sigma }_{x}}(d,y) = \pm \sigma (y),\quad {{\tau }_{{xy}}}(d,y) = \pm \tau (y)$

Верхним знакам перед функциями $\sigma (y)$, $\tau (y)$ в последней строке (2.3) соответствует четно-симметричная деформация прямоугольника относительно вертикальной оси симметрии $y$, а нижним – нечетно-симметричная.

При четно-симметричной деформации полуполосы и прямоугольника относительно горизонтальной оси симметрии $x$ функция $\sigma (y)$ должна удовлетворять требованию самоуравновешенности:

(2.4)

$\int\limits_{ - h}^h {\sigma (y)dy = 0} $

При нечетно-симметричной деформации условия самоуравновешенности внешних нагрузок будут такими:

(2.5)

$\int\limits_{ - h}^h {\sigma (y)ydy = \int\limits_{ - h}^h {\tau (y)dy = 0} } $

Характеристические уравнения для четно-симметричной и нечетно-симметричной деформаций относительно горизонтальной оси $x$ имеют вид соответственно

(2.6)

$L(\lambda ) = \lambda h \pm \sin \lambda h\cos \lambda h = 0$

Нулевым корням уравнений (2.6) отвечают известные элементарные решения. Кроме этого, уравнения (2.6) имеют бесконечные наборы комплексных корней. Они расположены симметрично относительно начала координат в комплексной плоскости $\lambda $ и имеют следующую асимптотику соответственно для четно-симметричной и нечетно-симметричной задач:

(2.7)

$\frac{{{{\lambda }_{k}}}}{h} \approx \left( {k\pi - \frac{\pi }{4}} \right) + \frac{i}{2}\ln (4k\pi - \pi ),\quad \frac{{{{\lambda }_{k}}}}{h} \approx \left( {k\pi + \frac{{5\pi }}{4}} \right) + \frac{i}{2}ln(4k\pi + 5\pi )$

Комплексным корням отвечают быстро затухающие решения в виде разложений по собственным функциям Папковича–Фадля.

Требования к гладкости граничных функций те же, что и в теории тригонометрических рядов Фурье. Это обусловлено асимптотической близостью в (2.7) чисел ${{\lambda }_{k}}$ и $k\pi $. Помимо этого, граничные функции должны обращаться в ноль в окрестности концов отрезка $[ - h,h]$ либо быть непрерывными здесь и равными нулю при $y = \pm h$. В противном случае решение краевой задачи может быть нерегулярным по Мусхелишвили [11].

Приведем группы формул, не связанных с переменной $x$ и поэтому остающихся неизменными как для полуполосы, так и для прямоугольника ($\nu $ – коэффициент Пуассона).

2.1. Четно-симметричная деформация относительно оси $x$. Собственные функции Папковича–Фадля:

$\xi ({{\lambda }_{k}},y) = \left( {\frac{{1 - \nu }}{2}\sin {{\lambda }_{k}}h - \frac{{1 + \nu }}{2}{{\lambda }_{k}}h\cos {{\lambda }_{k}}h} \right)\cos {{\lambda }_{k}}y - \frac{{1 + \nu }}{2}{{\lambda }_{k}}ysin{{\lambda }_{k}}h\sin {{\lambda }_{k}}y$

$\chi ({{\lambda }_{k}},y) = \left( {\frac{{1 + \nu }}{2}{{\lambda }_{k}}h\cos {{\lambda }_{k}}h + \sin {{\lambda }_{k}}h} \right)\sin {{\lambda }_{k}}y - \frac{{1 + \nu }}{2}{{\lambda }_{k}}ysin{{\lambda }_{k}}h\cos {{\lambda }_{k}}y$

(2.8)

${{s}_{x}}({{\lambda }_{k}},y) = (1 + \nu ){{\lambda }_{k}}\left[ {(\sin {{\lambda }_{k}}h - {{\lambda }_{k}}h\cos {{\lambda }_{k}}h)\cos {{\lambda }_{k}}y - {{\lambda }_{k}}ysin{{\lambda }_{k}}h\sin {{\lambda }_{k}}y} \right]$

${{s}_{y}}({{\lambda }_{k}},y) = (1 + \nu ){{\lambda }_{k}}\left[ {(\sin {{\lambda }_{k}}h + {{\lambda }_{k}}h\cos {{\lambda }_{k}}h)\cos {{\lambda }_{k}}y + {{\lambda }_{k}}ysin{{\lambda }_{k}}h\sin {{\lambda }_{k}}y} \right]$

${{t}_{{xy}}}({{\lambda }_{k}},y) = (1 + \nu )\lambda _{k}^{2}(h\cos {{\lambda }_{k}}h\sin {{\lambda }_{k}}y - ysin{{\lambda }_{k}}h\cos {{\lambda }_{k}}y)$

Коэффициенты Лагранжа (аналоги коэффициентов Фурье) ${{\sigma }_{k}}$, ${{\tau }_{k}}$ и нормирующие множители ${{M}_{k}}$:

(2.9)

$\begin{gathered} {{\sigma }_{k}} = \int\limits_{ - h}^h {\sigma (y){{x}_{k}}(y)dy,\quad {{x}_{k}}(y)} = \frac{{\cos {{\lambda }_{k}}y}}{{2(1 + \nu ){{\lambda }_{k}}h\sin {{\lambda }_{k}}h}} \\ {{\tau }_{k}} = \int\limits_{ - h}^h {\tau (y){{t}_{k}}(y)dy,\quad {{t}_{k}}(y)} = - \frac{{\sin {{\lambda }_{k}}y}}{{2(1 + \nu )h\sin {{\lambda }_{k}}h}},\quad {{M}_{k}} = {{\cos }^{2}}{{\lambda }_{k}}h \\ \end{gathered} $

2.2. Нечетно-симметричная деформация относительно оси $x$. Собственные функции Папковича–Фадля:

$\xi ({{\lambda }_{k}},y) = \left( {\sin {{\lambda }_{k}}h - \frac{{1 + \nu }}{2}{{\lambda }_{k}}h\cos {{\lambda }_{k}}h} \right)\sin {{\lambda }_{k}}y + \frac{{1 + \nu }}{2}{{\lambda }_{k}}y\sin {{\lambda }_{k}}h\cos {{\lambda }_{k}}y$

$\chi ({{\lambda }_{k}},y) = - \left( {\frac{{1 - \nu }}{2}\sin {{\lambda }_{k}}h + \frac{{1 + \nu }}{2}{{\lambda }_{k}}h\cos {{\lambda }_{k}}h} \right)\cos {{\lambda }_{k}}y - \frac{{1 + \nu }}{2}{{\lambda }_{k}}y\sin {{\lambda }_{k}}h\sin {{\lambda }_{k}}y$

(2.10)

${{s}_{x}}({{\lambda }_{k}},y) = (1 + \nu ){{\lambda }_{k}}[(2\sin {{\lambda }_{k}}h - {{\lambda }_{k}}h\cos {{\lambda }_{k}}h)\sin {{\lambda }_{k}}y + {{\lambda }_{k}}y\sin {{\lambda }_{k}}h\cos {{\lambda }_{k}}y]$

${{s}_{y}}({{\lambda }_{k}},y) = (1 + \nu )\lambda _{k}^{2}(h\cos {{\lambda }_{k}}h\sin {{\lambda }_{k}}y - y\sin {{\lambda }_{k}}h\cos {{\lambda }_{k}}y)$

${{t}_{{xy}}}({{\lambda }_{k}},y) = (1 + \nu ){{\lambda }_{k}}[(\sin {{\lambda }_{k}}h - {{\lambda }_{k}}h\cos {{\lambda }_{k}}h)\cos {{\lambda }_{k}}y - {{\lambda }_{k}}y\sin {{\lambda }_{k}}h\sin {{\lambda }_{k}}y]$

Коэффициенты Лагранжа ${{\sigma }_{k}}$, ${{\tau }_{k}}$ и нормирующие множители ${{M}_{k}}$:

(2.11)

$\begin{gathered} {{\sigma }_{k}} = \int\limits_{ - h}^h {\sigma (y){{x}_{k}}(y)dy,\quad {{x}_{k}}(y)} = \frac{1}{{2(1 + \nu )\lambda _{k}^{2}h}}\left( {\frac{{\sin {{\lambda }_{k}}y}}{{\sin {{\lambda }_{k}}h}} - y} \right) \\ {{\tau }_{k}} = \int\limits_{ - h}^h {\tau (y){{t}_{k}}(y)dy,\quad {{t}_{k}}(y)} = \frac{1}{{2(1 + \nu ){{\lambda }_{k}}h}}\frac{{\cos {{\lambda }_{k}}y}}{{\sin {{\lambda }_{k}}h}},\quad {{M}_{k}} = \frac{{{{{\sin }}^{2}}{{\lambda }_{k}}h}}{{{{\lambda }_{k}}}} \\ \end{gathered} $

В формулах (2.9) ${{x}_{k}}(y)$, ${{t}_{k}}(y)$ – финитные части функций, биортогональных к собственным функциям ${{s}_{x}}({{\lambda }_{k}},y)$, ${{t}_{{xy}}}({{\lambda }_{k}},y)$ (2.8), соответственно. Аналогично для формул (2.11), (2.10).

Требования самоуравновешенности внешних нагрузок обусловлены самоуравновешенностью соответствующих собственных функций.

3. Решение краевой задачи для полуполосы. Решение задачи ищется в виде рядов (элементарные решения опущены):

$U(x,y) = \sum\limits_{k = 1}^\infty \,{{a}_{k}}\xi ({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}x}}} + {{\bar {a}}_{k}}\xi ({{\bar {\lambda }}_{k}},y){{e}^{{{{{\bar {\lambda }}}_{k}}x}}}$

$V(x,y) = \sum\limits_{k = 1}^\infty \,{{a}_{k}}\chi ({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}x}}} + {{\bar {a}}_{k}}\chi ({{\bar {\lambda }}_{k}},y){{e}^{{{{{\bar {\lambda }}}_{k}}x}}}$

(3.1)

${{\sigma }_{x}}(x,y) = \sum\limits_{k = 1}^\infty \,{{a}_{k}}{{s}_{x}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}x}}} + {{\bar {a}}_{k}}{{s}_{x}}({{\bar {\lambda }}_{k}},y){{e}^{{{{{\bar {\lambda }}}_{k}}x}}}$

${{\sigma }_{y}}(x,y) = \sum\limits_{k = 1}^\infty \,{{a}_{k}}{{s}_{y}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}x}}} + {{\bar {a}}_{k}}{{s}_{y}}({{\bar {\lambda }}_{k}},y){{e}^{{{{{\bar {\lambda }}}_{k}}x}}}$

${{\tau }_{{xy}}}(x,y) = \sum\limits_{k = 1}^\infty \,{{a}_{k}}{{t}_{{xy}}}({{\lambda }_{k}},y){{e}^{{{{\lambda }_{k}}x}}} + {{\bar {a}}_{k}}{{t}_{{xy}}}({{\bar {\lambda }}_{k}},y){{e}^{{{{{\bar {\lambda }}}_{k}}x}}},$

где через $U(x,y),$ $V(x,y)$ обозначены соответственно продольное и поперечное перемещения, умноженные на модуль сдвига, ${{a}_{k}}$, ${{\bar {a}}_{k}}$ – неизвестные коэффициенты разложений.

Когда на торце полуполосы заданы нормальные напряжения, окончательно получим:

$U(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left( {{{\lambda }_{k}}{{\sigma }_{k}}\frac{{\xi ({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)} \frac{{\operatorname{Im} ( - {{{\bar {\lambda }}}_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} {{\lambda }_{k}}}}$

$V(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left( {{{\sigma }_{k}}\frac{{\chi ({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)} \frac{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} {{\lambda }_{k}}}}$

(3.2)

${{\sigma }_{x}}(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left( {{{\sigma }_{k}}\frac{{{{s}_{x}}({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)} \frac{{\operatorname{Im} ( - {{{\bar {\lambda }}}_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} {{\lambda }_{k}}}}$

${{\sigma }_{y}}(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left( {{{\sigma }_{k}}{{\lambda }_{k}}{{{\bar {\lambda }}}_{k}}\frac{{{{s}_{y}}({{\lambda }_{k}},y)}}{{\lambda _{k}^{2}{{M}_{k}}}}} \right)} \frac{{\operatorname{Im} ( - {{\lambda }_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} {{\lambda }_{k}}}}$

${{\tau }_{{xy}}}(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left( {{{\sigma }_{k}}{{\lambda }_{k}}{{{\bar {\lambda }}}_{k}}\frac{{{{t}_{{xy}}}({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)} \frac{{\operatorname{Im} ( - {{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} {{\lambda }_{k}}}}$

Если на торце полуполосы заданы касательные напряжения, то имеем:

$U(x,y) = - \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{\xi ({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)} \frac{{\operatorname{Im} ({{\lambda }_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} {{\lambda }_{k}}}}$

$V(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left( {\frac{{{{\tau }_{k}}}}{{{{\lambda }_{k}}}}\frac{{\chi ({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)} \frac{{\operatorname{Im} ({{\lambda }_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} {{\lambda }_{k}}}}$

(3.3)

${{\sigma }_{x}}(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{{{s}_{x}}({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)} \frac{{\operatorname{Im} ({{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} {{\lambda }_{k}}}}$

${{\sigma }_{y}}(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{{{s}_{y}}({{\lambda }_{k}},y)}}{{\lambda _{k}^{2}{{M}_{k}}}}} \right)} \frac{{\operatorname{Im} (\lambda _{k}^{2}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} {{\lambda }_{k}}}}$

${{\tau }_{{xy}}}(x,y) = \sum\limits_{k = 1}^\infty {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{{{t}_{{xy}}}({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)} \frac{{\operatorname{Im} ({{\lambda }_{k}}{{e}^{{{{\lambda }_{k}}x}}})}}{{\operatorname{Im} {{\lambda }_{k}}}}$

Для четно-симметричной деформации полуполосы нужно воспользоваться формулами (2.8), (2.9), а для нечетно-симметричной – формулами (2.10), (2.11).

4. Решение краевой задачи для прямоугольника.

4.1. Четно-симметричная деформация относительно вертикальной оси симметрии $y$. Решение задачи ищется в виде рядов (элементарные решения опущены):

$U(x,y) = \sum\limits_{k = 1}^\infty \,{{a}_{k}}\xi ({{\lambda }_{k}},y)\operatorname{sh} {{\lambda }_{k}}x + {{\bar {a}}_{k}}\xi ({{\bar {\lambda }}_{k}},y)\operatorname{sh} {{\bar {\lambda }}_{k}}x$

$V(x,y) = \sum\limits_{k = 1}^\infty \,{{a}_{k}}\chi ({{\lambda }_{k}},y)\operatorname{ch} {{\lambda }_{k}}x + {{\bar {a}}_{k}}\chi ({{\bar {\lambda }}_{k}},y)\operatorname{ch} {{\bar {\lambda }}_{k}}x$

(4.1)

${{\sigma }_{x}}(x,y) = \sum\limits_{k = 1}^\infty \,{{a}_{k}}{{s}_{x}}({{\lambda }_{k}},y)\operatorname{ch} {{\lambda }_{k}}x + {{\bar {a}}_{k}}{{s}_{x}}({{\bar {\lambda }}_{k}},y)\operatorname{ch} {{\bar {\lambda }}_{k}}x$

${{\sigma }_{y}}(x,y) = \sum\limits_{k = 1}^\infty \,{{a}_{k}}{{s}_{y}}({{\lambda }_{k}},y)\operatorname{ch} {{\lambda }_{k}}x + {{\bar {a}}_{k}}{{s}_{y}}({{\bar {\lambda }}_{k}},y)\operatorname{ch} {{\bar {\lambda }}_{k}}x$

${{\tau }_{{xy}}}(x,y) = \sum\limits_{k = 1}^\infty \,{{a}_{k}}{{t}_{{xy}}}({{\lambda }_{k}},y)\operatorname{sh} {{\lambda }_{k}}x + {{\bar {a}}_{k}}{{t}_{{xy}}}({{\bar {\lambda }}_{k}},y)\operatorname{sh} {{\bar {\lambda }}_{k}}x$

Когда на вертикальных сторонах прямоугольника $x = \pm d$ заданы нормальные напряжения, получим следующие конечные формулы:

$U(x,y) = \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\sigma }_{k}}{{\lambda }_{k}}\frac{{\xi ({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}d)}}} \right\}} $

$V(x,y) = - \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\sigma }_{k}}\frac{{\chi ({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}d)}}} \right\}} $

(4.2)

${{\sigma }_{x}}(x,y) = \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\sigma }_{k}}\frac{{{{s}_{x}}({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}d)}}} \right\}} $

${{\sigma }_{y}}(x,y) = \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\sigma }_{k}}{{\lambda }_{k}}{{{\bar {\lambda }}}_{k}}\frac{{{{s}_{y}}({{\lambda }_{k}},y)}}{{\lambda _{k}^{2}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}d)}}} \right\}} $

${{\tau }_{{xy}}}(x,y) = \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\sigma }_{k}}{{\lambda }_{k}}{{{\bar {\lambda }}}_{k}}\frac{{{{t}_{{xy}}}({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} (\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}d)}}} \right\}} $

Когда заданы касательные напряжения, решение задачи будет таким:

$U(x,y) = \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{\xi ({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}d)}}} \right\}} $

$V(x,y) = - \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {\frac{{{{\tau }_{k}}}}{{{{\lambda }_{k}}}}\frac{{\chi ({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}d)}}} \right\}} $

(4.3)

${{\sigma }_{x}}(x,y) = - \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{{{s}_{x}}({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)\frac{{\operatorname{Im} (\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}d)}}} \right\}} $

${{\sigma }_{y}}(x,y) = - \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{{{s}_{y}}({{\lambda }_{k}},y)}}{{\lambda _{k}^{2}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} (\lambda _{k}^{2}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}d)}}} \right\}} $

${{\tau }_{{xy}}}(x,y) = - \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{{{t}_{{xy}}}({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}d)}}} \right\}} $

4.2. Нечетно-симметричная деформация относительно вертикальной оси симметрии $y$. В этом случае в формулах (4.1)–(4.3) надо гиперболические синусы заменить на гиперболические косинусы и наоборот. В результате получим следующие формулы.

Когда на сторонах $x = \pm d$ известны нормальные напряжения:

$U(x,y) = - \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\sigma }_{k}}{{\lambda }_{k}}\frac{{\xi ({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}d)}}} \right\}} $

$V(x,y) = \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\sigma }_{k}}\frac{{\chi ({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}d)}}} \right\}} $

(4.4)

${{\sigma }_{x}}(x,y) = - \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\sigma }_{k}}\frac{{{{s}_{x}}({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}d)}}} \right\}} $

${{\sigma }_{y}}(x,y) = - \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\sigma }_{k}}{{\lambda }_{k}}{{{\bar {\lambda }}}_{k}}\frac{{{{s}_{y}}({{\lambda }_{k}},y)}}{{\lambda _{k}^{2}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}d)}}} \right\}} $

${{\tau }_{{xy}}}(x,y) = - \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\sigma }_{k}}{{\lambda }_{k}}{{{\bar {\lambda }}}_{k}}\frac{{{{t}_{{xy}}}({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} (\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{{\bar {\lambda }}}_{k}}\operatorname{ch} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}d)}}} \right\}} $

Когда известны касательные напряжения:

$U(x,y) = - \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{\xi ({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}d)}}} \right\}} $

$V(x,y) = \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {\frac{{{{\tau }_{k}}}}{{{{\lambda }_{k}}}}\frac{{\chi ({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}d)}}} \right\}} $

(4.5)

${{\sigma }_{x}}(x,y) = \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{{{s}_{x}}({{\lambda }_{k}},y)}}{{{{M}_{k}}}}} \right)\frac{{\operatorname{Im} (\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}d)}}} \right\}} $

${{\sigma }_{y}}(x,y) = \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{{{s}_{y}}({{\lambda }_{k}},y)}}{{\lambda _{k}^{2}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} (\lambda _{k}^{2}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{sh} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}d)}}} \right\}} $

${{\tau }_{{xy}}}(x,y) = \sum\limits_{k = 1}^\infty {\left\{ {2\operatorname{Re} \left( {{{\tau }_{k}}\frac{{{{t}_{{xy}}}({{\lambda }_{k}},y)}}{{{{\lambda }_{k}}{{M}_{k}}}}} \right)\frac{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}x)}}{{\operatorname{Im} ({{\lambda }_{k}}\operatorname{sh} {{{\bar {\lambda }}}_{k}}d\operatorname{ch} {{\lambda }_{k}}d)}}} \right\}} $

Так же, как и в случае полуполосы, для четно-симметричной относительно горизонтальной оси симметрии $x$ деформации прямоугольника нужно воспользоваться формулами (2.8), (2.9), а для нечетно-симметричной – формулами (2.10), (2.11).

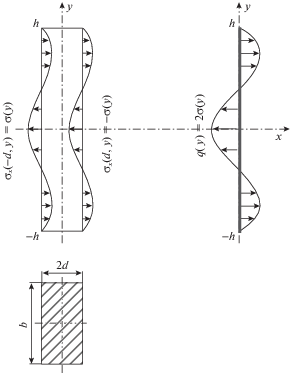
5. Пример. В качестве примера рассмотрим нечетно-симметричную относительно оси $y$ и четно-симметричную относительно оси $x$ деформацию достаточно узкого прямоугольника, полагая $h = 1$, $d = 0.1$, толщина пластинки $b = 1$ (по умолчанию во всех вышеприведенных формулах).

Примем

(5.1)

${{\sigma }_{x}}( \pm d,y) = \mp \frac{1}{2}(5{{y}^{4}} - 6{{y}^{2}} + 1),\quad {{\tau }_{{xy}}}( \pm d,y) = 0,\quad \nu = \frac{1}{3}$

Воспользовавшись формулами (4.4), (2.8), (2.9), получим решение задачи.

Сравним это решение с балочной теорией (схемы задач показаны на рис. 3).

Рис. 3.

Поперечная нагрузка, изгибающий момент и перерезывающая сила соответственно равны

(5.2)

$q(y) = (5{{y}^{4}} - 6{{y}^{2}} + 1),\quad M(y) = - \frac{1}{6}{{({{y}^{2}} - 1)}^{3}},\quad Q(y) = y{{({{y}^{2}} - 1)}^{2}}$

Нормальные и касательные напряжения в балке определяются по формулам

(5.3)

${{\sigma }_{b}}(x,y) = \frac{{M(y)}}{I}x,\quad {{\tau }_{b}}(x,y) = \frac{{6Q(y)}}{{b{{{(2d)}}^{3}}}}({{d}^{2}} - {{x}^{2}}),\quad I = \frac{{b{{{(2d)}}^{3}}}}{{12}}$

где $I$ – момент инерции поперечного сечения балки.

Сравним точное и приближенное решения. На графиках сплошным кривым соответствует решение в прямоугольнике, а точечным – балочное решение.

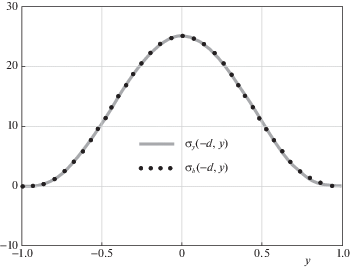
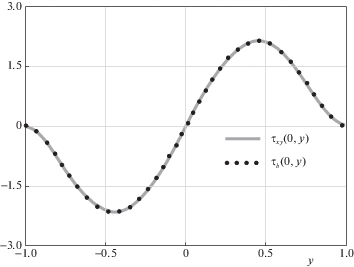
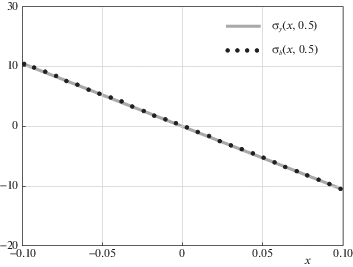
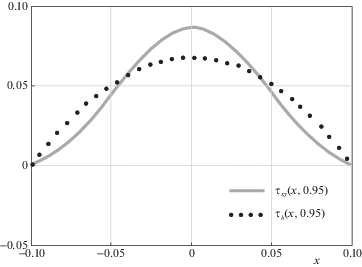
На рис. 4 показаны кривые распределения нормальных напряжений ${{\sigma }_{y}}( - d,y)$ в прямоугольнике и ${{\sigma }_{b}}( - d,y)$ в балке, а на рис. 5 показаны касательные напряжения ${{\tau }_{{xy}}}(0,y)$ в прямоугольнике и ${{\tau }_{b}}(0,y)$ в балке.

Рис. 4.

Рис. 5.

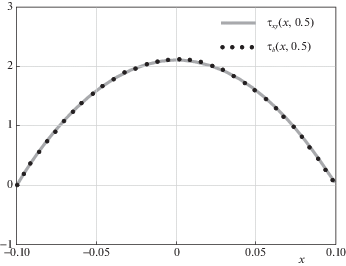
На рис. 6 и 7 соответственно показаны распределения нормальных и касательных напряжений в поперечных сечениях $x = 0.5$ прямоугольника и балки.

Рис. 6.

Рис. 7.

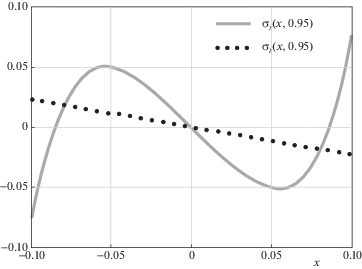
На всех графиках соответствующие кривые практически неразличимы. Заметные различия возникают вблизи концов $y = \pm h$, где и нормальные, и касательные напряжения уже очень малы. В частности, на рис. 8 и 9 показаны соответственно нормальные и касательные напряжения в сечении $y = 0.95$. Эти различия являются проявлениями, так называемых, “концевых эффектов” [3]. На расстоянии от узких торцов пластинки, равном примерно ее ширине $2d$, они практически исчезают в полном соответствии с принципом Сен-Венана [3]. Физически различия обусловлены тем, что в отличие от балочной теории, здесь перемещения $V(x, \pm 1) \ne 0$.

Рис. 8.

Рис. 9.

Заключение.

1. В статье приведены готовые точные решения краевой задачи теории упругости для прямоугольника. Горизонтальные стороны прямоугольника свободны, а на вертикальных заданы нормальные или касательные напряжения. Рассмотрены все случаи симметрии относительно центральных осей, комбинируя которые можно получить решения, не обладающие симметрией.

2. Добавляя к полученному решению решение, “повернутое” на 90 градусов, можно получить решения для прямоугольника с произвольными (самоуравновешенными) нагрузками на всех его сторонах.

3. Все формулы имеют одинаковую структуру: коэффициент Лагранжа, затем отношение собственной функции Папковича–Фадля к отвечающему ей нормирующему множителю и, наконец, выражение, зависящее только от переменной $x$.

4. Формулы остаются теми же для любых (непериодических) однородных граничных условий на вертикальных сторонах прямоугольника (жесткое защемление, ребра жесткости и т.д.). Однако другими будут собственные функции Папковича–Фадля, собственные числа ${{\lambda }_{k}}$, нормирующие множители ${{M}_{k}}$ и биортогональные функции ${{x}_{k}}(y)$, ${{t}_{k}}(y)$.

5. Распределение напряжений в достаточно узком прямоугольнике, длина которого в десять раз больше ширины, практически не отличается от балочного решения. Существенные различия имеются вблизи свободных торцов прямоугольника, где напряжения весьма малы. Эти различия обусловлены концевыми эффектами и быстро исчезают по мере удаления от торцов.

Исследование М.Д. Коваленко и И.В. Меньшовой выполнено при финансовой поддержке РФФИ и Государственного фонда естественных наук Китая в рамках научного проекта № 20-51-53021. Исследование А.П. Кержаева выполнено за счет гранта Российского научного фонда (проект № 19-71-00094).

Список литературы

Meleshko V.V. Selected topics in the history of two-dimensional biharmonic problem // Appl. Mech. Rev. 2003. V. 56. № 1. P. 33–85.
Meleshko V.V. Bending of an elastic rectangular clamped plate: Exact versus ‘engineering’ solutions // J. Elast. 1997. V. 48. № 1. P. 1–50.
Тимошенко С.П., Гудьер Дж. Теория упругости. М.: Наука, 1975. 576 с.
Коваленко М.Д., Шуляковская Т.Д. Разложения по функциям Фадля–Папковича в полосе. Основы теории // Изв. РАН. МTТ. 2011. № 5. С. 78–98.
Коваленко М.Д., Меньшова И.В., Шуляковская Т.Д. Разложения по функциям Фадля–Папковича. Примеры решений в полуполосе // Изв. РАН. МTТ. 2013. № 5. С. 121–144.
Kovalenko M.D., Menshova I.V., Kerzhaev A.P. On the exact solutions of the biharmonic problem of the theory of elasticity in a half-strip // Z. Angew. Math. Phys. 2018. V. 69. № 5. Art. 121. 30 p.
Kovalenko M.D., Abrukov D.A., Menshova I.V., Kerzhaev A.P., Yu G. Exact solutions of boundary value problems in the theory of plate bending in a half-strip: basics of the theory // Z. Angew. Math. Phys. 2019. V. 70. № 4. Art. 98. 22 p.
Kerzhaev A.P., Kovalenko M.D., Menshova I.V. Borel transform in the class W of quasi-entire functions // Complex Anal. Oper. Theory. 2018. V. 12. № 3. P. 571–587.
Гольденблат И.И. Нелинейные проблемы теории упругости. М.: Наука, 1969. 336 с.
Шерман Д.И. Об одной задаче теории упругости // Докл. АН СССР. 1940. Т. 27. № 9. С. 907–913.
Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. М.: Наука, 1966. 708 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал