Прикладная математика и механика, 2021, T. 85, № 3, стр. 347-357

1. Введение. Ляв [1] показал, что при некоторых условиях в системе изотропный слой на полупространстве может распространяться поверхностная волна, имеющая горизонтальную поперечную поляризацию и экспоненциально затухающая по глубине. Наряду с волнами Рэлея, волны Лява играют важную роль в передаче сейсмической энергии и весьма часто регистрируются при сейсмической активности и взрывах.

Поле перемещений, соответствующее волне Лява может быть представлено в виде:

где ${{{\mathbf{u}}}_{1}}$ и ${{{\mathbf{u}}}_{2}}$ относятся к перемещениям в слое и субстрате соответственно; ${\mathbf{m}}$ – единичная амплитуда (вектор поляризации), предполагается, что вектор ${\mathbf{m}}$ ортогонален к сагиттальной плоскости (последняя образована вектором ${\mathbf{n}}$, задающим направление распространения волнового фронта, и единичным вектором $\nu $, нормальным к свободной поверхности); $x{\kern 1pt} ' \equiv \nu \cdot {\mathbf{x}}$ – координата вдоль вектора $\nu $, в дальнейшем считается, что $x{\kern 1pt} '$ принимает отрицательные значения в полупространстве; $r$ – волновое число; c – фазовая скорость; $t$ – время; неизвестные (комплексные) коэффициенты ${{C}_{k}}$ определяются с точностью до множителя из граничных условий на внешней плоской границе: и контактных условий на поверхности раздела ($x{\kern 1pt} ' = 0$):

Параметры ${{\gamma }_{k}}$, $k = 1,2$ в (1.1) соответствуют комплексным корням уравнения Кристоффеля, это уравнение будет введено позже. В уравнениях (1.2), (1.3) ${{{\mathbf{C}}}_{k}}$, $k = 1,2$ – четырехвалентные тензоры упругости слоя и полупространства соответственно; $h$ – толщина слоя.

Замечание 1.1. В соответствии с представлением (1.1) затухание по глубине в полупространстве обеспечивается параметром Кристоффеля ${{\gamma }_{2}}$ с отрицательной мнимой частью.

Следующее утверждение фактически принадлежит Ляву:

Предложение 1.1. 1) Исследуемые волны могут возникать в изотропном слое и контактирующим с ним изотропном полупространстве, в том и только том случае, когда фазовая скорость удовлетворяет условию

где $c_{k}^{T} = \sqrt {{{\mu }_{k}}{\text{/}}{{\rho }_{k}}} $, $k = 1,2$ скорости поперечных объемных волн в слое и полупространстве соответственно, а ${{\mu }_{k}}$ и ${{\rho }_{k}}$ соответствующие константы Ламе и плотности.

2) Дисперсионное соотношение между фазовой скоростью $c$ и частотой $\omega $ может быть представлено в виде

Следствие 1. а) При фиксированной частоте $\omega $ существует конечное число волн Лява, распространяющихся с различными фазовыми скоростями $c \in (c_{1}^{T};c_{2}^{T})$.

б) При фиксированной фазовой скорости $c \in (c_{1}^{T};c_{2}^{T})$ существует бесконечное число волн Лява, распространяющихся с различными частотами $\omega $.

Следствие 2. Не существует волн Лява, если $c_{1}^{T} > \,\,c_{2}^{T}$.

В [2] было показано, что волны Лява могут распространяться в системе, состоящей из анизотропного слоя, контактирующего с полупространством, при этом предполагалось, что как слой, так и полупространство имеют ось упругой симметрии четвертого или шестого порядка, ориентированную вдоль вектора ${\mathbf{m}}$. Для такой системы условия распространения и дисперсионные соотношения оказывались аналогичными (1.4) и (1.5). В [3] на основе подхода [2] получены дисперсионные соотношения для трансверсально изотропного слоя и полупространства.

Для слоистых сред, состоящих из большего числа слоев, контактирующих с полупространством, не существует аналитических решений, аналогичных (1.5). Дисперсионные соотношения для волны Лява в таких средах могут быть получены численно с применением двух матричных методов, первоначально предложенных для анализа волн Лэмба. Эти подходы известны как метод передаточных Матриц (ПМ), иногда этот метод называют методом Томсона–Хаскелла, по имени разработчиков этого метода [4, 5]), и метод глобальной матрицы (ГМ), предложенный в [6, 7]. ПМ-метод основан на последовательном решении контактных граничных задач на интерфейсных поверхностях и построении соответствующих передаточных матриц. Ниже этот метод будет обсуждаться более подробно. ГМ-метод основан на решении обыкновенных дифференциальных уравнений с кусочно-однородными коэффициентами, который приводит в итоге к построению специальной “глобальной” матрицы.

С момента появления ГМ-метода считалось, что при численных реализациях он приводит к (численно) более устойчивым решениям, чем ПМ-метод. В дальнейшем предлагались разнообразные модификации ПМ- и ГМ-методов с целью сделать их более численно устойчивым, см. [8–14]. Проблема численной устойчивости становится особенно актуальной, когда слоистая среда состоит из большого числа слоев. В этом случае начинают сказываться преимущества ПМ-метода, поскольку порядок соответствующих матриц остается неизменным по отношению к числу слоев (в случае ГМ-метода порядок соответствующей матрицы линейно растет с числом слоев).

В связи с исследованиями распространения волн Лява необходимо отметить недавние работы [15–17] по анализу дисперсионных соотношений в средах, содержащих тонкие покрытия, а так же асимптотические методы для исследования SH-волн в трехслойных системах, содержащих слои с контрастными свойствами.

В настоящей работе развивается модифицированный ПМ-метод, основанный на использовании гиперболических функций в представлении для парциальных волн, и предназначенный как для аналитического исследования волн Лява в анизотропных средах с небольшим числом слоев (1–3), так и для численного анализа систем, содержащих большое число слоев. Далее будет показано, что представление (1.1) оказывается неверным, если в уравнении Кристоффеля появляются кратные корни. Верное представление и соответствующая модификация ПМ-метода будут даны ниже. Кроме того, ПМ-метод будет использоваться для получения разрешающих уравнений для волн с поперечной горизонтальной поляризацией, распространяющихся в слоистых пластинах со свободными и защемленными граничными поверхностями (в этом случае, в отличие от волн Лява, пластины не контактируют с полупространством).

2. Основные соотношения. Ниже как слои, так и полупространство считаются однородными и линейно гиперупругими. Уравнения движения для упругой однородной анизотропной могут быть представлены в виде:

где четырехвалентный тензор упругости ${\mathbf{C}}$ предполагается положительно определенным

Замечание 2.1. а) Другое замечание относится к симметрии тензора упругости. Предполагается, что все рассматриваемые среды имеют плоскости упругой симметрии, совпадающие с сагиттальной плоскостью ${\mathbf{m}} \cdot {\mathbf{x}} = 0$. Это эквивалентно принадлежности тензора упругости для всех материалов к моноклинной системе. Можно показать [18], что последнее влечет равенство нулю всех разложимых компонент тензора упругости, имеющих нечетное вхождение вектора ${\mathbf{m}}$ (в ортогональном базисе в ${{R}^{3}}$, образованном вектором ${\mathbf{m}}$ и любыми ортогональными векторами, принадлежащими сагиттальной плоскости). В случае моноклинной симметрии тензор упругости содержит 13 независимых разложимых компонент.

б) В дальнейшем будет показано, что моноклинная симметрия обеспечивает достаточное условие для того, чтобы поверхностные усилия на любой плоскости $\nu \cdot {\mathbf{x}} = \operatorname{const} $ были коллинеарные вектору ${\mathbf{m}}$.

Следуя [19–21], рассмотрим более общее, чем (1.1), представление для волны Лява

где $x{\kern 1pt} ' = \nu \cdot {\mathbf{x}}$, так же как и в представлении (1.1); $f$ – неизвестная скалярная функция; экспоненциальный множитель в правой части (2.3) соответствует распространению волнового фронта в направлении ${\mathbf{n}}$ с фазовой скоростью $c$; $r$ – волновое число. Подставляя представление (2.3) в уравнение (2.1) и принимая во внимание Замечание 2.1.а, получаем следующее дифференциальное уравнение

Характеристическое уравнение для (2.4), известное как уравнение Кристоффеля, имеет вид

Левая часть уравнения (2.5) представляет собой полином второго порядка относительно параметров Кристоффеля $\gamma $. Таким образом, для исследуемой упругой симметрии, волна Лява в слое может состоять только из двух парциальных волн.

3. Перемещения и поверхностные усилия в полупространстве. В дальнейшем предполагается, что слоистая среда состоит из $n$ слоев, контактирующих, если не оговорено противное, с полупространством, нижний индекс $n + 1$ будет относится к полупространству. Поскольку поле перемещений в полупространстве должно затухать с глубиной, соответствующий корень уравнения (2.5) должен быть комплексным с отрицательной мнимой частью, см. Замечание 1.1.

Имеет место следующее утверждение

Предложение 3.1. Затухание по глубине в моноклинном полупространстве возможно в том и только том случае, если фазовая скорость $c$ принадлежит (непустому) скоростному интервалу

где для произвольного тензора второго ранга ${\mathbf{A}}{\kern 1pt} :\;{\text{sym}}({\mathbf{A}}) \equiv \frac{1}{2}({\mathbf{A}} + {{{\mathbf{A}}}^{t}})$. Для скоростного интервала (3.1) соответствующий параметр Кристоффеля ${{\gamma }_{{n + 1}}}$ – комплексный с отрицательной мнимой частью

Доказательство. Непосредственный анализ корней уравнения (2.5) показывает, что эти корни комплексны при отрицательном дискриминанте, – это дает верхнюю границу в (3.1). Остается показать, что подкоренное выражение в (3.1) – положительно. Но это вытекает из анализа квадратичного полинома

Правая часть (3.3) положительна при любых действительных $x$, поскольку тензор упругости положительно определен. Несуществование действительных корней этого полинома завершает доказательство, поскольку дискриминант этого полинома совпадает (с точностью до множителя $ - {{\left( {{{\rho }_{{n + 1}}}} \right)}^{{ - 1/2}}}$) с верхней границей в (3.1). Остается заметить, что выражение (3.2) получено из решения уравнения (2.5).

Следствие 1. Параметр ${{\gamma }_{{n + 1}}}$ не может быть кратным корнем уравнения Кристоффеля (2.5).

Доказательство вытекает из условия неравенства нулю дискриминанта уравнения (3.2), что необходимо для затухания решения по глубине.

Следствие 2. Если рассматриваемый материал обладает еще одной плоскостью упругой симметрии, нормаль к которой совпадает с вектором ${\mathbf{n}}$ или $\nu $ (такой материал необходимо ортотропен), то допустимый скоростной диапазон имеет вид:

где $c_{{n + 1}}^{T}$ – скорость поперечной объемной волны, распространяющейся в направлении вектора ${\mathbf{n}}$, и имеющей поляризацию, совпадающую с вектором ${\mathbf{m}}$. Для рассматриваемого случая параметр Кристоффеля ${{\gamma }_{{n + 1}}}$ – чисто мнимый

Доказательство. Для такого материала выражение $({\text{sym}}({\mathbf{m}} \otimes {\mathbf{n}} \cdot \cdot \,{{{\mathbf{C}}}_{{n + 1}}} \cdot \cdot \,\nu \otimes {\mathbf{m}}))$, присутствующее в (3.2), становится равным нулю, поскольку это выражение содержит нечетное число вхождений векторов ${\mathbf{n}}$ и $\nu $. Далее, достаточно заметить, что остающееся подкоренное выражение в (3.1) совпадает со скоростью $c_{{n + 1}}^{T}$. Оставшаяся часть доказательства вытекает из анализа уравнения (2.5).

Представление (1.1) для полупространства дает следующее поле поверхностных усилий на плоскости $\nu \cdot {\mathbf{x}} = 0$:

Предложение 3.2. Усилия (3.6) колинеарны вектору ${\mathbf{m}}$.

Доказательство вытекает из предположенной моноклинной симметрии относительно вектора ${\mathbf{m}}$, что обеспечивает четное вхождение вектора ${\mathbf{m}}$ в разложимые компоненты тензора ${{{\mathbf{C}}}_{{n + 1}}}$ в базисе, образованном векторами m, v, n. Таким образом, векторы $\left( {\nu \cdot {{{\mathbf{C}}}_{{n + 1}}} \cdot \cdot \,\nu \otimes {\mathbf{m}}} \right)$ и $\left( {\nu \cdot {{{\mathbf{C}}}_{{n + 1}}} \cdot \cdot \,{\mathbf{n}} \otimes {\mathbf{m}}} \right)$ в правой части (3.6) коллинеарны вектору ${\mathbf{m}}$.

4. Перемещения и поверхностные усилия в слоях. В этом разделе нижний индекс $k$ ($1 \leqslant k \leqslant n$) относится к соответствующему слою.

4.1. Некратные корни. Для некратных корней уравнения Кристоффеля и ортотропного материала с главными осями упругости, совпадающими с векторами m, n и $\nu $, представление (1.1) остается верным. Все же, для целей настоящего анализа, который включает в себя более общий класс моноклинной симметрии, представление (1.1) будет модифицировано следующим образом

где ${{\gamma }_{k}} = {{\alpha }_{k}} + {{\beta }_{k}}$, и

Таким образом, ${{\alpha }_{k}}$ – действительный или мнимый параметр, в зависимости от значения фазовой скорости, а ${{\beta }_{k}}$ – действителен и независим от $c$.

Принимая во внимание (4.1), соответствующие поверхностные усилия на плоскости $\nu \cdot {\mathbf{x}} = x{\kern 1pt} '$ имеют вид

Предложение 4.1. Поверхностные усилия (4.3) коллинеарны вектору ${\mathbf{m}}$.

Доказательство аналогично доказательству Предложения 3.2.

Принимая во внимание (4.3) и тот факт, что $\nu \cdot {{{\mathbf{C}}}_{k}} \cdot \cdot \,{\mathbf{n}} \otimes {\mathbf{m}} = 0$, ${{\beta }_{k}} = 0$, и ${{\gamma }_{k}} = {{\alpha }_{k}}$ для ортотропного материала с осями упругой симметрии, совпадающими с векторами m, n, и $\nu $, получаем следующее выражение для поверхностных усилий

4.2. Кратные корни. Представление (4.1) для волн Лява в слое становится неверным, когда в уравнении Кристоффеля появляются кратные корни, см. [19, 20].

Кратные корни возникают, когда параметр ${{\alpha }_{k}}$ в (4.2) становится равным нулю, отсюда получаем

Предложение 4.2. а) Фазовая скорость, при которой появляются кратные корни, определяется следующим выражением

б) Соответствующий параметр Кристоффеля ${{\gamma }_{k}}$ (необходимо действительный) имеет вид

в) Представление поля перемещений, отвечающее кратным корням, имеет вид

г) Соответствующие поверхностные усилия на плоскости $\nu \cdot {\mathbf{x}} = x{\kern 1pt} '$ имеют вид

Доказательство. Условия а) и б) вытекают из условия обращения в нуль дискриминанта в правой части (3.2). Условие в) соответствует общему решению уравнения (2.4) в случае кратных корней; см. также [19–21].

Предложение 4.3. Поверхностные усилия (4.8) коллинеарны вектору ${\mathbf{m}}$.

Доказательство аналогично доказательству Предложения 3.2.

5. Модифицированный ПМ-метод. Ниже развивается модификация ПМ-метода применительно к разработанному четырехмерному комплексному формализму, см. [20, 21].

5.1. Передаточные матрицы. В соответствии с Предложениями 4.1 и 4.2 скалярные амплитуды перемещений и поверхностных усилий в $k$-м слое на плоскости $\nu \cdot {\mathbf{x}} = x{\kern 1pt} '$ могут быть представлены в виде:

где ${{u}_{k}}(x{\kern 1pt} ') \equiv \left| {{{{\mathbf{u}}}_{k}}(x{\kern 1pt} '){{e}^{{ - ir({\mathbf{n}} \cdot {\mathbf{x}} - ct)}}}} \right|$, ${{t}_{k}}(x{\kern 1pt} ') \equiv \left| {{{{\mathbf{t}}}_{k}}(x{\kern 1pt} '){{e}^{{ - ir({\mathbf{n}} \cdot {\mathbf{x}} - ct)}}}} \right|$ – соответствующие скалярные амплитуды, а ${{{\mathbf{M}}}_{k}}$ – $2 \times 2$ матрица. Принимая во внимание выражения (4.1), (4.3), (4.5) и (4.6), матрица ${{{\mathbf{M}}}_{k}}$ принимает вид

Некратные корни

б) Кратные корни

Заметим, что в соответствии с (4.2) параметр ${{\beta }_{k}}$ в (5.2) не зависит от фазовой скорости $c$. Справедливо следующее утверждение:

Предложение 5.1. Вне зависимости от кратности корней, матрицы ${{{\mathbf{M}}}_{k}}$ не вырождены при любых действительных x'.

Доказательство. Во-первых, заметим, что экспоненциальные множители ${{e}^{{ir{{\beta }_{k}}x'}}}$ в (5.2) и ${{e}^{{ir{{\gamma }_{k}}x'}}}$ в (5.3) отличны от нуля при любых $x{\kern 1pt} '$; далее, непосредственный анализ показывает, что матрицы в правых частях (5.2), (5.3) не вырождены при любых x' (определитель матрицы в (5.2) равен $ - {{\alpha }_{k}}\left( {{\mathbf{m}} \otimes \nu \cdot \cdot \,{{{\mathbf{C}}}_{k}} \cdot \cdot \,\nu \otimes {\mathbf{m}}} \right){{e}^{{ir{{\beta }_{k}}x'}}}$ с ${{\alpha }_{k}} \ne 0$, поскольку корни некратные; в случае матрицы (5.3) соответствующий определитель равен $\left( {{\mathbf{m}} \otimes \nu \cdot \cdot \,{{{\mathbf{C}}}_{k}} \cdot \cdot \,\nu \otimes {\mathbf{m}}} \right){{e}^{{ir{{\gamma }_{k}}x'}}}$).

Теперь, используя матрицы ${{{\mathbf{M}}}_{k}}$, перемещения и поверхностные усилия на границе раздела между $n$-м слоем и полупространством могут быть представлены в терминах только коэффициентов ${{C}_{1}}$ и ${{C}_{2}}$

где ${{h}_{k}}$, $k = 1,...,n$ – толщины соответствующих слоев.

5.2. Граничные условия на внешней границе. Выражения (4.3), (4.8) позволяют записать условия отсутствия касательных напряжений на внешней границе в виде первого слоя

где ${{t}_{1}}$ – соответствующая скалярная амплитуда; ${{\vec {B}}_{1}}({{h}_{1}}{\text{/}}2)$ = $({{X}_{1}}({{h}_{1}}{\text{/}}2)$; ${{Y}_{1}}({{h}_{1}}{\text{/2}}))$ и $\vec {C} = ({{C}_{1}};{{C}_{2}})$. Компоненты ${{X}_{1}}({{h}_{1}}{\text{/}}2)$ и ${{Y}_{1}}({{h}_{1}}{\text{/}}2)$ имеют вид

а) Некратные корни

б) Кратные корни

Уравнения (5.1) позволяют выразить (с точностью до множителя) коэффициенты ${{C}_{1}}$ и ${{C}_{2}}$ в виде решения следующего уравнения

Причем, выражение (5.8) эквивалентно

Из (5.8) видно, что двумерный вектор ${{\vec {T}}_{1}}({{h}_{1}}{\text{/}}2)$ коллинеарен вектору $\vec {C}$.

5.3. Граничные условия на границе раздела слой–полупространство. Контактные условия на соответствующей границе раздела могут быть представлены в виде:

где, по аналогии с (5.9), имеем

Условие (5.11) необходимо дополнить контактным условием

В (5.12) обозначено ${{t}_{{n + 1}}}(0) = \left| {{{{\mathbf{t}}}_{{n + 1}}}(0){{e}^{{ - ir({\mathbf{n}} \cdot {\mathbf{x}} - ct)}}}} \right|$, а вектор ${{{\mathbf{t}}}_{{n + 1}}}(0)$ определен по (3.6). Принимая во внимание (5.11), (5.12), видим, что уравнение (5.10) выражает собой колинеарность векторов ${{\vec {V}}_{n}}$ и $\left( {{{u}_{{n + 1}}}(0),\,{{t}_{{n + 1}}}(0)} \right)$, последнее эквивалентно условию коллинеарности перемещений и усилий при переходе через границу раздела компонент. В (5.12) предполагается, что в локальной системе координат для полупространства интерфейсная плоскость задается уравнением $\nu \cdot {\mathbf{x}} = 0$.

5.4. Разрешающее уравнение для волн Лява. Принимая во внимание уравнения (5.4), (5.8), (5.10) и (5.12), объединенное уравнение модифицированного ПМ-метода может быть представлено в виде

Уравнение (5.13) представляет собой искомое разрешающее уравнение для волн Лява.

Уравнение (5.13), в частности, позволяет получить аналитическое дисперсионное выражение для трансверсально-изотропного слоя, находящегося между двумя трансверсально-изотропными полупространствами

6. Численный пример. С помощью разработанного метода исследовалась дисперсия волн Лява в многослойной системе, состоящей из чередующихся упруго анизотропных слоев контактирующих с трансверсально изотропным полупространством [22]. Полупространство и слои имеют физико-механические характеристики, определяемые следующими выражениями:

Четные слои, монокристалл кремния (Si), ориентация 100

Нечетные слои, трансверсально изотропный карбид кремния (SiC)

Полупространство, трансверсально изотропный нитрид кремния (Si₃N₄)

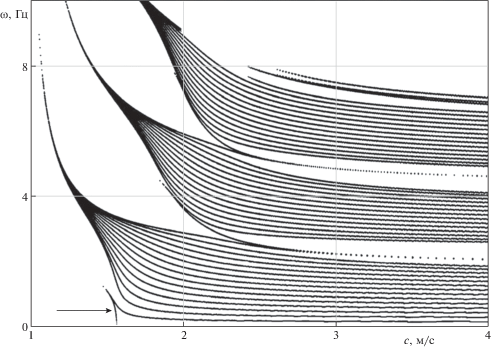
Для рассматриваемой 15-слойной системы (14 чередующихся слоев и контактирующее полупространство) на рис. 1 построены соответствующие дисперсионные кривые.

На рис. 1 стрелкой отмечена фундаментальная мода, имеющая нетривиальный предел фазовой скорости $\mathop {\lim }\limits_{\omega \to 0} c(\omega ) = {{c}_{0}}$. Для вычисления предельной фазовой скорости ${{c}_{0}}$ применимы асимптотические методы [15–17].

Заключительные замечания. Для анизотропной слоистой среды, обладающей моноклинной симметрией, проведен анализ дисперсионных уравнений для волн Лява, с горизонтальной поперечной поляризацией. В замкнутом виде получены дисперсионные уравнения для произвольного числа слоев, контактирующих с упругим анизотропным (моноклинным) полупространством. В случае SH-волн в трехслойной трансверсально изотропной среде, по-видимому, впервые удалось получить аналитические решения для соответствующих дисперсионных уравнений.

Полученные в последнем разделе результаты могут служить объяснением появления высокочастотного волновода для волн с поперечной горизонтальной поляризацией, распространяющихся в системе ортотропный слой, находящийся между ортотропными полупространствами.

Автор (СВК) благодарит РФФИ (Грант 20-08-00419) за частичную финансовую поддержку.