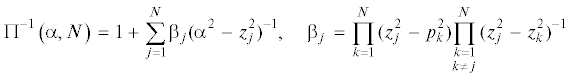Прикладная математика и механика, 2021, T. 85, № 3, стр. 332-346

1. Введение. Аппарат интегральных уравнений (ИУ) занимает важное место в решении смешанных задач механики деформируемого твердого тела, в том числе задач контактного взаимодействия. В [1, 2] проведено сравнение применяемых подходов и представлены результаты анализа применимости различных методов ИУ статических и динамических задач.

Задачи без начальных условий для установивших колебаний объектов на поверхности упругой среды, возникающие при исследовании взаимодействия источника с деформируемым основанием, сводятся к решению ИУ или систем интегральных уравнений (СИУ) с осциллирующими ядрами. В.А. Бабешко был предложен эффективный метод решения ИУ и СИУ с разностными ядрами I-го рода, названный методом фиктивного поглощения (МФП) [3]. Дальнейшее развитие этот метод получил в работах В.А. Бабешко и О.Д. Пряхиной [4–8] применительно к решению интегральных уравнений и СИУ для различных постановок смешанных задач и моделей сред, обладающих сложными свойствами, в том числе анизотропией. Примеры успешного применения МФП в задачах термо- и электроупругости при учете связности полей продемонстрированы в работах [9, 10]. В [9] в схему МФП включены прямые численные методы, позволяющие использовать точное представление символа ядра ИУ динамической задачи, не прибегая к его аппроксимации легко факторизуемыми функциями. Для невыпуклых односвязных областей МФП был применен в [11].

Идея МФП [3] заключается в преобразовании уравнения, имеющего осциллирующее ядро, к ИУ с быстро убывающим на бесконечности ядром. Подобное поведение свойственно ИУ задач для сред с большой вязкостью. МФП позволяет уверенно решать ИУ динамических задач, используя в качестве вспомогательных статические задачи или задачи для сред с затуханием. Для решения последних можно применять многочисленные методы, в частности, изложенные в [12].

МФП создан В.А. Бабешко на рубеже 70–80-х годов прошлого столетия и, к сожалению, нечасто используется в настоящее время. Цель статьи – вновь привлечь внимание к этому методу решения ИУ с осциллирующими ядрами. В работе описана модификация МФП в части выбора базисных функций, а также схема реализации метода для случая, когда штамп или дефект имеют невыпуклую область в плане. В отличие от представленной в [4–9] традиционно применяемой схемы, для вводимой вспомогательной составляющей решения использованы производные $\delta $-функций Дирака, в качестве носителя которых выбрано граничное множество области контакта.

2. МФП в односвязной области произвольной конфигурации. Пусть в плоскости изменения типа граничных условий (контакта штампа со средой или расположения внутреннего дефекта) введена декартова система координат ${{x}_{1}}O{{x}_{2}}$. Запишем ИУ рассматриваемой задачи в форме

Решение (2.1) будем искать в классе суммируемых функций $q\left( {{{x}_{1}},{{x}_{2}}} \right) \in {{{\mathbf{L}}}_{b}}\left( \Omega \right)$, b > 1 [7]. Будем рассматривать ситуацию, когда конечная область интегрирования Ω представляется объединением M ($1 < M < \infty $) выпуклых областей $\Omega = \bigcup\nolimits_{m = 1}^M {{{D}_{m}}} $, где области разбиения D_m ($\partial {{D}_{m}} = {{S}_{m}}$) могут иметь общие участки границ. ИУ (2.1) можно записать в виде системы

${{f}_{s}} = {{{\text{P}}}_{{[{{D}_{s}}]}}}f\left( {{{x}_{1}},{{x}_{2}}} \right)$, где ${{{\text{P}}}_{{[{{D}_{s}}]}}}$ – проекционный оператор на область ${{D}_{s}}$, положение ${{\Gamma }_{1}}$, ${{\Gamma }_{2}}$ в комплексной плоскости определено принципом предельного поглощения [7, 8].

Свойства символа ядра интегрального уравнения (2.1) K определяются выбранной моделью упругой среды и подробно описаны в [7, 8]. Здесь принимается, что $K\left( {{{\alpha }_{1}},{{\alpha }_{2}}} \right) \equiv K\left( \alpha \right)$ ($\alpha _{1}^{2} + \alpha _{2}^{2} = {{\alpha }^{2}}$), $K\left( \alpha \right) = K\left( { - \alpha } \right)$, $K\left( \alpha \right)$ = $C{{\left| \alpha \right|}^{{ - 1}}}[1 + O({{\alpha }^{{ - 1}}})]$, $\left| \alpha \right| \to \infty $. Мероморфная функция K может иметь конечное число вещественных полюсов ${{p}_{k}}$ и нулей ${{z}_{k}}$ $(k = \overline {1,N} )$, увеличивающееся с ростом частоты колебаний, и счетное множество комплексных ${{p}_{k}}$, ${{z}_{k}}$ $(k = \overline {N + 1,\infty } )$ [7, 8, 14].

В дальнейшем, кроме введенной системы координат ${{x}_{1}}O{{x}_{2}}$, будем использовать локальные декартовы системы координат $x_{1}^{m}{{O}_{m}}x_{2}^{m}$, ${{O}_{m}}\left( {{{a}_{m}},{{b}_{m}}} \right) \in {{D}_{m}}$, выбрав оси параллельными осям ${{x}_{1}}O{{x}_{2}}$.

Для системы штампов в ряде случаев единственность решения СИУ [13] не достигается, то же самое имеет место в задачах для установившихся колебаний структур с множественными неоднородностями. Далее для простоты полагается, что ИУ

где ${{R}_{m}} = {{R}_{m}}\left( \psi \right)$ – уравнения границ S_m в локальных координатах, ∀ $k = \overline {1,N} $, $s = \overline {1{\text{,}}M} $, ${{b}_{{ks}}} \in {\mathbf{C}}\left( {0,2\pi } \right)$ имеют единственное решение [7].

Представим решение (2.1) $q\left( {{{x}_{1}},{{x}_{2}}} \right) \in {{{\mathbf{L}}}_{b}}\left( \Omega \right)$, b > 1, в форме

Возьмем $\varphi $ в виде

где ${{g}_{{ks}}}$ – неизвестные однозначные функции, $\Delta = {{\partial }^{2}}{\text{/}}\partial x_{1}^{2} + {{\partial }^{2}}{\text{/}}\partial x_{2}^{2}$. Выбор базисных функций для φ может быть различным [7], в данной работе представлен МФП для $\varphi \left( {{{x}_{1}},{{x}_{2}}} \right)$ вида (2.6). Если все полюсы p_k функции K простые, то $\varphi \left( {{{x}_{1}},{{x}_{2}}} \right)$ и $p\left( {{{x}_{1}},{{x}_{2}}} \right)$ должны обладать свойствами

Здесь и далее через ${{{\text{V}}}_{{\text{2}}}}g\left( {{{x}_{1}},{{x}_{2}}} \right)$ обозначено двумерное изображение Фурье функции $g\left( {{{x}_{1}},{{x}_{2}}} \right)$. Условия для случая кратных полюсов сформулированы в [7]. Далее будем считать, что функция $K\left( \alpha \right)$ не имеет кратных нулей ${{z}_{k}}$ и полюсов ${{p}_{k}}$ (${{z}_{k}}$, ${{p}_{k}} \in \mathbb{R}$). Тогда для нее справедливо представление $K\left( \alpha \right)$ = ${{K}_{0}}\left( \alpha \right)\Pi \left( \alpha \right)$, где ${{K}_{0}}\left( \alpha \right)$ имеет то же асимптотическое поведение при $\left| \alpha \right| \to \infty $, что и $K\left( \alpha \right)$, и является регулярной на вещественной оси. Функция $\Pi \left( \alpha \right)$ имеет на вещественной оси конечное число нулей и полюсов, совпадающих с нулями и полюсами $K\left( \alpha \right)$.

Функция $\Pi \left( \alpha \right)$ приближается рациональной функцией с заданной точностью [14]. Для простоты введем функцию $\Pi \left( {\alpha ,N} \right)$ = ${{E}_{N}}({{\alpha }^{2}})Q_{N}^{{ - 1}}({{\alpha }^{2}})$, где ${{E}_{N}}({{\alpha }^{2}})$ = $\prod\nolimits_{k = 1}^N {({{\alpha }^{2}} - z_{k}^{2})} $, ${{Q}_{N}}({{\alpha }^{2}})$ ≡ $\prod\nolimits_{k = 1}^N {({{\alpha }^{2}} - p_{k}^{2})} $, ${{p}_{k}}$ и ${{z}_{k}}$ – полюсы и нули $K\left( \alpha \right)$ соответственно, ${{p}_{k}}$, ${{z}_{k}} \in \mathbb{R}$, $\Pi \left( {\alpha ,N} \right)$ = $1 + O({{\alpha }^{{ - 1}}})$, $\left| \alpha \right| \to \infty $.

Тогда функция ${{K}_{0}}\left( \alpha \right) = K\left( \alpha \right){{\Pi }^{{ - 1}}}\left( {\alpha ,N} \right)$ будет обладать свойствами, характерными для символа ядра ИУ статической задачи. Далее будем использовать представление

Из (2.1), принимая во внимание (2.8), в операторном виде можно записать соотношение для новой неизвестной $t\left( {{{x}_{1}},{{x}_{2}}} \right)$ = ${\text{V}}_{2}^{{ - 1}}\Pi \left( {\alpha ,N} \right){{{\text{V}}}_{{\text{2}}}}p\left( {{{x}_{1}},{{x}_{2}}} \right)$, где ${\text{V}}_{2}^{{ - 1}}$ – оператор обратного двумерного преобразования Фурье,

где ${{\mathcal{K}}_{0}}$ – интегральный оператор с символом ядра ${{K}_{0}}\left( \alpha \right)$,

Существуют различные техники построения обратного оператора $\mathcal{K}_{0}^{{ - 1}}$ в зависимости от свойств функции K₀(α), обзор их можно найти, в том числе, в [1]. Положим, что $\mathcal{K}_{0}^{{ - 1}}$ известен, тогда

и решение (2.1) в операторном виде запишется как

Чтобы $p\left( {{{x}_{1}},{{x}_{2}}} \right) \in {{{\mathbf{L}}}_{b}}\left( \Omega \right)$ имела носитель в Ω, требуется выполнение условий [7]

Выделим у функции ${\text{V}}_{2}^{{ - 1}}\Pi \left( {\alpha ,N} \right){{{\text{V}}}_{{\text{2}}}}\varphi $, в общем случае имеющей в качестве носителя всю плоскость, обобщенную составляющую ${{\varphi }_{0}}$ с носителем в Ω. Тогда ${{\varphi }_{2}} = {\text{V}}_{2}^{{ - 1}}\Pi \left( {\alpha ,N} \right){{{\text{V}}}_{{\text{2}}}}\varphi - {{\varphi }_{0}}$ будет классической функцией, имеющей носитель во всей плоскости. С этой целью в соотношении

из рациональных функций выделим полиномиальные составляющие

Будем иметь

Из (2.9)

В (2.12) использован проектор на Ω, так как носитель ${{\varphi }_{2}}$ – вся плоскость. Из (2.10)

Условия (2.11) перепишутся в форме

которую, в свою очередь, можно представить следующим образом:

Для (2.4) полагалась разрешимость левой части полученной системы относительно ${{g}_{{ks}}}\left( \psi \right)$. В правой части (2.13) неизвестные ${{g}_{{ks}}}\left( \psi \right)$ содержатся в ${{\varphi }_{2}}$. Обратив левую часть, придем к системе ИУ II-го рода относительно введенных в (2.6) функций ${{g}_{{ks}}}\left( \psi \right)$, которая, в свою очередь, может быть решена с помощью дискретизации.

С учетом вышесказанного для решения (2.1) справедливо представление

где

Можно проделать дальнейшие упрощения (2.14), представив ${{\varphi }_{2}}$ в виде ${{\varphi }_{2}}\left( {{{x}_{1}},{{x}_{2}}} \right)$ = = $\sum\nolimits_{s = 1}^M {\varphi _{{2s}}^{ + }} $ + $\varphi _{2}^{ - }$, где $\varphi _{{2s}}^{ + }$ = ${{{\text{P}}}_{{\left[ {{{D}_{s}}} \right]}}}\varphi _{2}^{ + }$. Обозначив ${{q}_{s}}\left( {{{x}_{1}},{{x}_{2}}} \right)$ ≡ $q\left( {{{x}_{1}},{{x}_{2}},{{D}_{s}}} \right)$, $\left( {{{x}_{1}},{{x}_{2}}} \right) \in {{D}_{s}}$, получим решения (2.2)

Неизвестные ${{g}_{{ks}}}$ при этом определяются из системы, аналогично [7]

Из полученных представлений решения видно, что введенная в виде (2.6) функция $\varphi $ присутствует лишь под знаками интегральных операторов.

3. МФП в осесимметричных задачах

3.1. Решение ИУ осесимметричной задачи с убывающим символом ядра. Рассмотрим интегральное уравнение пространственной задачи об установившихся колебаниях (с частотой $\omega $) круглого штампа на поверхности однородного упругого слоя толщины h с защемленной нижней гранью в отсутствии трения в области контакта штампа со средой при заданных вертикальных смещениях его подошвы. В декартовой системе координат плоскость x₁Ox₂ совмещена с поверхностью слоя, ось Ox₃ направлена вверх по нормали. В случае осевой симметрии в цилиндрических координатах ИУ принимает вид

где a – радиус штампа, ${{J}_{n}}\left( r \right)$ – функция Бесселя I рода порядка n, ${{\Gamma }_{0}}$ – часть контура Γ (2.3), расположенная в полуплоскости x₁ > 0. Неизвестная функция $q\left( r \right)$ описывает напряжения в области контакта штампа со средой, функция $f\left( r \right)$ – перемещения подошвы штампа. Вид символа ядра, соответствующий элементу матрицы-функции Грина $K\left( \alpha \right) \equiv {{K}_{{33}}}\left( {\alpha ,0} \right)$ упругого слоя, жестко сцепленного с недеформируемым основанием, приведен в [2, 7, 8]. Там же описаны свойства элементов матрицы Грина, зависящих от упругих характеристик, плотности среды и толщины слоя.

Рассмотрим в качестве вспомогательного для решения (3.1) уравнение с правой частью в виде функции Бесселя I рода вида

с ядром (3.2). Для произвольной правой части следует разложить $f\left( r \right)$ в ряд по функциям Бесселя или представить ее в виде интеграла Фурье–Бесселя.

Имеется много примеров применения МФП в осесимметричных задачах [5–8]. Но везде в качестве функции φ используется линейная комбинация δ-функций Дирака с непересекающимися носителями вида

Вместе с тем, справедлива лемма, позволяющая выбрать другой вид функции φ.

Лемма [7]: Пусть функция $q\left( r \right) \in {{{\mathbf{L}}}_{b}}\left( {0,a} \right)$ $\left( {b > 1} \right)$. Существует единственная функция $\varphi \left( r \right)$ вида

такая, что имеют место равенства $Q\left( {{{p}_{k}}} \right) = \Phi \left( {{{p}_{k}}} \right)$; $k = \overline {1{\text{,}}\,N} $, где

Здесь ${{{\text{V}}}_{{{{B}_{n}}}}}$ – оператор интегрального преобразования Ханкеля (Бесселя–Фурье), m_k выбирается таким образом, что ${{J}_{n}}\left( {a{{p}_{k}}} \right) \ne 0$. Далее рассматривается ${{m}_{k}} = 0$.

Функцию $K\left( \alpha \right)$ символа ядра представим в виде (2.8). Как, например в [7], выберем в качестве ${{K}_{0}}\left( \alpha \right)$ функцию ${{K}_{0}}\left( \alpha \right) = {{({{\alpha }^{2}} + {{B}^{2}})}^{{ - 1/2}}}$, где B – заданный параметр аппроксимации. Рациональная функция $\Pi \left( {\alpha ,N} \right)$ = $\prod\nolimits_{k = 1}^N {({{\alpha }^{2}} - z_{k}^{2})({{\alpha }^{2}}} $ – $p_{k}^{2}{{)}^{{ - 1}}}$ описана в предыдущем разделе. Здесь ${{p}_{k}}$ – полюса, лежащие выше контура ${{\Gamma }_{0}}$.

В соответствии с (2.5) представим решение (3.3) в виде

В качестве $\varphi \left( r \right)$ возьмем

где, как и ранее, ${{G}_{k}}({{\alpha }^{2}}) = ({{\alpha }^{2}} - p_{1}^{2}) \ldots ({{\alpha }^{2}} - p_{{k - 1}}^{2})({{\alpha }^{2}} - p_{{k + 1}}^{2}) \ldots ({{\alpha }^{2}} - p_{N}^{2})$, а ${{C}_{k}}$ – неизвестные константы, определяемые в дальнейшем.

В соответствии с (2.7)

Введем новую неизвестную $t\left( r \right)$, для которой, используя представление (2.8), приходим к ИУ с регулярным убывающим ядром

Решение ИУ (3.3) запишется в виде

Система для определения (2.13) примет вид

где ${{z}_{l}}$ – нули функции $\Pi \left( {\alpha ,N} \right)$, лежащие выше контура ${{\Gamma }_{0}}$.

Оценка точности построения решения ИУ для среды с поглощением определяется значением параметра B, порядок отбрасываемых при деформации контура интегрирования членов тем меньше, чем больше значение B [14]. Воспользуемся приведенным в [7] приближенным решением уравнения

с ядром (3.5) и представлением [7]

Применив процедуру перехода к интегрированию по развернутому контуру, $\Gamma $, используя свойства цилиндрических функций, в результате получим представление решения (3.3)

где

Здесь использованы обозначения, аналогичные [7], $H_{0}^{{\left( j \right)}}$ – функции Бесселя III рода (функции Ханкеля) $\left( {j = 1,2} \right)$. Присутствующие в представлении (3.6) ${{g}_{k}}$ содержат в себе неизвестные константы ${{C}_{k}}$, ${{g}_{k}}$ = $a{{C}_{k}}{{E}_{N}}(p_{k}^{2}){{J}_{n}}\left( {a{{p}_{k}}} \right)$.

Алгебраическая система для определения ${{g}_{k}}$ примет вид

Выражение (3.6) описывает решение (3.3) с точностью до множителя ${{C}^{{ - 1}}}$, где C характеризует поведение функции $K\left( \alpha \right)$ при $\left| \alpha \right| \to \infty $ ($K\left( \alpha \right)$ = $C{{\left| \alpha \right|}^{{ - 1}}}[1 + O({{\alpha }^{{ - 1}}})]$, $\left| \alpha \right| \to \infty $), а выбранное ядро вспомогательной статической задачи имеет асимптотику ${{K}_{0}}\left( \alpha \right)$ = ${{\left| \alpha \right|}^{{ - 1}}}[1 + O({{\alpha }^{{ - 1}}})]$, $\left| \alpha \right| \to \infty $.

Описанная схема МФП для осесимметричной задачи реализована в работе [15].

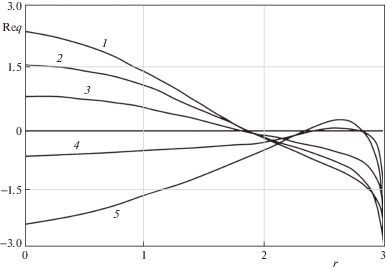
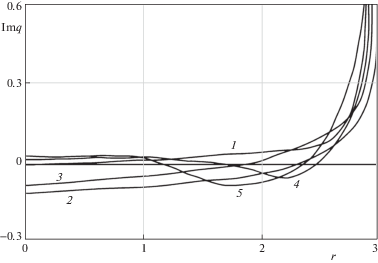
На рис. 1, 2 представлены результаты расчетов амплитудных значений контактных напряжений, когда форма подошвы описывается функцией $f\left( r \right) = {{J}_{n}}\left( {\eta r} \right)$. Все параметры отнесены к толщине слоя, безразмерная частота определяется формулой ${{\bar {\omega }}^{2}} = \rho {{\omega }^{2}}{{h}^{2}}{{\mu }^{{ - 1}}}$. Характеристики слоя: h = 1 – толщина, плотность $\rho = 1$; коэффициент Пуассона $\nu = 0.3$; модуль сдвига $\mu = 1$. Графики реальной части $q\left( r \right)$, отражающие изменения амплитуды напряжений с ростом частоты, приведены на рис. 1.

На рис. 2 представлены мнимые части амплитуды контактных напряжений. Кривым под номерами 1, 2, 3, 4, 5 соответствуют значения приведенной частоты 1.8; 2.2; 2.6; 3; 3.4 ($a = 3$, $n = 0$, $\eta = 1$).

МФП применим для любых частот колебаний. Преимуществом МФП также является правильное описание поведения решения не только во внутренних точках, но и в окрестности границ области контакта.

3.2. Решение ИУ осесимметричной задачи с растущим символом ядра. В контактных задачах для трещин символ ядра ИУ относительно неизвестного скачка перемещений в области дефекта имеет асимптотику $K\left( \alpha \right)$ = $C\left| \alpha \right|[1 + O({{\alpha }^{{ - 1}}})]$, $\left| \alpha \right| \to \infty $ [16], и ядро интегрального оператора является обобщенной функцией. В данном случае за счет выноса из обеих частей интегрального уравнения вида (3.3) дифференциального оператора можно привести ИУ к уравнению с классической функцией ядра, решение которого осуществляется в соответствии с приведенным алгоритмом МФП. При этом решение уравнения отыскивается в классе суммируемых функций $q\left( r \right) \in {{{\mathbf{L}}}_{b}}\left( {0,a} \right)$ $\left( {b > 1} \right)$, обращающихся в нуль на границе области трещины.

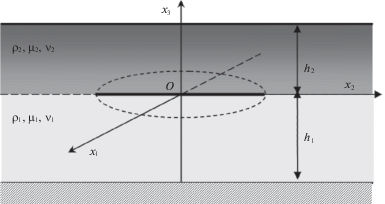
Рассмотрим в качестве примера ИУ осесимметричной задачи о возбуждении гармонических колебаний в упругой среде вибрацией берегов круглой трещины отрыва $(\Omega :{{x}^{2}} + {{y}^{2}} \leqslant {{a}^{2}})$. В качестве упругой среды будем рассматривать двухслойный пакет, считая, что трещина располагается в плоскости раздела физико-механических свойств (рис. 3).

Верхняя грань пакета свободна от нагрузок, нижняя – жестко защемлена, в области трещины заданы равные напряжения на противоположных ее берегах. Полагается, что в процессе колебаний берега трещины не взаимодействуют. Смешанная граничная задача может быть сведена к интегральному уравнению вида (3.1), где, для сохранения единых обозначений в ИУ, через $q\left( r \right)$ обозначено неизвестное амплитудное значение скачка перемещений в области трещины, $f\left( r \right)$ описывает амплитуду напряжения на ее берегах. Структура и свойства функции символа ядра описаны в работах [16, 17].

Будем строить решение ИУ вида (3.3), где символ ядра (3.6) – растущая функция.

Вынесем из обеих частей ИУ дифференциальный оператор вида $ - {{L}_{n}} + {{l}^{2}}$, где l – некоторая константа. Получим ИУ с убывающей при $\left| \alpha \right| \to \infty $ функцией символа ядра

$\varepsilon \left( r \right) = {{С}_{1}}{{I}_{n}}\left( {lr} \right)$ – ограниченное в нуле решение модифицированного уравнения Бесселя

Здесь ${{I}_{n}}\left( r \right)$ – модифицированная функция Бесселя I рода порядка n, ${{C}_{1}}$ – константа, подлежащая определению.

Используя свойства цилиндрических функций [18] и проведя разворот контура интегрирования на всю вещественную ось, можно преобразовать правую часть (3.7) так, что ИУ примет вид

где ${{C}_{1}}$ находится из заданного на краю трещины условия $q\left( a \right) = 0$.

Значения интегралов, стоящих в (3.8) справа, нетрудно посчитать с помощью таблиц [19], в результате чего приходим к ИУ с правой частью в виде комбинации функций Бесселя ${{J}_{n}}\left( {\eta r} \right)$ и ${{I}_{n}}\left( {lr} \right)$

где ${{K}_{n}}\left( r \right)$ – модифицированная функция Бесселя II рода (функция Макдональда).

Функция символа ядра K₁ c точностью до постоянного множителя приближается соотношением ${{K}_{1}}(\alpha )$ = $K(\alpha ){{({{\alpha }^{2}} + {{l}^{2}})}^{{ - 1}}}$ ≈ ${{K}_{0}}(\alpha )\Pi (\alpha ,N)$, далее для построения решения (3.8) может быть использован алгоритм МФП с базисными функциями вида (3.4).

Решение вспомогательной задачи для среды с поглощением для ИУ с правой частью в виде ${{I}_{n}}\left( {lr} \right)$ построено в работе [17]. В силу линейности задачи решение ИУ (3.9) запишется как

где ${{q}_{1}}\left( r \right)$ – приближенное решение ИУ для правой части в виде ${{J}_{n}}\left( {\eta r} \right)$, представляемое соотношением (3.6),

Здесь $b{\kern 1pt} *{\kern 1pt} (l) = \sqrt {\frac{{2\pi }}{a}} {{I}_{n}}\left( {al} \right)\sqrt {B + l} $,

Система для определения ${{d}_{k}}$, входящих в (3.10), принимает вид

Присутствующая в решении константа ${{С}_{1}}$ определяется из условия равенства нулю скачка перемещений на границе области трещины. С этой целью вычисляется предел $R = \mathop {{\text{lim}}}\limits_{r \to a - 0} q\left( r \right)\sqrt {a - r} $, соответствующий коэффициенту при корневой особенности, и приравнивается к нулю.

В работе [16] представлено решение интегральных уравнений плоской задачи для слоистого пакета при наличии интерфейсных трещин. Авторами также использован МФП, но вынос дифференциального оператора осуществлялся на этапе построения решения вспомогательной статической задачи.

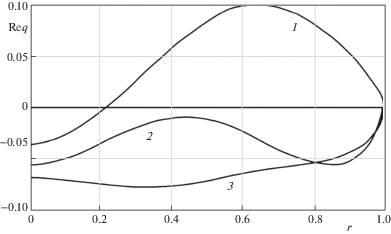
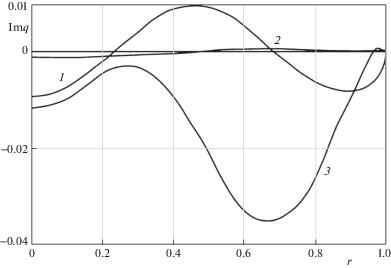
На рис. 4, 5 представлены результаты расчетов для трещины отрыва на границе раздела свойств в двухслойном пакете с защемленной нижней гранью. Все безразмерные величины приведены к параметрам верхнего слоя, в качестве характерного линейного размера выбран радиус трещины, приведенная частота определяется формулой ${{\bar {\omega }}^{2}} = {{\rho }_{2}}{{\omega }^{2}}{{a}^{2}}\mu _{2}^{{ - 1}}$. Параметры пакета: h₁ = 0.6 – толщина нижнего слоя, h₂ = 0.4 – толщина верхнего слоя; плотности слоев ${{\rho }_{1}} = {{\rho }_{2}} = 1$; коэффициенты Пуассона ${{\nu }_{1}} = {{\nu }_{2}} = 0.3$; ${{\mu }_{1}}{\text{/}}{{\mu }_{2}} = 0.5$.

На рис. 4 приведены реальные, на рис. 5 – мнимые части амплитудного значения скачка перемещений на берегах трещины, к которым приложена единичная нагрузка ($a = 1$, $n = 0$, $\eta = 0$).

Кривым под номерами 1, 2, 3 соответствуют значения приведенной частоты 4, 5, 7. Как видно из графиков, значения мнимой части возрастают, в вещественной – убывают с ростром частоты колебаний.

Заключение. В работе описана схема метода фиктивного поглощения решения интегральных уравнений смешанных задач механики деформируемого твердого тела для односвязной области, занимаемой штампом или дефектом. Применение нового вида вспомогательных функций продемонстрировано на примере ИУ осесимметричных задач о колебаниях штампа и трещины в упругой среде. Выбор более сложного вида базисных функций приводит к более простой форме решения. Для трещины отрыва в двухслойном пакете приведены результаты численных расчетов.

МФП может использоваться при решении ИУ задач для произвольных в плане областей штампов или дефектов (трещин и включений). Достоинство МФП состоит также в том, что область применимости полученных приближенных решений динамических задач определяется областью применения решений использованных в качестве вспомогательных статических задач.

Фрагменты работы выполнены в рамках задания ГЗ ЮНЦ РАН, проект № 01201354241 и при частичной поддержке РФФИ (проект 18-05-80008).