Прикладная математика и механика, 2021, T. 85, № 3, стр. 285-295

1. Введение. Контактные задачи теории упругости для полосы – важный раздел смешанных задач, в который ростовские механики внесли значительный вклад. Отметим пионерскую работу [1], а также монографию [2], оказавшую значительное влияние на многих исследователей и дальнейшее развитие теории контактных задач. При этом в монографии представлены общие вопросы контактного взаимодействия, вопросы разрешимости краевых задач в различных классах функций, методы исследования интегральных уравнений для малых областей контакта (метод больших лямбда, развитый В.М. Александровым), и метод бесконечных систем (метод малых лямбда, развитый В.А. Бабешко [3, 4]). В дальнейшем ряд результатов в рамках метода больших лямбда был распространен на неоднородную полосу [5], в контактных задачах для которой основная трудность состоит в том, что символы ядер интегральных операторов невозможно построить в явном виде для произвольных законов неоднородности. Символ ядра строился в два этапа. На первом этапе решалась краевая задача для матричного дифференциального оператора с параметром (параметром преобразования Фурье); на втором этапе строилась аппроксимация полученной численно функциональной зависимости дробно-рациональными и степенными функциями. В работах [6, 7] данный подход расширен для многослойных структур с неоднородным покрытием.

В настоящее время в инженерную практику внедряется все большее количество составных конструкций, покрытий, конструктивных элементов, изготовленных из композиционных материалов. Моделирование таких объектов, обладающих существенно неоднородными свойствами, требует изучения деформирования неоднородных слоистых структур при статических и динамических воздействиях. Одним из наиболее популярных и быстро развивающихся направлений в конструировании неоднородных объектов является изготовление функционально-градиентных материалов (ФГМ). ФГМ представляет из себя среду, свойства которой изменяются по некоторому закону, исходя из некоторых требований, например, для снижения уровня напряженного состояния внутри конструктивного элемента [8].

Одной из наиболее перспективных областей применения ФГМ является изготовление градиентных покрытий различного назначения. Нанесение покрытий из ФГМ широко применяется при изготовлении различных элементов инженерных конструкций, режущего инструмента, медицинских приборов, в конструкциях компонентов двигателей авиационной и космической техники [9]. Переменный состав и изменение свойств с глубиной покрытия приводит к уменьшению концентрации напряжений, что в свою очередь позволяет снизить вероятность образования трещин и других дефектов.

Альтернативным способом исследования деформирования неоднородных оснований является построение приближенных моделей. В монографии [10] построен ряд приближенных моделей контактного взаимодействия для тел с тонкими покрытиями и прослойками. Работы [11, 12] посвящены разработке моделей деформирования неоднородной упругой полосы в рамках использования некоторых гипотез о структуре полей, позволяющие рассматривать произвольные законы неоднородности, в том числе разрывные.

Большое число работ посвящено решению контактных задач для функционально-градиентных материалов на основе метода конечных элементов. Исследована [13] контактная задача для вязкоупругого основания и сферического индентора. Построено [14] решение задачи о контактном взаимодействии неоднородного слоя, лежащего на однородном полупространстве, и двух плоских штампов.

Рассмотрена [15] задача о контакте двух сфер, усиленных функционально-градиентными покрытиями. Задача сведена к решению интегрального уравнения Фредгольма второго рода. Неоднородность материала смоделирована путем создания многослойной области с постоянными свойствами в каждом слое.

Большое количество работ для полосы выполнено в предположении о том, что законы неоднородности изменяются экспоненциальным образом, что приводит к краевым задачам с постоянными коэффициентами и символы ядер интегральных операторов могут быть получены аналитически. В [16] исследована контактная задача для поперечно-неоднородного ортотропного слоя и цилиндрического штампа. Коэффициенты матрицы жесткостей изменяются с толщиной по экспоненциальному закону.

Настоящая работа посвящена развитию методов исследования контактных задач для неоднородной упругой полосы, где для изучения символа ядра интегрального оператора использованы численные и асимптотические методы, позволяющие выявить основные свойства этих функций при малых и больших значениях аргумента. Разработан метод граничных элементов для решения интегрального уравнения контактной задачи, позволяющий исследовать задачи с переменной областью контакта, не прибегая к затратной схеме его решения в расширенной области. Построены важные зависимости сила–внедрение для различных законов неоднородности.

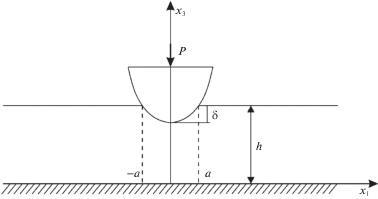
2. Постановка задачи. В рамках плоской задачи теории упругости рассмотрим контактное взаимодействие поперечно-неоднородной упругой полосы толщины $h$ и штампа с основанием гладкой формы. Свяжем с полосой прямоугольную систему координат $O{{x}_{1}}{{x}_{3}}$ с началом в основании полосы, ось $O{{x}_{3}}$ направлена вертикально вверх (рис. 1). Нижняя граница полосы ${{x}_{3}} = 0$ жестко сцеплена с недеформируемым основанием. Область контакта полосы и штампа расположена на отрезке ${\text{|}}{{x}_{1}}{\text{|}} \leqslant a$. Параметры Ламе полосы являются произвольными положительными функциями вертикальной координаты, $\lambda = \lambda ({{x}_{3}})$, $\mu = \mu ({{x}_{3}})$, ${{x}_{3}} \in [0,h]$.

Уравнения равновесия и определяющие соотношения задачи имеют вид

где ${{u}_{i}}$, ${{\sigma }_{{ij}}}$ – компоненты вектора перемещений и тензора напряжений соответственно.

Считая, что трение между контактными поверхностями штампа и полосы отсутствует, сформулируем граничные условия контактной задачи

где $\delta $ – глубина внедрения, $a$ – величина области контакта, функция $f({{x}_{1}})$ описывает форму основания штампа.

Связь между внедрением штампа $\delta $ и величиной области контакта $a$ определяется из условия равенства нулю контактных напряжений на границе контакта. Для определения силы, действующей на штамп, служит условие равновесия штампа

Обезразмерим задачу, введя безразмерные параметры следующим образом

где ${{\mu }_{0}}$ – характерное значение модуля сдвига (либо среднее значение функции, либо максимальное).

3. Равновесие неоднородной упругой полосы под действием нагрузки. Рассмотрим вспомогательную задачу о равновесии неоднородной упругой полосы под действием безразмерной нормальной нагрузки $\hat {q}({{\xi }_{1}})$, локализованной на отрезке $[ - \beta ,\beta ]$ верхней границы. Граничные условия задачи в безразмерных параметрах имеют вид

где

В работе [17] система дифференциальных уравнений в частных производных (2.1), (2.2) с помощью преобразования Фурье по координате ${{\xi }_{1}}$ сведена к канонической системе обыкновенных дифференциальных уравнений с переменными коэффициентами относительно трансформант вида

где знаком “~” обозначены символы Фурье соответствующих функций, а матрица коэффициентов системы не содержит производных от законов неоднородности, в отличие от [5, 18], и имеет вид

Граничные условия (3.1), (3.2) краевой задачи в трансформантах примут вид

где

Решение краевой задачи (3.3), (3.4) построим численно с помощью метода пристрелки. Для этого сформулируем следующие вспомогательные задачи Коши

В силу линейной независимости решений вспомогательных задач, решение краевой задачи (3.3), (3.4) запишем в виде их линейной комбинации

Находя константы ${{c}_{1}}$, ${{c}_{2}}$ из условий (3.4) в точке ${{\xi }_{3}} = 1$, получим решение краевой задачи (3.3), (3.4) в виде

Формула (3.7) позволяет установить связь трансформант нагрузки и вертикальной компоненты смещения верхней границы полосы в виде

где $K(\alpha )$ – передаточная функция, определяемая через решения вспомогательных задач Коши формулой

4. Анализ передаточной функции. Передаточная функция $K(\alpha )$ является важным объектом при исследовании контактных задач для полосы. Важную роль согласно [2] играет асимптотическое поведение этих функций при малых и больших значениях параметра преобразования. Значения в нуле характеризуют среднее значение контактного давления, а поведение на бесконечности – структуру контактного давления у границ области контакта. Исследуем поведение $K(\alpha )$ и проведем асимптотический анализ при малых и больших значениях параметра $\alpha $.

Меняя в системе (3.3) $\alpha $ на $ - \alpha $, нетрудно показать, что функция $K(\alpha )$ для любых законов неоднородности является четной функцией, т.е. $K( - \alpha ) = K(\alpha )$.

При проведении асимптотического анализа рассмотрим задачу (3.3), (3.4), для удобства полагая $Q(\alpha ) \equiv 1$, что соответствует действию сосредоточенной силы в точке ${{\xi }_{1}} = 0$ верхней границы полосы

Полагая параметр $\alpha $ малым, представим решение краевой задачи в виде регулярных асимптотических разложений

Подставляя выражение (4.2) в систему (3.3) и приравнивая между собой коэффициенты при одинаковых степенях $\alpha $, получим краевые задачи для систем дифференциальных уравнений первого порядка, анализ которых позволяет найти начальные коэффициенты разложений (4.2). На основе асимптотических представлений решения краевой задачи передаточная функция для малых значений параметра $\alpha $ с учетом четности может быть записана в виде

где главный член разложения имеет вид а остальные находятся рекуррентным образом [15].

Рассмотрим теперь случай больших $\alpha $ и исследуем поведение передаточной функции при $\alpha \to \infty $, что приводит к анализу для системы с переменными коэффициентами краевой задачи с малым параметром при старшей производной. Используем для анализа асимптотический метод, например метод Вишика–Люстерника [19]. Отметим, что спектр матрицы коэффициентов системы (3.3) состоит из двух двукратных значений $\left| \alpha \right|$ и $ - \left| \alpha \right|$, что приводит к существенному усложнению построения асимптотического решения в рамках известных подходов [20].

Будем искать решение задачи при больших $\alpha $ в окрестности ${{\xi }_{3}} = 1$ при $\alpha > 0$ в виде

Подставляя представление (4.3) в каноническую систему (3.3), решая возникающие краевые задачи и удовлетворяя граничным условиям (4.1), с учетом четности функции $K(\alpha )$ найдем главный член разложения передаточной функции при $\left| \alpha \right| \to \infty $ в явном виде

Построенное асимптотическое представление согласуется с известными результатами для однородного случая [2], а также с качественными результатами, полученными для неоднородной полосы, например в [5].

5. Интегральное уравнение контактной задачи. Метод граничных элементов. Найдем вертикальное смещение верхней границы полосы, для этого построим обращение преобразования Фурье. Из формулы (3.8) найдем

причем ядро интегрального оператора имеет вид

Учитывая условия (2.4), сформулируем интегральное уравнение контактной задачи в виде

Поскольку основные свойства функции $K(\alpha )$ идентичны свойствам этой функции в однородном случае, можно показать, что ядро интегрального уравнения (5.1) имеет логарифмическую особенность и для его решения может быть использован метод больших лямбда [5] или численные методы.

Решение интегрального уравнения (5.1) построим численно с помощью метода граничных элементов. Учитывая симметрию задачи в случае, когда функция $\gamma ({{\xi }_{1}})$, описывающая форму основания штампа, является четной, построим решение уравнения (5.1) в области $[0,\beta ]$. Проведем дискретизацию уравнения (5.1), для этого разобьем отрезок $[0,\beta ]$ на $N$ элементов ${{\Delta }_{p}} = [{{\eta }_{p}},{{\eta }_{{p + 1}}}]$, $p = \overline {1,N} $, границы отрезков ${{\Delta }_{p}}$ определяются формулой ${{\eta }_{j}} = (j - 1)s$, $s = \beta {{N}^{{ - 1}}}$, $j = \overline {1,N + 1} $; в качестве точек коллокаций выберем середины отрезков ${{\Delta }_{p}}$: ${{\xi }_{{1p}}} = (p - 0.5)s$. Будем считать, что функция $q({{\xi }_{1}})$ принимает постоянные значения на элементах и введем обозначение ${{q}_{p}} = {{\left. q \right|}_{{{{\Delta }_{p}}}}}$. Считая, что уравнение (5.1) выполнено в наборе точек $\{ {{\xi }_{{1p}}}\} $, составим алгебраическую систему относительно узловых значений неизвестной функции $q({{\xi }_{1}})$ вида

где

При исследовании контактных задач для штампов с гладким основанием область контакта является неизвестной величиной, зависящей от глубины внедрения штампа, и подлежит определению. При реализации вычислительных схем решения интегральных уравнений в контактных задачах в качестве исходных параметров, как правило, задается значение внедрения или силы, действующей на штамп, а затем определяется величина области контакта, которая нелинейным образом зависит от задаваемых величин. В работе [21] исследована контактная задача для трехслойного сферического шарнира, решение интегрального уравнения построено с помощью метода коллокаций. Для определения величины области контакта по заданному значению внедрения построен итерационный процесс, в котором область контакта определяется из условия неотрицательности контактного давления. Схожий подход применен при решении пространственных контактных задач в работах [22, 23], в которых область контакта изначально полагается заведомо бо́льшей, чем действительная, а затем уточняется на каждом шаге итерационного процесса.

При реализации вычислительной схемы, построенной в настоящей работе, задается значение $\beta $, а величина внедрения определяется из условия равенства нулю контактного давления на границах контактной области, которое после дискретизации является условием равенства нулю узлового значения ${{q}_{N}}$ искомой функции вблизи границы контакта и может быть записано в виде

где ${{\Delta }_{N}}$ – определитель матрицы, получающейся согласно методу Крамера заменой $N$-го столбца матрицы $H$ на вектор-столбец $g$. Отметим, что параметр ${{\delta }_{*}}$ входит в правые части интегральных уравнений линейно и уравнение (5.4) является линейным алгебраическим уравнением относительно ${{\delta }_{*}}$, что позволяет просто найти связь ${{\delta }_{*}}(\beta )$.

При вычислении коэффициентов алгебраической системы (5.2) интегралы в (5.3) вычисляются с использованием асимптотического представления символа ядра на бесконечности. Интегрирование осуществляется по отрезку $[0,b]$ c помощью квадратурных формул Гаусса, а при вычислении оставшейся части интеграла на полуинтервале $[b,\infty )$ функция $K(\alpha )$ заменяется ее асимптотическим представлением (4.4). Значение параметра $b$ определяется в вычислительном эксперименте.

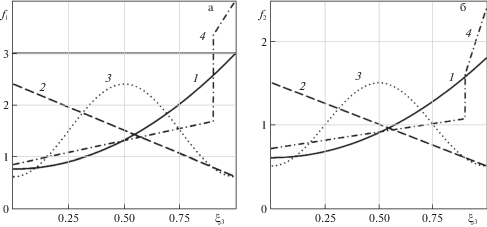
6. Результаты вычислительных экспериментов. При проведении вычислительных экспериментов были выбраны следующие законы неоднородности полосы

1. возрастающие: $f_{1}^{{(1)}}({{\xi }_{3}}) = 0.75 + 2.25\xi _{3}^{2}$, $f_{2}^{{(1)}}({{\xi }_{3}}) = 0.6 + 1.2\xi _{3}^{2}$;

2. убывающие: $f_{1}^{{(2)}}({{\xi }_{3}}) = 2.4 - 1.8{{\xi }_{3}}$, $f_{2}^{{(2)}}({{\xi }_{3}}) = 1.5 - {{\xi }_{3}}$;

3. немонотонные: $f_{1}^{{(3)}}({{\xi }_{3}}) = 1.5 - 0.9\cos \left( {2\pi {{\xi }_{3}}} \right)$, $f_{2}^{{(3)}}({{\xi }_{3}}) = 1 - 0.5\cos \left( {2\pi {{\xi }_{3}}} \right)$;

4. кусочно-линейные:

причем средние значения законов неоднородности на отрезке [0, 1] равны

Графики законов неоднородности 1–4 представлены на рис. 2.

С целью проверки сходимости вычислительной схемы решения задачи построены для различного количества граничных элементов на равномерной сетке при $N = 10$, 30, 90. Проведено сравнение значений искомого контактного давления в общих для разных разбиений точках коллокации. Проведенный анализ показал сходимость вычислительной схемы при увеличении количества отрезков разбиения. Более эффективным является построение неравномерной сетки граничных элементов со сгущением вблизи границ области контакта. Ниже представлены результаты вычислительных экспериментов, построенные для штампа с основанием параболической формы $\gamma ({{\xi }_{1}}) = \xi _{1}^{2}{\text{/2}}r$ при значениях параметров: $r = 5$, $N = 30$, ${{l}_{N}}{\text{/}}{{l}_{1}} = 0.01$, ${{l}_{p}}$ – длина отрезка ${{\Delta }_{p}}$.

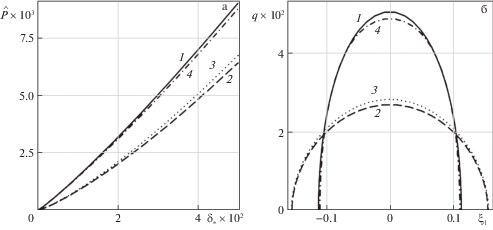
На рис. 3 представлены решения контактных задач для законов неоднородности 1–4. Распределение контактного давления для разных законов построено при одинаковом значении внедрения ${{\delta }_{*}} = 0.005$. Контактное давление достигает наибольшей величины для законов, значение которых на верхней границе полосы больше. Результаты решения контактной задачи получились близкими для законов с близкими значениями модулей упругости на верхней границе.

Заключение. Исследована задача о контактном взаимодействии без трения неоднородной упругой полосы и штампа с гладким основанием. Проведен асимптотический анализ символа ядра интегрального уравнения контактной задачи при малых и больших значениях параметра преобразования. Главные члены асимптотик найдены в аналитическом виде. Показано, что значение символа ядра в нуле, характеризующее среднее значение контактного давления, определяется среднеинтегральным значением податливости полосы, а поведение на бесконечности, определяющее структуру контактного давления у границ области контакта, определяется значениями упругих модулей на верхней границе полосы. На основе метода граничных элементов построено решение интегрального уравнения контактной задачи. Представлен подход, позволяющий исследовать задачи с переменной областью контакта, не прибегая к затратной схеме ее определения в расширенной области. Построены зависимости сила–внедрение и распределение контактного давления для различных законов неоднородности.

Работа выполнена при поддержке гранта Правительства РФ № 075-15-2019-1928.