Прикладная математика и механика, 2021, T. 85, № 5, стр. 576-586

1. Введение. Известно, что Румянцев В.В. уделял, вместе с учениками, особое внимание задаче о поступательно-вращательных движениях искусственных небесных тел. Так, в статье [1] спутник моделируется динамически-симметричным твердым телом, даны достаточные условия устойчивости его стационарных движений, когда центр масс спутника остается в точке либрации ограниченной задачи трех тел. Аналогичные исследования проведены в работе [2], но для спутника-гиростата. К сожалению, поступательно-вращательные движения твердого тела в ограниченной задаче трех тел исследованы мало. Приведем еще статьи [3, 4], в которых доказано существование частных движений гантели, расположенной в треугольной точке либрации круговой ограниченной задачи трех тел, исследована устойчивость этих движений. В статьях [5, 6] исследованы некоторые периодические режимы поступательно-вращательных движений космического аппарата в системе Земля–Луна и их устойчивость. В статье [7] исследуется движение материального отрезка в поле притяжения двух неподвижных притягивающих центров с равными массами и отстоящих друг от друга на чисто мнимом расстоянии $2ic$.

Рассмотрим задачу о поступательно-вращательном движении твердого тела (стержня) пренебрежимо малой массы в гравитационном поле двух одинаковых по массе основных тел (звезд) при условии, что основные тела вращаются вокруг общего центра масс по круговой орбите радиус $a$. С помощью стержня мы будем моделировать протяженный космический аппарат, длина которого существенно превалирует над его поперечными размерами. Если пренебречь размерами тела, рассматривая его как материальную точку, то движение тела описывается уравнениями копенгагенской ограниченной задачи трех тел. Известно, что уравнения этой задачи интегрируются для случая одномерного движения материальной точки вдоль оси, проходящей через центр масс основных тел перпендикулярно плоскости движения этих тел. Этот частный случай движения принято называть задачей Ситникова [8].

Исследуемую задачу будем называть обобщенной задачей Ситникова. Если классическая задача Ситникова (эллиптическая) имеет дело с частными движениями материальной точки вдоль указанной нормали в виде осциллирующих движений с нарастающей амплитудой, хаотических движений, периодических движений и движений с бифуркациями, с устойчивостью относительных равновесий и периодических движений [9–15], то в обобщенной задаче Ситникова исследуются вращения твердого тела, когда его центр масс перемещается вдоль нормали к плоскости движения основных тел. При этом следует различать два типа задач, отличающиехся друг от друга степенью сложности. К первому типу мы относим задачи динамики твердого тела, когда его силовая функция $U$ вычисляется строго (как для случая стержня). Ко второму типу – задачи с приближенными значениями силовой функции, когда удерживаются несколько первых зональных гармоник в разложении силовой функции в ряд.

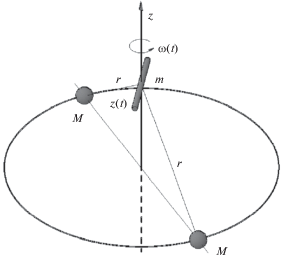
2. Уравнения движения стержня, силовая функция задачи. Запишем уравнения движения однородного стержня массы $m$ и длины $2l$ в гравитационном поле притяжения двух одинаковых по массе $M$ основных тел, вращающихся вокруг их общего центра масс $C$ по круговой орбите радиуса $a$. Пусть $C\xi \eta \zeta $ инерциальная система координат, $Cxyz$ – синодическая система координат, в которой ось $Cx$ соединяет основные тела во все время движения, ось $Cz$ направлена по нормали к плоскости движения этих тел, ось $Cy$ дополняет систему до правой тройки. Со стержнем свяжем оси $Ox{\kern 1pt} '{\kern 1pt} y{\kern 1pt} '{\kern 1pt} z{\kern 1pt} '$ где $O$ – центр масс стержня, $z{\kern 1pt} '$ направим вдоль стержня, оси $x{\kern 1pt} '$, y' – перпендикулярно стержню. Наряду со связанной системой координат $Ox{\kern 1pt} '{\kern 1pt} y{\kern 1pt} '{\kern 1pt} z{\kern 1pt} '$ рассмотрим также поступательно движущиеся оси $O\xi {\kern 1pt} '{\kern 1pt} \eta {\kern 1pt} '{\kern 1pt} \zeta {\kern 1pt} '$, ориентированные параллельно осям инерциальной системы $C\xi \eta \zeta $. Ориентацию осей $Ox{\kern 1pt} '{\kern 1pt} y{\kern 1pt} '{\kern 1pt} z{\kern 1pt} '$ относительно $O\xi {\kern 1pt} '{\kern 1pt} \eta {\kern 1pt} '{\kern 1pt} \zeta {\kern 1pt} '$ зададим с помощью углов Эйлера $\psi ,\varphi ,\theta $, где $\psi $ – угол прецессии, $\varphi $ – угол собственного вращения, $\theta $ – угол нутации. Тогда уравнения движения центра масс стержня примут вид

где $\xi ,\eta ,\zeta $ – координаты центра масс $O$ стержня, $U = U(\xi ,\eta ,\zeta ,\psi ,\varphi ,\theta ,t)$ – силовая функция задачи.

Уравнения вращения по углам Эйлера можно записать в виде уравнений Лагранжа второго рода:

Здесь

кинетическая энергия стержня. Заметим, что второе равенство из системы уравнений (2.2) удовлетворяется тождественно, так как $T$ и $U$ не зависят от угла $\varphi $ и ее производной по времени.

Подставляя кинетическую энергию в первое и третье уравнения системы (2.2), получим

Уравнения (2.1), (2.3) описывают абсолютные поступательно-вращательные движения стержня в поле притяжения двух массивных тел.

Опишем силовую функцию задачи $U = {{U}_{1}} + {{U}_{2}}$, где ${{U}_{j}}$ – силовая функция притяжения стержня со стороны основного тела с номером $j$. Фиксируем точку стержня массы $dm$ с координатами $x{\kern 1pt} ' = y{\kern 1pt} ' = 0,$ $z{\kern 1pt} ' = z{\kern 1pt} '$ в связанных осях. В поступательно движущихся осях $O\xi {\kern 1pt} '\eta {\kern 1pt} '\zeta {\kern 1pt} '$ имеем следующие координаты этой точки:

Здесь $\alpha {\kern 1pt} '{\kern 1pt} ',\;\beta {\kern 1pt} '{\kern 1pt} ',\;\gamma {\kern 1pt} '{\kern 1pt} '$ – направляющие косинусы оси $z{\kern 1pt} '$ с осями $O\xi {\kern 1pt} ',\;O\eta {\kern 1pt} '$, $O\zeta {\kern 1pt} '$ соответственно. Несложно видеть, что

Учитывая, что координаты центра масс $O$ стержня $AB$ в инерциальных осях есть $\xi ,\;\eta ,\;\zeta $, а координаты первой притягивающей массы есть $(a\cos {{\omega }_{0}}t$, $a\sin {{\omega }_{0}}t$, 0), где ${{\omega }_{0}}$ – частота движения основных тел по круговой орбите, получим выражение для полярного радиуса ${{r}_{1}}$ массы $dm$:

Полярный радиус ${{r}_{2}}$ вычисляется аналогично с условием замены $a$ на $( - a)$.

Силовая функция задачи есть

где $\rho $ – постоянная плотность однородного стержня. Вычисления показывают, что

Выражение для ${{U}_{2}}$ имеет аналогичный вид с учетом замены $a$ на $( - a)$.

Очевидно, область возможных движений стержня соответствует положительным значениям подкоренных выражений, входящих в функцию $U$, что возможно при выполнении неравенства

и родственного ему ($a$ заменяется на $ - a$) для любых значений углов $\theta ,\psi $ и времени $t$. Всюду ниже считаем, что $a > l$.

3. Интегральные многообразия уравнений движения стержня. Рассмотрим многообразие решений системы уравнений (2.1), (2.3) следующего вида:

Вычисления показывают, что уравнения по $\xi ,\;\eta ,\;\theta $ удовлетворяются тождественно, уравнения по $\zeta ,\psi $ приводятся к виду:

Здесь двоеточием сверху обозначена вторая производная по новому времени $\tau $

Величины ${{\Delta }_{1}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {{\Delta }_{2}}$ описываются формулами

Это значит, что (3.1) является интегральным многообразием, его конфигурационное пространство есть цилиндр $R \times {{S}^{1}}$. Система уравнений (3.2) описывает движения вдоль этого многообразия. Стержень совершает сложное движение: его центр масс движется вдоль неподвижной нормали (оси $Cz$) к плоскости $Cxy$ движения главных тел, проходящей через их центр масс, а сам стержень вращается вокруг этой оси с абсолютной угловой скоростью $({{\omega }_{0}} + \dot {\delta })$ в плоскостях, паралелльных плоскости $Cxy$, при этом поступательные и вращательные движения завязаны (рис. 1). Заметим, что эти вращения подобны ротационному движению вертолета, когда вертолет планирует при выключенном двигателе за счет вращения лопастей.

Уравнения (2.1), (2.3) допускают также дополнительные интегральные подмногообразия вида (3.1), когда угол $\delta = {\text{const}}$. Действительно, при $\delta = \pi {\text{/}}2$, $3\pi {\text{/}}2$, либо $\delta = 0$, π второе уравнение системы (3.2) удовлетворяется тождественно, в то время как первое уравнение задает закон движения вдоль оси $Cz$. Этот закон разный для разных значений $\delta $. Этим многообразиям отвечает абсолютное вращение стержня с постоянной угловой скоростью ${{\omega }_{0}}$, поэтому в синодической системе координат, вращающейся с той же самой угловой скоростью, стержень движется поступательно вдоль оси $Cz$.

Рассмотрим многообразия

Уравнение движения стержня вдоль оси z имеет вид

В этом случае стержень ориентирован параллельно оси $Cx$ во все время движения и перемещается поступательно относительно синодических осей вдоль оси $Cz$. Отметим, что существование интегрального многообразия (3.3) следует также из физических соображений. Действительно, в силу симметрии задачи силы гравитационного притяжения дают составляющую вдоль оси $Cz$, в то время как проекции этих сил вдоль стержня уничтожают друг друга для каждой пары точек стержня, расположенных симметрично относительно его центра масс $O$. В равномерно вращающихся синодических осях переносные силы инерции также уничтожают друг друга для указанных пар точек стержня, кориолисовые силы инерции равны нулю. Итак, главный вектор сил направлен по оси $Cz$, главный момент сил равен нулю. Стержень движется поступательно вдоль оси $Cz$.

Для многообразия

уравнение движения вдоль оси $z$ имеет вид

Здесь стержень движется вдоль оси $Cz$ поступательно (относительно синодических осей $Cxyz$) так, что он перпендикулярен оси $Cx$ во все время движения.

Отметим также интегральное подмногообразие

для которого уравнение по углу $\delta $ имеет вид

В этом случае стержень вращается неравномерно вокруг собственного центра масс, совпадающего с центром масс основных притягивающих тел, плоскость его вращений совпадает с плоскостью движения этих тел.

В заключение исследований укажем еще на одно интегральное многообразие

которому соответствует поступательное движение стержня вдоль оси $Cz$, при этом сам стержень ориентирован вдоль оси $Cz$ во все время движения. На этом многообразии вырождаются углы Эйлера и появляются особенности в правых частях уравнений (2.1), (2.3). Поэтому для доказательства интегральности многообразия (3.9) воспользуемся физическими соображениями. В силу симметрии расположения стержня в синодических осях и симметрии гравитационного воздействия главный вектор гравитационных сил ориентирован вдоль оси $Cz$, переносные и кориолисовые силы инерции равны нулю. Главный момент внешних сил относительно центра масс стержня равен нулю. Поэтому стержень, ориентированный вдоль оси $Cz$ в начальный момент времени и движущийся поступательно вдоль этой оси, сохранит это движение.

Силовая функция стержня на этом многообразии имеет вид

Тогда колебания центра масс стержня вдоль оси $Cz$ описываются уравнением

4. Исследование движений на одномерных многообразиях. Рассмотрим движения вдоль одномерных многообразий (3.3), (3.5), (3.7),(3.9). Исследуем многообразие ${\mathbf{Ia}}$ (см. (3.3)). Уравнение движений (3.4) стержня допускает частное решение $z = 0$, несмотря на то, что правая часть этого уравнения неопределена в нуле при $a > l$ (неопределенность 0/0 устраняется стандартно). Этому решению отвечает относительное равновесие стержня в синодических осях, когда он ориентирован вдоль прямой, соединяющей притягивающие тела, при этом его центр масс совпадает с центром масс притягивающих тел, а сам стержень находится в плоскости движения этих тел. Такое стационарное движение является аналогом относительного равновесия стержня типа “спица” в центральном гравитационном поле [16].

Интеграл энергии задачи приводится к виду

если движения стержня рассматривать в синодических осях. Вычисления показывают, что фазовый портрет задачи топологически подобен фазовому портрету колебаний материальной точки в круговой задаче Ситникова (рис. 2).

Отсюда следует, в частности, что положение относительного равновесия $z = 0$, в котором стержень принадлежит плоскости вращения основных тел и ориентирован вдоль оси $Cx$, соединяющей притягивающие тела, устойчиво по отношению к малым возмущениям в $z$ и $\dot {z}$, сохраняющим движение стержня вдоль интегрального многообразия (3.3).

Рассмотрим интегральное многообразие (3.5). Отметим, что уравнение движения стержня (3.6) допускает частное решение $z$, при котором стержень расположен в плоскости движения основных тел, при этом его центр масс совпадает с центром масс этих тел, стержень вращается с постоянной угловой скоростью ${{\omega }_{0}}$ в инерциальном пространстве так, что сохраняет постоянный угол $\pi {\text{/2}}$ с прямой, соединяющей основные тела. Такое стационарное движение является аналогом относительного равновесия типа “стрела”, обнаруженное Дубошиным Г.Н. [16] в центральном силовом поле. Интеграл энергии имеет следующий вид в синодических осях:

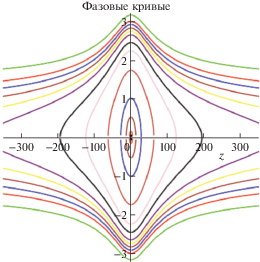
Фазовый портрет колебаний стержня вдоль оси $Cz$ подобен фазовому портрету колебаний материальной точки в круговой задаче Ситникова.

Исследуем многообразие (3.7). Интеграл энергии имеет вид

Заметим, что выражение, стоящее под знаком логарифма, положительно, область возможных движений – цилиндр $R \times {{S}^{1}}$. Фазовый портрет колебаний подобен фазовому портрету колебаний математического маятника.

В заключение рассмотрим многообразие ${\mathbf{II}}$ (см. (3.9)). Интеграл энергии на этом многообразии вычисляется по формуле

Вычисления показывают, что фазовый портрет колебаний стержня вдоль оси $Cz$ подобен фазовому портрету колебаний материальной точки в круговой задаче Ситникова.

Частное решение $z = 0$ отвечает абсолютному равновесию стержня, при котором он ориентирован вдоль оси $Cz$, а его центр масс совпадает с центром масс основных тел. Это равновесие подобно относительному равновесию стержня на круговой орбите в центральном гравитационном поле, когда стержень ориентирован по нормали к плоскости орбиты своего центра масс. Такие равновесия принято называть “поплавок” [16].

5. Описание движений на интегральном многообразии “гравитационный пропеллер”. Рассмотрим движение на сложном многообразии (3.1), (3.2), которые мы называем “гравитационный пропеллер”, если $z(t) \ne 0$. Воспользуемся асимптотическими методами исследования дифференциальных уравнений с малым параметром. В качестве малого параметра выбираем характерную длину стержня – $l$. При $l \to 0$ масса однородного стержня стремится к нулю, поэтому уравнения его поступательно-вращательных движений являются сингулярно возмущенными по δ.

Действительно, раскладывая правую часть второго уравнения системы (3.2) в ряд Тейлора по l, получим неопределенности 0/0 в первых трех членах разложения. Раскрывая эти неопределенности, имеем

Уравнение по $z$ является регулярным по малому параметру $l$, несмотря на то, что $l$ содержится в знаменателе правой части:

Отбрасываем члены порядка ${{l}^{2}}$, вводим новое время $\nu $:

Имеем приближенную систему уравнений, описывающую вращательные движения стержня:

Очевидно, в данном приближении по $l$ движение центра масс тела практически не зависит от вращения тела относительно центра масс и описывается гармонической функцией $\nu $.

Уравнение (5.3) является неавтономным уравнением второго порядка с малым параметром при старшей производной, исследованным в статье [17]. Это уравнение не содержит диссипативных членов c $\delta {\kern 1pt} '$. Поэтому уравнение (5.3) не охватывается теоремой Тихонова А.Н. [18], следовательно, отсутствует предельный переход при $l \to 0$ от решения уравнения (5.3) к решению вырожденного уравнения

Легко видеть, что все решения уравнения (5.4) имеют вид $\delta {\kern 1pt} * = 0,\pi ,\pi {\text{/}}2,3\pi {\text{/}}2$, отвечающий значениям угла $\delta $ на интегральных подмногообразиях, описанных выше.

Как следует из статьи [17], решение $\delta (\nu ,l)$ уравнения (5.3) не имеет предела при $l \to 0$, а колеблется с большой частотой порядка $1{\text{/}}l$ и конечной амплитудой, зависящей от начальных условий, около решения $\delta {\kern 1pt} *$ вырожденного уравнения (5.4). Совокупность максимумов и минимумов возмущения $\left( {\delta (\nu ,l) - \delta {\kern 1pt} *} \right)$ приближаются при $l \to 0$ к некоторым непрерывным кривым $\delta = {{F}_{1}}(\nu )$, $\delta = {{F}_{2}}(\nu )$, не зависящим от l. Эти кривые были названы опорными и получены дифференциальные уравнения, описывающие эти кривые.

Расчеты показали справедливость этих выводов. Выбирая в качестве величин $l,a$ характерные размеры объектов в солнечной системе ($l = 10$ км, $a = 1$ а.е.), имеем безразмерное значение $l \sim {{10}^{{ - 7}}}$. Исследовались колебания, описываемые уравнением (5.3) в окрестности интегрального многообразия $\delta {\kern 1pt} * = 0$, $\delta {\kern 1pt} *{\kern 1pt} ' = 0$ при начальных данных $\delta (0) = {{10}^{{ - 7}}}$, $\delta {\kern 1pt} '(0) = 0$ и параметрах ${{c}_{1}} = 0$, ${{c}_{2}} = 0.1$. Результаты расчетов изображены на рис. 3.

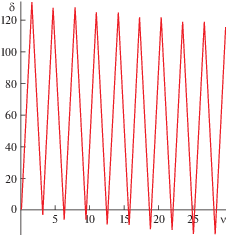
Отсюда следует, что в возмущенном движении стержень совершает в синодических осях приблизительно 21 оборот (130 рад) в одном направлении, потом 21 оборот – в противоположном и так далее, при этом величина прямого поворота со временем падает, что ведет к монотонному убыванию опорной кривой $\delta = {{F}_{1}}(\nu )$ проходящей через точки максимума решения $\delta (\nu ,l)$.

Случай больших $l$ не исследован.

Заключение. Исследование уравнений поступательно-вращательных движений стержня в круговой ограниченной задаче трех тел, когда основные тела имеют одинаковые массы и вращаются относительно собственного центра масс по круговым орбитам, показало, что существует семейство частных движений, когда центр масс стержня перемещается вдоль оси $Cz$, т.е. вдоль нормали к плоскости вращения основных тел. Сам стержень непрерывно вращается вокруг этой оси, сохраняя с ней неизменный угол $\pi {\text{/}}2$, при этом угловая скорость вращения стержня и скорость движения его центра масс вдоль оси $Cz$ взаимосвязаны. В частном случае возможны вращения стержня с постоянной угловой скоростью ${{\omega }_{0}}$, совпадающей с угловой скоростью орбитального движения основных тел, но при этом стержень постоянно ориентирован вдоль прямой, паралелльной отрезку, соединяющему основные тела, либо составляет с этим направлением угол, равный $\pi {\text{/}}2$; скорость движения его центра масс не зависит от ${{\omega }_{0}}$, но определяется текущей координатой $z$ (в силу наличия интеграла энергии). Возможны также неравномерные вращения стержня при $z(t) = 0$ (плоские движения стержня в плоскости вращения основных тел).

Особняком стоит частный вид движений стержня, когда он ориентирован вдоль оси $Cz$, перемещаясь вдоль неё поступательно, либо сохраняя абсолютное равновесие при $z(t) = 0$.

Показано, что на одномерных многообразиях колебания стержня подобны колебаниям материальной точки в круговой задаче Ситникова, либо подобны колебаниям математического маятника. В то же время, колебания стрежня малой длины вдоль двумерного многообразия “интегральный пропеллер” имеют сложный сингулярно-возмущенный характер в окрестности некоторых относительных равновесий: чатоты колебаний принимают большие значения при ограниченной амплитуде колебаний.