Прикладная математика и механика, 2021, T. 85, № 5, стр. 626-634

1. Введение. Поверхностные волновые движения в морской среде могут возникать как вследствие естественных причин, так и порождаться искусственными источниками возмущений [1–4]. Современное состояние результатов исследований линейных и нелинейных поверхностных волновых возмущений содержится в [5–10]. Основные результаты решений задач о генерации поверхностных волновых возмущений представляются в самой общей интегральной форме, и в этом случае полученные интегральные решения требуют разработки асимптотических методов их анализа, допускающих качественный анализ и проведение экспресс-оценок получаемых решений [11–16]. В ряде случаев первоначальное качественное представление об изучаемом круге волновых явлений можно получить на основе более простых асимптотических моделей и аналитических методов их исследования [1–4, 7, 8]. В этой связи необходимо отметить классические задачи гидродинамики о построении асимптотических решений, описывающих эволюцию поверхностных возмущений, возбуждаемых источниками различной природы в тяжелой однородной жидкости [1–4, 13, 15–17]. Модельные решения позволяют в дальнейшем получить представления поверхностных волновых полей с учетом изменчивости и нестационарности реальных природных сред. Ряд результатов асимптотического анализа линейных задач, описывающих различные режимы возбуждения и распространения поверхностных возмущений, лежит в основе активно развивающейся в настоящее время нелинейной теории генерации океанических волн экстремально большой амплитуды – волн-убийц [8–10]. Для мониторинга и предупреждения опасных природных волновых явлений в океане, в том числе обнаружения волн большой амплитуды, необходимо проводить оперативный анализ волновых явлений с помощью различных математических моделей. Одной из основных используемых моделей можно считать предположение о генерации волновых пакетов импульсным воздействием. Для проведения прогнозных расчетов необходимо подбирать параметры использованной модели так, чтобы приблизить смоделированную волновую систему к реально наблюдаемым, в том числе по фотоснимкам из космоса, волновым картинам [7, 8, 11, 12]. Таким образом, математические модели волновой генерации могут быть не только верифицированы, но и использованы для проведения прогнозных оценок.

Целью настоящей работы является построение равномерных и неравномерных асимптотик дальних полей поверхностных возмущений, возбуждаемых вспыхнувшим источником возмущений в тяжелой однородной жидкости конечной глубины.

2. Постановка задачи и интегральные формы решений. Рассматриваются волновые возмущения на поверхности идеальной тяжелой жидкости конечной глубины $H$, распространяющиеся от точечного импульсного источника возмущений, вспыхнувшего в момент $t = 0$. Источник находится на глубине ${{z}_{0}}$ (т.е. в точке $(0,0, - {{z}_{0}})$; $0 < {{z}_{0}} < H$) и мгновенно выбрасывает объем жидкости $Q$. Следуя [1–5, 7, 8] потенциал $\Phi (x,y,z,t)$ ($\nabla \Phi = (u,{v},w)$, $u,{v},w$ – компоненты возмущения вектора скорости поверхностных волн) в линейном приближении можно описать уравнением с соответствующим линеаризованным граничным условием на поверхности жидкости

где $\Delta = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}$, $g$ – ускорение свободного падения. Решение этой задачи получается путем применения преобразования Фурье по переменным $x,y,t$. Тогда возвышение свободной поверхности жидкости $\eta (x,y,t)$ можно представить в виде где ${{\Omega }^{2}}(k) = gkthkH$ – дисперсионное соотношение для поверхностных волн в слое конечной толщины [1–5, 7].

3. Неравномерные асимптотики решений. Далее будут исследоваться асимптотики интеграла (2.1), позволяющие эффективно рассчитывать амплитудно-фазовые характеристики волновых полей вдали от источника возмущений. Внутренний интеграл в (2.1) по переменной $\omega $ вычисляется с помощью теоремы о вычетах. Контур интегрирования необходимо сместить в область $\operatorname{Im} \omega > 0$, тогда замыкая его в нижнюю полуплоскость, учитывая полюса при $\omega = \pm \Omega (k)$, можно получить

Перейдем далее к полярным координатам: $\mu = k\cos \psi $, $\nu = k\sin \psi $, $x = r\cos \alpha $, $y = r\sin \alpha $, проинтегрируем по переменной $\psi $, в результате имеем

Заменим функцию Бесселя ${{J}_{0}}(kr)$ на ее асимптотику при $kr \gg 1$: ${{J}_{0}}(kr)$ ≈ $\cos (kr$ – –$\pi {\text{/4}})\sqrt {{\text{2/}}\pi kr} $ [18]. Получающийся в результате интеграл можно представить в виде

где $V = r{\text{/}}t$, функция $\Omega (k)$ продолжается при $k < 0$ нечетным образом, и $\sqrt k = i\sqrt {\left| k \right|} $ при $k < 0$. Далее рассматривается асимптотика интегралов ${{I}_{ \pm }}(r,t)$ при больших значениях $r,t$ и фиксированных значениях $V$, то есть в точке движущейся в радиальном направлении со скоростью $V$. Поскольку $\Omega (k)$ – монотонно возрастающая функция $k$, то фазовая функция интеграла ${{I}_{ + }}(r,t)$ не имеет стационарных точек на действительной оси $k$, потому этот интеграл экспоненциально мал при $t \to \infty $ (точнее, при $Vt{\text{/}}H \gg 1$). Фазовая функция интеграла ${{I}_{ - }}(r,t)$ имеет две стационарных точки на действительной оси: $ \pm {{k}_{0}}$, где ${{k}_{0}}$ – положительный корень уравнения: $q{\kern 1pt} '(k) = 0$, q(k) = = $kV - \Omega (k)$. Тогда главный член асимптотики возвышения $\eta (r,t)$ при $t \to \infty $, может быть вычислен по методу стационарной фазы

Асимптотика (3.2) становится непригодной при $V \to C$ ($C = \sqrt {gH} $ – максимальная групповая скорость поверхностных волн), то есть вблизи волнового фронта, где стационарные точки $ \pm {{k}_{0}}$ сливаются друг с другом, а также с точкой ветвления $k = 0$. Для построения локальных асимптотик с помощью подходящей замены следует свести исходный интеграл к эталонному интегралу. Выбор эталонного интеграла определяется распределением стационарных точек фазовой функции и особых точек подынтегральной функции в зависимости от параметров задачи. Построение асимптотики сводится к выбору соответствующей специальной функции, ее нескольких первых производных и к определению зависимости аргументов этой специальной функции, а также амплитудных и фазовых множителей [19–22]. Вычислим далее локальную асимптотику интеграла ${{I}_{ - }}(r,t)$ вблизи волнового фронта, то есть при $V \to C$, и, соответственно, при $r \approx Ct$. Очевидно, что основной вклад в локальную асимптотику дает окрестность значения $k = 0$, которая отвечает распространению длинных волн с максимальной групповой скоростью [1–4, 17]. При малых значениях $k$ функции $F(k)$, $q(k)$ допускают следующие разложения: $F(k)$ = $F{\kern 1pt} '(0)k$ + …, $q(k)$ = $q{\kern 1pt} '(0)k$ + $q{\kern 1pt} '''(0){{k}^{3}}{\text{/6}}$ + …, где $F{\kern 1pt} '(0)$ = = ${{(2\pi )}^{{ - 3/2}}}{{r}^{{ - 1/2}}}$, $q{\kern 1pt} '(0) = V - C$, $q{\kern 1pt} '''(0)$ = $\sqrt g {{H}^{{5/2}}}$. Тогда, аппроксимируя фазовую функцию $q(k)$ кубичным полиномом, $F(k)$ – линейной функцией, можно получить

Локальная асимптотика возвышения $\eta (r,t)$ при $t \to \infty $ в окрестности волнового фронта $r \approx Ct$ выражается через функцию Эйри и ее производную [20–22]

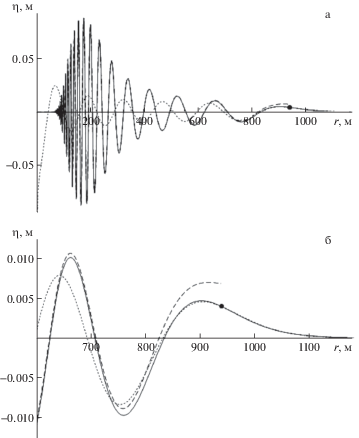
На рис. 1 изображены результаты расчетов по точным формулам (3.1) (сплошная линия), в приближении стационарной фазы (3.2) (штриховая линия), и по формуле (3.3) – локальная асимптотика (пунктирная линия), точкой отмечено положение волнового фронта. Для наглядности приведены результаты расчетов для двух пространственных масштабов. Полученные результаты показывают, что вне окрестности волнового фронта метод стационарной фазы позволяет точно описать поведение волнового поля. В окрестности волнового фронта локальная асимптотика практически совпадает с точным решением. Параметры расчетов были следующие: $Q = {{10}^{3}}$ м³, $t = 60$ с, $H = 25$ м, ${{z}_{0}} = 5$ м. Использованные в расчетах пространственно-временные параметры соответствуют возможным масштабам нелокальных источников возбуждения поверхностных волн в океане [5, 7, 8, 11, 12].

4. Равномерные асимптотики решений. Для построения равномерной асимптотики интеграла (3.1) выполним регулярную замену переменных $k = k(s)$, переводящую фазовую функцию $q(k)$ в новую функцию: $\tau (s)$ = $q(k(s))$ = $ - \sigma s + {{s}^{3}}{\text{/3}}$. При этом стационарные точки $ \pm {{k}_{0}}$ будут отвечать точкам ${{s}_{ \pm }} = \pm \sqrt \sigma $ соответственно. Из этого условия можно получить: $\sigma = {{( - 3q({{k}_{0}}){\text{/2}})}^{{2/3}}}$, в результате интеграл ${{I}_{ - }}(r,t)$ можно представить в виде

где $G(s) = F(k(s))\sqrt {s{\text{/}}k(s)} \frac{{dk}}{{ds}}$ – регулярная функция переменной $s$. Действительно, по построению функция $k = k(s)$ является нечетной регулярной функцией, принимающей положительные значения при $s > 0$. Поэтому $\frac{{dk}}{{ds}}$ – четная регулярная функция, $s{\text{/}}k(s)$ – четная регулярная функция, принимающая только положительные значения, $\sqrt {s{\text{/}}k(s)} $ – четная регулярная функция и, следовательно, $G(s)$ – регулярная функция, как произведение трех регулярных функций. Следуя общей схеме метода построения равномерных асимптотик (метода эталонных интегралов) функцию $G(s)$ представим в виде [20–22]: $G(s) = P(s) + R(s)$, $P(s) = a{{s}^{2}} + bs + c$, где $P(s)$ – интерполяционный многочлен Лагранжа для функции $G(s)$, построенный по точкам $ - \sqrt \sigma $, 0, $\sqrt \sigma $, $R(s) = s({{s}^{2}}$ – – $\sigma ){{R}_{1}}(s)$, где $\mathop R\nolimits_1 (s)$ – регулярная функция. В результате можно получить

Интеграл ${{I}_{0}}(r,t)$ вычисляется аналитически [19, 20]

где $\xi = - \sigma {{(t{\text{/2}})}^{{2/3}}}$. Для интеграла ${{I}_{1}}(r,t)$ справедлива оценка: ${{I}_{1}}(r,t)$ = $O({{I}_{0}}(r,t){\text{/}}t)$, так как этот интеграл интегрированием по частям можно привести к виду где ${{G}_{1}}(s)$ – регулярная функция. Таким образом ${{I}_{1}}(r,t)$ с точностью до множителя ${{t}^{{ - 1}}}$ того же вида, что интеграл ${{I}_{0}}(r,t)$. 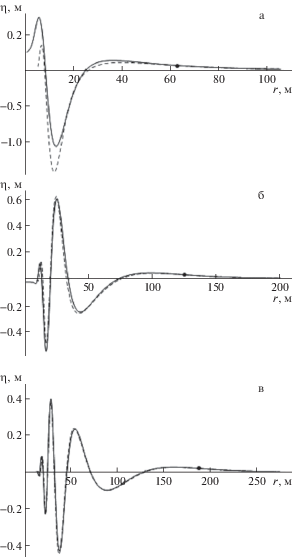Далее, в силу нечетности функции $F(k)$ можно получить: $a = c = 0$, $b$ = $G(\sqrt \sigma ){\text{/}}\sqrt \sigma $ = $F(\mathop k\nolimits_0 ){{({\text{2/}}{{k}_{0}}q{\kern 1pt} ''({{k}_{0}}))}^{{1/2}}}$. Тогда главный член равномерной (по параметру $V$) асимптотики $\eta (r,t)$ при $t \to \infty $ имеет вид

На рис. 2 представлены результаты расчетов по точным формулам (3.1) (сплошная линия), по формуле (4.1) – равномерная асимптотика (штриховая линия) для различных моментов времени, точкой отмечено положение волнового фронта.

Заключение. В работе изучены дальние поля поверхностных возмущений от вспыхнувшего локализованного источника в тяжелой жидкости конечной глубины. Построены равномерные и неравномерные асимптотические решения, выражающиеся через функцию Эйри и ее производную, позволяющие описывать амплитудно-фазовую структуру дальних полей поверхностных возмущений как вблизи, так и вдали от волнового фронта. Изучены характеристики возбуждаемых поверхностных возмущений в зависимости от основных параметров волновой генерации. Полученные асимптотики дальних полей поверхностных волновых возмущений дают возможность эффективно рассчитывать основные характеристики волновых полей, и, кроме того, качественно анализировать полученные решения, что важно для правильной постановки математических моделей волновой динамики поверхностных возмущений реальных природных сред. Использованное модельное представление вспыхнувшего источника возмущений может адекватно описать различные физически обоснованные механизмы генерации волновых пакетов, в том числе волн больших амплитуд [7, 9–12]. Полученные асимптотические результаты с различными значениями входящих в них физических параметров дают возможность в дальнейшем провести оценку основных характеристик начального возмущения.

Работа выполнена по темам государственного задания: В.В. Булатов, Ю.В. Владимиров (№ АААА-А20-120011690131-7), И.Ю. Владимиров (№ 0128-2021-0002), и частичной финансовой поддержке РФФИ проект № 20-01-00111А.