Прикладная математика и механика, 2021, T. 85, № 5, стр. 601-614

Ламинарное течение вязкой жидкости в начальном участке круглой трубы

Л. И. Казаков^1, *

¹ ФГУП НИИАЭ (Автоэлектроники)
Севастополь, Россия

Поступила в редакцию 21.01.2021
После доработки 07.07.2021
Принята к публикации 14.07.2021

DOI: 10.31857/S0032823521050052

Аннотация

Изложена приближенная теория стационарного осесимметричного ламинарного течения вязкой несжимаемой жидкости в начальном участке круглой трубы. Она дает расчетные значения разных физических характеристик устанавливающегося течения, совпадающие в пределах ±2% с известными ранее расчетными и экспериментальными данными. Вместо традиционного применения для всей длины начального участка уравнения Бернулли, в представленной работе для определения величины давления используется уравнение среднего по сечению трубы осевого градиента давления.

Ключевые слова: начальный участок, пограничный слой, ядро течения, закон Гагена–Пуазейля

1. Введение. Важная в научном и практическом отношениях проблема установления течения Пуазейля в трубах имеет более чем вековую историю. Первым задачу о движении вязкой жидкости в начальном участке круглой трубы приближенно решил в 1891 году Буссинеск. Ему удалось довольно точно найти (судя по [1], c. 232) длину начального участка $L = 0.2445a{{\operatorname{Re} }_{a}}$, где а – радиус трубы, Re_a – число Рейнольдса по радиусу. Затем задачу решали (также приближенно) Л. Шиллер и С.М. Тарг [1–3]. Большое значение имели экспериментальные исследования, прежде всего, самого Пуазейля (и его предшественника Гагена) [4], классические измерения Никурадзе [5], а также многочисленные и весьма тщательные измерения течения по капиллярам разных жидкостей при разных температурах [6]. В наше время, с развитием вычислительной техники пришла возможность выполнять математические эксперименты, т.е. решать задачи численно. В кратком, но емком обзоре исследований по обсуждаемой проблеме [7], отмечено неудовлетворительное состояние вопроса: так, длины начального участка, найденные разными авторами, отличаются в три раза; даже полученные численно длины разнятся более чем на 20%.

В отечественной литературе по гидравлике за 1956–2016 гг. – в монографиях, справочниках, учебниках, справочных и учебных пособиях, конспектах лекций – для длины L начального участка чаще всего приводят формулу Л. Шиллера, что, вообще говоря, неверно, поскольку она выведена в рамках теории, пригодной лишь для первой четверти начального участка, не дает необходимого асимптотического стремления с расстоянием относительной скорости по оси трубы к 2, что наглядно подтверждает рис. 3, где кривая Шиллера на некотором расстоянии упирается в уровень 2. Это расстояние и считают, по недоразумению, длиной начального участка. В мировой же литературе чаще ссылаются на Буссинеска, а в последнее время – на новые, более точные численные результаты. Так, в [7] для ${{\operatorname{Re} }_{a}} \gg 1$ найдено: $L = 0.2268a{{\operatorname{Re} }_{a}}$, что для ньютоновских жидкостей подтверждено в [8]. Близкое значение для Re_a > 100 (0.2248) получено ранее в [9]. Но в работе [10] аналогичный численный результат для Re_a > 250 (0.2181) на 4% меньше.

2. Нулевое приближение. Из уравнения Навье–Стокса и уравнения непрерывности при $\frac{\partial }{{\partial t}} = 0$, $\frac{\partial }{{\partial \varphi }} = 0$, ${{V}_{\varphi }} = 0$ имеем ([11], с. 76):

(2.1)

${{V}_{x}}\frac{{\partial {{V}_{x}}}}{{\partial x}} + {{V}_{r}}\frac{{\partial {{V}_{x}}}}{{\partial r}} = - \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} + \nu \left( {\frac{{{{\partial }^{2}}{{V}_{x}}}}{{\partial {{x}^{2}}}} + \frac{1}{r}\frac{{\partial {{V}_{x}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{V}_{x}}}}{{\partial {{r}^{2}}}}} \right)$

(2.2)

${{V}_{x}}\frac{{\partial {{V}_{r}}}}{{\partial x}} + {{V}_{r}}\frac{{\partial {{V}_{r}}}}{{\partial r}} = - \frac{1}{\rho }\frac{{\partial P}}{{\partial r}} + \nu \left( {\frac{{{{\partial }^{2}}{{V}_{r}}}}{{\partial {{x}^{2}}}} + \frac{1}{r}\frac{{\partial {{V}_{r}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{V}_{r}}}}{{\partial {{r}^{2}}}} - \frac{{{{V}_{r}}}}{{{{r}^{2}}}}} \right)$

(2.3)

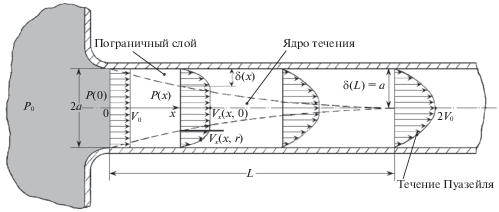
$\frac{{\partial \left( {r{{V}_{x}}} \right)}}{{\partial x}} + \frac{{\partial \left( {r{{V}_{r}}} \right)}}{{\partial r}} = 0$

Здесь ${{V}_{x}}$, ${{V}_{r}}$ – осевая и радиальная скорости частиц жидкости в потоке; $P = P\left( {x,r} \right)$ – давление; $\rho = \operatorname{const} $ – плотность жидкости; $\nu = \mu {\text{/}}\rho $ – ее кинематическая вязкость; $\mu $ – вязкость. На входе в трубу $\left( {x = 0} \right)$ скорость потока считаем однородной, т.е. ${{V}_{x}}(0,r)$ = ${{V}_{0}}$ = const. Далее благодаря вязкости жидкости на стенках трубы образуется и развивается пограничный слой, толщина которого $\delta (x)$ постепенно увеличивается от нуля $\delta \left( 0 \right) = 0$ до $\delta \left( L \right) = a$, где $L$ – длина начального участка, как показано на рис. 1. Центральные части сечений начального участка трубы заполнены внешним (по отношению к пограничному слою) потоком, называемым ядром течения с неизменной в каждом сечении скоростью. При $x \geqslant L$ в трубе устанавливается течение Пуазейля с параболическим профилем скоростей [11, с. 82]:

(2.4)

${{V}_{x}}\left( {x,r} \right) = 2{{V}_{0}}\left( {1 - \frac{{{{r}^{2}}}}{{{{a}^{2}}}}} \right)$

Рис. 1.

Схема ламинарного течения вязкой жидкости в начальном участке L круглой трубы.

Так обычно (вслед за Л. Прандтлем [5], c. 34) представляют качественную картину течения в начальном участке трубы.

С помощью уравнений (2.1) и (2.3) найдем среднее по площади $S = \pi {{a}^{2}}$ сечения трубы значение осевой компоненты градиента давления ([3], с. 358, (2.7)):

(2.5)

$\frac{{\overline {\partial P} }}{{\partial x}} = \frac{1}{S}\iint\limits_S {\frac{{\partial P}}{{\partial x}}}dS = - \frac{{4\rho }}{{{{a}^{2}}}}\int\limits_0^a {r{{V}_{x}}} \frac{{\partial {{V}_{x}}}}{{\partial x}}dr + {{\left. {\frac{{2\mu }}{a}\frac{{\partial {{V}_{x}}}}{{\partial r}}} \right|}_{{r = a}}}$

Выражение (2.5) – следствие уравнений движения, полученное без разделения течения на центральную область (ядро) и пограничный слой.

Обозначим через $V(x)$ скорость в ядре течения на оси трубы:

$V(x) = {{V}_{x}}(x,0),\quad 0 \leqslant x \leqslant L$

С учетом (2.4) имеем:

${{V}_{0}} \leqslant V(x) \leqslant 2{{V}_{0}}$

Поэтому вдоль трубы скорость заметно изменяется на расстоянии $x\sim L$, т.е.

(2.6)

$\frac{{\partial {{V}_{x}}}}{{\partial x}} \approx \frac{{V(x)}}{L} \approx \tfrac{{{{V}_{0}}}}{L} = \operatorname{const} $

В пределах пограничного слоя ${{\partial {{V}_{x}}} \mathord{\left/ {\vphantom {{\partial {{V}_{x}}} {\partial r}}} \right. \kern-0em} {\partial r}}$ ≈ ${{V(x)} \mathord{\left/ {\vphantom {{V(x)} {\delta (x)}}} \right. \kern-0em} {\delta (x)}}$. По опыту L обычно составляет десятки и более калибров трубы, и всегда можно считать

$\delta (x) \leqslant a \ll L$

Как далее станет ясно (см. (3.28)), второе неравенство эквивалентно требованию ${{\operatorname{Re} }_{a}} \gg 4$. Тогда из уравнения непрерывности (2.3) и уравнений (2.1), (2.2), соответственно, следует:

(2.7)

$~{{V}_{r}}\sim \frac{a}{L}V \ll V,\quad {\text{или}}\quad \frac{{{{V}_{r}}}}{{{{V}_{0}}}} \ll 1$

(2.8)

$\frac{{\left| {{{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial r}}} \right. \kern-0em} {\partial r}}} \right|}}{{\left| {{{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial x}}} \right. \kern-0em} {\partial x}}} \right|}} \sim \frac{\delta }{L} \ll 1,\quad {\text{или}}\quad \frac{{\partial P}}{{\partial x}} \approx \frac{{dP}}{{dx}},\quad P = P(x)$

Это дает возможность упростить исходную систему уравнений (2.1)–(2.3):

(2.9)

${{V}_{x}}\frac{{\partial {{V}_{x}}}}{{\partial x}} + {{V}_{r}}\frac{{\partial {{V}_{x}}}}{{\partial r}} + \frac{1}{\rho }\frac{{dP}}{{dx}} = \nu \left( {\frac{{{{\partial }^{2}}{{V}_{x}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{{\partial {{V}_{x}}}}{{\partial r}}} \right)$

(2.10)

$\frac{{\partial \left( {r{{V}_{x}}} \right)}}{{\partial x}} + \frac{{\partial \left( {r{{V}_{r}}} \right)}}{{\partial r}} = 0$

Согласно (2.7) и (2.8) зависимостью давления от радиальной переменной $r$ во всех сечениях вдоль трубы следует пренебречь и считать

(2.11)

$\frac{{\overline {\partial P} }}{{\partial x}} = \frac{{dP}}{{dx}}$

Для пограничного слоя удобно вместо $r$ ввести поперечную координату $y = a - r$. В качестве нулевого приближения представим осевую скорость ${{V}_{x}}\left( {x,r} \right)$ в виде

(2.12)

${{V}_{x}}\left( {x,y} \right) = V\left( x \right)f\left( \eta \right),\quad \eta = \frac{y}{{\delta \left( x \right)}},$

где профили скоростей во всех сечениях пограничного слоя определяет задаваемая подходящим образом функция $f\left( \eta \right)$, а функции $V(x)$ и $\delta (x)$ предстоит найти. Для слоя конечной толщины функция $f\left( \eta \right)$ должна удовлетворять условиям:

(2.13)

$f\left( 0 \right) = 0;\quad f\left( {\eta \geqslant 1} \right) = 1;\quad {{\lim }_{{\eta \to 1 - 0}}}\frac{{df}}{{d\eta }} = 0$

Эти условия вытекают из физической сути пограничного слоя.

Подставив (2.12) в (2.5), используя соотношения

(2.14)

$\begin{gathered} r = a - y,\quad dr = - dy,\quad \frac{\partial }{{\partial r}} = - \frac{\partial }{{\partial y}} \\ dy = \delta d\eta ,\quad \frac{\partial }{{\partial y}} = \frac{1}{\delta }\frac{\partial }{{\partial \eta }},\quad \frac{{\partial \eta }}{{\partial x}} = - \frac{{\delta {\kern 1pt} '}}{\delta }\eta \\ \end{gathered} $

(2.15)

$\frac{{\partial {{V}_{x}}}}{{\partial x}} = \frac{\partial }{{\partial x}}\left( {Vf} \right) = \frac{\nu }{{{{\delta }^{2}}}}\left( {\lambda f - \zeta \eta \frac{{\partial f}}{{\partial \eta }}} \right),$

где

(2.16)

$\lambda = \frac{{V{\kern 1pt} '{\kern 1pt} {{\delta }^{2}}}}{\nu }$

(2.17)

$\zeta = \frac{{V\delta \delta {\kern 1pt} '}}{\nu }$

и, учитывая (2.11), найдем:

(2.18)

$\frac{{dP}}{{dx}} = - \frac{{4\mu V}}{{a\delta }}\left\{ {\left( {\lambda + \frac{\zeta }{2}} \right)\int\limits_0^{{a \mathord{\left/ {\vphantom {a \delta }} \right. \kern-0em} \delta }} {{{f}^{2}}d\eta - \frac{\delta }{a}} \left( {\lambda + \zeta } \right){{{\int\limits_0^{{a \mathord{\left/ {\vphantom {a \delta }} \right. \kern-0em} \delta }} {\eta {{f}^{2}}d\eta + \frac{1}{2}\left. {\frac{{\partial f}}{{\partial \eta }}} \right|} }}_{{\eta = 0}}}} \right\}$

Параметры λ и ζ безразмерны. Штрих означает производную по x. Для любого профиля справедливо:

(2.19)

$\int\limits_0^{{a \mathord{\left/ {\vphantom {a \delta }} \right. \kern-0em} \delta }} {{{f}^{2}}} \left( \eta \right)d\eta = \frac{a}{\delta } - \alpha ,\quad \int\limits_0^{{a \mathord{\left/ {\vphantom {a \delta }} \right. \kern-0em} \delta }} {\eta {{f}^{2}}} d\eta = \frac{{{{a}^{2}}}}{{2{{\delta }^{2}}}} - \beta ,$

где $\alpha < 1$ и $\beta < 1$ – константы, зависящие от профиля $f\left( \eta \right)$. С учетом (2.19) выражение (2.18) можно представить в виде:

(2.20)

$\frac{{dP}}{{dx}} = - \rho VV{\kern 1pt} '\; - \frac{{6\mu V}}{{{{a}^{2}}}}R\left( x \right),$

где

(2.21)

$R\left( x \right) = \frac{1}{3}\left\{ {\lambda \left( {\frac{{{{a}^{2}}}}{{2{{\delta }^{2}}}} - 2\alpha \frac{a}{\delta } + 2\beta } \right) - \zeta \left( {\alpha \frac{a}{\delta } - 2\beta } \right) + \frac{a}{\delta }f{\kern 1pt} '\left( 0 \right)} \right\}$

В самом начале трубы пограничный слой на стенке весьма тонок, его влияние на течение пренебрежимо малó, и жидкость почти по всему сечению можно считать идеальной. Тогда из уравнения Бернулли ([11], с. 25, 37) $P + {{\rho {{V}^{2}}} \mathord{\left/ {\vphantom {{\rho {{V}^{2}}} 2}} \right. \kern-0em} 2}$ = const следует, что

(2.22)

${{\left. {\frac{{dP}}{{dx}}} \right|}_{{x = 0}}} = - \rho VV{\kern 1pt} '$

Л. Шиллер ([2], с. 58) предполагал, что “…падение давления в начальном участке происходит по уравнению Бернулли…”, т.е. считал для всего начального участка $0 < x < L$ справедливым уравнение (2.22), а не (2.20). По этой причине его “… теория очень хорошо передает распределение скоростей…” (([2], с. 62), ([5], с. 35)) лишь в первой четверти начального участка и дает заниженное вдвое значение его длины L (см. рис. 3).

Согласно (2.20) и (2.22) должно выполняться условие $\mathop {\lim }\limits_{x \to 0} R(x)$ = 0. За пределами начального участка трубы, где уже установилось течение Пуазейля, $\delta = a$, $\delta {\kern 1pt} ' = 0$, V_r = 0, $V = 2{{V}_{0}}$, $V{\kern 1pt} ' = 0$ и, следовательно, по (2.16) и (2.17) $\lambda = \zeta = 0$. Согласно (2.1), (2.4), (2.20), (2.21) здесь:

(2.23)

$\frac{{dP}}{{dx}} = - \frac{{8\mu {{V}_{0}}}}{{{{a}^{2}}}} = - \frac{{4\mu {{V}_{0}}f{\kern 1pt} '\left( 0 \right)}}{{{{a}^{2}}}}$

Отсюда следует, что функция $f\left( \eta \right)$ должна удовлетворять также условию

(2.24)

$f{\kern 1pt} '(0) = 2,\quad {\text{т}}{\text{.е}}{\text{.}}\quad f\left( \eta \right) \approx 2\eta ;\quad \eta \ll 1$

Условиям (2.13), (2.24) удовлетворяет параболический профиль (([5], с. 34), ([2], с. 58))

(2.25)

$f(\eta ) = \left\{ \begin{gathered} 2\eta - {{\eta }^{2}},\quad \eta \leqslant 1 \hfill \\ 1,\quad \eta \geqslant 1 \hfill \\ \end{gathered} \right.$

который примем за основу. Тогда из уравнения постоянства расхода Q жидкости

$Q = \pi {{a}^{2}}{{V}_{0}} = 2\pi \int\limits_{a - \delta (x)}^a {{{V}_{x}}} (x,r)rdr + \pi {{(a - \delta (x))}^{2}}V(x),$

подставив в него (2.12) и используя (2.14), найдем в нулевом приближении осевую скорость в ядре течения:

(2.26)

$V(x) = {{V}_{0}}(\varepsilon ) = \frac{{{{V}_{0}}}}{{1 - \frac{2}{3}\varepsilon + \frac{1}{6}{{\varepsilon }^{2}}}},$

где

(2.27)

$\varepsilon (x) = \delta (x){\text{/}}a$

относительная толщина пограничного слоя. Теперь на основании (2.12), (2.14), (2.25)–(2.27) осевая скорость по сечению трубы в нулевом приближении примет вид:

(2.28)

${{V}_{x}}(x,r) = \left\{ \begin{gathered} {{V}_{0}}(\varepsilon )\left( {2\eta - {{\eta }^{2}}} \right),\quad \eta \leqslant 1 \hfill \\ {{V}_{0}}(\varepsilon ),\quad 1 \leqslant \eta \leqslant \frac{1}{{\varepsilon (x)}} \hfill \\ \end{gathered} \right.$

где

(2.29)

$\eta (x,r) = \frac{1}{{\varepsilon (x)}}\left( {1 - \frac{r}{a}} \right)$

При $x > L$ будет $\varepsilon (x) = 1$ и (2.28) переходит в течение Пуазейля (2.4). Из (2.28) видно, что в нулевом приближении осевая скорость течения от параметров $\lambda $ (2.16) и $\zeta $ (2.17) не зависит. Можно установить, что эти параметры связаны соотношением:

(2.30)

$\lambda = \frac{\varepsilon }{V}\frac{{dV}}{{d\varepsilon }}\zeta $

Из (2.17) также найдем выражение для обратной $\varepsilon (x)$ функции:

(2.31)

$\frac{{\nu x(\varepsilon )}}{{{{a}^{2}}{{V}_{0}}}} = \int\limits_0^\varepsilon {\frac{{\varepsilon V(\varepsilon )}}{{\zeta (\varepsilon ){{V}_{0}}}}} d\varepsilon $

В нулевом приближении легко найти радиальные скорости течения. Из (2.10) и (2.14) следует:

(2.32)

$\left( {1 - \frac{y}{a}} \right){{V}_{r}}(x,y) = \int\limits_0^y {\left( {1 - \frac{y}{a}} \right)} \frac{{\partial {{V}_{x}}(x,y)}}{{\partial x}}dy$

Используя (2.15), (2.16), (2.25), найдем:

(2.33)

$\frac{{\partial {{V}_{x}}(x,r)}}{{\partial x}} = \left\{ \begin{gathered} V{\kern 1pt} '\left[ {2\eta \left( {1 - \frac{\zeta }{\lambda }} \right) - {{\eta }^{2}}\left( {1 - \frac{{2\zeta }}{\lambda }} \right)} \right],\quad \eta \leqslant 1 \hfill \\ V{\kern 1pt} ',\quad \eta \geqslant 1 \hfill \\ \end{gathered} \right.$

Подставив это в (2.32) с учетом (2.12), получим:

(2.34)

${{V}_{r}}\left( {x,r} \right) = \left\{ \begin{gathered} \frac{{\varepsilon {{a}^{2}}V{\kern 1pt} '}}{r}\left[ {\left( {1 - \frac{\zeta }{\lambda }} \right)\left( {{{\eta }^{2}} - \frac{{2\varepsilon }}{3}{{\eta }^{3}}} \right) - \left( {1 - \frac{{2\zeta }}{\lambda }} \right)\left( {\frac{{{{\eta }^{3}}}}{3} - \frac{{\varepsilon {{\eta }^{4}}}}{4}} \right)} \right],\quad \eta \leqslant 1 \hfill \\ - \frac{{V{\kern 1pt} '}}{2}r,\quad \eta \geqslant 1 \hfill \\ \end{gathered} \right.$

3. Первое приближение. Подставив (2.20) в уравнение (2.9), представим уравнения (2.9) и (2.10) соответственно в виде:

$\frac{{\partial (rV_{x}^{2})}}{{\partial x}} + \frac{{\partial (r{{V}_{r}}{{V}_{x}})}}{{\partial r}} - rVV{\kern 1pt} '\; - \frac{{6\nu V}}{{{{a}^{2}}}}rR(x) = \nu \frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{V}_{x}}}}{{\partial r}}} \right)$

$\frac{{\partial (r{{V}_{x}}V)}}{{\partial x}} + \frac{{\partial (r{{V}_{r}}V)}}{{\partial r}} - r{{V}_{x}}V{\kern 1pt} ' = 0$

Вычтем первое уравнение из второго и, проинтегрировав обе части полученного уравнения по $y$ от $y = 0$ до $y$ с учетом (2.14), найдем:

(3.1)

$\begin{gathered} \frac{\nu }{V}\left( {1 - \frac{y}{a}} \right)\frac{\partial }{{\partial y}}\left( {\frac{{{{V}_{x}}}}{V}} \right) - \frac{\tau }{{\rho {{V}^{2}}}} = - \frac{{V{\kern 1pt} '}}{V}\left[ {2\delta {\text{*}}{\kern 1pt} {\text{*}}(y) + \delta {\text{*}}(y)} \right] - \int\limits_0^y {\left( {1 - \frac{y}{a}} \right)} \frac{\partial }{{\partial x}}\left[ {\frac{{{{V}_{x}}}}{V}\left( {1 - \frac{{{{V}_{x}}}}{V}} \right)} \right]dy + \\ + \;\frac{1}{V}\left( {1 - \frac{y}{a}} \right){{V}_{r}}(y)\left( {1 - \frac{{{{V}_{x}}}}{V}} \right) - \frac{{6\nu }}{{{{a}^{2}}V}}R(x)\left( {y - \frac{{{{y}^{2}}}}{{2a}}} \right), \\ \end{gathered} $

где обозначено:

(3.2)

$\tau = {{\left. {\mu \frac{{\partial {{V}_{x}}}}{{\partial y}}} \right|}_{{y = 0}}}$

– напряжение трения на стенке трубы,

(3.3)

$\delta {\text{*}}(y) = \int\limits_0^y {\left( {1 - \frac{{{{V}_{x}}}}{V}} \right)} \left( {1 - \frac{y}{a}} \right)dy$

(3.4)

$\delta {\text{*}}{\kern 1pt} {\text{*}}(y) = \int\limits_0^y {\frac{{{{V}_{x}}}}{V}\left( {1 - \frac{{{{V}_{x}}}}{V}} \right)} \left( {1 - \frac{y}{a}} \right)dy$

При $y \to a$ должно быть: ${{V}_{x}} \to V$, $\delta {\text{*}}(y) \to \delta {\text{*}}$, $\delta {\text{*}}{\kern 1pt} {\text{*}}(y) \to \delta {\text{*}}{\kern 1pt} {\text{*}}$, где $\delta {\text{*}} = \delta {\text{*}}(a)$ – “толщина вытеснения”, $\delta {\text{*}}{\kern 1pt} {\text{*}} = \delta {\text{*}}{\kern 1pt} {\text{*}}(a)$ – “толщина потери импульса” ([12], с. 59, 60). Тогда (3.1) перейдет в “уравнение импульсов” ([12], с. 89)

(3.5)

$\int\limits_0^a {\left( {1 - \frac{y}{a}} \right)} \frac{\partial }{{\partial x}}\left[ {\frac{{{{V}_{x}}}}{V}\left( {1 - \frac{{{{V}_{x}}}}{V}} \right)} \right]dy + \frac{{V{\kern 1pt} '}}{V}\left[ {2\delta {\text{*}}{\kern 1pt} {\text{*}} + \delta {\text{*}}} \right] = \frac{\tau }{{\rho {{V}^{2}}}} - \frac{{3\nu }}{{aV}}R(x)$

При $x \to \infty $ согласно (2.21) имеем: $\frac{\partial }{{\partial x}} = 0$, $V{\kern 1pt} ' = 0$, $\lambda = \zeta = 0$, $R(\infty )$ = ${{\left. {\frac{a}{{3\delta }}\frac{{df}}{{d\eta }}} \right|}_{{\eta = 0}}}$. Тогда из (3.5) следует: $\tau $ = $\frac{{3\mu V}}{a}R(\infty )$ = ${{\left. {\frac{{\mu V}}{\delta }\frac{{df}}{{d\eta }}} \right|}_{{\eta = 0}}}$ = ${{\left. {\mu \frac{{\partial {{V}_{x}}}}{{\partial y}}} \right|}_{{y = 0}}}$ ч.т.д.

Исключим из уравнения (3.1) величины $\tau $ и ${{V}_{r}}(y)$ с помощью соотношений (3.5) и (2.32) и учтем (3.3), (3.4). Проинтегрировав обе части полученного уравнения по $y$, найдем:

$\left( {1 - \tfrac{y}{a}} \right)\tfrac{{{{V}_{x}}(x,y)}}{{V(x)}} = - \frac{1}{a}\int\limits_0^y {\tfrac{{{{V}_{x}}}}{V}} dy + $

$\begin{gathered} + \;\frac{{V{\kern 1pt} '}}{\nu }\left\{ {2\int\limits_0^y {\int\limits_y^a {\frac{{{{V}_{x}}}}{V}\left( {1 - \frac{{{{V}_{x}}}}{V}} \right)\left( {1 - \tfrac{y}{a}} \right)dy} } dy + \int\limits_0^y {\int\limits_y^a {\left( {1 - \frac{{{{V}_{x}}}}{V}} \right)\left( {1 - \tfrac{y}{a}} \right)dy} dy} } \right\} + \\ + \;\frac{V}{\nu }\int\limits_0^y {\int\limits_y^a {\left( {1 - \tfrac{y}{a}} \right)\frac{\partial }{{\partial x}}} \left[ {\frac{{{{V}_{x}}}}{V}\left( {1 - \frac{{{{V}_{x}}}}{V}} \right)} \right]dy} dy + \\ \end{gathered} $

(3.6)

$ + \;\frac{1}{\nu }\int\limits_0^y {\left\{ {\left( {1 - \frac{{{{V}_{x}}}}{V}} \right)\int\limits_0^y {\left( {1 - \tfrac{y}{a}} \right)\frac{{d{{V}_{x}}}}{{dx}}dy} } \right\}} dy + R(x)\left( {1 - \frac{{{{r}^{3}}}}{{{{a}^{3}}}}} \right)$

Первое приближение к искомому профилю скорости $V{}_{x}(x,y)$ получим, подставив в правую часть (3.6) функцию нулевого приближения (2.12) и перейдя к переменным (2.29), (2.27) $\eta $ и $\varepsilon $:

$\left( {1 - \tfrac{y}{a}} \right)\frac{{{{V}_{x}}(x,y)}}{{V(x)}} = \left( {2\lambda + \zeta } \right)\int\limits_0^\eta {\int\limits_\eta ^{{{\varepsilon }^{{ - 1}}}} {\left( {1 - {{f}^{2}}} \right)\left( {1 - \varepsilon \eta } \right)d\eta } d\eta } + $

$ + \;\left( {\lambda + \zeta } \right)\int\limits_0^\eta {\left\{ {\left( {1 - f} \right)\int\limits_0^\eta {f\left( {1 - \varepsilon \eta } \right)d\eta - \int\limits_\eta ^{{{\varepsilon }^{{ - 1}}}} {\left( {1 - f} \right)\left( {1 - \varepsilon \eta } \right)d\eta } } } \right\}} d\eta - $

(3.7)

$ - \;\varepsilon \int\limits_0^\eta {\left\{ {f + \zeta \int\limits_\eta ^{{1 \mathord{\left/ {\vphantom {1 \varepsilon }} \right. \kern-0em} \varepsilon }} {\eta f\left( {1 - f} \right)d\eta + \left( {1 - f} \right)\zeta \int\limits_0^\eta {\eta fd\eta } } } \right\}} d\eta + R(\varepsilon )\left( {1 - {{{\left( {1 - \tfrac{y}{a}} \right)}}^{3}}} \right)$

Последнее слагаемое здесь имеет “кубический” профиль $\left( {1 - {{r}^{3}}{\text{/}}{{a}^{3}}} \right)$, который по мере роста этого слагаемого с ростом $x$ будет несколько “скруглять” края плоской части ядра течения, придавая пограничному слою асимптотические черты так, что для первого приближения в отличие от (2.13)

$\mathop {\lim }\limits_{\eta \to 1 - 0} \frac{\partial }{{\partial \eta }}\left( {\frac{{{{V}_{x}}}}{V}} \right) \ne 0$

Поэтому только на оси трубы ($r = 0$, $y = a$) будет верным условие

$\frac{{V(x,0)}}{{V(x)}} = 1,$

как и в случае асимптотического пограничного слоя, например, при начальном профиле Блазиуса для пластины ([12], с. 29).

Подставив в (3.7) исходный параболический профиль (2.25), вычислив для него по формулам (2.19) входящие в $R(x)$ (2.21) постоянные

(3.8)

$\alpha = \frac{7}{{15}},\quad \beta = \frac{2}{{15}}$

и по результатам интегрирования, найдем первое приближение для функции ${{V}_{x}}(x,r)$ в переменных

(3.9)

$\eta = \frac{1}{{\varepsilon (x)}}\left( {1 - \frac{r}{a}} \right);\quad \varepsilon (x) = \frac{{\delta (x)}}{a}$

(3.10)

$\frac{{{{V}_{x}}(x,r)}}{{{{V}_{0}}}}\frac{r}{a} = {\rm Z}(\varepsilon )\left[ {F\left( {\varepsilon ,\eta } \right) + R(\varepsilon )\left( {1 - \frac{{{{r}^{3}}}}{{{{a}^{3}}}}} \right)} \right],$

где

(3.11)

${\text{{\rm Z}}}(\varepsilon ) = \frac{{V(\varepsilon )}}{{{{V}_{0}}}}$

$F(\varepsilon ,\eta ) = \left( {1 - \frac{r}{a}} \right)\left[ { - \eta + \frac{{{{\eta }^{2}}}}{3}} \right. + \frac{{\lambda (\varepsilon )}}{\varepsilon }\left\{ {\frac{3}{5}} \right. - \frac{\eta }{2} + \frac{{{{\eta }^{3}}}}{6} - \frac{{{{\eta }^{4}}}}{{15}} + \frac{{{{\eta }^{5}}}}{{90}} - $

(3.12)

$\begin{gathered} - \;\left. {\varepsilon \left( {\frac{{11}}{{60}} - \frac{{{{\eta }^{2}}}}{6} + \frac{2}{{15}}{{\eta }^{4}} - \frac{{13}}{{180}}{{\eta }^{5}} + \frac{1}{{84}}{{\eta }^{6}}} \right)} \right\} + \frac{{\zeta (\varepsilon )}}{\varepsilon }\left\{ {\frac{2}{{15}}} \right. - \frac{{{{\eta }^{3}}}}{6} + \\ + \;\frac{2}{{15}}{{\eta }^{4}} - \frac{1}{{45}}{{\eta }^{5}} - \left. {\varepsilon \left. {\left( {\frac{1}{{10}} - \frac{2}{{15}}{{\eta }^{4}} + \frac{{11}}{{90}}{{\eta }^{5}} - \frac{1}{{42}}{{\eta }^{6}}} \right)} \right\}} \right] \\ 0 \leqslant \eta \leqslant 1,\quad \varepsilon \geqslant 1 - \frac{r}{a} \\ \end{gathered} $

(3.13)

$\frac{{{{V}_{x}}(x,r)}}{{{{V}_{0}}}}\frac{r}{a} = {\rm Z}(\varepsilon )\left[ {\frac{r}{a} - 1 + \varepsilon + F(\varepsilon ,1) + R(\varepsilon )\left( {1 - \frac{{{{r}^{3}}}}{{{{a}^{3}}}}} \right)} \right];\quad 1 \leqslant \eta \leqslant \frac{1}{\varepsilon },\quad \varepsilon \leqslant 1 - \frac{r}{a}$

При $r = 0$ $\left( {\eta = {{\varepsilon }^{{ - 1}}} \geqslant 1} \right)$ из (3.13) и (3.12) следует:

(3.14)

$R(\varepsilon ) = 1 - \varepsilon - F(\varepsilon ,1) = 1 - \frac{\varepsilon }{3} - \lambda (\varepsilon )\left( {\frac{{19}}{{90}} - \frac{{113}}{{1260}}\varepsilon } \right) - \zeta (\varepsilon )\left( {\frac{7}{{90}} - \frac{{41}}{{630}}\varepsilon } \right)$

Выразив в (3.13) $F(\varepsilon ,1)$ через $R(\varepsilon )$ из (3.14), получим:

(3.15)

$\frac{{{{V}_{x}}(x,r)}}{{{{V}_{0}}}} = {\rm Z}(\varepsilon )\left[ {1 - R(\varepsilon )\frac{{{{r}^{2}}}}{{{{a}^{2}}}}} \right];\quad \varepsilon \leqslant 1 - \frac{r}{a}$

Приравняв (3.14) и (2.21) с учетом (2.24), (3.8), найдем соотношение между параметрами $\lambda (\varepsilon )$ и $\zeta (\varepsilon )$, соответствующее первому приближению:

(3.16)

$\lambda \left( {1 - \frac{{28}}{{15}}\varepsilon + \frac{9}{5}{{\varepsilon }^{2}} - \frac{{113}}{{210}}{{\varepsilon }^{3}}} \right) - \zeta \left( {\frac{{14}}{{15}}\varepsilon - {{\varepsilon }^{2}} + \frac{{41}}{{105}}{{\varepsilon }^{3}}} \right) = - 4\varepsilon + 6{{\varepsilon }^{2}} - 2{{\varepsilon }^{3}}$

Используя выражения (3.10)–(3.14), (3.9), (2.14), запишем уравнение постоянства расхода жидкости для первого приближения осевой скорости:

$Q = \pi {{a}^{2}}{{V}_{0}} = 2\pi {{a}^{2}}V(\varepsilon )\left\{ {\frac{1}{2}{{{\left( {1 - \varepsilon } \right)}}^{2}} + \left( {\varepsilon - \frac{1}{4}} \right)R(\varepsilon ) + \varepsilon \int\limits_0^1 {F(\varepsilon ,\eta )d\eta } } \right\}$

Вычисляя по (3.12)

$\int\limits_0^1 {F(\varepsilon ,\eta )d\eta = - \frac{\varepsilon }{4}} + \lambda \left( {\frac{{11}}{{70}} - \frac{{71}}{{1120}}\varepsilon } \right) + \zeta \left( {\frac{{11}}{{210}} - \frac{{71}}{{1680}}\varepsilon } \right)$

и учитывая (3.14), получим:

(3.17)

$V(\varepsilon ) = \frac{{2{{V}_{0}}}}{{1 + \frac{\varepsilon }{3}(1 - \varepsilon ) + \lambda \left( {\frac{{19}}{{90}} - \frac{{11}}{{36}}\varepsilon + \frac{{53}}{{504}}{{\varepsilon }^{2}}} \right) + \zeta \left( {\frac{7}{{90}} - \frac{1}{6}\varepsilon + \frac{{23}}{{252}}{{\varepsilon }^{2}}} \right)}}$

Найденные соотношения первого приближения (3.16), (3.17) и точное выражение (2.30) составляют систему уравнений для определения неизвестных функций $V(\varepsilon )$ (или ${\rm Z}(\varepsilon )$ (3.11)), $\lambda (\varepsilon )$, $\zeta (\varepsilon )$. Исключив из нее $\lambda $ и $\zeta $, для ${\rm Z}(\varepsilon )$ получим дифференциальное уравнение

(3.18)

${\text{{\rm Z}}}{\kern 1pt} '(\varepsilon ) = - \frac{{\text{{\rm Z}}}}{\varepsilon }\frac{{{{a}_{{22}}}{{b}_{1}} - {{a}_{{12}}}\left( {\frac{2}{{\text{{\rm Z}}}} - 1 - \frac{\varepsilon }{3}\left( {1 - \varepsilon } \right)} \right)}}{{{{a}_{{21}}}{{b}_{1}} - {{a}_{{11}}}\left( {\frac{2}{{\text{{\rm Z}}}} - 1 - \frac{\varepsilon }{3}\left( {1 - \varepsilon } \right)} \right)}},$

где ${{b}_{1}}(\varepsilon )$, ${{a}_{{ik}}}(\varepsilon )$ – известные полиномы. Уравнение (3.18) – уравнение Абеля второго рода ([13], с. 48, п. 4.11(б)). Его приближенное решение найдем сначала, для граничных условий ${\text{Z}}(0) = 1$, ${\rm Z}(1) = 2$, а затем вычисляя по (3.18) наклоны интегральной кривой ${\rm Z}(\varepsilon )$ в начальной и конечной точках и применяя метод последовательных приближений [13, с. 23], найдем:

(3.19)

${\rm Z}(\varepsilon ) = 1 + \frac{{28}}{{45}}\varepsilon + \frac{{64}}{{195}}{{\varepsilon }^{2}} + \frac{{71}}{{585}}{{\varepsilon }^{3}} - \frac{{14}}{{195}}{{\varepsilon }^{4}}$

(3.20)

${\rm Z}{\kern 1pt} '(\varepsilon ) = \frac{{28}}{{45}} + \frac{{128}}{{195}}\varepsilon + \frac{{71}}{{195}}{{\varepsilon }^{2}} - \frac{{56}}{{195}}{{\varepsilon }^{3}}$

Приближенное решение (3.19) уравнения (3.18) хорошо удовлетворяет последнему: значения ${{{\rm Z}{\kern 1pt} '(\varepsilon )} \mathord{\left/ {\vphantom {{{\rm Z}{\kern 1pt} '(\varepsilon )} {{\rm Z}(\varepsilon )}}} \right. \kern-0em} {{\rm Z}(\varepsilon )}}$, вычисленные по (3.19), (3.20), а также при подстановке функции (3.19) в правую часть уравнения (3.18), разнятся менее чем на 0.27%.

Зная ${\rm Z}(\varepsilon )$ и ${\rm Z}{\kern 1pt} '(\varepsilon )$, найдем параметры $\lambda (\varepsilon )$ и $\zeta (\varepsilon )$:

(3.21)

$\lambda (\varepsilon ) = \frac{{90\varepsilon }}{{7S(\varepsilon )}}\left( {1 - \frac{3}{2}\varepsilon + \frac{{{{\varepsilon }^{2}}}}{2}} \right){\text{Z}}{\kern 1pt} '(\varepsilon )$

(3.22)

$\zeta (\varepsilon ) = \frac{{90}}{{7S(\varepsilon )}}\left( {1 - \frac{3}{2}\varepsilon + \frac{{{{\varepsilon }^{2}}}}{2}} \right){\rm Z}(\varepsilon ),$

где

(3.23)

$S(\varepsilon ) = 1 + \frac{{251}}{{910}}\varepsilon - \frac{{1886}}{{3185}}{{\varepsilon }^{2}} + \frac{{10}}{{21}}{{\varepsilon }^{3}} - \frac{{9198}}{{3185}}{{\varepsilon }^{4}} + \frac{{20443}}{{7644}}{{\varepsilon }^{5}} - \frac{{267}}{{455}}{{\varepsilon }^{6}}$

Отсюда при $\varepsilon \ll 1$ следует:

(3.24)

$\lambda (\varepsilon ) \approx 8\varepsilon ,\quad \zeta (\varepsilon ) \approx \frac{{90}}{7};\quad \lambda (1) = \zeta (1) = 0$

Подставив полученные разложения в (2.31), после интегрирования найдем:

(3.25)

$\begin{gathered} \frac{{\nu x(\varepsilon )}}{{{{a}^{2}}{{V}_{0}}}} = \frac{{x(\varepsilon )}}{{a{{{\operatorname{Re} }}_{a}}}} = \frac{1}{{100}}\left\{ {\frac{{24\,301}}{{351}}} \right.\varepsilon + \frac{{4633}}{{234}}{{\varepsilon }^{2}} + \frac{{727}}{{81}}{{\varepsilon }^{3}} + \frac{{1007}}{{252}}{{\varepsilon }^{4}} + \\ + \;\frac{{2687}}{{945}}{{\varepsilon }^{5}} - \frac{{178}}{{117}}{{\varepsilon }^{6}} + \frac{{52\,528}}{{351}}\ln \left( {1 - \frac{\varepsilon }{2}} \right) - \left. {\frac{{151}}{{27}}\ln \left( {1 - \varepsilon } \right)} \right\}, \\ \end{gathered} $

где

(3.26)

${{\operatorname{Re} }_{a}} = \frac{{{{V}_{0}}a}}{\nu }$

– число Рейнольдса.

В (3.25) разложение правой части начинается с квадратичного члена, как это и должно быть в силу того, что при $\varepsilon \ll 1$

$\frac{{\nu x(\varepsilon )}}{{{{a}^{2}}{{V}_{0}}}} \approx \frac{7}{{90}}\int\limits_0^\varepsilon {\varepsilon d\varepsilon = \frac{{7{{\varepsilon }^{2}}}}{{180}}} = \frac{7}{{180}}\frac{{{{\delta }^{2}}}}{{{{a}^{2}}}}$

Отсюда для самого начала трубы имеем:

(3.27)

$\delta \left( x \right) = 5.071\sqrt {\frac{{\nu x}}{{{{V}_{0}}}}} ,$

что совпадает с оценкой толщины пограничного слоя на пластине в задаче Блазиуса ([12], с. 32). При $x \to \infty $ из (3.25) следует:

$\delta \left( x \right) \approx a\left[ {1 - \exp \left( { - 0.08 - \frac{{17.88}}{{{{{\operatorname{Re} }}_{a}}}}\frac{x}{a}} \right)} \right]$

Графическое представление относительной толщины пограничного слоя вдоль начального участка (пунктир на рис. 1) дает рис. 2, где показана зависимость $\varepsilon (s)$, $s = {x \mathord{\left/ {\vphantom {x {\left( {a{{{\operatorname{Re} }}_{a}}} \right)}}} \right. \kern-0em} {\left( {a{{{\operatorname{Re} }}_{a}}} \right)}}$, соответствующая уравнению (3.25).

Рис. 2.

Относительная толщина $\varepsilon (s)$ пограничного слоя в начальном участке трубы, $s = {x \mathord{\left/ {\vphantom {x {\left( {a{{{\operatorname{Re} }}_{a}}} \right)}}} \right. \kern-0em} {\left( {a{{{\operatorname{Re} }}_{a}}} \right)}}$.

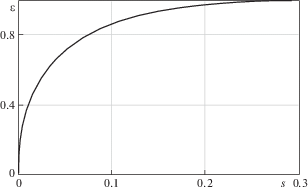
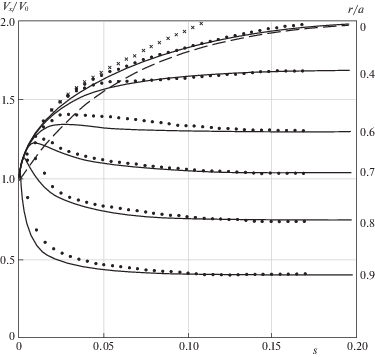
Рис. 3.

Зависимость осевых скоростей ${{{{V}_{x}}\left( {x,r} \right)} \mathord{\left/ {\vphantom {{{{V}_{x}}\left( {x,r} \right)} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$ на начальном участке круглой трубы при ламинарном течении вязкой жидкости от $s = {x \mathord{\left/ {\vphantom {x {\left( {a{{{\operatorname{Re} }}_{a}}} \right)}}} \right. \kern-0em} {\left( {a{{{\operatorname{Re} }}_{a}}} \right)}}$: • • • • – экспериментальные кривые Никурадзе; – – – теория Буссинеска; ×××× – теория Шиллера; $ - - - $ – расчет по формулам (3.10), (3.15) с учетом (3.14), (3.19)–(3.23).

Длину $L$ начального участка трубы, следуя Прандтлю ([1], с. 225), определим условием $V(L)$ = $0.99 \cdot 2{{V}_{0}}.$ Согласно (3.19) этому соответствует значение $\varepsilon (L) = 0.9852$. Тогда по (3.25) найдем:

(3.28)

$L = 0.2305a{{\operatorname{Re} }_{a}}$

Эта величина меньше, чем дает формула Буссинеска $L = 0.26a{{\operatorname{Re} }_{a}}$ (([5], с. 36), ([14], с. 164)), заметно больше расчетных значений Л. Шиллера ($L = 0.115a{{\operatorname{Re} }_{a}}$, ([2], с. 60)) и С.М. Тарга ($L = 0.16a{{\operatorname{Re} }_{a}}$, ([1], с. 248)) и почти совпадает с численным результатом работы [7] $L = 0.2268a{{\operatorname{Re} }_{a}}$.

Теперь, зная $V\left( \varepsilon \right)$, $\lambda \left( \varepsilon \right)$ и $\zeta \left( \varepsilon \right)$, можем вычислить по формулам первого приближения (3.9)–(3.15) осевую скорость жидкости в сечениях трубы. При этом найдем, что, поскольку при $x > L$ $\varepsilon \to 1$, $\lambda \left( \varepsilon \right) \to 0$, $\zeta \left( \varepsilon \right) \to 0$, $\eta \to 1 - \frac{r}{a}$, $V\left( \varepsilon \right)$ → $2{{V}_{0}}$, то

${{V}_{x}}\left( {\infty ,r} \right) = \frac{{2{{V}_{0}}}}{{{r \mathord{\left/ {\vphantom {r a}} \right. \kern-0em} a}}}\left[ { - {{{\left( {1 - \frac{r}{a}} \right)}}^{2}}\left( {\frac{2}{3} + \frac{r}{{3a}}} \right) + \frac{2}{3}\left( {1 - \frac{{{{r}^{3}}}}{{{{a}^{3}}}}} \right)} \right] = 2{{V}_{0}}\left( {1 - \frac{{{{r}^{2}}}}{{{{a}^{2}}}}} \right),$

т.е. на больших расстояниях x > L течение переходит в течение Пуазейля.

Далее вычислим распределение удельного трения жидкости о стенки начального участка трубы. Согласно (3.2), (2.14), (3.9)–(3.12), (3.14)

$\tau = \frac{{\mu V\left( \varepsilon \right)}}{{a\varepsilon }}\left\{ {3\varepsilon - {{\varepsilon }^{2}} + \lambda \left( \varepsilon \right)\left( {\frac{3}{5} - \frac{{49}}{{60}}\varepsilon + \frac{{113}}{{420}}{{\varepsilon }^{2}}} \right) + \zeta \left( \varepsilon \right)\left( {\frac{2}{{15}} - \frac{1}{3}\varepsilon + \frac{{41}}{{210}}{{\varepsilon }^{2}}} \right)} \right\}$

При $\varepsilon \ll 1$, учитывая (3.24) и (3.27), получим:

$\tau = \frac{{12}}{7}\frac{{\mu {{V}_{0}}}}{{\delta (x)}} = 0.3381\sqrt {\frac{{\rho \mu V_{0}^{3}}}{x}} ,$

что лишь на 1.8% превышает результат Блазиуса для пластины ([12], с. 29). При $\varepsilon \to 1$

$\tau = \frac{{4\mu {{V}_{0}}}}{a},$

как и должно быть для течения Пуазейля.

Рисунок 3 демонстрирует степень соответствия расчета по первому приближению (3.10), (3.15) относительных осевых скоростей ${{{{V}_{x}}(x,r)} \mathord{\left/ {\vphantom {{{{V}_{x}}(x,r)} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$ результатам измерений ([5], с. 36, рис. 13). Совпадение расчета с экспериментом в начале трубы не очень хорошее, что, видимо, обусловлено наличием “закругления” на входе в трубу, обеспечивающего ламинарность течения, но не учитываемого всеми известными теориями, однако, в дальнейшем расчетные и экспериментальные кривые асимптотически сливаются. Показаны также теоретические кривые Буссинеска и Шиллера установления с расстоянием скорости жидкости на оси трубы.

На рис. 4 приведено сравнение рассчитанных по (3.10), (3.15) кривых ${{{{V}_{x}}(x,r)} \mathord{\left/ {\vphantom {{{{V}_{x}}(x,r)} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$ с результатами численных расчетов, взятыми из работ [10, 14]. Почти все расчетные точки этих работ точно ложатся на соответствующие приближенные кривые. На рис. 5, 6 показано сравнение ${{{{V}_{x}}(x,r)} \mathord{\left/ {\vphantom {{{{V}_{x}}(x,r)} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$ с численными данными работы [10] для малых значений аргумента s.

Рис. 4.

Сравнение приближенных кривых ${{{{V}_{x}}\left( {x,r} \right)} \mathord{\left/ {\vphantom {{{{V}_{x}}\left( {x,r} \right)} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$ с численными расчетами: $ - - - $ – расчет по формулам (3.10), (3.15); $ \bullet $ – данные работы [10]; × – данные работы [14].

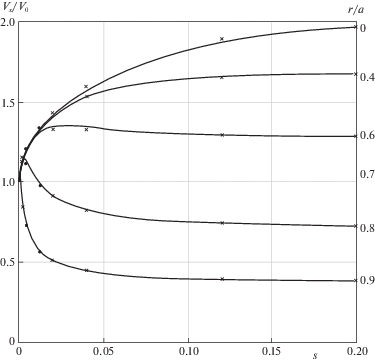
Рис. 5.

Сравнение приближенных кривых ${{{{V}_{x}}\left( {x,r} \right)} \mathord{\left/ {\vphantom {{{{V}_{x}}\left( {x,r} \right)} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$ с точными данными работы [10] при малых аргументах s для r/a = 0 ($\bigcirc $) и r/a = 0.8 ($ \bullet $).

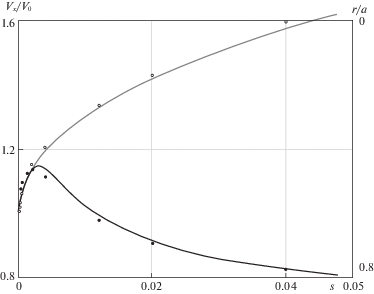
Рис. 6.

Сравнение приближенных кривых ${{{{V}_{x}}\left( {x,r} \right)} \mathord{\left/ {\vphantom {{{{V}_{x}}\left( {x,r} \right)} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$ с точными данными работы [10] при малых аргументах s для r/a = 0 ($\bigcirc $) и r/a = 0.9 ($ \bullet $).

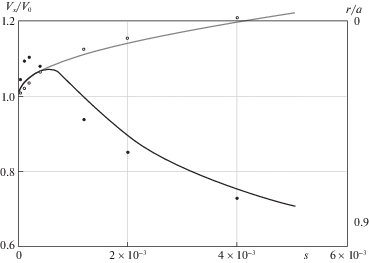
Заключение. Развита теория установления течения Гагена–Пуазейля в начальном участке круглой трубы. Найденная длина начального участка L = 0.2305aRe_a [15] близка к современному значению, полученному численным методом [7]. Теория хорошо объясняет известные экспериментальные результаты И. Никурадзе [5] и подтверждается численными данными работ [10, 14].

Список литературы

Тарг С.М. Основные задачи теории ламинарных течений. М.; Л.: ГИТТЛ, 1951. 420 с.
Шиллер Л. Движение жидкости в трубах М.; Л.: ОНТИ НКТП СССР, 1936. 230 с.
Слёзкин Н.А. Динамика вязкой несжимаемой жидкости. М.: ГИТТЛ, 1955. 519 с.
Воларович М.П. Работы Пуазейля о течении жидкости в трубах // Изв. АН СССР. Серия физ. 1947. Т. 11. № 1.
Прандтль Л., Титьенс О. Гидро- и аэромеханика. Т. 2 М.; Л.: ОНТИ НКТП СССР, 1935. 283 с.
Schiller L. und Kirsten H. Über den Widerstand strömender Flüssigkeit in kurzen Rohrstücken // Physikalische Zeitschrift. 1921. V. 22. S. 523–528.
Durst F., Ray S., Ünsal B., Bayoumi O.A. The development lengths of laminar pipe and channel flows // J. Fluid. Eng. 2005. V. 127. № 6. P. 1154–1160.
Poole R.J., Ridley B.S. Development – length requirements for fully developed laminar pipe flow of inelastic non-Newtonian liquids // J. Fluid. Eng. 2007. V. 129. P. 1281–1287.
Mehrotra A.K., Patience G.S. Unified entry length for Newtonian and power – law fluids in laminar pipe flow // Can. J. Chem. Eng. 1990. V. 68. P. 529–533.
Shimomukay K., Kanda H. Numerical study of normal pressure distribution in entrance pipe flow // Electr. Trans. Numer. Anal. 2008. V. 30. P. 10–25.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Т. VI. Гидродинамика. М.: Наука, 1986. 736 с.
Лойцянский Л.Г. Ламинарный пограничный слой. М.: ГИФМЛ, 1962. 479 с.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976. 576 с.
Hornbeck R.W. Laminar flow in the entrance region of a pipe // Appl. Sci. Res. A. 1964. V. 13. P. 224–236.
Казаков Л.И. Развитие течения Пуазейля в круглой трубе. Севастополь: 2019. 32 с. – Деп. в ВИНИТИ 07.10.2019 № 80-В2019.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал