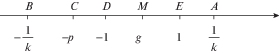Прикладная математика и механика, 2021, T. 85, № 5, стр. 664-674

Гидродинамическая модель явления “струйности” при электрохимической обработке металлов

Н. М. Миназетдинов^1, *

¹ Российский новый университет
Москва, Россия

Поступила в редакцию 02.02.2021
После доработки 19.06.2021
Принята к публикации 14.07.2021

DOI: 10.31857/S0032823521050064

Аннотация

При электрохимической обработке металлов в межэлектродном промежутке в местах с пониженным статическим давлением возникает кавитация. В рамках модели “идеального процесса” электрохимической обработки решена двумерная задача, связанная с определением формы обрабатываемой поверхности с учетом присоединенной кавитации. Применяется условие, позволяющее учесть влияние электрического поля на гидродинамику кавитационного течения идеальной несжимаемой жидкости в межэлектродном промежутке.

Ключевые слова: электрохимическая обработка металлов, кавитация, идеальная несжимаемая жидкость

1. Введение. Существенное влияние на процесс электрохимической обработки металлов оказывают гидродинамические факторы. Поток раствора электролита в межэлектродном промежутке между границами электрода-инструмента (катода) и обрабатываемой заготовки (анода) должен обеспечивать стабильное протекание электродных реакций, удаление продуктов этих реакций и охлаждение электродов: анода и катода [1–3].

При определенных условиях в результате обтекания потоком электролита острых кромок катода возникают каверны, заполненные парами жидкости и газом, выделяющимся в процессе электрохимической обработки. Электропроводность газовой среды, заполняющей каверну, существенно ниже электропроводности электролита, и как следствие, происходит неравномерное растворение металла на различных участках анода, чем можно объяснить появление струйных неровностей в виде волнистой поверхности, ориентированной в направлении потока электролита [1].

В монографии [4] выполнен обзор различных механизмов образования и способов устранения данного нежелательного явления, которое в научно-технической литературе получило название “струйности”. Там же отмечено, что значительная роль в образовании “струйности” принадлежит явлению присоединенной кавитации [5].

В работах [6, 7], представлены решения двумерных задач, связанных с определением установившейся [8] анодной границы c учетом кавитации в предположение, что течение электролита описывается моделью идеальной несжимаемой жидкости. Для описания кавитационного обтекания острой кромки катода бесконечно длинной каверной была применена схема Кирхгофа [5].

В данной работе в рамках математической модели [6], рассматривается двумерная схема электрохимического формообразования с учетом каверны конечной протяженности.

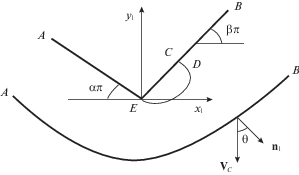
2. Схема электрохимической обработки. Геометрия сечения межэлектродного промежутка представлена на рис. 1. Двугранный угол AEB соответствует границе катода. Введем систему декартовых координат $\left( {{{x}_{1}},{{y}_{1}}} \right)$, связанную с катодом. Начало координат выбрано в точке E, точки A и B являются бесконечно удаленными. Углы наклона граней AE и EB к оси абсцисс определяется значениями $\alpha \pi $ и $\beta \pi $ соответственно, причем $0 \leqslant \alpha < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, $0 \leqslant \beta < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Катод совершает поступательное перемещение в направлении, противоположном оси ординат, с постоянной скоростью ${{V}_{c}}$. В процессе обработки с течением времени формируется установившаяся анодная граница AB. В установившемся режиме геометрия межэлектродного промежутка не меняется во времени [8].

Рис. 1.

Граница AEB катода отделена от границы AB анода зазором, в котором осуществляется установившееся течение идеальной несжимаемой жидкости. Для определенности будем считать, что течение осуществляется в направлении от входа в межэлектродный канал в окрестности точки A к точке B. В точке E происходит отрыв потока с поверхности катода-инструмента с образованием каверны. В модели задачи считается, что граница каверны DE, согласно схеме Рябушинского [5], замыкается на фиктивную пластинку DC, перпендикулярную грани EB катода.

При постановке задачи и ее решении рассматриваются два векторных поля: стационарное электрическое поле и поле скоростей установившегося течения идеальной несжимаемой жидкости в межэлектродном промежутке, а также их взаимосвязь.

3. Математическая модель процесса электрохимической обработки. Согласно [9] введем аналитическую функцию ${{W}_{1}}({{z}_{1}})$ = ${v}({{x}_{1}},{{y}_{1}})$ + $iu({{x}_{1}},{{y}_{1}})$ комплексной переменной ${{z}_{1}} = {{x}_{1}} + i{{y}_{1}}$, где ${v}({{x}_{1}},{{y}_{1}})$ – функция тока, а $u({{x}_{1}},{{y}_{1}})$ – потенциал электрического поля. Величина $u({{x}_{1}},{{y}_{1}})$ принимает постоянные значения на границах электродов

(3.1)

${{\left. u \right|}_{{AB}}} = {{u}_{a}},\quad {{\left. u \right|}_{{AE}}} = {{\left. u \right|}_{{BC}}} = {{u}_{c}}$

В модели каверна считается диэлектриком [6], и ее граница CDE является участком линии тока, и на ее поверхности существует точка M раздвоения этой линии. Для определенности рассмотрим случай, когда точка M расположена между точками D и E. Будем считать, что

(3.2)

${{\left. {{v}({{x}_{1}},{{y}_{1}})} \right|}_{{CDE}}} = 0$

Нормальная производная потенциала электрического поля на искомой установившейся анодной границе AB удовлетворяет условию

(3.3)

$\frac{{\partial u}}{{\partial {{n}_{1}}}} = \frac{1}{{\kappa {{a}_{0}}}}\left( { - {{a}_{1}} + \frac{{\rho {{V}_{c}}}}{\varepsilon }\cos \theta } \right),$

где $\kappa $ − удельная электропроводность среды, $\varepsilon $ − электрохимический эквивалент металла, $\rho $ − плотность материала анода, $\theta $ − угол между вектором ${{{\mathbf{V}}}_{c}}$ скорости подачи катода и вектором ${{{\mathbf{n}}}_{1}}$ нормали к анодной границе (рис. 1), ${{a}_{0}}$, ${{a}_{1}}$ – постоянные величины [10].

Произведем замену переменных по формулам

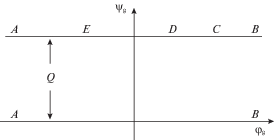
$\psi = {{\left( {u - {{u}_{c}}} \right)} \mathord{\left/ {\vphantom {{\left( {u - {{u}_{c}}} \right)} {\left( {{{u}_{a}} - {{u}_{c}}} \right)}}} \right. \kern-0em} {\left( {{{u}_{a}} - {{u}_{c}}} \right)}},\quad \varphi = {\nu \mathord{\left/ {\vphantom {\nu {\left( {{{u}_{a}} - {{u}_{c}}} \right)}}} \right. \kern-0em} {\left( {{{u}_{a}} - {{u}_{c}}} \right)}},\quad z = {{{{z}_{1}}} \mathord{\left/ {\vphantom {{{{z}_{1}}} H}} \right. \kern-0em} H} = x + iy,$

где $H = {{{{a}_{0}}\kappa \left( {{{u}_{a}} - {{u}_{c}}} \right)} \mathord{\left/ {\vphantom {{{{a}_{0}}\kappa \left( {{{u}_{a}} - {{u}_{c}}} \right)} {{{j}_{0}}}}} \right. \kern-0em} {{{j}_{0}}}}$ – характерная длина, ${{j}_{0}} = {{\rho {{V}_{c}}} \mathord{\left/ {\vphantom {{\rho {{V}_{c}}} \varepsilon }} \right. \kern-0em} \varepsilon }$ – характерная плотность тока [11].

Безразмерный комплексный потенциал $W\left( z \right)$ = $\varphi \left( {x,y} \right)$ + $i\psi \left( {x,y} \right)$, согласно формулам (3.1)–(3.3) удовлетворяет граничным условиям

(3.4)

${{\left. \psi \right|}_{{AB}}} = 1,\quad {{\left. \psi \right|}_{{AE}}} = {{\left. \psi \right|}_{{BC}}} = 0$

(3.5)

${{\left. \varphi \right|}_{{CDE}}} = 0$

(3.6)

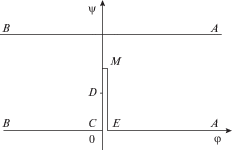
${{\left| {\frac{{dW}}{{dz}}} \right|}_{{AB}}} = {{\left. {\frac{{\partial \psi }}{{\partial n}}} \right|}_{{AB}}} = b + \cos \theta ,\quad b = - \frac{{{{a}_{1}}}}{{{{j}_{0}}}}$

Область изменения безразмерного комплексного потенциала электрического поля представлена на рис. 2.

Рис. 2.

Из условий (3.4), (3.6) следует, что безразмерные величины межэлектродных зазоров на бесконечности в окрестностях точек A и B равны соответственно

(3.7)

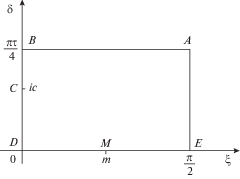
${{h}_{1}} = \frac{1}{{b + \cos \alpha \pi }},\quad {{h}_{2}} = \frac{1}{{b + \cos \beta \pi }}$

4. Параметрическое представление безразмерного комплексного потенциала электрического поля. Введем параметрическую комплексную переменную $t = \xi + i\delta $, изменяющуюся в области ${{G}_{t}}$ ($0 < \xi < {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$, $0 < \delta < {{\pi \left| \tau \right|} \mathord{\left/ {\vphantom {{\pi \left| \tau \right|} 4}} \right. \kern-0em} 4}$) $\left( {\tau = i\left| \tau \right|} \right)$ (рис. 3).

Рис. 3.

Согласно условиям (3.4) и (3.5) функция $W(t)$ удовлетворяет граничным условиям

(4.1)

$\begin{gathered} \varphi \left( \xi \right) = 0;\quad \xi \in \left[ {0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right],\quad \varphi \left( {i\delta } \right) = 0;\quad \delta \in \left[ {0,c} \right],\quad \psi \left( {i\delta } \right) = 0;\quad \delta \in \left[ {c,{{\pi \left| \tau \right|} \mathord{\left/ {\vphantom {{\pi \left| \tau \right|} 4}} \right. \kern-0em} 4}} \right) \\ \psi \left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + i\delta } \right) = 0;\quad \delta \in \left[ {0,{{\pi \left| \tau \right|} \mathord{\left/ {\vphantom {{\pi \left| \tau \right|} 4}} \right. \kern-0em} 4}} \right),\quad \psi \left( {\xi + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right) = 1;\quad \xi \in \left( {0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right) \\ \end{gathered} $

Введем вспомогательную комплексную переменную u, область изменения которой – верхняя полуплоскость ${{G}_{u}}$ (рис. 4) и выполним конформное отображение прямоугольника ${{G}_{t}}$ (рис. 3) на полуплоскость ${{G}_{u}}$ с помощью эллиптического синуса [12]

(4.2)

$\begin{gathered} u = \operatorname{sn} \left( {2K(k)\left( {\frac{{2t}}{\pi } - \frac{1}{2}} \right),k} \right) = - \frac{1}{{\sqrt k }}\frac{{{{\vartheta }_{2}}\left( {2t} \right)}}{{{{\vartheta }_{3}}\left( {2t} \right)}};\quad k = {{\left( {\frac{{{{\vartheta }_{2}}}}{{{{\vartheta }_{3}}}}} \right)}^{2}} \\ K\left( k \right) = \int\limits_0^1 {\frac{{du}}{{\sqrt {\left( {1 - {{u}^{2}}} \right)\left( {1 - {{k}^{2}}{{u}^{2}}} \right)} }} = \frac{{\pi \vartheta _{3}^{2}}}{2}} ,\quad g = - \frac{{{{\vartheta }_{3}}}}{{{{\vartheta }_{2}}}}\frac{{{{\vartheta }_{2}}\left( {2m} \right)}}{{{{\vartheta }_{3}}\left( {2m} \right)}},\quad p = \frac{{{{\vartheta }_{3}}}}{{{{\vartheta }_{2}}}}\frac{{{{\vartheta }_{2}}\left( {2ci} \right)}}{{{{\vartheta }_{3}}\left( {2ci} \right)}}, \\ \end{gathered} $

где ${{\vartheta }_{i}}\left( t \right)$, $i = 1,2,3,4$ – тета-функции для периодов $\pi $ и $\pi \tau $, ${{\vartheta }_{i}} = {{\vartheta }_{i}}\left( 0 \right)$ [12].

Рис. 4.

С помощью интеграла Кристоффеля–Шварца [13], найдем производную функции, отображающей область ${{G}_{u}}$ на область изменения комплексного потенциала (рис. 2)

(4.3)

$\frac{{dW}}{{du}} = N\frac{{u - g}}{{\left( {1 - {{u}^{2}}{{k}^{2}}} \right)\sqrt {\left( {u - 1} \right)\left( {u + p} \right)} }};\quad N = {\text{const}}$

Используя эллиптические функции Якоби [12]

${\text{cn}}\left( w \right) = \frac{{{{\vartheta }_{4}}}}{{{{\vartheta }_{2}}}}\frac{{{{\vartheta }_{2}}\left( {{w \mathord{\left/ {\vphantom {w {\vartheta _{3}^{2}}}} \right. \kern-0em} {\vartheta _{3}^{2}}}} \right)}}{{{{\vartheta }_{4}}\left( {{w \mathord{\left/ {\vphantom {w {\vartheta _{3}^{2}}}} \right. \kern-0em} {\vartheta _{3}^{2}}}} \right)}},\quad {\text{dn}}\left( w \right) = \frac{{{{\vartheta }_{4}}}}{{{{\vartheta }_{3}}}}\frac{{{{\vartheta }_{3}}\left( {{w \mathord{\left/ {\vphantom {w {\vartheta _{3}^{2}}}} \right. \kern-0em} {\vartheta _{3}^{2}}}} \right)}}{{{{\vartheta }_{4}}\left( {{w \mathord{\left/ {\vphantom {w {\vartheta _{3}^{2}}}} \right. \kern-0em} {\vartheta _{3}^{2}}}} \right)}}$

и равенство [12]

$\frac{d}{{dw}}{\text{sn}}\left( w \right) = {\text{cn}}\left( w \right){\text{dn}}\left( w \right),$

из соотношения (4.2) найдем

(4.4)

$\frac{{du}}{{dt}} = \frac{{4K\left( k \right)}}{\pi }\frac{{\vartheta _{4}^{2}}}{{{{\vartheta }_{2}}{{\vartheta }_{3}}}}\frac{{{{\vartheta }_{1}}\left( {2t} \right){{\vartheta }_{4}}\left( {2t} \right)}}{{\vartheta _{3}^{2}\left( {2t} \right)}}$

Подставляя формулы (4.2)–(4.4) в соотношение

$\frac{{dW}}{{dt}} = \frac{{dW}}{{du}}\frac{{du}}{{dt}},$

получим

$\frac{{dW}}{{dt}} = {{N}_{1}}\frac{{{{\vartheta }_{1}}\left( {2t} \right){{\vartheta }_{4}}\left( {2t} \right)}}{{\vartheta _{3}^{2}\vartheta _{3}^{2}\left( {2t} \right) - \vartheta _{2}^{2}\vartheta _{2}^{2}\left( {2t} \right)}}\frac{{F(t,m)}}{{\sqrt {F(t,ci)\left( {{{\vartheta }_{3}}{{\vartheta }_{2}}\left( {2t} \right) + {{\vartheta }_{2}}{{\vartheta }_{3}}\left( {2t} \right)} \right)} }};\quad {{N}_{1}} = {\text{const}}$

$F(t,a) = {{\vartheta }_{3}}\left( {2a} \right){{\vartheta }_{2}}\left( {2t} \right) - {{\vartheta }_{2}}\left( {2a} \right){{\vartheta }_{3}}\left( {2t} \right)$

Из формулы [12]

(4.5)

${{\vartheta }_{4}}\left( {y + z} \right){{\vartheta }_{4}}\left( {y - z} \right)\vartheta _{4}^{2} = \vartheta _{3}^{2}\left( y \right)\vartheta _{3}^{2}\left( z \right) - \vartheta _{2}^{2}\left( y \right)\vartheta _{2}^{2}\left( z \right)$

следует

$\vartheta _{3}^{2}\vartheta _{3}^{2}\left( {2t} \right) - \vartheta _{2}^{2}\vartheta _{2}^{2}\left( {2t} \right) = \vartheta _{4}^{2}\left( {2t} \right)\vartheta _{4}^{2}$

Тогда

(4.6)

$\frac{{dW}}{{dt}} = {{N}_{2}}\frac{{{{\vartheta }_{1}}\left( {2t} \right)}}{{{{\vartheta }_{4}}\left( {2t} \right)}}\frac{{F\left( {t,m} \right)}}{{\sqrt {F\left( {t,ci} \right)\left( {{{\vartheta }_{3}}{{\vartheta }_{2}}\left( {2t} \right) + {{\vartheta }_{2}}{{\vartheta }_{3}}\left( {2t} \right)} \right)} }};\quad {{N}_{2}} = {\text{const}}$

Используя формулы прибавления полупериодов для тета-функций [12]

(4.7)

${{\vartheta }_{4}}\left( {2t} \right) = i{{q}^{{\frac{1}{4}}}}{{{\text{e}}}^{{ - 2ti}}}{{\vartheta }_{1}}\left( {2t - {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 2}} \right. \kern-0em} 2}} \right);\quad q = {{e}^{{ - \pi \left| \tau \right|}}},$

затем, используя формулу удвоения [12]

(4.8)

${{\vartheta }_{1}}\left( {2t} \right){{\vartheta }_{2}}{{\vartheta }_{3}}{{\vartheta }_{4}} = 2{{\vartheta }_{1}}\left( t \right){{\vartheta }_{2}}\left( t \right){{\vartheta }_{3}}\left( t \right){{\vartheta }_{4}}\left( t \right),$

найдем

${{\vartheta }_{4}}\left( {2t} \right) = 2i{{q}^{{\frac{1}{4}}}}{{{\text{e}}}^{{ - 2ti}}}\frac{{{{\vartheta }_{1}}\left( {{{t}_{2}}} \right){{\vartheta }_{2}}\left( {{{t}_{2}}} \right){{\vartheta }_{3}}\left( {{{t}_{2}}} \right){{\vartheta }_{4}}\left( {{{t}_{2}}} \right)}}{{{{\vartheta }_{2}}{{\vartheta }_{3}}{{\vartheta }_{4}}}};\quad {{t}_{2}} = t - {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}$

Выражение (4.6) с учетом формул (4.7), (4.8) представим в виде

(4.9)

$\frac{{dW}}{{dt}} = {{N}_{2}}\frac{{ - i{{q}^{{ - \frac{1}{4}}}}{{{\text{e}}}^{{2ti}}}{{\vartheta }_{2}}{{\vartheta }_{3}}{{\vartheta }_{4}}{{\vartheta }_{1}}\left( {2t} \right)}}{{2{{\vartheta }_{1}}\left( {{{t}_{2}}} \right){{\vartheta }_{2}}\left( {{{t}_{2}}} \right){{\vartheta }_{3}}\left( {{{t}_{2}}} \right){{\vartheta }_{4}}\left( {{{t}_{2}}} \right)}}\frac{{F\left( {t,m} \right)}}{{\sqrt {F\left( {t,ci} \right)\left( {{{\vartheta }_{3}}{{\vartheta }_{2}}\left( {2t} \right) + {{\vartheta }_{2}}{{\vartheta }_{3}}\left( {2t} \right)} \right)} }}$

Из граничных условий (4.1) следует

(4.10)

$\frac{1}{4}\oint\limits_{t = {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} {\frac{{dW}}{{dt}}dt = i} ,\quad \frac{1}{4}\oint\limits_{t = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} {\frac{{dW}}{{dt}}dt = - i} $

В формулах (4.10) выражение (4.9) интегрируется соответственно по четверти дуг окружностей бесконечно малого радиуса с центрами в точках $B$ ($t = {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}$) и $A$ ($t = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}$) против часовой стрелки. Используя соотношение (4.9), и первую формулу из (4.10) с помощью теории вычетов [13], найдем

(4.11)

${{N}_{2}} = \frac{{4{{\vartheta }_{2}}{{\vartheta }_{3}}}}{\pi }\frac{{\sqrt {\left( {\vartheta _{3}^{2} + \vartheta _{2}^{2}} \right)\left( {{{\vartheta }_{3}}{{\vartheta }_{3}}\left( {2ci} \right) - {{\vartheta }_{2}}{{\vartheta }_{2}}\left( {2ci} \right)} \right)} }}{{{{\vartheta }_{3}}{{\vartheta }_{3}}\left( {2m} \right) - {{\vartheta }_{2}}{{\vartheta }_{2}}\left( {2m} \right)}}$

Далее, с помощью выражений (4.9), (4.11), и второй формулы из (4.10) получим уравнение

(4.12)

$\sqrt {\frac{{\left( {\vartheta _{3}^{2} + \vartheta _{2}^{2}} \right)\left( {{{\vartheta }_{3}}{{\vartheta }_{3}}\left( {2ci} \right) - {{\vartheta }_{2}}{{\vartheta }_{2}}\left( {2ci} \right)} \right)}}{{\left( {\vartheta _{3}^{2} - \vartheta _{2}^{2}} \right)\left( {{{\vartheta }_{3}}{{\vartheta }_{3}}\left( {2ci} \right) + {{\vartheta }_{2}}{{\vartheta }_{2}}\left( {2ci} \right)} \right)}}} \left( {\frac{{{{\vartheta }_{3}}{{\vartheta }_{3}}\left( {2m} \right) + {{\vartheta }_{2}}{{\vartheta }_{2}}\left( {2m} \right)}}{{{{\vartheta }_{3}}{{\vartheta }_{3}}\left( {2m} \right) - {{\vartheta }_{2}}{{\vartheta }_{2}}\left( {2m} \right)}}} \right) = 1$

5. Гидродинамика кавитационного течения идеальной жидкости в межэлектродном промежутке. Введем комплексный потенциал двумерного установившегося течения идеальной несжимаемой жидкости ${{W}_{g}}\left( z \right)$ = ${{\varphi }_{g}}\left( {x,y} \right)$ + $i{{\psi }_{g}}\left( {x,y} \right)$, где ${{\varphi }_{g}}\left( {x,y} \right)$ – потенциал скорости ${\mathbf{V}} = {\text{grad}}\,{{\varphi }_{g}}$, ${{\psi }_{g}}\left( {x,y} \right)$ – функция тока [5].

Твердые и свободные границы течения являются линиями тока, следовательно

(5.1)

$\begin{gathered} {{\psi }_{g}}\left( \xi \right) = Q;\quad \xi \in \left[ {0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right],\quad {{\psi }_{g}}\left( {i\delta } \right) = Q;\quad \delta \in \left[ {0,{{\pi \left| \tau \right|} \mathord{\left/ {\vphantom {{\pi \left| \tau \right|} 4}} \right. \kern-0em} 4}} \right) \\ {{\psi }_{g}}\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + i\delta } \right) = Q;\quad \delta \in \left[ {0,{{\pi \left| \tau \right|} \mathord{\left/ {\vphantom {{\pi \left| \tau \right|} 4}} \right. \kern-0em} 4}} \right),\quad {{\psi }_{g}}\left( {\xi + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right) = 0;\quad \xi \in \left( {0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right) \\ \end{gathered} $

В плоскости комплексного потенциала ${{W}_{g}}$ области течения соответствует полоса ширины $Q$ = ${{V}_{1}}{{h}_{1}}$ = ${{V}_{2}}{{h}_{2}}$, ${{V}_{1}}$, ${{V}_{2}}$ – значения скорости в точках A и B соответственно (рис. 5).

Рис. 5.

Функция ${{d{{W}_{g}}} \mathord{\left/ {\vphantom {{d{{W}_{g}}} {dt}}} \right. \kern-0em} {dt}}$ на горизонтальных сторонах прямоугольника ${{G}_{t}}\;$ принимает действительные значения, а на вертикальных – мнимые, имеет нули первого порядка в точках $D$ ($t = 0$), $E$ ($t = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$), полюса первого порядка в точках $B$ ($t = {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}$), $A$ ($t = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ + + ${{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}$). Согласно принципу симметрии Шварца [13], функцию ${{d{{W}_{g}}} \mathord{\left/ {\vphantom {{d{{W}_{g}}} {dt}}} \right. \kern-0em} {dt}}$ можно аналитически продолжить через границы области ${{G}_{t}}$ на всю плоскость. Продолженная таким образом функция будет двоякопериодической с периодами $\pi $, $\pi \tau $ и известными особенностями в прямоугольнике периодов [12]. Согласно теории эллиптических функций функцию ${{d{{W}_{g}}} \mathord{\left/ {\vphantom {{d{{W}_{g}}} {dt}}} \right. \kern-0em} {dt}}$ можно представить в виде [14]

$\frac{{d{{W}_{g}}}}{{dt}} = {{N}_{3}}\frac{{{{\vartheta }_{1}}\left( t \right){{\vartheta }_{2}}\left( t \right){{\vartheta }_{3}}\left( t \right){{\vartheta }_{4}}\left( t \right)}}{{{{\vartheta }_{1}}\left( {t - {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right){{\vartheta }_{2}}\left( {t - {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right){{\vartheta }_{1}}\left( {t + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right){{\vartheta }_{2}}\left( {t + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)}};\quad {{N}_{3}} = {\text{const}}$

Применяя преобразование (4.8) представим полученное выражение в виде

(5.2)

$\frac{{d{{W}_{g}}}}{{dt}} = \frac{{{{N}_{3}}{{\vartheta }_{2}}{{\vartheta }_{3}}{{\vartheta }_{4}}}}{2}\frac{{{{\vartheta }_{1}}\left( {2t} \right)}}{{{{\vartheta }_{1}}\left( {t - {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right){{\vartheta }_{2}}\left( {t - {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right){{\vartheta }_{1}}\left( {t + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right){{\vartheta }_{2}}\left( {t + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)}}$

Интегрируя выражения (5.2) по четверти дуги окружности бесконечно малого радиуса с центром в точке $B$ ($t = {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}$) против часовой стрелки и используя равенство $\frac{1}{4}\oint_{t = {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} {\left( {{{d{{W}_{g}}} \mathord{\left/ {\vphantom {{d{{W}_{g}}} {dt}}} \right. \kern-0em} {dt}}} \right)dt} $ = $ - iQ$, вытекающее из граничных условий (5.1), найдем

(5.3)

${{N}_{3}} = - \frac{{4Q}}{\pi }{{\vartheta }_{2}}{{\vartheta }_{3}}{{q}^{{ - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}};\quad q = \exp \left( {\pi \tau i} \right)$

Применяя формулы (4.7), (4.8) и (5.3) выражения (5.2) представим в виде

(5.4)

$\frac{{d{{W}_{g}}}}{{dt}} = - \frac{{4Q}}{\pi }{{\vartheta }_{2}}{{\vartheta }_{3}}\frac{{{{\vartheta }_{1}}\left( {2t} \right)}}{{{{\vartheta }_{4}}\left( {2t} \right)}}$

Введем в рассмотрение функцию Жуковского [5]

(5.5)

$\chi \left( t \right) = \ln \frac{{{{V}_{0}}dz}}{{d{{W}_{g}}}} = r + i{{\theta }_{g}};\quad r = \ln \frac{{{{V}_{0}}}}{V}$

где $V$ – модуль скорости, ${{V}_{0}}$ – величина скорости на свободной поверхности DE, ${{\theta }_{g}}$ – угол скорости с осью абсцисс $x$.

Представим функцию $\chi \left( t \right)$ в виде суммы [5, 15]

(5.6)

$\chi \left( t \right) = {{\chi }_{0}}\left( t \right) + \omega \left( t \right),$

где ${{\chi }_{0}}\left( t \right) = {{r}_{0}} + i{{\theta }_{0}}$ – функция Жуковского для вспомогательного течения жидкости по заданной схеме при условии, что на границе AB модуль скорости постоянный и равен ${{V}_{*}}$, $\omega (t)$ – функция, аналитическая в области ${{G}_{t}}$ и непрерывная в ее замыкании ${{\bar {G}}_{t}}$.

Согласно схеме течения, выполняются граничные условия

(5.7)

$\begin{gathered} \operatorname{Im} \chi \left( {i\delta } \right) = \operatorname{Im} {{\chi }_{0}}\left( {i\delta } \right) = \left( {0.5 + \beta } \right)\pi ;\quad \delta \in \left[ {0,c} \right) \\ \operatorname{Im} \chi \left( {i\delta } \right) = \operatorname{Im} {{\chi }_{0}}\left( {i\delta } \right) = \beta \pi ;\quad \delta \in \left( {c,{{\pi \left| \tau \right|} \mathord{\left/ {\vphantom {{\pi \left| \tau \right|} 4}} \right. \kern-0em} 4}} \right] \\ \operatorname{Im} \chi \left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + i\delta } \right) = \operatorname{Im} {{\chi }_{0}}\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + i\delta } \right) = - \alpha \pi ;\quad \delta \in \left[ {0,{{\pi \left| \tau \right|} \mathord{\left/ {\vphantom {{\pi \left| \tau \right|} 4}} \right. \kern-0em} 4}} \right] \\ \end{gathered} $

(5.8)

$\begin{gathered} Re\chi \left( \xi \right) = Re{{\chi }_{0}}\left( \xi \right) = 0;\quad \xi \in \left[ {0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right] \\ Re{{\chi }_{0}}\left( {\xi + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right) = \ln \frac{{{{V}_{0}}}}{{{{V}_{*}}}} = {{r}_{0}};\quad \xi \in \left[ {0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right] \\ \end{gathered} $

на границе AB при $t = \xi + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}$, граничные значения гармонически сопряженных функций $r\left( {\xi + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)$ и ${{\theta }_{g}}\left( {\xi + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)$ связаны соотношением [6]

(5.9)

${{e}^{{ - r\left( {\xi + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)}}} = \frac{{\left( {b + \cos {{\theta }_{g}}\left( {\xi + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)} \right)}}{{{{V}_{0}}}}\left| {\frac{{d{{\varphi }_{g}}}}{{d\xi }}\frac{{d\xi }}{{d\varphi }}} \right|$

Используя формулы (4.6), (4.11) и (5.4) условие (5.9) представим в виде

$C\frac{Q}{{{{V}_{0}}}}{{F}_{2}}\left( \xi \right)\left( {b + \cos {{\theta }_{g}}\left( {\xi + \frac{{\pi \tau }}{4}} \right)} \right){{{\text{e}}}^{{r\left( {\xi + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)}}} = 1,$

(5.10)

$C = \frac{{{{F}_{1}}\left( {0,m} \right)}}{{\sqrt {{{F}_{1}}\left( {0,ci} \right)\left( {\vartheta _{3}^{2} + \vartheta _{2}^{2}} \right)} }},\quad {{F}_{1}}(t,a) = {{\vartheta }_{3}}\left( {2a} \right){{\vartheta }_{3}}\left( {2t} \right) - {{\vartheta }_{2}}\left( {2a} \right){{\vartheta }_{2}}\left( {2t} \right),$

${{F}_{2}}\left( \xi \right) = \frac{{\sqrt {{{F}_{1}}\left( {\xi ,ci} \right)\left( {{{\vartheta }_{3}}{{\vartheta }_{3}}\left( {2\xi } \right) + {{\vartheta }_{2}}{{\vartheta }_{2}}\left( {2\xi } \right)} \right)} }}{{{{F}_{1}}\left( {\xi ,m} \right)}}$

Используя условия ${{\theta }_{g}}\left( {{{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)$ = $\operatorname{Im} \chi \left( {{{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)$ = $\beta \pi $ из соотношения (5.10) найдем

(5.11)

$\frac{Q}{{{{V}_{0}}}} = \frac{{{{{\text{e}}}^{{ - r\left( {{{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)}}}}}{{b + \cos \beta \pi }}$

С учетом равенства (5.11) выражение (5.10) представим в виде

(5.12)

$\frac{{С{{F}_{2}}\left( \xi \right)}}{{b + \cos \beta \pi }}\left( {b + \cos {{\theta }_{g}}\left( {\xi + \frac{{\pi \tau }}{4}} \right)} \right){{{\text{e}}}^{{r\left( {\xi + {{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right) - r\left( {{{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right)}}} = 1$

Функция ${{d{{\chi }_{0}}} \mathord{\left/ {\vphantom {{d{{\chi }_{0}}} {dt}}} \right. \kern-0em} {dt}}$ в точке $C$ ($t = ic$) имеет полюс первого порядка с вычетом равным 1/2. Учитывая, что на сторонах прямоугольника ${{G}_{t}}$ выполняется условие $\operatorname{Re} \left( {{{d{{\chi }_{0}}} \mathord{\left/ {\vphantom {{d{{\chi }_{0}}} {dt}}} \right. \kern-0em} {dt}}} \right) = 0$, продолжим функцию ${{d{{\chi }_{0}}} \mathord{\left/ {\vphantom {{d{{\chi }_{0}}} {dt}}} \right. \kern-0em} {dt}}$ по принципу симметрии Шварца на всю плоскость и получим эллиптическую функцию с периодами $\pi $, $\pi \tau $. Представляя функцию ${{d{{\chi }_{0}}} \mathord{\left/ {\vphantom {{d{{\chi }_{0}}} {dt}}} \right. \kern-0em} {dt}}$ в виде линейной комбинации логарифмических производных тета-функций [12] и затем интегрированием получим выражение функции ${{\chi }_{0}}\left( t \right)$ [15]

(5.13)

${{\chi }_{0}}\left( t \right) = \frac{1}{2}\ln \frac{{{{\vartheta }_{1}}\left( {t + ic} \right){{\vartheta }_{4}}\left( {t + ic} \right)}}{{{{\vartheta }_{1}}\left( {t - ic} \right){{\vartheta }_{4}}\left( {t - ic} \right)}} + i{{A}_{0}}t + i{{B}_{0}}$

Используя условия

$\operatorname{Im} {{\chi }_{0}}\left( 0 \right) = \left( {0.5 + \beta } \right)\pi ,\quad \operatorname{Im} {{\chi }_{0}}\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right) = - \alpha \pi ,$

получим

${{A}_{0}} = - 2\left( {\alpha + \beta } \right)\quad {\text{и}}\quad {{B}_{0}} = \beta \pi $

Учитывая, что ${{\chi }_{0}}\left( {{{\pi \tau } \mathord{\left/ {\vphantom {{\pi \tau } 4}} \right. \kern-0em} 4}} \right) = {{r}_{0}} + i\beta \pi $ из соотношения (5.13) выразим величину ${{r}_{0}}$

(5.14)

${{r}_{0}} = c + \left( {\alpha + \beta } \right)\frac{{\pi \left| \tau \right|}}{2}$

Для неизвестной функции $\omega (t)$, выполняются граничные условия

(5.15)

$\operatorname{Im} \omega \left( {i\delta } \right) = 0,\quad \operatorname{Im} \omega \left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} + i\delta } \right) = 0,\quad \delta \in \left[ {0,{{\pi \left| \tau \right|} \mathord{\left/ {\vphantom {{\pi \left| \tau \right|} 4}} \right. \kern-0em} 4}} \right]$

(5.16)

$Re\omega \left( \xi \right) = 0,\quad \xi \in \left[ {0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right]$

(5.17)

$\begin{gathered} \frac{{С{{F}_{2}}\left( \xi \right)}}{{b + \cos \beta \pi }}\left( {b + \cos \left( {T\left( \xi \right) + \mu \left( \xi \right)} \right)} \right){{{\text{e}}}^{{\nu \left( \xi \right) - \nu \left( 0 \right)}}} = 1 \\ T\left( \xi \right) = \operatorname{Im} {{\chi }_{0}}\left( {\xi + \frac{{\pi \tau }}{4}} \right),\quad \mu \left( \xi \right) = \operatorname{Im} \omega \left( {\xi + \frac{{\pi \tau }}{4}} \right),\quad \nu \left( \xi \right) = \operatorname{Re} \omega \left( {\xi + \frac{{\pi \tau }}{4}} \right) \\ \end{gathered} $

Учитывая граничные условия (5.15), (5.16) функцию $\omega (t)$ можно разложить в ряд с вещественными коэффициентами [6, 15]

(5.18)

$\omega \left( t \right) = 2i\sum\limits_{k = 1}^\infty {{{b}_{k}}\sin (2tk)} $

Тогда $\mu \left( \xi \right)$ = $2\sum\nolimits_{k = 1}^\infty {{{b}_{k}}sin\left( {2\xi k} \right){\text{ch}}\left( {\frac{{\pi \left| \tau \right|}}{2}k} \right)} $, $\nu \left( \xi \right)$ = $ - 2\sum\nolimits_{k = 1}^\infty {{{b}_{k}}\cos \left( {2\xi k} \right){\text{sh}}\left( {\frac{{\pi \left| \tau \right|}}{2}k} \right)} $.

Используя условия

$\chi \left( {\frac{{\pi \tau }}{4}} \right) = \ln \frac{{{{V}_{0}}}}{{{{V}_{2}}}} + \beta \pi i,\quad \chi \left( {\frac{\pi }{2} + \frac{{\pi \tau }}{4}} \right) = \ln \frac{{{{V}_{0}}}}{{{{V}_{1}}}} - \alpha \pi i,$

найдем

(5.19)

$\frac{{{{V}_{0}}}}{{{{V}_{2}}}} = \exp \left( {{{r}_{0}} - 2\sum\limits_{k = 1}^\infty {{{b}_{k}}\operatorname{sh} \left( {\frac{{\pi \left| \tau \right|k}}{2}} \right)} } \right),\quad \frac{{{{V}_{0}}}}{{{{V}_{1}}}} = \exp \left( {{{r}_{0}} - 2\sum\limits_{k = 1}^\infty {{{{\left( { - 1} \right)}}^{k}}{{b}_{k}}\operatorname{sh} \left( {\frac{{\pi \left| \tau \right|k}}{2}} \right)} } \right)$

Из условия ${{V}_{1}}{{h}_{1}} = {{V}_{2}}{{h}_{2}}$, формул (3.7) и (5.19) следует, что должно выполняться равенство

(5.20)

$\frac{{{{V}_{1}}}}{{{{V}_{2}}}} = \exp \left( {2\sum\limits_{k = 1}^\infty {{{b}_{k}}\left( {{{{\left( { - 1} \right)}}^{k}} - 1} \right){\text{sh}}\left( {\frac{{\pi \left| \tau \right|k}}{2}} \right)} } \right) = \frac{{{{h}_{2}}}}{{{{h}_{1}}}} = \frac{{b + \cos \alpha \pi }}{{b + \cos \beta \pi }}$

Зависимость $z(t)$ может быть получена интегрированием функции

(5.21)

$\frac{{dz}}{{dt}} = \frac{{\exp (\chi (t))}}{{{{V}_{0}}}}\frac{{d{{W}_{g}}}}{{dt}}$

Подставляя в (5.21) формулы (5.4), (5.6), (5.13) и (5.18) получим

(5.22)

$\frac{{dz}}{{dt}} = M\frac{{{{\vartheta }_{1}}\left( {2t} \right)}}{{{{\vartheta }_{4}}\left( {2t} \right)}}{{\left( {\frac{{{{\vartheta }_{1}}\left( {t + ic} \right){{\vartheta }_{4}}\left( {t + ic} \right)}}{{{{\vartheta }_{1}}\left( {t - ic} \right){{\vartheta }_{4}}\left( {t - ic} \right)}}} \right)}^{{0.5}}}\exp \left( {2i\sum\limits_{k = 1}^\infty {{{c}_{k}}\sin (2tk)} - 2\left( {\alpha + \beta } \right)ti} \right)$,

где $M = - \frac{{4Q}}{{\pi {{V}_{0}}}}{{\vartheta }_{2}}{{\vartheta }_{3}}\exp \left( {\beta \pi i} \right)$.

Согласно схеме течения (см. рис. 1) точка C принадлежит лучу EB, расположенному под углом $\beta \pi $ относительно оси абсцисс, следовательно, должно выполняться равенство

(5.23)

$\frac{{\operatorname{Im} {{z}_{C}}}}{{\operatorname{Re} {{z}_{C}}}} = \frac{{\operatorname{Im} z\left( {ic} \right)}}{{\operatorname{Re} z(ic)}} = \operatorname{tg} \beta \pi $

Длина $L$ отрезка EC, характеризующая длину каверны, определяется по формуле

(5.24)

$L = \sqrt {{{{\operatorname{Re} }}^{2}}{{z}_{C}} + {{{\operatorname{Im} }}^{2}}{{z}_{C}}} = \sqrt {{{{\operatorname{Re} }}^{2}}z\left( {ic} \right) + {{{\operatorname{Im} }}^{2}}z\left( {ic} \right)} $

Для численного решения задачи задаются геометрические величины $\alpha $, $\beta $, L и параметры ${{a}_{0}}$, ${{a}_{1}}$, ${{j}_{0}}$. В разложении (5.18) сохраняется конечное число n слагаемых и составляется система уравнений, в которой требуется выполнение условия (5.17) в дискретных точках ${{\xi }_{k}} = {\pi \mathord{\left/ {\vphantom {\pi {\left( {2k} \right)}}} \right. \kern-0em} {\left( {2k} \right)}}$, где $k = \overline {1,n} $. К полученной системе добавляются уравнения (4.12), (5.23) и (5.24). В процессе решения определяются коэффициенты ${{b}_{k}}$, $k = \overline {1,n} $ и параметры m, c, $\left| \tau \right|$. Затем с помощью соотношений (5.11), (5.19), (5.20) и (5.22) определяются гидродинамические и геометрические характеристики течения.

6. Результаты расчетов. Задача решена при

$\alpha = 0,\quad \beta = 0.25,\quad {{a}_{0}} = 0.906,\quad {{a}_{1}} = - 12.82,\quad {{j}_{0}} = 100\;{{\text{A}} \mathord{\left/ {\vphantom {{\text{A}} {{\text{с}}{{{\text{м}}}^{2}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{2}}}}$

Для заданных значений получаем, что ${{{{h}_{2}}} \mathord{\left/ {\vphantom {{{{h}_{2}}} {{{h}_{1}}}}} \right. \kern-0em} {{{h}_{1}}}} = 1.35065$. В табл. 1 представлены результаты расчетов величин ${{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} {{{V}_{1}}}}} \right. \kern-0em} {{{V}_{1}}}}$, ${{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} {{{V}_{2}}}}} \right. \kern-0em} {{{V}_{2}}}}$, ${{{{V}_{1}}} \mathord{\left/ {\vphantom {{{{V}_{1}}} {{{V}_{2}}}}} \right. \kern-0em} {{{V}_{2}}}}$, ${Q \mathord{\left/ {\vphantom {Q {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$ для трех значений величины L: 0.5, 0.7, 0.9. Величина отношения ${{{{V}_{1}}} \mathord{\left/ {\vphantom {{{{V}_{1}}} {{{V}_{2}}}}} \right. \kern-0em} {{{V}_{2}}}}$ при различных значениях L одна и та же, и совпадает с величиной отношения ${{{{h}_{2}}} \mathord{\left/ {\vphantom {{{{h}_{2}}} {{{h}_{1}}}}} \right. \kern-0em} {{{h}_{1}}}}$.

Таблица 1.

Результаты расчета гидродинамических характеристик

L	${{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} {{{V}_{1}}}}} \right. \kern-0em} {{{V}_{1}}}}$	${{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} {{{V}_{2}}}}} \right. \kern-0em} {{{V}_{2}}}}$	${{{{V}_{1}}} \mathord{\left/ {\vphantom {{{{V}_{1}}} {{{V}_{2}}}}} \right. \kern-0em} {{{V}_{2}}}}$	${Q \mathord{\left/ {\vphantom {Q {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$
0.5	1.93258	2.61023	1.35065	0.45865
0.7	2.03995	2.75523	1.35065	0.43451
0.9	2.24487	3.03204	1.35065	0.39485

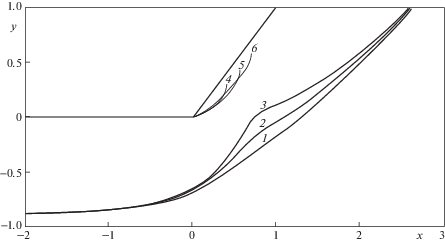
На рис. 6 представлены графики анодных границ и каверн. Линии 1 и 4 соответствуют анодной границе и границе каверны для значения $L = 0.5$, линии 2 и 5 для значения $L = 0.7$, линии 3 и 6 для значения $L = 0.9$.

Рис. 6.

Заключение. Результаты решения отражают качественные эффекты, связанные с влиянием каверны и ее размеров на образование макродефектов обрабатываемой поверхности, высота которых может составлять от 10 до 100 мк [1].

Список литературы

Мороз И.И., Алексеев Г.А., Водяницкий О.А и др. Электрохимическая обработка металлов. М.: Машиностроение, 1969. 208 с.
Wilson J.F. Practice and Theory of Electrochemical Machining. R.E. Publishing Company, 1982. 252 p.
Rajurkar K.P., Sundaram M.M., Malshe A.P. Review of electrochemical and electrodischarge machining // Proc. Seventeenth SIRP conference of electro physicals and chemical machining (ISEM). 2013. V. 6. P. 13–26.
Житников В.П., Зайцев А.Н. Импульсная электрохимическая размерная обработка. М.: Машиностроение, 2008, 413 с.
Гуревич М.И. Теория струй идеальной жидкости. М.: Наука, 1979. 536 с.
Миназетдинов Н.М. О кавитационном течении идеальной несжимаемой жидкости при электрохимической обработке металлов // ПММ. 2017. Т. 81. Вып. 1. С. 45–53.
Миназетдинов Н.М. Об одной модели кавитационного течения при электрохимической обработке // Вестн. Российского нового университета. Сер.: Сложные системы: модели, анализ и управление. 2020. № 3. С. 41–51.
Давыдов А.Д., Козак Е. Высокоскоростное электрохимическое формообразование. М.: Наука, 1990. 272 с.
Крылов А.Л. Задача Коши для уравнения Лапласа в теории электрохимической обработки металлов // Докл. АН СССР. 1968. Т. 178. № 2. С. 321–323.
Миназетдинов Н.М. Гидродинамическая интерпретация одной задачи теории размерной электрохимической обработки металлов // ПММ. 2009. Т. 73. Вып. 1. С. 60–68.
Клоков В.В. Электрохимическое формообразование. Казань: Изд-во Казан. ун-та, 1984. 80 с.
Уитекер Э.Т., Ватсон Дж.Н. Курс современного анализа Т. 2. Трансцендентные функции. М.: Физматгиз, 1963. 515 с.
Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука, 1987. 688 с.
Терентьев А.Г. Струйное обтекание системы двух препятствий // Тр. сем. по краевым задачам. Казань: Изд-во Казан. ун-та, 1964. Вып. 1. С. 110–123.
Киселев О.М., Котляр, Л.М. К задаче о течении тяжелой жидкости с двумя свободными поверхностями. // ПММ. 1973. Т. 37. № 5. С. 849–856.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал