1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 85, № 6, 2021

Прикладная математика и механика, 2021, T. 85, № 6, стр. 748-757

Автомодельные течения вязкого газа в плоском канале при произвольной зависимости коэффициентов переноса от температуры

М. А. Брутян 1, 2, *, У. Г. Ибрагимов 2, **

1 Центральный аэрогидродинамический институт им. Н.Е. Жуковского
Жуковский, Россия

2 Московский физико-технический институт
Долгопрудный, Россия

* E-mail: murad.brutyan@tsagi.ru
** E-mail: umar.ibragimov@phystech.edu

Поступила в редакцию 18.05.2021
После доработки 24.08.2021
Принята к публикации 10.09.2021

Полный текст (PDF)

Аннотация

Рассматривается течение вязкого сжимаемого газа, истекающего из вершины плоского клина. Для случая теплоизолированных стенок установлена возможность построения автомодельных решений при произвольной зависимости коэффициентов вязкости и теплопроводности от температуры. Полученные аналитические решения сравниваются с найденными ранее автомодельными решениями при постоянных коэффициентах переноса. Для течений газа в микродиффузорах проведено сравнение полученных автомодельных решений с результатом эксперимента других авторов.

Ключевые слова: точные решения, уравнения Навье–Стокса, течения вязкого газа

1. Введение. Начиная со второй половины 20 века, во всем мире наблюдается повышенный интерес к исследованиям течений жидкости и газа в “микроустройствах”, которые используются в различных технических изделиях, например в струйных принтерах [1–3], а также в целом ряде медицинских и химических технологических процессах, таких как газовая хроматография [4–6]. К такого рода микроустройствам относятся датчики течения, клапаны регуляризации давления, сепараторы, химические датчики и др. Экспериментально и на основе инженерного подхода изучаются [7, 8] течения в микродиффузорах.

Впервые автомодельные решения уравнений Навье–Стокса для течения вязкого сжимаемого газа от источника массы в плоских и осесимметричных конических диффузорах теоретически изучались в работах [9–12]. Рассматривается [9] осесимметричное течение в конусе с непроницаемыми стенками и условием скольжения для скорости и температуры на стенке. Изучались [10–12] течения в осесимметричных и плоских каналах с массоотводом газа на стенке.

Для несжимаемых течений [13] дано описание широкого класса известных и новых точных решений уравнений Навье–Стокса, в частности известного решения Джеффри–Гамеля для течения вязкой несжимаемой жидкости в плоском диффузоре.

Рассмотрено [14, 15] течение в клине при условии адиабатической стенки и показано, что автомодельные решения, удовлетворяющие условию сплошной среды, реализуются в каналах с малыми углами раствора. Число Рейнольдса на оси клина при этом оказывается небольшим, что соответствует течениям сильно разреженного газа либо течениям газа в микроканалах при нормальных условиях. Найдены [15] аналитические решения для течения в плоском канале с коэффициентами динамической вязкости η и теплопроводности $\kappa $, зависящими от температуры по степенному закону Фроста ($\eta ,\kappa \propto {{T}^{k}}$). Рассмотрено [16] аналогичное автомодельное течение вязкого сжимаемого газа от струи (источника импульса), истекающей в область между двумя расходящимися стенками.

В настоящей работе получено точное автомодельное решение уравнений движения вязкого теплопроводного газа в плоском клиновидном канале при произвольной зависимости коэффициентов переноса от температуры. Найденные аналитические решения сравниваются с полученными ранее решениями для степенной зависимости коэффициентов переноса от температуры. Для течений газа в микродиффузорах проведено сравнение полученных автомодельных решений с экспериментом других авторов.

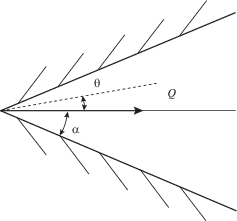
2. Автомодельные течения. Рассмотрим течение вязкого газа, истекающего из вершины плоского клина, рис. 1.

Рис. 1.

Схема течения в плоском клине.

Уравнения движения в полярных координатах (r, θ) имеют вид [17]:

(2.1)
$\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\rho u} \right) = 0$
(2.2)
$\rho u\frac{{\partial u}}{{\partial r}} = - \frac{{\partial p}}{{\partial r}} + \frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\sigma }_{{rr}}}} \right) + \frac{1}{r}\frac{{\partial {{\sigma }_{{r\theta }}}}}{{\partial \theta }} - \frac{{{{\sigma }_{{\theta \theta }}}}}{r}} \right]$
(2.3)
$0 = - \frac{1}{r}\frac{{\partial p}}{{\partial \theta }} + \frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {\frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\sigma }_{{r\theta }}}} \right) + \frac{1}{r}\frac{{\partial {{\sigma }_{{\theta \theta }}}}}{{\partial \theta }} + \frac{{{{\sigma }_{{r\theta }}}}}{r}} \right]$
(2.4)
$\frac{{\rho u}}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}}}\frac{{\partial T}}{{\partial r}} = u\frac{{\partial p}}{{\partial r}} + \frac{{\nabla \cdot \left( {\kappa \nabla T} \right)}}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}\Pr {{{\operatorname{Re} }}_{0}}}} + \frac{1}{{{{{\operatorname{Re} }}_{0}}}}\left[ {\frac{{1\eta }}{2}\left( {\varepsilon _{{rr}}^{2} + \varepsilon _{{\theta \theta }}^{2}} \right) + \varepsilon _{{r\theta }}^{2}\eta - \frac{2}{3}\eta {{{\left( {\nabla \cdot {\mathbf{V}}} \right)}}^{2}}} \right]$

Течение предполагается радиальным, ${\mathbf{V}} = (u,0)$. В уравнениях (2.1)–(2.4) безразмерные переменные связанны с размерными газодинамическими параметрами, помеченными звездочкой, следующим образом:

$\rho = \frac{{\rho {\kern 1pt} *}}{{{{\rho }_{0}}}},\quad p = \frac{{p{\kern 1pt} *}}{{{{\rho }_{0}}u_{0}^{2}}},\quad T = \frac{{T{\kern 1pt} *}}{{{{T}_{0}}}},\quad u = \frac{{u{\kern 1pt} *}}{{{{u}_{0}}}},\quad \eta = \frac{{\eta {\kern 1pt} *}}{{{{\eta }_{0}}}},$
где ${{\rho }_{0}}$, ${{u}_{0}}$, ${{T}_{0}}$ – соответственно плотность, скорость и температура в некоторой точке $({{r}_{0}},0)$ на оси клина. Газ считается совершенным, так что $\gamma {\text{M}}_{0}^{2}p = \rho T$. Стенки канала предполагаются теплоизолированными.

Компоненты тензора вязких напряжений $\sigma $ и тензора скоростей деформации $\varepsilon $ имеют вид:

${{\sigma }_{{rr}}} = \eta {{\varepsilon }_{{rr}}} - \frac{2}{3}\eta \nabla \cdot {\mathbf{V}},\quad {{\sigma }_{{\theta \theta }}} = \eta {{\varepsilon }_{{\theta \theta }}} - \frac{2}{3}\eta \nabla \cdot {\mathbf{V}},\quad {{\sigma }_{{r\theta }}} = \eta {{\varepsilon }_{{r\theta }}}$
${{\varepsilon }_{{rr}}} = 2\frac{{\partial u}}{{\partial r}},\quad {{\varepsilon }_{{r\theta }}} = \frac{1}{r}\frac{{\partial u}}{{\partial \theta }},\quad {{\varepsilon }_{{\theta \theta }}} = \frac{{2u}}{r}$

В уравнения (2.1)–(2.4) входят параметры подобия: число Маха ${{{\text{M}}}_{0}}$, число Рейнольдса ${{\operatorname{Re} }_{0}}$ и число Прандтля $\Pr $, которые вычисляются следующим образом:

${{\operatorname{Re} }_{0}} = \frac{{{{\rho }_{0}}{{u}_{0}}{{r}_{0}}}}{{{{\eta }_{0}}}},\quad {{{\text{M}}}_{0}} = \frac{{{{u}_{0}}}}{{\sqrt {\gamma R{{T}_{0}}} }},\quad \Pr = \frac{{{{c}_{p}}{{\eta }_{0}}}}{{{{\kappa }_{0}}}}$

Автомодельное решение уравнений (2.1)–(2.4) ищем в виде:

(2.5)
$\rho = \frac{{\rho (\theta )}}{r},\quad p = \frac{{p(\theta )}}{r},\quad u = u(\theta ),\quad T = T(\theta ),\quad \eta = \eta (\theta ),\quad \kappa = \kappa (\theta )$

Тогда уравнение неразрывности (2.1) выполняется автоматически, а определяющие уравнения (2.2)–(2.4) можно переписать в следующем виде:

(2.6)
${{\operatorname{Re} }_{0}}p - \frac{4}{3}u\eta + \frac{d}{{d\theta }}\left( {\eta \frac{{du}}{{d\theta }}} \right) = 0$
(2.7)
${{\operatorname{Re} }_{0}}\frac{{dp}}{{d\theta }} = \eta \frac{{du}}{{d\theta }} + \frac{4}{3}\frac{d}{{d\theta }}\left( {\eta u} \right)$
(2.8)
${{\operatorname{Re} }_{0}}up = \frac{1}{{\left( {\gamma - 1} \right){\text{M}}_{0}^{2}\Pr }}\frac{d}{{d\theta }}\left( {\eta \frac{{dT}}{{d\theta }}} \right) + \eta \left[ {\frac{4}{3}{{u}^{2}} + {{{\left( {\frac{{du}}{{d\theta }}} \right)}}^{2}}} \right]$
с граничными условиями прилипания на теплоизолированной стенке:

(2.9)
$u( \pm \alpha ) = 0,\quad {{\left. {\frac{{dT}}{{d\theta }}} \right|}_{{\theta = \pm \alpha }}} = 0$

Течение будем предполагать симметричным относительно оси клина:

(2.10)
${{\left. {\frac{{du}}{{d\theta }}} \right|}_{{\theta = 0}}} = 0,\quad {{\left. {\frac{{dT}}{{d\theta }}} \right|}_{{\theta = 0}}} = 0$

Из условия нормировки для параметров течения на оси клина при $\theta = 0$ имеем:

(2.11)
$u(0) = 1,\quad T(0) = 1,\quad p(0) = \frac{1}{{\gamma {\text{M}}_{0}^{2}}}$

Продифференцируем уравнение (2.6) по $\theta $ и вычтем полученное выражение из уравнения (2.7). В результате приходим к следующему обыкновенному дифференциальному уравнению:

$\frac{{{{d}^{2}}}}{{d{{\theta }^{2}}}}\left( {\eta \frac{{du}}{{d\theta }}} \right) + \eta \frac{{du}}{{d\theta }} = 0,$
решение которого, с учетом условий симметрии (2.10) имеет вид:
(2.12)
$\eta \frac{{du}}{{d\theta }} = {{\tau }_{0}}\sin \theta ,$
где ${{\tau }_{0}}$ – некоторая константа. Из уравнений (2.6) и (2.12) находим выражение для давления:
(2.13)
${{\operatorname{Re} }_{0}}p = \frac{4}{3}\eta u - {{\tau }_{0}}\cos \theta $
откуда, используя условия (2.11), находим неизвестную константу ${{\tau }_{0}}$:

(2.14)
${{\tau }_{0}} = \frac{4}{3} - \frac{{{{{\operatorname{Re} }}_{0}}}}{{\gamma {\text{M}}_{0}^{2}}}$

Подставляя (2.13) в уравнение энергии (2.8), имеем:

$0 = \frac{1}{{{\text{M}}_{0}^{2}\Pr (\gamma - 1)}}\frac{d}{{d\theta }}\left( {\eta \frac{{dT}}{{d\theta }}} \right) + \frac{{du}}{{d\theta }}{{\tau }_{0}}\sin \theta + {{\tau }_{0}}u\cos \theta $

Интегрируя полученное выражение по $\theta $ с учетом симметрии находим:

$0 = \frac{1}{{{\text{M}}_{0}^{2}\Pr (\gamma - 1)}}\eta \frac{{dT}}{{d\theta }} + u{{\tau }_{0}}\sin \theta $

Подставляя вместо выражения ${{\tau }_{0}}\sin \theta $ соответствующее выражение из формулы (2.12), получаем следующее обыкновенное дифференциальное уравнение относительно скорости и температуры:

$0 = \frac{1}{{{\text{M}}_{0}^{2}\Pr (\gamma - 1)}}\eta \frac{{dT}}{{d\theta }} + \eta \frac{{du}}{{d\theta }}u,$
которое с учетом граничных условий (2.9) легко интегрируется:

(2.15)
$T = 1 + \frac{{1 - {{u}^{2}}}}{2}{\text{M}}_{0}^{2}\Pr (\gamma - 1)$

Формула (2.15) дает зависимость температуры от скорости, $T = T(u)$. Тогда уравнение (2.12) с учетом (2.14) может быть решено в квадратурах. Окончательно получаем:

(2.16)
$\int\limits_0^u {\eta (U)dU} = \left( {\frac{4}{3} - \frac{{{{{\operatorname{Re} }}_{0}}}}{{\gamma {\text{M}}_{0}^{2}}}} \right)\left( {\cos \alpha - \cos \theta } \right)$

Заметим, что в силу условий нормировки (2.11) должно выполняться условие:

(2.17)
$\int\limits_0^1 {\eta (U)dU} = \left( {\frac{4}{3} - \frac{{{{{\operatorname{Re} }}_{0}}}}{{\gamma {\text{M}}_{0}^{2}}}} \right)\left( {\cos \alpha - 1} \right),$
из которого находится связь между безразмерными параметрами ${{\operatorname{Re} }_{0}}$ и ${{{\text{M}}}_{0}}$:

(2.18)
${{\operatorname{Re} }_{0}} = \gamma {\text{M}}_{0}^{2}\left( {\frac{4}{3} + \frac{1}{{1 - \cos \alpha }}\int\limits_0^1 {\eta (U)dU} } \right)$

В случае $\eta = \operatorname{const} $, формула (2.18) приобретает вид конечного соотношения:

(2.19)
${{\operatorname{Re} }_{0}} = \gamma {\text{M}}_{0}^{2}\left( {\frac{4}{3} + \frac{1}{{1 - \cos \alpha }}} \right),$
а в случае произвольной степенной зависимости $\eta = {{T}^{k}}$ она принимает следующую форму:

(2.20)
${{\operatorname{Re} }_{0}} = \gamma {\text{M}}_{0}^{2}\left( {\frac{4}{3} + \frac{1}{{1 - \cos \alpha }}\int\limits_0^1 {{{{\left( {1 + \frac{{1 - {{U}^{2}}}}{2}{\text{M}}_{0}^{2}\Pr (\gamma - 1)} \right)}}^{k}}dU} } \right)$

Заметим, что формулы (2.19) и (2.20) совпадают с соответствующими формулами, полученными ранее в работе [15], в которой изначально предполагалась степенная зависимость коэффициентов переноса от температуры [18, 19]. Отметим также, что число Кнудсена ${\text{Kn}} = {{{\text{M}}}_{{\text{0}}}}{\text{/R}}{{{\text{e}}}_{{\text{0}}}}$, как следует из формулы (2.18), имеет порядок ${\text{Kn}} \propto 1{\text{/}}\gamma {{{\text{M}}}_{{\text{0}}}}f(\alpha )$, где $f(\alpha )$ меняется от некоторого конечного значения $4{\text{/}}3 + \int_0^1 {\eta (U)dU} $ при $\alpha = \pi {\text{/}}2$ до бесконечности при $\alpha \to 0$. Откуда можно сделать вывод, что для течений в микродиффузорах при умеренных числах ${{{\text{M}}}_{{\text{0}}}}$ условие сплошной среды, ${\text{Kn}} \ll 1$, выполняется.

3. Результаты расчетов параметров течения газа в плоском канале для различных зависимостей коэффициентов переноса от температуры. Рассмотрим течение воздуха, для которого число Прандтля Pr при нормальных условиях приблизительно равно 0.71. Сравним полученные нами автомодельные решения для двух различных моделей газа:

1. модель газа с постоянными коэффициентами переноса: $\eta ,\kappa = \operatorname{const} $;

2. модель газа с коэффициентами переноса, зависящими от температуры по более близкому к реальности закону Сазерленда [20].

Точное решение уравнений Навье–Стокса для течений Куэтта и Пуазейля горячего газа с коэффициентом вязкости, зависящим от температуры по закону Сазерленда, получено в недавних работах [21, 22].

Как отмечалось выше, в первом случае задача допускает аналитическое решение, полученное ранее в работе [15]. Ниже исследуется автомодельное решение для принятого на практике закона Сазерленда, который в безразмерной форме при ${{\eta }_{0}} = 18.27$ × × 10–6 Па с и ${{T}_{0}} = 291.15$ K записывается в следующем виде:

(3.1)
$\eta (T) = \frac{{1 + 120{\text{/}}291.15}}{{T + 120{\text{/}}291.15}}{{T}^{{3/2}}}$

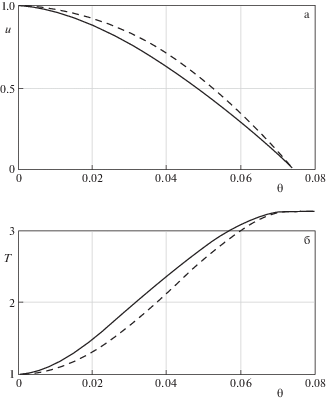
Проведенные по формулам (2.16), (2.17) расчеты течений воздуха в микродиффузорах показали, что при малых и умеренных числах ${{{\text{M}}}_{0}}$ автомодельные решения для различных зависимостей $\eta = \eta (T)$ практически совпадают. Заметные отличия появляются при числах ${{{\text{M}}}_{0}} > 2$. На рис. 2а и 2б, представлены сравнения профилей скорости $u = u(\theta )$ и температуры $T = T(\theta )$ при ${{{\text{M}}}_{0}} = 4$ для различных зависимостей $\eta = \eta (T)$.

Рис. 2.

Профили скорости а) и температуры б); сплошная линия – формула Сазерленда, пунктирная линия – $\eta = 1$.

Значение полуугла раствора клина $\alpha = 0.074$ рад выбрано таким же, как в работе [23], где экспериментально изучалось течение воздуха в микроканале.

На рис. 3 приведена зависимость числа ${{\operatorname{Re} }_{0}}$ от числа ${{{\text{M}}}_{0}}$ на оси симметрии клина для различных законов $\eta = \eta (T)$.

Рис. 3.

Зависимость числа ${{\operatorname{Re} }_{0}}$ от числа ${{{\text{M}}}_{0}}$ на оси симметрии; сплошная линия – формула Сазерленда, пунктирная линия – $\eta = 1$.

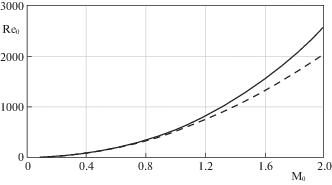
Из представленных на рис. 3 зависимостей видно, что для клина с полууглом раствора $\alpha = 0.074$ рад, автомодельные режимы течения при ${{{\text{M}}}_{0}} \propto 1$ реализуются при ${\text{R}}{{{\text{e}}}_{0}} \propto 500$ как для газа с постоянными коэффициентами переноса, так и для газа “Сазерленда”. Из определения числа Рейнольдса ${{\operatorname{Re} }_{0}} = {{\rho }_{0}}{{u}_{0}}{{r}_{0}}{\text{/}}{{\eta }_{0}}$ следует, что при нормальных условиях ($T \propto 300$ K, $p \propto 100$ кПа) автомодельное течение реализуется в клине длиной ${{r}_{0}} \propto {{10}^{{ - 4}}}$, которая характерна для микроканалов [23].

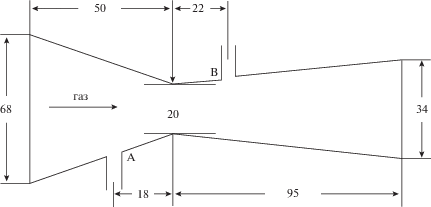
Ранее [7, 8, 23] рассматривались течения в плоских и осесимметричных микроканалах. В частности [23], экспериментально и численно исследуется течение в плоском микродиффузоре при различных значениях давления в выходном сечении канала. Схема канала показана на рис. 4, размеры даны в мкм. Стенки канала выполнены из полимерного материала с низкой теплопроводностью, поэтому в численном расчете, основанном на решении уравнений Навье–Стокса, на границах канала ставилось условие прилипания и условие теплоизолированной стенки.

Рис. 4.

Схема течения внутри микроканала.

Согласно расчетным и экспериментальным данным [23], в наиболее узкой части канала (см. рис. 4) давление и температура имели значения: p $ \simeq $ 40 кПа и T $ \simeq $ 245 K.

Представим число Рейнольдса ${{\operatorname{Re} }_{0}} = {{\rho }_{0}}{{u}_{0}}{{r}_{0}}{\text{/}}{{\eta }_{0}}$ в следующей форме:

(3.2)
${{\operatorname{Re} }_{0}} = \frac{{{{\rho }_{0}}{{u}_{0}}{{r}_{0}}}}{{{{\eta }_{0}}}} = \frac{{{{\rho }_{0}}{{a}_{0}}{{r}_{0}}}}{{{{\eta }_{0}}}}{{{\text{M}}}_{0}} \simeq 1500{{{\text{M}}}_{0}}$

Тогда с учетом формулы (2.18) данное выражение принимает вид:

$1500{{{\text{M}}}_{0}} = \gamma {\text{M}}_{0}^{2}\left( {\frac{4}{3} + \frac{1}{{1 - \cos \alpha }}\int\limits_0^1 {\eta (U)dU} } \right)$

Решая полученное уравнение с учетом зависимости $\eta = \eta (T)$, рассчитываемой по формуле Сазерленда (3.1), из соотношения (3.2) находим значение числа ${{\operatorname{Re} }_{0}} \simeq 3300$. Оценим теперь расход газа Q по формуле:

(3.3)
$Q = {{r}_{0}}D{{\rho }_{0}}{{u}_{0}}\int\limits_{ - \alpha }^\alpha {\rho (\theta )u(\theta )d\theta } = D{{\mu }_{0}}{{\operatorname{Re} }_{0}}\int\limits_{ - \alpha }^\alpha {\rho (\theta )u(\theta )d\theta } ,$
где $D$ – ширина поперечного сечения канала. При значениях ${{\operatorname{Re} }_{0}} \simeq 3300$ и $D = 120$ мкм, получаем: $Q \simeq 2.5 \times {{10}^{{ - 4}}}$ г/с, что по порядку величины согласуется с экспериментальным значением [23]: $Q \approx 3.8 \times {{10}^{{ - 4}}}$ г/с. Некоторое отличие расхода, рассчитанного с помощью полученного в настоящей работе автомодельного решения от экспериментального значения можно объяснить тем, что в работе [23] газ в диффузор конечной длины попадает из входного сечения конечного размера, в то время как в автомодельном решении газ истекает из точечного источника в канал бесконечной длины.

Заключение. Установлена возможность построения автомодельных решений для течения вязкого сжимаемого газа в плоском канале при произвольной зависимости коэффициентов переноса от температуры. При $\eta = \operatorname{const} $ и $\eta = {{T}^{k}}$ найденные аналитические решения согласуются с полученными ранее [15].

Для течения воздуха в микроканале проведено сравнение автомодельных решений для двух различных зависимостей коэффициента вязкости от температуры: $\eta = \operatorname{const} $ и $\eta $, рассчитанной по формуле Сазерленда. Оказалось, что существенные различия начинают проявляться при значениях числа Маха на оси клина ${{{\text{M}}}_{0}} > 2$.

Проведенные численные расчеты автомодельных решений сравниваются с экспериментальными данными [23]. Показано что расход газа $Q$ в микроканале, рассчитанный по формуле (3.3), удовлетворительно согласуется с экспериментальными данными.

Список литературы

  1. Bassous E., Taub H.H., Kuhn L. Ink jet printing nozzle arrays etched in silicon // Appl. Phys. Lett. 1977. V. 31. P. 135–137.

  2. Petersen K.E. Fabrication of an integrated planar silicon ink-iet structure // IEEE Trans. Electron Devices. 1979. V. 26. P. 1918–1920.

  3. Petersen K.E. Silicon as a mechanical material // Proc. IEEE. 1983. V. 70. P. 420–457.

  4. Terry S.C., Jerman J.H., Angell J.B. A gas chromatographic air analyzer fabricated on a silicon wafer // IEEE Trans. Electron Devices. 1979. V. 26. P. 1880–1886.

  5. Tuckerman D.B., Pease R.F.W. High-performance heat sinking for VLSI // IEEE Electron Device Lett. 1981. V. 2. P. l26–129.

  6. Zdeblick M.J., Barth P.W., Angell J.A. Microminiature fluidic amplifier // Sensors&Actuators. 1988. V. 15. P. 427–433.

  7. Jiang X.N., Zhou Z.Y., Huang X.Y., Li Y., Yang Y., Liu C.Y. Micronozzle/diffuser flow and its application in micro valveless pumps // Sensors&Actuation. 1998. V. 70. P. 81–87.

  8. Li Xiu-Han, Yu Xiao-Mei, Zhang Da-Cheng, Cui Hai-Hang, Li Ting, Wang Ying, Wang Yang-Yuan. Characteristics of gas flow within a micro diffuser/nozzle pump // Chin. Phys. Lett. 2006. V. 23. № 5. P. 1230–1233.

  9. Williams J.C. Conical nozzle flow with velocity slip and temperature jump // AIAA J. 1967. V. 5. № 12. P. 2128–2134.

  10. Быркин А.П. О точных решениях уравнений Навье–Стокса для течения сжимаемого газа в каналах // Уч. зап. ЦАГИ. 1970. Вып. 1. № 6. С. 15–21.

  11. Быркин А.П. Об одном точном решении уравнений Навье–Стокса для сжимаемого газа // ПММ. 1969. Т. 33. Вып. 1. С. 152–157.

  12. Быркин А.П., Межиров И.И. О некоторых автомодельных течениях вязкого газа в канале // Изв. АН СССР. МЖГ. 1969. Вып. 1. С. 100–105.

  13. Аристов С.Н., Князев Д.В., Полянин А.Д. Точные решения уравнений Навье–Стокса с линейной зависимостью компонент скорости от двух пространственных переменных // Теоретич. основы химич. технол. 2009. Т. 43. № 5. С. 547–566.

  14. Брутян М.А., Ибрагимов У.Г. Автомодельные турбулентные течения вязкого газа в клине // Труды МФТИ. 2020. Вып. 12. № 3. С. 141–149.

  15. Брутян М.А. Автомодельные решения типа Джеффери–Гамеля для течения вязкого сжимаемого газа // Уч. зап. ЦАГИ. 2017. Вып. XLVIII. № 6. С. 13–22.

  16. Брутян М.А., Крапивский П.Л. Точные решения стационарных уравнений Навье–Стокса вязкого теплопроводного газа для плоской струи из линейного источника // ПММ. 2018. Вып. 82. № 5. С. 644–656.

  17. Probstein R.F., Kemp N.H. Viscous Aerodynamic Characteristics in Hypersonic Rarefied Gas Flow // J. Aerosp. Sci. 1960. V. 27. № 3. P. 174–192.

  18. Лифшиц Е.М., Питаевский Л.П. Физическая кинетика. М.: Наука, 1979. 527 с.

  19. Чепмен С., Каулинг Т. Математическая теория неоднородных газов. М.: Изд-во иностр. лит., 1960. 510 с.

  20. Sutherland W. LII. The viscosity of gases and molecular force // The London, Edinburgh&Dublin Philos. Mag.&J. Sci. 1893. V. 36. № 223. P. 507–531.

  21. Голубкин В.Н., Сизых Г.Б. О сжимаемом течении Куэтта // Уч. зап. ЦАГИ. 2018. Вып. 49. № 1. С. 27–38.

  22. Хорин А.Н., Конюхова А.А. Течение Куэтта горячего вязкого газа // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2020. Вып. 24. № 2 С. 365–378.

  23. Hao P.F., Ding Y.T., Yao Z.H., He F., Zhu K.Q. Size effect on gas flow in micro nozzles // J. Micromech. Microeng. 2005. V. 15. P. 2069–2073.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал