Прикладная математика и механика, 2021, T. 85, № 6, стр. 699-718

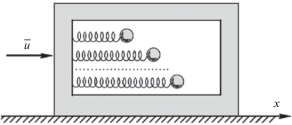
1. Объект исследования. Рассматривается управляемое перемещение системы из $(n + 1)$ тел (рис. 1). Первое тело (платформа массы ${{m}_{0}}$) движется поступательно вдоль горизонтальной оси Ох. Действующая на него управляющая сила u ограничена по модулю наперед заданной величиной $a$. К платформе крепятся посредством линейных пружин n материальных точек (массами ${{m}_{1}},{{m}_{2}}, \ldots ,{{m}_{n}}$), которые могут совершать колебания параллельно оси Ох. Трение отсутствует. Такая система является упрощенной моделью для описания малых перемещений платформы с упругими звеньями или сосуда, частично заполненного жидкостью. Проблемы управления такими объектами формулировались в [1], но до сих пор остаются актуальными. Им посвящены, например, недавние работы [2–4]. Известную трудность представляет поиск управления, оптимального по быстродействию. В работах [1, 5] приведено решение задачи оптимального перемещения платформы с одним осциллятором, моделирующим маятник в линейном приближении, где оптимальное управление оказалось кусочно-постоянным с тремя переключениями. В нелинейной постановке эта задача исследовалась численно [6], где обнаружились не только режимы с семью переключениями, но и особые управления. Ввиду практической невозможности аналитического решения задачи оптимального быстродействия для платформы с несколькими осцилляторами разрабатывались методы квазиоптимального управления. Предложен [7] алгоритм гашения колебаний платформы с осцилляторами посредством ограниченного управления в виде обратной связи. Здесь сочетаются метод [8] аппроксимации множества достижимости (для больших энергий системы) и метод [9, 10] обобщенных функций Ляпунова (для построения локального синтеза в окрестности терминального положения). Подход развивался в дальнейшем, исследовались [11] проблемы существования и единственности движения под действием предлагаемого управления, также подробно рассмотрен случай [12] платформы с двумя осцилляторами. Далее речь пойдет о задаче оптимального по быстродействию перемещения платформы с осцилляторами, где будут существенно использоваться свойства симметрии краевых условий.

Обозначим через ${{k}_{1}},{{k}_{2}}, \ldots ,{{k}_{n}}$ – коэффициенты жесткости, ${{q}_{1}},{{q}_{2}}, \ldots ,{{q}_{n}}$ – удлинения пружин осцилляторов, $M = \sum\nolimits_{i = 0}^n {{{m}_{i}}} $ – массу всей системы, ${{q}_{0}}$ – координату платформы. Конфигурация системы задается вектором ${\mathbf{q}} = {{\left( {{{q}_{0}},{{q}_{1}}, \ldots ,{{q}_{n}}} \right)}^{{\text{т}}}}$, а уравнения движения имеют вид

где $B = {\text{diag}}\left( {0,{{k}_{1}}, \ldots ,{{k}_{n}}} \right)$ – матрица потенциальной энергии, ${\mathbf{b}} = {{\left( {1,0, \ldots ,0} \right)}^{{\text{т}}}}$. Матрицу $A$ кинетической энергии и обратную ей матрицу ${{A}^{{ - 1}}}$ можно записать в блочном виде где $G = {\text{diag}}\left( {{{m}_{1}},{{m}_{2}}, \ldots ,{{m}_{n}}} \right)$, ${\mathbf{m}} = {{\left( {{{m}_{1}},{{m}_{2}}, \ldots ,{{m}_{n}}} \right)}^{{\text{т}}}}$, ${\mathbf{e}} = {{\left( {1,1, \ldots ,1} \right)}^{{\text{т}}}}$. Квадратная матрица H имеет на главной диагонали элементы ${{h}_{{ii}}} = \left( {{{m}_{0}} + {{m}_{i}}} \right){\text{/}}{{m}_{i}}$ ($i = 1,2, \ldots ,n$), а все элементы вне диагонали равны 1. Частоту колебаний каждой отдельной пружины обозначим ${{\vartheta }_{i}} = \sqrt {{{k}_{i}}{\text{/}}{{m}_{i}}} $ ($i = 1,2, \ldots ,n$).

Замечание 1. Система (1.1) является управляемой, если выполнено условие

Действительно, заменяя $A{\mathbf{q}} = {\mathbf{p}}$ и преобразуя уравнение (1.1) к виду

применим “ранговый” критерий управляемости [13], который одинаков [14] для (1.3) и для системы вдвое меньшего порядка, т.е. вычислим ранг матрицы

Определитель матрицы W можно упростить, вынося общие сомножители у элементов строк и вычитая столбцы, пропорциональные другим столбцам (подробности опускаем). В результате останется (с ненулевым коэффициентом) определитель Вандермонда относительно квадратов частот ${{\vartheta }_{i}}$, идентичный полученному ранее в ([1], с. 342) для линеаризованной модели платформы с маятниками и не равный нулю при условии (1.2). Таким образом, если собственные частоты колебаний осцилляторов попарно различны, то выполняется условие ${\text{det}}\,K \ne 0$, гарантирующее управляемость системы (1.1).

Следуя [1], преобразуем систему (1.1) к совокупности подсистем с независимыми переменными, но общим управлением. Для этого в уравнение (1.3) подставим ${\mathbf{p}} = S{\kern 1pt} {\mathbf{z}}$, где S – матрица из собственных векторов матрицы N. Получим

где у диагональной матрицы $D = {\text{diag}}\left( {0,{{\omega }}_{1}^{2},{{\omega }}_{2}^{2}, \ldots ,{{\omega }}_{n}^{2}} \right)$ на главной диагонали – собственные числа матрицы N (1.3), причем первое равно нулю, а остальные положительны в силу свойств матриц А и B. Элементы вектора ${\mathbf{r}} = {{\left( {{{r}_{1}},{{r}_{2}}, \ldots ,{{r}_{{n + 1}}}} \right)}^{{\text{т}}}}$ не равны нулю, так как в противном случае при ${{r}_{j}} = 0$ ($j = 2, \ldots ,n + 1$) (либо при ${{r}_{1}} = 0$) в системе (1.4) оказалась бы неуправляемая подсистема ${{\ddot {z}}_{j}} + {{\omega }}_{j}^{2}{{z}_{j}} = 0$ (либо ${{\ddot {z}}_{1}} = 0$).

Вводя безразмерные переменные ${{\omega }}_{i}^{'} = \frac{{{{{{\omega }}}_{i}}}}{{{{{{\omega }}}_{1}}}}$, ${{x}_{i}} = \frac{{{{z}_{{i + 1}}}{{\omega }}_{1}^{2}}}{{{{r}_{{i + 1}}}a}}$ ($i = 1,2, \ldots ,n$), $u{\text{'}} = \frac{u}{a}$, ${{x}_{0}} = \frac{{{{z}_{1}}{{\omega }}_{1}^{2}}}{{{{r}_{1}}a}}$ и время $t{\text{'}} = {{{{\omega }}}_{1}}t$, получим (опуская штрихи)

Здесь и далее для определенности пронумеруем частоты в порядке возрастания значений, т.е. $1 = {{{{\omega }}}_{1}} < {{{{\omega }}}_{2}} < \ldots < {{{{\omega }}}_{n}}$.

2. Постановка задачи и ее симметрии. Систему (1.5) представим в нормальной форме

Полагая, что требуемому перемещению платформы соответствует изменение переменной ${{x}_{0}}$, равное безразмерному отрезку 2b, назначим в середине этого отрезка начало отсчета координаты ${{x}_{0}}$. Аналогичную “удвоенную” запись удобно применять и для искомого общего времени 2Т движения системы, что придаст краевым условиям симметричный вид.

Задача оптимального по быстродействию перемещения платформы с осцилляторами формулируется следующим образом: требуется определить управление $u\left( t \right)$, $t \in \left[ {0,2T} \right]$, переводящее систему (2.1) из состояния

за наименьшее время 2T (заранее неизвестное) в состояние

Используя принцип максимума Понтрягина [15], составим гамильтониан

Тогда оптимальное управление получит вид

где сопряженные переменные должны удовлетворять системе

В силу замечания 1, искомое оптимальное управление существует при условии (1.2). Однако специфика краевых условий (2.1), (2.2) такова, что даже при совпадении собственных частот ${{\vartheta }_{i}} = {{\vartheta }_{j}}~$ ($i \ne j$) решение задачи существует, поскольку два осциллятора с одинаковой частотой будут двигаться синхронно.

Замечание 2. В задаче (2.1)–(2.5) записанное в смещенном времени $\tilde {t} = t - T$, $\tilde {t} \in \left[ { - T,T} \right]$ оптимальное управление $u\left( {\tilde {t}} \right)$, а также решения ${{x}_{i}}\left( {\tilde {t}} \right)$, ${{{{\lambda }}}_{i}}\left( {\tilde {t}} \right)$ ($i = 0,1, \ldots ,n$) будут нечетными функциями, а ${{y}_{i}}\left( {\tilde {t}} \right)$, ${{{{\mu }}}_{i}}\left( {\tilde {t}} \right)$ ($i = 0,1, \ldots ,n$) – четными функциями.

Для доказательства достаточно убедиться, что в новом времени $\tilde {t}$ все соотношения (2.1)–(2.5) инвариантны относительно замены $\tilde {t} \to - \tilde {t}$, $u \to - u$, ${{x}_{i}} \to - {{x}_{i}}$, ${{{{\lambda }}}_{i}} \to - {{{{\lambda }}}_{i}}$ ($i = 0,1, \ldots ,n$) при неизменных ${{y}_{i}}$, ${{{{\mu }}}_{i}}$ ($i = 0,1, \ldots ,n$).

Из замечания 2 вытекают соотношения

характеризующие состояние системы в конце оптимальной полутраектории.

Замечание 3. В задаче (2.1)–(2.5) оптимальное управление (2.4) является кусочно-постоянным с конечным числом переключений, число которых нечетно.

Действительно, в формуле (2.4) под знаком sign выражение не может быть тождественно равным нулю в силу линейной независимости известных решений системы (2.5). Поэтому особые режимы, моделируемые бесконечно быстрыми переключениями управления, здесь невозможны. При этом количество переключений нечетно, поскольку наряду с моментом времени переключения T возможны лишь “попарно симметричные” моменты вида ${{\tau }}$ и $(2T - {{\tau }})$, где ${{\tau }} < T$.

Можно доказать, что зависимость $T(b)$ значений наименьшего времени от задаваемых значений дальности будет монотонной. Ей соответствует обратная монотонная зависимость $b$ от $T$, которую можно затем, в свою очередь, “обратить”, чтобы получить $T(b)$. Поэтому далее поставленную задачу быстродействия будем рассматривать для взаимной к быстродействию вариационной задачи на максимум дальности ($2b$) при заданном времени ($2T$).

3. Свойства движений, удовлетворяющих необходимым условиям оптимальности. Далее моменты времени переключения управления будем обозначать ${{\tau }_{j}}$, увеличивая индексы j с ростом значений времени.

Утверждение 1. Если в задаче (2.1)–(2.3) полутраектория оптимальна по быстродействию и реализуется кусочно-постоянным управлением с $(n + 1)$ переключениями в моменты времени ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{n}}$, T, то управляющая функция имеет вид

Доказательство. Поскольку оптимальное управление должно удовлетворять соотношению (2.4), то будем искать решение системы (2.5) с учетом замечания 2, согласно которому функции ${{{{\lambda }}}_{0}}$, ${{{{\lambda }}}_{1}}$, …, ${{{{\lambda }}}_{n}}$ должны быть нечетными в смещенном времени $\tilde {t} = t - T$. Поэтому можно положить

В обозначениях (3.2) эта запись упрощается: ${{{{\lambda }}}_{i}}\left( t \right) = {{c}_{i}}{{f}_{i}}\left( t \right)$ $\left( {i = 0,1, \ldots ,n} \right)$.

Вектор ${\mathbf{c}} = {{\left( {{{c}_{0}},{{c}_{1}}, \ldots ,{{c}_{n}}} \right)}^{{\text{т}}}}$, составленный из констант интегрирования, найдем из условия обращения в ноль управления (2.4) в моменты времени ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{n}}$, T, т.е. из соотношений

где ${\mathbf{f}}\left( t \right) = {{\left( {{{f}_{0}}\left( t \right),{{f}_{1}}\left( t \right), \ldots ,{{f}_{n}}\left( t \right)} \right)}^{{\text{т}}}}$.

Решению однородной системы (3.3) соответствует в пространстве ${{R}^{n}}{{^{ + }}^{1}}$ вектор ${\mathbf{c}}$, перпендикулярный одновременно к n линейно независимым векторам ${\mathbf{f}}\left( {{{{{\tau }}}_{j}}} \right)$, $j = 1,2, \ldots ,n$, порождающим подпространство ${{R}^{n}}$. Известно, что сумма произведений элементов столбца определителя на алгебраические дополнения элементов другого столбца равна нулю. Поэтому координаты ${{c}_{0}},{{c}_{1}}, \ldots ,{{c}_{n}}$ можно взять (с точностью до сомножителя $~\kappa \ne 0~$) в виде алгебраических дополнений элементов первого столбца матрицы ${{Q}_{{n + 1}}}\left( t \right)$ (3.1). Тогда сумма $({{{{\lambda }}}_{0}}\left( t \right) + \ldots + {{{{\lambda }}}_{n}}\left( t \right))$, стоящая под знаком sign в выражении для управления (2.4), будет равна ${\text{det}}\,{{Q}_{{n + 1}}}\left( t \right)$, что и доказывает утверждение 1.

В формуле (3.1) знак коэффициента $~\kappa ~$ определяется известным (по условию) значением управления $u\left( t \right)$ при $t \in \left[ {0,{{{{\tau }}}_{1}}} \right]$.

Нетрудно убедиться, что определитель (3.1) обращается в нуль и при значениях времени $2T - {{{{\tau }}}_{n}}$, …, $2T - {{{{\tau }}}_{2}}$, $2T - {{{{\tau }}}_{1}}$, что соответствует свойствам симметрии из замечания 2.

Замечание 4. Если в задаче (2.1)–(2.3) полутраектория оптимальна по быстродействию и реализуется кусочно-постоянным управлением с количеством переключений большим, чем $(n + 1)$, то вид управляющей функции будет тот же (3.1).

Действительно, пусть смена знака управления осуществляется в моменты времени ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{n}}$, ${{{{\tau }}}_{{n + 1}}}$, …, ${{{{\tau }}}_{{n + k}}}$, T. Тогда к системе (3.3) добавятся соотношения, описывающие перпендикулярность вектора c к векторам ${\mathbf{f}}({{{{\tau }}}_{{n + 1}}})$, …, ${\mathbf{f}}\left( {{{{{\tau }}}_{{n + k}}}} \right)~$. Решение расширенной системы (3.3) останется прежним, а принадлежность векторов ${\mathbf{f}}({{{{\tau }}}_{{n + 1}}})$, …, ${\mathbf{f}}\left( {{{{{\tau }}}_{{n + k}}}} \right)~$ к упомянутому подпространству ${{R}^{n}}$ проявится в том, что при действии управления (3.1) определитель ${\text{det}}\,{{Q}_{{n + 1}}}\left( t \right)$ обратится в ноль не только в моменты времени ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{n}}$, T, но и в моменты ${{{{\tau }}}_{{n + 1}}}$, …, ${{{{\tau }}}_{{n + k}}}$, предшествующие значению T.

Замечание 5. Если в задаче (2.1)–(2.3) полутраектория оптимальна по быстродействию и реализуется кусочно-постоянным управлением с количеством переключений $m < (n + 1)$, то вид управляющей функции будет

где $~\kappa \ne 0~$, ${\text{det}}{{Q}_{m}}\left( t \right)$ – угловой $m \times m$ минор из ${\text{det}}\,{{Q}_{{n + 1}}}\left( t \right)$ (3.1).

Особенность управляющей функции вида (3.1) – в ее предназначении для конкретного типа траектории (с заранее известным количеством моментов переключения). Описанное в замечании 5 управление не является частным случаем формулы (3.1). Например, при ${{{{\tau }}}_{n}} \to T$, когда в пределе количество переключений убывает на единицу, определитель (3.1) стремится к нулю и в этом смысле вырождается, так как не может задавать функцию времени. Замена управления вида (3.1) на управление (3.4) равносильна тому, что компоненты ${{{{\lambda }}}_{{m + 1}}}$, …, ${{{{\lambda }}}_{n}}$ сопряженного вектора принимаются тождественно равными нулю.

Из вышеизложенного следует схема построения управляемых движений, удовлетворяющих необходимым условиям оптимальности. Для отыскания наибольшей дальности перемещения при заданном времени 2T сначала строится траектория с предполагаемым количеством переключений управления. Далее проверяется вдоль этой траектории действие управления вида (3.4) (если число переключений $m < (n + 1)$) или вида (3.1) – в остальных случаях. Если кроме ожидаемых моментов переключения возникают другие, при которых управление тоже обращается в ноль, то такое управление не удовлетворяет необходимым условиям оптимальности.

Основные вычислительные трудности связаны с обеспечением краевых условий (2.3) путем отыскания для заданного значения T моментов переключения управления. Можно показать (подробности опускаем), что если движение системы (2.1) началось при действии управления $u = 1$ на участке $t \in \left[ {0,{{{{\tau }}}_{1}}} \right]$, то на j-м участке постоянства управления при $t \in \left[ {{{{{\tau }}}_{{j - 1}}},{{{{\tau }}}_{j}}} \right]$ координата i-го осциллятора ($i = 1,2, \ldots ,n$) будет явной функцией времени

Если бы движение началось при $u = - 1$, то выражение в правой части (3.5) изменило бы знак на противоположный. В любом из этих случаев, согласно соотношению (2.6), в конце оптимальной полутраектории (т.е. при $t = T$) для всех $i = 1,2, \ldots ,n$ должны выполняться условия

где ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{{j - 1}}}$, T – моменты переключения управления на полутраектории.

Замечание 6. Если все числа ${{{{\omega }}}_{i}}$ ($i = 2, \ldots ,n$) рациональны, то в задаче (2.1)–(2.3) существует оптимальное движение с одним переключением управления.

Действительно, пусть ${{{{\omega }}}_{i}} = {{l}_{i}}{\text{/}}{{n}_{i}}$, где ${{l}_{i}} \in N$, ${{n}_{i}} \in N$ ($i = 2, \ldots ,n$) и все дроби несократимые. Тогда из уравнений (3.6) при $t = T$, $j = 1$ (т.е. в конце первого участка постоянства управления) получается система соотношений

Ей удовлетворяет длительность полутраектории $T = {{T}_{*}}$, где ${{T}_{*}} = 2{{n}_{*}}{{\pi }}$, ${{n}_{*}}$ – общий знаменатель всех дробей ${{{{\omega }}}_{i}}$. За это время ${{T}_{*}}$ каждый из n осцилляторов выполнит целое число полных колебаний, а платформа завершит этап разгона при постоянном управлении $u = 1$. Вторым этапом будет ее торможение при $u = - 1$, что соответствует наибольшей дальности за время $2{{T}_{*}}$.

Заметим, что введенное значение ${{T}_{*}}$ не только задает параметры “тривиального” режима (с одним переключением управления). Роль числа ${{T}_{*}}$ важна и для описания других режимов, так как оно является общим периодом всех функций в (3.6). Поэтому, если множество значений ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{{j - 1}}}$, T является решением решений системы (3.6), то множество ${{{{\tau }}}_{1}} + {{T}_{*}}$, ${{{{\tau }}}_{2}} + {{T}_{*}}$, …, ${{{{\tau }}}_{{j - 1}}} + {{T}_{*}}$, $T + {{T}_{*}}$ тоже им удовлетворит. Кроме того, система (3.6) обладает еще одной симметрией.

Замечание 7. Если все числа ${{{{\omega }}}_{i}}$ ($i = 2, \ldots ,n$) рациональны и управление с моментами переключения ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, …, ${{{{\tau }}}_{{j - 1}}}$, T при $T < {{T}_{*}}{\text{/}}2$ удовлетворяет краевым условиям (3.6), то и управление с моментами переключения ${{{{\tau }}}_{1}} + \Delta $, ${{{{\tau }}}_{2}} + \Delta $, …, ${{{{\tau }}}_{{j - 1}}} + \Delta $, $T + \Delta $ (где $\Delta = {{T}_{*}} - 2T$) тоже удовлетворит условиям (3.6).

Действительно, в уравнениях (3.6) аргументы $\left( {T - {{{{\tau }}}_{k}}} \right)$ $\left( {k = 1,2, \ldots ,j - 1} \right)$ инвариантны относительно замены ${{{{\tau }}}_{k}} \to {{{{\tau }}}_{k}} + \Delta $, $T \to T + \Delta $. Поскольку при этом $\Delta = {{T}_{*}} - 2T$, то $T \to {{T}_{*}} - T$, значит, выражение $\cos {{{{\omega }}}_{i}}T$ заменится равным по значению $\cos ({{\omega }_{i}}{{T}_{*}} - {{\omega }_{i}}T)$, так как величина ${{{{\omega }}}_{i}}{{T}_{*}}$ кратна ${\text{2}}\pi $ (согласно определению ${{T}_{*}}$).

Отметим также, что если хотя бы одно из значений ${{{{\omega }}}_{i}}$ иррационально (при ${{{{\omega }}}_{1}} = 1$), то система (3.7) не имеет решения, поэтому оптимальное движение с одним переключением управления невозможно.

4. Оптимальное перемещение платформы с двумя осцилляторами. Далее рассмотрим подробнее случай $n = 2$. Для системы (2.1) имеем $1 = {{{{\omega }}}_{1}} < {{{{\omega }}}_{2}}$, обозначая для краткости ${{{{\omega }}}_{2}} = {{\omega }}$. Уравнения движения принимают вид

Краевые условия повторяются из (2.2), (2.3):

Если число ${{\omega }}$ рациональное, то в силу замечания 6 для системы (4.1)–(4.3) существует оптимальное движение с одним переключением управления.

Движение с тремя переключениями управления, как увидим далее из численных экспериментов, встречается не при каждом значении ${{\omega }}$. Его условия следуют из уравнений (3.6) при $t = T$, $j = 2$ в виде

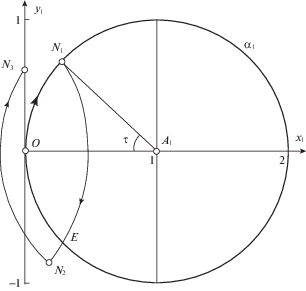
Рассмотрим режимы с пятью переключениями управления, иллюстрируя движение первого осциллятора на фазовой плоскости $({{x}_{1}},{{y}_{1}})$ (рис. 2). Пусть переключения управления происходят в моменты времени ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, T, $2T - {{{{\tau }}}_{2}}$, $2T - {{{{\tau }}}_{1}}$. При $u\left( t \right) = 1$, $t \in (0,{{{{\tau }}}_{1}})$ изображающая точка выходит из точки О с координатами (0, 0) и перемещается по дуге ON₁ окружности ${{\alpha }_{1}}$ с центром А₁(1, 0). Далее при $u\left( t \right) = - 1$, $t \in ({{{{\tau }}}_{1}},{\text{\;}}{{{{\tau }}}_{2}})$ движение происходит по дуге N₁N₂ с центром А₂(–1, 0), затем вновь при $u\left( t \right) = 1$, $t \in ({{{{\tau }}}_{2}},T)$ – по дуге N₂N₃ с центром А₁(1, 0). Угловые меры дуг численно равны времени движения по ним. Согласно условию (2.6) оптимальная полутраектория завершается в точке с координатой ${{x}_{1}}\left( T \right) = 0$. Вторая часть траектории, в силу замечания 2, симметрична первой относительно оси ${{x}_{1}} = 0$ с заменой управлений на противоположные. Далее ограничимся иллюстрацией только полутраекторий (при $t \in [0,T]$).

Уравнение второго осциллятора ${{\ddot {x}}_{2}} = - {{{{\omega }}}^{2}}{{x}_{2}} + u$ заменой переменной ${{\theta }} = {{{{\omega }}}^{2}}{{x}_{2}}$ и времени $t{\text{'}} = {{\omega }}t$ преобразуется к виду ${{\ddot {\theta }}} = - {{\theta }} + u$. Поэтому его движение можно изображать на тех же окружностях в плоскости $({{x}_{1}},{{y}_{1}})$, но в измененном времени, так что соответствующие дуги будут в ${{\omega }}$ раз длиннее. Согласно условию (2.6) полутраектория, составленная из дуг с угловыми мерами ${{\omega }}{{{{\tau }}}_{1}}$, ${{\omega }}\left( {{{{{\tau }}}_{2}} - {{{{\tau }}}_{1}}} \right)$, ${{\omega }}\left( {T - {{{{\tau }}}_{2}}} \right)$ тоже должна завершаться на вертикальной координатной оси. В одновременном выполнении соотношений ${{x}_{1}}\left( T \right) = 0$ и ${{x}_{2}}\left( T \right) = 0$ заключается вычислительная трудность отыскания моментов переключения ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$ при заданном значении T. Для режима движения с пятью переключениями из уравнений (3.6) при $t = T$, $j = 3$ (т.е. в конце третьего участка постоянства управления) получим

Существование режима движения с пятью переключениями управления (при заданном T) равносильно разрешимости системы (4.5) относительно ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, где $0 < {{{{\tau }}}_{1}} < {{{{\tau }}}_{2}} < T$.

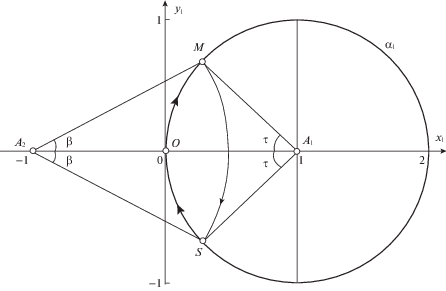
Утверждение 2. При любом значении ${{\omega }}$ в задаче (4.1)–(4.3) существует режим движения с пятью переключениями управления, при котором

Действительно, при подстановке соотношений (4.6) второе уравнение (4.5) становится тождеством, а первое уравнение (4.5) приобретает вид

откуда при оставлении слева только первого и последнего слагаемых получим

На фазовой плоскости $({{x}_{1}},{{y}_{1}})$ обсуждаемому движению O → M → S → O (рис. 3) соответствуют (в силу (4.6)) одинаковые угловые меры дуг OM = SO = ${{\tau }}$, ${{\tau }} = {{{{\tau }}}_{1}}$, изображающих движение при $u = 1$. Длительность второго участка MS (при $u = - 1$) определяется длиной дуги $2{{\beta }}$, где

В таких обозначениях имеем $T{\text{/}}2 = {{\tau }} + {{\beta }}$, $\left( {T - 2{{{{\tau }}}_{1}}} \right){\text{/}}2 = {{\beta }}$, так что с учетом $0 < T < 2{{\pi }}$, ${\text{sin}}\left( {T{\text{/}}2} \right) \ne 0$ уравнение (4.7) равносильно верному равенству

вытекающему из теоремы синусов для треугольника A₂MA₁. Из симметричного ему треугольника A₂SA₁ внутренний угол $\angle S$ = ${{\pi }} - \left( {{{\tau }} + {{\beta }}} \right)$ = ${{\pi }} - T{\text{/}}2$, будет определяться соотношением

При заданном значении ${{\omega }}$ можно геометрически определять на окружности ${{{{\alpha }}}_{1}}$ точку S (а также M), из которой отрезок A₂A₁ виден под заданным углом $\angle S$ (4.9). Далее будем обозначать ${{{{\tau }}}_{s}}$ – угловой размер дуги OS (а также дуги OM), ${{T}_{s}} = 2{{\pi /}}\omega $ – длительность найденной полутраектории с условием (4.6).

Утверждение 3. В задаче (4.1)–(4.3) при каждом значении $T \in \left( {0,{{T}_{s}}} \right]$ существует режим движения с пятью переключениями управления.

Подробное доказательство утверждения 3 приведено в Приложении.

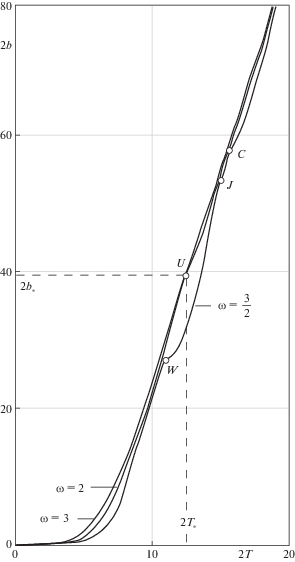
5. Результаты численных экспериментов. Для платформы с двумя осцилляторами (4.1) задача оптимального по быстродействию перемещения (4.2), (4.3) решалась численно при некоторых конкретных ${{\omega }}$. Для возрастающих значений времени 2T вычислялись величины наибольшей дальности 2b перемещения платформы, чтобы затем на графике обратить эту зависимость, т.е. для каждого перемещения 2b получать наименьшее время 2T.

Алгоритм сводился к подбору таких моментов переключения кусочно-постоянного управления, при которых в конце полутраектории достигались соотношения

Например, при поиске режима с пятью переключениями управления (в моменты времени ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, $T$, $2T - {{{{\tau }}}_{2}}$, $2T - {{{{\tau }}}_{1}}$) задавалось значение ${{{{\tau }}}_{1}}$, табулировалось ${{{{\tau }}}_{2}}$, при каждом из которых интегрировалась система (4.1) с начальными условиями (4.2) вплоть до фиксации такого момента T, когда выполнялись соотношения (5.1). Затем такая траектория проверялась на соответствие необходимым условиям оптимальности, для чего вновь интегрировалась система (4.1), (4.2), но уже при действии управляющей функции (3.1) в виде

Если эта функция обращалась в ноль только в упомянутые моменты времени ${{{{\tau }}}_{1}}$, ${{{{\tau }}}_{2}}$, $T$, $2T - {{{{\tau }}}_{2}}$, $2T - {{{{\tau }}}_{1}}$, то, согласно утверждению 1, управление признавалось соответствующим необходимым условиям оптимальности. Для проверки режимов с количеством переключений, большим пяти, согласно замечанию 4 применялась та же функция (5.2). Если требовалось проверить выполнение необходимых условий оптимальности для режима с тремя переключениями ${{{{\tau }}}_{1}}$, $T$, $2T - {{{{\tau }}}_{1}}$, то, в силу замечания 5, применялось управление в виде

Отметим, что раскрытие определителя ${{Q}_{2}}\left( t \right)$ дает функцию управления того же вида, что и найденную в ([1], с. 273) для платформы с одним осциллятором.

Далее приведем численные результаты для трех случаев.

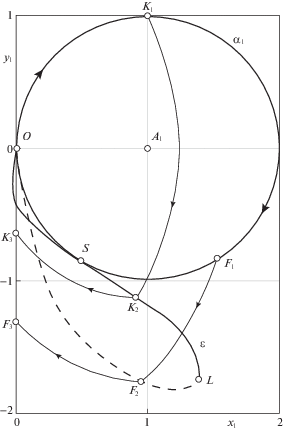
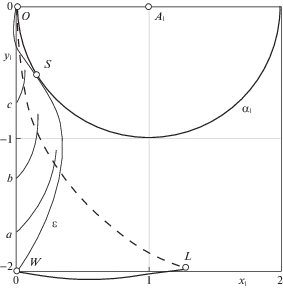
1. Случай ${{\omega }} = 2$. На рис. 4 показаны оптимальные полутраектории на фазовой плоскости $({{x}_{1}},{{y}_{1}})$ первого осциллятора. Изображающая точка выходит из пункта О с координатами (0, 0) и перемещается при $u\left( t \right) = 1$, $t \in \left( {0,{{{{\tau }}}_{1}}} \right)$ по окружности ${{{{\alpha }}}_{1}}$ с центром А₁(1, 0). После первого переключения управления, например, в точке K₁ с параметром ${{{{\tau }}}_{1}} = \pi {\text{/2}}$, движение продолжается при $u\left( t \right) = - 1$, $t \in \left( {{{{{\tau }}}_{1}},{{{{\tau }}}_{2}}} \right)$ по окружности с центром А₂(–1, 0) до переключения управления в точке K₂. Последний участок K₂K₃ полутраектории проходит при $u\left( t \right) = 1$, $t \in \left( {{{{{\tau }}}_{2}},T} \right)$ и завершается на оси ординат. Все точки окружности ${{{{\alpha }}}_{1}}$ (кроме O) являются точками первого переключения управления при разных значениях ${{{{\tau }}}_{1}}$. На рис. 4 показана линия ${{\varepsilon }}$, составленная из точек второго переключения управления. На ее первую часть OSL (сплошную) приходят точки из верхней полуокружности ${{\alpha }_{1}}$ (где ${{{{\tau }}}_{1}} \in \left( {0,{{\pi }}} \right]$), а на вторую часть (пунктирную) – из нижней полуокружности (где ${{{{\tau }}}_{1}} \in \left( {{{\pi }},2{{\pi }}} \right)$). Например, для полутраектории O → F₁ → F₂ → F₃ первое переключение происходит в точке F₁ (при ${{{{\tau }}}_{1}} = 4\pi {\text{/}}3$), а второе – в точке F₂. Случай, когда изображающая точка проходит до первого переключения всю окружность ${{{{\alpha }}}_{1}}$ (однократно или многократно), соответствует режиму с одним переключением управления, описанному в замечании 6. Построенные численно полутраектории с моментами первого переключения ${{{{\tau }}}_{1}}$ и $\left( {{{{{\tau }}}_{1}} + 2{{\pi }}} \right)$ на фазовой плоскости $({{x}_{1}},{{y}_{1}})$ отличаются лишь предварительным обходом окружности ${{{{\alpha }}}_{1}}$. То есть здесь $2{{T}_{*}} = 4{{\pi }}$ – период, через который повторяются все типы оптимальных движений осцилляторов. Для рассматриваемого случая ${{\omega }} = 2$ из соотношения (4.9) имеем $\angle S = \pi {\text{/}}2$, откуда ${{{{\tau }}}_{s}} = \pi {\text{/}}3$ – угловая мера дуги OS, смысл которой заимствован из рис. 3. В точке S окружность ${{\alpha }_{1}}$ касается линии ${{\varepsilon }}$.

2. Случай ${{\omega }} = 3$. На рис. 5 линия ${{\varepsilon }}$, составленная из точек второго переключения управления, имеет изломы. Смысл ее сплошной и пунктирной частей тот же, что и на рис. 4. В точке W, лежащей на оси ординат, совпали значения ${{{{\tau }}}_{2}}$ и T. Эта траектория – единственная для ${{\omega }} = 3$, реализуемая функцией оптимального управления (5.3) с тремя переключениями (в моменты времени ${{{{\tau }}}_{1}} = \pi {\text{/}}2$, $T = {{\pi }}$, $2T - {{{{\tau }}}_{1}} = 3\pi {\text{/}}2$). Режим с одним переключением соответствует полному обходу окружности ${{{{\alpha }}}_{1}}$ целое число раз. Все остальные режимы при ${{\omega }} = 3$ имеют пять переключений. На фазовой плоскости все типы оптимальных движений осцилляторов повторяются через период $2{{T}_{*}} = 4{{\pi }}$. Из соотношения (4.9) угол $\angle S = 2\pi {\text{/}}3$ задает точку S (касания линии ${{\varepsilon }}$ с окружностью ${{\alpha }_{1}}$) на конце дуги с угловой мерой OS ≈ 33°. На рис. 5 для сравнения показаны дуги a, b, c – фрагменты аналогов линии ${{\varepsilon }}$ соответственно при ω = 3.1, $\sqrt {12} $ и 5.

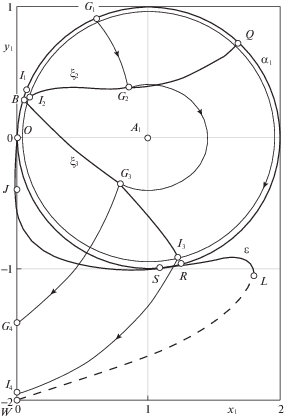
3. Случай ${{\omega }} = 3{\text{/}}2$. Здесь величина ${{T}_{*}} = 4{{\pi }}$ – в два раза больше, чем для целочисленных значений ${{\omega }}$. На рис. 6 показана лишь часть линии ${{\varepsilon }}$ второго переключения управления. В точки ее “сплошной” дуги OSL приходят траектории после переключения на верхней полуокружности ${{{{\alpha }}}_{1}}$ (с параметрами ${{{{\tau }}}_{1}} \in \left( {0,\pi } \right]$), а на “пунктирную” дугу LW – из участка нижней полуокружности ${{{{\alpha }}}_{1}}$. В точке W завершается полутраектория с параметрами ${{{{\tau }}}_{1}} \approx 4.571$, ${{{{\tau }}}_{2}} = T \approx 5.2575$. Ей соответствуют три переключения управления вместо пяти, которые встречались для всех случаев $T \in (0,5.2575)$. Согласно замечанию 7, пять переключений получились и при всех $T \in (7.3089,4{{\pi )}}$. Можно показать, что дуга LW линии ${{\varepsilon }}$ не имеет непрерывного продолжения и что в диапазоне $T \in (5.2575,7.3089)$ не существует оптимальных движений с пятью переключениями управления. Например, при $T = 2{{\pi }}$, ${{\omega }} = 3{\text{/}}2$ система (4.5) имеет единственное решение ${{{{\tau }}}_{1}} = 2\pi {\text{/}}9$, ${{{{\tau }}}_{2}} = 16\pi {\text{/}}9$, но оно может быть реализовано лишь при $u\left( t \right) = - 1$ для $t \in \left( {0,~{{{{\tau }}}_{1}}} \right)$, где получаемое в результате перемещение платформы невелико.

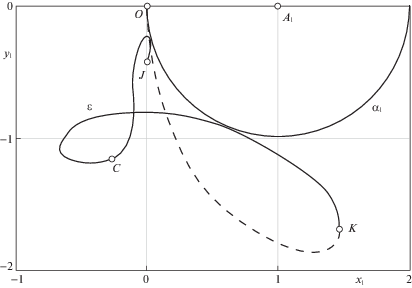
Численные расчеты показывают, что при $T \in (5.2575,7.3089)$ реализуются движения с семью переключениями управления, причем с увеличением значения T эволюция графика функции $u\left( t \right)$ происходит следующим образом. При T → 5.2575 продолжительность третьего промежутка постоянства управления стремится к нулю, т.е. ${{{{\tau }}}_{2}} \to T$, так что на интервале $t \in \left( {0,T} \right)$ остается лишь один момент переключения ${{{{\tau }}}_{1}} \approx 4.571$. При T = 5.2575 в график $u\left( t \right)$ в точке $t \approx 0.309$ “вставляется” узкий промежуток постоянства управления $u = - 1$, т.е. на интервале $t \in \left( {0,T} \right)$ становится сразу на два переключения больше. С дальнейшим ростом значения T “вставка” расширяется и дрейфует вправо. На рис. 6 упомянутому значению ${{{{\tau }}}_{1}} \approx 4.571$ соответствует точка B. Из нее выходят линия второго переключения BQ, обозначенная ${{{{\xi }}}_{2}}$, и линия третьего переключения BR, обозначенная ${{{{\xi }}}_{3}}$. Например, при $T = 2{{\pi }}$ полутраектория имеет вид O → G₁ → G₂ → G₃ → G₄, где ${{{{\tau }}}_{1}} \approx 1.17050$, ${{{{\tau }}}_{2}} \approx 1.46418$, ${{{{\tau }}}_{3}} \approx 5.51026$. Полутраектория O → I₁ → I₂ → I₃ → I₄, реализуется управлением с переключениями в моменты времени ${{{{\tau }}}_{1}} \approx 0.30987$, ${{{{\tau }}}_{2}} \approx 0.31977$, ${{{{\tau }}}_{3}} \approx 4.56519$, $T \approx 5.27637$. Точка I₄ на оси ординат близка к точке W, как близки и соответствующие им значения T. С этой полутраекторией “согласована” (в смысле замечания 7) кривая с параметрами ${{{{\tau }}}_{1}} \approx 2.32350$, ${{{{\tau }}}_{2}} \approx 2.33340$, ${{{{\tau }}}_{3}} \approx 6.57882$, $T = 7.2900$. Для нее первое и второе переключения происходят (на линиях ${{{{\alpha }}}_{1}}$ и ${{{{\xi }}}_{2}}$) в двух точках, близких к Q. Третье переключение – на линии ${{{{\xi }}}_{3}}$ возле точки B, а четвертое – на оси ординат возле точки J. Из этой точки J далее выходит линия второго переключения управления в режимах при $T \in \left( {7.3089,4\pi } \right)$, которые показаны на рис. 7 и реализуются с пятью переключениями управления. Здесь участок JC – единственный, где с ростом T убывает значение ${{{{\tau }}}_{1}}$ (от ≈379° до ≈322°). От точки K (где ${{{{\tau }}}_{1}} = 3{{\pi }}$) до точки O (где ${{{{\tau }}}_{1}} = 4{{\pi }}$), линия второго переключения управления показана пунктиром. Таким образом, на рис. 6 показана первая часть линии ${{\varepsilon }}$ (в виде OSLW), а на рис. 7 – ее вторая часть (в виде JCKO). В промежуток между точками W и J на ось ординат приходят полутраектории после трех переключений (на линиях ${{{{\alpha }}}_{1}}$, ${{{{\xi }}}_{2}}$ и ${{{{\xi }}}_{3}}$).

Заметим, что на рис. 6 после достижения линией ${{\varepsilon }}$ оси ординат (в точке W) с дальнейшим ростом параметра T начинаются режимы с семью переключениями управления. Аналогичным свойством обладают дуги a, b, c на рис. 5, т.е. при ${{\omega }} > 3$ линии второго переключения сразу после касания (в точке S) с окружностью ${{{{\alpha }}}_{1}}$ устремляются к оси ординат, где начинаются режимы с числом переключений, большим пяти.

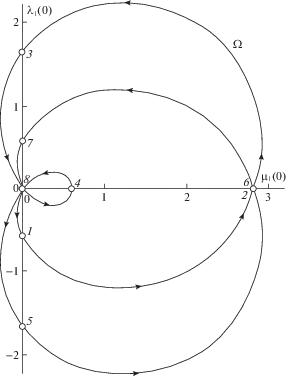
Для случая ${{\omega }} = 3{\text{/}}2$ диаграмма начальных значений ${{{{\mu }}}_{1}}\left( 0 \right)$, ${{{{\lambda }}}_{1}}\left( 0 \right)$ компонент сопряженного вектора показана на рис. 8 в виде непрерывной линии ${{\Omega }}$, точки которой параметризованы величинами $T \in (0,{{T}_{*}}]$, ${{T}_{*}} = 4{{\pi }}$. Замкнутость этой кривой обусловлена ранее упомянутой (после замечания 6) периодичностью функций. При этом линия симметрична в силу замечания 2, а из соотношений (5.2) следует

где ${{c}_{1}}$ – константа интегрирования, вычисляемая при фиксированном T и равная алгебраическому дополнению элемента “21” в определителе ${{Q}_{3}}\left( t \right)$.

На рис. 8 на линии ${{\Omega }}$ номерами помечены точки с параметрами $T = i\pi {\text{/}}2$ ($i = 1,2, \ldots ,8$), причем точки с нечетными i лежат на оси ординат, а с четными – на оси абсцисс. “Прочитывая” последовательно номера i, можно следить за ростом параметра $T$ вдоль кривой ${{\Omega }}$: она выходит из начала координат (при $i = 0$) и возвращается в него (при $i = 8$), попутно дважды заходя в него при $T \approx 5.2575$ и $T \approx 7.3089$. При этих значениях T, согласно замечанию 5, определитель ${{Q}_{3}}\left( t \right)$ (5.2) заменяется на ${{Q}_{2}}\left( t \right)$ (5.3), так что в формуле (5.4) следует взять ${{c}_{1}} = {{{{\tau }}}_{1}} - T$. На рис. 8 маленькая внутренняя петля соответствует диапазону $T \in (5.2575,7.3089)$, т.е. движениям с семью переключениями управления.

На рис. 9 показаны оптимальные зависимости безразмерной дальности 2b перемещения платформы от безразмерного времени 2T при трех разных ${{\omega }}$. Для целочисленных значений ${{\omega }}$ имеем $2{{T}_{*}} = 4{{\pi }}$, $2{{b}_{*}} = 4{{{{\pi }}}^{2}}$, поэтому линии ${{\omega }} = 2$ и ${{\omega }} = 3$ имеют общую точку $U(4\pi ,4{{\pi }^{2}})$. Дуге WJ соответствуют движения с семью переключениями управления при ${{\omega }} = 3{\text{/}}2$. На этой же линии участок JC – единственный, где с ростом T убывает ${{{{\tau }}}_{1}}$. После точки C линия ${{\omega }} = 3{\text{/}}2$ вновь “отстает” от двух других, но при $2T > 19$ они становятся весьма близки и пересекаются втроем при $2T = 8{{\pi }}$.

Заключение. Все построенные на рис. 4–7 полутраектории (вместе с их симметричными продолжениями) удовлетворяют необходимым условиям оптимальности в виде принципа максимума Понтрягина, поскольку реализованы посредством управлений вида (5.2) (с пятью или семью переключениями), вида (5.3) (с тремя переключениями) либо с одним переключением (по замечанию 6). Для платформы с двумя осцилляторами типы оптимальных траекторий оказались существенно зависящими от отношения $\omega $ двух частот системы. При рациональных значениях $\omega $ существует значение дальности перемещения, для которой возможно “тривиальное” оптимальное движение с одним переключением управления (за время $2{{T}_{*}}$). Кроме того, численные эксперименты демонстрируют повторяемость оптимальных режимов с периодом $2{{T}_{*}}$. В случае иррациональных значений $\omega $ не только исключается возможность “тривиального” режима, но и возникает проблема формального представления зависимости дальности перемещения системы от задаваемого времени $2T$. Эта зависимость не может быть предъявлена в каком-либо завершенном виде из-за непредсказуемого появления все новых типов движений с бесконечным ростом значений $2T$.

Случай ${{\omega }} = 2$ оказался единственным (среди целочисленных), где все оптимальные перемещения, кроме “тривиального”, реализуются только с пятью переключениями управления. При любых ${{\omega }}$ для малых значений дальности оптимальные управления имеют пять переключений. Чем больше ${{\omega }}$, тем раньше (по времени маневрирования) функция управления эволюционирует к виду, имеющему семь переключений, при этом проходя через критическую форму с тремя переключениями.

Приложение. Для доказательства утверждения 3 нужно обосновать, что при каждом значении $T \in \left( {0,{{T}_{s}}} \right]$ у системы уравнений (4.5) найдутся корни $0 < {{{{\tau }}}_{1}} < {{{{\tau }}}_{2}} < T$.

Поскольку случай $T = {{T}_{s}}$ уже упомянут в утверждении 2, то далее положим $T < {{T}_{s}}$. Обозначая длительности промежутков постоянства управления ${{\tau }} = {{{{\tau }}}_{1}}$, ${{\sigma }} = {{{{\tau }}}_{2}} - {{{{\tau }}}_{1}}$, ${{\delta }} = T - {{{{\tau }}}_{2}}$, запишем первое уравнение (4.5) в виде

На рис. 2 промежуткам времени ${{\tau }}$, ${{\sigma }}$, ${{\delta }}$ соответствуют угловые меры дуг ON₁, N₁N₂, N₂N₃. Точка N₂ должна лежать вне круга с границей ${{{{\alpha }}}_{1}}$, иначе из нее не удастся попасть на ось ординат при $u = 1$. Отсюда следует ${{N}_{1}}{{N}_{2}} \geqslant {{N}_{1}}E$, т.е.

Для решения системы (4.5) достаточно найти такие корни ${{\tau }}$, ${{\sigma }}$, ${{\delta }}$ уравнения (П.1), которые удовлетворят ему и при их замене на ${{\omega \tau }}$, ${{\omega \sigma }}$, ${{\omega \delta }}$. Такое изменение масштаба в ${{\omega }}$ раз рассмотрим на координатной плоскости. На рис. 10 показана зависимость 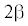от ${{\tau }}$ (4.8) в виде кривой g, которая выпукла вверх. На этой же плоскости введем координаты ${{\delta }}$, ${{\sigma }}$ и построим линии, заданные уравнениями (П.1) при каждом фиксированном значении ${{\tau }}$. На рис. 2 при заданном значении ${{\tau }}$ (т.е. при выборе точки N₁) наименьшему значению ${{\sigma }} = 2{{\beta }}$ (в точке E) соответствует наименьшее значение ${{\delta }} = {{\tau }}$. Поэтому при заданном ${{\tau }}$ уравнение (П.1) на рис. 10 опишет кривую ${{{{\gamma }}}_{1}}$, выходящую из точки ${{E}_{1}}\left( {{{\tau }},2{{\beta }}\left( {{\tau }} \right)} \right) \in g$. Если каждой точке кривой ${{{{\gamma }}}_{1}}$ поставить в соответствие числовой параметр $T = {{\tau }} + {{\sigma }} + {{\delta }}$, то значению $T = 2{{\pi }}$ будет соответствовать точка ${{Z}_{1}}\left( {{{\tau }},2{{\pi }} - 2{{\tau }}} \right)$. Действительно, подставляя $T = 2{{\pi }}$ в (3.10), получим ${\text{cos}}\,{{\delta }} = {\text{cos}}\left( {{{\sigma }} + {{\delta }}} \right)$, откуда

Если же подставить $T = 2{{\pi }}$ в первое уравнение (4.5), то получим $\cos {{{{\tau }}}_{2}} = \cos {{{{\tau }}}_{1}}$, т.е. ${\text{cos}}\left( {{{\tau }} + {{\sigma }}} \right)$ = $\cos {{\tau }}$, откуда следует ${{\sigma }} + 2{{\tau }} = 2{{\pi }}$. Таким образом, на плоскости с координатами ${{\delta }}$, ${{\sigma }}$ точка ${{Z}_{1}}$ располагается над точкой ${{E}_{1}}$ и принадлежит прямой l с уравнением (П.3). На дуге ${{E}_{1}}{{Z}_{1}}$ точку с параметром $T = 2{{\pi /}}\omega $ обозначим ${{H}_{1}}$.

Дифференцируя (П.1) по ${{\sigma }}$ (при ${{\tau }} = {\text{const}}$) и выражая отсюда $d{{\delta /}}d{{\sigma }}$, можно показать, что функция ${{\delta }}\left( {{\sigma }} \right)$ на отрезке ${{\sigma }} \in \left[ {2{{\beta }}\left( {{\tau }} \right),2{{\pi }} - 2{{\tau }}} \right]$ имеет единственный экстремум. При этом ${{d}^{2}}{{\delta /}}d{{{{\sigma }}}^{2}} < 0$, а также $d{{\delta /}}d{{\sigma }} \to - 1{\text{/}}2$ при $T \to 2{{\pi }}$, т.е. точки ${{E}_{1}}$ и ${{Z}_{1}}$ соединяет кривая ${{{{\gamma }}}_{1}}$, “выпуклая вправо” и касающаяся прямой l в точке ${{Z}_{1}}$. Семейство таких кривых (при каждом фиксированном ${{\tau }} \in \left( {0,{{\pi }}} \right)$), выходящих из точек линии g, изображает множество решений уравнения (П.1) в диапазоне значений ${{\tau }} + {{\sigma }} + {{\delta }} \leqslant 2{{\pi }}$.

Используем эти линии для графического решения системы (4.5) по следующей схеме. Задав конкретное значение ${{\omega }}$, определим из (4.9) угол $\angle S$ и найдем угловой размер ${{{{\tau }}}_{s}}$ дуги OS, равный моменту переключения управления в точке M на рис. 3. Для произвольного ${{\tau }} \in (0,{{{{\tau }}}_{s}})$ рассматриваем соответствующую ему кривую ${{{{\gamma }}}_{1}}$ (в виде ${{E}_{1}}{{Z}_{1}}$), а для значения ${{\omega \tau }}$ – аналогичную кривую ${{{{\gamma }}}_{2}}$, соединяющую точки ${{E}_{2}}\left( {{{\omega \tau }},2{{\beta }}\left( {{{\omega \tau }}} \right)} \right) \in g$ и ${{Z}_{2}}\left( {{{\omega \tau }},2{{\pi }} - 2{{\omega \tau }}} \right) \in l$ (рис. 10). На кривой ${{{{\gamma }}}_{1}}$ выделяем участок ${{E}_{1}}{{H}_{1}}$, где в точке ${{H}_{1}}$ параметр $T = 2{{\pi /}}\omega $.

Покажем, что при гомотетии с центром O и коэффициентом 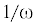(т.е. при сжатии плоскости в ${{\omega }}$ раз) образ ${{{{\gamma }}}_{3}}$ кривой ${{{{\gamma }}}_{2}}$ пересечет дугу ${{E}_{1}}{{H}_{1}}$ в ее внутренней точке. Действительно, прямоугольный треугольник ${{E}_{2}}{{Z}_{2}}{{D}_{2}}$, описанный около кривой ${{{{\gamma }}}_{2}}$, отобразится в ${{E}_{3}}{{Z}_{3}}{{D}_{3}}$ (рис. 10). Точка ${{E}_{3}}$ окажется ниже ${{E}_{1}}$ в силу выпуклости кривой g (по неравенству Йенсена). Точка ${{Z}_{3}}\left( {{{\tau }},\frac{{2{{\pi }}}}{{{\omega }}} - 2{{\tau }}} \right)$ попадет на вертикаль ${{E}_{3}}{{E}_{1}}$, причем выше точки ${{E}_{1}}$, поскольку $\frac{{2{{\pi }}}}{{{\omega }}} - 2{{\tau }} > 2{{\beta }}\left( {{\tau }} \right)$ (это следует из $\frac{{2{{\pi }}}}{{{\omega }}}$ = $2{{{{\tau }}}_{s}} + 2{{\beta }}\left( {{{{{\tau }}}_{s}}} \right)$ > $2{{\tau }} + 2{{\beta }}\left( {{\tau }} \right)$, так как ${{{{\tau }}}_{s}} > {{\tau }}$ и функция ${{\varphi }}\left( {{\tau }} \right)$ = ${{\tau }} + {{\beta }}\left( {{\tau }} \right)$ – монотонно возрастающая). Через точку ${{Z}_{3}}$ пройдет образ прямой l в виде прямой ${{Z}_{3}}{{D}_{3}}$ с уравнением ${{\sigma }} = \frac{{2{{\pi }}}}{{{\omega }}} - 2{{\delta }}$. Точка ${{H}_{1}}$ лежит выше прямой ${{Z}_{3}}{{D}_{3}}$, ибо ее координаты ${{{{\delta }}}_{h}}$, ${{{{\sigma }}}_{h}}$ удовлетворяют условию ${{{{\sigma }}}_{h}} > \frac{{2{{\pi }}}}{{{\omega }}} - 2{{{{\delta }}}_{h}}$. Это следует из соотношений ${{\sigma }_{h}} + {{\delta }_{h}} + {{\delta }_{h}}$ > ${{\sigma }_{h}} + {{\delta }_{h}} + {{\tau }_{h}}$ = $\frac{{2{{\pi }}}}{{{\omega }}}$ в силу ${{{{\delta }}}_{h}} > {{{{\tau }}}_{h}}$.

Поскольку вертикальный отрезок ${{Z}_{3}}{{E}_{3}}$ содержит точку ${{E}_{1}}$ внутри, а наклонная прямая ${{Z}_{3}}{{D}_{3}}$ пересекает дугу ${{E}_{1}}{{H}_{1}}$, то и кривая ${{{{\gamma }}}_{3}}$ (соединяющая ${{Z}_{3}}$ и${{E}_{3}}$, располагаясь левее ${{Z}_{3}}{{D}_{3}}$) пересечет дугу ${{E}_{1}}{{H}_{1}}$ в некоторой точке ${{X}_{1}}$. Ее координаты ${{\delta }}$, ${{\sigma }}$ вместе с выбранным значением ${{\tau }}$ являются решением уравнения (3.10), как и кратные им значения ${{\omega \delta }}$, ${{\omega \sigma }}$, ${{\omega \tau }}$, поскольку гомотетичная точка ${{X}_{2}}\left( {{{\omega \delta }},~{{\omega \sigma }}} \right)$ лежит на кривой ${{{{\gamma }}}_{2}}$ с параметром ${{\omega \tau }}$. Значит, при любом $T \in \left( {0,{{T}_{s}}} \right]$ система (4.4), (4.5) имеет решение, что доказывает утверждение 3.