Прикладная математика и механика, 2022, T. 86, № 1, стр. 18-34

1. Введение. Формулировки задач о плоскопараллельном течении слоев идеальной несжимаемой жидкости в бесконечном горизонтальном канале хорошо известны. В частности, в случае одного слоя с одной твердой и другой свободной границами – это задача о поведении мелкой воды. Более сложные варианты, например, когда течение нескольких слоев жидкости происходит в канале с твердыми плоскими границами подробно описаны ранее [1–5]. Интерес к таким задачам объясняется тем, что они достаточно просто описывают неустойчивости либо Рэлея–Тейлора (в случае различной плотности слоев жидкости), либо Кельвина–Гельмгольца (в случае слоев жидкости, движущихся с различными скоростями), позволяя получать важную информацию о наиболее типичная чертах указанных неустойчивостей.

В предлагаемой работе рассмотрена одна из наиболее простых, с математической точки зрения, моделей – течение двухслойной жидкости в канале с твердыми крышками, когда слои жидкости с малой разницей плотности движутся с различными скоростями ([1], модель III; [2], с. 133–140; [3], с. 56–58). Основное внимание фокусируется на способе конструирования решения задачи Коши для системы двух квазилинейных уравнений гиперболического типа в частных производных первого порядка. Для этих целей используется метод годографа на основе закона сохранения, предложенный первоначально в [6], и развитый в ряде работ [7–11]. Заметим, что такой метод можно применять и для решения уравнений эллиптического типа (см., напр., [10, 12–14]) и, в частности, практически для всех задач о неустойчивых сплошных средах, описанных в [15]. Уместно напомнить, что для рассматриваемой задачи о двухслойной мелкой воде при большой разнице между скоростями движения слоев (больше единицы в безразмерных переменных) гиперболический тип уравнений изменяется на эллиптический ([1], модель III; [2], с. 133–140). Метод годографа с дополнительными модификациями позволяет преобразовать решение исходной задачи Коши для системы двух квазилинейных уравнений, записанной в инвариантах Римана, в некоторую задачу для одного линейного уравнения в частных производных второго порядка с переменными коэффициентами. Такой метод эффективен, когда имеется явная зависимость между исходными переменными и инвариантами Римана, а также явное выражение для функции Римана–Грина соответствующего линейного уравнения. Для указанной модели ([1], модель III, [2], с. 133–140; [3], с. 56–58) явная зависимость между инвариантами Римана известна. Более того, замена переменных переводит уравнения двухслойной мелкой воды (для рассматриваемой модели) к обычным уравнениям мелкой воды, точнее к уравнениям некоторого политропного газа. Однако, инварианты Римана, приведенные в ([1], с. 11, (3.5)), неоднозначно связаны с исходными переменными – содержат радикалы, выбор знака перед которыми далеко нетривиален. Аналогичная неоднозначность возникает и при замене переменных, приводящих уравнения двухслойной мелкой воды к уравнениям обычной мелкой воды в ([1], с. 13, (4.1), (4.3)).

В предлагаемой работе предложена замена переменных, позволяющая устранить неоднозначность между исходными переменными и инвариантами Римана, а также для соответствующего линейного уравнения метода годографа найти явное выражение функции Римана–Грина (гипергеометрическая функция). В конечном итоге, это позволяет построить неявное двухпараметрическое решение исходной задачи Коши. Явное решение задачи восстанавливается на линиях уровня неявного решения при помощи интегрирования некоторой задачи Коши для системы обыкновенных дифференциальных уравнений.

Во избежание недоразумений, вновь, подчеркнем, что несмотря на то, что задача о поведении двухслойной мелкой воды под крышкой достаточно хорошо исследована (см. например, [1–3]), точное решение задачи Коши, насколько известно авторам, отсутствует.

2. Постановка задачи. Уравнения для описания поведения двухслойной идеальной несжимаемой жидкости с малым скачком плотности в безразмерных переменных возьмем в форме (приближение мелкой воды)

дополнив их начальными условиями

Здесь $h\left( {x,t} \right)$ – положение границы раздела слоев жидкости, ${v}\left( {x,t} \right)$ – полуразность скоростей верхнего и нижнего слоев (см. рис. 1), ${{h}_{0}}\left( x \right)$, ${{{v}}_{0}}\left( x \right)$ – заданные функции, определяющие первоначальное расположение границы раздела между жидкостями и полуразность скоростей движения слоев.

Уравнения (2.1) предложены в ([2], с. 67, (9.22)) и ([1], Модель III), в которых они представлены в ином виде (для слоя $0 < \tilde {h} < 1$)

Переход от (2.3) к (2.1) производится при помощи замены $2\tilde {h} \to \left( {h + 1} \right)$. Другой вариант замены уравнений (2.3), осуществляющий переход от слоя $0 < \tilde {h} < 1$ к слою $\left| h \right| < 1$, использован в ([2], с. 135, (3.6)).

Область ${{\Omega }}$, в которой уравнения (2.1) имеют гиперболический тип, определяется неравенствами

Известно (см., например, [16]), что в процессе эволюции решение $h\left( {x,t} \right)$, ${v}\left( {x,t} \right)$ может покидать пределы области ${{\Omega }}$. В частности, при $\left| {v} \right| = 1$ происходит “слияние” двух вещественных характеристик уравнений (2.1) в одну кратную характеристику, а при $\left| {v} \right| > 1$ уравнения имеют эллиптический тип. Более подробное описание процессов при переходе в область $\left| {v} \right| > 1$ имеется в монографии ([2], с. 133–140), в которой, в частности, указано, что переход их области гиперболичности в область эллиптичности в случае классических (неразрывных) решений невозможен ([2], с. 135).

2.1. Замена переменных и инварианты Римана. Задача Коши (2.1), (2.2) после замены переменных

принимает вид

Используя обычную технику (см., например, [16], с. 27–31) нетрудно найти инварианты Римана ${{R}^{1}}$, ${{R}^{2}}$ и соответствующие характеристические направления ${{{{\lambda }}}^{1}}$, ${{{{\lambda }}}^{2}}$

Хорошо известно, что инварианты Римана могут быть определены различными способами – произвольная функция от инварианта также является инвариантом. В частности, аналогом инвариантов ([1], с. 11, (3.5)) для уравнений (2.1) будут

Связь между инвариантами ${{\tilde {R}}^{1}}$, ${{\tilde {R}}^{2}}$ и исходными переменными определяется уравнениями

Уравнения (2.11), в итоге, например, для $h$ приводят к уравнению четвертого порядка, и величины $h$ и ${v}$ не могут быть однозначно определены по ${{\tilde {R}}^{1}}$, ${{\tilde {R}}^{2}}$.

Напротив, предложенная замена (2.5) приводит к взаимнооднозначному соответствию $({{R}^{1}},{{R}^{2}})$ $ \rightleftarrows $ $(h,{v})$, естественно, при условии $( - {{\pi /2}} < {{\xi }}$, ${{\eta }} < {{\pi /2}})$. Более того, при любых эволюциях решения $\left( {h,{v}} \right) \in {{\Omega }}$ (см. (2.4), (2.5)), то есть уравнения (2.5) (и (2.1)), всегда являются гиперболическими. Нетрудно понять, что для исследования уравнений в эллиптической области удобно, например, использовать замену $h = \sin \xi $, ${v} = \operatorname{ch} \eta $, $\left| h \right| < 1$, $\left| {v} \right| > 1$ (см. [14]).

2.2. Задача Коши для инвариантов Римана. Записанная для инвариантов Римана задача Коши, соответствующая (2.6), (2.7) (или (2.1), (2.2)), имеет вид

где $R_{0}^{1}\left( x \right)$, $R_{0}^{2}\left( x \right)$ – заданные функции, ${{\lambda }}({{R}^{1}},{{R}^{2}})$, ${{\lambda (}}{{R}^{1}},{{R}^{2}}{\text{)}}$ определены с учетом (2.8), (2.9).

Основная цель работы – построение неявного двухпараметрического решения задачи Коши (2.12), (2.13) и указание способа (как правило, численного) восстановления явного решения на линиях уровня неявного решения (изохронах).

3. Построение решения. Для построения решения задачи Коши (2.12), (2.13) применяем метод годографа на основе закона сохранения, впервые предложенный в [6] и развитый в [10], а также использованный в ряде работ [7–9, 11]). На самом деле можно использовать и иные варианты метода – классический вариант (взаимозамена зависимых и независимых переменных $({{R}^{1}},{{R}^{2}}) \rightleftarrows \left( {{{\xi }},{{\eta }}} \right)$, см., например, ([16], с. 33, 34)), или обобщенный метод годографа [17]. Почти очевидно, что, в конечном итоге, все указанные методы приведут к одинаковому результату. С точки зрения авторов, метод на основе закона сохранения более “прозрачен” и лучше приспособлен к решению задачи Коши для системы двух квазилинейных уравнений гиперболического типа. В данном разделе описание метода дается для общего случая произвольных зависимостей ${{{{\lambda }}}^{1}}({{R}^{1}},{{R}^{2}})$, ${{{{\lambda }}}^{2}}({{R}^{1}},{{R}^{2}})$ и лишь затем рассмотрен конкретный вариант (2.9).

3.1. Неявное двухпараметрическое решение. Следуя [6, 10] двухпараметрическое неявное решение задачи Коши (2.12), (2.13) разыскиваем в виде

где $a$, $b$ – параметры.

Для определения связи между переменными $\left( {x,t} \right)$ и параметрами $\left( {a,b} \right)$ в форме

используем закон сохранения где ${{\varphi }}$, ${{\psi }}$ – плотность и плотность потока закона сохранения.

Выполняя дифференцирование в (3.3), и исключая при помощи (2.12) производные, например, $R_{t}^{1}$, $R_{t}^{2}$, получаем линейную систему для определения функций ${{\varphi }}({{R}^{1}},{{R}^{2}})$, ${{\psi (}}{{R}^{1}},{{R}^{2}}{\text{)}}$

Условия разрешимости уравнений (3.4) приводят к линейному дифференциальному уравнению в частных производных второго порядка для функции ${{\varphi }}$ (аналогичное для функции ${{\psi }}$)

которое дополняем условиями (см. [10], условия модифицированы по сравнению с [6])

Легко показать, что решение задачи (3.4)–(3.6) имеет вид

где ${{\Phi }}({{R}^{1}},{{R}^{2}}\,|\,{{r}^{1}},{{r}^{2}})$ – функция Римана–Грина уравнения (3.5), которая по переменным ${{R}^{1}}$, ${{R}^{2}}$ удовлетворяет уравнению (3.5), а по переменным ${{r}^{1}}$, ${{r}^{2}}$ – сопряженному уравнению, функцию ${{\varphi }}({{R}^{1}},{{R}^{2}}\,|\,{{r}^{1}},{{r}^{2}})$, по аналогии с функцией Римана–Грина, удобно записывать как зависящую от параметров ${{r}^{1}}$, ${{r}^{2}}$.

Действительно, дифференцируя соотношения (3.6) соответственно по ${{R}^{2}}$ и ${{R}^{1}}$, с учетом (3.4) получим условия, возникающие при определении функции Римана–Грина (см. [18], с. 446–457), а дополнительный множитель в формуле (3.7) появляется из условий (3.6) если положить ${{R}^{1}} = {{r}^{1}}$, ${{R}^{2}} = {{r}^{2}}$ и учесть нормировку ${{\Phi }}({{r}^{1}},{{r}^{2}}\,|\,{{r}^{1}},{{r}^{2}})$ = 1.

Функция $t\left( {a,b} \right)$, связывающая переменную $t$ с $a$, $b$, определяется соотношением

Здесь приведен частный вид формулы, справедливый для случая, когда начальные условия задаются при $t = 0$. Более общий вид формулы для начальных данных задаваемых на некоторой кривой в плоскости $\left( {x,t} \right)$ см. в [6, 10], а также [7–9, 12]. Опуская подробности, укажем, что соотношение (3.8) получено интегрированием по замкнутому контуру PQM дифференциальной 1-формы $\left( {\psi dt - \varphi dx} \right)$, соответствующей закону сохранения (3.3). Часть контура PQ – это отрезок $\left[ {a,b} \right]$ на оси $t = 0$. Части контура QM, PM отвечают характеристикам, соответственно, $dx = {{\lambda }^{1}}dt$ и $dx = {{\lambda }^{2}}dt$, на которых сохраняются инварианты Римана – ${{R}^{1}} = {{r}^{1}}\left( b \right)$ и ${{R}^{2}} = {{r}^{2}}\left( a \right)$ (см. рис. 2). Фактически, значения ${{r}^{1}}\left( b \right)$, ${{r}^{2}}\left( a \right)$ идентифицируют характеристики.

Аналогичным образом определяется функция $x\left( {a,b} \right)$, необходимая для окончательного построения неявного решения (3.1), (3.2). Однако, для нахождения явного решения функция $x\left( {a,b} \right)$, непосредственно, не требуется (см. [10]).

Обратим внимание на то, что роль “параметров” $a$, $b$ достаточно многогранна. Во-первых, можно считать, что $a$, $b$ – это обычные числовые параметры, задающие двухпараметрическое решение. Во-вторых, если при помощи (3.2) удается построить обратные функции $a = a\left( {x,t} \right)$, $b = b\left( {x,t} \right)$, то (3.1) попросту является явным решением задачи. В-третьих, ввиду (3.1), величины $a$, $b$ можно считать инвариантами Римана, так как функции от инвариантов Римана также инварианты. Наконец, в-четвертых, $a$, $b$ – это лагранжевы переменные, то есть значения координаты $x$ в момент $t = 0$. Последнее, в частности, означает, что построен аналог метода характеристик для системы двух квазилинейных уравнений – начальные данные из точек $x = a$, $x = b$ оси $x$ переносятся вдоль характеристик $PM$, $QM$ в точку $M$ (см. рис. 2).

3.2. Явное решение на изохронах. Для построенния явного решения на плоскости $\left( {a,b} \right)$ рассматриваем линии уровня функции $t\left( {a,b} \right)$ (изохроны). Задавая значение ${{t}_{{\text{*}}}}$, выбираем некоторую изохрону, считая ее параметризованной при помощи параметра $\mu $

где ${{t}_{{\text{*}}}}$ – момент времени, идентифицирующий линию уровня, $a\left( {{\mu }} \right)$, $b\left( {{\mu }} \right)$ – значения $a$, $b$, соответствующие параметру ${{\mu }}$.

Считая изохрону достаточно гладкой (кусочно-гладкой), и дифференцируя соотношение (3.9) по параметру ${{\mu }}$, получаем задачу Коши для обыкновенных дифференциальных уравнений (подробнее см. ([10], с. 46–51))

где $({{a}_{*}},{{b}_{*}})$ – точка на изохроне, соответствующая ${{\mu }} = 0$, функция $X\left( {{\mu }} \right)$ отвечает координате $x$ на изохроне: $X\left( \mu \right)$ = $x\left( {a,b} \right)$ = $x\left( {a\left( \mu \right),b\left( \mu \right)} \right)$, ${{X}_{{\text{*}}}}$ – значение координаты $x$ на изохроне при ${{\mu }} = 0$, производные ${{t}_{a}}\left( {a,b} \right)$, ${{t}_{b}}\left( {a,b} \right)$ вычисляются при помощи (3.8), $J\left( {a,b} \right)$ – якобиан преобразования $\left( {a,b} \right)$ $ \rightleftarrows $ $\left( {x,t} \right)$.

Таким образом, интегрируя задачу Коши (3.10), с учетом (3.1) для момента времени ${{t}_{{\text{*}}}}$ получаем явное решение, которое полностью определяется начальными данными $R_{0}^{1}\left( x \right)$, $R_{0}^{2}\left( x \right)$

Конечно, предварительно следует решить задачу (3.5), (3.6) для нахождения функции ${{\varphi }}$, входящую в соотношение (3.8). Ограничения накладываемые на начальные данные, фактически, определяются условиями существования интеграла (3.8), в частности, $R_{0}^{1}\left( x \right)$, $R_{0}^{2}\left( x \right)$ могут быть кусочно-гладкими функциями и даже кусочно-непрерывными (в этом случае потребуются дополнительные условия на разрывах, см., например, [27]).

Заметим, что явное решение (3.12), по-прежнему, является двухпараметрическим. Роль параметров играют момент времени ${{t}_{{\text{*}}}}$ и ${{\mu }}$. На практике, вычисление интегралов в выражениях для $t\left( {a,b} \right)$, ${{t}_{a}}\left( {a,b} \right)$, ${{t}_{b}}\left( {a,b} \right)$ сводится к решению некоторых задач Коши для обыкновенных дифференциальных уравнений, что существенно упрощает вычисления (подробнее см. [10]).

Наконец, обратим внимание на то, что правая часть уравнения для $X\left( {{\mu }} \right)$ совпадает с якобианом $J\left( {a,b} \right)$ преобразования $\left( {a,b} \right)$ $ \rightleftarrows $ $\left( {x,t} \right)$ (см. (3.11)). В частности, это означает, что знак производной $dX(\mu ){\text{/}}d\mu $ может измениться, и при нарушении монотонности функции $X\left( {{\mu }} \right)$ по параметру ${{\mu }}$ на изохроне может возникнуть неоднозначность решения по переменной $x$. Иными словами, метод позволяет строить опрокидывающиеся (неоднозначные) решения, конечно, если физический смысл задачи, как в случае границы раздела между двумя слоями жидкости, допускает такие решения.

4. Функция Римана–Грина для уравнения (3.5). Для нахождения функции $t\left( {a,b} \right)$ требуется функция ${{\varphi }}({{R}^{1}},{{R}^{2}}\,|\,{{r}^{1}},{{r}^{2}})$, определяемая, в свою очередь, функцией Римана–Грина уравнения (3.5) (см. (3.7)). Именно возможность явного определения функции Римана–Грина является ключевым фактором эффективности метода, описанного в разд. 2.

Уравнение (3.5) удобно представить в общей форме

где коэффициенты $A({{R}^{1}},{{R}^{2}})$, $B({{R}^{1}},{{R}^{2}})$, $C({{R}^{1}},{{R}^{2}})$ определены соотношениями (с учетом (2.9))

Вычисляя инварианты Лапласа $k$ и $h$ ([19], с. 117, (3.2)), а также инварианты Овсянникова $p$ и $q$ ([19], с. 120, (4.6)), имеем

Это означает, что в соответствии с классификационной теоремой ([19], с. 123) уравнение (4.1), (4.2) эквивалентно одному из вариантов уравнения Эйлера–Пуассона–Дарбу (такой вид уравнение имеет только при $p = 1$)

Переход от уравнения (4.1), (4.2) к эквивалентному уравнению (4.6) осуществляется при помощи замены переменных [19, с. 117, (3.1)]

где $\alpha ({{R}^{1}})$, ${{\beta }}({{R}^{2}})$, ${{\omega }}({{R}^{1}},{{R}^{2}})$ определяются уравнениями (см. ([19], с. 123, (5.3) и с. 118 (3.3))), которые при переходе от (4.1) к (4.6) принимают вид

Нетрудно показать, что с учетом формул (4.3)–(4.5) уравнения (4.8), (4.9) допускают решения

где $K$ – произвольный постоянный множитель.

Функция Римана–Грина для уравнения (4.8) хорошо известна (см., например, [20–23]) и впервые получена Риманом ([24], с. 73). В рассматриваемом случае функция имеет вид

где ${{{\text{\;}}}_{2}}{{F}_{1}}$ – гипергеометрическая функция Гаусса.

Окончательный результат для функций ${{\Phi }}({{R}^{1}},{{R}^{2}}\,|\,{{r}^{1}},{{r}^{2}})$ и ${{\varphi }}({{R}^{1}},{{R}^{2}}\,|\,{{r}^{1}},{{r}^{2}})$ (см. (3.7), (3.8)) имеет вид

Обратим внимание, что множитель $K$ выбран с учетом нормировки ${{\Phi }}({{r}^{1}},{{r}^{2}}\,|\,{{r}^{1}},{{r}^{2}})$ = 1 для функции Римана–Грина.

5. Результаты расчетов и анализ. С использованием алгоритма, изложенного в разд. 2, и с учетом выражения для функции Римана–Грина (4.13), (4.14), приведем результаты решения задачи Коши в исходных переменных (2.1), (2.2) для некоторых начальных данных.

5.1. Периодическое возмущение границы между слоями. Начальные данные для функции ${{h}_{0}}\left( x \right)$, ${{{v}}_{0}}\left( x \right)$ выбираем в виде $T$-периодического пространственного возмущения границы раздела

где ${{\varepsilon }}$ – амплитуда возмущения, ${{{v}}_{0}}$ – начальная постоянная полуразность скоростей слоев жидкости, $T = 2{{\pi }}$ – период, выбор которого не играет существенной роли, ввиду $ - \infty < x < \infty $.

5.2. Выбор начальных данных для задачи Коши (3.10), (3.11). Для решения задачи Коши (3.10), (3.11) требуются начальные данные – значения ${{a}_{{\text{*}}}}$, ${{b}_{{\text{*}}}}$, идентифицирующие изохрону, и значение ${{X}_{{\text{*}}}}$, связывающее начало отсчета координаты $x$ и параметра ${{\mu }}$. Способ определения ${{X}_{{\text{*}}}}$ по заданным ${{a}_{{\text{*}}}}$, ${{b}_{{\text{*}}}}$ подробно описан в ([10], с. 50, 51), а также в [7–9, 11–13] и, в конечном итоге, сводится к однократному (для каждой изохроны) вычислению интеграла

Здесь $Y\left( b \right) = x({{a}_{{\text{*}}}},b)$ и учтено соотношение ${{x}_{b}} = {{{{\lambda }}}^{2}}{{t}_{b}}$ (${{x}_{a}} = {{{{\lambda }}}^{1}}{{t}_{a}}$), которое следует из (3.1) после подстановки в (2.12) при тождественно не равных константе функциях ${{r}^{1}}\left( b \right)$, ${{r}^{2}}\left( a \right)$.

Очевидно, что ${{X}_{{\text{*}}}} = Y({{b}_{{\text{*}}}})$ = $x({{a}_{{\text{*}}}},{{b}_{{\text{*}}}})$. Заметим, что в случае периодических решений выбор ${{X}_{{\text{*}}}}$ существенной роли не играет.

Для выбора ${{a}_{{\text{*}}}}$, ${{b}_{{\text{*}}}}$ следует построить на плоскости $\left( {a,b} \right)$ линии уровня функции $t\left( {a,b} \right)$ (см., в частности, рис. 3). Изображение изохрон на плоскости $\left( {a,b} \right)$ крайне информативно. Дело в том, что первые два уравнения системы (3.10) представляют гамильтонову систему, в которой роль гамильтониана играет функция $t\left( {a,b} \right)$. Это означает, что стационарные точки (если таковые имеются, как в рассматриваемом случае) могут быть либо седлом, либо центром. Сказанное демонстрирует рис. 3, на котором показаны изохроны в окрестности точки $\left( {{{a}_{0}},{{b}_{0}}} \right)$ = (–267.819, –2.358) и отмечены стационарные точки системы (3.10)

в которых ${{t}_{a}}\left( {{{a}_{k}},{{b}_{k}}} \right) = 0$, ${{t}_{b}}\left( {{{a}_{k}},{{b}_{k}}} \right) = 0$. Точки $\left( {{{a}_{1}},{{b}_{1}}} \right)$, $\left( {{{a}_{3}},{{b}_{3}}} \right)$ являются центрами, а точки $\left( {{{a}_{2}},{{b}_{2}}} \right)$, $\left( {{{a}_{4}},{{b}_{4}}} \right)$ соответствуют седловым точкам.

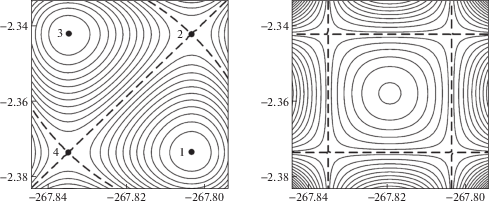
В совокупности с линиями уровня якобиана $J\left( {a,b} \right)$ (см. рис. 3) поведение изохрон позволяет качественно описать структуру решения, в частности, на линиях смены знака якобиана может происходить опрокидывание решения.

Важно отметить, что при построении решений $h(x,{{t}_{{\text{*}}}})$, ${v}(x,{{t}_{{\text{*}}}})$ для различных моментов ${{t}_{{\text{*}}}} = t({{a}_{{\text{*}}}},{{b}_{{\text{*}}}})$ выбираемые начальные точки $({{a}_{{\text{*}}}},{{b}_{{\text{*}}}})$, идентифицирующие изохроны, не должные попадать на замкнутые линии уровня (см. окрестности центров $\left( {{{a}_{1}},{{b}_{1}}} \right)$, $\left( {{{a}_{3}},{{b}_{3}}} \right)$ на рис. 3), по крайней мере, для рассматриваемой задачи. Таким замкнутым линиям соответствуют изолированые решения, не реализуемые для рассматриваемых начальных данных. Иными словами, характеристики, выходящие с оси $t = 0$ (см. рис. 2), не попадают на замкнутые линии. Заметим, что характеристики, выходящие с оси $t = 0$, не попадают и в седловые точки $\left( {{{a}_{2}},{{b}_{2}}} \right)$, $\left( {{{a}_{4}},{{b}_{4}}} \right)$.

5.3. Периодичность решения. В случае периодических начальных данных (5.1), очевидно, что $R_{0}^{1}\left( \tau \right)$, $R_{0}^{2}\left( \tau \right)$, ${{r}^{1}}\left( b \right)$, ${{r}^{2}}\left( a \right)$ являются $T$-периодическими функциями своих аргументов. Это, в частности, означает, что функция Римана–Грина ${{\varphi }}(R_{0}^{1}\left( \tau \right)$, $R_{0}^{2}\left( \tau \right)\,|\,{{r}^{1}}\left( b \right)$, ${{r}^{2}}(a))$ (подынтегральное выражение в (3.8)) является $T$-периодической по каждому аргументу ${{\tau }}$, $a$, $b$. Легко показать, что выполнено соотношение $t\left( {a + T,b + T} \right)$ = = $t\left( {a,b} \right)$, и решение задачи (2.1), (2.2) с начальными данными (5.1) сохраняет пространственную $T$-периодичность. Действительно, интегрируя тождество

с учетом начального условия (см. (3.10)) ${{\left. X \right|}_{{{{\mu }} = 0}}}$ = ${{X}_{{\text{*}}}}$ получим

Принимая во внимание (5.2), имеем

и, ввиду периодичности подынтегрального выражения,

Тогда с учетом (5.4), (5.5)

Окончательно, учитывая вид решения (3.12), получим искомую $T$-периодичность решения по переменной $x$

Заметим, что в случае начальных данных (5.1), по причине периодичности $t\left( {a + T,b + T} \right)$ = $t\left( {a,b} \right)$, построение линий уровня существенно упрощается – на плоскости $\left( {a,b} \right)$ возникает некоторая периодическая структура изолиний. В частности, точки $({{a}_{k}} + 2{{\pi }}n$, ${{b}_{k}} + 2{{\pi }}n)$ (см. (5.3)) также являются стационарными точками.

5.4. Многозначность и опрокидывание решения. Одной из важных характеристик решений казилинейных уравнений является момент времени ${{t}_{z}}$, при котором происходит “опрокидывание” профиля решения – решение может становиться многозначным по пространственной координате, и/или происходит градиентная катастрофа. Многозначность решения, обычно, как, например, в газовой динамике, устраняется при помощи разрывного решения (ударной волны). В рассматриваемой задаче о поведении границы раздела слоев жидкости, многозначность не противоречит физике процесса – граница раздела, в принципе, может иметь произвольную форму, которая описывается многозначной по $x$ функцией $h\left( {x,t} \right)$. Ясно, что ${{t}_{z}}$ зависит от вида начального распределения и, в случае (5.1), от параметров ${{\varepsilon }}$, ${{{v}}_{0}}$, то есть ${{t}_{z}} = {{t}_{z}}\left( {{{\varepsilon }},{{{v}}_{0}}} \right)$.

Момент ${{t}_{z}}$ вычисляется из условий наличия точки перегиба координтаты $x = X\left( {{\mu }} \right)$ (см. (3.12)) в некоторой точке изохроны, то есть условий $x = X\left( {{\mu }} \right)$, ${{X}_{{{\mu }}}}\left( {{\mu }} \right) = 0$, ${{X}_{{{{\mu \mu }}}}}\left( {{\mu }} \right) = 0$, которые приводят к одной из систем

или

Решение $\left( {{{a}_{z}},{{b}_{z}}} \right)$ одной из систем (5.8) и/или (5.9) определяет момент времени ${{t}_{z}} = t\left( {{{a}_{z}},{{b}_{z}}} \right)$.

Обратим внимание на то, что в стационарных точках $\left( {{{a}_{k}},{{b}_{k}}} \right)$ якобиан $J\left( {{{a}_{k}},{{b}_{k}}} \right) = 0$ и ${{X}_{{{{\mu \mu }}}}}\left( \mu \right) = 0$. Однако, как уже указывалось, характеристики с оси $x = 0$ не попадают в точки $\left( {{{a}_{k}},{{b}_{k}}} \right)$ и такие точки не следует рассматривать как точки опрокидывания решения.

Результаты расчетов ${{t}_{z}}$ для параметров ${{\varepsilon }} = 0.1$, $ - 0.99 < {{{v}}_{0}} < 0.99$ и ${{{v}}_{0}} = 0$, $0.1 \leqslant {{\varepsilon \;}} \leqslant 0.891$, приведены на рис. 4. При $\varepsilon = 0.1$, ${{{v}}_{0}} = 0$ значение ${{t}_{z}} = 265.9985$ (${{a}_{z}} = - 267.2250$, ${{b}_{z}} = - 2.3578$).

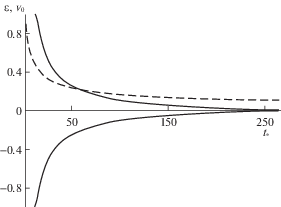
Как и следовало ожидать, наибольшее значения ${{t}_{z}}$ принимает в случае, когда в начальный момент времени различие в скоростях между слоями отсутствует (${{{v}}_{0}} = 0$), и ${{t}_{z}}$ убывает с ростом $\left| {{{{v}}_{0}}} \right|$. Аналогичное убывание ${{t}_{z}}$ имеет место и при росте амплитуды возмущения $\varepsilon $.

5.5. Поведение границы раздела. На рис. 5 в моменты времени ${{t}_{{\text{*}}}}$ (на изохронах) показаны граница раздела $h(x,{{t}_{{\text{*}}}})$ и изменения полуразности скоростей ${v}(x,{{t}_{{\text{*}}}})$ в слоях жидкости.

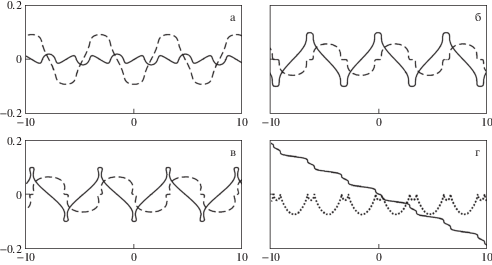
Кроме этого, на рис. 5 г изображены функция ${{\mu }} = {{\mu }}\left( x \right)$ и функция ${{t}_{{bb}}}\left( {a\left( {{\mu }} \right),b\left( {{\mu }} \right)} \right)$ по переменной $x$. Это позволяет отслеживать опрокидывание профиля решения, то есть ситуацию, при которой ${{X}_{{{\mu }}}}\left( {{\mu }} \right) = 0$ (или ${{{{\mu }}}_{x}}\left( x \right) = \infty $) и ${{t}_{{bb}}} = 0$ или ${{t}_{{aa}}} = 0$ (см. (5.8), (5.9)). Многозначность решения по переменной $x$, в частности, видна на рис. 5 в.

5.6. О построении асимптотики. Соотношение (3.8) для определения функции $t\left( {a,b} \right)$ с учетом вида функции Римана–Грина (4.12)–(4.14) для малых значений параметра ${{\varepsilon }}$ в случае начальных данных (5.1) позволяет достаточно просто построить асимптотику решения. Для этого, принимая во внимание, что при ${{{v}}_{0}} = 0$ имеем ${{\theta }} = O({{{{\varepsilon }}}^{4}})$, а при ${{{v}}_{0}} \ne 0$ имеем ${{\theta }} = O({{{{\varepsilon }}}^{2}})$ (см. (4.12), (4.10), (2.5), (2.8), (5.1)), достаточно взамен гипергеометрической функции ${{{\text{\;}}}_{2}}{{F}_{1}}$ использовать разложение в ряд, сохраняя члены порядка $O({{{{\varepsilon }}}^{4}})$ и явно вычисляя интеграл в (3.8). Вычислительный эксперимент показал, что при ${{\varepsilon }} = 0.1$, ${{{v}}_{0}} = 0$ разложение в ряды до членов порядка $O({{{{\varepsilon }}}^{4}})$ позволяет воспроизводить вычисление изохрон и якобиана (см. рис. 3) с точностью до трех знаков после запятой. Конечно, задачу Коши (3.10), (3.11), все равно, приходится решать численно, но использование разложения ${{{\text{\;}}}_{2}}{{F}_{1}}$ позволяет существенно ускорить расчет. Заметим, что при этом и результаты, показанные на рис. 5, также воспроизводятся с указанной точностью.

В принципе, решение задачи (2.6), (2.7), по крайней мере, для начальных данных (5.1), можно разыскивать в виде асимптотических рядов по степеням $\varepsilon $

Однако, величины $\left\{ {{{{{\xi }}}_{{2k + 1}}}\left( {x,t} \right),{{{{\eta }}}_{{2k + 1}}}\left( {x,t} \right)} \right\}$ включают в себя члены порядка $O({{t}^{k}})$ и при больших значениях $t$ сходимость рядов крайне плохая. На рис. 6 для параметров ${{\varepsilon }} = 0.1$, ${{{v}}_{0}} = 0$ приведены результаты расчетов с сохранением членов ряда до порядка $O({{{{\varepsilon }}}^{7}})$, включительно, в моменты времени $t = 210$, $t = 265.5$ (сравни с рис. 6б). Удовлетворительный результат с точностью до 1% удается получить лишь при $t < 140$ (напомним, что момент опрокидывания решения для данных параметров ${{t}_{z}} \approx 266$). При дальнейшем росте $t$ асимптотическое решение значительно отличается от точного. Дальнейшее увеличение количества членов ряда лишь ухудшает ситуацию, ввиду того, что ряды являются асимптотическими.

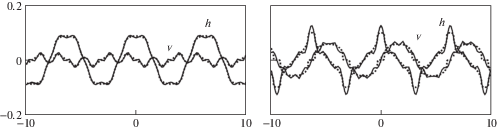
Заметим, что построение решения в виде рядов делает практически невозможным определение момента опрокидывания решения.

Заключение. Рассмотренный в работе алгоритм решения задачи (2.6), (2.7), конечно, применим и к начальным данным, отличным от (5.1). Выбор периодических начальных данных и представление результатов расчетов для параметра ${{{v}}_{0}} = 0$ обусловлено лишь тем, что в этом случае, ввиду различных симметрий (отсутствие начального сдвига скорости, симметричное расположение границы раздела и т.п.), наиболее ярко проявляются особенности решения, такие как, например, наличие стационарных точек. Расчеты для других начальных данных, в частности, для движущихся навстречу солитоноподобных возмущений границы, не приведены по причине того, что основной целью работы является построение эффективного алгоритма решения систем гиперболических уравнений, а не детальное исследование различных вариантов начальных данных. Обратим внимание на то, что метод, фактически, является точным – не используются никакие аппроксимации задачи, типичные для конечно-разностных методов, проекционных методов, метода конечных элементов и конечных объемов. Точность решения ограничена лишь точностью интегрирования задач Коши для систем обыкновенных дифференциальных уравнений.

Конечно, серьезным ограничением метода являются требования существования явных соотношений, связывающих исходные переменные с инвариантами Римана, и наличие явного выражения для функции Римана–Грина. Последнее, впрочем, при отсутствии явного выражения лишь усложнит алгоритм, тогда как возможность записи задачи в инвариантах Римана весьма важна. Однако, круг задач, для которых такие требования выполнены достаточно широко (см., в частности, [6–15, 25, 26]). Помимо исследования конкретных оригинальных задач, одним из применений метода построения точного решения является использование результатов в качестве эталонных тестовых примеров для проверки при разработке иных численных алгоритмов решения систем (двух) квазилинейных уравнений. При этом, как уже указывалось, начальные данные могут быть кусочно-непрерывными и метод позволяет строить как разрывные решения (при наличии дополнительных соотношений на разрывах), так и автомодельные, решать задачу Гурса с данными на характеристиках (см., в частности, [27]), а также решать системы двух квазилинейных уравнений эллиптического типа (см., например, [10, 12, 14, 25, 28]). Наконец, заметим, что на основе закона сохранения, обобщенного и классического доказана [29] эквивалентность различных методов годографа.

Работа выполнена при поддержке гранта Правительства РФ № 075-15-2019-1928.