Прикладная математика и механика, 2022, T. 86, № 1, стр. 66-76
Непериодические колебания микро- и наноструны в газовой среде
М. А. Ильгамов 1, 2, 3, *, И. М. Утяшев 1, 2, **
1 Институт механики им. Р.Р. Мавлютова УФИЦ РАН
Уфа, Россия
2 Башкирский государственный университет
Уфа, Россия
3 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: ilgamov@anrb.ru
** E-mail: utyashevim@mail.ru
Поступила в редакцию 28.06.2021
После доработки 06.09.2021
Принята к публикации 25.09.2021
- EDN: IFCRNN
- DOI: 10.31857/S0032823522010052
Аннотация
Рассмотрены линейные колебания микро- и наноструны с изменяющимся давлением в газовой среде. При этом учитываются два поверхностных эффекта. Первый обусловлен различием упругих свойств в приповерхностном слое и в основном объеме материала. В зависимости от материала эффективная жесткость на растяжение может быть больше или меньше, чем обычная жесткость. Второй эффект обусловлен наличием разности сил давления среды на выпуклой и вогнутой сторонах круговой поверхности, появляющейся при отклонении от прямой линии. Эти эффекты определяются безразмерными параметрами. Решение определяется в зависимости от заданного закона изменения давления по времени. Повышение давления приводит к уменьшению амплитуды и повышению частоты колебаний. С вакуумированием связаны увеличение амплитуды и уменьшение частоты. В обратной задаче определяется закон изменения давления, а также параметр первого эффекта.
1. Введение. Нанопроволоки, микро- и наноструны находят применение в электронных, оптоэлектронных и электромеханических устройствах, в литографии, в качестве химических и биологических детекторов и сенсоров и т.д. [1–4]. Изучение их эксплуатационных свойств, в частности, статической и динамической деформации под действием приложенных сил, спектра частот, устойчивости формы представляет большой интерес.
Как показано экспериментально и теоретически в работах [5, 6], а также в последующих исследованиях, при диаметрах струны порядка 10 мкм и меньше начинает влиять на деформацию поверхностный эффект, связанный с различием упругих характеристик в тонком слое около поверхности и в основном объеме тела. Влияние указанного и других эффектов объясняется тем, что с уменьшением диаметра d струны увеличивается удельная поверхность пропорционально d–1. Укажем на исследования [7–11] в этом направлении, в которых приводится также обзор литературы. В частности, статический изгиб проволоки, устойчивость ее формы, свободные колебания рассматриваются в [9–13]. Принято, что в теории изгиба проволоки учитывается изгибающий момент, а струны – не учитывается.
Согласно указанным работам, продольная сила N выражается через деформацию ε осевой линии формулой
(1.1)
$N = EF\varepsilon (1 + \beta ),\quad F{\text{ = }}{{\pi {{d}^{2}}} \mathord{\left/ {\vphantom {{\pi {{d}^{2}}} 4}} \right. \kern-0em} 4},\quad \beta = {{4{{E}_{s}}} \mathord{\left/ {\vphantom {{4{{E}_{s}}} {Ed}}} \right. \kern-0em} {Ed}},$Второй поверхностный эффект связан с образующейся разностью площадей выпуклой и вогнутой частей боковой поверхности струны в результате ее отклонения от прямой линии. Эта разность площадей приводит к появлению распределенной поперечной силы [14, 15]
где р – равномерное давление на боковую поверхность струны, κ –кривизна осевой линии. Сила q при p > 0 направлена в сторону вогнутости осевой линии, при p < 0 – в сторону выпуклости. Равновесие тонкостенных упругих тел в предположениях, приводящих к формуле (1.2), было рассмотрено в работах [16, 17].В [18–24] рассмотрены различные задачи поперечных линейных и нелинейных колебаний струн, тросов, в том числе в динамике космических тросовых систем. Обратная задача по определению граничных условий по собственным частотам приведена в [25, 26]. В [27, 28] изучены разрывные волновые явления в сильно деформируемых нитях. Спектр частот продольных колебаний в нанострунах и нанопленках из интерметаллидов, обладающих сложной зависимостью между напряжением и деформацией, определен в [29].
В настоящей работе одновременно учитываются указанные поверхностные эффекты при рассмотрении линейных поперечных колебаний микро- и нанострун, находящихся под давлением газа. При этом задается закон изменения давления. Непериодические колебания струны возбуждаются в начальный период приложения давления. В случае его установления на определенном уровне с течением времени колебания струны переходят на периодический режим.
При анализе не учитываются другие факторы, оказывающие влияние на колебания (внутреннее трение в материале, излучение в окружающую среду, ее присоединенная масса и т.д.) Эти факторы пропорциональны плотности. Поэтому пренебрежение ими может быть приемлемым в случае легких газов. Кроме того хорошо известно, как учитывать влияние излучения и присоединенной массы на колебания тела.
2. Постановка задачи. Струна диаметром d и длиной L закреплена неподвижно на опорах с некоторым удлинением u0. Относительно продольной и поперечной компонент перемещения u(x, t), w(x, t) граничные и начальные условия имеют вид
(2.1)
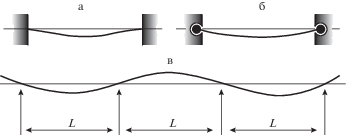
$u\left( {0,t} \right) = 0,\quad u\left( {L,t} \right) = {{u}_{0}},\quad w\left( {0,t} \right) = 0,\quad w\left( {L,t} \right) = 0$Эти условия характерны для двухопорных микро- и нанорезанаторов [2, 13]. Предполагается, что опоры исключают передачу силы сжатия от возможного торцевого давления на область 0 < x < L. На рис. 1 приведены примеры таких опор, в которых торцевые площади изолированы от избыточного давления (а) или в случае его действия передача силы сжатия в область 0 < x < L не происходит из-за шарнирного закрепления (б) (то же самое в случае многоопорной струны (в)). Условия (2.2) реализуются, например, в момент наибольшего отклонения струны при ее свободных колебаниях. Этот момент принимается за начало отсчета времени.
На круговую поверхность струны действует равномерное давление газов p0 + p(t). Под p0 будем подразумевать постоянное давление, в частности, атмосферное давление. Струна под этим всесторонним давлением является прямой и растянутой в соответствии с первыми двумя условиями (2.1). Поэтому p0 может быть названо давлением сборки системы струна–концевые опоры.
Малое отклонение от прямой линии струны при действии избыточного динамического давления p(t) описывается уравнением
(2.3)
$D\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} - N\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \rho F\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = q,\quad D = \frac{{\pi E{{d}^{4}}}}{{64}}\quad (0 \leqslant x \leqslant L),$Сила N образуется в результате указанного выше осевого растяжения, а также поперечного перемещения струны и является постоянной по всей длине L. Деформация ε осевой линии связана с компонентами перемещения формулой
Подстановка ее в выражение (1.1) и интегрирование по x от 0 до L дает
(2.4)
$\frac{{NL}}{{EF(1 + \beta )}} = u(L) - u(0) + \frac{1}{2}\int\limits_0^L {{{{\left( {\frac{{\partial w}}{{\partial x}}} \right)}}^{2}}} dx$В соответствии с первыми условиями (2.1) u(L) – u(0) = u0.
Отношение первого члена ко второму в уравнении (2.3) при функции прогиба $w = \sin ({{\pi x} \mathord{\left/ {\vphantom {{\pi x} L}} \right. \kern-0em} L})$ равно
В дальнейшем ограничимся законом изменения избыточного давления в виде
(2.5)
$p = {{p}_{0}}{{({t \mathord{\left/ {\vphantom {t {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}})}^{\alpha }},$(2.6)
$\begin{gathered} \frac{{{{\partial }^{2}}w}}{{\partial {{\tau }^{2}}}} - \left[ {{{\tau }^{\alpha }} + \eta + \gamma \int\limits_0^1 {{{{\left( {\frac{{\partial w}}{{\partial \xi }}} \right)}}^{2}}d\xi } } \right]\frac{{{{\partial }^{2}}w}}{{\partial {{\xi }^{2}}}} = 0 \\ \xi = \frac{x}{L},\quad \tau = \frac{t}{{{{t}_{0}}}},\quad {{t}_{0}} = L\sqrt {\frac{\rho }{{{{p}_{0}}}}} ,\quad \eta = \frac{{E{{u}_{0}}(1 + \beta )}}{{{{p}_{0}}L}},\quad \gamma = \frac{{E(1 + \beta )}}{{2{{p}_{0}}}} \\ \end{gathered} $В уравнении (2.6) и в условиях (2.1), (2.2) прогиб w отнесен к длине L. Первый поверхностный эффект при β > 0 увеличивает упругие силы (параметры η и γ возрастают), при β < 0 – уменьшает. В качестве примера приведем данные из [9]: $\beta d = 765$ нм (железо) и $\beta d = - 4.5$ нм (железо на стеклянном субстрате). Эффект начинает проявляться при $d < {{10}^{6}}$ нм в первом случае и $d < {{10}^{2}}$нм во втором. При $E = {{10}^{5}}$ МПа, ${{p}_{0}} = 0.1$ МПа и принятом выше отношении ${{{{u}_{0}}} \mathord{\left/ {\vphantom {{{{u}_{0}}} L}} \right. \kern-0em} L} = {{10}^{{ - 7}}}$ параметр $\eta = {{10}^{{ - 1}}}(1 + \beta )$.
3. Колебания предварительно слаборастянутой струны. Рассмотрим сначала решение линейного уравнения (2.6) для случая слаборастянутой струны, под которым будем подразумевать $\eta \ll {{\tau }^{\alpha }}$ в (2.6). Это условие выполняется за исключением начального момента. В интервале $0 \leqslant \tau \leqslant 0.1$ происходит малое изменение w ввиду нулевой скорости в начальных условиях (2.2) и инерционности струны. Это имеет место особенно при больших значениях показателя α, когда давление мало отличается от p0 до $\tau = 0.1$. Это можно показать по решению уравнения ${{w}_{{\tau \tau }}} - (\eta + 0.1){{w}_{{\xi \xi }}}$ = 0, следующего из (2.6) при $\alpha = 1$. В интервале до $\tau = 0.1$ оно дает значение прогиба с превышением. Принимая в условиях (2.2) ${{w}_{0}}(\xi )$ = ${{W}_{1}}\sin \pi \xi $ и решение уравнения в виде $w = W(\tau )\sin \pi \xi $, получаем W = ${{W}_{1}}\cos \sqrt {\eta + 0.1} \tau $. При $\eta = 0.1$ и $\tau = 0.1$ находим $W = {{W}_{1}}$ × 0.999. Таким образом, нарушение условия $\eta \ll {{\tau }^{\alpha }}$ при малых значениях τ не приводит к искажению дальнейшего колебательного процесса. Тогда решение уравнения (2.6), удовлетворяющее условиям (2.1), (2.2), имеет вид [30]
(3.1)
$\begin{gathered} w = \sqrt \tau \sum\limits_{k = 1} {{{A}_{k}}{{J}_{{ - \mu }}}} \left( {kz} \right)\sin (k\pi \xi );\quad z = 2\pi \mu {{\tau }^{{\tfrac{1}{{2\mu }}}}} \\ {{A}_{k}} = 2\Gamma (1 - \mu ){{(k\pi \mu )}^{\mu }}\int\limits_0^1 {{{w}_{0}}(\xi )\sin (k\pi \xi )d\xi ;\quad \mu = \frac{1}{{2 + \alpha }},} \\ \end{gathered} $Как видно из (2.6) и вида параметров η и γ, в данной постановке первый поверхностный эффект не оказывает влияния на решение (второй эффект выражен в члене ${{\tau }^{\alpha }}{{\partial }^{2}}w{\text{/}}\partial {{\xi }^{2}}$). Целью этой упрощенной постановки задачи является в частности анализ влияния показателя α в законе изменения давления на решение. Анализ сходимости ряда (3.1) показывает, что при плавных функциях w0(ξ) с достаточной точностью можно ограничиться первым членом (k = 1) [31]. Решение (3.1) при k = 1, w0(ξ) = W1 sin πξ приводится к виду
(3.2)
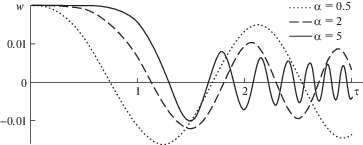
$w = {{W}_{1}}{{\pi }^{\mu }}{{\mu }^{\mu }}\Gamma (1 - \mu ){{\tau }^{{\tfrac{1}{2}}}}{{J}_{{ - \mu }}}\left( z \right)\sin \pi \xi $На рис. 2 представлено изменение безразмерного прогиба w в средней точке (W1 = 0.02, ξ = 1/2 в (3.2)) по безразмерному времени τ при различных значениях показателя α и соответственно параметра μ. Чем больше показатель α (т.е. больше давление p), тем быстрее уменьшается амплитуда колебаний струны с течением времени, а частота возрастает. В начале процесса (до τ ≈ 1) наблюдается малое изменение w, особенно для больших значений α. Это объясняется тем, что при больших значениях α давление p остается малым до τ = 1.
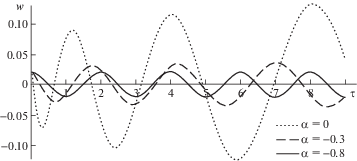
Показателю α = 0 (p = p0) соответствуют гармонические колебания с постоянной частотой и амплитудой. Амплитуда определяется первым начальным условием (2.2). При отрицательных значениях α происходит увеличение амплитуды и уменьшение частоты колебаний, что объясняется снижением давления p (рис. 3). При такой раскачке колебаний линейное решение перестает быть удовлетворительным. Становится заметной роль нелинейного члена в (2.6). Он является положительным и соответствует растягивающей силе, возникающей при отклонении струны от прямой линии. При положительном значении параметра β первого поверхностного эффекта (в составе γ) эта сила обеспечивает большее ограничение амплитуды, чем при отрицательном значении β. Однако анализ нелинейных колебаний не входит в задачу данной работы.
Ограничиваемся тремя членами ряда Стирлинга гамма-функции
Известные точные значения $\Gamma (1) = 1$, $\Gamma (1{\text{/}}2) = \sqrt \pi $ получаются из двух членов этого ряда без заметных погрешностей. Аргумент $1 - \mu = (1 + \alpha ){{(2 + \alpha )}^{{ - 1}}}$ изменяется от 1/3 до 2/3 при $ - {1 \mathord{\left/ {\vphantom {1 {2 < \alpha < 1}}} \right. \kern-0em} {2 < \alpha < 1}}$. Воспользуемся также асимптотическими приближениями функции Бесселя для малого и большого аргументов
(3.3)
${{J}_{{ - \mu }}}(z)\mathop \approx \limits_{z \to 0} \frac{{{{z}^{{ - \mu }}}}}{{{{2}^{{ - \mu }}}\Gamma (1 - \mu )}},\quad {{J}_{{ - \mu }}}(z)\mathop \approx \limits_{z \to \infty } {{\left( {\frac{2}{{\pi z}}} \right)}^{{\frac{1}{2}}}}\cos \left( {z + \frac{{\pi \mu }}{2} - \frac{\pi }{4}} \right)$4. Определение скорости изменения давления. Представляет интерес определение показателя α по известному значению периода колебаний T, который в данной задаче зависит от времени. Из равенства z = 2πτ/T с учетом значения z из (3.1) получаем T = = (2 + α)τ–α/2. Считая, что моментам времени τ1 и τ2 соответствуют периоды T1 и T2, можно записать (из-за использования асимптотических представлений учет времени на рис. 4 начинается не с нуля)
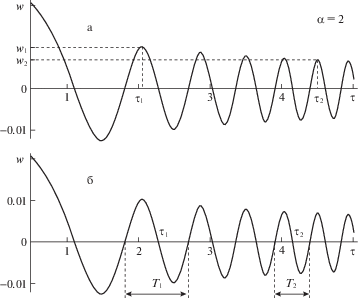
В качестве моментов τ1 и τ2 принимаются значения τ при w(τ) = 0. Поскольку определение (4.1) значения α является приближенным (ввиду непериодичности процесса) целесообразно привлечь также другую процедуру. Например, можно использовать значение прогиба w(ξ, τ) в определенной точке ξ в разные моменты времени [31]. В соответствии с (3.2), (3.3) определяем амплитуду по длине струны и по времени w(ξ, τ). Моменты времени τ1 и τ2 соответствуют амплитудам w1 и w2 (рис. 4 (б)). Тогда
Из решения (3.2) прямой задачи получены: моментам τ1 = 5.4933, τ2 = 8.5214 соответствуют периоды Т1 = 0.8542, Т2 = 0.6853. По ним из (4.1) получаем α = 1.0034 (вместо точного значения α = 1). Пусть известны амплитуды w1 = 0.0100, w2 = 0.0089 и соответствующие моменты τ1 = 5.2769, τ2 = 8.3488. Тогда по формуле (4.2) α = 0.9999. Объяснение большей погрешности (4.1) по сравнению с (4.2) состоит в том, что периоды Т1 и Т2 являются усредненными, в то время как величины w1 и w2 в (4.2) определяются более точно. Для давления р = р0τα при τ = 5 в первом случае имеем погрешность около 0.544% (р = 5.027р0 вместо точного значения 5р0), во втором случае 0.023%. Погрешность уменьшается при уменьшении непериодичности (с приближением показателя α к нулю).
5. Колебания предварительно растянутой струны. Рассмотрим случай предварительно растянутой струны при α = 1. Из уравнения (2.6) следует
(5.1)
$\frac{{{{\partial }^{2}}w}}{{\partial \tau _{1}^{2}}} - {{\tau }_{1}}\frac{{{{\partial }^{2}}w}}{{\partial {{\xi }^{2}}}} = 0;\quad {{\tau }_{1}} = \eta + \tau $Решение уравнения (5.1) имеет вид (3.2), (3.3), где вместо τ нужно подставить τ1 (либо η + τ). Входящие в них величины при α = 1 равны: μ = 1/3, Г(2/3) = 1.354. Решение (3.2) при учете (3.3) приобретает вид:
(5.2)
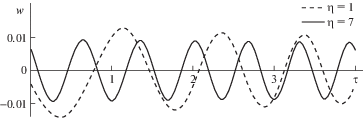
$w \approx {{W}_{1}}{{\pi }^{{ - \tfrac{2}{3}}}}1.626{{(\eta + \tau )}^{{ - \tfrac{1}{4}}}}\cos \left( {z - \frac{\pi }{{12}}} \right)\sin \pi \xi ;\quad z = \frac{{2\pi }}{3}{{(\eta + \tau )}^{{\tfrac{3}{2}}}}$График этого решения в точке ξ = 1/2 при W1 = 0.02 и различных значениях η дан на рис. 5.
Для определения параметра натяжения η может быть поставлена обратная задача. Положив τi = τi + η в (5.2), находим:
(5.3)
$\eta = \frac{{T_{1}^{2}{{\tau }_{1}} - T_{2}^{2}{{\tau }_{2}}}}{{T_{2}^{2} - T_{1}^{2}}},\quad \eta = \frac{{{{\tau }_{1}}w_{1}^{4} - {{\tau }_{2}}w_{2}^{4}}}{{w_{2}^{4} - w_{1}^{4}}}$По найденному значению η может быть определено либо предварительное продольное перемещение u0 (при известных данных E, p0, L, β)
либо параметр первого поверхностного эффектаКак во всякой обратной задаче, предъявляются повышенные требования к точности экспериментальных данных τ1, τ2, T1, T2, w1, w2, входящих в (4.1), (4.2), (5.3). То же самое относится к параметрам E, p0, L, входящим в (5.4) и (5.5). Отметим, в (5.5) имеется разность близких чисел.
Заключение. Приведенная постановка задачи отличается от обычной теории свободных колебаний струн тем, что учитываются два поверхностных эффекта. Первый из них, связанный различием упругих свойств приповерхностного слоя и основного объема, приводит к изменению эффективной жесткости струны на растяжение, модуль упругости которой определяется безразмерным параметром β в (1.1).
Второй эффект характеризируется безразмерным параметром α, данным в (2.5). В зависимости от возрастания (α > 0) или убывания (α < 0) избыточного давления происходит увеличение или уменьшение эффективной жесткости и частот поперечных колебаний струны по сравнению с частотами, возбуждаемыми при давлении сборки системы струна–опоры (α = 0). Без учета второго эффекта колебания струны могут быть только периодическими и обусловленными начальными условиями. Предложен способ определения параметра α изменения давления на поверхность струны по экспериментальным данным периодов и амплитуд колебаний в различные моменты времени. Разные формулировки соответствующей обратной задачи приводят к соотношениям (4.1), (4.2), позволяющим получать результаты с различной точностью.
Для многих материалов в литературе отсутствуют значения параметра первого поверхностного эффекта β. Их определение представляет очевидные сложности. Один из возможных способов определения параметра β (или величины Es) состоит в решении обратной задачи для предварительно растянутой струны. Для этого служит формула (5.5). Если параметр β известен для материала, то в этом случае по формуле (5.4) может быть определена трудно измеряемая величина продольного перемещения.
Работа выполнена по государственному заданию на 2019–2022 годы (№ 0246-2019-0088).
Список литературы
Raman A., Melcher J., Tung R. Cantilever dynamics in atomic force microscopy // Nano Today. 2008. V. 3. № 1–2. P. 20–27.
Eom K., Park H.S., Yoon D.S., Kwon T. Nanomechanical resonators and their applications in biological/chemical detection: Nanomechanics principles // Phys. Rep. 2011. V. 503. № 4–5. P. 115–163.
Elnathan R., Kwiat M., Patolsky F., Voelcker N.H. Engineering vertically aligned semiconductor nanowire arrays for applications in the life sciences // Nano Today. 2014. V. 9. № 2. P. 172–196.
Guo L.J. Nanoimprint lithography: methods and material requirements // Adv. Mater. 2007. V. 19. № 4. P. 495–513.
Sheehan P.E., Lieber C.M. Nanotribology and nanofabrication of MoO3 structures by atomic force microscopy // Science. 1996. V. 272. № 5265. P. 1158–1161.
Wong E., Sheehan P.E., Lieber C.M. Nanobeam mechanics: Elasticity, strength, and toughness of nanorods and nanotubes // Science. 1997. V. 277. № 5334. P. 1971–1975.
Gurtin M.E., Murdoch A.I. Surface stress in solids // Int. J. Solids Struct. 1978. V. 14. № 6. P. 431–440.
Miller R.E., Shenoy V.B. Size-dependent elastic properties of nanosized structural elements // Nanotechnology. 2000. V. 11. № 3. P. 139–147.
Sharma P., Ganti S., Bhate N. Effect of surfaces on the size-dependent elastic state of nano-inhomogeneities // Appl. Phys. Lett. 2003. V. 82. № 4. P. 535–537.
He L.H., Lim C.W., Wu B.S. A continuum model for size-dependent deformation of elastic films of nano-scale thickness // Int. J. Solids Struct. 2004. V. 41. № 3–4. P. 847–857.
Hajjaj A.Z., Jaber N., Ilyas S., Alfosail F.K., Younis M.I. Linear and nonlinear dynamics of micro and nano-resonators: Review of recent advances // Int. J. Non-Lin. Mech. 2020. V. 119. 103328.
Lim C.W., He L.H. Size-dependent non-linear response of thin elastic films with nano-scale thickness // Int. J. Mech. Sci. 2004. V. 46. № 11. P. 1715–1726.
Wu J.X., Li X.F., Tang A.Y., Lee K.Y. Free and forced transverse vibration of nanowires with surface effects // J. Vib. Control. 2017. V. 23. № 13. P. 2064−2077.
Link H. Über den geraden Druckstab in Flüssigkeit // Ingenieur-Archiv. 1960. V. 31. № 3. P. 149–167.
Ilgamov M.A. Static Problems of Hydroelasticity. Moscow: Nauka, 1998. 208 p.
Peterson J.P. Axially loaded column subjected to lateral pressure // AIAA J. 1963. V. 1. № 6. P. 1458–1459.
Ильгамов М.А. Спектр частот проволочного микро- и нанорезонатора // Докл. РАН. 2020. Т. 494. № 1. С. 21–24.
Белецкий В.В., Новикова Е.Т. Об относительном движении связки двух тел на орбите // Космич. исслед. 1969. Т. 7. № 3. С. 377–384.
Демьянов Ю.А., Кокорева Д.В., Малашин А.А. Взаимовлияние поперечных и продольных колебаний в музыкальных инструментах // ПММ. 2003. Т. 67. № 2. С. 273–283.
Асланов В.С. Влияние упругости орбитальной тросовой системы на колебания спутника // ПММ. 2010. Т. 74. № 4. С. 582–593.
Демьянов Ю.А., Малашин А.А. Влияние жесткости на поперечно-продольные движения музыкальных струн // ПММ. 2011. Т. 75. № 1. С. 95–100.
Холодовский С.Е. О движении полуограниченной струны с точечной массой на конце // ПММ. 2018. Т. 82. № 6. С. 751–756.
Русских С.В., Шклярчук Ф.Н. Передвижение тяжелого твердого тела, подвешенного на тросе переменной длины, с устранением колебаний // ПММ. 2019. Т. 83. № 4. С. 549–561.
Садов Ю.А., Нуралиева А.Б. О линейных поперечных колебаниях троса космического лифта // ПММ. 2020. Т. 84. № 5. С. 543–553.
Ахтямов А.М. Теория идентификации краевых условий и ее приложения. М.: Физматлит, 2009. С. 232–251.
Ахтямов А.М., Утяшев И.М. Идентификация краевых условий на обоих концах струны по собственным частотам колебаний // Акустич. ж. 2015. Т. 61. № 6. С. 647–655.
Ильгамов М.А., Ридель В.В. Режимы разрывных колебаний в абсолютно гибкой нити // Докл. РАН. 1995. Т. 343. № 4. С. 478–481.
Ридель В.В., Ильгамов М.А. Нелинейные волны в абсолютно гибкой нити // ПМТФ. 1997. Т. 38. № 6. С. 139–146.
Ильгамов М.А. Скорость волны и спектр частот продольных колебаний растянутых нанопленок из интерметаллидов // ФТТ. 2015. Т. 57. № 5. С. 950–954.
Зайцев В.Ф., Полянин А.Д. Справочник по дифференциальным уравнениям с частными производными: Точные решения. М.: МПО, 1996. 496 с.
Утяшев И.М. Анализ поперечных колебаний струны в зависимости от изменяющегося натяжения // Вестн. Башкирского унив. 2013. Т. 18. № 4. С. 973–977.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика