Прикладная математика и механика, 2022, T. 86, № 1, стр. 77-87

1. Введение. Анализу кинематики шарнирных четырехзвенников, в частности, исследованию передаточной функции посвящено немало работ [1, 2]. В последнее время появились работы, исследующие приводимость конфигурационного пространства и использующие методы алгебраической геометрии [2–4]. Эти работы основаны на применении базисов Гребнера, дающих мощный инструмент исследования идеалов в кольцах многочленов над полем $\mathbb{Q}$ рациональных чисел и его конечными расширениями. Метод связан с громоздкими вычислениями в пакетах символьной математики, которые невозможно проверить вручную. В данной работе с привлечением элементарных сведений из алгебраической геометрии путем простых рассуждений и вычислений проводится классификация четырехзвенных механизмов по геометрическим свойствам их конфигурационного пространства. На ее основе исследуется связь передаточной функции четырехзвенника с приводимостью его конфигурационного пространства.

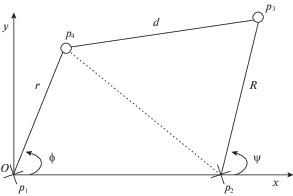
Рассматриваем плоский шарнирный четырехзвенник с вращательными парами (шарнирами) ${{p}_{i}}$, $1 \leqslant i \leqslant 4$ (рис. 1). Пусть его закрепленные шарниры (обозначены на рис. 1 крестиками, свободные – кружочками) ${{p}_{1}} = (0,0)$ и ${{p}_{2}} = (1,0)$, где координаты записаны в декартовой системе, которой мы будем пользоваться и впредь. Звенья (рычаги) четырехзвенника перенумеруем следующим образом: неподвижному звену ${{p}_{1}}{{p}_{2}}$ присвоим номер 0, звену ${{p}_{1}}{{p}_{4}}$ – номер 1, ${{p}_{2}}{{p}_{3}}$ – номер 2, ${{p}_{4}}{{p}_{3}}$ – номер 3. Зависимость $\psi = \psi (\varphi )$ углов, образуемых первым и вторым рычагами четырехзвенника и осью абсцисс, называют передаточной функцией четырехзвенника.

Мы решим вопрос: могут ли и когда различным четырехзвенникам отвечать одинаковые передаточные функции? Этот вопрос не так прост, как может показаться. Например, для двух различных шарнирных параллелограммов передаточная функция $\psi = \varphi $ одинакова. Но если непрерывно сдвинуть эти параллелограммы в антипараллелограммы, то передаточные функции станут различны. Они зависят от длины $r$ первого рычага – боковой стороны параллелограмма: ψ = $2\operatorname{arctg} \left( {\frac{{r - 1}}{{r + 1}}\operatorname{tg} \frac{\varphi }{2}} \right)$. Мы исследуем связь передаточной функции с приводимостью как алгебраической кривой конфигурационного пространства четырехзвенника. Для четырехзвенников с неприводимым конфигурационным пространством будет доказана теорема о том, что для двух различных (с точностью до подобия) таких четырехзвенников передаточные функции различны.

Приведем определение конфигурационного пространства механизма (в ряде математических работ шарнирный механизм и его конфигурационное пространство определяются по другому) следуя [5–7]. Ключевым является понятие рычажного отображения, сопоставляющего положениям свободных шарниров квадраты длин рычагов. Для нашего четырехзвенника с ${{p}_{4}} = ({{x}_{4}},{{y}_{4}})$, ${{p}_{3}} = ({{x}_{3}},{{y}_{3}})$ это отображение $F:{{\mathbb{R}}^{4}} \to {{\mathbb{R}}^{3}}$, задающееся формулами:

Точку $d = \{ {{r}^{2}},{{R}^{2}},{{d}^{2}}\} \in {{\mathbb{R}}^{3}}$ называем кинематической шарнирной схемой (КШС), или сокращенно – кинематической схемой. Мы будем задавать КШС тройкой длин рычагов: $\left\{ {\left| {{{p}_{1}}{{p}_{4}}} \right|,\left| {{{p}_{2}}{{p}_{3}}} \right|,\left| {{{p}_{3}}{{p}_{4}}} \right|} \right\}$ = $\{ r,R,d\} $, записанной в приданном рычагам порядке. Выбрав единичное расстояние между закрепленными шарнирами, мы тем самым не рассматриваем геометрически подобных четырехзвенников с одинаковыми передаточными функциями.

Полный прообраз $K = {{F}^{{ - 1}}}(d)$ точки при рычажном отображении называем конфигурационным пространством КШС $d$. Неодноточечную компоненту связности его мы называем конфигурационным пространством шарнирного механизма. Таким образом, шарнирный механизм есть подвижная конструкция, которую можно из одного положения непрерывно перевести в любое другое ее положение. Например, КШС $\left\{ {2,\;2,\;\frac{1}{{10}}} \right\}$ отвечает два шарнирных механизма с одной степенью свободы, отличающихся отражением относительно оси $Ox$.

Алгебраическим множеством называют множество общих нулей совокупности многочленов. Конфигурационные пространства КШС, будучи множествами решений полиномиальных систем уравнений, являются алгебраическими множествами. Алгебраическое множество называют приводимым, если оно является объединением двух меньших алгебраических множеств, и неприводимым в противном случае. Конфигурационное пространство шарнирного механизма, являясь, вообще говоря, частью алгебраического множества, не всегда есть алгебраическое множество. Назовем алгебраическим замыканием (часто его называют замыканием по Зарисскому) множества $M \subset {{\mathbb{R}}^{n}}$ наименьшее алгебраическое множество из ${{\mathbb{R}}^{n}}$, содержащее $M$. И будем называть конфигурационное пространство $K$ шарнирного механизма и сам механизм приводимым или неприводимым, если алгебраическое замыкание $K$ приводимо, и соответственно, неприводимо.

Будем обозначать конфигурационное пространство четырехзвенника как: ${{K}_{i}}(r,R,d)$, где нижний индекс $i$ различает механизмы с одной кинематической схемой $\{ r,R,d\} $. Если конфигурационное пространство механизма состоит из нескольких неприводимых компонент (иногда их называют кинематическими модами механизма), то их будем дополнительно нумеровать верхним индексом.

2. Передаточная функция четырехзвенника. Нам удобно параметризовать окружности, по которым движутся шарниры ${{p}_{3}}$ и ${{p}_{4}}$, через тангенсы половинных углов $u = \operatorname{tg} \frac{\psi }{2}$ и $t = \operatorname{tg} \frac{\varphi }{2}$:

Параметры $t$ и $u$ здесь изменяются от $ - \infty $ до $ + \infty $, но точки окружностей ($ - r,0$) и ($1 - R$, 0) не получаются ни при каких конечных значениях параметров. Вводя эту параметризацию, мы начинаем работать не с самим конфигурационным пространством, как мы его определили, а с бирационально изоморфным ему алгебраическим множеством. Но свойство приводимости не меняется при бирациональном изоморфизме.

Подставляя параметризации в уравнение (1.1) придем к уравнению относительно $t$ и $u$:

с достаточно громоздкими коэффициентами $A$, $C$, зависящими от $r$, $R$, $d$ и $t$, и являющимися по $t$ многочленами, вообще говоря, второй степени:

Решения уравнения (2.1) и дают передаточную функцию. Почти всегда их можно записать как корни числителя дроби, стоящей в левой части (2.1), – многочлена $P = P(u,t)$:

где коэффициенты зависят от $r$, $R$ и $d$. Два значения функции отвечают двум возможным углам $\psi $, для положений механизма с симметричной относительно прямой ${{p}_{2}}{{p}_{4}}$ двуповодковой группой ${{p}_{4}}{{p}_{3}}{{p}_{2}}$.

Однако, возможны и особые случаи. Ввиду того, что мы параметризовали не все точки окружностей, у исходной системы может оказаться решение $\psi \equiv \pi $, не зависящее от угла $\varphi $, которому отвечает значение $u = \infty $, не учитываемое формулой (2.2). Так оно и есть при $R = 1$, $d = r$. Этому решению отвечают положения четырехзвенника, в которых шарнир ${{p}_{3}}$ совпадает с ${{p}_{1}}$. Угол $\varphi $ меняется произвольно при постоянном $\psi $.

Исследуем эту возможность подробнее. В этом случае степень многочлена $P(u,t)$ по $u$ должна быть ниже второй. Действительно, коэффициент $A$ при ${{u}^{2}}$ в многочлене $P$ тождественно равен нулю тогда и только тогда, когда $A$ есть нулевой многочлен от $t$. У него всего два ненулевых коэффициента при второй и нулевой степенях $t$:

При этом ${{a}_{0}} - {{a}_{2}} = 4r(R - 1)$, и поскольку $r > 0$, то $R = 1$. Подставляя $R = 1$ в ${{a}_{0}} = 0$, получим ${{r}^{2}} - {{d}^{2}} = 0$, и $d = r$. Таким образом, получаем единственную кинематическую схему $\left\{ {r,1,r} \right\}$. Ей отвечает единственный механизм с приводимым конфигурационным пространством $K(r,1,r)$. Оно состоит из двух компонент, на одной ${{K}^{1}}(r,1,r)$ из которых ${{p}_{3}} = (0,0)$, а на другой ${{K}^{2}}(r,1,r)$ координаты шарнира ${{p}_{3}}$ переменны. На ${{K}^{1}}(r,1,r)$ передаточная функция постоянна: $\psi (\varphi ) = \pi $, на ${{K}^{2}}(r,1,r)$ она переменна и однозначна:

Приводимость конфигурационного пространства привела к существенно различным передаточным функциям для разных положений одного четырехзвенного механизма. Очевидно, необходимо исследовать все случаи приводимости конфигурационного пространства четырехзвенного механизма.

В случае произвольного поля $\mathbb{K}$ критерием приводимости алгебраического множества $V \subset {{\mathbb{K}}^{n}}$ является существование в кольце $\mathbb{K}[{{x}_{1}},{{x}_{2}}, \ldots ,{{x}_{n}}]$ многочленов от $n$ переменных над полем $\mathbb{K}$ таких многочленов $f$ и $g$, что произведение $fg = 0$ на $V$, но ни один из этих многочленов не обладает таким свойством [8]. Будем опираться на лемму [8], справедливую для любого поля $\mathbb{K}$. Но далее мы будем работать лишь в полях $\mathbb{R}$ и $\mathbb{C}$ вещественных и комплексных чисел.

Лемма 1. Пусть $f(x,y) \in \mathbb{K}[x,y]$ неприводимый, а $g(x,y) \in \mathbb{K}[x,y]$ – произвольный многочлен. Если $g$ не делится на $f$, то система уравнений $f(x,y) = 0$, $g(x,y) = 0$ имеет разве лишь конечное число решений.

Над полем вещественных чисел неприводимый многочлен может задавать приводимое алгебраическое множество. Например, неприводимый над полем вещественных чисел многочлен ${{x}^{2}}{{(x - 1)}^{2}} + {{y}^{2}}$ задает приводимое алгебраическое множество, состоящее из двух точек $(0,0)$ и $(1,0)$. Ведь каждая точка есть алгебраическое множество. Однако, справедливо следующее утверждение.

Лемма 2. Если многочлен $f(x,y)$ положительной степени неприводим в поле $\mathbb{C}$ комплексных чисел, то множество его нулей ${{V}_{\mathbb{C}}}(f) \subset {{\mathbb{C}}^{2}}$ неприводимо.

Заметим во-первых, что алгебраическое множество ${{V}_{\mathbb{C}}}(h)$ состоит из бесконечного числа точек. Действительно, если $f(x,y)$ содержит одночлен $a{{x}^{k}}$, $a \in \mathbb{C}$, $k > 0$, то в поле комплексных чисел при любом постоянном ${{y}_{0}}$ многочлен положительной степени $f(x,{{y}_{0}})$ имеет хотя бы один корень. Так же разбирается и случай наличия в $f(x,y)$ одночлена $a{{y}^{k}}$, $a \in \mathbb{C}$, $k > 0$. Если же таких одночленов в $f(x,y)$ нет, то многочлен $f(x,{{y}_{0}})$ имеет ненулевую степень по $x$ при любых кроме конечного числа значений ${{y}_{0}}$. А значит, уравнение $f(x,y) = 0$ и в этом случае имеет бесконечно много решений.

Допустим теперь, что ${{V}_{\mathbb{C}}}(f)$ приводимо, и произведение $g(x,y)h(x,y)$ двух многочленов зануляется на ${{V}_{\mathbb{C}}}(f)$, но ни один из этих многочленов не зануляется на ${{V}_{\mathbb{C}}}(f)$. Поскольку ${{V}_{\mathbb{C}}}(f)$ содержит бесконечно много точек, то $g(x,y)h(x,y)$ по лемме 1 делится на $f(x,y)$. В силу неприводимости $f(x,y)$ на него делится хотя бы один из многочленов $g(x,y)$ и $h(x,y)$. Но тогда этот многочлен зануляется на ${{V}_{\mathbb{C}}}(f)$, что противоречит приводимости множества ${{V}_{\mathbb{C}}}(f)$. Лемма доказана.

Пусть вещественный многочлен $P(u,t)$ задает вещественную алгебраическую кривую ${{V}_{\mathbb{R}}}(P) \subset {{\mathbb{R}}^{2}}$, то есть одномерное алгебраическое множество.

Лемма 3. Если многочлен $P(u,t)$ неприводим над полем комплексных чисел, то кривая неприводима.

Многочлен $P(u,t)$ положительной степени, поскольку он задает кривую. В силу предыдущей леммы множество ${{V}_{\mathbb{C}}}(P)$ неприводимо. Допустим приводимость кривой ${{V}_{\mathbb{R}}}(P)$, тогда найдутся такие вещественные многочлены $R(u,t)$ и $Q(u,t)$, что произведение $RQ = 0$ на ${{V}_{\mathbb{R}}}(P)$, но ни один из этих многочленов не обладает таким свойством. Поскольку число точек в ${{V}_{\mathbb{R}}}(P)$ бесконечно, и ${{V}_{\mathbb{C}}}(P) \supset {{V}_{\mathbb{R}}}(P)$, то система уравнений $RQ = 0$, $P = 0$ имеет бесконечно много решений. По лемме 1 многочлен $RQ$ делится на $P$. Следовательно, $RQ$ зануляется на ${{V}_{\mathbb{C}}}(P)$, но ни один из многочленов $R$ и $Q$ не зануляется на ${{V}_{\mathbb{R}}}(P)$, а значит и на ${{V}_{\mathbb{C}}}(P)$. То есть, мы получили приводимость ${{V}_{\mathbb{C}}}(P)$ в противоречии лемме 2.

3. Исследование приводимости многочлена $P$. Разберем случаи приводимости $P(u,t)$ над полем комплексных чисел в зависимости от положительных параметров $r$, $R$, $d$. Заметим, что поскольку коэффициент $ - 8Rr \ne 0$, то степень $\deg P(u,t) \geqslant 2$. Как правило $\deg P(u,t) = 4$, но при некоторых значениях параметров она равна двум. Степень $P(u,t)$ по каждому из переменных $u$ и $t$ не превосходит двух.

I. Допустим $P(u,t) = Q(t)R(u,t)$, где многочлен $Q(t)$ зависит лишь от $t$. Если допустить $\deg Q(t) = 2$, то многочлен $R(u,t) = R(u)$ зависит лишь от $u$, иначе степень многочлена $P(u,t)$ по $t$ была бы больше двух. Поскольку $P(u,t)$ содержит одночлен $ut$, то $R(u)$ содержит одночлен $u$. Но тогда произведение $Q(t)R(u)$ содержит член ${{t}^{2}}u$, которого нет в $P(u,t)$. Таким образом $\deg Q(t) = 1$, и можно считать $Q(t) = t + \beta $, $\beta \in \mathbb{C}$. Но тогда, поскольку $R(u,t)$ содержит первую степень $u$, то $\beta = 0$, ибо иначе $P(u,t)$ будет содержать моном $u$, которого в нем нет. Итак, коэффициенты $A$, $ - 8Rrt$, $C$ квадратного трехчлена $P(u,t)$ по $u$ имеют общим множителем $t$. Свободные члены многочленов $A$ и $C$ от $t$ равные соответственно

должны равняться нулю. Это дает ${{b}_{A}} - {{b}_{C}} = 4R(r - 1) = 0$, и поскольку $R > 0$, то $r = 1$. Подставляя $r = 1$ в ${{b}_{C}} = 0$, получим ${{R}^{2}} - {{d}^{2}} = 0$, и $R = d$. Таким образом, приходим к механизму $K(1,d,d)$ складывающегося четырехзвенника с конфигурационным пространством из двух неприводимых компонент. Здесь все подобно случаю, разобранному в предыдущем пункте.

II. Пусть $P(u,t) = Q(u)R(u,t)$, где многочлен $Q(u)$ зависит лишь от $u$. Если предположить $\deg Q(u) = 2$, то $R(u,t) = R(t)$, и мы приходим к уже разобранному случаю. В случае линейного многочлена $Q(u)$ получаем как и выше $P(u,t) = uR(u,t)$. В этом случае многочлен $C$ должен быть нулевым. Но приравнивание его коэффициента при ${{t}^{2}}$:

к нулю дает $d = r + 1 + R$, что отвечает ферме, а не механизму. Для механизмов этот случай приводимости не осуществляется.

III. Пусть $P(u,t)$ разлагается на два множителя, зависящих от обоих переменных: $P(u,t)$ = $Q(u,t)R(u,t)$. Поскольку степень по переменному $u$ $\mathop {\deg }\nolimits_u P = 2$ и верно равенство $\mathop {\deg }\nolimits_u QR$ = $\mathop {\deg }\nolimits_u Q$ + $\mathop {\deg }\nolimits_u R$, то $\mathop {\deg }\nolimits_u Q$ = $\mathop {\deg }\nolimits_u R$ = 1. То же самое верно и для степеней этих многочленов по $t$.

а) В случае $\deg P(u,t) = 4$ разложение имеет вид

Поскольку в $P(u,t)$ нет членов с ${{u}^{2}}t$ и $u{{t}^{2}}$, то $e = - fa$ и $g = - bf$. Поскольку в $P(u,t)$ нет членов с $u$ и $t$, то

И тогда, либо $a = b = 0$, и в этом случае:

Что приводит к

Однако, второе равенство не может выполняться для механизма.

Следовательно, этот случай отпадает, и остается случай $h = fc$, и тогда

Приравнивая коэффициенты, получаем систему уравнений:

Возводя последнее равенство дважды в квадрат и подставляя при этом в него выражения для $f$, $f{{c}^{2}}$, $f{{a}^{2}}$, $f{{b}^{2}}$ из первых четырех равенств, приходим к равенству

Но это равенство у нас не выполняется.

б) Остается случай $\deg P(u,t) = 2$. Но тогда

Случаю механизма отвечает лишь возможность $d = r + 1 - R$. После такой подстановки многочлен $\frac{1}{4}P(u,t)$ приобретает вид:

Пусть он разлагается в произведение

Допустим, хотя бы один из свободных членов $c$, $h$ не равен нулю. Поскольку $P(u,t)$ не содержит первых степеней $u$ и $t$, то

Эта однородная система линейных уравнений относительно неизвестных $c$, $h$ имеет ненулевое решение, лишь если столбцы ее определителя пропорциональны. Но тогда квадратный трехчлен $r(R - 1){{u}^{2}}$ + $R(r + 1){{t}^{2}}$ – 2Rrut является полным квадратом, что влечет равенство нулю его дискриминанта:

Это при наших условиях невозможно. Таким образом, $c = h = 0$, откуда следует $R = r$ и $d = 1$. Что отвечает шарнирному параллелограмму.

Остается заметить, что во всех найденных случаях приводимости многочлена $P(u,t)$ над полем комплексных чисел он приводим и над полем вещественных чисел, и распадается в произведение множителей, определяющих вещественные алгебраические кривые. Конфигурационное пространство шарнирного параллелограмма $K(r,r,1)$, $r \ne 1$ бирационально изоморфно кривой, задающейся уравнением $r(t - u)(rt - ru - t$ – – u) = 0, дельтоида $K(1,R,R)$, $R \ne 1$ – кривой $u( - R{{t}^{2}}u + {{t}^{2}}u - 2Rt + Ru + u)$ = 0, шарнирного ромба $K(1,1,1)$ – кривой $ut(u - t) = 0$.

Итак, доказано следующее утверждение.

Лемма 4. Конфигурационное пространство шарнирного четырехзвенного механизма приводимо лишь в двух случаях: когда механизм – шарнирный параллелограмм, у нас $K(r,r,1)$, либо когда это складывающийся механизм (дельтоид), у нас $K(r,1,r)$ или $K(1,R,R)$ (ромб $K(1,1,1)$ является и параллелограммом и дельтоидом).

4. Классификация четырехзвенных механизмов. Перечислим все существенно различные с точки зрения геометрии конфигурационных пространств случаи КШС четырехзвенных механизмов, и отвечающих им механизмов. Эта классификация уточняет классификацию, приведенную в работе [5], заостряя внимание на случаях приводимости конфигурационного пространства. Ее легко представить наглядно, пользуясь рис. 2, 3.

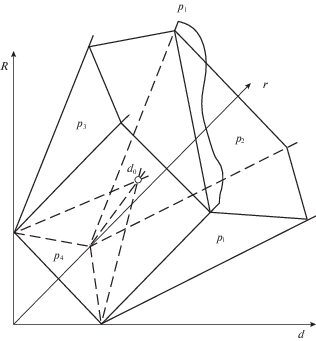
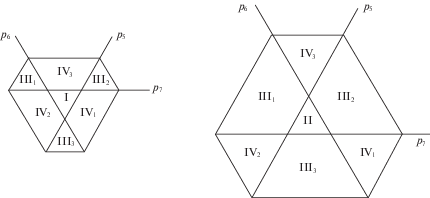
На рис. 2, изображено множество $C$ существенных КШС, то есть тех, которым отвечает хотя бы один шарнирник. Оно лежит в неотрицательном октанте координатной системы $OrRd$ и кроме координатных плоскостей ограничено плоскостями: P₄ : r + + $R + d = 1$ со стороны вершины октанта, и ${{P}_{1}}: - r - R + d = 1$; ${{P}_{2}}:r - R - d = 1$; ${{P}_{3}}: - r + R - d = 1$ с боков. На границе множества $C$ лежат КШС, которым отвечают одна или две фермы. Внутри $C$ лежат КШС, которым отвечают механизмы. Ранг дифференциала рычажного отображения падает лишь в тех положениях четырехзвенного механизма, где все его шарниры оказываются на одной прямой. Мы называем такие механизмы и их КШС распрямляемыми. Их КШС лежат в плоскостях P₅ : r + + $R - d = 1$, ${{P}_{6}}: - r + R + d = 1$, ${{P}_{7}}:r - R + d = 1$ рис. 2, проходящих через точку ${{d}_{0}}$ = = (1, 1, 1) и стороны треугольной грани множества $C$. На рис. 3 показаны сечения множества $C$ плоскостями, параллельными плоскости ${{P}_{4}}$; первое – “ниже” точки ${{d}_{0}}$, второе – “выше”. Плоскости ${{P}_{5}}$, ${{P}_{6}}$, ${{P}_{7}}$ разбивают $C$ на 8 частей (областей типов КШС), пронумерованных на рис. 3 римскими цифрами с индексами. Механизмы, отвечающие КШС, лежащей внутри области типа, являются нераспрямляемыми и правильными, а следовательно неприводимыми. Кривошипом будем называть рычаг механизма, совершающий полный оборот.

Опуская КШС, которым отвечают фермы, получим следующую классификацию.

I. Нераспрямляемые случаи. Конфигурационное пространство КШС правильно, следовательно не содержит особых точек.

а) Кинематическим схемам, лежащим в областях I, III₁, III₂, III₃ типов, отвечает по одному неприводимому шарнирному механизму с конфигурационным пространством гомеоморфным окружности. Эти механизмы не имеют кривошипов.

б) Кинематическим схемам из областей II, IV₁, IV₂, IV₃ отвечают по два неприводимых механизма с конфигурационными пространствами гомеоморфными окружностям. У механизмов из области ${\text{II}}$ все три рычага кривошипы, у механизмов из остальных областей есть по одному кривошипу.

II. Распрямляемые случаи, им отвечают КШС, лежащие внутри в плоскостях ${{P}_{5}}$, ${{P}_{6}}$, ${{P}_{7}}$. Всем этим КШС отвечает один неправильный шарнирный механизм.

а) Конфигурационное пространство механизма неприводимо, если его КШС не лежит в пересечении плоскостей, то есть на прямых $\{ R = r$, $d = 1\} $, $\{ r = 1$, $R = d\} $ и $\{ r = d$, $R = 1\} $. Конфигурационное пространство механизма гомеоморфно букету двух окружностей, то есть паре окружностей, склеенных в одной точке. Можно выделить 12 типов таких механизмов, отвечающих областям, вырезаемым в каждой из плоскостей ${{P}_{i}}$, $i = 5,6,7$ остальными плоскостями. Мы не будем их перечислять.

б) Конфигурационное пространство механизма приводимо $\{ R = r$, $d = 1\} $, $\{ r = 1$, $R = d\} $ или $\{ r = d$, $R = 1\} $.

б1) Параллелограмм: $\{ R = r$, $d = 1\} $, но $r \ne 1$. Конфигурационное пространство $K$ состоит из пары неприводимых компонент: одна (${{K}^{1}}$) отвечает параллелограммам, другая (${{K}^{2}}$) – антипараллелограммам. Топологически $K$ представляет собой две окружности, склеенные в двух точках. Для компоненты имеется два кривошипа. Для компоненты антипараллелограмма имеется два кривошипа при $r < d$, и три кривошипа при $r > d$. В случае $r < d$ механизм $K$ имеет всего два кривошипа.

б2) Дельтоид: $\{ r = 1,R = d\} $ но $d \ne 1$, или $\{ r = d,R = 1\} $, но $r \ne 1$. Конфигурационное пространство состоит из пары неприводимых компонент: одна ${{K}^{1}}$ отвечает положениям механизма с остановившимся свободным шарниром, совпавшим с закрепленным, другая ${{K}^{2}}$ – положениям без остановивишихся шарниров. Топологически также представляет собой две окружности, склеенные в двух точках. Имеется два кривошипа для компоненты ${{K}^{1}}$. Для компоненты ${{K}^{2}}$ имеется два кривошипа при $r < 1$, и три кривошипа при $r > 1$. В случае когда пара рычагов меньшей длины имеет длину меньшую единицы механизм имеет всего два кривошипа.

б3) Ромб: $r = R = d = 1$. Конфигурационное пространство состоит из трех неприводимых компонент: две из которых ${{K}^{1}}$, ${{K}^{2}}$ отвечают положениям механизма со свободным шарниром, совпавшим с закрепленным, третья ${{K}^{3}}$ – ромбическим положениям (без совпавших шарниров). Топологически представляет собой три окружности, попарно склеенные в трех точках так, что в разных точках склеиваются разные пары окружностей. Имеется по два кривошипа для каждой из компонент. Для механизма в целом все три подвижных рычага кривошипы.

5. Теорема о единственности четырехзвенника с данной передаточной функцией.

Теорема 1. Пусть $K(r,R,d)$ неприводимый четырехзвенный механизм, тогда для любого четырехзвенника с единичным расстоянием между закрепленными шарнирами и набором $\{ r{\kern 1pt} ',R{\kern 1pt} ',d{\kern 1pt} '\} $ длин рычагов, отличным от $\{ r,R,d\} $, на произвольном интервале изменения угла $\varphi $ передаточная функция $\psi {\kern 1pt} ' = \psi {\kern 1pt} '(\varphi )$ четырехзвенника $K(r{\kern 1pt} ',R{\kern 1pt} ',d{\kern 1pt} ')$ отлична от передаточной функции $\psi = \psi (\varphi )$ четырехзвенника $K(r,R,d)$.

Конфигурационное пространство $K(r,R,d)$ бирационально изоморфно компоненте связности кривой $P(u,t) = 0$, где многочлен $P(u,t)$ неприводим. Если конфигурационное пространство четырехзвенника $K(r{\kern 1pt} ',R{\kern 1pt} ',d{\kern 1pt} ')$ изоморфно кривой $P{\kern 1pt} '(u,t)$, то передаточные функции могут совпадать на интервале, лишь если система уравнений $P(u,t) = 0$, $P{\kern 1pt} '(u,t) = 0$ имеет бесконечное число решений. Вследствие леммы 1 это возможно, лишь если многочлен $P{\kern 1pt} '(u,t)$ делится на $P(u,t)$. Поскольку $\deg P{\kern 1pt} '(u,t)$ ≤ ≤ $\deg P(u,t)$, это возможно лишь в случае $P{\kern 1pt} '(u,t)$ = $aP(u,t)$, $a \in \mathbb{R}{{\backslash 0}}$. Доказательство нашей теоремы завершает следующая лемма.

Лемма 5. Пусть передаточная функция четырехзвенника $K(r,R,d)$ задается неприводимым многочленом $P(u,t)$, а передаточная функция четырехзвенника $K(r{\kern 1pt} ',R{\kern 1pt} ',d{\kern 1pt} ')$ – многочленом $P{\kern 1pt} '(u,t)$ = $aP(u,t)$, $a \in \mathbb{R}{{\backslash 0}}$, тогда $r{\kern 1pt} ' = r$, $R{\kern 1pt} ' = R$, $d{\kern 1pt} ' = d$.

Приравнивая нулю коэффициенты многочлена $F = P{\kern 1pt} '(u,t) - aP(u,t)$, получаем систему уравнений на длины рычагов. Пусть ${{k}_{{ij}}}$ – коэффициент при ${{u}^{i}}{{t}^{j}}$ в $F$. Тогда:

Подставляя в первое уравнение $R{\kern 1pt} '$ и $r{\kern 1pt} '$, выраженные через $R$ и $r$ из двух последних, получим:

откуда $a = 1$. Теперь два последних уравнения дают $R{\kern 1pt} ' = R$ и $r{\kern 1pt} ' = r$. Подставляя эти значения в ${{k}_{{00}}}$ получаем

Таким образом, и $d{\kern 1pt} ' = d$, и лемма доказана.

Еще проще доказывается, что передаточные функции антипараллелограммов и передаточные функции дельтоидов на компоненте с несовпадающими шарнирами также при заданных закрепленных шарнирах однозначно определяются длинами их рычагов. Передаточная функция дельтоида с совпавшими шарнирами не зависит от длины вращающихся рычагов. Но здесь по существу есть лишь одна постоянная функция. В случае параллелограмма прямая и обратная передаточные функции совпадают и не зависят от длин боковых рычагов.