Прикладная математика и механика, 2022, T. 86, № 1, стр. 35-65

1. Постановка задачи. Опишем общую геометрию волновода, однако при некоторых ограничениях, которые будут сниматься в работе по мере надобности. Пусть $\Omega = \omega \times \mathbb{R}$ – цилиндр с сечением $\omega $, областью на плоскости ${{\mathbb{R}}^{2}}$ с липшицевой границей $\partial \omega $ и компактным замыканием $\bar {\omega } = \omega \cup \partial \omega $. Масштабированием сведем характерный размер сечения к единице и сделаем безразмерными системы декартовых координат $x = (y,z) \in {{\mathbb{R}}^{3}}$, $y = ({{y}_{1}},{{y}_{2}}): = ({{x}_{1}},{{x}_{2}})$ и все геометрические параметры. Начало тех или иных координат обозначаем $O$. Пусть еще ${{\omega }_{*}}$ – внутренняя подобласть области $\omega $ и ${{P}^{1}}, \ldots ,{{P}^{J}}$ – попарно различные точки в ней, т.е. ${{\bar {\omega }}_{*}} \subset \omega $ и ${{P}^{j}} \in {{\omega }_{*}}$, ${{P}^{j}} \ne {{P}^{k}}$ при $j \ne k$. Наконец, зафиксируем точки ${{z}^{1}} < \ldots < {{z}^{N}}$ на оси аппликат $z = {{x}_{3}}$ и подберем коэффициенты растяжения/сжатия ${{\gamma }_{n}} > 0$ и векторы сдвигов ${{y}^{n}} \in {{\mathbb{R}}^{2}}$ так, чтобы

Акустический волновод ${{\Pi }^{\varepsilon }}$ с резонатором (рис. 1, а–г) составлен из полубесконечных цилиндрических рукавов

и конечных цилиндров (1.1), зауженных или расширенных камер-вставок, которые соединены через мелкие отверстия в поперечных перегородках $\partial {{\Omega }_{n}} \cap \partial {{\Omega }_{{n - 1}}}$. При этом ${{\theta }_{1}}, \ldots ,{{\theta }_{J}}$ – ограниченные липшицевы области на плоскости, $\varepsilon \in (0,{{\varepsilon }_{0}}]$ – малый параметр, а величина ${{\varepsilon }_{0}} > 0$ зафиксирована так, что замыкания проекций множеств (1.3) на плоскость $\{ x:z = 0\} $ попадают вовнутрь области ${{\omega }_{*}}$, т.е. $\overline {\theta _{j}^{\varepsilon }} ({{z}^{n}}) \subset \partial {{\omega }_{*}} \times \{ {{z}^{n}}\} $.

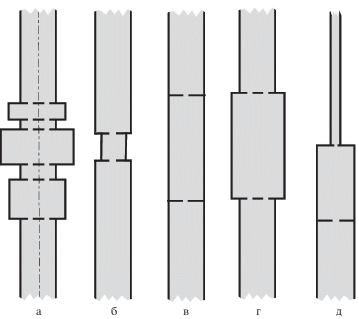
Гармонические во времени колебания акустической среды в волноводе с жесткими стенками и перфорированными перегородками

описываются при помощи спектральной задачи Неймана для оператора Лапласа ${{\Delta }_{x}}$ в дифференциальной форме или вариационной форме

Здесь ${{\nabla }_{x}} = \operatorname{grad} $, ${{\partial }_{\nu }}$ – производная вдоль внешней нормали $\nu $, определенная почти всюду на липшицевой поверхности $\partial \Pi _{N}^{\varepsilon }$, а ${{u}^{\varepsilon }}$ – давление в среде, $\lambda = {{\kappa }^{2}}$ – спектральный параметр и $\kappa > 0$ – частота колебаний (масштабированием постоянная плотность сведена к единице). Наконец, ${{({\kern 1pt} {\kern 1pt} \cdot {\kern 1pt} {\kern 1pt} ,\; \cdot {\kern 1pt} {\kern 1pt} )}_{{\Pi _{N}^{\varepsilon }}}}$ – натуральное скалярное произведение в пространстве Лебега ${{L}^{2}}\left( {\Pi _{N}^{\varepsilon }} \right)$ и ${{H}^{1}}\left( {\Pi _{N}^{\varepsilon }} \right)$ – пространство Соболева.

При гладких или кусочно-гладких границах задействованных областей можно оперировать исключительно дифференциальной постановкой (1.5) задачи в обычных или весовых пространствах Соболева ([1] гл. 5 и 6), однако при собственно липшицевых поверхностях приходится иметь дело с интегральным тождеством (1.6). Далее ограничиваемся классическими формулировками возникающих краевых задач, так как переход к обобщенным проводится по стандартной схеме [2].

Левая часть равенства (1.6) – положительная, симметричная и замкнутая в ${{H}^{1}}\left( {{{\Pi }^{\varepsilon }}} \right)$ форма, а значит, задаче (1.5) ставится в соответствие ([3] гл. 10) положительный самосопряженный оператор ${{A}^{\varepsilon }}$ в ${{L}^{2}}\left( {{{\Pi }^{\varepsilon }}} \right)$, область определения которого шире пространства Соболева ${{H}^{2}}\left( {{{\Pi }^{\varepsilon }}} \right)$ из-за корневых сингулярностей градиента решения на ребре $\partial \theta _{j}^{\varepsilon }({{z}^{n}})$ = $\{ x:y \in \partial \theta _{j}^{\varepsilon }$, $z = {{z}^{n}}\} $ (см. [4, 5] и, например, ([1] гл. 2 и 12)). Непрерывный спектр $\sigma _{c}^{\varepsilon }$ оператора ${{A}^{\varepsilon }}$ занимает замкнутую полуось $\overline {{{\mathbb{R}}_{ + }}} = [0, + \infty )$ и разбивается на участки постоянной кратности собственными числами

модельной задачи на сечении

Дискретный спектр $\sigma _{d}^{\varepsilon }$ заведомо пуст, но у оператора ${{A}^{\varepsilon }}$ могут быть собственные числа, вкрапленные в непрерывный спектр и образующие точечный спектр $\sigma _{p}^{\varepsilon }$. В разд. 3 при дополнительных условиях симметрии (рис. 1, a)

и “раздутия” ${{\gamma }_{n}} > 1$ хотя бы одной из камер при помощи приема [6] показано, что множество $\sigma _{p}^{\varepsilon } \cap (0,{{\Lambda }_{1}})$ не пусто. В то же время для уменьшенных камер (рис. 1, б) на интервале $(0,{{\Lambda }_{1}})$ собственных чисел оператора ${{A}^{\varepsilon }}$ нет – этот факт вытекает из априорных оценок решений в сингулярно возмущенных областях [7]. В общей ситуации, в частности, выше первой положительной точки отсечки ${{\Lambda }_{1}}$ строение точечного спектра осталось неизученным.

Зафиксируем спектральный параметр $\lambda = {{\kappa }^{2}}$ в первом интервале $(0,{{\Lambda }_{1}})$ непрерывного спектра; при этом $\kappa \in (0,{{\kappa }_{\dag }})$ и ${{\kappa }_{\dag }} = \sqrt {{{\Lambda }_{1}}} $. Тогда в прямом бесконечном цилиндре $\Omega $ распространяются только поршневые волны, не зависящие от поперечных координат $y$

Нормирующий множитель $\alpha $ включает площадь $\left| \omega \right|$ сечения $\omega $.

Волна ${{w}^{ + }}$, приходящая из бесконечности в рукаве ${{\Omega }^{ - }}$, порождает рассеянное акустическое поле и вместе с ним образует решение задачи (1.5)

При этом ${{R}^{\varepsilon }}$ и ${{T}^{\varepsilon }}$ – коэффициенты отражения и прохождения при уходящих в рукавах ${{\Omega }^{ \pm }}$ волнах (1.11), ${{\tilde {u}}^{\varepsilon }}$ – остаток, затухающий на бесконечности со скоростью $O({{e}^{{ - {{\beta }_{\lambda }}|z|}}})$, ${{\beta }_{\lambda }} = \sqrt {{{\Lambda }_{1}} - \lambda } $, а ${{\chi }_{ \pm }}$ – гладкие срезающие функции, локализующие волны в рукавах ${{\Omega }^{ \pm }}$

Длина ${{z}_{*}} > 0$ зафиксирована так, что $ - {{z}_{*}} < {{z}^{1}} < \ldots < {{z}^{{N + 1}}} < {{z}_{*}}$.

Технический результат работы – вывод асимптотических формул для коэффициентов рассеяния

Формулы (1.13) с достаточно явными выражениями для ${{R}^{0}}$ и ${{T}^{0}}$ применяются для обеспечения почти полного прохождения поршневой волны через семейство перфорированных перегородок, т.е. достижению равенства ${{R}^{0}} = 0$. Основное внимание в статье уделяется случаю двух ($N = 2$) перегородок, причем не только для волновода (1.4) с двумя рукавами (1.2), имеющими одинаковое сечение $\omega $ (рис. 1, б–г), но и для волновода (рис. 1, д)

у которого рукава и камера имеют неодинаковые сечения ${{\omega }_{ \pm }}$, ${{\omega }_{\# }} \subset {{\mathbb{R}}^{2}}$, а перегородки – различающуюся перфорацию

При этом ${{\omega }_{ \pm }} \cap {{\omega }_{\# }} \ne \emptyset $ и $P_{{( \pm )}}^{j} \in {{\omega }_{ \pm }} \cap {{\omega }_{\# }}$, $j = 1, \ldots ,{{J}_{ \pm }}$. Используемые в формулах (1.14)–(1.17) обозначения вполне аналогичны введенным в начале раздела и не нуждаются в пояснениях. Упомянем лишь, что нормирующий множитель ${{\alpha }_{ \pm }}$ в поршневых волнах равен ${{\left( {2\kappa \left| {{{\omega }_{ \pm }}} \right|} \right)}^{{ - 1/2}}}$.

В разд. 2 приводятся известные результаты, относящиеся к случаям $N = J = 1$ (одна перегородка), $N = 2$, $J = 1$ (одна камера) и $N = \infty $ (периодическое семейство перегородок). В отличие от многих предшествующих публикаций используется метод [7] построения асимптотики решений статических и спектральных сингулярно возмущенных краевых задач, приспособленный [8–10] к дифракционным задачам о волноводах. В разд. 4 содержится вспомогательный материал, а в разд. 5 проведен асимптотический анализ решения (1.12) в волноводе $\Pi _{2}^{\varepsilon }$ с двумя перегородками, но произвольным количеством отверстий, и как следствие в разд. 6 сформулированы условия, гарантирующие упомянутое почти полное прохождение поршневой волны. Этот эффект, называемый инвертированной аномалией Вайнштейна (терминология [11]), достигается путем подбора полувысоты вставки-камеры (1.16)

Благодаря свойству унитарности матрицы рассеяния названная аномалия распространения волны ${{w}^{ + }}$ в направлении от $ - \infty $ к $ + \infty $ гарантирует такую же аномалию волны ${{w}^{ - }}$ в направлении от $ + \infty $ к $ - \infty $. Почти полное прохождение отличающихся от поршневых волн не исследовалось.

Многие геометрические ограничения введены в начаде разд. 1 исключительно для предварительной фиксации объекта, но в разд. 5 и 7 обсуждаются разнообразные допустимые изменения геометрии волновода, в частности, широкие трубы, оканчивающиеся “глушителем” (рис. 1, д) или “камерой обскура” (рис. 2, а). Новый результат из разд. 6.2 – критерий (6.9) возможности достижения эффекта почти полного прохождения поршневой волны в волноводе (1.14) с разными рукавами (1.15) и количествами отверстий в двух перегородках. Если $J = 1$, а ${{\omega }_{ \pm }}$ и ${{\theta }_{{1 \pm }}}$ – круги с радиусами $\rho _{ \pm }^{\omega }$ и $\rho _{ \pm }^{\theta }$ соответственно (рис. 1, б), то упомянутый критерий выглядит просто

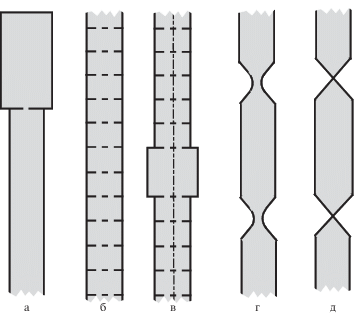
В общем случае критерий содержит площади $\left| {{{\omega }_{ \pm }}} \right|$ сечений и, что весьма неожиданно, гармонические емкости [12, 13] множеств $\{ x \in {{\mathbb{R}}^{3}}:y \in \overline {{{\theta }_{{j \pm }}}} $, $z = 0\} $.

2. Известные факты

2.1. Периодический волновод. В рамках теории Флоке–Блоха–Гельфанда (см. [1, 14–17] и др.) существенный спектр $\sigma _{e}^{\varepsilon }$ задачи (1.5) в цилиндре $\Pi _{\infty }^{\varepsilon }$ со счетным периодическим семейством перфорированных перегородок ${{\{ {{\Theta }^{\varepsilon }}(n)\} }_{{n \in \mathbb{Z}}}}$ (рис. 2, б)

определяется при помощи преобразования Гельфанда [18] и требует исследовать модельную задачу на ячейке периодичности ${{\varpi }^{\varepsilon }}$

Именно, существенный спектр $\sigma _{e}^{\varepsilon }$ – объединение спектральных сегментов

образованных собственными числами модельной спектральной задачи Неймана для оператора Лапласа с зависящими от параметра Флоке $\tau \in \mathbb{R}$ условиями квазипериодичности на торцах $\omega ( \pm 1{\text{/}}2)$ ячейки (2.3)

В волноводе (2.1) к единице сведен период, т.е. расстояние между соседними перегородками, а не характерный размер сечения $\omega $. Ячейка периодичности, на которой ставится модельная задача со спектром (2.5), имеет единичную длину, но может быть вырезана из периодической области (2.1) произвольно; например, в случае $\varpi _{ \bullet }^{\varepsilon }$ = = $\omega \times (0,1)$ условия квазипериодичности устанавливают связь значений решения и его производных только на малых множествах $\theta _{j}^{\varepsilon }(0)$ и $\theta _{j}^{\varepsilon }(1)$, $j = 1, \ldots ,J$, лежащих на торцах $\omega (0)$ и $\omega (1)$, а на оставшейся части границы $\partial \omega _{ \bullet }^{\varepsilon }$ выставлены краевые условия Неймана.

Вариационная постановка [2] задачи (2.6), (2.7) порождает ([3], гл. 10) положительный самосопряженный оператор ${{B}^{\varepsilon }}(\tau )$ в гильбертовом пространстве ${{L}^{2}}(\varpi )$ с дискретным спектром (2.5). Функции $\tau \mapsto M_{k}^{\varepsilon }(\tau )$ непрерывны и $2\pi $-периодичны, т.е. сегменты (2.4) – связные компакты на полуоси $\overline {{{\mathbb{R}}_{ + }}} $.

Для собственных чисел задачи (2.6), (2.7) установлены [19, 20] формулы

Здесь ${{c}_{k}}$ и ${{\varepsilon }_{k}}$ – положительные величины, зависящие от номера $k$ члена последовательности (2.5), а $M_{k}^{0}$ – собственные числа предельной задачи Неймана

Ячейки $\varpi _{ \bullet }^{\varepsilon }$ и $\varpi _{ \bullet }^{0}$ совпадают как множества, но на торцах $\omega (0)$ и $\omega (1)$ второй из них уничтожены следы перфорации $\{ \theta _{j}^{\varepsilon }\} _{{j = 1}}^{J}$.

Соотношения (2.8) показывают, что длины сегментов (2.4) не превосходят $2{{c}_{k}}\varepsilon $, и в случае $M_{k}^{0} < M_{{k + 1}}^{0}$ между сегментами ${{\sigma }^{\varepsilon }}(k)$ и ${{\sigma }^{\varepsilon }}(k + 1)$ раскрыта лакуна шириной $M_{{k + 1}}^{0} - M_{k}^{0} + O(\varepsilon )$. Лакуны называются зонами торможения волн, так как на соответствующих частотах распространение волн в волноводе (2.1) невозможно. Вместе с тем при $\lambda \in \sigma _{e}^{\varepsilon }(k)$, т.е. в весьма узких частотных диапазонах (2.4), существуют волны, переносящие энергию без каких-либо потерь вдоль волновода через счетное семейство мелких отверстий. Поэтому спектральные сегменты называются зонами прохождения волн, а сами волны имеют вид

При этом $V({\kern 1pt} {\kern 1pt} \cdot {\kern 1pt} {\kern 1pt} ;\tau )$ – собственная функция задачи (2.6), (2.7), отвечающая собственному числу $M(\tau )$ при некотором $\tau \in ( - \pi ,\pi ]$. Функция (2.9) именуется волной Флоке, оказывается гладкой благодаря условиям квазипериодичности (2.7) и в силу равенств (2.6) удовлетворяет задаче (1.5) в периодическом волноводе (2.1).

2.2. Одна перегородка. Исследована [21] дифракция волн в волноводе (1.4) с одной перегородкой и одним малым отверстием в ней, т.е. $N = 1$, $J = 1$, ${{y}^{1}} = 0$ и $\Pi _{1}^{\varepsilon } = (\Omega {{\backslash }}\omega (0)) \cup \theta _{1}^{\varepsilon }(0)$ (в случае $J > 1$ выводы остаются без существенных изменений). На околопороговых частотах в $\Pi _{1}^{\varepsilon }$ обнаружены разнородные аномалии Вайнштейна [22]. Опишем эти эффекты на примере малой частоты вблизи основного порога ${{\Lambda }_{0}} = 0$ и увеличивающемся, но также малом размере $\varepsilon $ отверстия $\theta _{1}^{\varepsilon }(0)$. Если отверстие совсем мало и $\varepsilon = o(\kappa )$, то поршневая волна претерпевает почти полное отражение и коэффициент прохождения ${{T}^{\varepsilon }}$ – бесконечно малая $O(\varepsilon )$ (прямая аномалия Вайнштейна). В случае “большего” диаметра отверстия, т.е. при $\kappa = o(\varepsilon )$ наблюдается почти полное прохождение волны ${{w}^{ + }}$ (инвертированная аномалия Вайнштейна по терминологии [11]), а именно, для коэффициентов рассеяния (1.13) верны соотношения ${{R}^{0}} = 0$, ${{R}^{\varepsilon }} = O(\varepsilon )$ и $\left| {{{T}^{\varepsilon }}} \right| = 1 + O(\varepsilon )$.

Если величины $\varepsilon $ и $\kappa $ сравнимы по порядку, то оба коэффициента рассеяния ${{R}^{\varepsilon }}$ и ${{T}^{\varepsilon }}$ перестают быть малыми. Изучены [11, 23–26] родственные двумерные и трехмерные задачи, связанные с аномалиями Вайнштейна [22].

2.3. Две перегородки. Далее волноводам $\Pi _{2}^{\varepsilon }$ (рис. 1, б–г) уделяется основное внимание.

Описан [27] эффект почти полного прохождения волн в случае $J = 1$, но для волновода $\Pi _{2}^{\varepsilon }$ с мягкими стенками (задача Дирихле для уравнения Гельмгольца) при помощи подхода, опирающегося на разложение в ряды Фурье и потому излишне громоздкого. Метод [7] построения асимптотики решений краевых задач в сингулярно возмущенных областях применен [28, 29] для исследования прохождения волн в плоском волноводе с зауженными участками, образующими в пределе при $\varepsilon \to + 0$ двойной угол (рис. 2, г и д). Как и в статье [27], на границе назначены условия Дирихле. В указанных публикациях процедуры настройки формы камер для обеспечения почти полного прохождения волн не разрабатывались.

Алгоритмы построения асимптотики в краевых задачах Дирихле и Неймана [7] различаются существенно хотя бы потому, что предельные задачи обладают разными свойствами, а их решения – разным поведением около выделенных особых точек. Поэтому упомянутые результаты неприменимы к рассматриваемой задаче (1.5).

3. Собственные числа

3.1. Захваченные волны. Предположим, что волновод (1.4) обладает плоскостью $\{ x:{{x}_{1}} = 0\} $ зеркальной симметрии (см. формулу (1.9) и рис. 1, a). Сузим задачу (1.5) на половину $\Pi _{{N + }}^{\varepsilon }$ = $\{ x \in \Pi _{N}^{\varepsilon }:{{x}_{1}} = {{y}_{1}} > 0\} $ волновода и на его срединной плоскости ${{\Gamma }^{\varepsilon }}$ = = $\{ x \in \Pi _{N}^{\varepsilon }:{{x}_{1}} = 0\} $ назначим исскуственные условия Дирихле [6]

Сечение $\omega $ рукавов ${{\Omega }^{ \pm }}$ наследуют симметрию от самого волновода $\Pi _{N}^{\varepsilon } \supset {{\Omega }^{ \pm }}$. Первое собственное число ${{\Lambda }_{{0 + }}} > 0$ соответствующей модельной смешанной краевой задачи на половине ${{\omega }_{ + }} = \{ y \in \omega :{{y}_{1}} > 0\} $ сечения

определяет нижнюю грань непрерывного спектра $\sigma _{{c + }}^{\varepsilon }$ оператора $A_{ + }^{\varepsilon }$ задачи (3.1) (обозначения аналогичны введенным в разд. 1) и совпадает с каким-то положительным членом ${{\Lambda }_{k}}$ последовательности (1.7). Например, для прямоугольника $\omega = ( - {{d}_{1}},{{d}_{1}})$ × × $( - {{d}_{2}},{{d}_{2}})$ в случае ${{d}_{2}} \geqslant {{d}_{1}}$ имеем ${\mathbf{k}} = 1$, однако индекс ${\mathbf{k}}$ можно сделать сколь угодно большим, увеличивая дробь ${{d}_{1}}{\text{/}}{{d}_{2}}$. В любом случае продолжение по нечетности соответствующей собственной функции ${{U}_{{0 + }}}$ задачи (1.9) через среднюю линию $\{ y \in \omega :{{y}_{1}} = 0\} $ фигуры $\omega $ есть не что иное, как собственная функция ${{U}_{{\mathbf{k}}}}$ задачи (1.8). Таким образом, непрерывный спектр $\sigma _{{c + }}^{\varepsilon }$ оператора $A_{ + }^{\varepsilon }$ задачи (3.1) (обозначения аналогичны введенным в разд. 1) занимает луч $[{{\Lambda }_{k}}, + \infty ) \subset {{\mathbb{R}}_{ + }}$, а интервал $(0,{{\Lambda }_{k}}) \supset (0,{{\Lambda }_{1}})$ может содержать собственные числа задачи (3.1), образующие ее дискретный спектр

Соответствующие собственные функции $u_{{0 + }}^{\varepsilon },\; \ldots ,\;u_{{{{Q}^{\varepsilon }} + }}^{\varepsilon }$ ортонормируем в пространстве ${{L}^{2}}(\Pi _{{N + }}^{\varepsilon })$. Наконец, нечетное продолжение собственных функций задачи (3.1) в $\Pi _{{N + }}^{\varepsilon }$ через плоскость ${{\Gamma }^{\varepsilon }}$ дает собственные функции задачи (1.5) в $\Pi _{N}^{\varepsilon }$ и тем самым показывает, что множество $\sigma _{{d + }}^{\varepsilon }$ содержится в точечном спектре $\sigma _{p}^{\varepsilon }$, который состоит из собственных чисел оператора ${{A}^{\varepsilon }}$, вкрапленных в его непрерывный спектр $\sigma _{c}^{\varepsilon }$. Дискретный спектр $\sigma _{d}^{\varepsilon }$ задачи (1.5) заведомо пуст.

Для того чтобы обнаружить дискретный спектр в задаче (3.1), предположим, что среди коэффициентов ${{\gamma }_{1}}, \ldots ,{{\gamma }_{N}}$ в определении (1.1) есть превосходящие единицу. Пусть ${{\gamma }_{n}} > 1$, а число $Q \in {{\mathbb{N}}_{0}}$ и высота ${{L}_{n}} = {{z}^{{n + 1}}} - {{z}^{n}}$ цилиндра ${{\Omega }_{n}}$ таковы, что

Рассмотрим вспомогательную задачу на половине ${{\Omega }_{{n + }}} = \{ x \in {{\Omega }_{ + }}:{{x}_{1}}$ > 0} цилиндра ${{\Omega }_{n}}$

Здесь $\Gamma _{n}^{\varepsilon }$ – объединение искусственно образованной поверхности $\Gamma _{n}^{0} = \{ x \in {{\Omega }_{n}}:{{y}_{1}} = 0\} $ и частей отверстий $\theta _{j}^{\varepsilon }(n)$ и $\theta _{j}^{\varepsilon }(n + 1)$, $j = 1, \ldots ,J$, попадающих на границу $\partial {{\Omega }_{{n + }}}$. При $\varepsilon = 0$ отверстия исчезают и задача (3.4) превращается в предельную спектральную смешанную краевую задачу

у которой в силу ограничения (3.3) есть собственные числа

Проверено ([7] гл. 9, [30]), что задача (3.4) имеет собственные числа $M_{{n0 + }}^{\varepsilon }$, …, $M_{{nQ + }}^{\varepsilon }$, подчиненные неравенствам

с некоторыми ${{c}_{0}} > 0$ и ${{\varepsilon }_{0}} > 0$. Таким образом, при малом $\varepsilon $ упомянутые собственные числа содержатся в интервале $(0,{{\Lambda }_{1}})$. Соответствующие собственные функции $V_{{n0 + }}^{\varepsilon }$, …, $V_{{nQ + }}^{\varepsilon }$ ортонормируем в пространстве ${{L}^{2}}({{\Omega }_{{n + }}})$ и продолжим нулем через отверстия $\Gamma _{n}^{\varepsilon }{{\backslash }}\Gamma _{n}^{0}$ на волновод $\Pi _{{N + }}^{\varepsilon }$. Наконец, $\mathcal{L}_{n}^{\varepsilon }$ – линейная оболочка указанных продолжений, $dim\mathcal{L}_{n}^{\varepsilon }$ = Q + 1.

Для вывода оценки кратности дискретного спектра (3.2)

применим минимальный принцип ([30] теор. 10.2.1)

Здесь $\mathcal{E}_{0}^{\varepsilon } = H_{0}^{1}(\Pi _{{N + }}^{\varepsilon };{{\Gamma }^{\varepsilon }})$ = $\{ u_{ + }^{\varepsilon } \in {{H}^{1}}(\Pi _{{N + }}^{\varepsilon }):u_{ + }^{\varepsilon } = 0\;{\text{на}}\;{{\Gamma }^{\varepsilon }}\} $, ${{\Gamma }^{\varepsilon }}$ – срединная плоскость симметричного тела $\Pi _{N}^{\varepsilon }$, и

Итак, $\mathcal{L}_{n}^{\varepsilon } \subset \mathcal{E}_{0}^{\varepsilon }$, и в силу формулы (3.7) при $q = 0$ имеем

Функции $V_{{n0 + }}^{\varepsilon }, \ldots ,V_{{nQ + }}^{\varepsilon }$ взаимно ортогональны в пространстве ${{L}^{2}}(\Pi _{N}^{\varepsilon })$, и поэтому $dim\mathcal{L}_{{n1}}^{\varepsilon } \geqslant Q$, где

Следовательно

Здесь $p = 0$ в случае $V_{{n0 + }}^{\varepsilon } \in \mathcal{L}_{{n1}}^{\varepsilon }$, но $p = 1$ в противном случае, так как какая-то нетривиальная линейная комбинация $c_{0}^{\varepsilon }V_{{n0 + }}^{\varepsilon } + c_{1}^{\varepsilon }V_{{n1 + }}^{\varepsilon }$ обязательно содержится в множестве (3.8) при $q = 1$.

Продолжив рассуждения, находим, что $\lambda _{{Q + }}^{\varepsilon } \leqslant M_{{nQ + }}^{\varepsilon } < {{\Lambda }_{1}}$, и доказываем искомое неравенство (3.6). После этого может оказаться, что $dim\mathcal{L}_{{nQ}}^{\varepsilon } = 0$, а значит, обнаружить еще одно собственное число $\lambda _{{Q + 1 + }}^{\varepsilon } \in \sigma _{{d + }}^{\varepsilon }$ по изложенной схеме не удается. Вместе с тем соотношение (3.6) не всегда превращается в равенство. Во-первых, на интервале $(0,{{\Lambda }_{1}})$ спектр рассмотренной предельной задачи в ${{\Omega }_{{n + }}}$, вообще говоря, не исчерпывается собственными числами (3.5). Во-вторых, среди цилиндров (1.1) могут найтись несколько штук с коэффициентами растяжения ${{\gamma }_{n}} > 1$. Наконец, не все собственные числа в дискретном спектре $\sigma _{d}^{\varepsilon }$ удается найти по изложенной схеме.

В любой ситуации при указанной симметрии волновода (1.4) увеличение размеров хотя бы одного из цилиндров (1.1) позволяет по прежней схеме образовать любое заданное наперед количество собственных чисел задачи (1.5), вкрапленных в ее непрерывный спектр.

3.2. Отсутствие точечного спектра. Для применения известных априорных оценок будем считать, что контуры $\partial \omega $ и $\partial {{\theta }^{1}}, \ldots ,\partial {{\theta }^{J}}$ гладкие. Пусть еще $\Pi _{N}^{\varepsilon }$ – цилиндр $\Omega $ с перегородками ${{\Theta }^{\varepsilon }}({{z}^{1}})$, …, ${{\Theta }^{\varepsilon }}({{z}^{N}})$ (рис. 1, б), т.е. ${{y}^{1}}$, …, ${{y}^{N}} = 0 \in {{\mathbb{R}}^{2}}$ и ${{\Omega }_{n}} = \omega \times {{\Upsilon }_{n}}$, где ${{\Upsilon }_{n}} = ({{z}^{n}},{{z}^{{n + 1}}})$, $n = 1, \ldots ,N - 1$ и ${{\Upsilon }_{0}} = ( - \infty ,{{z}^{1}})$, ${{\Upsilon }_{N}} = ({{z}^{N}}, + \infty )$. Вставки (1.1) невысокие, что обеспечено вторым требованием (1.10), а первое выполнено потому, что ${{\gamma }_{1}} = \ldots {{\gamma }_{{N - 1}}} = 1$ по построению.

Предположим, что у задачи (1.5) есть собственное число

Соответствующую собственную функцию ${{u}^{\varepsilon }}$ нормируем в пространстве ${{L}^{2}}({{\Pi }^{\varepsilon }})$ и разобьем ее на компоненты

Условие ортогональности в списке (3.10) обеспечивает неравенство Пуанкаре

Кроме того, при $n = 1, \ldots ,N - 1$ одномерное неравенство Харди [31], записанное в сферических координатах, влечет за собой весовую оценку

Подставим в интегральное тождество (1.6) пробную функцию ${{\psi }_{n}} \in C_{c}^{\infty }({{\Upsilon }_{n}})$, не зависящую от переменных $y$ и продолженную нулем с камеры ${{\Omega }_{n}}$ на весь волновод $\Pi _{N}^{\varepsilon }$. В результате получим соотношение

Интегралы по множеству ${{\Omega }_{n}}$, содержащие произведения $u_{ \bot }^{\varepsilon }(y,z){{\psi }_{n}}(z)$ и ${{\partial }_{z}}u_{ \bot }^{\varepsilon }(y,z){{\partial }_{z}}{{\psi }_{n}}(z)$ исчезли по причине условия ортогональности в списке (3.10), которое сохраняется при почти всех $z \in {{\Upsilon }_{n}}$ и для производной ${{\partial }_{z}}u_{ \bot }^{\varepsilon }$. Следовательно

Поскольку ${{\lambda }^{\varepsilon }}$ не является собственным числом задачи Неймана для обыкновенного дифференциального уравнения (3.13) в силу предположений (1.10) и (3.9), справедливы соотношения

В силу соотношений (1.5), (3.13) и (3.15) функция $u_{ \bot }^{\varepsilon }$ удовлетворяет краевой задаче

Приведем несколько известных априорных оценок [7] решений эллиптических краевых задач в сингулярно возмущенных областях применительно к краевой задаче (3.16), правые части которой временно зафиксируем. Прежде всего, поскольку гладкие ребра $\partial \omega \times \{ {{z}^{n}}\} $ и $\partial \omega \times \{ {{z}^{{n + 1}}}\} $ на границе $\partial {{\Omega }_{n}}$ имеют раствор $\pi {\text{/2}}$, а точки $({{P}^{j}},{{z}^{n}})$ и $({{P}^{j}},{{z}^{{n + 1}}})$ являются вершинами конусов $\mathbb{R}_{ \pm }^{3}$, локальные весовые оценки решений задачи Неймана ([1] гл. 9 §4, 32–34) показывают, что

Радиус $R > 0$ выбран так, чтобы $\overline {{{\theta }_{j}}} \subset \mathbb{B}_{R}^{2}(\mathcal{O}) = \left\{ {y:\left| y \right| < R} \right\}$ при $j = 1, \ldots ,J$.

Обработаем окрестности отверстий $\overline {\theta _{j}^{\varepsilon }(n)} $. Сделаем растяжение координат

Замена (3.17) переводит множество $\Pi _{N}^{\varepsilon } \cap {{\mathbb{B}}_{{\varepsilon R}}}({{P}^{j}},{{z}^{n}})$ в пересечение шара $\mathbb{B}_{R}^{3}(\mathcal{O})$ и двух полупространств $\mathbb{R}_{ \pm }^{3} = \{ \xi : \pm {{\xi }_{3}} > 0\} $, соединенных через отверстие ${{\theta }_{j}}(0)$ = $\{ \xi :\eta \in {{\theta }_{j}},{{\xi }_{3}} = 0\} $

На ребре $\partial {{\theta }_{j}} \times \{ 0\} $ трещины $\overline {{{\theta }_{j}}} $ градиент решения задачи Неймана приобретает сингулярность $O(\rho _{\theta }^{{ - 1/2}})$, где ${{\rho }_{\theta }}$ – расстояние до ребра. Это обстоятельство предопределяет весовой показатель ${{\beta }_{\theta }} \in ( - {\text{1/2}},0)$ в локальной оценке ([1] гл. 10 и 12 § 8, [32–34])

для функции ${{\xi }^{{jn}}} \mapsto {\mathbf{u}}_{{jn}}^{\varepsilon }({{\xi }^{{jn}}})$ = $u_{ \bot }^{\varepsilon }({{P}^{j}} + \varepsilon {{\eta }^{{jn}}},{{z}^{n}} + \varepsilon {{\zeta }^{{jn}}})$, подчиненной уравнению $ - {{\Delta }_{\xi }}{\mathbf{u}}_{{jn}}^{\varepsilon }$ = = ${{\varepsilon }^{2}}{{\lambda }^{\varepsilon }}{\mathbf{u}}_{{jn}}^{\varepsilon }$ и краевым условиям $ \pm {{\partial }_{\zeta }}{\mathbf{u}}_{{jn}}^{\varepsilon }$ = $ \mp \varepsilon F_{{n \pm }}^{\varepsilon }$ соответственно на примыкающих к отверстию частях бесконечного множества (3.18) и его границы.

Итак, составляющая $u_{ \bot }^{\varepsilon }$, а значит, и само решение ${{u}^{\varepsilon }}$ принадлежат весовому классу Соболева с показателем гладкости два. В то же время из-за упомянутых сингулярностей на ребрах трещин нормальные производные ${{\partial }_{z}}{{u}^{\varepsilon }}({\kern 1pt} {\kern 1pt} \cdot {\kern 1pt} {\kern 1pt} ,{{z}^{n}})$ и $ - {{\partial }_{z}}{{u}^{\varepsilon }}({\kern 1pt} {\kern 1pt} \cdot {\kern 1pt} {\kern 1pt} ,{{z}^{{n + 1}}})$ на торцах камеры ${{\Omega }_{n}}$ не попадают в пространство ${{L}^{2}}(\omega )$, но все-таки принадлежат пространству ${{L}^{q}}(\omega )$ с показателем $q \in [1,2)$. В итоге гладкая на интервале ${{\Upsilon }_{n}} \mathrel\backepsilon z$ функция

по крайней мере непрерывна в концевых точках ${{z}^{n}}$ и ${{z}^{{n + 1}}}$. Имеем

При этом сначала воспользовались неравенством Коши–Буняковского и сходимостью интеграла от выражения $\rho _{\theta }^{{ - 2{{\beta }_{\theta }} - 1}}$ с показателем ${{\beta }_{\theta }} < 0$ по области ${{\theta }_{j}} \in {{\mathbb{R}}^{2}}$, затем сделали обратную замену координат (3.17) и применили известное следовое весовое неравенство Кондратьева ([1] гл. 9 § 4, [35]) вместе с оценкой (3.19) и, наконец, учли неравенство Харди (3.12) и тот факт, что ${{r}_{{jn}}} \leqslant {{c}_{j}}\varepsilon $ при $x \in \mathbb{B}_{{3\varepsilon R}}^{3}({{P}^{j}},{{z}^{n}})$.

Просуммируем полученные соотношения по $n = 1, \ldots ,N$ и при малом $\varepsilon $ придем к ключевой оценке

Согласно определениям (3.10) интегральное тождество (1.6) с ингредиентами $\lambda = {{\lambda }^{\varepsilon }}$ и ${{\psi }^{\varepsilon }} = {{u}^{\varepsilon }}$ принимает вид

В силу формул (3.9) и (3.11) левая часть равенства (3.21) больше величины $\delta {{\left\| {u_{ \bot }^{\varepsilon };{{H}^{1}}(\Pi _{N}^{\varepsilon })} \right\|}^{2}}$. Вместе с тем соотношения (3.15) и (3.20) показывают, что правая часть равенства (3.21) мажорируется величиной ${{c}_{F}}\sqrt \varepsilon {{\left\| {u_{ \bot }^{\varepsilon };{{H}^{1}}(\Pi _{N}^{\varepsilon })} \right\|}^{2}}$. В результате при малом $\varepsilon $ выводим равенства $\left\| {u_{ \bot }^{\varepsilon };{{L}^{2}}(\Pi _{N}^{\varepsilon })} \right\|$ = 0 и $u_{ \bot }^{\varepsilon } = 0$, и при учете формул (3.14) находим, что ${{u}^{\varepsilon }} = 0$ на объединении рукавов ${{\Omega }_{0}} \cup {{\Omega }_{N}}$, а значит, и всюду на волноводе $\Pi _{N}^{\varepsilon }$ по теореме о единственности продолжения [36]. В итоге видим, что сделанное изначально предположение ложно, и при указанных ограничениях на интервале $(0,{{\Lambda }_{1}})$ собственных чисел (3.9) у оператора ${{A}^{\varepsilon }}$ задачи (1.5) нет.

3.3. Несколько замечаний. Схему проверки отсутствия собственных чисел на интервале $(0,{{\Lambda }_{1}})$ непрерывного спектра $\sigma _{c}^{\varepsilon }$ оператора ${{A}^{\varepsilon }}$ нетрудно приспособить к волноводу (1.4), у которого вставки (1.1) имеют коэффициенты сжатия ${{\gamma }_{n}} \leqslant 1$ и любых допустимых векторах сдвигов ${{y}^{n}} \in {{\mathbb{R}}^{2}}$, $n = 1, \ldots ,N$. Более того, расположение отверстий в перегородках $\partial {{\Omega }_{n}} \cap \partial {{\Omega }_{{n - 1}}}$ и их форма также не играют существенной роли.

Если нарушить ограничения (1.10) или (3.9), то перестанут быть верными неравенства (3.11), (3.15) и ход доказательства нарушится.

Если возмутить одну или несколько ячеек (рис. 2, в) периодического волновода (2.1) в предположении (1.9) о его зеркальной симметрии, то по схеме из разд. 3 (1°) нетрудно образовать собственные числа, попадающие как вовнутрь лакун (дискретный спектр $\sigma _{{d\infty }}^{\varepsilon }$), так и на сегменты (2.4) (точечный спектр $\sigma _{{p\infty }}^{\varepsilon }{{\backslash }}\sigma _{{d\infty }}^{\varepsilon }$). Известны [37–40] приемы образования таких собственных без предположения о симметрии при помощи малых сингулярных возмущений задачи.

4. Специальные решения вспомогательных задач

4.1. Пограничный слой. Растяжение координат (3.17) и формальный переход к $\varepsilon = 0$ переделывают волновод (1.4) в бесконечную область (3.18). В данном разделе индексы $j$ и $n$ у символов ${{\xi }^{{jn}}}$ и ${{\Xi }^{j}}$ не пишем.

Поскольку ${{\Delta }_{x}} + {{\kappa }^{2}} = {{\varepsilon }^{{ - 2}}}({{\Delta }_{\xi }} + {{\varepsilon }^{2}}{{\kappa }^{2}})$ в растянутых координатах (3.17), поведение поля ${{u}^{\varepsilon }}$ около отверстий (1.3) описывается при помощи решений предельной задачи Неймана для уравнения Лапласа

В рамках метода сращиваемых асимптотических разложений ([7] гл. 2, [41, 42]) требуется перечислить все ограничненные решения задачи (4.1). Одно из них очевидно – константа. Еще одно определено равенством

Здесь ${\mathbf{P}}$ – емкостной потенциал двумерного множества $\overline {\theta (0)} $ в пространстве ${{\mathbb{R}}^{3}}$, т.е. затухающее на бесконечности решение задачи Дирихле во внешности плоской трещины

Функция ${\mathbf{P}}$ четна по переменной $\zeta = {{\xi }_{3}}$, а значит, функция ${\mathbf{Z}}$ нечетна. Согласно краевому условию в задаче (4.3) функция ${\mathbf{Z}}$ обращается в нуль на трещине $\theta (0)$, имеет непрерывную производную $\partial {\mathbf{Z}}{\text{/}}\partial {{\xi }_{3}}$ и потому оказывается гладкой всюду в области $\Xi $, кроме ребра $\partial \theta \times \{ 0\} $. Наконец, в силу определения емкостного потенциала (см. [12, 13] и др.) справедливо представление

При этом ${{\left( {2\pi \left| \xi \right|} \right)}^{{ - 1}}}$ – функция Грина задачи Неймана для оператора ${{\Delta }_{\xi }}$ в полупространстве $\mathbb{R}_{ \pm }^{3}$ с особенностью в начале координат $O$, коэффициенты ${{C}_{1}}(\theta )$ и ${{C}_{2}}(\theta )$, имеющие отношение к тензору поляризации [12] множества $\overline {\theta (0)} \subset {{\mathbb{R}}^{3}}$, востребованы не будут, и

Кроме того, ${{\operatorname{cap} }_{3}}\theta $ – гармоническая емкость [12, 13] множества $\overline {\theta (0)} \subset {{\mathbb{R}}^{3}}$.

Доказано ([34] § 2 и 5, [43, 44]), что всякое ограниченное решение задачи (4.1) – линейная комбинация ${{c}_{0}} + {{c}_{1}}{{{\mathbf{Z}}}^{j}}$.

В следующих разделах используются обозначения ${{{\mathbf{Z}}}^{j}}$ и $C({{\theta }_{j}})$, $j = 1, \ldots ,J$.

4.2. Полубесконечный цилиндр. Рассмотрим задачу Неймана в зафиксированном полуцилиндре ${{\Omega }_{ \sqcup }} = \omega \times {{\mathbb{R}}_{ + }}$

У однородной ($g = 0$) задачи (4.6) есть единственное ограниченное решение, порожденное приходящей волной ${{w}^{ - }}$

Таким образом, условие существования затухающего решения задачи (4.6) имеет вид

При $z \to + \infty $ решение $u(y,z)$ – бесконечно малая $O({{e}^{{ - {{\beta }_{1}}z}}})$, ${{\beta }_{1}} = \sqrt {{{\Lambda }_{1}} - \lambda } $.

В рамках теории обобщенных функций [45] задача (4.6) с правой частью

содержащей дельта-функцию Дирака и потому удовлетворяющей условию (4.8), имеет затухающее решение ${{G}^{j}}$ – обобщенную функцию Грина, которая допускает представление

Здесь ${{r}_{j}} = {{\left( {{{{\left| {y - {{P}^{j}}} \right|}}^{2}} + {{z}^{2}}} \right)}^{{1/2}}}$, ${{\chi }^{j}}$ – гладкая срезающая функция с малым носителем, равная единице в окрестности точки ${{P}^{j}}$, ${{\chi }^{j}}{{\chi }^{k}} = 0$ при $j \ne k$. Числовая ($J \times J$)-матрица $G$ с элементами ${{G}_{{jk}}} = {{\tilde {G}}^{j}}({{P}^{k}})$ симметрична.

4.3. Составной конечный цилиндр. В цилиндре ${{\Omega }_{\# }}(\ell ) = {{\omega }_{\# }} \times ( - \ell ,\ell )$, определенном по формуле (1.16), рассмотрим краевую задачу с условиями скачков на срединной плоскости ${{\omega }_{\# }}(0) = {{\omega }_{\# }} \times \{ 0\} $

Здесь $[{v}](y) = {v}(y, + 0) - {v}(y, - 0)$ – скачок функции ${v}$, и $\gamma $, $\ell $ – положительные параметры.

Предположим, что ${{\lambda }_{q}} = (2\ell {{)}^{{ - 1}}}{{\pi }^{2}}{{q}^{2}}$ – простое собственное число задачи (4.11)–(4.14) при некотором $q \in \mathbb{N}$. Условие разрешимости задачи (4.11)–(4.14) с параметром $\lambda = {{\lambda }_{q}}$ и собственной функцией

имеет вид

Далее понадобятся сингулярные правые части краевых условий (4.13)

При этом ${{h}_{{\operatorname{reg} \pm }}}$ – гладкие функции на множестве $\overline {{{\omega }_{\# }}} $. Согласно предназначению дельта-функции интегралы из соотношения (4.16) превращаются в суммы

5. Асимптотика коэффициентов рассеяния. Пусть $\Pi _{2}^{\varepsilon }$ (рис. 1, б и в) – волновод (1.4) с двумя перфорированными перегородками и одной вставкой (см. формулы (1.16), (1.17), разд. 2.3 и рис. 1, б–г), причем высота $2{{\ell }^{\varepsilon }}$ удовлетворяет соотношению (1.18), в котором величины $\ell {\kern 1pt} '$, $\ell {\kern 1pt} ''$ подлежат определению и

При этом $N = 2$, но число отверстий $J \in \mathbb{N}$ произвольно, а положение точек ${{z}^{1}} = - {{\ell }^{\varepsilon }}$, ${{z}^{2}} = {{\ell }^{\varepsilon }}$ зависит от малого параметра $\varepsilon $, в частности, ${{L}_{1}} = 2{{\ell }^{\varepsilon }}$.

Асимптотические разложения на рукавах (1.2)

дополним разложением на цилиндрической вставке (1.16)

При этом ${\mathbf{v}}$ – собственная функция (4.15), числа ${{R}^{0}}$, ${{T}^{0}}$, ${{a}^{0}}$ и функции $u_{ \pm }^{0}$, ${v}_{\varepsilon }^{'}$ подлежат определению, а многоточие заменяет младшие асимптотические члены, не существенные в предпринимаемом анализе. Слагаемые разложений (5.2)–(5.4) зависят от малого параметра $\varepsilon $, что позволит определить их как решения задач (4.6) и (4.11)–(4.14) в фиксированных областях ${{\Omega }_{ \sqcup }}$ и ${{\Omega }_{\# }}(\ell )$ соответственно.

Воспользуемся методом сращиваемых асимптотических разложений ([7] гл. 2, [41, 42]) и, интерпретируя разложения (5.2)–(5.4) как внешние, согласуем их с внутренними разложениями около отверстий $\theta _{j}^{\varepsilon }( \pm {{\ell }^{\varepsilon }})$, заданных формулой (1.3) и использующих растянутые координаты ${{\xi }^{{\varepsilon j \pm }}}$ = $({{\varepsilon }^{{ - 1}}}(y - {{P}^{j}})$, ${{\varepsilon }^{{ - 1}}}(z \mp {{\ell }^{\varepsilon }}))$ (ср. определение (3.17) с ${{z}^{n}} = \pm {{\ell }^{\varepsilon }}$)

В силу формулы (4.15) для главного члена разложения (5.4) верны соотношения

Поскольку функции (5.2) и (5.3) остаются ограниченными на рукавах при $\varepsilon \to + 0$, первое слагаемое суммы (5.5) затухает при $\xi _{3}^{{\varepsilon j \pm }} \to \pm \infty $ и, являясь решением задачи (4.1) в области ${{\Xi }^{j}}$, согласно представлениям (4.4) и (5.6) принимает вид

Здесь ${{{\mathbf{Z}}}^{j}}$ – гармоническая функция (4.2) в области (3.18), и ее представление (4.16) включает коэффициент $C({{\theta }_{j}})$, находящийся в связи (4.15) с гармонической емкостью трещины $\overline {{{\theta }_{j}}(0)} $. Таким образом, выполнены разложения

При этом многоточие заменяет величины $O\left( {{{{\left| {{{\xi }^{{\varepsilon j \pm }}}} \right|}}^{{ - 2}}}} \right)$, которые находятся согласно формуле (4.4), но в дальнейших вычислениях значимой роли не играют.

В силу соотношения

процедура согласования разложений (5.2), (5.3) и (5.9) (нижняя строка) показывает, что поправочные члены $u_{ \pm }^{0}$ суть обладающие сингулярностями ${{a}^{0}}{{( \mp 1)}^{q}}C({{\theta }_{j}})(4\pi {{r}_{j}}{{)}^{{ - 1}}}$ решения задачи (4.6) в цилиндре ${{\Omega }_{ \sqcup }}$ с правыми частями

Поршневые волны (1.11), помещенные в правые части разложений (5.2) и (5.3), имеют множителями первые члены асимптотики коэффициентов рассеяния (1.13) и поэтому в главном учитывают поведение функции (1.12) на бесконечности в волноводе (1.14), а значит, поля $u_{ \pm }^{0}(y,z)$ должны исчезать при $z \to + \infty $. Следовательно, учет сингулярных составляющих у данных Неймана (5.11) приводит к равенству

Здесь ${{G}^{j}}$ – обобщенные функции Грина с требуемым поведением (4.10) при ${{r}_{j}} \to + 0$. Постоянные составляющие $i\kappa \alpha ({{R}^{0}} - 1)$ и $i\kappa \alpha {{T}^{0}}$ в формулах (5.11) компенсировать затухающими решениями задачи (4.6) нельзя, однако данное Неймана (4.9) функции Грина также содержит регулярную составляющую $ - {{\left| \omega \right|}^{{ - 1}}}$, а значит, суммы (5.12) действительно удовлетворяет указанным задачам при условиях

Кроме того, около точек $({{P}^{j}},0) \in \partial {{\Omega }_{ \sqcup }}$ верны представления

Согласование разложений (5.4) и (5.9) (верхняя строка) вместе с соотношением (5.7) приводят к задаче (4.11)–(4.14) в фиксированном цилиндре ${{\Omega }^{\gamma }}(\ell )$ для предельного ($\varepsilon = 0$) поправочного слагаемого ${v}_{0}^{'}$ на вставке ${{\Omega }^{\gamma }}({{\ell }^{\varepsilon }})$ переменной высоты. Правые части этой задачи имеют вид

При этом в краевых условиях на торцах ${{\omega }_{\# }}( - \ell )$ и ${{\omega }_{\# }}( + \ell )$ учтены невязки, порожденные сдвигом границ ${{\omega }_{\# }}( - {{\ell }^{\varepsilon }})$ и ${{\omega }_{\# }}( + {{\ell }^{\varepsilon }})$, а также сингулярности, привнесенные согласованием с главными членами (5.8) внутренних разложений около отверстий $\theta _{j}^{\varepsilon }( \pm {{\ell }^{\varepsilon }})$. Выберем слагаемое

в формуле (1.18) для полувысоты ${{\ell }^{\varepsilon }}$ цилиндрической вставки ${{\Omega }_{\# }}({{\ell }^{\varepsilon }})$. При нарушении равенства (5.18) искомый эффект пропадает (см. разд. 8.2). Согласно определению (5.18) условие разрешимости (4.16) задачи (4.11)–(4.14) с правыми частями (5.17) (см. формулы (4.17) и (4.18)) выполнено, а значит, существует ее решение которое определено с точностью до слагаемого $a{\kern 1pt} '{\kern 1pt} {\mathbf{v}}$ и может быть подчинено условию ортогональности, фиксирующему постоянные ${\mathbf{v}}_{{j \pm }}^{'} \in \mathbb{R}$ в представлении (5.19)

В силу соотношения (5.18) множитель $a{\kern 1pt} '$ при собственной функции (4.15), присутствующий в формуле (5.4), не влияет на изучаемые главные члены асимптотики поля (1.12).

Составим задачу для третьего члена ${v}_{0}^{{''}}$ разложения (5.4). Поскольку торцы ${{\omega }_{\# }}( \pm {{\ell }^{\varepsilon }})$ цилиндра ${{\Omega }_{\# }}({{\ell }^{\varepsilon }})$ смещаются при $\varepsilon \to + 0$, сингулярности $O{{({{r}_{{j \pm }}})}^{{ - 1}}}$ самой функции (5.19) порождают невязки порядка $r_{{\varepsilon j \pm }}^{{ - 3}}$ в краевых условиях Неймана на торцах ${{\omega }_{\# }}( \pm {{\ell }^{\varepsilon }})$ цилиндра ${{\Omega }_{\# }}({{\ell }^{\varepsilon }})$ (ср. формулы (5.19) и (5.10)). Для устранения нежелательных – слишком сильных – сингулярностей положим

Функция (5.20) задана на самой вставке ${{\Omega }_{\# }}({{\ell }^{\varepsilon }})$, и ее сингулярности сосредоточены в “правильных” точках $({{P}^{j}}, \pm {{\ell }^{\varepsilon }})$, а значит, могут быть согласованы с внутренними разложениями (5.5). Вместе с тем функция ${v}_{\varepsilon }^{'}$ и ее производные приобрели скачки на срединном сечении ${{\omega }_{\# }}(0)$, которые нужно компенсировать очередным асимптотическим членом ${v}_{\varepsilon }^{{''}}$ – подчиним его условиям сопряжения (5.5), где

Формулы (5.7) и (5.4) предоставляют регулярные составляющие правых частей условий Неймана (4.13)

Появление в этих краевых условиях суммы $h_{{\operatorname{dir} \pm }}^{{''}}$ дельта-функций Дирака и их производных обусловлено согласованием внешних и внутренних разложений около отверстий. Учитывая слагаемые $O(1)$ при ${{r}_{j}} \to + 0$ в выражениях (5.15) и (5.20) выводим условия на бесконечности

Здесь величины ${\mathbf{u}}_{{j \pm }}^{0}$ и ${\mathbf{v}}_{{j \pm }}^{'}$ взяты из формул (5.16) и (5.19) соответственно. Таким образом, представление (4.4) решений ${{{\mathbf{Z}}}^{j}}$ задачи (4.1) в области ${{\Xi }^{j}}$ показывает, что

Продолжим процедуру согласования и извлечем слагаемые $O\left( {{{{\left| {{{\xi }^{{\varepsilon j \pm }}}} \right|}}^{{ - 2}}}} \right)$ и $O\left( {{{{\left| {{{\xi }^{{\varepsilon j \pm }}}} \right|}}^{{ - 1}}}} \right)$ соответственно из членов $Z_{ \pm }^{{j0}}\left( {{{\xi }^{{\varepsilon j \pm }}}} \right)$ и $Z_{ \pm }^{{j'}}\left( {{{\xi }^{{\varepsilon j \pm }}}} \right)$ разложения (4.4), которые предписывают функции ${v}_{0}^{{''}}$ поведение около точек $({{P}^{j}}, \pm \ell )$. В результате согласно особенности (4.10) функции Грина и данным Неймана (4.9) для нее находим сингулярную составляющую правой части краевого условия (4.13)

Как и ранее в формуле (5.17), дельта-функции Дирака и их производные – результат процедуры согласования при учете слагаемых порядков ${{\left| {{{\xi }^{{\varepsilon j \pm }}}} \right|}^{{ - 1}}}$ = $\varepsilon r_{{\varepsilon j \pm }}^{{ - 1}}$ и ${{\varepsilon }^{{ - 1}}}{{\left| {{{\xi }^{{\varepsilon j \pm }}}} \right|}^{{ - 2}}}$ = = $\varepsilon r_{{\varepsilon j \pm }}^{{ - 2}}$ соответственно из разложений функций (5.24) и (5.8), полученных согласно представлениям (4.4) и (5.8), (5.24). Вместе с тем производные $\partial \delta {\text{/}}\partial {{y}_{p}}$, порождающие сингулярности $O(r_{{\varepsilon j \pm }}^{{ - 2}})$ внутри камеры ${{\Omega }_{\# }}({{\ell }^{\varepsilon }})$, не сказываются на условии (4.16) разрешимости задачи (4.11)–(4.14) с правыми частями (5.21), (5.22) и (5.26), так как собственная функция (4.15) не зависит от переменных $y$ и дифференцирование уничтожает ее следы на торцах ${{\omega }_{\# }}( \pm \ell )$. Кроме того, определение (5.18) поправки в представлении (1.18) размера ${{\ell }^{\varepsilon }}$ уничтожает в названном условии разрешимости коэффициент $a{\text{'}}$, фигурировавший в формулах (5.4) и (5.22). В силу соотношений (5.23) и (5.25) оно принимает вид

Величина ${\mathbf{B}}(\kappa )$, получающаяся при вычислении интеграла (4.16) с подынтегральными выражениями (5.21), (5.22) и (5.26), из которых удалены коэффициенты ${{S}_{ \pm }}$, $a{\kern 1pt} '$, $\ell {\kern 1pt} ''$, а множитель $\ell {\kern 1pt} '$ заменен выражением (5.18), зависит от выбранной частоты $\kappa $ и формы волновода $\Pi _{2}^{0}$, т.е. от областей $\omega $, ${{\omega }_{\# }}$, ${{\theta }_{1}}, \ldots ,{{\theta }_{J}}$, точек ${{P}^{1}}, \ldots ,{{P}^{J}}$ и размеров $\ell $, $\ell {\kern 1pt} '$. Вместе с тем явная формула для функции $\kappa \mapsto {\mathbf{B}}(\kappa )$ недоступна без применения численных методов, так как она определяется через вспомогательные решения ${\mathbf{u}}_{ \pm }^{0}$ и ${\mathbf{v}}_{0}^{'}$, точнее их скалярные характеристики из соотношений (5.12), (5.15), (5.19) и (5.25). Единственное используемое далее важное свойство: функции ${\mathbf{u}}_{ \pm }^{0}$ и ${\mathbf{v}}_{0}^{'}$, а вместе с ними и число ${\mathbf{B}}(\kappa )$ вещественны.

6. Почти полное прохождение поршневой волны. Покажем, как можно добиться равенств

в представлениях (1.13) коэффициентов рассеяния. При учете соотношений (5.13) и (6.1) имеем

Коэффициент (6.2) чисто мнимый, а число (5.28) вещественное. Таким образом, соотношение

уничтожает мнимую часть выражения (5.27). Его вещественная часть исчезает в силу равенств (6.1). Итак, последнее из нужных требований соблюдено.

Определение высоты $2{{\ell }^{\varepsilon }}$ вставки ${{\Omega }^{\gamma }}({{\ell }^{\varepsilon }})$ по формулам (1.18), (5.1) и (5.18), (6.3) следует интерпретировать как настройку параметров волновода для обеспечения почти полного прохождения поршневой волны через две перфорированные перегородки. Поскольку поправка (5.18) положительна, найденная высота $2{{\ell }^{\varepsilon }}$ больше критической $\pi q{\text{/}}\kappa $.

Обсудим несколько вариантов изменения геометрии волновода $\Pi _{2}^{\varepsilon }$.

6.1. Нарушение настройки. Пусть $t \ne 0$ – вещественный параметр, и в противоположность формуле (6.3)

Теперь, решив систему линейных уравнений (5.13) и (5.27), находим

Графики функций $\mathbb{R} \mathrel\backepsilon t \mapsto {{R}^{0}}(t)$, ${{T}^{0}}(t)$ на комплексной плоскости $\mathbb{C}$ суть окружности с радиусом $\frac{1}{2}$ и центрами в точках $\frac{1}{2}$, $\frac{1}{2}{{( - 1)}^{{q + 1}}}$ на вещественной оси. В случае $t = 0$ получаем равенства (6.1), но ${{R}^{0}}(t) \to 1$, ${{T}^{0}}(t) \to 0$ при $t \to \pm \infty $. Наконец, модули коэффициентов отражения и прохождения

соответственно монотонно возрастает и убывает при увеличении переменной $\left| t \right|$. Приведенные формулы показывают, как при изменении высоты вставки (1.1), $n = 1$, почти полное прохождение поршневой волны превращается в ее почти полное отражение.

Формула (6.4) означает искажение настройки высоты вставки на втором шаге асимптотической процедуры. Сделаем то же на первом шаге (5.18), а именно положим

Тогда задача (4.11)–(4.14) с правыми частями (5.17) разрешима только в случае ${{a}^{0}} = 0$, а значит, представление (5.4) теряет главный асимптотический член $O({{\varepsilon }^{{ - 1}}})$ и поэтому реализуется почти полное отражение поршневой волны.

6.2. Разные перфорация перегородок и сечения рукавов. Пусть $P_{\vartheta }^{1}, \ldots ,P_{\vartheta }^{{{{J}_{\vartheta }}}}$ – два ($\vartheta = \pm $) семейства попарно различных точек в области ${{\omega }_{*}}$, и $\theta _{{j \pm }}^{\varepsilon }( \pm {{\ell }^{\varepsilon }})$ – отверстия, определенные аналогами формул (1.3) по фиксированным областям ${{\theta }_{{j \pm }}} \subset {{\mathbb{R}}^{2}}$; здесь ${{J}_{ \pm }} \in \mathbb{N}$ и $j = 1, \ldots ,{{J}_{ \pm }}$. Повторим с понятными изменениями выкладки из разд. 4 применительно к измененному волноводу (1.14) (рис. 1, д), у которого рукава (1.15) имеют неодинаковые сечения ${{\omega }_{ \pm }}$ и перегородки (1.17) перфорированы по-разному. В результате получим заменители формул (5.27) и (5.13), (5.14)

Новая перфорация перегородок (1.17) приводит к сингулярным составляющим

в правых частях (5.11) краевых условий Неймана в задаче (4.11)–(4.14) для $u_{ \pm }^{0}$ и, соответственно, к равенствам (6.6), проистекающим от условия (4.8) ее разрешимости. Похожие изменения происходят и в сингулярных составляющих (5.26) задачи (4.11)–(4.14) для ${v}_{0}^{{''}}$ и в коэффициентах при ${{T}^{0}}$, $1 + {{R}^{0}}$ и ${{a}^{0}}$ в формуле (6.7). Модифицированное выражение (5.28), обозначенное ${{{\mathbf{B}}}_{\# }}(\kappa )$, появляется в формуле (6.7) и, следовательно, в условии (6.4), однако для существования решения (6.1) полученной системы алгебраических уравнений для ${{T}^{0}}$ и ${{R}^{0}}$ требуется еще одно ограничение

Равенство (6.9) следует интерпретировать как критерий возможности обеспечить эффект почти полного прохождения поршневой волны в волноводе (1.14) путем настройки высоты $2{{\ell }^{\varepsilon }}$ камеры. В критерии фигурируют площади $\left| {{{\omega }_{ \pm }}} \right|$ сечений рукавов и гармонические емкости [12] двумерных трещин $\{ x:y \in \overline {{{\theta }_{{j \pm }}}} ,z = 0\} $ в пространстве ${{\mathbb{R}}^{3}}$, определенные по емкостному потенциалу ${\mathbf{P}}$ согласно формулам (4.3) и (4.5).

Если требование (6.9) нарушено, то при соблюдении условия (6.3) с заменой ${\mathbf{B}}(\kappa ) \mapsto {{{\mathbf{B}}}_{\# }}(\kappa )$ находим

Таким образом, наблюдаются значимые как отражение, так и прохождение волн, однако при слабой проницаемости одной из перегородок ($\varphi \to + 0$ или $\varphi \to + \infty $) легко предсказуемо почти полное отражение, т.е. $\left| {{{R}^{0}}(\varphi )} \right| \to 1$.

6.3. Волновые фильтры и дампферы. Отсутствие в ограничении (6.9) частоты $\kappa $ позволяет создать примитивный волновой фильтр (рис. 1, д), в котором

Именно, если расстояние $2{{\ell }^{\varepsilon }}$ между первой перегородкой ${{\Theta }^{\varepsilon }}( - {{\ell }^{\varepsilon }})$ = ${{\omega }_{ - }}( - {{\ell }^{\varepsilon }}){{\backslash }}\overline {\theta _{{1 + }}^{\varepsilon }} $ и “выхлопной трубой” ${{\omega }_{ + }}({{\ell }^{\varepsilon }})$ = ${{\omega }_{ + }} \times ({{\ell }^{\varepsilon }}, + \infty )$ подобрано согласно модифицированным формулам (1.18), (5.1), (5.18), (6.3) (ср. соотношения (6.6)–(6.8) и (5.13), (5.27), (5.14)) при заданной частоте ${{\kappa }_{*}}$ := $\kappa \in (0,\min \Lambda _{{1 \pm }}^{{1/2}})$, где ${{\Lambda }_{{1 \pm }}}$ – первые положительные собственные числа задач (1.8) в областях ${{\omega }_{ \pm }}$, то поршневая волна с волновым числом ${{\alpha }_{*}} = {{(2{{\kappa }_{*}}\left| {{{\omega }_{ - }}} \right|)}^{{ - 1/2}}}$ почти не отражается, однако при изменении волнового числа (вариации частоты) настройка камеры ${{\Omega }_{\# }}({{\ell }^{\varepsilon }})$ пропадает, и она работает как “глушитель”, т.е. почти полностью отражает волну.

Если ${{\omega }_{ \pm }}$ и ${{\theta }_{ \pm }}$ – круги с радиусами $\rho _{ \pm }^{\omega }$ и $\rho _{ \pm }^{\theta }$ соответственно, то простейшее свойство линейности гармонической емкости [12] показывает, что критерий (6.9) почти полного прохождения соблюдается при ограничении (1.19).

7. Замечания

7.1. Полные асимптотические разложения. Развитие изложенной асимптотической процедуры позволяет построить бесконечные ряды для коэффициентов рассеяния ${{R}^{\varepsilon }}$ и ${{T}^{\varepsilon }}$. Вместе с тем в рамках метода сращиваемых разложений [41, 42] на следующих шагах итерационных процессов в асимптотические конструкции привлекаются решения предельных задач в областях ${{\Omega }_{ \sqcup }}$, ${{\Omega }_{\# }}(\ell )$ и ${{\Xi }_{j}}$ из разд. 4 с все более и более сильными сингулярностями в точках $({{P}^{j}},0)$, $({{P}^{j}}, \pm \ell )$ и на бесконечности. Это обстоятельство значительно усложняет реализацию процедуры cогласования. Более простым оказывается метод составных разложений [7, 46, 47], в котором на каждом шаге требуется решать задачи с фиксированным поведением вблизи особых точек. Показано ([7] гл. 2, [48]), как старшие асимптотические члены, полученные при помощи метода сращивания, переделываются в члены, пригодные для метода составных разложений. В частности, в рамках последнего метода задачи в цилиндрах ${{\Omega }_{\# }}(\ell )$ и ${{\Omega }_{ \sqcup }}$ всегда решаются в классе ограниченных и затухающих на бесконечности функций, а сингулярности использованных в разд. 5 решений $u_{ \pm }^{0}$ и ${v}_{0}^{'}$ присоединяются к решениям задач в неограниченных областях ${{\Xi }^{1}}, \ldots ,{{\Xi }^{J}}$, которым (решениям) предписывается затухание со скоростью $O\left( {{{{\left| {{{\xi }^{j}}} \right|}}^{{ - 1}}}} \right)$.

Младшие члены асимптотики понадобятся наверняка при попытке обеспечить почти полное прохождение волн, отличающихся от поршневых и приобретающих зависимость от поперечных координат $y = ({{y}_{1}},{{y}_{2}})$. Например, если амплитудная часть $U(y)$ волны ${{e}^{{i\mu z}}}U(y)$ обращается в нуль в точке ${{P}^{j}}$, вокруг которой образованы отверстия $\theta _{j}^{\varepsilon }({{z}^{n}})$ в перегородках, то в задаче (4.1) о пограничном слое нужно учесть специальные решения, которые имеют отношение к тензору поляризации [12 прил. G] трещины $\overline {{{\theta }_{j}}(0)} $, включают коэффициенты ${{C}_{1}}({{\theta }_{j}})$ и ${{C}_{2}}({{\theta }_{j}})$, уже фигурировавшие в формулах (4.4) и (5.26). При этом производные дельта-функции Дирака в краевых условиях (4.13) оказывают влияние на условия разрешимости (4.16) задачи (4.11)–(4.14) в случае зависимости собственной функции ${v}$ от поперечных переменных $y$. В результате критерий (6.9) возможности почти полного прохождения поршневых волн (1.11) существенно изменяется для волн иного строения.

7.2. Обоснование асимптотики. Общие методы исследования сингулярно возмущенных статических и спектральных краевых задач [7] требуют лишь незначительных изменений при переходе к дифракционным задачам о распространении волн в волноводах с цилиндрическими выходами на бесконечность. При этом полезной оказывается техника весовых пространств с отделенной асимптотикой ([1] гл. 6, 7, § 3) (см. также [49, 50] для уравнения Гельмгольца в квантовых и акустических волноводах). Нормы в таких пространствах включают модули коэффициентов рассеяния и поэтому для проверки соотношений (1.11) достаточно из построенных членов асимптотических разложений (5.2)–(5.5) соорудить подходящее глобальное асимптотическое приближение к решению (1.12) задачи (1.5), обработать появившуюся малую невязку в вариационной задаче (1.6) и применить равномерные по параметру $\varepsilon $ априорные оценки решений. Нужные асимптотические конструкции для обоих методов сращиваемых и составных разложений известны ([7] гл. 2). Благодаря возможности нахождения младших членов асимптотик заботиться о точности априорных оценок не нужно (ср. подход [47]), но метод [7] все-таки предоставляет асимптотически точные оценки.

7.3. Вариация частоты. Изменим постановку вопроса, а именно, зафиксируем высоту $L$ вставки (1.15) и попытаемся найти частоту

при которой происходит почти полное прохождение поршневых волн (1.11) в волноводе $\Pi _{2}^{\varepsilon }$ с рукавами (1.17) одинакового сечения $\omega $.

При помощи соотношений (1.18), (5.1) и (5.18) находим два первых члена разложения (7.1)

К сожалению, явную формулу для коэффициента $\kappa {\kern 1pt} ''$ в третьем члене представления (1.18) получить не удается, так как величина ${\mathbf{B}}(\kappa )$ сложным образом зависит от частоты $\kappa $: в выражении (5.28) присутствуют интегралы от решений ${\mathbf{u}}_{ \pm }^{0}$ и ${\mathbf{v}}_{0}^{'}$ краевых задач для оператора Гельмгольца ${{\Delta }_{x}} + {{\kappa }^{2}}$.

8. Варианты, обобщения и следствия

8.1. Изменение геометрии перфорированных перегородок. Разработаны общие алгоритмы, позволяющие приспособить предложенные асимптотические процедуры к цилиндрическим волноводам с препятствиями, изображенными на рис. 3, а и б. Вместе с тем по сравнению с волноводами на рис. 1, а–г, вспомогательные решения предельных задач из разд. 4 теряют явный вид. Например, в случае косых перегородок (рис. 3, а) искажается дифракционное поле (4.7), и коэффициент отражения в полубесконечном цилиндре ${{\Omega }_{\angle }}$ со скошенным торцом отличен от единицы, а в случае утолщенных перегородок (рис. 3, б) вместо решения (4.2), найденного по емкостному потенциалу ${\mathbf{P}}$, используется решение $Z$ задачи (4.1) в полупространствах, соединенных через трубу ${{\theta }_{j}} \times [ - {{H}_{n}},{{H}_{n}}]$ (рис. 3, в)

с зафиксированным поведением на бесконечности

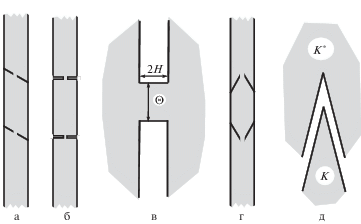
Здесь $2\varepsilon {{H}_{n}}$ – толщина перегородки с номером $n = 1, \ldots ,N$, ${{H}_{n}} > 0$, а $C({{\theta }_{j}},{{H}_{n}})$ – величина, зависящая от формы отверстия ${{\theta }_{j}}$ и от длины $2{{H}_{n}}$ трубы, однако не выражающаяся через классические объекты гармонического анализа.

Для конических перегородок с отверстиями диаметром $O(\varepsilon )$ в вершинах (рис. 3, г) алгоритм построения асимптотики изменяется мало (ср. публикации [28, 29] для двумерной задачи Дирихле, рис. 2, г и д), однако разложение ведется по степеням малого параметра $\varepsilon $ с показателями, определенными по сингулярностям решений ([43, 51], гл. 7) задачи Неймана для оператора Лапласа в выпуклом конусе ${\mathbf{K}}$ и его дополнении ${\mathbf{K}}* = {{\mathbb{R}}^{3}}{{\backslash }}\overline {\mathbf{K}} $ (рис. 3, д). Впрочем для подобных задач разработанная в данной статье процедура настройки параметров волновода ранее не применялась и эффект почти полного прохождения волн через перфорированные перегородки обнаружен не был (ср. разд. 6.2).

8.2. Почти полное отражение. Если $\lambda = {{\kappa }^{2}}$ – не собственное число задачи (4.11)–(4.14), то поршневая волна ${{w}^{ + }}$, приходящая из бесконечности в рукаве ${{\Omega }_{ - }}(\ell )$ волновода $\Pi _{2}^{\varepsilon }$, почти полностью отражается от первой перегородки ${{\Theta }^{\varepsilon }}( - \ell )$ (обозначения из формул (2.2) и (1.14)). Коэффициенты рассеяния у решения (1.12) принимают вид

Алгоритм построения асимптотики значительно упрощается по сравнению с разд. 5 и разд. 6, в частности, бесполезно проводить настройку высоты вставки ${{\Omega }_{\# }}({{\ell }^{\varepsilon }})$ и можно взять $\ell {\kern 1pt} ' = 0$ и $\ell {\kern 1pt} '' = 0$ в определении (1.18).

Укажем начальные члены асимптотики в разных частях волновода.

Поправочный член внешнего разложения на рукаве ${{\Omega }_{ - }}(\ell )$

находится в результате согласования с внутренним разложением около отверстий $\theta _{j}^{\varepsilon }( - \ell )$

Здесь использованы обозначения, введенные в разд. 5. Формула (8.2) означает, что в представлении (8.1) фигурирует величина

Продолжение процедуры согласования показывает, что в силу соотношений (8.3) и (4.4) первый член внешнего разложения на камере ${{\Omega }^{\gamma }}(\ell )$

находится из однозначно разрешимой по предположению задачи (4.11)–(4.14) с правыми частями

Наконец, внутреннее разложение вблизи отверстий $\theta _{j}^{\varepsilon }( + \ell )$ и внешнее на рукаве ${{\Omega }_{ + }}(\ell )$ выглядят так:

Последняя формула приводит ко второму соотношению (8.1).

Проведенные вычисления позволяют заключить, что прохождение поршневой волны через одну перегородку с отверстием диаметром $O(\varepsilon )$ понижает амплитуду в $\varepsilon $ раз. Таким образом, при условии, что число $\lambda = {{\kappa }^{2}}$ не является собственным для задачи Неймана на каждой ($n = 1, \ldots ,N - 1$) из камер (1.1), коэффициент прохождения ${{T}^{\varepsilon }}$ в волноводе (1.4) с $N$ перегородками приобретает порядок ${{\varepsilon }^{N}}$.

8.3. Камера обскура. Рассмотрим решение

задачи (1.5) в полубесконечном волноводе $\Pi _{ \sqcap }^{\varepsilon }$ (рис. 2, а), который образован рукавом ${{\Omega }_{ - }}({{\ell }^{\varepsilon }}) = \omega \times ( - \infty , - {{\ell }^{\varepsilon }})$ и камерой $\Omega _{ \sqcap }^{\varepsilon } = {{\omega }_{\# }} \times ( - {{\ell }^{\varepsilon }},0)$, соединенными одним отверстием $\theta _{1}^{\varepsilon }( - {{\ell }^{\varepsilon }})$. Множество $\Pi _{ \sqcap }^{\varepsilon }$ – половина $\{ x \in \Pi _{2}^{\varepsilon }:z < 0\} $ симметричного множества $\Pi _{2}^{\varepsilon }$ из разд. 5 в случае $J = 1$, а значит, решения (8.4) и (1.12) связаны соотношением

При этом коэффициент отражения $R_{ \sqcap }^{\varepsilon }$ в волноводе $\Pi _{ \sqcap }^{\varepsilon }$ равен сумме ${{R}^{\varepsilon }} + {{T}^{\varepsilon }}$ коэффициентов рассеяния в волноводе $\Pi _{2}^{\varepsilon }$. Таким образом, асимптотические формулы из разд. 6 позволяют найти асимптотику фазы ${{\psi }_{\varepsilon }} \in ( - \pi ,\pi ]$ у коэффициента отражения

Если ${{\kappa }^{2}}$ не является собственным числом задачи Неймана в половине $\Omega _{ \sqcap }^{\varepsilon }(\ell )$ цилиндра ${{\Omega }^{\varepsilon }}(\ell )$, т.е. $\kappa \ne \pi p{\text{/}}\ell $ при всех $p \in \mathbb{N}$, или настройка высоты ${{\ell }^{\varepsilon }}$ нарушена на первом шаге (5.18), то ${{\psi }_{0}} = 0$ в представлении фазы

Если же $\kappa = \pi p{\text{/}}\ell $, $p \in \mathbb{N}$, т.е. $q = 2p$ в формуле (5.1), а настройка высоты ${{\ell }^{\varepsilon }}$ нарушена на втором шаге и поправка $\ell {\kern 1pt} ''$ имеет вид (6.4) с параметром $t \in \mathbb{R}$, то согласно формулам (6.5) и (1.13)

Главная часть фазы (8.5) удовлетворяет соотношениям

Иными словами, для спектрального параметра $\lambda = {{\kappa }^{2}}$, близкого к собственному числу задачи Неймана в камере $\Omega _{ \sqcap }^{\varepsilon }$ с заклееным отверстием, происходит быстрое, со скоростью $O({{\varepsilon }^{{ - 1}}})$, изменение фазы ${{\psi }_{\varepsilon }}$ коэффициента отражения $R_{ \sqcap }^{\varepsilon }$.