Прикладная математика и механика, 2022, T. 86, № 1, стр. 121-150
Моделирование термоупруговязкопластического деформирования гибких армированных пластин
А. П. Янковский *
Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
Новосибирск, Россия
* E-mail: lab4nemir@rambler.ru
Поступила в редакцию 27.07.2021
После доработки 10.11.2021
Принята к публикации 25.11.2021
- EDN: EKGCRN
- DOI: 10.31857/S003282352201009X
Аннотация
Разработана модель термоупруговязкопластического деформирования композитного материала, перекрестно армированного непрерывными волокнами в произвольных направлениях. Материалы компонентов композиции изотропны, их пластическое деформирование описывается теорией течения с изотропным упрочнением при учете зависимости функции нагружения от температуры и скорости деформирования. Построена математическая модель термоупруговязкопластического изгибного поведения армированных пластин. Слабое сопротивление поперечным сдвигам таких тонкостенных конструкций учитывается в рамках теории Амбарцумяна, а геометрическая нелинейность описывается в приближении Кармана. Учитывается связанность механической и теплофизической составляющих задачи о динамическом неупругом деформировании композитных пластин. Температура по толщине конструкций аппроксимируется полиномами разных порядков. Решение сформулированной двумерной задачи строится на основе явной численной схемы. Исследовано термоупруговязкопластическое поведение плоско-перекрестно и пространственно армированных стеклопластиковых и металлокомпозитных пластин, динамически изгибаемых под действием воздушной взрывной волны. Показано, что для адекватного определения температуры в таких конструкциях ее необходимо аппроксимировать полиномами 6–7-го порядков по толщине пластин. Продемонстрировано, что относительно тонкие композитные пластины нагреваются на 15…30°C, а относительно толстые – на 1.5…2.5°C. В силу такого малого уровня нагрева армированных конструкций их динамический расчет при действии нагрузок типа воздушной взрывной волны можно проводить без учета теплового воздействия при отсутствии дополнительных источников тепла немеханического происхождения. При этом обязательно необходимо учитывать чувствительность пластических свойств компонентов композиции к скорости их деформирования.
1. Введение. Тонкостенные армированные конструкции типа пластин и оболочек широко используются в инженерной практике [1–6]. Современные изделия из композиционных материалов (КМ) часто подвергаются интенсивному силовому и тепловому нагружению [5–7], при котором компоненты композиции могут вести себя неупруго [7–10]. Поэтому проблема моделирования термоупругопластического поведения КМ-конструкций является актуальной. Однако на данный момент времени теоретические исследования, выполненные в этом направлении, немногочисленны [7–11]. Обычно моделируется линейно-упругое поведение КМ-изделий [5–7, 12–16]. Упругопластическое динамическое деформирование слоистых тонкостенных элементов конструкций с изотропными слоями рассматривалось в [7]. Аналогичное механическое поведение армированных пластин моделировалось в [17]. Возникающий при этом тепловой отклик в [7, 17] не учитывался. Однако известно, что высокоинтенсивное кратковременное силовое воздействие на конструкцию может приводить к значительному выделению тепловой энергии [5]. При наличии же температурного поля компоненты композиции могут изменить свои физико-механические свойства [18, 19]. Кроме того, при динамическом нагружении пластин и оболочек необходимо учитывать и такой экспериментальный факт [18, 19], как чувствительность пластических свойств материалов к изменению скорости их деформирования (упруговязкопластичность [20]). Оба эти обстоятельства могут существенно отразиться на неупругом динамическом поведении тонкостенных КМ-конструкций. Некоторые варианты теории термоупругопластического поведения однородных материалов (в рамках теории пластического течения) рассматривались в [21], но при этом не учитывались их вязкопластические свойства. Упруговязкопластическое деформирование армированных пластин моделировалось в [22], но тепловой отклик при этом не рассматривался. Структурные модели механики композитов, учитывающие влияние теплового воздействия на упруговязкопластическое поведение материалов композиции, на данный момент времени не разработаны. Согласно терминологии, принятой в [20], такое деформирование КМ будем называть термоупруговязкопластическим. При этом следует принимать во внимание и связанность температурной и механической составляющей динамической задачи.
Для учета возможного ослабленного сопротивления тонкостенных КМ-конструкций поперечному сдвигу и расчета волновых процессов, которые возникают в них при динамическом нагружении, традиционно используют неклассические теории Рейсснера [5, 7, 12, 23], Редди [13, 14] или Амбарцумяна [15, 17, 22]. Реже используются более точные теории, как правило, базирующиеся на гипотезе ломаной линии [7, 16].
Численное интегрирование физически и геометрически нелинейных динамических задач для тонкостенных конструкций обычно осуществляют, применяя явные схемы [7, 17, 22, 24] или неявные методы Ньюмарка [9, 25].
Согласно вышеизложенному, настоящее исследование посвящено моделированию термоупруговязкопластического динамического деформирования гибких армированных пластин при учете возможного их слабого сопротивления поперечным сдвигам. Численное решение возникающих при этом связанных термомеханических задач предполагается строить на основе явных пошаговых алгоритмов.
2. Численно-аналитическое моделирование термоупруговязкопластического деформирования КМ. Рассматривается КМ, состоящий из матрицы, регулярно усиленной N семействами волокон в разных направлениях с плотностями армирования ${{\omega }_{k}}$ ($1 \leqslant k \leqslant N$). Как и в [21, 22], предполагаем, что малые деформации $\varepsilon _{{ij}}^{{(k)}}$ однородного изотропного k-го материала композиции можно представить в виде упругих $e_{{ij}}^{{(k)}}$, несжимаемых пластических $p_{{ij}}^{{(k)}}$ и температурных ${{\delta }_{{ij}}}\varepsilon _{\Theta }^{{(k)}}$ составляющих:
(2.1)
$\varepsilon _{{ij}}^{{(k)}} = e_{{ij}}^{{(k)}} + p_{{ij}}^{{(k)}} + {{\delta }_{{ij}}}\varepsilon _{\Theta }^{{(k)}};\quad i,j = \overline {1,3} ,\quad 0 \leqslant k \leqslant N\quad \left( {p_{{ii}}^{{(k)}} = 0,\quad \varepsilon _{\Theta }^{{(k)}} = \int\limits_{{{t}_{0}}}^t {{{\alpha }_{k}}\dot {\Theta }dt} } \right),$(2.2)
$\bar {e}_{{ij}}^{{(k)}} = s_{{ij}}^{{(k)}}{\text{/}}\left( {2{{G}_{k}}} \right),\quad e_{0}^{{(k)}} = \sigma _{0}^{{(k)}}{\text{/}}\left( {3{{K}_{k}}} \right);\quad i,j = 1,2,3,\quad 0 \leqslant k \leqslant N,$(2.3)
$\begin{gathered} s_{{ij}}^{{(k)}} = \sigma _{{ij}}^{{(k)}} - {{\delta }_{{ij}}}\sigma _{0}^{{(k)}},\quad \bar {e}_{{ij}}^{{(k)}} = e_{{ij}}^{{(k)}} - {{\delta }_{{ij}}}e_{0}^{{(k)}},\quad e_{0}^{{(k)}} = \varepsilon _{0}^{{(k)}} - \varepsilon _{\Theta }^{{(k)}} \\ \sigma _{0}^{{(k)}} = \frac{1}{3}\sigma _{{ll}}^{{(k)}},\quad \varepsilon _{0}^{{(k)}} = \frac{1}{3}\varepsilon _{{ll}}^{{(k)}},\quad 2{{G}_{k}} = \frac{{{{E}_{k}}}}{{1 + {{\nu }_{k}}}},\quad 3{{K}_{k}} = \frac{{{{E}_{k}}}}{{1 - 2{{\nu }_{k}}}}, \\ \end{gathered} $Пластическое течение k-го материала композиции ассоциировано с поверхностью нагружения ${{f}_{k}} = 0$, соответствующей условию текучести Мизеса [20–22]:
(2.4)
${{f}_{k}}\left( {{{T}_{k}},{{\chi }_{k}},{{H}_{k}},\Theta } \right) \equiv T_{k}^{2} - \tau {{_{s}^{{(k)}}}^{2}}\left( {{{\chi }_{k}},{{H}_{k}},\Theta } \right) = 0;\quad 0 \leqslant k \leqslant N,$(2.5)
$\begin{gathered} {{T}_{k}} = \sqrt {\frac{1}{2}s_{{ij}}^{{(k)}}s_{{ij}}^{{(k)}}} ,\quad {{\chi }_{k}} = \int\limits_0^t {\sqrt {2\dot {p}_{{ij}}^{{(k)}}\dot {p}_{{ij}}^{{(k)}}} } dt,\quad {{H}_{k}} = \sqrt {2\xi _{{ij}}^{{(k)}}\xi _{{ij}}^{{(k)}}} ;\quad \xi _{{ij}}^{{(k)}} = \dot {\bar {e}}_{{ij}}^{{(k)}} + \dot {p}_{{ij}}^{{(k)}} \\ i,j = 1,2,3,\quad 0 \leqslant k \leqslant N, \\ \end{gathered} $С одной стороны, в соотношении (2.4) при учете выражений (2.5) функция $\tau _{s}^{{(k)}}$ отличается от рассмотренной в [22] дополнительным аргументом $\Theta $; с другой стороны, $\tau _{s}^{{(k)}}$ отличается от случая, рассмотренного в [21], наличием аргумента ${{H}_{k}}$. Поэтому, повторяя рассуждения из [21, 22], в конечном итоге при учете формул (2.1) и (2.2) получим определяющие уравнения термоупруговязкопластического деформирования k-го компонента композиции, которые для удобства дальнейшего изложения целесообразно записать в матричной форме:
(2.6)
${{\dot {\sigma }}_{k}} = {{{\mathbf{Z}}}_{k}}{{\dot {\varepsilon }}_{k}} + {{{\mathbf{Y}}}_{k}}{{\ddot {\varepsilon }}_{k}} + {{\beta }_{k}}\dot {\Theta };\quad 0 \leqslant k \leqslant N$Здесь и далее:
(2.7)
$\begin{gathered} {{\sigma }_{k}} = {{\left( {\sigma _{1}^{{(k)}}\;\sigma _{2}^{{(k)}}\;\sigma _{3}^{{(k)}}\;\sigma _{4}^{{(k)}}\;\sigma _{5}^{{(k)}}\;\sigma _{6}^{{(k)}}} \right)}^{{\text{т}}}} \equiv {{\left( {\sigma _{{11}}^{{(k)}}\;\sigma _{{22}}^{{(k)}}\;\sigma _{{33}}^{{(k)}}\;\sigma _{{23}}^{{(k)}}\;\sigma _{{31}}^{{(k)}}\;\sigma _{{12}}^{{(k)}}} \right)}^{{\text{т}}}} \\ {{\varepsilon }_{k}} = {{\left( {\varepsilon _{1}^{{(k)}}\;\varepsilon _{2}^{{(k)}}\;\varepsilon _{3}^{{(k)}}\;\varepsilon _{4}^{{(k)}}\;\varepsilon _{5}^{{(k)}}\;\varepsilon _{6}^{{(k)}}} \right)}^{{\text{т}}}} \equiv {{\left( {\varepsilon _{{11}}^{{(k)}}\;\varepsilon _{{22}}^{{(k)}}\;\varepsilon _{{33}}^{{(k)}}\;2\varepsilon _{{23}}^{{(k)}}\;2\varepsilon _{{31}}^{{(k)}}\;2\varepsilon _{{12}}^{{(k)}}} \right)}^{{\text{т}}}} \\ {{{\mathbf{s}}}_{k}} = {{\left( {s_{1}^{{(k)}}\;s_{2}^{{(k)}}\;s_{3}^{{(k)}}\;s_{4}^{{(k)}}\;s_{5}^{{(k)}}\;s_{6}^{{(k)}}} \right)}^{{\text{т}}}} \equiv {{\left( {s_{{11}}^{{(k)}}\;s_{{22}}^{{(k)}}\;s_{{33}}^{{(k)}}\;s_{{23}}^{{(k)}}\;s_{{31}}^{{(k)}}\;s_{{12}}^{{(k)}}} \right)}^{{\text{т}}}} \\ {{\xi }_{k}} = {{\left( {\xi _{1}^{{(k)}}\;\xi _{2}^{{(k)}}\;\xi _{3}^{{(k)}}\;\xi _{4}^{{(k)}}\;\xi _{5}^{{(k)}}\;\xi _{6}^{{(k)}}} \right)}^{{\text{т}}}} \equiv {{\left( {\xi _{{11}}^{{(k)}}\;\xi _{{22}}^{{(k)}}\;\xi _{{33}}^{{(k)}}\;\xi _{{23}}^{{(k)}}\;\xi _{{31}}^{{(k)}}\;\xi _{{12}}^{{(k)}}} \right)}^{{\text{т}}}} \\ \end{gathered} $(2.8)
${{{\mathbf{Z}}}_{k}} = {{{\mathbf{\bar {Z}}}}_{k}} - {{G}_{k}}{{{\mathbf{\bar {\bar {Z}}}}}_{k}},\quad {{{\mathbf{Y}}}_{k}} = \tau _{H}^{{(k)}}{{{\mathbf{\bar {\bar {Z}}}}}_{k}};\quad k = 0,1, \ldots ,N,$(2.9)
$\begin{gathered} \beta _{l}^{{(k)}} = \frac{{s_{l}^{{(k)}}}}{{{{G}_{k}}}}\left[ {G_{\Theta }^{{(k)}} - \tau _{s}^{{(k)}}\left( {\tau _{s}^{{(k)}}G_{\Theta }^{{(k)}} - \tau _{\Theta }^{{(k)}}{{G}_{k}}} \right){{A}_{k}}} \right]\quad (i,j = \overline {1,3} ,\;\;l = \overline {4,6} ) \\ \bar {\bar {z}}_{{ij}}^{{(k)}} = {{A}_{k}}s_{i}^{{(k)}}s_{j}^{{(k)}}\quad (i,j = \overline {1,6} ),\quad {{\lambda }_{k}} = \frac{{{{\nu }_{k}}{{E}_{k}}}}{{\left( {1 + {{\nu }_{k}}} \right)\left( {1 - 2{{\nu }_{k}}} \right)}} \\ \end{gathered} $(2.10)
$\begin{gathered} {{c}_{k}} = \left\{ \begin{gathered} 0\quad {\text{при}}\quad {{T}_{k}} < \tau _{s}^{{(k)}}\quad {\text{или}}\quad {{T}_{k}} = \tau _{s}^{{(k)}},\quad {{W}_{k}} \leqslant 0 \hfill \\ 1\quad {\text{при}}\quad {{T}_{k}} = \tau _{s}^{{(k)}},\quad {{W}_{k}} > 0 \hfill \\ \end{gathered} \right. \\ {{W}_{k}} = {{G}_{k}}{\mathbf{s}}_{k}^{{\text{т}}}{{{\dot {\varepsilon }}}_{k}} + \tau _{s}^{{(k)}}G_{k}^{{ - 1}}\left( {\tau _{s}^{{(k)}}G_{\Theta }^{{(k)}} - \tau _{\Theta }^{{(k)}}{{G}_{k}}} \right)\dot {\Theta } - 2\tau _{s}^{{(k)}}\tau _{H}^{{(k)}}H_{k}^{{ - 1}}\xi _{k}^{{\text{т}}}{{{\ddot {\varepsilon }}}_{k}} \\ T_{k}^{2} = \frac{1}{2}\sum\limits_{i = 1}^3 {s{{{_{i}^{{(k)}}}}^{2}}} + \sum\limits_{i = 4}^6 {s{{{_{i}^{{(k)}}}}^{2}}} ,\quad H_{k}^{2} = 2\sum\limits_{i = 1}^3 {\xi {{{_{i}^{{(k)}}}}^{2}}} + 4\sum\limits_{i = 4}^6 {\xi {{{_{i}^{{(k)}}}}^{2}}} ,\quad 0 \leqslant k \leqslant N, \\ \end{gathered} $Если пластические свойства материала не зависят от скорости деформирования ($\tau _{H}^{{(k)}} \equiv 0$), то уравнения (2.6) при учете соотношений (2.8)–(2.10) редуцируются в определяющие соотношения термоупругопластического деформирования k-го компонента композиции, которые полностью совпадают с уравнениями, полученными в [21] при отсутствии трансляционного упрочнения. Если же рассматривается изотермическая задача ($\dot {\Theta } \equiv 0$), то уравнение (2.6) редуцируется в матричное соотношение (2.2) из [22]. При $\dot {\Theta } \equiv 0$ равенство (2.6) связывает между собой скорости напряжений ${{\dot {\sigma }}_{k}}$ и деформаций ${{\dot {\varepsilon }}_{k}}$ и вторые производные по времени от деформаций ${{\ddot {\varepsilon }}_{k}}$. Ранее в [27] на основе теории дислокаций было получено, что определяющее уравнение вязкопластичности в одномерном случае должно связывать между собой скорости напряжения и деформации и вторую производную по времени от деформации. Таким образом, соотношение (2.6) обобщает определяющие уравнения, полученные в [21, 22], и качественно полностью соответствует результатам работы [27].
Как и в [22], условия активного нагружения k-го материала композиции можно записать в форме, отличной от выражения (2.10):
(2.11)
${{c}_{k}} = 1\quad {\text{при}}\quad {{T}_{k}} = \tau _{s}^{{(k)}}\left( {{{\chi }_{k}},{{H}_{k}},\Theta } \right)\quad {\text{и}}\quad {{\dot {T}}_{k}} - \tau _{H}^{{(k)}}{{\dot {H}}_{k}} - \tau _{\Theta }^{{(k)}}\dot {\Theta } > 0;\quad 0 \leqslant k \leqslant N$Из экспериментов известно [18, 19, 26], что $\tau _{H}^{{(k)}}\left( {{{\chi }_{k}},{{H}_{k}},\Theta } \right) > 0$ и, как правило, $\tau _{\Theta }^{{(k)}}\left( {{{\chi }_{k}},{{H}_{k}},\Theta } \right) < 0$ (исключение составляют разве что стали в диапазоне температур $0 \leqslant \Theta $ ≤ 110…120°C), поэтому из соотношений (2.11) вытекает: 1) в упругопластическом случае ($\dot {\Theta } \equiv 0$ и $\tau _{H}^{{(k)}} \equiv 0$) прирост пластических деформаций возможен только при увеличении интенсивности касательных напряжений (${{\dot {T}}_{k}} > 0$); 2) при постоянстве ${{T}_{k}}$ (${{\dot {T}}_{k}} \equiv 0$) и нечувствительности материала к скорости деформирования ($\tau _{H}^{{(k)}} \equiv 0$) прирост пластических деформаций возможен только при увеличении температуры ($\dot {\Theta } > 0$); 3) в изотермическом случае ($\dot {\Theta } \equiv 0$) при отсутствии приращений интенсивности напряжений (${{\dot {T}}_{k}} \equiv 0$) прирост пластических деформаций возможен только при уменьшении скорости деформирования (${{\dot {H}}_{k}} < 0$, $0 \leqslant k \leqslant N$). Эти результаты полностью согласуются с известными экспериментальными данными [18, 19, 26].
Как отмечалось во Введении, решение моделируемой задачи предполагается строить с использованием явных численных схем [7, 22, 24, 28], поэтому значения неизвестных функций будем вычислять в дискретные моменты времени ${{t}_{{n + 1}}} = {{t}_{n}} + \Delta $ ($n = 0,1,2, \ldots $), где $\Delta = {\text{const}} > 0$ – шаг по времени. Имея целью воспользоваться результатами работы [22], считаем, что при $t = {{t}_{{n - 1}}}$, ${{t}_{n}}$ уже известны значения следующих величин
(2.12)
$\begin{gathered} \mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^{n - 1} \left( {\mathbf{r}} \right) \equiv {{{\dot {\varepsilon }}}_{k}}\left( {{{t}_{{n - 1}}},{\mathbf{r}}} \right),\quad \mathop {{{{\ddot {\varepsilon }}}_{k}}}\limits^{n - 1} \left( {\mathbf{r}} \right) \equiv {{{\ddot {\varepsilon }}}_{k}}\left( {{{t}_{{n - 1}}},{\mathbf{r}}} \right),\quad \mathop {\dot {\Theta }}\limits^{n - 1} \left( {\mathbf{r}} \right) \equiv \dot {\Theta }\left( {{{t}_{{n - 1}}},{\mathbf{r}}} \right) \\ \mathop \Theta \limits^m \left( {\mathbf{r}} \right) \equiv \Theta \left( {{{t}_{m}},{\mathbf{r}}} \right),\quad 0 \leqslant k \leqslant N,\quad m = n - 1,n,\quad {\mathbf{r}} = \left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right), \\ \end{gathered} $(2.13)
$\mathop {{{{\ddot {\varepsilon }}}_{k}}}\limits^n = \frac{2}{\Delta }\left( {\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^n \; - \;\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^{n - 1/2} } \right),\quad \mathop {\dot {\Theta }}\limits^n = \frac{2}{\Delta }\left( {\mathop \Theta \limits^n \; - \;\mathop \Theta \limits^{n - 1/2} } \right);\quad 0 \leqslant k \leqslant N,$(2.14)
$\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^{n - 1/2} \equiv \mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^{n - 1} \; + \frac{\Delta }{2}\mathop {{{{\ddot {\varepsilon }}}_{k}}}\limits^{n - 1} ,\quad \mathop \Theta \limits^{n - 1/2} \equiv \mathop \Theta \limits^{n - 1} \; + \frac{\Delta }{2}\mathop {\dot {\Theta }}\limits^{n - 1} ;\quad 0 \leqslant k \leqslant N$Из равенств (2.14) при учете предположений (2.12) получаем, что шестикомпонентный вектор-столбец $\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^{n - 1/2} $ и величины $\mathop \Theta \limits^{n - 1/2} $, $\mathop \Theta \limits^n $ в правых частях соотношений (2.13) в текущий момент времени ${{t}_{n}}$ уже известны. Подставим выражения (2.13) в правую часть уравнения (2.6), тогда при учете обозначений, аналогичных (2.12), при $t = {{t}_{n}}$ будем иметь
(2.15)
$\mathop {{{{\dot {\sigma }}}_{k}}}\limits^n = \mathop {{{{\mathbf{B}}}_{k}}}\limits^n \mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^n \; + \;\mathop {{{{\mathbf{p}}}_{k}}}\limits^n ;\quad k = 0,1,2, \ldots ,N,$(2.16)
$\mathop {{{{\mathbf{B}}}_{k}}}\limits^n \equiv \mathop {{{{\mathbf{Z}}}_{k}}}\limits^n \; + \frac{2}{\Delta }\mathop {{{{\mathbf{Y}}}_{k}}}\limits^n ,\quad \mathop {{{{\mathbf{p}}}_{k}}}\limits^n \equiv - \frac{2}{\Delta }\mathop {{{{\mathbf{Y}}}_{k}}}\limits^n \mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^{n - 1/2} \; + \frac{2}{\Delta }\left( {\mathop \Theta \limits^n \; - \;\mathop \Theta \limits^{n - 1/2} } \right)\mathop {{{\beta }_{k}}}\limits^n ;\quad 0 \leqslant k \leqslant N,$Матричное равенство (2.15) – это искомое определяющее уравнение для термоупруговязкопластического k-го материала композиции. Согласно соотношениям (2.8)–(2.10) и (2.16), матрицы ${{{\mathbf{Z}}}_{k}}$, ${{{\mathbf{Y}}}_{k}}$, ${{{\mathbf{B}}}_{k}}$ и векторы-столбцы ${{\beta }_{k}}$, ${{{\mathbf{p}}}_{k}}$ зависят от решения задачи, поэтому уравнение (2.15) является нелинейным. Для его линеаризации, как и в [22], используем метод, аналогичный методу переменных параметров упругости [24]. Тогда при $t = {{t}_{n}}$ на текущей итерации этого метода элементы матрицы $\mathop {{{{\mathbf{B}}}_{k}}}\limits^n = \left( {\mathop {b_{{ij}}^{{(k)}}}\limits^n } \right)$ и вектора $\mathop {{{{\mathbf{p}}}_{k}}}\limits^n = \left( {\mathop {p_{i}^{{(k)}}}\limits^n } \right)$ в определяющем уравнении (2.15) будут известны.
Линеаризованное матричное равенство (2.15) формально полностью совпадает с соотношением (2.10) в [22]. Поэтому, используя для КМ исходные допущения, аналогичные принятым в [22, 30], и повторяя рассуждения из [22], на базе соотношения (2.15) в рассматриваемый момент времени ${{t}_{n}}$ на текущей итерации получим следующее линеаризованное матричное уравнение, характеризующее термоупруговязкопластическое состояние КМ:
(2.17)
$\mathop {\dot {\sigma }}\limits^n = \mathop {\mathbf{B}}\limits^n \mathop {\dot {\varepsilon }}\limits^n \; + \mathop {\mathbf{p}}\limits^n ;\quad n = 0,1,2, \ldots ,$(2.18)
$\begin{gathered} {\mathbf{B}} \equiv \left( {{{\omega }_{0}}{{{\mathbf{B}}}_{0}} + \sum\limits_{k = 1}^N {{{\omega }_{k}}} {{{\mathbf{B}}}_{k}}{{{\mathbf{E}}}_{k}}} \right){{{\mathbf{H}}}^{{ - 1}}},\quad {\mathbf{p}} \equiv {\mathbf{f}} - {\mathbf{Bg}},\quad {\mathbf{f}} \equiv {{\omega }_{0}}{{{\mathbf{p}}}_{0}} + \sum\limits_{k = 1}^N {{{\omega }_{k}}} \left( {{{{\mathbf{p}}}_{k}} + {{{\mathbf{B}}}_{k}}{{{\mathbf{r}}}_{k}}} \right) \\ {\mathbf{H}} \equiv {{\omega }_{0}}{\mathbf{I}} + \sum\limits_{k = 1}^N {{{\omega }_{k}}} {{{\mathbf{E}}}_{k}},\quad {\mathbf{g}} \equiv \sum\limits_{k = 1}^N {{{\omega }_{k}}} {{{\mathbf{r}}}_{k}},\quad {{\omega }_{0}} \equiv 1 - \sum\limits_{k = 1}^N {{{\omega }_{k}}} ,\quad {{{\mathbf{r}}}_{k}} \equiv {\mathbf{D}}_{k}^{{ - 1}}{{\varsigma }_{k}},\quad {{{\mathbf{E}}}_{k}} \equiv {\mathbf{D}}_{k}^{{ - 1}}{{{\mathbf{C}}}_{k}}, \\ \end{gathered} $(2.19)
$\begin{gathered} c_{{1j}}^{{(k)}} = d_{{1j}}^{{(k)}} = q_{{1j}}^{{(k)}},\quad c_{{ij}}^{{(k)}} = \sum\limits_{l = 1}^6 {g_{{il}}^{{(k)}}b_{{lj}}^{{(0)}}} ,\quad d_{{ij}}^{{(k)}} = \sum\limits_{l = 1}^6 {g_{{il}}^{{(k)}}b_{{lj}}^{{(k)}}} \\ \varsigma _{1}^{{(k)}} = 0,\quad \varsigma _{i}^{{(k)}} = \sum\limits_{l = 1}^6 {g_{{il}}^{{(k)}}\left( {p_{l}^{{(0)}} - p_{l}^{{(k)}}} \right)} ;\quad i = \overline {2,6} ,\quad j = \overline {1,6} ,\quad 1 \leqslant k \leqslant N \\ \end{gathered} $(2.20)
$\begin{gathered} g_{{11}}^{{(k)}} = q_{{11}}^{{(k)}} = l_{{11}}^{{(k)}}l_{{11}}^{{(k)}},\quad g_{{12}}^{{(k)}} = q_{{12}}^{{(k)}} = l_{{12}}^{{(k)}}l_{{12}}^{{(k)}},\quad \ldots ,\quad g_{{16}}^{{(k)}} = 2q_{{16}}^{{(k)}} = 2l_{{12}}^{{(k)}}l_{{11}}^{{(k)}},\quad \ldots \\ 2g_{{61}}^{{(k)}} = q_{{61}}^{{(k)}} = 2l_{{21}}^{{(k)}}l_{{11}}^{{(k)}},\quad \ldots ,\quad g_{{66}}^{{(k)}} = q_{{66}}^{{(k)}} = l_{{11}}^{{(k)}}l_{{22}}^{{(k)}} + l_{{12}}^{{(k)}}l_{{21}}^{{(k)}};\quad 1 \leqslant k \leqslant N \\ \end{gathered} $(2.21)
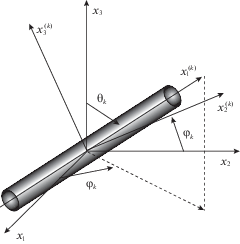
$\begin{gathered} l_{{11}}^{{(k)}} = \sin {{\theta }_{k}}\cos {{\varphi }_{k}},\quad l_{{12}}^{{(k)}} = \sin {{\theta }_{k}}\sin {{\varphi }_{k}},\quad l_{{13}}^{{(k)}} = \cos {{\theta }_{k}} \\ l_{{21}}^{{(k)}} = - \sin {{\varphi }_{k}},\quad l_{{22}}^{{(k)}} = \cos {{\varphi }_{k}},\quad l_{{23}}^{{(k)}} = 0 \\ l_{{31}}^{{(k)}} = - \cos {{\theta }_{k}}\cos {{\varphi }_{k}},\quad l_{{32}}^{{(k)}} = - \cos {{\theta }_{k}}\sin {{\varphi }_{k}},\quad l_{{33}}^{{(k)}} = \sin {{\theta }_{k}};\quad 1 \leqslant k \leqslant N \\ \end{gathered} $Не выписанные в равенствах (2.20) элементы $6 \times 6$-матриц ${{{\mathbf{G}}}_{k}}$ = $\left( {g_{{ij}}^{{(k)}}} \right)$ и ${{{\mathbf{Q}}}_{k}}$ = $\left( {q_{{ij}}^{{(k)}}} \right)$ приведены в табл. (21.40) и (21.44) в [30]. Матрицы ${{{\mathbf{G}}}_{k}}$ и ${{{\mathbf{Q}}}_{k}}$ определяют преобразования вектор-столбцов ${{\sigma }_{k}}$ и ${{\varepsilon }_{k}}$ (см. соотношения (2.7)) при переходе от глобальной прямоугольной системы координат ${{x}_{j}}$ к локальной прямоугольной системе $x_{i}^{{(k)}}$, связанной с волокнами k-го семейства. Ось $x_{1}^{{(k)}}$ при этом предполагается направленной вдоль арматуры и задается двумя углами сферической системы координат ${{\theta }_{k}}$ и ${{\varphi }_{k}}$ (рис. 1). Направляющие косинусы $l_{{ij}}^{{(k)}}$ между осями $x_{i}^{{(k)}}$ и ${{x}_{j}}$ ($i,j = 1,2,3$) определяются равенствами (2.21). (В выражениях (2.18) и (2.19) опущен верхний индекс n.)
Как и в [22], при выводе соотношений (2.17) и (2.18) попутно получаем линеаризованные матричные равенства
(2.22)
$\mathop {{{{\dot {\varepsilon }}}_{0}}}\limits^n = \mathop {{{{\mathbf{H}}}^{{ - 1}}}}\limits^n \mathop {\dot {\varepsilon }}\limits^n \; - \mathop {{{{\mathbf{H}}}^{{ - 1}}}}\limits^n \mathop {\mathbf{g}}\limits^n ,\quad \mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^n = \mathop {{{{\mathbf{E}}}_{k}}}\limits^n \mathop {{{{\dot {\varepsilon }}}_{0}}}\limits^n \; + \mathop {{{{\mathbf{r}}}_{k}}}\limits^n ;\quad 1 \leqslant k \leqslant N$Первое равенство (2.22) при $t = {{t}_{n}}$ на данной итерации выражает скорости деформаций связующего материала ${{\dot {\varepsilon }}_{0}}$ через скорости осредненных деформаций КМ $\dot {\varepsilon }$. Второе соотношение (2.22) определяет скорости деформаций арматуры k-го семейства ${{\dot {\varepsilon }}_{k}}$ через скорости деформаций связующего ${{\dot {\varepsilon }}_{0}}$.
Согласно формулам (2.9), (2.10) и (2.18)–(2.21) в момент времени ${{t}_{n}}$ на текущей итерации матрицы B, ${{{\mathbf{H}}}^{{ - 1}}}$, ${{{\mathbf{E}}}_{k}}$ и вектор-столбцы p, g, ${{{\mathbf{r}}}_{k}}$ в равенствах (2.17) и (2.22) известны. Если тепловое воздействие не учитывается ($\dot {\Theta } \equiv 0$), то соотношение (2.17) при учете выражений (2.14), (2.16), (2.18) и (2.19) редуцируется в определяющее уравнение для КМ, полученное в [22] в предположении об упруговязкопластическом поведении компонентов композиции. Следовательно, соотношение (2.17) обобщает структурные уравнения, выведенные в [22].
Предположим, что в текущий момент времени ${{t}_{n}}$ итерационный процесс сошелся с требуемой точностью, т.е. в соотношении (2.17) известны скорости деформаций КМ $\mathop {\dot {\varepsilon }}\limits^n $. Тогда по формулам (2.22) последовательно определяем скорости деформаций компонентов композиции $\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^n $, а из равенств (2.15) – скорости напряжений $\mathop {{{{\dot {\sigma }}}_{k}}}\limits^n $ в этих же материалах. Используя центральные конечные разности по времени на трехточечном шаблоне $\left\{ {{{t}_{{n - 1}}},{{t}_{n}},{{t}_{{n + 1}}}} \right\}$, получаем
(2.23)
$\frac{1}{{2\Delta }}\left( {\mathop {{{\sigma }_{k}}}\limits^{n + 1} \; - \;\mathop {{{\sigma }_{k}}}\limits^{n - 1} } \right) = \mathop {{{{\dot {\sigma }}}_{k}}}\limits^n ,\quad \frac{1}{{2\Delta }}\left( {\mathop {{{\varepsilon }_{k}}}\limits^{n + 1} \; - \;\mathop {{{\varepsilon }_{k}}}\limits^{n - 1} } \right) = \mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^n ;\quad 0 \leqslant k \leqslant N$,(2.24)
$\begin{gathered} \mathop {e_{{ii}}^{{(k)}}}\limits^{n + 1} = \frac{1}{{{{E}_{k}}}}\left( {\mathop {\sigma _{{ii}}^{{(k)}}}\limits^{n + 1} \; - {{\nu }_{k}}\mathop {\sigma _{{jj}}^{{(k)}}}\limits^{n + 1} \; - {{\nu }_{k}}\mathop {\sigma _{{ll}}^{{(k)}}}\limits^{n + 1} } \right),\quad \mathop {e_{{ij}}^{{(k)}}}\limits^{n + 1} = \frac{1}{{2{{G}_{k}}}}\mathop {\sigma _{{ij}}^{{(k)}}}\limits^{n + 1} \\ i \ne j \ne l \ne i,\quad i,j,l = 1,2,3,\quad 0 \leqslant k \leqslant N, \\ \end{gathered} $Из соотношения (2.1) при учете выражения для $\varepsilon _{\Theta }^{{(k)}}$ в момент времени ${{t}_{{n + 1}}}$ будем иметь
(2.25)
$\begin{gathered} \mathop {p_{{ij}}^{{(k)}}}\limits^{n + 1} = \mathop {\varepsilon _{{ij}}^{{(k)}}}\limits^{n + 1} - \mathop {e_{{ij}}^{{(k)}}}\limits^{n + 1} - {{\delta }_{{ij}}}\mathop {{{{\bar {\alpha }}}^{{(k)}}}}\limits^{n + 1} (\mathop \Theta \limits^{n + 1} - \mathop \Theta \limits^n ) - {{\delta }_{{ij}}}\mathop {\varepsilon _{\Theta }^{{(k)}}}\limits^n ,\quad \mathop {{{{\bar {\alpha }}}^{{(k)}}}}\limits^{n + 1} \equiv \frac{1}{2}\left( {\mathop {{{\alpha }^{{(k)}}}}\limits^{n + 1} + \mathop {{{\alpha }^{{(k)}}}}\limits^n } \right) \\ i,j = \overline {1,3} ,\quad 0 \leqslant k \leqslant N, \\ \end{gathered} $Согласно второму соотношению (2.5), для вычисления параметра Одквиста ${{\chi }_{k}}$ при $t = {{t}_{{n + 1}}}$ имеем равенство
(2.26)
$\mathop {{{\chi }_{k}}}\limits^{n + 1} = \int\limits_0^{{{t}_{{n + 1}}}} {\sqrt {2\dot {p}_{{ij}}^{{(k)}}\dot {p}_{{ij}}^{{(k)}}} dt} = \mathop {{{\chi }_{k}}}\limits^n \; + \int\limits_{{{t}_{n}}}^{{{t}_{{n + 1}}}} {\sqrt {2dp_{{ij}}^{{(k)}}dp_{{ij}}^{{(k)}}} } \approx \mathop {{{\chi }_{k}}}\limits^n \; + \sqrt {2\Delta \mathop {p_{{ij}}^{{(k)}}}\limits^{n + 1} \Delta \mathop {p_{{ij}}^{{(k)}}}\limits^{n + 1} } ,$(2.27)
$\Delta \mathop {p_{{ij}}^{{(k)}}}\limits^{n + 1} \equiv \mathop {p_{{ij}}^{{(k)}}}\limits^{n + 1} \; - \mathop {p_{{ij}}^{{(k)}}}\limits^n ;\quad i,j = 1,2,3,\quad 0 \leqslant k \leqslant N$В правой части выражений (2.27) значения пластических деформаций уже известны (см. соотношение (2.25)), а значит в равенстве (2.26) известно последнее слагаемое. Таким образом, по формуле (2.26) при учете выражений (2.23)–(2.25) и (2.27) можно рассчитать величину параметра Одквиста $\mathop {{{\chi }_{k}}}\limits^{n + 1} $ при $t = {{t}_{{n + 1}}}$. С вычислительной точки зрения такой способ определения величины $\mathop {{{\chi }_{k}}}\limits^{n + 1} $ удобен тем, что в следующий момент времени ${{t}_{{n + 1}}}$ он не требует уточнения параметра Одквиста в процессе итерационной процедуры по методу переменных параметров упругости.
3. Теплофизическая структурная модель армированного материала. При моделировании динамического термоупруговязкопластического деформирования КМ необходимо учитывать связанность механической и теплофизической задач. Поэтому кроме определяющих механических соотношений (2.17) необходимо использовать закон теплопроводности Фурье для КМ, который в матричной форме можно записать так [31]:
где(3.2)
$\begin{gathered} {\mathbf{q}} = {{\left( {{{q}_{1}}\;{{q}_{2}}\;{{q}_{3}}} \right)}^{{\text{т}}}},\quad {\mathbf{g}} = {{\left( {{{g}_{1}}\;{{g}_{2}}\;{{g}_{3}}} \right)}^{{\text{т}}}} = \operatorname{grad} \Theta ,\quad \Lambda = \left( {{{\omega }_{0}}{{\Lambda }_{0}} + \sum\limits_{k = 1}^N {{{\omega }_{k}}{\mathbf{L}}_{k}^{{\text{T}}}{{\Lambda }_{k}}} {{{{\mathbf{\bar {E}}}}}_{k}}} \right){\mathbf{\bar {H}}} \\ {\mathbf{\bar {H}}} = {{\left( {{{\omega }_{0}}{\mathbf{\bar {I}}} + \sum\limits_{k = 1}^N {{{\omega }_{k}}{\mathbf{L}}_{k}^{{\text{T}}}} {{{{\mathbf{\bar {E}}}}}_{k}}} \right)}^{{ - 1}}},\quad {{{{\mathbf{\bar {E}}}}}_{k}} = {\mathbf{\bar {B}}}_{k}^{{ - 1}}{{{{\mathbf{\bar {C}}}}}_{k}};\quad 1 \leqslant k \leqslant N, \\ \end{gathered} $(3.3)
$\begin{gathered} \bar {b}_{{11}}^{{(k)}} = 1,\quad \bar {b}_{{1i}}^{{(k)}} = 0,\quad \bar {b}_{{ij}}^{{(k)}} = \lambda _{{ij}}^{{(k)}},\quad \bar {c}_{{1j}}^{{(k)}} = l_{{1j}}^{{(k)}},\quad \bar {c}_{{ij}}^{{(k)}} = l_{{im}}^{{(k)}}\lambda _{{mj}}^{{(0)}} \\ i = 2,3,\quad j = 1,2,3,\quad 1 \leqslant k \leqslant N \\ \end{gathered} $Если материалы композиции термочувствительны, то $\lambda _{{ij}}^{{(k)}} = \lambda _{{ij}}^{{(k)}}\left( \Theta \right)$ ($0 \leqslant k \leqslant N$), поэтому согласно формулам (3.2), (3.3) и эффективные коэффициенты КМ в выражении (3.1) зависят от температуры (${\mathbf{\Lambda }} = {\mathbf{\Lambda }}\left( \Theta \right)$, ${{\lambda }_{{ij}}} = {{\lambda }_{{ij}}}\left( \Theta \right)$, $i,j = 1,2,3$).
4. Постановка задачи термоупруговязкопластического изгибного деформирования КМ-пластины. Рассматриваем динамическое поведение КМ-пластины толщиной 2h (рис. 2), с которой свяжем декартову прямоугольную систему координат ${{x}_{i}}$: плоскость $O{{x}_{1}}{{x}_{2}}$ – срединная; ось $O{{x}_{3}}$ – поперечная ($\left| {{{x}_{3}}} \right| \leqslant h$). Конструкция может быть армирована плоско-перекрестно (рис. 2а) или пространственно (рис. 2б). Структура армирования в направлении $O{{x}_{3}}$ квазиоднородна.
Рис. 2.
Элемент КМ-пластины с ортогональной 2D-структурой армирования (а) и с пространственной 4D-структурой армирования (б).
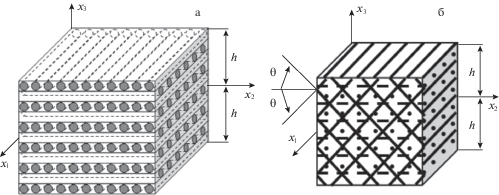
Для моделирования волновых процессов и возможного слабого сопротивления гибкой КМ-пластины поперечному сдвигу (например в случаях плоско-перекрестных структур армирования или в случае пространственной структуры армирования, изображенной на рис. 2б, при сдвиге в плоскости $O{{x}_{1}}{{x}_{3}}$) используем теорию Амбарцумяна [15, 17, 22], а геометрическую нелинейность задачи учтем в приближении Кармана.
Замечание. В [22] было показано, что в случае упруговязкопластического деформирования гибкой пластины с произвольными пространственными структурами армирования не удается построить явную схему типа “крест” при использовании теории Амбарцумяна, если на лицевых поверхностях касательными внешними силами нельзя пренебречь. Очевидно, что этот результат переносится и на более общий случай термоупруговязкопластического деформирования КМ-пластин. В связи с этим в настоящем исследовании рассматриваем только частные случаи пространственных структур армирования и нагружения КМ-конструкций, при которых можно использовать явную численную схему типа “крест”. Поэтому далее предполагаем: исследуется частный, но практически важный случай нагружения пластины, когда на лицевых поверхностях можно пренебречь внешними касательными силами; структура пространственного армирования такова, что если волокно некоторого k-го семейства имеет наклонное направление ($0 < {{\theta }_{k}} < \pi {\text{/}}2$; см. соотношения (2.21) и рис. 1), то обязательно найдется другое m-е семейство наклонных волокон с параметрами армирования ${{\theta }_{m}} = \pi - {{\theta }_{k}}$, ${{\varphi }_{m}} = {{\varphi }_{k}}$ и ${{\omega }_{m}} = {{\omega }_{k}}$ ($1 \leqslant k$, $m \leqslant N$, $m \ne k$), изготовленных из того же материала, что и волокна k-го семейства. Структуры с такой особенностью армирования часто встречаются на практике [32]. В частности, к ним относится структура армирования, изображенная на рис. 2б, а также структуры с ортогональным пространственным армированием [32] или структуры с плоско-перекрестным армированием [26] (см. рис. 2а).
Согласно этому замечанию, в рамках теории Амбарцумяна осредненные деформации композиции ${{\varepsilon }_{{ij}}}$ и перемещения точек КМ-пластины ${{U}_{i}}$ аппроксимируем формулами [15, 22]:
(4.1)
$\begin{gathered} {{\varepsilon }_{{ij}}}\left( {t,{\mathbf{r}}} \right) = \frac{1}{2}\left( {{{\partial }_{i}}{{u}_{j}} + {{\partial }_{j}}{{u}_{i}}} \right) - {{x}_{3}}{{\partial }_{i}}{{\partial }_{j}}w + \frac{{{{x}_{3}}}}{{3{{h}^{2}}}}\left( {3{{h}^{2}} - x_{3}^{2}} \right)\left( {{{\partial }_{i}}\varepsilon _{{j3}}^{0} + {{\partial }_{j}}\varepsilon _{{i3}}^{0}} \right) + \frac{1}{2}{{\partial }_{i}}w{{\partial }_{j}}w \\ {{\varepsilon }_{{i3}}}\left( {t,{\mathbf{r}}} \right) = \frac{{{{h}^{2}} - x_{3}^{2}}}{{{{h}^{2}}}}\varepsilon _{{i3}}^{0}\left( {t,{\mathbf{x}}} \right);\quad {\mathbf{x}} = \left( {{{x}_{1}},{{x}_{2}}} \right),\quad i,j = 1,2 \\ \end{gathered} $(4.2)
$\begin{gathered} {{U}_{i}}\left( {t,{\mathbf{r}}} \right) = {{u}_{i}}\left( {t,{\mathbf{x}}} \right) - {{x}_{3}}{{\partial }_{i}}w + \frac{{2{{x}_{3}}}}{{3{{h}^{2}}}}\left( {3{{h}^{2}} - x_{3}^{2}} \right)\varepsilon _{{i3}}^{0} \\ {{U}_{3}}\left( {t,{\mathbf{r}}} \right) = w\left( {t,{\mathbf{x}}} \right);\quad {\mathbf{x}} \in \Omega ,\quad \left| {{{x}_{3}}} \right| \leqslant h,\quad t \geqslant {{t}_{0}},\;\;i = 1,2, \\ \end{gathered} $В данной работе моделируется механическое поведение КМ-пластины как гибкой тонкостенной системы, поэтому поперечное нормальное напряжение ${{\sigma }_{{33}}}\left( {t,{\mathbf{r}}} \right)$ с приемлемой для практических приложений точностью можно аппроксимировать так [12]:
(4.3)
${{\sigma }_{{33}}}\left( {t,{\mathbf{r}}} \right) \equiv {{\sigma }_{3}}\left( {t,{\mathbf{r}}} \right) = \frac{{\sigma _{{33}}^{{( + )}}\left( {t,{\mathbf{x}}} \right) - \sigma _{{33}}^{{( - )}}\left( {t,{\mathbf{x}}} \right)}}{{2h}}{{x}_{3}} + \frac{{\sigma _{{33}}^{{( + )}}\left( {t,{\mathbf{x}}} \right) + \sigma _{{33}}^{{( - )}}\left( {t,{\mathbf{x}}} \right)}}{2},$Матричное определяющее уравнение (2.17) – это система шести алгебраических уравнений. Согласно соотношениям соответствия, аналогичным (2.7), из третьего уравнения этой системы в дискретный момент времени ${{t}_{n}}$ определяем скорость поперечной линейной деформации композиции
(4.4)
$\mathop {{{{\dot {\varepsilon }}}_{{33}}}}\limits^n \equiv \mathop {{{{\dot {\varepsilon }}}_{3}}}\limits^n = \frac{1}{{\mathop {{{b}_{{33}}}}\limits^n }}\left( {\mathop {{{{\dot {\sigma }}}_{3}}}\limits^n } \right. - \sum\limits_{i = 1}^6 {\left( {1 - {{\delta }_{{3i}}}} \right)} \mathop {{{b}_{{3i}}}}\limits^n \left. {\mathop {{{{\dot {\varepsilon }}}_{i}}}\limits^n \; - \mathop {{{p}_{3}}}\limits^n } \right),$К кинематическим соотношениям (4.1) и (4.2) необходимо добавить двумерные уравнения движения гибкой пластины и соответствующие им начальные и граничные условия, которые общеизвестны [15] (см. формулы (16)–(19) в [17]), поэтому не будем их здесь приводить.
В случае связанности механической и теплофизической задач термоупруговязкопластического деформирования армированных пластин дополнительно необходимо использовать уравнение теплового баланса для КМ [33, 34]:
где(4.6)
$\rho \equiv \sum\limits_{k = 0}^N {{{\omega }_{k}}{{\rho }_{k}}} ,\quad c \equiv \frac{1}{\rho }\sum\limits_{k = 0}^N {{{\omega }_{k}}{{c}_{k}}{{\rho }_{k}}} ,\quad W\left( {t,{\mathbf{r}}} \right) \equiv {{\sigma }_{{ij}}}{{\dot {\varepsilon }}_{{ij}}},$Предполагаем, что на лицевых поверхностях пластины заданы комбинации тепловых граничных условий II и III рода [35]:
(4.7)
$\begin{gathered} q_{3}^{{( + )}}\left( {t,{\mathbf{x}}} \right) \equiv {{q}_{3}}\left( {t,{\mathbf{x}},h} \right) = {{\alpha }^{{( + )}}}{{\left. {\left( {\Theta - \Theta _{\infty }^{{( + )}}} \right)} \right|}_{{{{x}_{3}} = h}}} + q_{\infty }^{{( + )}}\left( {t,{\mathbf{x}}} \right) \\ q_{3}^{{( - )}}\left( {t,{\mathbf{x}}} \right) \equiv {{q}_{3}}\left( {t,{\mathbf{x}}, - h} \right) = - {{\alpha }^{{( - )}}}{{\left. {\left( {\Theta - \Theta _{\infty }^{{( - )}}} \right)} \right|}_{{{{x}_{3}} = - h}}} + q_{\infty }^{{( - )}}\left( {t,{\mathbf{x}}} \right);\quad {\mathbf{x}} \in \Omega ,\quad t \geqslant {{t}_{0}}, \\ \end{gathered} $На торцевой поверхности ${{\Omega }_{*}}$ могут быть заданы тепловые граничные условия общего вида
(4.8)
$\begin{gathered} {{q}_{1}}{{n}_{1}} + {{q}_{2}}{{n}_{2}} = {{\alpha }_{*}}(\Theta - \Theta _{\infty }^{*}) + q_{\infty }^{*}\left( {t,{\mathbf{r}}} \right);\quad {\mathbf{x}} \in \Gamma \\ \left| {{{x}_{3}}} \right| \leqslant h,\quad t \geqslant {{t}_{0}}\quad ({{n}_{1}} = \cos \beta ,\quad {{n}_{2}} = \sin \beta ), \\ \end{gathered} $Для понижения размерности уравнения (4.5) аппроксимируем температуру пластины $\Theta $ полиномом M-й степени по поперечной координате ${{x}_{3}}$:
(4.9)
$\Theta \left( {t,{\mathbf{r}}} \right) - {{\Theta }^{0}} = \sum\limits_{l = 0}^M {{{\Theta }_{l}}\left( {t,{\mathbf{x}}} \right)x_{3}^{l}} ;\quad {\mathbf{x}} \in \Omega ,\quad \left| {{{x}_{3}}} \right| \leqslant h,\quad t \geqslant {{t}_{0}},$Согласно сделанному замечанию, при рассматриваемых структурах армирования ось $O{{x}_{3}}$ совпадает с одним из главных направлений теплофизической анизотропии КМ, поэтому
где ${{\lambda }_{{ij}}}$ – элементы матрицы $\Lambda $ в законе Фурье (3.1).Подставим разложение (4.9) в граничные условия (4.7) и используем соотношение (3.1) при учете равенств (4.10), тогда после элементарных преобразований получим
(4.11)
$\begin{gathered} - \sum\limits_{l = 0}^M {{{{\left( { - 1} \right)}}^{l}}{{h}^{{l - 1}}}} \left( {l\lambda _{{33}}^{{( - )}} + h{{\alpha }^{{( - )}}}} \right){{\Theta }_{l}}\left( {t,{\mathbf{x}}} \right) = {{\alpha }^{{( - )}}}\left( {\Theta _{\infty }^{{( - )}} - {{\Theta }^{0}}} \right) + q_{\infty }^{{( - )}}\left( {t,{\mathbf{x}}} \right) \\ \sum\limits_{l = 0}^M {{{h}^{{l - 1}}}} \left( {l\lambda _{{33}}^{{( + )}} + h{{\alpha }^{{( + )}}}} \right){{\Theta }_{l}}\left( {t,{\mathbf{x}}} \right) = {{\alpha }^{{( + )}}}\left( {\Theta _{\infty }^{{( + )}} - {{\Theta }^{0}}} \right) - q_{\infty }^{{( + )}}\left( {t,{\mathbf{x}}} \right);\quad {\mathbf{x}} \in \Omega ,\quad t \geqslant {{t}_{0}}, \\ \end{gathered} $(4.12)
$\lambda _{{33}}^{{( \pm )}} \equiv {{\left. {{{\lambda }_{{33}}}} \right|}_{{\Theta = \Theta \left( {t,{\mathbf{x}}, \pm h} \right)}}}{\kern 1pt} {\text{,}}$Система двух уравнений (4.11) при учете соотношений (4.10) и (4.12) содержит $M + 1$ неизвестных двумерных функции ${{\Theta }_{l}}\left( {t,{\mathbf{x}}} \right)$ ($0 \leqslant l \leqslant M$). Для замыкания этой системы используем обобщенный метод Галеркина [36], т.е. проинтегрируем уравнение теплового баланса (4.5) по толщине пластины с весами $x_{3}^{m}$ ($0 \leqslant m \leqslant M - 2$), тогда получим
(4.13)
$\begin{gathered} \rho {{{\dot {U}}}^{{(m)}}} = - {{\partial }_{1}}Q_{1}^{{(m)}} - {{\partial }_{2}}Q_{2}^{{(m)}} - \bar {Q}_{3}^{{(m)}} + {{W}^{{(m)}}}\left( {t,{\mathbf{x}}} \right) \\ {\mathbf{x}} \in \Omega ,\quad t \geqslant {{t}_{0}},\quad 0 \leqslant m \leqslant M - 2, \\ \end{gathered} $(4.14)
$\begin{gathered} {{U}^{{(m)}}}\left( {t,{\mathbf{x}}} \right) \equiv \int\limits_{ - h}^h {U\left( {t,{\mathbf{r}}} \right)} x_{3}^{m}d{{x}_{3}} \\ \bar {Q}_{3}^{{(m)}}\left( {t,{\mathbf{x}}} \right) \equiv \int\limits_{ - h}^h {{{\partial }_{3}}{{q}_{3}}\left( {t,{\mathbf{r}}} \right)} x_{3}^{m}d{{x}_{3}} = {{q}_{3}}\left( {t,{\mathbf{r}}} \right)\left. {x_{3}^{m}} \right|_{{ - h}}^{h} - m\int\limits_{ - h}^h {{{q}_{3}}\left( {t,{\mathbf{r}}} \right)} x_{3}^{{m - 1}}d{{x}_{3}} = \\ = {{h}^{m}}\left[ {q_{3}^{{( + )}} - {{{\left( { - 1} \right)}}^{m}}q_{3}^{{( - )}}} \right] - mQ_{3}^{{(m - 1)}}\left( {t,{\mathbf{x}}} \right),\quad Q_{i}^{{(m)}}\left( {t,{\mathbf{x}}} \right) \equiv \int\limits_{ - h}^h {{{q}_{i}}\left( {t,{\mathbf{r}}} \right)} x_{3}^{m}d{{x}_{3}}\quad (i = \overline {1,3} ) \\ {{W}^{{(m)}}}\left( {t,{\mathbf{x}}} \right) \equiv \int\limits_{ - h}^h {W\left( {t,{\mathbf{r}}} \right)x_{3}^{m}} d{{x}_{3}},\quad \frac{{\partial U}}{{\partial \Theta }} = c\left( \Theta \right), \\ \end{gathered} $Анализ экспериментальных данных показывает [18, 37], что с приемлемой для практических приложений точностью в достаточно широком диапазоне температур теплоемкость k-го компонента композиции ${{c}_{k}}$ можно аппроксимировать квадратной параболой от разности $\Theta - {{\Theta }^{0}}$ (могут быть использованы и более сложные зависимости ${{c}_{k}}(\Theta - {{\Theta }^{0}})$, это не принципиально). Тогда согласно второму равенству (4.6) удельную теплоемкость композиции в случае учета термочувствительности можно представить в виде
(4.15)
$c\left( {{\mathbf{x}};\Theta - {{\Theta }^{0}}} \right) = {{C}_{0}}\left( {\mathbf{x}} \right) + {{C}_{1}}\left( {\mathbf{x}} \right)\left( {\Theta - {{\Theta }^{0}}} \right) + {{C}_{2}}\left( {\mathbf{x}} \right){{\left( {\Theta - {{\Theta }^{0}}} \right)}^{2}};\quad {\mathbf{x}} \in \Omega $,(4.16)
${{C}_{i}}\left( {\mathbf{x}} \right) \equiv \frac{1}{\rho }\sum\limits_{k = 0}^N {c_{i}^{{(k)}}{{\rho }_{k}}{{\omega }_{k}}\left( {\mathbf{x}} \right)} ;\quad i = 0,1,2,$Из последней формулы (4.14) при учете выражений (4.15) и (4.16) получаем
(4.17)
$U\left( {{\mathbf{x}};\Theta - {{\Theta }^{0}}} \right) = {{U}_{0}} + {{C}_{0}}\left( {\mathbf{x}} \right)\left( {\Theta - {{\Theta }^{0}}} \right) + \frac{{{{C}_{1}}\left( {\mathbf{x}} \right)}}{2}{{\left( {\Theta - {{\Theta }^{0}}} \right)}^{2}} + \frac{{{{C}_{2}}\left( {\mathbf{x}} \right)}}{3}{{\left( {\Theta - {{\Theta }^{0}}} \right)}^{3}},$Подставим разложение (4.17) в первое равенство (4.14) и учтем формулу (4.9), тогда получим
(4.18)
$\begin{gathered} {{C}_{0}}\sum\limits_{i = 0}^M {H\left( {i + m} \right){{\Theta }_{i}}} + \frac{{{{C}_{1}}}}{2}\sum\limits_{i = 0}^M {\sum\limits_{j = 0}^M {H\left( {i + j + m} \right){{\Theta }_{i}}{{\Theta }_{j}}} } + \\ + \;\frac{{{{C}_{2}}}}{3}\sum\limits_{i = 0}^M {\sum\limits_{j = 0}^M {\sum\limits_{l = 0}^M {H\left( {i + j + l + m} \right)} } } {{\Theta }_{i}}{{\Theta }_{j}}{{\Theta }_{l}} = {{U}^{{(m)}}}\left( {t,{\mathbf{x}}} \right) \\ {\mathbf{x}} \in \Omega ,\quad t \geqslant {{t}_{0}},\quad 0 \leqslant m \leqslant M - 2, \\ \end{gathered} $(4.19)
$H\left( s \right) \equiv \frac{{{{h}^{{s + 1}}}}}{{s + 1}}\left[ {1 - {{{\left( { - 1} \right)}}^{{s + 1}}}} \right]$Если в текущий момент времени t из каких-то соображений известны значения функций ${{U}^{{(m)}}}$, то система нелинейных (в случае учета термочувствительности) уравнений (4.11) и (4.18) при учете выражений (4.12) и (4.19) замкнута относительно функций ${{\Theta }_{l}}\left( {t,{\mathbf{x}}} \right)$, $0 \leqslant l \leqslant M$.
Для получения граничных условий, соответствующих двумерным уравнениям теплового баланса (4.13), необходимо проинтегрировать равенство (4.8) по толщине пластины с весами $x_{3}^{m}$, тогда с учетом обозначений (4.14) и разложения (4.9) получим
(4.20)
$\begin{gathered} Q_{1}^{{(m)}}{{n}_{1}} + Q_{2}^{{(m)}}{{n}_{2}} - {{\alpha }_{*}}\sum\limits_{l = 0}^M {H\left( {l + m} \right){{\Theta }_{l}}} = - {{\alpha }_{*}}H\left( m \right)(\Theta _{\infty }^{*} - {{\Theta }^{0}}) + Q_{\infty }^{{(m)}}\left( {t,{\mathbf{x}}} \right) \\ {\mathbf{x}} \in \Gamma ,\quad t \geqslant {{t}_{0}},\quad 0 \leqslant m \leqslant M - 2, \\ \end{gathered} $(4.21)
$Q_{\infty }^{{(m)}}\left( {t,{\mathbf{x}}} \right) \equiv \int\limits_{ - h}^h {q_{\infty }^{*}\left( {t,{\mathbf{r}}} \right)x_{3}^{m}d{{x}_{3}}} ;\quad 0 \leqslant m \leqslant M - 2$Начальные условия для уравнений (4.13) имеют вид
(4.22)
${{U}^{{(m)}}}\left( {{{t}_{0}},{\mathbf{x}}} \right) = U_{0}^{{(m)}}\left( {\mathbf{x}} \right);\quad {\mathbf{x}} \in \Omega ,\quad 0 \leqslant m \leqslant M - 2,$Из замкнутой системы двумерных уравнений (4.11) и (4.13) при учете соотношений (4.14) и (4.18) следует, что число M в разложении (4.9) должно быть не меньше двух ($M \geqslant 2$), если учитываются теплофизические граничные условия на лицевых поверхностях пластины (см. равенства (4.11)).
5. Метод расчета. Как отмечалось во Введении, для интегрирования рассматриваемой задачи будем использовать явные пошаговые численные схемы, определяя решение в дискретные моменты времени ${{t}_{n}}$ ($n = 0,1,2, \ldots $). В связи с этим считаем, что при $t = {{t}_{m}}$ помимо функций (2.12) уже известны также и значения следующих величин
(5.1)
$\mathop {{{\Theta }_{s}}}\limits^n \left( {\mathbf{x}} \right) \equiv {{\Theta }_{s}}\left( {{{t}_{n}},{\mathbf{x}}} \right),\quad \mathop {q_{\infty }^{{( \pm )}}}\limits^n \left( {\mathbf{x}} \right) \equiv q_{\infty }^{{( \pm )}}\left( {{{t}_{n}},{\mathbf{x}}} \right),\quad \mathop {\sigma _{{ij}}^{{(k)}}}\limits^m \left( {\mathbf{r}} \right) \equiv \sigma _{{ij}}^{{(k)}}\left( {{{t}_{m}},{\mathbf{r}}} \right),$(5.2)
${{\gamma }_{i}}\left( {t,{\mathbf{x}}} \right) \equiv \frac{8}{5}\varepsilon _{{i3}}^{0} - {{\partial }_{i}}w;\quad i = 1,2$Производные по времени в механической составляющей исследуемой связанной термоупруговязкопластической задачи (за исключением левой части первого равенства (2.13)) будем аппроксимировать центральными конечными разностями на трехточечном шаблоне $\left\{ {{{t}_{{n - 1}}},{{t}_{n}},{{t}_{{n + 1}}}} \right\}$, что позволяет разработать явную численную схему. Заменяя вторые производные по времени от кинематических переменных w, ${{u}_{i}}$ и ${{\gamma }_{i}}$ в уравнениях движения гибкой КМ-пластины их конечно-разностными аналогами и учитывая выражения (5.2) и обозначения, аналогичные (5.1), получим [22]
(5.3)
$\frac{{2h\rho }}{{{{\Delta }^{2}}}}\left( {\mathop {{{u}_{i}}}\limits^{n + 1} \; - 2\mathop {{{u}_{i}}}\limits^n \; + \;\mathop {{{u}_{i}}}\limits^{n - 1} } \right) = \sum\limits_{j = 1}^2 {{{\partial }_{j}}} \left( {\mathop {{{F}_{{ij}}}}\limits^n \; - \;\mathop {{{F}_{{j3}}}}\limits^n {{\partial }_{j}}\mathop w\limits^n } \right) - \left( {\mathop {\sigma _{{33}}^{{( + )}}}\limits^n \; - \;\mathop {\sigma _{{33}}^{{( - )}}}\limits^n } \right){{\partial }_{i}}\mathop w\limits^n $(5.4)
${{F}_{{ij}}} = \int\limits_{ - h}^h {{{\sigma }_{{ij}}}} d{{x}_{3}},\quad {{F}_{{i3}}} = \int\limits_{ - h}^h {{{\sigma }_{{i3}}}} d{{x}_{3}},\quad {{M}_{{ij}}} = \int\limits_{ - h}^h {{{\sigma }_{{ij}}}} {{x}_{3}}d{{x}_{3}};\quad i,j = 1,2,$Используя выражения (5.4) и предположения (5.1) в данный момент времени ${{t}_{n}}$ можно вычислить все силовые факторы ${{F}_{{ij}}}$, ${{F}_{{i3}}}$, ${{M}_{{ij}}}$ и внешние нагрузки $\sigma _{{33}}^{{( \pm )}}$, входящие в правые части равенств (5.3). Следовательно, при учете соответствующих граничных условий [15, 17, 22] из уравнений (5.3) можно вычислить по явной схеме значения неизвестных функций $\mathop w\limits^{n + 1} $, $\mathop {{{u}_{i}}}\limits^{n + 1} $ и $\mathop {{{\gamma }_{i}}}\limits^{n + 1} $ в следующий момент времени ${{t}_{{n + 1}}}$. После этого по формулам (4.1) при учете равенств (5.2) определяем осредненные деформации композиции $\mathop {{{\varepsilon }_{{ij}}}}\limits^{n + 1} $. Согласно соотношениям (4.1) и (5.1), деформации $\mathop {{{\varepsilon }_{{ij}}}}\limits^{n - 1} $ уже известны при $t = {{t}_{{n - 1}}}$, поэтому на основании формул численного дифференцирования по t при учете выражения (4.4) можно вычислить и скорости деформаций $\mathop {{{{\dot {\varepsilon }}}_{{ij}}}}\limits^n $ в каждой точке пластины в момент времени ${{t}_{n}}$. Далее по формулам (2.22) при учете соответствий (2.7) определяем скорости деформаций компонентов композиции $\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^n $, а из соотношений (2.15) при учете формул (2.16) – скорости напряжений $\mathop {{{{\dot {\sigma }}}_{k}}}\limits^n $. Используя аппроксимации (2.23) при учете предположений (5.1), вычисляем напряжения $\mathop {{{\sigma }_{k}}}\limits^{n + 1} $ и деформации $\mathop {{{\varepsilon }_{k}}}\limits^{n + 1} $ в k-м компоненте композиции, затем по формуле (2.26) при учете соотношений (2.24), (2.25) и (2.27) определяем значение параметра Одквиста $\mathop {{{\chi }^{{(k)}}}}\limits^{n + 1} $ в том же материале в следующий момент времени при ${{t}_{{n + 1}}}$. Согласно равенствам (2.10) и (2.13) параметр переключения ${{c}^{{(k)}}}$ при $t = {{t}_{n}}$ зависит от $\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^n $, поэтому в текущий момент времени ${{t}_{n}}$ определяющее соотношение (2.15) (или (2.6)) необходимо итерационно уточнять по методу переменных параметров упругости [24]. Проведенные расчеты показывают, что для получения приемлемой в практических приложениях точности достаточно использовать две итерации на каждом шаге по времени.
Для интегрирования теплофизической составляющей рассматриваемой задачи будем также использовать явную схему, но на двухточечном шаблоне по времени $\left\{ {{{t}_{n}},{{t}_{{n + 1}}}} \right\}$. Тогда система двумерных уравнений теплового баланса (4.13) при учете обозначений, аналогичных (5.1), примет вид [28]:
(5.5)
$\begin{gathered} \frac{\rho }{\Delta }\left( {\mathop {{{U}^{{(m)}}}}\limits^{n + 1} \; - \mathop {{{U}^{{(m)}}}}\limits^n } \right) = - {{\partial }_{1}}\mathop {Q_{1}^{{(m)}}}\limits^n \; - {{\partial }_{2}}\mathop {Q_{1}^{{(m)}}}\limits^n \; - \mathop {\bar {Q}_{3}^{{(m)}}}\limits^n \; + \mathop {{{W}^{{(m)}}}}\limits^n \\ {\mathbf{x}} \in \Omega ,\quad 0 \leqslant m \leqslant M - 2,\quad n = 0,1,2, \ldots \\ \end{gathered} $На основании формул (4.14) при учете предположений (5.1) в текущий момент времени ${{t}_{n}}$ можно вычислить правые части в равенствах (5.5), а затем по явной схеме при учете соотношений (4.20), (4.21) определяем значения функций $\mathop {{{U}^{{(m)}}}}\limits^{n + 1} $ в следующий момент времени ${{t}_{{n + 1}}}$. Далее, рассматривая при $t = {{t}_{{n + 1}}}$ уравнения (4.11) и (4.18) (в которых правые части уже известны) при учете обозначений (4.12) и (4.19), определяем коэффициенты разложения температуры $\mathop {{{\Theta }_{l}}}\limits^{n + 1} \left( {\mathbf{x}} \right)$ ($0 \leqslant l \leqslant M$) в формуле (4.9). В случае учета термочувствительности материалов композиции система уравнений (4.11) и (4.18) нелинейна. Для ее линеаризации можно использовать метод переменных теплофизических параметров, аналогичный методу переменных параметров упругости [24]. Расчеты показали, что для сходимости такого итерационного процесса с приемлемой для приложений точностью достаточно использовать две–три итерации.
Согласно структуре левых частей уравнений (5.3) и (5.5), для начала расчетов по предложенной численной схеме необходимо предварительно знать функции $\mathop w\limits^m $, $\mathop {{{u}_{i}}}\limits^m $, $\mathop {{{\gamma }_{i}}}\limits^m $ ($m = 0,1$) и $\mathop {{{U}^{{(l)}}}}\limits^0 $. При этом функции $\mathop w\limits^0 $, $\mathop {{{u}_{i}}}\limits^0 $, $\mathop {{{\gamma }_{i}}}\limits^0 $ и $\mathop {{{U}^{{(l)}}}}\limits^0 $ ($0 \leqslant l \leqslant M - 2$) определяются из начальных условий (см. равенства (4.22) и формулы (18) в [17]). Если при $t = {{t}_{0}}$ КМ-пластина покоится в естественном состоянии и внешние нагрузки отсутствуют ($\mathop {\sigma _{{33}}^{{( + )}}}\limits^0 $ = = $\mathop {\sigma _{{33}}^{{( - )}}}\limits^0 $ = 0), то по формуле Тейлора с точностью ${{\Delta }^{3}}$ получаем $\mathop w\limits^1 \approx \mathop {{{u}_{i}}}\limits^1 $ ≈ 0, $\mathop {{{\gamma }_{i}}}\limits^1 $ ≈ 0, $i = 1,2$ [17, 22].
Заменяя в уравнениях (5.3) и (5.5) производные ${{\partial }_{i}}\left( \centerdot \right)$ их конечно-разностными аналогами и присоединяя к этим уравнениям необходимые граничные условия (см. равенства (4.20) и (4.21), а также формулы (19) в [17]) окончательно получим явную пошаговую схему численного интегрирования связанной задачи термоупруговязкопластического деформирования гибкой КМ-пластины.
6. Обсуждение результатов расчетов. В качестве конкретных примеров рассмотрим неизотермическое динамическое поведение прямоугольных удлиненных пластин ($\Omega $: $\left| {{{x}_{1}}} \right| \leqslant a$, $\left| {{{x}_{2}}} \right| \leqslant b$, $a = 3b$) толщиной $2h = 2$ см и разной ширины 2b. По всему контуру Γ конструкции жестко закреплены ($w = {{u}_{i}} = 0$, ${{\gamma }_{i}} = 0$, ${\mathbf{x}} \in \Gamma $, $t \geqslant {{t}_{0}}$ [22]) и в начальный момент времени $t = {{t}_{0}} = 0$ покоятся ($w = {{u}_{i}} = 0$, ${{\gamma }_{i}} = 0$, ${\mathbf{x}} \in \Omega $, $t = {{t}_{0}}$, $i = 1,2$ [22]) при температуре естественного состояния ($\Theta = {{\Theta }^{0}}$ = const, ${\mathbf{x}} \in \Omega $, $\left| {{{x}_{3}}} \right| \leqslant h$, $t = {{t}_{0}}$). Со стороны нижних лицевых поверхностей пластины нагружаются давлением, порожденным воздушной взрывной волной [25]:
(6.1)
$\begin{gathered} \sigma _{{33}}^{{( + )}} \equiv 0,\quad - {\kern 1pt} \sigma _{{33}}^{{( - )}} = p\left( t \right) = \left\{ \begin{gathered} {{p}_{{\max }}}t{\text{/}}{{t}_{{{\text{max}}}}},\quad 0 \leqslant t \leqslant {{t}_{{{\text{max}}}}} \hfill \\ {{p}_{{\max }}}\exp \left[ { - \alpha \left( {t - {{t}_{{{\text{max}}}}}} \right)} \right],\quad t > {{t}_{{{\text{max}}}}} \hfill \\ \end{gathered} \right. \\ \alpha = - \ln (0.01){\text{/}}\left( {{{t}_{{{\text{min}}}}} - {{t}_{{{\text{max}}}}}} \right) > 0,\quad {{t}_{{{\text{min}}}}} \gg {{t}_{{{\text{max}}}}},\quad p\left( {{{t}_{{{\text{min}}}}}} \right) = 0.01{{p}_{{\max }}}, \\ \end{gathered} $Через лицевые поверхности (${{x}_{3}} = \pm h$) реализуется конвективный теплообмен с окружающей средой ($q_{\infty }^{{( \pm )}} \equiv 0$) в условиях естественной конвекции (${{\alpha }^{{( \pm )}}}$ = 30 Вт/(м2 К) [38]) при температуре воздуха, равной температуре естественного состояния пластин: $\Theta _{\infty }^{{( \pm )}}$ = ${{\Theta }^{0}}$ = 20°С (см. равенства (4.7) и (4.11)). На торцевых поверхностях заданы граничные условия I рода, причем температура конструкций поддерживается равной температуре их естественного состояния: ${{\alpha }_{*}} \to \infty $, $\Theta _{\infty }^{*} = {{\Theta }^{0}}$ (см. соотношения (4.8), (4.20) и (4.21)).
Пластины изготовлены из высокопрочного магниевого сплава ВТ65 [18] и армированы высокопрочной стальной проволокой У8А [26] (металлокомпозиция) или из эпоксидной смолы [39] и усилены стекловолокнами [26] (стеклопластик). Упругопластическое деформирование материалов композиции на стадии активного нагружения при постоянстве скорости деформации $\dot {\varepsilon }$ и температуры $\Theta $ характеризуется диаграммой с линейным упрочнением
(6.2)
$\sigma = \left\{ \begin{gathered} {{E}^{{(k)}}}\varepsilon ,\quad \left| \varepsilon \right| \leqslant \varepsilon _{{\text{s}}}^{{(k)}} = \sigma _{{\text{s}}}^{{(k)}}{\text{/}}{{E}^{{(k)}}} \hfill \\ {\text{sign}}\left( \varepsilon \right)\sigma _{{\text{s}}}^{{(k)}} + E_{{\text{s}}}^{{(k)}}\left( {\varepsilon - {\text{sign}}\left( \varepsilon \right)\varepsilon _{{\text{s}}}^{{(k)}}} \right);\quad \left| \varepsilon \right| > \varepsilon _{{\text{s}}}^{{(k)}},\quad 0 \leqslant k \leqslant N, \hfill \\ \end{gathered} \right.$Таблица 1.
| Характеристика материала | Эпоксидная смола | Стеклянные волокна | Магниевый сплав ВМ65 (Mg) | Стальная проволока У8А |
|---|---|---|---|---|
| $\dot {\varepsilon } = 5 \times {{10}^{{ - 4}}}$ c–1 | ||||
| $\rho $, кг/м3 | 1210.0 (20) | 2520.0 (20) | 1800.0 (20) | 7800.0 (20) |
| 1208.0 (40) | 2519.6 (80) | 1796.2 (100) | 7791.8 (100) | |
| $E$, ГПа | 2.8 (20) | 86.8 (20) | 43.0 (20) | 210.0 (20) |
| 2.3 (40) | 86.3 (80) | 38.5 (100) | 195.0 (100) | |
| $\nu $ | 0.330 (20) | 0.250 (20) | 0.330 (20) | 0.300 (20) |
| 0.333 (40) | 0.254 (80) | 0.334 (100) | 0.305 (100) | |
| ${{\sigma }_{{\text{s}}}}$, МПа | 20 (20) | 4500 (20) | 267 (20) | 3968 (20) |
| 18 (40) | 4400 (80) | 219 (100) | 3971 (200) | |
| ${{E}_{{\text{s}}}},\,\,{\text{ГПа}}$ | 1.114 (20) | 6.230 (20) | 0.379 (20) | 6.973 (20) |
| 0.783 (40) | 5.168 (80) | 0.367 (100) | 5.014 (200) | |
| $\lambda $, Вт/(м K) | 0.243 (20) | 0.89 (20) | 117.23 (20) | 42.7 (20) |
| 0.240 (40) | 0.86 (80) | 121.42 (100) | 41.7 (100) | |
| $\alpha \times {{10}^{6}}$, K–1 | 68.1 (20) | 2.5 (20) | 20.9 (20) | 12.3 (20) |
| 70.3 (40) | 2.6 (80) | 22.6 (100) | 13.2 (100) | |
| $c$, кДж/(кг K) | 1.54 (20) | 0.800 (20) | 1.032 (20) | 0.485 (20) |
| 1.60 (40) | 0.839 (80) | 1.054 (100) | 0.488 (100) | |
| $\bar {c}$, м/с | 1521 (20) | 5869 (20) | 4888 (20) | 5189 (20) |
| 1380 (40) | 5852 (80) | 4635 (100) | 5003 (100) | |
| $\bar {a}$, м2/с | $2.60 \times {{10}^{{ - 7}}}$ (20) | $8.80 \times {{10}^{{ - 7}}}$ (20) | $1.27 \times {{10}^{{ - 4}}}$ (20) | $2.26 \times {{10}^{{ - 5}}}$ (20) |
| $2.48 \times {{10}^{{ - 7}}}$ (40) | $8.14 \times {{10}^{{ - 7}}}$ (80) | $1.29 \times {{10}^{{ - 4}}}$ (100) | $2.19 \times {{10}^{{ - 5}}}$ (100) | |
| $\dot {\varepsilon } = 0.417$ с–1 | ||||
| ${{\sigma }_{{\text{s}}}}$, МПа | – | – | 306 (20) | – |
| – | – | 243 (100) | – | |
| ${{E}_{{\text{s}}}}$, МПа | – | – | 0.589 (20) | – |
| – | – | 0.596 (100) | – | |
| $\dot {\varepsilon } = 104.0$ с–1 | ||||
| ${{\sigma }_{{\text{s}}}}$ МПа | 22.0 (20) | 4600 (20) | 385 (20) | 4100 (20) |
| 19.5 (40) | 4550 (80) | 340 (100) | 4075 (200) | |
| ${{E}_{{\text{s}}}}$, ГПа | 1.238 (20) | 6.314 (20) | 1.010 (20) | 7.035 (20) |
| 0.853 (40) | 5.458 (80) | 0.625 (100) | 6.158 (200) | |
Для проведения расчетов по пространственным переменным ${{x}_{1}}$ и ${{x}_{2}}$ вводилась равномерная сетка $\Delta {{x}_{1}} = \Delta {{x}_{2}}$ = b/50, а шаг по времени $\Delta $ выбирался равным 0.25 мкс. Рассматривались относительно тонкие ($b = 50$ см, $h{\text{/}}b$ = 1/50) и относительно толстые ($b = 10$ см, $h{\text{/}}b$ = 1/10) КМ-пластины, для которых
(6.3)
$\begin{gathered} \Delta {{x}_{1}}{\text{/}}\Delta = 40\;{\text{км/с,}}\quad 2h{\text{/}}\Delta = 80\;{\text{км/с,}}\quad {{\left( {\Delta {{x}_{1}}} \right)}^{2}}{\text{/}}\Delta = 400\;{{{\text{м}}}^{{\text{2}}}}{\text{/с}}\quad {\text{при}}\quad b = 50\;{\text{cм}} \\ \Delta {{x}_{1}}{\text{/}}\Delta = 8\;{\text{км/с,}}\quad 2h{\text{/}}\Delta = 80\;{\text{км/с,}}\quad {{\left( {\Delta {{x}_{1}}} \right)}^{2}}{\text{/}}\Delta = 16\;{{{\text{м}}}^{{\text{2}}}}{\text{/с}}\quad {\text{при}}\quad b = 10\;{\text{см}} \\ \end{gathered} $Для обеспечения устойчивости явной схемы (5.3) необходимо выполнение условий Куранта–Фридрихса–Леви: $\Delta {{x}_{1}}{\text{/}}\Delta \geqslant \bar {c}$ и $2h{\text{/}}\Delta \geqslant \bar {c}$ [7], а для устойчивости явной схемы (5.5) необходимо, чтобы ${{\left( {\Delta {{x}_{1}}} \right)}^{2}}{\text{/}}\Delta \geqslant \bar {a}$ [28]. Согласно числовым данным, полученным в (6.3), указанные отношения существенно превосходят соответствующие значения $\bar {c}$ и $\bar {a}$ для материалов композиций, представленные в табл. 1. Следовательно, аналогичные необходимые условия устойчивости явной схемы (5.3)–(5.5) будут с запасом выполняться и для рассматриваемых композиций. Отметим, что схема (5.5) имеет первый порядок точности по $\Delta $ [28], однако малый шаг по времени ($\Delta = 0.25$ мкс), гарантирующий устойчивость всей численной схемы в целом (см. уравнения (5.3) и (5.5)), обеспечивает вполне приемлемую для практических расчетов точность.
Структуры армирования однородны, т.е. ${{\omega }_{k}} = {\text{const}}$, ${{\theta }_{k}} = {\text{const}}$, ${{\varphi }_{k}} = {\text{const}}$, $1 \leqslant k \leqslant N$ (см. рис. 1). Рассматриваются два типа структур: 1) плоское ортогональное армирование (рис. 2а), когда два ($N = 2$) семейства волокон уложены по направлениям $O{{x}_{1}}$ и $O{{x}_{2}}$ с плотностями армирования ${{\omega }_{1}} = 0.1$ и ${{\omega }_{2}} = 0.3$; 2) пространственное 4D-армирование (рис. 2б), когда два первых семейства волокон укладываются по направлениям $O{{x}_{1}}$ и $O{{x}_{2}}$, а третье и четвертое семейства – наклонно по направлениям, определяемым углами (см. рис. 1): ${{\theta }_{3}} = \pi {\text{/}}4$, ${{\theta }_{4}} = 3\pi {\text{/}}4$, ${{\varphi }_{3}} = {{\varphi }_{4}} = \pi {\text{/2}}$ (на рис. 2б угол $\theta = \pi {\text{/}}4$). Во второй структуре плотности армирования имеют значения: ${{\omega }_{1}} = 0.1$, ${{\omega }_{2}} = 0.2$, ${{\omega }_{3}} = {{\omega }_{4}} = 0.05$. В обоих случаях армирования общий расход арматуры одинаков.
Для выяснения вопроса о выборе значения M в разложении (4.9), обеспечивающем приемлемую точность расчетов температуры $\Theta $, рассмотрим зависимости от M максимальных значений ${{\Theta }_{{{\text{max}}}}}\left( M \right)$ = $\mathop {\max }\limits_{t,{\mathbf{r}}} \Theta \left( {t,{\mathbf{r}};M} \right)$ ($\left| {{{x}_{1}}} \right| \leqslant a$, $\left| {{{x}_{2}}} \right| \leqslant b$, $\left| {{{x}_{3}}} \right| \leqslant h$; расчеты проводились на интервале времени $0 \leqslant t \leqslant 0.1$ с). На рис. 3 изображены указанные зависимости для относительно тонких ($b = 50$ см) стеклопластиковых пластин (рис. 3а), рассчитанные при ${{p}_{{\max }}} = 4$ МПа (см. соотношения (6.1)), для относительно толстых ($b = 10$ см) стеклопластиковых конструкций при ${{p}_{{\max }}} = 7$ МПа (рис. 3б) и для относительно тонких металлокомпозитных пластин при ${{p}_{{\max }}} = 10$ МПа (рис. 3в). При указанных нагрузках ${{p}_{{\max }}}$ во всех КМ-конструкциях возникают пластические деформации. На рис. 3 значению $M = 0$ условно соответствует случай, когда тепловое влияние вообще не учитывается, поэтому принято, что ${{\Theta }_{{{\text{max}}}}}\left( 0 \right)$ = ${{\Theta }^{0}}$ = 20°С. Номера кривых на рис. 3 совпадают с номерами структур армирования; кривые, номера которых помечены штрихом, рассчитаны без учета влияния скорости деформирования на пластические свойства материалов композиции – термоупругопластический расчет (при этом использовались данные из табл. 1, соответствующие случаю квазистатического нагружения: $\dot {\varepsilon } = 5 \times 1{{{\text{0}}}^{{ - 4}}}$ с–1). Кривые 2 и 2' на рис. 3б визуально почти не различаются.
Рис. 3.
Зависимость максимального значения температуры от порядка аппроксимирующего полинома в относительно тонкой (а) и толстой (б) стеклопластиковых пластинах и в относительно тонкой металлокомпозитной конструкции (в).
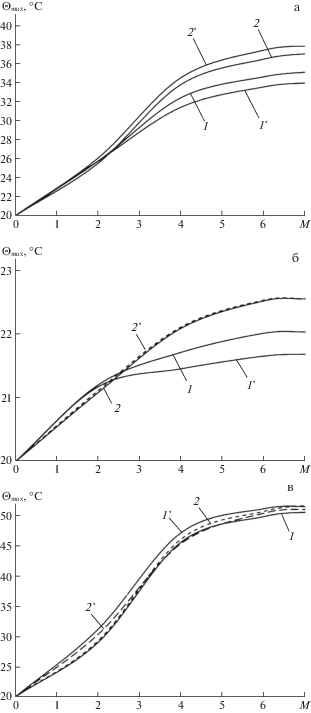
Поведение всех кривых на рис. 3 свидетельствует о том, что при переходе от значения $M = 6$ к $M = 7$ приращение величины ${{\Theta }_{{{\text{max}}}}}$ становится практически пренебрежимо малым. При значениях $M \geqslant 8$ линеаризованная система уравнений (4.11) и (4.18) (при учете выражений (4.19)), из которой в каждый момент времени определяются коэффициенты разложения температуры (4.9), является плохо обусловленной, в результате чего зависимость ${{\Theta }_{{{\text{max}}}}}\left( M \right)$ становится расходящейся. Поэтому кривые на рис. 3 при $M \geqslant 8$ не изображены.
Традиционно принято считать, что для проведения практических расчетов с приемлемой точностью в тонкостенных конструкциях вполне достаточно использовать линейное ($M = 1$) или квадратичное ($M = 2$) распределение температуры по их толщине [5, 14]. Сравнение же ординат точек на кривых рис. 3 при $M = 1$ или $M = 2$ и при $M = 7$ показывает, что в случаях неупругого динамического изгибного деформирования КМ-пластин линейное и квадратичное распределение температуры в них приводит к существенному занижению максимальных расчетных значений температуры. Для получения же адекватных расчетов температурных полей в таких случаях деформирования тонкостенных КМ-конструкций температуру в них по толщине следует аппроксимировать полиномами 6-го или 7-го порядков (см. разложение (4.9) при $M = 6$ или $M = 7$).
Для получения более наглядного представления о различии температурных полей, рассчитанных в рассматриваемых КМ-пластинах при $M = 2$ и $M = 7$, на рис. 4 изображены осцилляции наибольших значений температуры ${{\Theta }_{{\text{m}}}}\left( {t;M} \right)$ = $\mathop {\max }\limits_{\mathbf{r}} \Theta \left( {t,{\mathbf{r}};M} \right)$ в зависимости от времени t. Кривые на рис. 4а–в рассчитаны для тех же КМ-конструкций, что и на рис. 3а–в соответственно, но на рис. 4, чтобы его не загромождать, представлены зависимости ${{\Theta }_{{\text{m}}}}\left( {t;M} \right)$ только для пластин с 2D-структурами армирования. Все кривые на рис. 4 рассчитаны по термоупруговязкопластической теории; сплошные кривые 1 соответствуют случаю $M = 2$, а штриховые линии 2 – $M = 7$. Сравнение кривых 1 и 2 на рис. 4 свидетельствует о том, что расчет зависимости ${{\Theta }_{{\text{m}}}}\left( {t;M} \right)$ в простейшем случае при $M = 2$ лишь качественно (причем весьма приближенно), но не количественно, позволяет определить осцилляции максимальных значений температуры в рассматриваемых КМ-пластинах.
Рис. 4.
Зависимости от времени наибольших значений температуры в относительно тонкой (а) и толстой (б) стеклопластиковых пластинах и в относительно тонкой металлокомпозитной конструкции (в), рассчитанные с использованием разных аппроксимаций температурного поля в поперечном направлении.
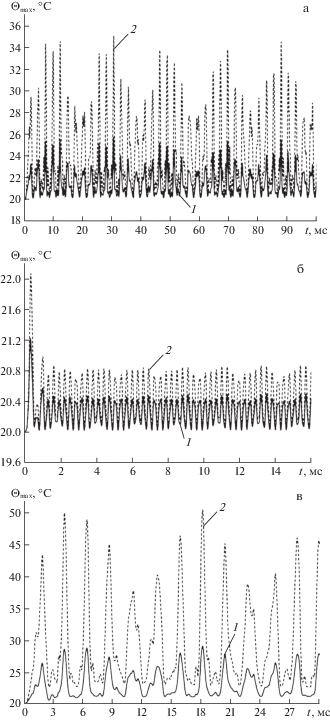
Поведение кривых на рис. 4а и 4в демонстрирует, что максимальные значения температуры в относительно тонких КМ-конструкциях достигаются в моменты времени (на рис. 4а – при $t \approx 31$ мс, а на рис. 4в – при $t \approx 18$ мс), которые много больше времени действия внешней интенсивной кратковременной нагрузки, т.е. значительно больше ${{t}_{{\min }}} = 2$ мс (см. выражения (6.1)). Отметим, что в некоторых расчетах, выполненных при $M = 2$ и $M = 7$, наблюдалось существенное различие моментов времени, в которые достигается наибольшее значение температуры ${{\Theta }_{{{\text{max}}}}}$. Следовательно, использование простейшей аппроксимации температуры по толщине КМ-пластины (при $M = 2$) может приводить к неверному определению момента времени, в который температура конструкции достигает максимального значения.
Поведение же кривых на рис. 4б показывает, что в случае относительно толстых стеклопластиковых пластин зависимости ${{\Theta }_{{\text{m}}}}\left( {t;M} \right)$ при разных M достигают своих наибольших значений на первой осцилляции, т.е. в моменты времени, близкие к ${{t}_{{\min }}} = 2$ мс. Качественно аналогичное поведение зависимостей ${{\Theta }_{{\text{m}}}}\left( {t;M} \right)$ при $M = 2$ и $M = 7$ наблюдается и в случае относительно толстых металлокомпозитных пластин (при ${{p}_{{\max }}} = 50$ МПа), поэтому соответствующие кривые на рис. 4 не приведены.
На рис. 5 изображены осцилляции максимальных значений интенсивности деформаций связующего материала $\varepsilon _{*}^{{(0)}}$ рассматриваемых композиций ($\varepsilon _{{\text{m}}}^{{(0)}}\left( t \right)$ = $\mathop {\max }\limits_{\mathbf{r}} \varepsilon _{*}^{{(0)}}\left( {t,{\mathbf{r}}} \right)$, $\left| {{{x}_{1}}} \right| \leqslant a$, $\left| {{{x}_{2}}} \right| \leqslant b$, $\left| {{{x}_{3}}} \right| \leqslant h$). Кривые на рис. 5а–в получены для тех же КМ-пластин, что и на рис. 3а–в соответственно. Номера кривых на рис. 5 имеют тот же смысл, что и на рис. 3. Все кривые на рис. 5 рассчитаны при значении $M = 7$ (см. разложение (4.9)).
Рис. 5.
Зависимость от времени максимального значения интенсивности деформаций связующего в относительно тонкой (а) и толстой (б) стеклопластиковых пластинах и в относительно тонкой металлокомпозитной конструкции при 2D-структуре (в) и при 4D-структуре армирования (г).
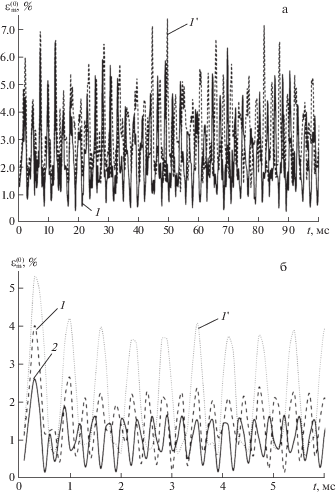
Рис. 5.
Окончание
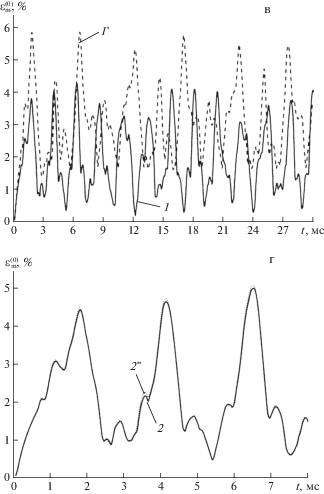
В работе [22] рассматривались только относительно толстые КМ-пластины. На рис. 5а, 5в и 5г представлены результаты расчетов относительно тонких стеклопластиковых и металлокомпозитных пластин соответственно, а на рис. 5б – относительно толстых стеклопластиковых конструкций. Сравнение кривых 1 и 1' на рис. 5а–в показывает, что расчет по термоупругопластической теории (кривые 1') приводит к существенному завышению наибольших значений $\varepsilon _{{\text{m}}}^{{(0)}}$ как в относительно тонких, так и в относительно толстых КМ-пластинах по сравнению с расчетами, выполненными по термоупруговязкопластической теории (кривые 1), даже в случаях, когда пластические свойства компонентов композиции весьма слабо зависят от скорости деформирования, как это имеет место в случае стеклопластиковой композиции (см. табл. 1).
Несмотря на то, что кривые 1 и 1' на рис. 5а–в существенно различаются, аналогичные кривые 1 и 1' на рис. 3а–в различаются незначительно. Следовательно, неучет чувствительности пластических свойств материалов композиции к скорости деформирования не оказывает настолько существенного влияния на температурное поле в КМ-конструкции, как на деформированное состояние компонентов композиции в них.
Сравнение кривых 1 и 2 на рис. 5б свидетельствует о том, что в относительно толстой стеклопластиковой пластине замена традиционной 2D-структуры армирования (см. рис. 2а) на пространственную структуру 4D-армирования (см. рис. 2б) позволяет существенно уменьшить интенсивность деформаций связующего материала, но при этом, согласно поведению кривых 1 и 2 на рис. 3б, увеличивается максимальное значение температуры ${{\Theta }_{{\max }}}$ в КМ-пластине. Однако это увеличение значения ${{\Theta }_{{\max }}}$ невелико и составляет примерно 0.5°С.
Аналогичная замена структур армирования в относительно тонкой стеклопластиковой пластине также приводит к уменьшению наибольшего значения интенсивности деформаций связующего материала в ней. Однако это уменьшение практически пренебрежимо мало, поэтому соответствующая кривая 2 на рис. 5а не изображена, чтобы его не загромождать. В случаях металлокомпозитных пластин как относительно тонких, так и относительно толстых указанная замена структур армирования является неэффективной, так как приводит к увеличению интенсивности деформаций связующего материала (ср. поведение кривых 1 и 2 на рис. 5в и 5г).
Поведение кривых на рис. 4а–в и 5а–в качественно схоже. Так, на рис. 5б наибольшее значение зависимости $\varepsilon _{{\text{m}}}^{{(0)}}\left( t \right)$ достигается на первой осцилляции при $t \approx 0.4$ мс; аналогично и на рис. 4б наибольшее значение зависимости ${{\Theta }_{{\text{m}}}}\left( t \right)$ достигается на первой осцилляции в тот же момент времени, т.е. примерно тогда, когда внешняя нагрузка достигает своего наибольшего значения (см. формулу (6.1)). Наибольшие же значения величин ${{\Theta }_{{\text{m}}}}$ и $\varepsilon _{{\text{m}}}^{{(0)}}$ на рис. 4а, 4в, 5а и 5в достигаются в моменты времени, существенно превосходящие значение ${{t}_{{\min }}}$, т.е. после прекращения действия внешней нагрузки. При этом моменты времени, в которые достигаются наибольшие значения величин ${{\Theta }_{{\text{m}}}}$ и $\varepsilon _{{\text{m}}}^{{(0)}}$ не совпадают.
Тот факт, что при нелинейном динамическом деформировании тонкостенных КМ-конструкций деформации могут достигать своих наибольших значений значительно позже времени прекращения действия кратковременной интенсивной нагрузки, был обнаружен еще в [12] для упругих оболочек.
Сравнение кривых с одинаковыми номера на рис. 5а и 5б показывает, что наибольшие значения интенсивности деформаций связующего материала в стеклопластиковых пластинах разной относительной толщины сопоставимы между собой. Однако сопоставление аналогичных кривых на рис. 3а и 3б свидетельствует о том, что относительно толстая конструкция (см. рис. 3б) нагревается существенно меньше, чем относительно тонкая (см. рис. 3а). Объясняется это тем, что в относительно толстой КМ-конструкции наиболее интенсивное деформирование материалов компонентов композиции происходит в узких зонах в окрестности жестко закрепленных кромок. При этом в указанных зонах доминируют деформации поперечных сдвигов. В относительно же тонких пластинах наиболее интенсивно деформируется основная часть конструкции (удаленная от опорных кромок), в которой доминируют изгибные деформации. Поэтому в относительно тонких КМ-пластинах механическая энергия более активно диссипирует в тепловую энергию, чем в относительно толстых конструкциях даже при сопоставимых уровнях максимальных деформаций в их компонентах композиции.
Все обсуждаемые выше результаты были получены при учете термочувствительности компонентов композиции. Расчеты, проведенные без учета термочувствительности (при использовании значений характеристик компонентов композиции, приведенных в табл. 1 для температуры естественного состояния ${{\Theta }^{0}}$ = 20°С), показывают, что зависимости ${{\Theta }_{{\text{m}}}}\left( t \right)$ и $\varepsilon _{{\text{m}}}^{{(0)}}\left( t \right)$ при этом визуально не отличаются от кривых, изображенных на рис. 3, 4а–в и 5а–в. Объясняется это малым приращением температуры при динамическом деформировании КМ-пластин (всего на 2…30°С) под воздействием воздушной взрывной волны. Подчеркнем, что аналогичный (порядка 10°С) уровень нагрева образцов из однородных материалов наблюдается и в экспериментах по ударному нагружению [19].
В связи с малым уровнем нагрева рассматриваемых конструкций целесообразно сравнить полученные выше результаты с расчетами, выполненными по упруговязкопластической теории [22], т.е. при полном неучете теплового воздействия. Было установлено, что для рассматриваемых КМ-пластин результаты таких расчетов по прогибам (соответствующие зависимости не изображены) визуально не отличаются от расчетов, выполненных по термоупруговязкопластической теории. Однако для зависимостей $\varepsilon _{{\text{m}}}^{{(0)}}\left( t \right)$ наблюдается некоторое различие. Так, кривая 2 на рис. 5г получена при учете теплового воздействия, а кривая 2'' – без учета этого воздействия. Видно, что в этом случае уже в окрестности начального момента времени проявляется заметное различие в поведении кривых 2 и 2'', однако ординаты точек глобальных максимумов на этих кривых, которые достигаются в момент времени $t = 6.5$ мс, различаются всего на 1.4%. Аналогичное пренебрежимо малое различие зависимостей $\varepsilon _{{\text{m}}}^{{(0)}}\left( t \right)$, рассчитанных с учетом и без учета теплового воздействия, наблюдается во всех остальных рассмотренных выше случаях, причем с увеличением времени это различие становится все более заметным, но по-прежнему остается пренебрежимо малым.
На рис. 5 не приведены зависимости $\varepsilon _{{\text{m}}}^{{(k)}}\left( t \right)$ для арматуры k-го семейства ($1 \leqslant k \leqslant N$), потому что они качественно аналогичны кривым, изображенным на рис. 5 для связующего материала, но имеют меньшие значения по оси ординат. Например, для арматуры второго семейства ($k = 2$), которая испытывает наибольшие деформации, максимальные значения $\varepsilon _{{\text{m}}}^{{(2)}}$ примерно в 1.5 раза меньше, чем для зависимостей, приведенных на рис. 5.
Таким образом, полученные результаты свидетельствуют о том, что расчет неупругого динамического поведения изгибаемых КМ-пластин при нагружении их воздушной взрывной волной можно проводить без учета влияния тепловых полей, которые возникают за счет механической диссипации энергии в таких КМ-конструкциях.
Заключение. Разработанная структурная модель, ориентированная на использование явных пошаговых схем, позволяет численно-аналитически моделировать поведение термоупруговязкопластически деформируемых КМ волокнистого строения в рамках теории течения с изотропным упрочнением, когда функция нагружения чувствительна к изменению температуры и скорости деформирования материала композиции. Полученные условия термоупругого деформирования, разгрузки, нейтрального и активного нагружения компонентов композиции с учетом изменения температуры и скорости деформирования позволяют проводить расчеты в условиях переменного во времени термосилового нагружения КМ.
Разработанная модель термоупруговязкопластического деформирования гибких пластин с произвольными структурами армирования позволяет учитывать возможное слабое сопротивление таких КМ-конструкций поперечным сдвигам и связанность теплофизической и механической составляющих задачи. Разработанный численный метод позволяет по явной схеме интегрировать сформулированную связанную начально-краевую задачу. Установлено, что величину шага по времени следует выбирать из необходимого условия устойчивости Куранта–Фридрихса–Леви для волнового уравнения, а не из необходимого условия устойчивости явной численной схемы для уравнения теплового баланса.
Установлено, что для адекватного расчета температурных полей в динамически изгибаемых неупругих КМ-пластинах температуру в поперечном направлении следует аппроксимировать полиномами 6–7-го порядков.
Проведенные расчеты показали, что при поперечном нагружении КМ-пластин воздушной взрывной волной стеклопластиковые конструкции нагреваются на 2…18°С, а металлокомпозитные – на 30°С, причем относительно тонкие пластины нагреваются сильней, чем относительно толстые (даже при сопоставимых величинах наибольших значений интенсивностей деформаций компонентов композиции). Замена плоской ортогональной структуры армирования (рис. 2а) на пространственную структуру армирования (рис. 2б) при сохранении общего расхода волокон в относительно толстой стеклопластиковой пластине позволяет уменьшить интенсивность деформаций связующего материала на 35.1%, однако максимальное значение температуры при такой замене возрастает, хотя и незначительно (от 2 до 2.5°С). Аналогичная замена структур армирования в относительно тонких стеклопластиковых, а также относительно тонких и относительно толстых металлокомпозитных пластинах является неэффективной, так как приводит к увеличению интенсивности деформаций связующего материала и к увеличению приращения температуры в них.
Для проведения адекватных динамических расчетов неупруго деформируемых изгибаемых КМ-пластин под действием нагрузки, порожденной воздушной взрывной волной, можно вполне обоснованно не учитывать влияние теплового воздействия, если отсутствуют дополнительные источники нагрева или охлаждения немеханического происхождения. Однако при этом нельзя пренебрегать чувствительностью пластических свойств материалов композиции к скорости их деформирования как в относительно толстых [22], так и в относительно тонких КМ-конструкциях.
Работа выполнена в рамках государственного задания (№ госрегистрации 121030900260-6).
Список литературы
Mouritz A.P., Gellert E., Burchill P., Challis K. Review of advanced composite structures for naval ships and submarines // Compos. Struct. 2001. V. 53. № 1. P. 21–42.
Bannister M. Challenger for composites into the next millennium – a reinforcement perspective // Composites. 2001. Part A32. P. 901–910.
Soutis C. Fibre reinforced composites in aircraft construction // Progr. in Aerospace Sci. 2005. V. 41. № 2. P. 143–151.
Gill S.K., Gupta M., Satsangi P. Prediction of cutting forces in machining of unidirectional glass-fiber-reinforced plastic composites // Frontiers Mech. Eng. 2013. V. 8. № 2. P. 187–200.
Соломонов Ю.С., Георгиевский В.П., Недбай А.Я., Андрюшин В.А. Прикладные задачи механики композитных цилиндрических оболочек. М.: Физматлит, 2014. 408 с.
Димитриенко Ю.И. Механика композитных конструкций при высоких температурах. М.: Физматлит, 2019. 448 с.
Абросимов Н.А., Баженов В.Г. Нелинейные задачи динамики композитных конструкций. Нижний Новгород: Изд-во ННГУ, 2002. 400 с.
Qatu M.S., Sullivan R.W., Wang W. Recent research advances on the dynamic analysis of composite shells: 2000–2009 // Compos. Struct. 2010. V. 93. P. 14–31.
Kazanci Z. Dynamic response of composite sandwich plates subjected to time-dependent pressure pulses // Int. J. Non-Lin. Mech. 2011. V. 46. P. 807–817.
Morinière F.D., Alderliesten R.C., Benedictus R. Modelling of impact damage and dynamics in fibre-metal laminates. A review // Int. J. Impact Eng. 2014. V. 67. P. 27–38.
Mao-hong Yu. Advances in strength theories for materials under complex stress state in the 20th century // ASME. Appl. Mech. Rev. 2002. V. 55. № 3. P. 169–200.
Богданович А.Е. Нелинейные задачи динамики цилиндрических композитных оболочек. Рига: Зинатне, 1987. 295 с.
Reddy J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis. New York: CRC Press, 2004. 831 p.
Андреев А. Упругость и термоупругость слоистых композитных оболочек. Математическая модель и некоторые аспекты численного анализа. Saarbrucken (Deutschland): Palmarium Acad. Publ., 2013. 93 с.
Амбарцумян С.А. Теория анизотропных пластин. Прочность, устойчивость и колебания. М.: Наука, 1987. 360 с.
Пикуль В.В. Механика оболочек. Владивосток: Дальнаука, 2009. 536 с.
Янковский А.П. Упругопластическое деформирование гибких пластин с пространственными структурами армирования // ПМТФ. 2018. Т. 59. № 6. С. 112–122.
Безухов Н.И., Бажанов В.Л., Гольденблат И.И., Николаенко Н.А., Синюков А.М. Расчеты на прочность, устойчивость и колебания в условиях высоких температур / Под ред. Гольденблата И.И. М.: Машиностроение, 1965. 567 с.
Белл Дж. Экспериментальные основы механики деформируемых твердых тел. Ч. II. Конечные деформации. М.: Наука, 1984. 432 с.
Коларов Д., Балтов А., Бончева Н. Механика пластических сред, М.: Мир, 1979. 302 с.
Бондарь В.С. Неупругость. Варианты теории. М.: Физматлит, 2004. 144 с.
Янковский А.П. Моделирование упругопластического изгиба пространственно-армированных пластин при учете чувствительности компонентов композиции к изменению скорости деформирования // ПММ. 2019. Т. 83. № 4. С. 660–686.
Reissner E. The effect of transverse-shear deformation on the bending of elastic plates // J. Appl. Mech. 1945. V. 12. № 2. P. 69–77.
Хажинский Г.М. Модели деформирования и разрушения металлов. М: Научный мир, 2011. 231 с.
Houlston R., DesRochers C.G. Nonlinear structural response of ship panels subjected to air blast loading // Comput.&Struct. 1987. V. 26. № 1/2. P. 1–15.
Композиционные материалы. Справочник / Под ред. Карпиноса Д.М. Киев: Наукова думка, 1985. 592 с.
Simmons J.A., Hauser F.E., Dorn J.E. Mathematical theories of plastic deformation under impulsive loading // Univ. Calif. Publ. in Engng. 1962. № 2. P. 177–230.
Рихтмайер Р., Мортон К. Разностные методы решения краевых задач. М.: Мир, 1972. 418 с.
Деккер К., Вервер Я. Устойчивость методов Рунге–Кутты для жестких нелинейных дифференциальных уравнений. М.: Мир, 1988. 334 с.
Малмейстер А.К., Тамуж В.П., Тетерс Г.А. Сопротивление жестких полимерных материалов. Рига: Зинатне, 1972. 500 с.
Янковский А.П. Моделирование процессов теплопроводности в пространственно-армированных композитах с произвольной ориентацией волокон // Прикл. физика. 2011. № 3. С. 32–38.
Тарнопольский Ю.М., Жигун И.Г., Поляков В.А. Пространственно-армированные композиционные материалы: Справочник. М.: Машиностроение, 1987. 224 с.
Киселев С.П. Механика сплошных сред. Новосибирск: Изд-во НГТУ, 2017. 164 с.
Грешнов В.М. Физико-математическая теория больших необратимых деформаций металлов. М.: Физматлит, 2018. 232 с.
Кудинов А.А. Тепломассообмен. М.: ИНФРА-М, 2012. 375 с.
Васидзу К. Вариационные методы в теории упругости и пластичности. М.: Мир, 1987. 542 с.
Новицкий Л.А., Кожевников И.Г. Теплофизические свойства материалов при низких температурах. Справочник. М.: Машиностроение, 1975. 216 с.
Луканин В.Н., Шатров М.Г. и др. Теплотехника. М.: Высш. шк., 2003. 671 с.
Справочник по композитным материалам: В 2-х кн. Кн. 1 / Под. ред. Любина Дж. М.: Машиностроение, 1988. 448 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика