Прикладная математика и механика, 2022, T. 86, № 2, стр. 263-275
Напряженно-деформированное состояние подкрепленного трехслойной оболочкой тоннеля мелкого заложения при действии транспортных нагрузок
Л. А. Алексеева 1, *, В. Н. Украинец 2, **, С. Р. Гирнис 2, ***
1 Институт математики и математического моделирования
Алма-Ата, Казахстан
2 НАО “Торайгыров университет”
Павлодар, Казахстан
* E-mail: alexeeva@math.kz
** E-mail: ukrainets.v@teachers.tou.edu.kz
*** E-mail: girnis.s@teachers.tou.edu.kz
Поступила в редакцию 10.08.2021
После доработки 20.01.2022
Принята к публикации 25.01.2022
- EDN: CAOKFS
- DOI: 10.31857/S0032823522020023
Аннотация
Решена задача о действии движущейся с постоянной скоростью нагрузки на трехслойную круговую цилиндрическую оболочку в упругом полупространстве. Для описания движения полупространства и внутреннего слоя оболочки используются динамические уравнения теории упругости в потенциалах Ламе. Колебания внешних слоев оболочки описываются классическими уравнениями теории тонких оболочек. Решение получено для случая, когда скорость движения нагрузки меньше скорости волны Рэлея и ее критических скоростей. На основе аналитического решения задачи исследуется напряженно-деформированное состояние подкрепленного трехслойной сталебетонной обделкой тоннеля мелкого заложения при действии равномерно движущейся по его лотку симметричной или несимметричной нормальной нагрузки от внутритуннельного транспорта.
1. Введение. Одной из модельных задач, применяемых для исследования динамики тоннелей мелкого заложения под воздействием транспортной нагрузки (нагрузки от движущегося внутритуннельного транспорта), является задача о действии на расположенную в упругом полупространстве круговую цилиндрическую оболочку нагрузки, равномерно движущейся по внутренней поверхности оболочки вдоль ее образующей, параллельной свободной границе полупространства. В отличие от аналогичной задачи для упругого пространства, моделирующей тоннель глубокого заложения, данная задача является более сложной, так как возникает необходимость учитывать отражаемые границей полупространства волны. Поэтому количество публикаций, посвященных исследованию этой проблеме, немногочисленно и охватывает, в основном, последние годы, в частности [1–8]. В настоящей работе построена математическая модель динамики подкрепленного трехслойной обделкой тоннеля мелкого заложения под воздействием транспортной нагрузки. С использованием метода неполного разделения переменных и переразложения цилиндрических и плоских волн построено аналитическое решение задачи, на основе которого разработан алгоритм и программный комплекс на языке ФОРТРАН для расчета напряженно-деформированного состояния обделки тоннеля и породного массива с учетом скорости движения транспортной нагрузки, глубины заложения тоннеля и физико-механических свойств массива и материала оболочек. Рассмотрен дозвуковой случай, когда скорость движения меньше скоростей распространения упругих волн в массиве, в том числе релеевской для упругого полупространства. Приводятся и анализируются результаты численных экспериментов.
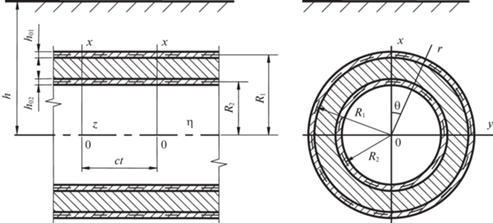
2. Постановка и аналитическое решение задачи. В качестве расчетной схемы подкрепленного трехслойной обделкой тоннеля мелкого заложения рассматривается бесконечно длинная круговая цилиндрическая трехслойная оболочка в линейно-упругом, однородном и изотропном полупространстве (массиве), отнесенному к неподвижным цилиндрической $r$, $\theta $, $z$ и декартовой $x$, $y$, $z$ системам координат, ось $z$ которых совпадает с осью оболочки и параллельна свободной от нагрузок горизонтальной границе полупространства (земной поверхности), ось $x$ – перпендикулярна к этой границе: $x \leqslant h$ (рис. 1). Внутренним слоем оболочки является толстостенная оболочка (заполнитель), а внешние слои (обшивка) представляют собой тонкостенные оболочки с радиусами срединных поверхностей ${{R}_{1}}$, ${{R}_{2}}$ и толщинами ${{h}_{{01}}}$, ${{h}_{{02}}}$. В силу малости толщин составляющих обшивку слоев допускается, что они контактируют с заполнителем и окружающим массивом вдоль своих срединных поверхностей. Контакт между слоями оболочки полагается жестким, а контакт между оболочкой и массивом полагается либо жестким, либо скользящим при двусторонней связи в радиальном направлении.
По внутренней поверхности оболочки в направлении ее оси $z$ с постоянной скоростью c движется нагрузка интенсивностью $P$, вид которой не меняется с течением времени (стационарная нагрузка). Скорость движения нагрузки принимается дозвуковой, т.е. меньше скоростей распространения волн сдвига в заполнителе и массиве (характерной для современных транспортных средств). Физико-механические свойства массива и заполнителя характеризуются соответственно следующими постоянными: ${{\nu }_{1}}$, ${{\mu }_{1}}$, ${{\rho }_{1}}$; ${{\nu }_{2}}$, ${{\mu }_{2}}$, ${{\rho }_{2}}$, где ${{\nu }_{k}}$ – коэффициент Пуассона, ${{\mu }_{k}}$ – модуль сдвига, ${{\rho }_{k}}$ – плотность ($k = 1,\;2$). В дальнейшем индекс $k = 1$ относится к массиву, а $k = 2$ – к заполнителю.
Поскольку рассматривается установившийся процесс, то картина деформаций стационарна по отношению к движущейся нагрузке. Поэтому можно перейти к связанной с нагрузкой подвижной декартовой ($x,y,\eta = z - ct$) или цилиндрической (r, θ, η = = $z - ct$) системе координат.
Для описания движения массива и заполнителя используются динамические уравнения теории упругости в подвижной системе координат [4]
(2.1)
$\left( {M_{{pk}}^{{ - 2}} - M_{{sk}}^{{ - 2}}} \right)\operatorname{grad} \operatorname{div} {{{\mathbf{u}}}_{k}} + M_{{sk}}^{{ - 2}}{{\nabla }^{2}}{{{\mathbf{u}}}_{k}} = {{{{\partial }^{2}}{{{\mathbf{u}}}_{k}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{{\mathbf{u}}}_{k}}} {\partial {{\eta }^{2}}}}} \right. \kern-0em} {\partial {{\eta }^{2}}}};\quad k = 1,\;2,$Колебания слоев обшивки описываются классическими уравнениями теории тонких оболочек в подвижной системе координат [2–4]
(2.2)
$\begin{gathered} \frac{{1 + {{\nu }_{{0k}}}}}{{2{{R}_{k}}}}\frac{{{{\partial }^{2}}{{u}_{{0\eta k}}}}}{{\partial \eta \partial \theta }} + \frac{{\left( {1 - {{\nu }_{{0k}}}} \right)}}{2}\left( {1 - \frac{{{{\rho }_{{0k}}}{{c}^{2}}}}{{{{\mu }_{{0k}}}}}} \right)\frac{{{{\partial }^{2}}{{u}_{{0\theta k}}}}}{{\partial {{\eta }^{2}}}} + \\ + \;\frac{1}{{R_{k}^{2}}}\frac{{{{\partial }^{2}}{{u}_{{0\theta k}}}}}{{\partial {{\theta }^{2}}}} + \frac{1}{{R_{k}^{2}}}\frac{{\partial {{u}_{{0rk}}}}}{{\partial \theta }} = \frac{{1 - {{\nu }_{{0k}}}}}{{2{{\mu }_{{0k}}}{{h}_{{0k}}}}}\left( {{{q}_{{\theta k}}} - {{q}_{{\theta {{R}_{k}}}}}} \right), \\ \end{gathered} $Здесь для наружного слоя обшивки $k = 1$, для внутреннего – $k = 2$; ${{\nu }_{{0k}}}$, ${{\mu }_{{0k}}}$, ${{\rho }_{{0k}}}$ – соответственно коэффициент Пуассона, модуль сдвига и плотность материалов слоев обшивки; ${{u}_{{0\eta k}}}$, ${{u}_{{0\theta k}}}$, ${{u}_{{0rk}}}$ – перемещения точек срединных поверхностей слоев обшивки; ${{q}_{{j{{R}_{2}}}}} = {{\left. {{{\sigma }_{{rj2}}}} \right|}_{{r = {{R}_{2}}}}}$, ${{q}_{{j1}}} = {{\left. {{{\sigma }_{{rj2}}}} \right|}_{{r = {{R}_{1}}}}}$, ${{q}_{{j{{R}_{1}}}}} = {{\left. {{{\sigma }_{{rj1}}}} \right|}_{{r = {{R}_{1}}}}}$ – составляющие реакции заполнителя и массива, $j = \eta ,\theta ,r$ (при скользящем контакте оболочки с массивом ${{q}_{{\eta {{R}_{1}}}}} = {{q}_{{\theta {{R}_{1}}}}} = 0$), ${{\sigma }_{{rj1}}}$, ${{\sigma }_{{rj2}}}$ – компоненты тензоров напряжений в массиве и заполнителе, ${{q}_{{j2}}} = {{P}_{j}}\left( {\theta ,\eta } \right)$, ${{P}_{j}}\left( {\theta ,\eta } \right)$ – составляющие интенсивности подвижной нагрузки $P\left( {\theta ,\eta } \right)$, $j = \eta ,\theta ,r$.
Поскольку граница полупространства свободна от нагрузок, то при $x = h$
При различных контактных условиях оболочки с массивом граничные условия имеют вид:
– для скользящего контакта оболочки с массивом
(2.4)
$\begin{gathered} {\text{при}}\quad r = {{R}_{1}}\quad {{u}_{{r1}}} = {{u}_{{r2}}},\quad {{u}_{{j2}}} = {{u}_{{0j1}}},\quad {{\sigma }_{{r\eta 1}}} = 0,\quad {{\sigma }_{{r\theta 1}}} = 0 \\ {\text{при}}\quad r = {{R}_{2}}\quad {{u}_{{j2}}} = {{u}_{{0j2}}};\quad j = r,\theta ,\eta \\ \end{gathered} $– для жесткого контакта оболочки с массивом
(2.5)
$\begin{gathered} {\text{при}}\quad r = {{R}_{1}}\quad {{u}_{{j1}}} = {{u}_{{j2}}},\quad {{u}_{{j1}}} = {{u}_{{0j1}}}\,\,\,\, \\ {\text{при}}\quad r = {{R}_{2}}\quad {{u}_{{j2}}} = {{u}_{{0j2}}},\quad j = r,\theta ,\eta , \\ \end{gathered} $Векторы ${{{\mathbf{u}}}_{k}}$ можно выразить через потенциалы Ламе [1, 4]
(2.6)
${{{\mathbf{u}}}_{k}} = grad{{\varphi }_{{1k}}} + \operatorname{rot} \left( {{{\varphi }_{{2k}}}{{{\mathbf{e}}}_{\eta }}} \right) + \operatorname{rot} \operatorname{rot} \left( {{{\varphi }_{{3k}}}{{{\mathbf{e}}}_{\eta }}} \right);\quad k = 1,\;2,$(2.7)
${{\nabla }^{2}}{{\varphi }_{{jk}}} = M_{{jk}}^{2}{{{{\partial }^{2}}{{\varphi }_{{jk}}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}{{\varphi }_{{jk}}}} {\partial {{\eta }^{2}}}}} \right. \kern-0em} {\partial {{\eta }^{2}}}};\quad j = 1,\;2,\;3,\quad k = 1,\;2$Здесь ${{{\mathbf{e}}}_{\eta }}$ – орт оси $\eta $, ${{M}_{{1k}}} = {{M}_{{pk}}}$, ${{M}_{{2k}}} = {{M}_{{3k}}} = {{M}_{{sk}}}$.
Через эти же потенциалы, используя (2.6) и закон Гука, можно выразить компоненты тензоров напряжений $\sigma _{{lmk}}^{{}}$ в массиве ($k = 1$) и заполнителе ($k = 2$) в цилиндрической $\left( {l,m = r,\theta ,\eta } \right)$ системе координат, а также $\sigma _{{lm1}}^{{}}$ в декартовой ($l,m = x,y,\eta $) системе координат.
Таким образом, для определения компонент напряженно-деформированного состояния (НДС) массива и заполнителя необходимо решить уравнения (2.7), используя граничные условия (2.3) и, в зависимости от условия контакта оболочки с массивом, (2.4) или (2.5).
Рассмотрим случай действия на оболочку синусоидальной по $\eta $ подвижной нагрузки с произвольной зависимостью от угловой координаты
(2.8)
$\begin{gathered} P\left( {\theta ,\eta } \right) = p\left( \theta \right){{e}^{{i\xi \eta }}},\quad p\left( \theta \right) = \sum\limits_{n = - \infty }^\infty {{{P}_{n}}{{e}^{{in\theta }}}} \\ {{P}_{j}}\left( {\theta ,\eta } \right) = {{p}_{j}}\left( \theta \right){{e}^{{i\xi \eta }}},\quad {{p}_{j}}\left( \theta \right) = \sum\limits_{n = - \infty }^\infty {{{P}_{{nj}}}{{e}^{{in\theta }}}} ;\quad j = r,\theta ,\eta , \\ \end{gathered} $В установившемся состоянии зависимость всех величин от $\eta $ имеет вид (2.8), поэтому
(2.9)
${{\phi }_{{jk}}}\left( {r,\theta ,\eta } \right) = {{\Phi }_{{jk}}}\left( {r,\theta } \right){{e}^{{i\xi \eta }}};\quad j = 1,\;2,\;3,\quad k = 1,\;2$(2.10)
${{u}_{{0jk}}}\left( {\theta ,\eta } \right) = \sum\limits_{n = - \infty }^\infty {{{u}_{{0njk}}}{{e}^{{in\theta }}}} {{e}^{{i\xi \eta }}};\quad j = r,\theta ,\eta ,\quad k = 1,2$Подставляя (2.9) в (2.7), получим
(2.11)
$\nabla _{2}^{2}{{\Phi }_{{jk}}} - m_{{jk}}^{2}{{\xi }^{2}}{{\Phi }_{{jk}}} = 0;\quad j = 1,2,3,\quad k = 1,2,$Используя (2.9) можно получить выражения для перемещений $u_{{lk}}^{*}$ и напряжений $\sigma _{{lmk}}^{*}$ ($l,m = r,\theta ,\eta $) в массиве ($k = 1$) и заполнителе ($k = 2$), а также $u_{{l1}}^{*}$, $\sigma _{{lm1}}^{*}$ ($l,m = x,y$, η) в массиве от синусоидальной нагрузки как функции от ${{\Phi }_{{jk}}}$ (знак * означает, что данные компоненты найдены при действии на оболочку синусоидальной подвижной нагрузки).
При дозвуковой скорости движения нагрузки ${{M}_{{sk}}} < 1$, $\;{{m}_{{sk}}} > 0$, $k = 1,\;2$, и решения уравнений (2.11) можно представить в виде [3, 4]
(2.12)
${{\Phi }_{{jk}}} = \Phi _{{jk}}^{{(1)}} + \Phi _{{jk}}^{{(2)}};\quad j = 1,2,3,\quad k = 1,2,$для массива
(2.13)
$\Phi _{{j1}}^{{(1)}} = \sum\limits_{n = - \infty }^\infty {{{a}_{{nj}}}{{K}_{n}}\left( {{{k}_{{j1}}}r} \right){{e}^{{in\theta }}}} ,\quad \Phi _{{j1}}^{{(2)}} = \int\limits_{ - \infty }^\infty {{{g}_{j}}\left( {\xi ,\zeta } \right)\exp \left( {iy\zeta + (x - h)\sqrt {{{\zeta }^{2}} + k_{{j1}}^{2}} } \right)} d\zeta $для заполнителя
(2.14)
$\Phi _{{j2}}^{{(1)}} = \sum\limits_{n = - \infty }^\infty {{{a}_{{nj + 3}}}{{K}_{n}}\left( {{{k}_{{j2}}}r} \right){{e}^{{in\theta }}}} ,\quad \Phi _{{j2}}^{{(2)}} = \sum\limits_{n = - \infty }^\infty {{{a}_{{nj + 6}}}{{I}_{n}}({{k}_{{j2}}}r)} {{e}^{{in\theta }}}$Здесь ${{I}_{n}}({{k}_{j}}r)$, ${{K}_{n}}({{k}_{j}}r)$ – соответственно модифицированные функции Бесселя и функции Макдональда, ${{k}_{{j1}}} = \left| {{{m}_{{j1}}}\xi } \right|$, ${{k}_{{j2}}} = \left| {{{m}_{{j2}}}\xi } \right|$; ${{g}_{j}}\left( {\xi ,\zeta } \right)$, ${{a}_{{n1}}}, \ldots ,{{a}_{{n9}}}$ – неизвестные функции и коэффициенты, подлежащие определению, $j = 1,2,3$.
Как показано в [1, 2, 4], представление потенциалов для полупространства в форме (2.12) приводит к их следующим выражениям в декартовой системе координат:
(2.15)
${{\Phi }_{{j1}}} = \int\limits_{ - \infty }^\infty {\left[ {\frac{{{{e}^{{ - x{{f}_{j}}}}}}}{{2{{f}_{j}}}}\sum\limits_{n = - \infty }^\infty {{{a}_{{nj}}}{{\Phi }_{{nj}}}} + {{g}_{j}}(\xi ,\zeta ){{e}^{{(x - h){{f}_{j}}}}}} \right]} {{e}^{{iy\zeta }}}d\zeta ,$Воспользуемся переписанными для $\sigma _{{xx1}}^{*}$, $\sigma _{{xy1}}^{*}$, $\sigma _{{x\eta 1}}^{*}$ граничными условиями (2.3), с учетом (2.15). Выделяя коэффициенты при ${{e}^{{iy\zeta }}}$ и приравнивая, в силу произвольности y, их нулю, получим систему трех уравнений, из которой выражаем функции ${{g}_{j}}\left( {\xi ,\zeta } \right)$ через неизвестные коэффициенты ${{a}_{{n1}}}$, ${{a}_{{n2}}}$, ${{a}_{{n3}}}$:
(2.16)
${{g}_{j}}(\xi ,\zeta ) = \frac{1}{{\Delta {\text{*}}}}\sum\limits_{l = 1}^3 {\Delta _{{jl}}^{*}{{e}^{{ - h{{f}_{l}}}}}\sum\limits_{n = - \infty }^\infty {{{a}_{{nl}}}{{\Phi }_{{nl}}}} } $Вид определителя $\Delta {\text{*}}$ и алгебраических дополнений $\Delta _{{jl}}^{*}$ совпадает с аналогичными определителями для неподкрепленной полости в упругом полупространстве и определен в [2, 4]. В частности, здесь $\Delta {\text{*}}$ – это определитель Рэлея, который в данном случае имеет вид
Ограничимся случаем $c < {{c}_{R}}$. Тогда все подынтегральные функции в (2.15) непрерывны и экспоненциально стремятся к нулю на бесконечности. С учетом (2.16), потенциалы (2.15) имеют вид
(2.17)
${{\Phi }_{{j1}}} = \int\limits_{ - \infty }^\infty {\left[ {\frac{{{{e}^{{ - x{{f}_{j}}}}}}}{{2{{f}_{j}}}}\sum\limits_{n = - \infty }^\infty {{{a}_{{nj}}}{{\Phi }_{{nj}}}} + {{e}^{{(x - h){{f}_{j}}}}}\sum\limits_{l = 1}^3 {\frac{{\Delta _{{jl}}^{*}}}{{\Delta {\text{*}}}}{{e}^{{ - h{{f}_{l}}}}}\sum\limits_{n = - \infty }^\infty {{{a}_{{nl}}}{{\Phi }_{{nl}}}} } } \right]} {{e}^{{iy\zeta }}}d\zeta $Следует отметить, что рэлеевская скорость ${{c}_{R}}$ несколько ниже скорости волн сдвига в массиве.
Используя известное при $x < h$ соотношение [1, 2]
Подставляя в последнее выражение из (2.16) ${{g}_{j}}\left( {\xi ,\zeta } \right)$, для $c < {{c}_{R}}$ получим
(2.18)
${{\Phi }_{{j1}}} = \sum\limits_{n = - \infty }^\infty {\left( {{{a}_{{nj}}}{{K}_{n}}({{k}_{{j1}}}r) + {{b}_{{nj}}}{{I}_{n}}({{k}_{{j1}}}r)} \right)} {{e}^{{in\theta }}},$Подставляя (2.18), при $k = 1$ и (2.12), при $k = 2$ в выражения для $u_{{lk}}^{*}$, $\sigma _{{lmk}}^{*}$ ($l,m = r,\theta ,\eta $), получим новые выражения для компонент НДС массива и заполнителя в цилиндрических координатах при $c < {{c}_{R}}$, где неизвестными будут только коэффициенты ${{a}_{{n1}}}, \ldots ,{{a}_{{n9}}}$.
Подставляя (2.10) в (2.2) и разрешая полученную для n-го члена разложения систему уравнений относительно $u_{{0n\eta k}}^{{}}$, $u_{{0n\theta k}}^{{}}$, $u_{{0nrk}}^{{}}$ можно найти их выражения.
Для определения коэффициентов ${{a}_{{n1}}}, \ldots ,{{a}_{{n9}}}$ воспользуемся, в зависимости от условия сопряжения оболочки с массивом, переписанными для $u_{{lk}}^{*}$ ($l = r,\theta ,\eta $) и $\sigma _{{r\eta 1}}^{*}$, $\sigma _{{r\theta 1}}^{*}$ граничными условиями (2.4) или (2.5). Подставляя в граничные условия соответствующие выражения и приравнивая коэффициенты рядов при ${{e}^{{in\theta }}}$, получим бесконечную систему ($n = 0, \pm 1, \pm 2, \ldots $) линейных алгебраических уравнений, для решения которой можно использовать метод редукции или более удобный для решения поставленной задачи метод последовательных отражений [2], позволяющий при каждом последовательном отражении решать систему линейных уравнений блочно-диагонального вида с матрицами размером 9 × 9 и определителями ${{\Delta }_{n}}\left( {\xi ,c} \right)$ вдоль главной диагонали.
Зная решение задачи для синусоидальной нагрузки, реакцию оболочки и окружающей ее среды на движущуюся с постоянной скоростью апериодическую (локальную) нагрузку вида $P\left( {\theta ,\xi } \right) = p\left( \theta \right)p\left( \eta \right)$ (характерного для транспортных средств) можно найти при помощи суперпозиции, используя представление нагрузки и компонент НДС массива и заполнителя в виде интегралов Фурье
Здесь $p{\kern 1pt} *{\kern 1pt} \left( \xi \right) = \int_{ - \infty }^\infty {p\left( \eta \right){{e}^{{ - i\xi \eta }}}d\eta } $.
Для вычислений перемещений и напряжений (2.19) можно использовать любой численный метод интегрирования, если определители ${{\Delta }_{n}}\left( {\xi ,c} \right)$ (n = 0, ±1, ±2, …) отличны от нуля, т.е. когда скорость движения нагрузки c меньше ее критических скоростей ${{c}_{{(n)*}}}$. Значения ${{c}_{{(n)*}}}$ определяются из дисперсионных уравнений ${{\Delta }_{n}}\left( {\xi ,c} \right) = 0$ [3] и могут оказаться меньше рэлеевской скорости. Окончательное решение будет зависеть от конкретного вида движущейся нагрузки.
Следует заметить, что исключая из постановки задачи граничные условия (2.3) и исключая из (2.12) $\Phi _{{j1}}^{{(2)}}$, получим решение аналогичной задачи для упругого пространства.
3. Численные эксперименты. Рассмотрим подкрепленный трехслойной обделкой тоннель глубиной заложения h = 6 м в породном массиве со следующими характеристиками: ${{\nu }_{1}}$ = 0.294, ${{\mu }_{1}} = \mu $ = 1.094 × 108 Па, ${{\rho }_{1}}$ = 1.5 × 103 кг/м3. Расчетные параметры для обделки: обшивка – стальные (ν01 = ν02 = 0.3, μ01 = μ02 = 8.08 × 1010 Па, ρ01 = ρ02 = = 7.8 × 103 кг/м3) тонкостенные оболочки одинаковой толщины h01 = h02 = 0.02 м с радиусами срединных поверхностей R1 = 3.0 м и R2 = 2.5 м; заполнитель – толстостенная бетонная (ν2 = 0.2, μ2 = 1.21 × 1010 Па, ρ2 = 2.5 × 103 кг/м3) оболочка. Контакт между породным массивом и обделкой, а также между ее слоями полагаем жестким.
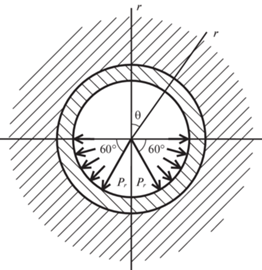
Исследуем напряженно-деформированное состояние рассматриваемого тоннеля при действии изображенной на рис. 2 цилиндрической нормальной нагрузки от внутритуннельного транспорта, движущейся по его лотку со скоростью c = 100 м/с. Нагрузка равномерно распределена вдоль оси η в интервале $\left| \eta \right| \leqslant {{l}_{0}}$ = 0.2 м.
Рассмотрим два случая нагружения: симметричное и несимметричное. В первом случае будем считать, что интенсивность нагрузки постоянна по всей поверхности ее приложения, то есть ${{P}_{r}} = q$.
Во втором случае интенсивность равномерно распределенной по угловой координате нагрузки, расположенной слева от вертикальной диаметральной плоскости тоннеля, в два раза больше интенсивности такой же нагрузки, действующей справа от этой плоскости, то есть при 90° ≤ θ ≤ 150° ${{P}_{r}} = q$; при 210° ≤ θ ≤ 270° ${{P}_{r}} = 2q$.
Параметр нагрузки $q$ (Па) подбираем таким образом, чтобы общая нагрузка по всей длине $2{{l}_{0}}$ (м) участка нагружения ${{P}_{r}} = q$ равнялась эквивалентной сосредоточенной нормальной кольцевой нагрузке интенсивностью P°° (Н/м), то есть $q = P{\text{/}}2{{l}_{0}}$.
Численные исследования соответствующих данному случаю дисперсионных уравнений показали, что в дозвуковом интервале скоростей они корней не имеют.
Введем обозначения: $u_{r}^{^\circ }$ = urμ/P° (м), (м), $\sigma _{{r\theta }}^{^\circ }$ = σrθ/P°, $\sigma _{{\theta \theta }}^{^\circ }$ = σθθ/P°, $\sigma _{{\eta \eta }}^{^\circ }$ = σηη/P°, $u_{x}^{^\circ }$ = uxμ/P° (м), (м), $u_{y}^{^\circ }$ = uyμ/P° (м), $\sigma _{{yy}}^{^\circ }$ = σyy/P°, где P° = P°°/м (Па).
В табл. 1, 2 помещены данные расчетов НДС поперечного сечения (η = 0) тоннеля при действии симметричной и несимметричной движущейся нагрузки.
Таблица 1.
Компоненты НДС поперечного сечения ($\eta = 0$) тоннеля при действии симметричной подвижной нагрузки
| r | Комп. НДС | θ, град | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | ||
| –20 | –40 | –60 | –80 | –100 | –120 | –140 | –160 | ||||
| Заполнитель (бетонный слой) | |||||||||||
| R2 | $u_{r}^{^\circ }$ × 10 | –0.25 | –0.23 | –0.17 | –0.07 | 0.08 | 0.23 | 0.30 | 0.27 | 0.18 | 0.13 |
| $\sigma _{{r\theta }}^{^\circ }$ | 0.0 | 0.15 | 0.17 | 0.12 | 0.07 | 0.0 | –0.11 | –0.15 | –0.09 | 0.0 | |
| –0.15 | –0.17 | –0.12 | –0.07 | 0.11 | 0.15 | 0.09 | |||||
| $\sigma _{{\theta \theta }}^{^\circ }$ | 0.02 | 0.10 | 0.29 | 0.45 | 0.34 | 0.02 | –0.10 | 0.24 | 0.80 | 1.08 | |
| $\sigma _{{\eta \eta }}^{^\circ }$ | –0.10 | –0.16 | –0.15 | –0.13 | –0.67 | –1.72 | –2.25 | –1.61 | –0.47 | 0.08 | |
| R1 | $u_{r}^{^\circ }$ × 10 | –0.24 | –0.22 | –0.17 | –0.07 | 0.07 | 0.21 | 0.28 | 0.25 | 0.17 | 0.13 |
| $\sigma _{{r\theta }}^{^\circ }$ | 0.0 | 0.04 | 0.04 | 0.05 | 0.10 | 0.10 | –0.03 | –0.02 | –0.02 | 0.0 | |
| –0.04 | –0.04 | –0.05 | –0.10 | –0.10 | 0.03 | 0.02 | 0.02 | ||||
| $\sigma _{{\theta \theta }}^{^\circ }$ | –0.09 | –0.07 | 0.07 | 0.01 | 0.50 | 1.32 | 1.74 | 1.23 | 0.24 | –0.25 | |
| $\sigma _{{\eta \eta }}^{^\circ }$ | –0.54 | –0.48 | –0.35 | –0.10 | 0.52 | 1.33 | 1.67 | 1.18 | 0.32 | –0.10 | |
| Массив | |||||||||||
| R1 | $u_{r}^{^\circ }$ × 10 | –0.24 | –0.22 | –0.17 | –0.07 | 0.07 | 0.21 | 0.28 | 0.25 | 0.17 | 0.13 |
| $\sigma _{{r\theta }}^{^\circ }$ × 10 | 0.0 | 0.03 | 0.05 | 0.04 | –0.02 | –0.07 | –0.08 | –0.05 | –0.02 | 0.0 | |
| –0.03 | –0.05 | –0.04 | 0.02 | 0.07 | 0.08 | 0.05 | 0.02 | ||||
| $\sigma _{{\theta \theta }}^{^\circ }$ × 10 | –0.02 | –0.02 | 0.01 | 0.05 | 0.05 | –0.01 | –0.06 | –0.04 | 0.02 | 0.06 | |
| $\sigma _{{\eta \eta }}^{^\circ }$ × 10 | –0.05 | –0.04 | –0.01 | 0.02 | 0.01 | –0.01 | –0.03 | –0.01 | 0.02 | 0.04 | |
Таблица 2.
Компоненты НДС поперечного сечения ($\eta = 0$) тоннеля при действии несимметричной подвижной нагрузки
| r | Комп. НДС | θ, град | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | ||
| Заполнитель (бетонный слой) | |||||||||||
| R2 | $u_{r}^{^\circ }$ × 10 | –0.38 | –0.35 | –0.28 | –0.17 | –0.02 | 0.13 | 0.21 | 0.20 | 0.16 | 0.20 |
| $\sigma _{{r\theta }}^{^\circ }$ | 0.10 | 0.29 | 0.26 | 0.12 | –0.01 | –0.14 | –0.21 | –0.16 | –0.03 | 0.11 | |
| $\sigma _{{\theta \theta }}^{^\circ }$ | 0.03 | 0.03 | 0.20 | 0.36 | 0.26 | –0.03 | –0.08 | 0.41 | 1.18 | 1.61 | |
| $\sigma _{{\eta \eta }}^{^\circ }$ | –0.15 | –0.28 | –0.31 | –0.28 | –0.82 | –1.83 | –2.28 | –1.63 | –0.44 | 0.11 | |
| R1 | $u_{r}^{^\circ }$ × 10 | –0.36 | –0.35 | –0.29 | –0.19 | –0.04 | 0.11 | 0.19 | 0.18 | 0.15 | 0.19 |
| $\sigma _{{r\theta \theta }}^{^\circ }$ | 0.03 | 0.09 | 0.08 | 0.06 | 0.07 | 0.05 | –0.06 | –0.19 | –0.17 | 0.05 | |
| $\sigma _{{\theta \theta }}^{^\circ }$ | –0.14 | –0.06 | 0.02 | 0.14 | 0.60 | 1.35 | 1.71 | 1.16 | 0.81 | –0.38 | |
| $\sigma _{{\eta \eta }}^{^\circ }$ | –0.80 | –0.64 | –0.42 | –0.12 | 0.47 | 1.19 | 1.43 | 0.89 | 0.05 | –0.15 | |
| Массив | |||||||||||
| R1 | $u_{r}^{^\circ }$ × 10 | –0.36 | –0.35 | –0.29 | –0.19 | –0.04 | 0.11 | 0.19 | 0.18 | 0.15 | 0.19 |
| $\sigma _{{r\theta }}^{^\circ }$ × 10 | 0.06 | 0.07 | 0.05 | 0.01 | –0.03 | –0.05 | –0.10 | –0.17 | –0.15 | 0.01 | |
| $\sigma _{{\theta \theta }}^{^\circ }$ × 10 | –0.01 | 0.0 | 0.02 | 0.03 | 0.0 | –0.01 | 0.03 | 0.05 | –0.02 | –0.05 | |
| $\sigma _{{\eta \eta }}^{^\circ }$ × 10 | –0.07 | –0.06 | –0.02 | 0.01 | –0.01 | –0.03 | –0.02 | 0.01 | 0.02 | 0.02 | |
| r | Комп. НДС | θ, град | |||||||||
| 0 | –20 | –40 | –60 | –80 | –100 | –120 | –140 | –160 | –180 | ||
| Заполнитель (бетонный слой) | |||||||||||
| R2 | $u_{r}^{^\circ }$ × 10 | –0.38 | –0.33 | –0.22 | –0.02 | 0.26 | 0.56 | 0.71 | 0.61 | 0.38 | 0.20 |
| $\sigma _{{r\theta }}^{^\circ }$ | 0.10 | –0.16 | –0.25 | –0.23 | –0.23 | –0.14 | 0.11 | 0.30 | 0.26 | 0.11 | |
| $\sigma _{{\theta \theta }}^{^\circ }$ | 0.03 | 0.25 | 0.68 | 1.00 | 0.77 | 0.10 | –0.22 | 0.32 | 1.23 | 1.61 | |
| $\sigma _{{\eta \eta }}^{^\circ }$ | –0.15 | –0.19 | –0.13 | –0.11 | –1.18 | –3.33 | –4.46 | –3.21 | –0.97 | 0.11 | |
| R1 | $u_{r}^{^\circ }$ × 10 | –0.36 | –0.32 | –0.22 | –0.03 | 0.24 | 0.52 | 0.66 | 0.57 | 0.36 | 0.19 |
| $\sigma _{{r\theta \theta }}^{^\circ }$ | 0.03 | –0.03 | –0.03 | –0.10 | –0.26 | –0.25 | 0.04 | 0.32 | 0.31 | 0.05 | |
| $\sigma _{{\theta \theta }}^{^\circ }$ | –0.14 | –0.15 | –0.23 | –0.11 | 0.91 | 2.63 | 3.50 | 2.52 | 0.63 | –0.38 | |
| $\sigma _{{\eta \eta }}^{^\circ }$ | –0.80 | –0.80 | –0.65 | –0.17 | 1.09 | 2.80 | 3.59 | 2.66 | 0.90 | –0.15 | |
| Массив | |||||||||||
| R1 | $u_{r}^{^\circ }$ × 10 | –0.36 | –0.32 | –0.22 | –0.03 | 0.24 | 0.52 | 0.66 | 0.57 | 0.36 | 0.19 |
| $\sigma _{{r\theta }}^{^\circ }$ × 10 | 0.06 | 0.02 | –0.02 | –0.03 | –0.01 | –0.01 | 0.03 | 0.12 | 0.14 | 0.01 | |
| $\sigma _{{\theta \theta }}^{^\circ }$ × 10 | –0.01 | –0.01 | 0.01 | 0.03 | 0.0 | –0.04 | –0.01 | 0.03 | –0.01 | –0.05 | |
| $\sigma _{{\eta \eta }}^{^\circ }$ × 10 | –0.07 | –0.05 | –0.01 | 0.03 | 0.02 | –0.03 | –0.04 | 0.01 | 0.03 | 0.02 | |
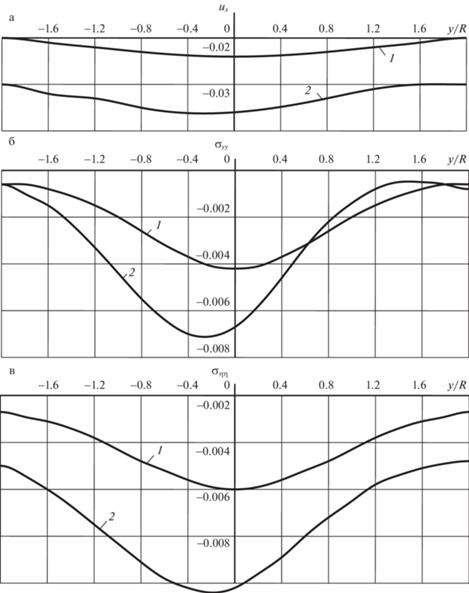
Согласно данным таблиц 1, 2 на рис. 3 построены эпюры нормальных напряжений $\sigma _{{\theta \theta }}^{^\circ }$, $\sigma _{{\eta \eta }}^{^\circ }$ и радиальных перемещений $u_{r}^{^\circ }$ на контуре r = R2 контактирующего с внутренней оболочкой обшивки бетонного слоя при η = 0.
Рис. 3.
Эпюры напряжений (${{\sigma }_{{\theta \theta }}}$ – а, ${{\sigma }_{{\eta \eta }}}$ – б) и перемещений (${{u}_{r}}$ – в) на контуре $r = {{R}_{2}}$ ($\eta = 0$) контактной поверхности заполнителя: симметричное нагружение (2.1); несимметричное нагружение (2.2).
Из анализа результатов расчетов следует, что в случае несимметричной нагрузки, т.е. при увеличении интенсивности левой половины симметричной нагрузки в два раза, симметричный характер распределения перемещений и напряжений по контурам сечения тоннеля нарушается. При этом, в заполнителе (бетонном слое) экстремальные радиальные перемещения ${{u}_{r}}$ при θ = –120° возрастают в 3.4 раза, а экстремальные напряжения ${{\sigma }_{{r\theta }}}$, ${{\sigma }_{{\theta \theta }}}$ и ${{\sigma }_{{\eta \eta }}}$ увеличиваются соответственно в 2.0 (при θ = –140°), 1.5 (при θ = 180°) и 2.0 (при θ = –120°) раза. На контактирующей с обделкой поверхности массива при любом нагружении тоннеля экстремальные напряжения значительно ниже, чем в бетонном слое обделки.
На земной поверхности также нарушается симметрия в распределении напряжений и перемещений. Результаты расчетов НДС земной поверхности в координатной плоскости $xy$ ($\eta = 0$) при действии на тоннель симметричной и несимметричной движущейся нагрузки представлены в табл. 3.
Таблица 3.
Компоненты НДС земной поверхности в плоскости xy ($\eta = 0$) при симметричном и несимметричном нагружении тоннеля
| Комп. НДС | y/R | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | –0.2 | –0.4 | –0.6 | –0.8 | –1.0 | –1.2 | –1.4 | –1.6 | –1.8 | –2.0 | |
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 | ||
| Симметричное нагружение | |||||||||||
| $u_{x}^{^\circ }$ × 10 | –0.24 | –0.24 | –0.23 | –0.23 | –0.23 | –0.22 | –0.22 | –0.21 | –0.21 | –0.20 | –0.20 |
| $u_{y}^{^\circ }$ × 100 | 0.0 | 0.04 | 0.07 | 0.09 | 0.11 | 0.12 | 0.12 | 0.11 | 0.10 | 0.08 | 0.07 |
| –0.04 | –0.07 | –0.09 | –0.11 | –0.12 | –0.12 | –0.11 | –0.10 | –0.08 | –0.07 | ||
| $\sigma _{{yy}}^{^\circ }$ × 100 | –0.42 | –0.41 | –0.37 | –0.32 | –0.26 | –0.20 | –0.15 | –0.11 | –0.08 | –0.06 | –0.06 |
| $\sigma _{{\eta \eta }}^{^\circ }$ × 100 | –0.80 | –0.79 | –0.76 | –0.72 | –0.68 | –0.63 | –0.58 | –0.54 | –0.51 | –0.49 | –0.47 |
| Несимметричное нагружение | |||||||||||
| $u_{x}^{^\circ }$ × 10 | –0.36 | –0.36 | –0.36 | –0.36 | –0.35 | –0.34 | –0.33 | –0.33 | –0.32 | –0.31 | –0.30 |
| –0.35 | –0.35 | –0.34 | –0.33 | –0.32 | –0.31 | –0.31 | –0.30 | –0.30 | –0.30 | ||
| $u_{y}^{^\circ }$ × 10 | –0.17 | –0.17 | –0.16 | –0.15 | –0.15 | –0.14 | –0.14 | –0.14 | –0.14 | –0.14 | –0.15 |
| –0.18 | –0.18 | –0.18 | –0.18 | –0.18 | –0.18 | –0.18 | –0.17 | –0.17 | –0.17 | ||
| $\sigma _{{yy}}^{^\circ }$ × 100 | –0.67 | –0.71 | –0.70 | –0.64 | –0.55 | –0.44 | –0.33 | –0.23 | –0.15 | –0.10 | –0.06 |
| –0.58 | –0.46 | –0.33 | –0.22 | –0.14 | –0.08 | –0.05 | –0.05 | –0.06 | –0.08 | ||
| $\sigma _{{\eta \eta }}^{^\circ }$ × 100 | –1.22 | –1.24 | –1.22 | –1.18 | –1.11 | –1.03 | –0.95 | –0.87 | –0.80 | –0.74 | –0.70 |
| –1.16 | –1.09 | –1.00 | –0.92 | –0.85 | –0.78 | –0.74 | –0.71 | –0.69 | –0.68 | ||
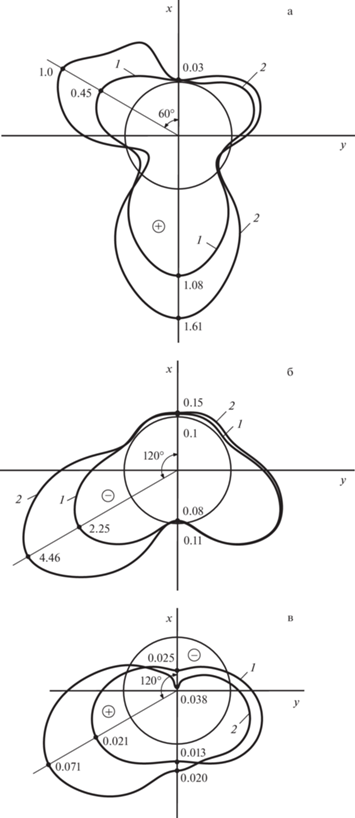
На рис. 4 в координатной плоскости $xy$ ($\eta = 0$) показаны изменения компонент НДС земной поверхности при действии на тоннель симметричной и несимметричной подвижных нагрузок. Обозначения кривых: симметричное нагружение (2.1); несимметричное нагружение (2.2). Как следует из анализа результатов расчетов, во втором случае нагружения (несимметричное нагружение) максимальный прогиб ${{u}_{x}}$ земной поверхности в 1.5 раза больше, чем в первом случае (при симметричном нагружении), а ее наибольшее горизонтальное смещение ${{u}_{y}}$ возрастает в 15 раз. Экстремальные нормальные напряжения ${{\sigma }_{y}}$ и ${{\sigma }_{{\eta \eta }}}$ увеличиваются соответственно в 1.7 и 1.5 раза.
Заключение. Полученное решение и разработанный на его основе программный комплекс позволяет методами математического моделирования исследовать динамику породного массива и его поверхности вдоль трассы тоннеля на разной глубине заложения с учетом физико-механических свойств массива и материала конструктивных элементов его обделки. Скорость движения транспортной нагрузки существенно влияет на динамику поверхности массива, что необходимо учитывать, например, при строительстве метрополитенов особенно в настоящее время в связи с интенсивным развитием высокоскоростного железнодорожного транспорта. Подбор материала и толщины слоев оболочек в обделке тоннеля позволяет снизить вибрацию поверхности массива вдоль трассы, которая негативно влияет на сейсмоустойчивость близ расположенных зданий и сооружений.
Отметим также, что диапазон скоростей современных транспортных средств лежит в рассмотренном здесь диапазоне дозвуковых скоростей и много меньше его верхнего предела.
Список литературы
Ержанов Ж.С., Айталиев Ш.М., Алексеева Л.А. Динамика тоннелей и подземных трубопроводов. Алма-Ата: Наука, 1989. 240 с.
Украинец В.Н. Динамика тоннелей и трубопроводов мелкого заложения под воздействием подвижных нагрузок. Павлодар: НИЦ ПГУ, 2006. 123 с.
Alekseyeva L.A., Ukrainets V.N. Dynamics of an elastic half-space with a reinforced cylindrical cavity under moving loads // Int. Appl. Mech. 2009. V. 45. № 9. P. 75–85.
Украинец В.Н., Гирнис С.Р. Математическое моделирование динамики подкрепленных двухслойными оболочками тоннелей при действии транспортных нагрузок. Павлодар: Кереку, 2018. 116 с.
Coşkun İ., Dolmaseven D. Dynamic response of a circular tunnel in an elastic half space // J. Engng. 2017. Article ID 6145375 https://doi.org/10.1155/2017/6145375
Dwivedia J.P., Singha V.P., Lalb R.K., Devia S. Dynamic response of lined circular tunnel in linear viscoelastic medium due to moving ring load // Materials Today: Proc. V. 4. Iss. 2. Pt. A. 2017. P. 3767–3775.
Cao Z., Sun S., Yuan Z., Cai Y. Analytical study on the effect of moving surface load on underground tunnel // in: Ed. by Wu W., Yu H.S. Proc. China-Europe Conf. on Geotechn. Engng. Cham: Springer, 2018.
Shunhua Zhou. Dynamics of Rail Transit Tunnel Systems. London: Acad. Press, 2019. 276 p.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика