Прикладная математика и механика, 2022, T. 86, № 2, стр. 251-262

Конечно-элементный алгоритм расчета эллипсоидальной оболочки при учете смещения как жесткого целого

А. Ш. Джабраилов^1, *, А. П. Николаев¹, Ю. В. Клочков¹, Н. А. Гуреева², Т. Р. Ищанов¹

¹ ФГБОУ ВО Волгоградский государственный аграрный университет
Волгоград, Россия

² ФГБОУ ВО Финансовый университет при Правительстве РФ
Москва, Россия

^* E-mail: arsen82@yandex.ru

Поступила в редакцию 30.03.2021
После доработки 06.12.2021
Принята к публикации 15.12.2021

EDN: SBCVXG
DOI: 10.31857/S0032823522020059

Полный текст (PDF)

Аннотация

Для прочностного расчета эллипсоидальной оболочки при использовании непрерывной параметризации срединной поверхности разработан конечный элемент четырёхугольной формы, являющийся фрагментом срединной поверхности эллипсоида. В качестве узловых неизвестных приняты перемещения узловых точек и их производные. Для получения аппроксимирующих функций искомых величин внутренней точки конечного элемента через узловые неизвестные использованы традиционные аппроксимирующие выражения вектора перемещения внутренней точки конечного элемента через векторы перемещений узлов элемента и производные этих векторов. При координатном преобразовании использованы матричные соотношения между базисными векторами узловых точек и векторами базиса внутренней точки конечного элемента, реализация которых позволяет аппроксимирующие выражения между векторными величинами представить в виде аппроксимирующих функций между компонентами вектора перемещения внутренней точки конечного элемента и компонентами векторов перемещений его узловых точек. На конкретном примере показано, что использование полученных аппроксимирующих функций позволяет учитывать смещение конечного элемента как абсолютно твердого тела. Полученные аппроксимирующие функции приводят к более быстрой сходимости результатов и при отсутствии смещения как жесткого целого.

Ключевые слова: оболочка, тензор деформаций, конечный элемент, вектор перемещения, векторная апроксимация, матрица жесткости, тензор напряжений

1. Введение. На сегодняшний день одним из самых распространенных и перспективных типов конструкций являются тонкостенные оболочки. Они находят весьма разнообразное применение в широком спектре инженерных сооружений. В настоящее время вопросы напряженно-деформированного состояния тонкостенных конструкций изучены достаточно глубоко, а теория оболочек получила законченные очертания [1–3]. В основном все расчеты оболочечных конструкций выполняются с помощью численных методов. Практически безальтернативным здесь является метод конечных элементов (МКЭ), развитию и совершенствованию которого посвящены работы многих отечественных и зарубежных авторов [4–11]. Обычно в МКЭ каждая компонента вектора перемещения внутренней точки конечного элемента аппроксимируется через узловые значения этой же компоненты независимо от других [12, 13], что вполне корректно при использовании прямоугольной декартовой системы координат. В криволинейной системе координат использование классической аппроксимации не дает возможности учитывать смещения оболочки как жесткого целого, что является общепризнанной проблемой МКЭ [14, 15]. В настоящей работе для криволинейной системы координат авторами на основе векторной интерполяции получены аппроксимирующие функции между компонентами вектора перемещения внутренней точки конечного элемента и компонентами векторов перемещений его узловых точек, что позволяет автоматически учитывать возможные смещения конструкции как абсолютно твердого тела.

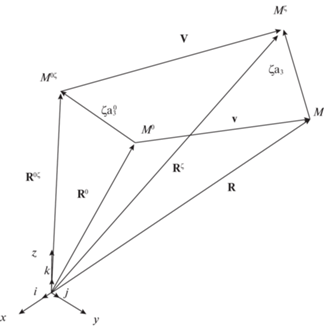
2. Материалы и методы. Геометрия оболочки. Произвольная точка срединной поверхности эллипсоида рассматривается в исходном (точка ${{M}^{0}}$) и деформированном состояниях (точка M, вектор перемещения v). Положение точки в произвольном слое оболочки, отстоящем на расстоянии ${{\xi }}$ от срединной поверхности, обозначаются символами: ${{M}^{{0\xi }}}$ и ${{M}^{\xi }}$ соответственно указанным состояниям (рис. 1).

Рис. 1.

Положение рассматриваемых точек при деформировании оболочки.

Положение точки M⁰ определяется радиус-вектором [16]

(2.1)

${{{\mathbf{R}}}^{0}} = a\sin T{\mathbf{i}} + b\cos T\sin t{\mathbf{j}} + c\cos T\cos t{\mathbf{k}},$

где a, b, c – отрезки, отсекаемые на осях Ох, Оy, Oz; ${\mathbf{i}},{\mathbf{j}},{\mathbf{k}}$ – орты декартовой системы координат; $T$ – параметр эллипса в плоскости xOz; $t$ – параметр эллипса в плоскости, перпендикулярной оси Ох.

Векторы, касательные к срединной поверхности эллипсоида в точке М⁰, определяются дифференцированием (2.1)

(2.2)

$\begin{gathered} {\mathbf{a}}_{1}^{0} = {\mathbf{R}}_{{,T}}^{0} = a\cos T{\mathbf{i}} - b\sin T\sin t{\mathbf{j}} - c\sin T\cos t{\mathbf{k}} \\ {\mathbf{a}}_{2}^{0} = {\mathbf{R}}_{{,t}}^{0} = b\cos T\cos t{\mathbf{j}} - c\cos T\sin t{\mathbf{k}} \\ \end{gathered} $

Нормаль к срединной поверхности определяется векторным произведением

(2.3)

${\mathbf{a}}_{3}^{0} = \frac{{{\mathbf{a}}_{1}^{0} \times {\mathbf{a}}_{2}^{0}}}{{\left| {{\mathbf{a}}_{1}^{0} \times {\mathbf{a}}_{2}^{0}} \right|}} = \frac{{{{u}_{1}}}}{u}{\mathbf{i}} + \frac{{{{u}_{2}}}}{u}{\mathbf{j}} + \frac{{{{u}_{3}}}}{u}{\mathbf{k}},$

где ${{u}_{1}} = bc\sin T\cos T$; ${{u}_{2}} = ac\sin t{{\cos }^{2}}T$; ${{u}_{3}} = ab\cos t{{\cos }^{2}}T$; $u = \sqrt {u_{1}^{2} + u_{2}^{2} + u_{3}^{2}} $.

Зависимости (2.2) и (2.3) представляются в матричном виде

(2.4)

$\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{3 \times 1} = \mathop {\left[ {\tau \left( {T,t} \right)} \right]}\limits_{3 \times 3} \mathop {\left\{ {\mathbf{i}} \right\}}\limits_{3 \times 1} ;\quad \mathop {\left\{ {\mathbf{i}} \right\}}\limits_{3 \times 1} = {{\mathop {\left[ {\tau \left( {T,t} \right)} \right]}\limits_{3 \times 3} }^{{ - 1}}}\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{3 \times 1} ,$

где ${{\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{1 \times 3} }^{T}} = \left\{ {{\mathbf{a}}_{1}^{0}{\mathbf{a}}_{2}^{0}{\mathbf{a}}_{3}^{0}} \right\}$; ${{\mathop {\left\{ {\mathbf{i}} \right\}}\limits_{1 \times 3} }^{T}} = \left\{ {{\mathbf{ijk}}} \right\}$.

Производные базисных векторов (2.4) произвольной точки срединной поверхности можно представить компонентами в этом же базисе матричными соотношениями

(2.5)

$\begin{gathered} \mathop {\left\{ {{{{\mathbf{a}}}^{0}}{{,}_{T}}} \right\}}\limits_{3 \times 1} = \mathop {\left[ {\tau \left( {T,t} \right){{,}_{T}}} \right]}\limits_{3 \times 3} \mathop {\left\{ {\mathbf{i}} \right\}}\limits_{3 \times 1} = \mathop {\left[ {\tau \left( {T,t} \right){{,}_{T}}} \right]}\limits_{3 \times 3} {{\mathop {\left[ {\tau \left( {T,t} \right)} \right]}\limits_{3 \times 3} }^{{ - 1}}}\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{3 \times 1} = \mathop {\left[ M \right]}\limits_{3 \times 3} \mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{3 \times 1} \\ \\ \mathop {\left\{ {{{{\mathbf{a}}}^{0}}{{,}_{t}}} \right\}}\limits_{3 \times 1} = \mathop {\left[ {\tau \left( {T,t} \right){{,}_{t}}} \right]}\limits_{3 \times 3} \mathop {\left\{ {\mathbf{i}} \right\}}\limits_{3 \times 1} = \mathop {\left[ {\tau \left( {T,t} \right){{,}_{t}}} \right]}\limits_{3 \times 3} {{\mathop {\left[ {\tau \left( {T,t} \right)} \right]}\limits_{3 \times 3} }^{{ - 1}}}\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{3 \times 1} = \mathop {\left[ N \right]}\limits_{3 \times 3} \mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{3 \times 1} , \\ \end{gathered} $

где ${{\mathop {\left\{ {{{{\mathbf{a}}}^{0}}{{,}_{T}}} \right\}}\limits_{1 \times 3} }^{T}} = \left\{ {{\mathbf{a}}_{{1,T}}^{0}{\mathbf{a}}_{{2,T}}^{0}{\mathbf{a}}_{{3,T}}^{0}} \right\}$; ${{\mathop {\left\{ {{{{\mathbf{a}}}^{0}}{{,}_{t}}} \right\}}\limits_{1 \times 3} }^{T}} = \left\{ {{\mathbf{a}}_{{1,t}}^{0}{\mathbf{a}}_{{2,t}}^{0}{\mathbf{a}}_{{3,t}}^{0}} \right\}$.

Положения точек M, ${{M}^{{0\xi }}}$и ${{M}^{\xi }}$ описываются радиус-векторами

(2.6)

${\mathbf{R}} = {{{\mathbf{R}}}^{0}} + {\mathbf{v}};{{{\mathbf{R}}}^{{0\xi }}} = {{{\mathbf{R}}}^{0}} + \xi {\mathbf{a}}_{3}^{0},\quad {{{\mathbf{R}}}^{\xi }} = {{{\mathbf{R}}}^{{0\xi }}} + {\mathbf{v}} + \xi \left( {{{{\mathbf{a}}}_{3}} - {\mathbf{a}}_{3}^{0}} \right)$

Входящий в (2.6) вектор перемещения ${\mathbf{v}}$ определяется компонентами в исходном базисе точки ${{M}^{0}}$

(2.7)

${\mathbf{v}} = {{{v}}^{i}}{\mathbf{a}}_{i}^{{\text{o}}}$

Дифференцированием (2.7) с учетом (2.5) определяются производные вектора ${\mathbf{v}}$

(2.8)

${{{\mathbf{v}}}_{{,\alpha }}} = z_{\alpha }^{m}{\mathbf{a}}_{m}^{0},\quad {{{\mathbf{v}}}_{{,\alpha \beta }}} = z_{{\alpha \beta }}^{m}{\mathbf{a}}_{m}^{0},$

где $z_{\alpha }^{m}$ и $z_{{\alpha \beta }}^{m}$ – функции компонент вектора перемещения ${\mathbf{v}}$ и их производных; при α = 1 понимается производная по параметру T; при α = 2 – дифференцирование по параметру t.

Орт нормали ${{{\mathbf{a}}}_{3}}$ к срединной поверхности в деформированном состоянии, входящий в (2.6), выражается векторным произведением

(2.9)

${{{\mathbf{a}}}_{3}} = \frac{{{{{\mathbf{a}}}_{1}} \times {{{\mathbf{a}}}_{2}}}}{{\sqrt a }},$

где ${{{\mathbf{a}}}_{1}} = \left( {{{{\mathbf{R}}}^{0}} + {\mathbf{v}}} \right){{,}_{T}}$, ${{{\mathbf{a}}}_{2}} = \left( {{{{\mathbf{R}}}^{0}} + {\mathbf{v}}} \right){{,}_{t}}~$, $a \approx {{a}^{0}} = a_{{11}}^{0}a_{{22}}^{0} - a_{{12}}^{0}a_{{21}}^{0}$ – детерминант метрического тензора в точке $M$.

Базисные векторы в точках ${{M}^{{0\xi }}}$ и ${{M}^{\xi }}$ находятся дифференцированием (2.6) с учетом (2.5) и (2.9)

(2.10)

$\begin{gathered} {\mathbf{g}}_{1}^{0} = {\mathbf{R}},_{T}^{{0\xi }},\quad {{{\mathbf{g}}}_{1}} = {\mathbf{R}},_{T}^{\xi }\; + {\mathbf{v}}{{,}_{T}}\; + \xi \left( {{{{\mathbf{a}}}_{{3,T}}} - {\mathbf{a}}_{{3,T}}^{0}} \right) \\ {\mathbf{g}}_{2}^{0} = {\mathbf{R}},_{t}^{{0\xi }},\quad {{{\mathbf{g}}}_{2}} = {\mathbf{R}},_{t}^{\xi }\; + \;{\mathbf{v}}{{,}_{t}}\; + \xi \left( {{{{\mathbf{a}}}_{{3,t}}} - {\mathbf{a}}_{{3,t}}^{0}} \right), \\ \end{gathered} $

где ${{{\mathbf{a}}}_{{3,\alpha }}} = \frac{1}{{\sqrt {{{a}^{0}}} }}\left( {{{{\mathbf{a}}}_{{1,\alpha }}} \times {{{\mathbf{a}}}_{2}} + {{{\mathbf{a}}}_{1}} \times {{{\mathbf{a}}}_{{2,\alpha }}}} \right)$.

Для определения деформаций в произвольном слое оболочки, отстоящем на расстоянии ${{\xi }}$ от срединной поверхности, используются соотношения механики сплошной среды [17]

(2.11)

$\varepsilon _{{\alpha \beta }}^{\xi } = \frac{1}{2}\left( {{{g}_{{\alpha \beta }}} - g_{{\alpha \beta }}^{0}} \right),$

где $g_{{\alpha \beta }}^{0} = {\mathbf{g}}_{\alpha }^{0}{\mathbf{g}}_{\beta }^{0}$, ${{g}_{{\alpha \beta }}} = {{{\mathbf{g}}}_{\alpha }}{{{\mathbf{g}}}_{\beta }}$ – ковариантные компоненты метрических тензоров в соответствующих точках.

При использовании (2.6), (2.8) и (2.9) деформации в произвольной точке оболочки (2.11) представляются выражением

(2.12)

$\varepsilon _{{\alpha \beta }}^{\xi } = {{\varepsilon }_{{\alpha \beta }}} + \xi {{\chi }_{{\alpha \beta }}},$

где ${{\varepsilon }}_{{{{\alpha \beta }}}}^{{}}$, ${{{{\chi }}}_{{{{\alpha \beta }}}}}$ – деформации и искривления срединной поверхности оболочки в точке $M$.

Равенство (2.12), с учетом (2.6), (2.8) и (2.9) представляется в матричном виде

(2.13)

$\mathop {\left\{ {{{\varepsilon }^{\xi }}} \right\}}\limits_{3 \times 1} = \mathop {\left[ G \right]}\limits_{3 \times 6} \mathop {\left\{ \varepsilon \right\}}\limits_{6 \times 1} = \mathop {\left[ G \right]}\limits_{3 \times 6} \mathop {\left[ L \right]}\limits_{6 \times 3} \mathop {\left\{ {v} \right\}}\limits_{3 \times 1} ,$

где ${{\left\{ {{{\varepsilon }^{\xi }}} \right\}}^{T}} = \left\{ {\varepsilon _{{11}}^{\xi }\varepsilon _{{22}}^{\xi }2\varepsilon _{{12}}^{\xi }} \right\}$, ${{\left\{ {v} \right\}}^{T}} = \left\{ {{{{v}}^{1}}{{{v}}^{2}}{{{v}}^{3}}} \right\}$; ${{\left\{ \varepsilon \right\}}^{T}} = \left\{ {{{\varepsilon }_{{11}}}{{\varepsilon }_{{22}}}2{{\varepsilon }_{{12}}}{{\chi }_{{11}}}{{\chi }_{{22}}}2{{\chi }_{{12}}}} \right\}$, $~\left[ L \right]$ – матрица дифференциальных и алгебраических операторов.

Компоненты тензора упругих деформаций в произвольном слое, отстоящем на расстоянии ${{\xi }}$ от срединной поверхности, могут быть определены с помощью соотношения [17]

(2.14)

${{\sigma }^{{\alpha \beta }}} = \lambda {{I}_{1}}\left( {{{\varepsilon }^{\xi }}} \right){{g}^{{\alpha \beta }}} + 2\mu {{g}^{{\alpha \rho }}}{{g}^{{\beta \gamma }}}\varepsilon ~_{{\rho \gamma }}^{\xi },$

где $\lambda $, μ – параметры Ляме, ${{g}^{{\alpha \beta }}}$ – контравариантные компоненты метрического тензора, ${{\sigma }^{{\alpha \beta }}}$ – контравариантные компоненты тензора напряжений, ${{I}_{1}}({{\varepsilon }^{\xi }}) = {{g}^{{\rho \gamma }}}\varepsilon ~_{{\rho \gamma }}^{\xi }$ – первый инвариант тензора деформаций.

Напряжения в точке произвольного слоя оболочки, отстоящем на расстоянии ${{\xi }}$ от срединной поверхности, в соответствии с (2.14) можно представить в матричном виде

(2.15)

$\mathop {\left\{ {{{\sigma }^{{\alpha \beta }}}} \right\}}\limits_{3 \times 1} = \mathop {\left[ C \right]}\limits_{3 \times 3} \mathop {\left\{ {{{\varepsilon }^{\xi }}} \right\}}\limits_{3 \times 1} $

Конечный элемент. В качестве элемента дискретизации принимается произвольный четырёхугольный фрагмент срединной поверхности оболочки с узлами i, j, k, l. Для реализации численного интегрирования фрагмент отображается на квадрат с локальными координатами ${{\zeta }}$ и η, изменяющимися в пределах–1 ≤ $\zeta $, η ≤ 1. Отображение осуществляется с использованием билинейных функций

(2.16)

$\lambda = {{\mathop {\left\{ {f\left( {\zeta ,~\eta } \right)} \right\}}\limits_{1 \times 4} }^{T}}\mathop {\left\{ {{{\lambda }_{y}}} \right\}}\limits_{4 \times 1} ,$

где ${{\left\{ {{{\lambda }_{y}}} \right\}}^{T}} = \left\{ {{{\lambda }^{i}}{{\lambda }^{j}}{{\lambda }^{k}}{{\lambda }^{l}}} \right\}$, а под символом ${{\lambda }}$ понимаются значения узловых параметров T и t, которые в дальнейшем обозначаются координатами ${{{{\theta }}}^{1}}$ и ${{{{\theta }}}^{2}}$ соответственно.

Дифференцированием (2.16) определяются производные координат ${{{{\theta }}}^{{{\alpha }}}}$ в системе ${{\zeta }}$, η($\theta ,_{\zeta }^{\alpha }$, $\theta ,_{\eta }^{\alpha }$, $\theta ,_{{\zeta \eta }}^{\alpha }$) и производные локальных координат ${{\zeta }}$, η по глобальным переменным ${{\theta }^{\alpha }}$ ($\zeta {{,}_{\alpha }}$,$\eta {{,}_{\alpha }}$, $\zeta {{,}_{{\alpha \beta }}}$, $\eta {{,}_{{\alpha \beta }}}$).

Для получения аппроксимирующих выражений перемещений внутренней точки конечного элемента рассматривается векторная формулировка алгоритма аппроксимации.

В качестве узловых варьируемых параметров принимаются векторы перемещений узловых точек и их производные в локальной и глобальной системах координат

(2.17)

$\begin{gathered} {{\mathop {\left\{ {{{{\mathbf{v}}}^{l}}} \right\}}\limits_{1 \times 12} }^{T}} = \left\{ {{{{\mathbf{v}}}^{i}}{{{\mathbf{v}}}^{j}}{{{\mathbf{v}}}^{k}}{{{\mathbf{v}}}^{l}}{\mathbf{v}},_{\zeta }^{i}{\mathbf{v}},_{\zeta }^{j}{\mathbf{v}},_{\zeta }^{k}{\mathbf{v}},_{\zeta }^{l}{\mathbf{v}},_{\eta }^{i}{\mathbf{v}},_{\eta }^{j}{\mathbf{v}},_{\eta }^{k}{\mathbf{v}},_{\eta }^{l}} \right\} \\ {{\mathop {\left\{ {{{{\mathbf{v}}}^{g}}} \right\}}\limits_{1 \times 12} }^{T}} = \left\{ {{{{\mathbf{v}}}^{i}}{{{\mathbf{v}}}^{j}}{{{\mathbf{v}}}^{k}}{{{\mathbf{v}}}^{l}}{\mathbf{v}},_{{{{\theta }^{1}}}}^{i}{\mathbf{v}},_{{{{\theta }^{1}}}}^{j}{\mathbf{v}},_{{{{\theta }^{1}}}}^{k}{\mathbf{v}},_{{{{\theta }^{1}}}}^{l}{\mathbf{v}},_{{{{\theta }^{2}}}}^{i}{\mathbf{v}},_{{{{\theta }^{2}}}}^{j}{\mathbf{v}},_{{{{\theta }^{2}}}}^{k}{\mathbf{v}},_{{{{\theta }^{2}}}}^{l}} \right\} \\ \end{gathered} $

На основании дифференциальных зависимостей

(2.18)

${\mathbf{v}},_{\zeta }^{n}\; = {\mathbf{v}},_{{{{\theta }^{1}}}}^{{}}\theta ,_{\zeta }^{1}\; + {\mathbf{v}},_{{{{\theta }^{2}}}}^{{}}\theta ,_{\zeta }^{2},\quad {\mathbf{v}},_{\eta }^{n}\; = {\mathbf{v}},_{{{{\theta }^{1}}}}^{n}\theta ,_{\eta }^{1}\; + {\mathbf{v}},_{{{{\theta }^{2}}}}^{n}\theta ,_{\eta }^{2}$

между узловыми неизвестными (2.17) записывается матричное соотношение

(2.19)

$\mathop {\left\{ {{{{\mathbf{v}}}^{l}}} \right\}}\limits_{12 \times 1} = \mathop {\left[ H \right]}\limits_{12 \times 12} \mathop {\left\{ {{{{\mathbf{v}}}^{g}}} \right\}}\limits_{12 \times 1} $

Вектор перемещения внутренней точки конечного элемента в деформированном состоянии определяется через узловые величины (2.17) следующими выражениями

(2.20)

${\mathbf{v}} = {{\mathop {\left\{ {\varphi \left( {\zeta ,~\eta } \right)} \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left\{ {{{{\mathbf{v}}}^{l}}} \right\}}\limits_{12 \times 1} = {{\mathop {\left\{ {\varphi \left( {\zeta ,~\eta } \right)} \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left[ H \right]}\limits_{12 \times 12} \mathop {\left\{ {{{{\mathbf{v}}}^{g}}} \right\}}\limits_{12 \times 1} = {{\mathop {\left\{ \gamma \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left\{ {{{{\mathbf{v}}}^{g}}} \right\}}\limits_{12 \times 1} ,$

где элементы матрицы ${{\left\{ {\varphi \left( {\zeta ,~\eta } \right)} \right\}}^{T}}$ являются полиномами Эрмита третьей степени [18].

Производные аппроксимирующей функции $\left\{ {\varphi \left( {\zeta ,~\eta } \right)} \right\}$ в глобальной системе координат определяются выражениями

$\frac{{\partial {{{\left\{ \varphi \right\}}}^{T}}}}{{\partial {{\theta }^{\alpha }}}} = \left[ {{{{\mathop {\left\{ {\varphi {{,}_{\zeta }}} \right\}}\limits_{1 \times 12} }}^{T}}\zeta {{,}_{\alpha }} + {{{\mathop {\left\{ {\varphi {{,}_{{~\eta }}}} \right\}}\limits_{1 \times 12} }}^{T}}~\eta {{,}_{\alpha }}} \right] = {{\mathop {\left\{ {\varphi {{,}_{{~\alpha }}}} \right\}}\limits_{1 \times 12} }^{T}}$

(2.21)

$\frac{{{{\partial }^{2}}{{{\left\{ \varphi \right\}}}^{T}}}}{{\partial {{\theta }^{\alpha }}\partial {{\theta }^{\beta }}}} = \left[ {{{{\mathop {\left\{ {\varphi {{,}_{{\zeta \zeta }}}} \right\}}\limits_{1 \times 12} }}^{T}}\zeta {{,}_{\alpha }}\zeta {{,}_{\beta }} + {{{\mathop {\left\{ {\varphi {{,}_{\zeta }}} \right\}}\limits_{1 \times 12} }}^{T}}\zeta {{,}_{{\alpha \beta }}} + {{{\mathop {\left\{ {\varphi {{,}_{{\zeta \eta }}}} \right\}}\limits_{1 \times 12} }}^{T}}\zeta {{,}_{\alpha }}\eta {{,}_{\beta }} + } \right.$

$ + \;\left. {{{{\mathop {\left\{ {\varphi {{,}_{{\eta \zeta }}}} \right\}}\limits_{1 \times 12} }}^{T}}\eta {{,}_{\alpha }}\zeta {{,}_{\beta }} + {{{\mathop {\left\{ {\varphi {{,}_{{\eta \eta }}}} \right\}}\limits_{1 \times 12} }}^{T}}\eta {{,}_{\alpha }}\eta {{,}_{\beta }} + {{{\mathop {\left\{ {\varphi {{,}_{{~\eta }}}} \right\}}\limits_{1 \times 12} }}^{T}}~\eta {{,}_{{\alpha \beta }}}} \right] = {{\mathop {\left\{ {\varphi {{,}_{{~\alpha \beta }}}} \right\}}\limits_{1 \times 12} }^{T}}$

С учетом (2.21) производные вектора перемещения внутренней точки конечного элемента запишутся в матричном виде

(2.22)

$\begin{gathered} {\mathbf{v}}{{,}_{\alpha }} = {{\mathop {\left\{ {\varphi {{,}_{{~\alpha }}}} \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left\{ {{{{\mathbf{v}}}^{l}}} \right\}}\limits_{12 \times 1} = {{\mathop {\left\{ {\varphi {{,}_{{~\alpha }}}} \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left[ H \right]}\limits_{12 \times 12} \mathop {\left\{ {{{{\mathbf{v}}}^{g}}} \right\}}\limits_{12 \times 1} = {{\mathop {\left\{ {\gamma {{,}_{\alpha }}} \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left\{ {{{{\mathbf{v}}}^{g}}} \right\}}\limits_{12 \times 1} \\ {\mathbf{v}}{{,}_{{\alpha \beta }}} = {{\mathop {\left\{ {\varphi {{,}_{{~\alpha \beta }}}} \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left\{ {{{{\mathbf{v}}}^{l}}} \right\}}\limits_{12 \times 1} = {{\mathop {\left\{ {\varphi {{,}_{{~\alpha \beta }}}} \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left[ H \right]}\limits_{12 \times 12} \mathop {\left\{ {{{{\mathbf{v}}}^{g}}} \right\}}\limits_{12 \times 1} = {{\mathop {\left\{ {\gamma {{,}_{{\alpha \beta }}}} \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left\{ {{{{\mathbf{v}}}^{g}}} \right\}}\limits_{12 \times 1} \\ \end{gathered} $

Столбец узловых неизвестных $\mathop {\left\{ {{{{\mathbf{v}}}^{g}}} \right\}}\limits_{12 \times 1} $ можно представить матричным произведением

(2.23)

$\mathop {\left\{ {{{{\mathbf{v}}}^{g}}} \right\}}\limits_{12 \times 1} = \mathop {\left[ {\mathbf{S}} \right]}\limits_{12 \times 36} \; \cdot \;\mathop {\left\{ {{{f}_{u}}} \right\}}\limits_{36 \times 1} ,$

где ${{\mathop {\left\{ {{{f}_{u}}} \right\}}\limits_{36 \times 1} }^{T}} = \left\{ {{{{v}}^{{1i}}}{{{v}}^{{2i}}}{{{v}}^{{3i}}} \ldots {{{v}}^{{1l}}}{{{v}}^{{2l}}}{{{v}}^{{3l}}}} \right.f_{1}^{{1i}}f_{1}^{{2i}}f_{1}^{{3i}} \ldots f_{2}^{{1i}}f_{2}^{{2i}}f_{2}^{{3i}} \ldots \left. {f_{2}^{{1l}}f_{2}^{{2l}}f_{2}^{{3l}}} \right\}$; $\mathop {\left[ {\mathbf{S}} \right]}\limits_{12 \times 36} $ – матрица, ненулевыми элементами которой являются базисные векторы узловых точек $\left\{ {{{{\mathbf{a}}}^{{ow}}}} \right\}$ = $\left\{ {{\mathbf{a}}_{1}^{{0w}}{\mathbf{a}}_{2}^{{0w}}{\mathbf{a}}_{3}^{{0w}}} \right\}$, ($w = i,j,k,l$).

С использованием (2.23) выражения (2.20) и (2.22) перепишутся следующим образом

${\mathbf{v}} = \left\{ {{{\gamma }_{1}}{{{\mathop {\left\{ {{{{\mathbf{a}}}^{{0i}}}} \right\}}\limits_{1 \times 3} }}^{T}}} \right. \ldots {{\gamma }_{4}}{{\mathop {\left\{ {{{{\mathbf{a}}}^{{0l}}}} \right\}}\limits_{1 \times 3} }^{T}}{{\gamma }_{5}}{{\mathop {\left\{ {{{{\mathbf{a}}}^{{0i}}}} \right\}}\limits_{1 \times 3} }^{T}} \ldots {{\gamma }_{8}}{{\mathop {\left\{ {{{{\mathbf{a}}}^{{0l}}}} \right\}}\limits_{1 \times 3} }^{T}}{{\gamma }_{9}}{{\mathop {\left\{ {{{{\mathbf{a}}}^{{0i}}}} \right\}}\limits_{1 \times 3} }^{T}} \ldots \left. {{{\gamma }_{{12}}}{{{\mathop {\left\{ {{{{\mathbf{a}}}^{{0l}}}} \right\}}\limits_{1 \times 3} }}^{T}}} \right\}\mathop {\left\{ {{{f}_{u}}} \right\}}\limits_{36 \times 1} $

(2.24)

${\mathbf{v}}{{,}_{\alpha }} = \left\{ {{{\gamma }_{{1,\alpha }}}{{{\mathop {\left\{ {{{{\mathbf{a}}}^{{0i}}}} \right\}}\limits_{1 \times 3} }}^{T}}} \right. \ldots \left. {{{\gamma }_{{12,\alpha }}}{{{\mathop {\left\{ {{{{\mathbf{a}}}^{{0l}}}} \right\}}\limits_{1 \times 3} }}^{T}}} \right\}\mathop {\left\{ {{{f}_{u}}} \right\}}\limits_{36 \times 1} $

${\mathbf{v}}{{,}_{{\alpha \beta }}} = \left\{ {{{\gamma }_{{1,\alpha \beta }}}{{{\mathop {\left\{ {{{{\mathbf{a}}}^{{0i}}}} \right\}}\limits_{1 \times 3} }}^{T}}} \right. \ldots \left. {{{\gamma }_{{12,\alpha \beta }}}{{{\mathop {\left\{ {{{{\mathbf{a}}}^{{0l}}}} \right\}}\limits_{1 \times 3} }}^{T}}} \right\}\mathop {\left\{ {{{f}_{u}}} \right\}}\limits_{36 \times 1} $

Входящие в (2.24) базисные векторы узловых точек можно выразить через базисные векторы внутренней точки конечного элемента с использованием (2.4)

(2.25)

$\mathop {\left\{ {{{{\mathbf{a}}}^{{0w}}}} \right\}}\limits_{3 \times 1} = \mathop {\left[ {{{\tau }^{w}}} \right]}\limits_{3 \times 3} \mathop {\left\{ {\mathbf{i}} \right\}}\limits_{3 \times 1} = \mathop {\left[ {{{\tau }^{w}}} \right]}\limits_{3 \times 3} {{\mathop {\left[ \tau \right]}\limits_{3 \times 3} }^{{ - 1}}}\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{3 \times 1} = \mathop {\left[ {{{z}^{w}}} \right]}\limits_{3 \times 3} \mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{3 \times 1} \quad \left( {w = i,j,k,l} \right)$

На основании (2.25) с учетом (2.8) соотношения (2.24) можно представить в виде

${{\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{1 \times 3} }^{T}}\mathop {\left\{ {v} \right\}}\limits_{3 \times 1} = {{\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{1 \times 3} }^{T}}\left[ {{{\gamma }_{1}}{{{\mathop {\left[ {{{z}^{i}}} \right]}\limits_{3 \times 3} }}^{T}} \ldots {{\gamma }_{{12}}}{{{\mathop {\left[ {{{z}^{l}}} \right]}\limits_{3 \times 3} }}^{T}}} \right]\mathop {\left[ Y \right]}\limits_{36 \times 36} \mathop {\left\{ {{{{v}}_{y}}} \right\}}\limits_{36 \times 1} $

(2.26)

${{\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{1 \times 3} }^{T}}\left\{ {\begin{array}{*{20}{c}} {f_{\alpha }^{1}} \\ {f_{\alpha }^{2}} \\ {f_{\alpha }^{3}} \end{array}} \right\} = {{\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{1 \times 3} }^{T}}\left[ {{{\gamma }_{{1,\alpha }}}{{{\mathop {\left[ {{{z}^{i}}} \right]}\limits_{3 \times 3} }}^{T}} \ldots {{\gamma }_{{12,\alpha }}}{{{\mathop {\left[ {{{z}^{l}}} \right]}\limits_{3 \times 3} }}^{T}}} \right]\mathop {\left[ Y \right]}\limits_{36 \times 36} \mathop {\left\{ {{{{v}}_{y}}} \right\}}\limits_{36 \times 1} $

${{\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{1 \times 3} }^{T}}\left\{ {\begin{array}{*{20}{c}} {f_{{\alpha \beta }}^{1}} \\ {f_{{\alpha \beta }}^{2}} \\ {f_{{\alpha \beta }}^{3}} \end{array}} \right\} = {{\mathop {\left\{ {{{{\mathbf{a}}}^{0}}} \right\}}\limits_{1 \times 3} }^{T}}\left[ {{{\gamma }_{{1,\alpha \beta }}}{{{\mathop {\left[ {{{z}^{i}}} \right]}\limits_{3 \times 3} }}^{T}} \ldots {{\gamma }_{{12,\alpha \beta }}}{{{\mathop {\left[ {{{z}^{l}}} \right]}\limits_{3 \times 3} }}^{T}}} \right]\mathop {\left[ Y \right]}\limits_{36 \times 36} \mathop {\left\{ {{{{v}}_{y}}} \right\}}\limits_{36 \times 1} ,$

где ${{\mathop {\left\{ {{{{v}}_{y}}} \right\}}\limits_{36 \times 1} }^{T}} = \left\{ {{{{v}}^{{1i}}} \ldots {{{v}}^{{1l}}}{v},_{1}^{{1i}} \ldots {v},_{1}^{{1l}}{v},_{2}^{{1i}} \ldots {v},_{2}^{{1l}}{{{v}}^{{2i}}} \ldots {{{v}}^{{2l}}} \ldots \ldots {v},_{2}^{{3i}} \ldots {v},_{2}^{{3l}}} \right\}$, $\mathop {\left[ Y \right]}\limits_{36 \times 36} $ – матрица преобразования между узловыми величинами $\left\{ {{{f}_{u}}} \right\}$ из (2.23) и $\left\{ {{{{v}}_{y}}} \right\}$.

Аппроксимирующие функции искомых величин можно представить из соотношения (2.26) следующим образом

(2.27)

$\begin{gathered} \mathop {\left\{ {v} \right\}}\limits_{3 \times 1} = \mathop {\left[ m \right]}\limits_{3 \times 36} \mathop {\left\{ {{{{v}}_{y}}} \right\}}\limits_{36 \times 1} \\ \left\{ {\begin{array}{*{20}{c}} {f_{\alpha }^{1}} \\ {f_{\alpha }^{2}} \\ {f_{\alpha }^{3}} \end{array}} \right\} = \mathop {\left[ {{{m}_{\alpha }}} \right]}\limits_{3 \times 36} \mathop {\left\{ {{{{v}}_{y}}} \right\}}\limits_{36 \times 1} ,\quad \left\{ {\begin{array}{*{20}{c}} {f_{{\alpha \beta }}^{1}} \\ {f_{{\alpha \beta }}^{2}} \\ {f_{{\alpha \beta }}^{3}} \end{array}} \right\} = \mathop {\left[ {{{m}_{{\alpha \beta }}}} \right]}\limits_{3 \times 36} \mathop {\left\{ {{{{v}}_{y}}} \right\}}\limits_{36 \times 1} \\ \end{gathered} $

При традиционной интерполяции компонент вектора перемещения как независимых скалярных величин их аппроксимирующие функции определяются выражениями

(2.28)

$\lambda = {{\mathop {\left\{ {\varphi \left( {\zeta ,~\eta } \right)} \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left\{ {{{\lambda }_{y}}} \right\}~}\limits_{12 \times 1} ,\quad \lambda {{,}_{\alpha }} = {{\mathop {\left\{ {\varphi {{,}_{\alpha }}\left( {\zeta ,~\eta } \right)} \right\}}\limits_{1 \times 12} }^{T}}\mathop {\left\{ {{{\lambda }_{y}}} \right\}~}\limits_{12 \times 1} ,$

где под символом ${{\lambda }}$ понимаются величины ${{{v}}^{1}},{{{v}}^{2}}$ и ${{{v}}^{3}}$.

Деформации (2.13) в произвольной точке оболочки с учетом (2.27) представляются в матричном виде

(2.29)

$\mathop {\left\{ {{{\varepsilon }^{\xi }}} \right\}}\limits_{3 \times 1} = \mathop {\left[ G \right]}\limits_{3 \times 6} \mathop {\left[ L \right]}\limits_{6 \times 3} \mathop {\left\{ {v} \right\}}\limits_{3 \times 1} = \mathop {\left[ G \right]}\limits_{3 \times 6} \mathop {\left[ L \right]}\limits_{6 \times 3} \mathop {\left[ m \right]}\limits_{3 \times 36} \mathop {\left\{ {{{{v}}_{y}}} \right\}}\limits_{36 \times 1} = \mathop {\left[ G \right]}\limits_{3 \times 6} \mathop {\left[ B \right]}\limits_{6 \times 36} \mathop {\left\{ {{{{v}}_{y}}} \right\}}\limits_{36 \times 1} $

Матрица жесткости конечного элемента. Матрица жесткости и столбец узловых усилий четырехугольного конечного элемента формируются на основе функционала, отражающего равенство действительных работ внешних и внутренних сил

(2.30)

$\Phi = \frac{1}{2}\mathop \smallint \limits_V^{} {{\left\{ {{{\varepsilon }^{\xi }}} \right\}}^{T}}\left\{ {{{\sigma }^{{\alpha \beta }}}} \right\}dV - \frac{1}{2}\mathop \smallint \limits_F^{} {{\left\{ {v} \right\}}^{T}}\left\{ P \right\}dF,$

где ${{\left\{ {{{\sigma }^{{\alpha \beta }}}} \right\}}^{T}} = \left\{ {{{\sigma }^{{11}}}{{\sigma }^{{22}}}{{\sigma }^{{12}}}} \right\}$ – матрица-строка напряжений в произвольном слое оболочки, отстоящем на расстоянии ${{\xi }}$ от срединной поверхности; ${{\left\{ P \right\}}^{T}} = \left\{ {{{p}_{1}}{{p}_{2}}{{p}_{3}}} \right\}$ – столбец внешней нагрузки.

С учетом (2.15) и (2.29) функционал (2.30) может быть преобразован к виду

(2.31)

$\begin{gathered} \Phi = \frac{1}{2}\mathop {{{{\left\{ {{v}_{y}^{g}} \right\}}}^{T}}}\limits_{1 \times 36~~~~} \mathop {{{{\left[ {PR} \right]}}^{T}}}\limits_{36 \times 36~} \mathop \smallint \limits_V^{} \mathop {{{{\left[ В \right]}}^{T}}}\limits_{36 \times 6~~~~} \mathop {{{{\left[ G \right]}}^{T}}}\limits_{6 \times 3~~~~} \mathop {\left[ C \right]}\limits_{~3 \times 3~} \mathop {\left[ G \right]}\limits_{3 \times 6~} \mathop {\left[ В \right]}\limits_{6 \times 36~} dV\mathop {\left[ {PR} \right]}\limits_{36 \times 36~} \mathop {\left\{ {{v}_{y}^{g}} \right\}}\limits_{36 \times 1~} \; - \\ - \;\mathop {\frac{1}{2}{{{\left\{ {{v}_{y}^{g}} \right\}}}^{T}}}\limits_{1 \times 36~~~} \mathop {{{{\left[ {PR} \right]}}^{T}}}\limits_{36 \times 36~} \mathop \smallint \limits_F^{} \mathop {{{{\left[ A \right]}}^{T}}}\limits_{36 \times 3~} \mathop {\left\{ P \right\}}\limits_{~3 \times 1~} dF, \\ \end{gathered} $

где $\mathop {\left[ {PR} \right]}\limits_{36 \times 36~} $ – матрица перехода от столбца $\left\{ {{v}_{y}^{l}} \right\}$ к столбцу $\left\{ {{v}_{y}^{g}} \right\}$.

В результате минимизации (2.31) по ${{\left\{ {{v}_{y}^{g}} \right\}}^{T}}$ можно получить следующее матричное выражение

(2.32)

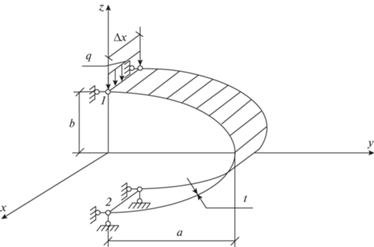
$\mathop {\left[ {{{K}^{g}}} \right]}\limits_{36 \times 36~} \mathop {\left\{ {{v}_{y}^{g}} \right\}}\limits_{36 \times 1~} = \mathop {\left[ {{{R}^{g}}} \right]}\limits_{36 \times 1~} ,$

где $\mathop {\left[ {{{K}^{g}}} \right]}\limits_{36 \times 36~} = \mathop {{{{\left[ {PR} \right]}}^{T}}}\limits_{36 \times 36~} \int_V {\mathop {{{{\left[ В \right]}}^{T}}}\limits_{36 \times 6~~~~} } \mathop {{{{\left[ G \right]}}^{T}}}\limits_{6 \times 3~~~~} \mathop {\left[ C \right]}\limits_{~3 \times 3~} \mathop {\left[ G \right]}\limits_{3 \times 6~} \mathop {\left[ В \right]}\limits_{6 \times 36~} dV\mathop {\left[ {PR} \right]}\limits_{36 \times 36~} $ – матрица жесткости; $\mathop {\left[ {{{R}^{g}}} \right]}\limits_{36 \times 1~} $ = = $\mathop {{{{\left[ {PR} \right]}}^{T}}}\limits_{36 \times 36~} \int_F {\mathop {{{{\left[ A \right]}}^{T}}}\limits_{36 \times 3~} \mathop {\left\{ P \right\}}\limits_{~3 \times 1~} dF} $ – столбец узловых усилий четырехугольного конечного элемента в глобальной системе координат.

3. Результаты. В качестве примера была решена тестовая задача по определению напряженно-деформированного состояния фрагмента эллиптического цилиндра, нагруженного вдоль образующей линейной нагрузкой интенсивности q, с шарнирно-подвижными опорами на меридиане точки 1 и с шарнирно-неподвижными на меридиане точки 2 (рис. 2).

Рис. 2.

Фрагмент эллиптического цилиндра.

Были приняты следующие исходные данные: $q = 5 \times {{10}^{{ - 3}}}$ кН/м; большая полуось эллипса $a = 0.1$ м; $E = 2 \times {{10}^{5}}$ МПа; ${v} = 0.3$; t = 0.001 м. Малая полуось эллипса $b$ была принята равной 0.025 м. Вследствие наличия плоскостей симметрии рассчитываемая оболочка моделировалась полоской конечных элементов шириной Δx = 0.01 м.

Расчет выполнялся в двух вариантах. В первом варианте при формировании матрицы жесткости использовалась традиционная интерполяционная процедура, полученная по (2.28). Во втором варианте при формировании матрицы жесткости конечного элемента использовались разработанные аппроксимирующие выражения (2.27).

В табл. 1 представлены значения физических кольцевых напряжений на внутренней $\sigma _{{22}}^{{v}}$ и наружной $\sigma _{{22}}^{n}$ поверхностях цилиндра в точках 1 и 2 в зависимости от густоты сетки дискретизации оболочки для скалярной и векторной форм аппроксимаций перемещений.

Таблица 1.

Расчет фрагмента эллиптического цилиндра при использовании скалярной и векторной форм аппроксимаций перемещений

Варианты аппроксимаций	Координаты точек (x, t)	Напряжения, МПа	Сетка дискретизации
Варианты аппроксимаций	Координаты точек (x, t)	Напряжения, МПа	37 × 2	49 × 2	97 × 2
Скалярная аппроксимация	Точка (1) приложения силы (0; 0)	$\sigma _{{22}}^{{v}}$	134.62	148.12	157.80
	Точка (1) приложения силы (0; 0)	$\sigma _{{22}}^{n}$	–135.12	–148.10	–157.42
	Точка (2) шарнирного опирания (0; π)	$\sigma _{{22}}^{{v}}$	64.10	118.61	156.23
	Точка (2) шарнирного опирания (0; π)	$\sigma _{{22}}^{n}$	–63.07	–117.90	–155.81
Векторная аппроксимация	Точка (1) приложения силы (0; 0)	$\sigma _{{22}}^{{v}}$	158.27	158.46	158.58
	Точка (1) приложения силы (0; 0)	$\sigma _{{22}}^{n}$	–158.53	–158.35	–158.22
	Точка (2) шарнирного опирания (0; π)	$\sigma _{{22}}^{{v}}$	158.27	158.46	158.58
	Точка (2) шарнирного опирания (0; π)	$\sigma _{{22}}^{n}$	–158.53	–158.35	–158.22

Замена шарнирных опор на пружинные позволит рассчитываемой конструкции перемещаться вертикально вниз, как абсолютно твердому телу, под действием линейно распределенной нагрузки.

Результаты расчетов напряженно-деформированного состояния рассчитываемой оболочки с пружинными опорами для скалярной и векторной форм аппроксимаций перемещений представлены в табл. 2. Для скалярной аппроксимации использовалась сетка дискретизации (337 × 2), для векторной – 49 × 2.

Таблица 2.

Расчет напряженно-деформированного состояния оболочки с пружинными опорами при использовании скалярной и векторной форм аппроксимаций перемещений

Жесткость пружины, 10² Н/м			∞	0.1	0.01	0.02
Величина жесткого смещения, 10^–2 м			0.00	1.00	10.00	20.00
Варианты аппроксимаций	Координаты точек (x, t)	Напряжения, МПа	Значения напряжений в контролируемых точках, при заданных смещениях оболочки
Скалярная аппроксимация	Точка (1) приложения силы (0; 0)	$\sigma _{{22}}^{{v}}$	157.19	153.22	117.74	–213.55
	Точка (1) приложения силы (0; 0)	$\sigma _{{22}}^{n}$	–156.79	–152.89	–117.96	208.22
	Точка (2) шарнирного опирания (0; π)	$\sigma _{{22}}^{{v}}$	157.21	161.07	195.54	517.45
	Точка (2) шарнирного опирания (0; π)	$\sigma _{{22}}^{n}$	–156.81	–160.61	–194.54	–511.36
Вертикальное смещение оболочки, 10^–2 м			0	0.99928	9.92892	19.32095
Векторная аппроксимация	Точка (1) приложения силы (0; 0)	$\sigma _{{22}}^{{v}}$	157.20	157.20	157.20	157.20
	Точка (1) приложения силы (0; 0)	$\sigma _{{22}}^{n}$	–156.81	–156.81	–156.81	–156.81
	Точка (2) шарнирного опирания (0; π)	$\sigma _{{22}}^{{v}}$	157.20	157.20	157.20	157.20
	Точка (2) шарнирного опирания (0; π)	$\sigma _{{22}}^{n}$	–156.81	–156.81	–156.81	–156.81
Вертикальное смещение оболочки, 10^–2 м			0.00	1.00	10.00	20.00

4. Обсуждение. Оценка достоверности результатов конечно-элементных решений определялась следующими критериями: сходимостью вычислительного процесса и условием равенства численных значений кольцевых напряжений в точках 1 и 2. Из табл. 1 видно, что использование векторной аппроксимации требует значительно меньшего числа элементов дискретизации для достижения приемлемых численных значений окружных напряжений. Достоверные численные значения кольцевых напряжений в первом варианте расчета наблюдаются при минимальной густоте сетки 97 × 2, в то время как при векторном способе интерполяции перемещений эти значения достигаются уже при сетке 37 × 2.

В точках 1 и 2 должно соблюдаться равенство значений кольцевых напряжений во внутренних и наружных волокнах. Данные табл. 1 показывают, что при использовании скалярной аппроксимации перемещений данное условие выполняется не сразу и вызывает необходимость значительно сгущать сетку дискретизации. Векторная интерполяция полей перемещений приводит к выполнению этого условия уже при сетке дискретизации 37 × 2.

Из табл. 2 видно, что при отсутствии жесткого смещения первый и второй варианты расчета позволяют получать достоверные конечно-элементные решения.

При смещении оболочки как жесткого целого в первом варианте расчета условие равенства кольцевых напряжений в точках 1 и 2 не выполняется, а при значительной величине смещения (0.2 м) численные показатели напряжений достигают и вовсе неприемлемых значений.

Как видно из табл. 2 инвариантная интерполяционная процедура векторных полей перемещений дает возможность получать приемлемые значения напряжений даже при значительной величине смещения оболочки как жесткого целого. Условие равенства кольцевых напряжений в точках 1 и 2 также выполняется.

Заключение. Опираясь на анализ вышеизложенных результатов, можно сделать следующие выводы. Разработанный алгоритм может быть рекомендован к расчету произвольных оболочечных конструкций, так как соответствует геометрическому смыслу при использовании реальной матрицы $[{{z}^{w}}]$ в координатном преобразовании аппроксимирующих выражений.

Предложенный способ интерполяции векторов перемещений позволяет с высокой степенью точности определять параметры напряженно-деформированного состояния в характерных точках рассчитываемой конструкции.

Сравнительный анализ предложенного способа интерполяции полей перемещений в сравнении с общепринятым показал, что использование традиционной интерполяции требует значительно большего сгущения сетки элементов дискретизации для достижения сходимости вычислительного процесса даже при отсутствии смещения как жесткого целого.

Скалярная аппроксимация не дает возможности получать достоверные значения контролируемых параметров напряженно-деформированного состояния при наличии смещения конструкции как жесткого целого, что является общепризнанной проблемой МКЭ. Предложенные аппроксимирующие функции позволяют автоматически учитывать смещения конечного элемента оболочки как абсолютно твёрдого тела.

Исследование проведено при поддержке грантов РФФИ и администрации Волгоградской области № 19-41-340002 р_а и № 19-41-343003р_мол_а.

Список литературы

Новожилов В.В. Краткий очерк развития теории оболочек в СССР // Исслед. по теории пластин и оболочек. Казань: Изд-во Казанского ун-та, 1970. Вып. 6–7. С. 3–22.
Григолюк Э.И., Кабанов В.В. Устойчивость оболочек. М.: Наука, 1978. 360 с.
Железнов Л.П., Кабанов В.В., Бойко Д.В. Нелинейное деформирование и устойчивость дискретно-подкрепленных овальных цилиндрических композитных оболочек при поперечном изгибе и внутреннем давлении // Пробл. машиностр. и надежн. машин. 2014. № 6. С. 23–30.
Zienkiewicz O.C., Taylor R.L. The finite element method // B: A Division of Reed Educ. & Prof. Publishing Ltd. 2010. V. 2. P. 477.
Голованов А.И. Современные конечно-элементные модели и методы исследования тонкостенных конструкций. Казань: Казан. гос. ун-т, 2005. 440 с.
Lalin V., Rybakov V., Sergey A. The finite elements for design of frame of thin-walled beams // Appl. Mech. & Mater. 2014. V. 578–579. P. 858–863.
Ефанов К.В. Расчет нефтяных аппаратов методом конечных элементов. Литрес: Самиздат, 2020. 132 с.
Badriev I.B., Paimushin V.N. Refined models of contact interaction of a thin plate with postioned onboth sides deformable foundations // Lobachevskii J. Math. 2017. V. 38 (5). P. 779–793.
Агапов В.П. Метод конечных элементов в статике, динамике и устойчивости пространственных тонкостенных подкрепленных конструкций. М.: Изд-во АСВ, 2000. 152 с.
Aldakheel F., Hudobivnik B., Wriggers P. Virtual element formulation for phase-field modeling of ductile fracture // Int. J. for Multiscale Comput. Engng. 2019. V. 17 (2). P. 181–200.
Magisano D., Leonetti L., Garcea G. Koiter asymptotic analysis of multilayered composite structures using mixed solid-shell finite elements // Composite Struct. 2016. V. 154. P. 296–308. https://doi.org/10.1016/j.compstruct.2016.07.046
Голованов А.И., Корнишин М.С. Введение в метод конечных элементов статики тонких оболочек. Казань: КФ АН СССР, 1989. 271 с.
Тюкалов Ю.Я. Равновесные конечные элементы для плоских задач теории упругости // Инж.-строит. ж. 2019. № 7 (91). С. 80–97.
Голованов А.И., Песошин А.В., Тюленева О.Н. Современные конечно-элементные модели и методы исследования тонкостенных конструкций. Казань: КГУ, 2005. 442 с.
Скопинский В.Н. Напряжения в пересекающихся оболочках. М.: Физматлит, 2008. 400 с.
Гуреева Н.А., Клочков Ю.В., Николаев А.П., Клочков М.Ю. Непрерывная параметризация срединной поверхности эллипсоидальной оболочки и ее геометрические параметры // Матем. физика и компьют. моделир. 2020. Т. 23. № 1. С. 5–12.
Седов Л.И. Механика сплошной среды: учебник для студентов университетов и высших технических учебных заведений. Т. 1. М.: Наука, 1983. 528 с.
Dzhabrailov A.Sh., Klochkov Yu.V., Marchenko S.S., Nikolaev A.P. The finite element approximation of vector fields in curvilinear coordinates // Rus. Aeron. 2007. V. 50(2). P. 115–120.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал