Прикладная математика и механика, 2022, T. 86, № 2, стр. 216-222
О подъемной силе в потоке разреженного газа
С. Л. Горелов 1, 2, *, А. В. Могорычная 2, **
1 ФГУП ЦАГИ
Жуковский, Россия
2 Московский физико-технический институт
Долгопрудный, Россия
* E-mail: gorelovsl@yandex.ru
** E-mail: anna.magorychnaya@phystech.edu
Поступила в редакцию 05.12.2021
После доработки 19.01.2022
Принята к публикации 23.01.2022
- EDN: GHNSYF
- DOI: 10.31857/S0032823522020060
Аннотация
Вычисляются аэродинамические силы, действующие на клин и конус в потоке разреженного газа. Доказывается, что существует такой угол полураствора клина и конуса, что при увеличении этого угла подъемная сила становится отрицательной при произвольном угле атаки. Для высокоскоростных течений показано, что такой эффект существует при произвольном числе Рейнольдса.
1. Введение. Эффект изменения знака подъемной силы при изменении угла атаки в высокоскоростных плоских течениях впервые был обнаружен в [1]. В свободномолекулярном течении такой эффект был найден в [2]. Данная работа является развитием идей из [2]. Показано, что при обтекании клина разреженным газом при определенным соотношении угла полураствора и угла атаки подъемная сила клина может стать отрицательной. Причем, этот эффект проявляется при любых скоростях газа и отношениях температур поверхности клина и газа. Более того, такой эффект есть и в случае гиперзвукового течения невязкого газа (модель Ньютона). Для высокоскоростных течений на основе локального метода [3] показано, что эффект изменения знака подъемной силы при определенных значениях угла полураствора существует для клина и конуса при произвольном числе Рейнольдса.
2. Свободномолекулярный случай. Обтекание клина. Рассматривается свободномолекулярное обтекание клина конечной длины с углом полураствора $\delta $ и углом атаки $0 \leqslant \alpha \leqslant \pi {\text{/}}2$.
Теорема 1. Существует такое значение $\delta = {{\delta }_{0}}$, что при $\delta \geqslant {{\delta }_{0}}$ коэффициент подъемной силы клина $Cy \leqslant 0$, и $0 \leqslant \alpha \leqslant \pi {\text{/}}2$, а при $\delta < {{\delta }_{0}}$ имеем $Cy > 0$ в некотором интервале значений угла атаки $\alpha $ из множества $0 \leqslant \alpha \leqslant \pi {\text{/}}2$. Значение $\delta = {{\delta }_{0}}$ определяется из уравнения
Доказательство. Коэффициенты давления и трения для плоской пластины под углом атаки $\theta $ равны [5]
(2.1)
$\begin{gathered} Cp = \frac{1}{{{{S}^{2}}\sqrt \pi }}\left[ {{{S}_{\theta }}\exp \left( { - S_{\theta }^{2}} \right) + \sqrt \pi \left( {\frac{1}{2} + S_{\theta }^{2}} \right)\left( {1 + \operatorname{erf} {{S}_{\theta }}} \right) + \frac{{\sqrt {\pi t} }}{2}\chi \left( {{{S}_{\theta }}} \right)} \right] \\ C\tau = \frac{{\cos \theta }}{{S\sqrt \pi }}\chi \left( {{{S}_{\theta }}} \right),\quad \chi \left( x \right) = \exp \left( { - {{x}^{2}}} \right) + x\sqrt \pi \left( {1 + \operatorname{erf} x} \right) \\ \end{gathered} $Здесь $S = {{U}_{\infty }}\sqrt {m{\text{/}}2k{{T}_{\infty }}} $, ${{U}_{\infty }}$ – скорость газа, $m$ – масса молекулы, $k$ – постоянная Больцмана, ${{T}_{\infty }}$ – температура газа, ${{T}_{w}}$ – температура поверхности, $t = {{T}_{w}}{\text{/}}{{T}_{\infty }}$ = = ${{t}_{w}}\left( {1 + {{S}^{2}}\left( {\gamma - 1} \right){\text{/}}\gamma } \right)$, ${{t}_{w}}$ – температурный фактор, $\gamma $ – отношение теплоемкостей, ${{S}_{\theta }} = S\sin \theta $.
Коэффициент подъемной силы выражается
Для верхней части клина $\theta = {{\theta }_{u}} = \delta - \alpha $, для нижней части $\theta = {{\theta }_{b}} = \delta + \alpha $.
(2.3)
$\begin{gathered} C{{y}_{b}} = Cp\cos \left( {\delta + \alpha } \right) - C\tau \sin \left( {\delta + \alpha } \right) \\ C{{y}_{u}} = - Cp\cos \left( {\delta - \alpha } \right) - C\tau \sin \left( {\delta - \alpha } \right) \\ \end{gathered} $Коэффициент подъемной силы клина выражается формулой
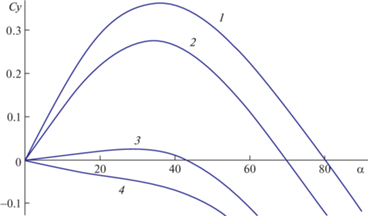
На рис. 1 представлены графики зависимостей $Cy$ от угла атаки $\alpha $ для разных величин угла полураствора $\delta $. Из графиков хорошо видно, что с увеличением $\delta $ кривая $Cy\left( \alpha \right)$ отходит от точки $\alpha = 0$ все ближе к горизонтали. И при некотором значении $\delta = {{\delta }_{0}}$ кривая при $\alpha = 0$ становится горизонтальной, а затем при увеличении $\delta $ значения $Cy$ становятся отрицательными. Определить эту величину ${{\delta }_{0}}$ можно из уравнения
(2.5)
${{\left. {\frac{{dCy\left( {\alpha ,\delta } \right)}}{{d\alpha }}} \right|}_{{\alpha = 0}}} = 0$Рис. 1.
Зависимость $Cy$ от угла атаки $\alpha $ при разных значениях $\delta $ ($S = 2$, ${{t}_{w}} = 0.1$, $\gamma = 1.4$): кривые 1–4 соответствуют значениям $\delta $ = 10°; 20°; 36°; 40°.
Из уравнения (2.5) определяем значения ${{\delta }_{0}}$ в зависимости от скорости набегающего потока $S$ и температурного фактора ${{t}_{w}}$.
Из рис. 1 видно, что зависимость $Cy\left( \alpha \right)$ немонотонна. Причем при любом угле полураствора $\delta $, начиная с некоторого угла, эта зависимость величина $Cy\left( \alpha \right)$ становится отрицательной. Отсюда следует
Теорема 2. При любом значении угла полураствора $\delta < {{\delta }_{0}}$ найдется такой угол атаки $\alpha = {{\alpha }_{0}}$ из множества $0 \leqslant \alpha \leqslant \pi {\text{/}}2$, что при $\alpha > {{\alpha }_{0}}$ коэффициент подъемной силы $Cy < 0$.
Рис. 2.
Зависимость ${{\delta }_{0}}$ от скоростного отношения $S$ для разных температурных факторов: кривые 1–3 соответствуют значениям ${{t}_{w}} = 1$; 0.1; 0.01.
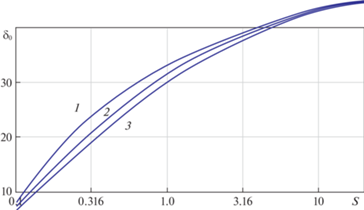
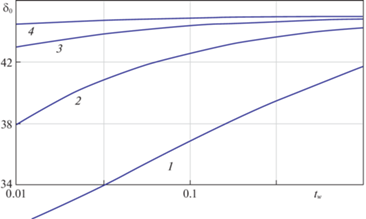
Рис. 3.
Зависимость ${{\delta }_{0}}$ от температурного фактора ${{t}_{w}}$ при разных значениях скоростного отношения: кривые 1–4 соответствуют значениям $S = 2$; 5; 10; 20.
Доказательство.
Эту теорему можно доказать непосредственным нахождением ${{\alpha }_{0}}$ из решения уравнения
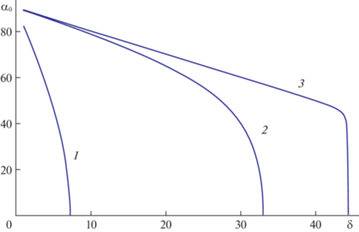
На рис. 4 показан пример зависимости ${{\alpha }_{0}}\left( \delta \right)$.
Рис. 4.
Зависимость ${{\alpha }_{0}}\left( \delta \right)$ для ${{t}_{w}} = 0.1$: кривые 1–3 соответствуют значениям $S = 0.1$; 1.0; 10.0.
3. Высокоскоростные течения. Локальный метод. Клин. В высокоскоростном потоке при $S \to \infty $ возможно использовать метод, основанный на гипотезе локальности [6], которая состоит в следующем: аэродинамические коэффициенты сил, действующие на элемент поверхности, зависят только от местного угла наклона $\theta $ этого элемента к вектору скорости набегающего потока ${{U}_{\infty }}$, от характерного для всего тела числа ${{\operatorname{Re} }_{0}} = {{\rho }_{\infty }}{{U}_{\infty }}L{\text{/}}{{\mu }_{0}}$ и температурного фактора ${{t}_{w}} = {{T}_{w}}{\text{/}}{{T}_{0}}$, где ${{\mu }_{0}} = \mu \left( {{{T}_{0}}} \right)$ – коэффициент вязкости, вычисляемый по температуре торможения; ${{T}_{0}}$ = ${{T}_{\infty }}[1 + {{S}^{2}}\left( {\gamma - 1} \right){\text{/}}\gamma ]$, ${{T}_{w}}$ – температура торможения и температура элемента поверхности, соответственно; $\gamma $ – отношение удельных теплоемкостей; $L$ – характерный размер тела. В соответствие с гипотезой локальности предполагается, что для аэродинамических коэффициентов справедливы соотношения [6]
(3.1)
$\begin{gathered} Cp = {{p}_{0}}{{\sin }^{2}}\theta + {{p}_{1}}\sin \theta \\ C\tau = {{\tau }_{0}}\cos \theta \sin \theta \\ \end{gathered} $Тогда, в свободномолекулярном случае $\left( {{{{\operatorname{Re} }}_{0}} \to 0} \right)$ из (2.1) при $S \to \infty $ следует:
Теорема 1 доказывается так же как в разд. 2 и критический угол вычисляется из решения уравнения (2.5).
В свободномолекулярном случае $\left( {{{{\operatorname{Re} }}_{0}} \to 0} \right)$ уравнение (2.5) имеет вид
Теорема 2 как и в случае разд. 2 доказывается прямым решением уравнения (2.6). Получается, что в этом случае такого угла нет, то есть ${{\alpha }_{0}}$ = 90°.
В случае невязкого газа (${{\operatorname{Re} }_{0}} \to \infty $) используется формула Ньютона и нахождение критического угла сводится к решению уравнения
Исключая нефизичные значения корней ($\left| \delta \right| > \pi {\text{/}}2$) и отрицательные значения (вследствие симметрии), получаем
Решение уравнения (2.6) дает доказательство теоремы 2. Результат этого решения показан на рис. 5.
Рис. 5.
Зависимость ${{\alpha }_{0}}\left( \delta \right)$ для клина в случае модели Ньютона (${{\operatorname{Re} }_{0}} \to \infty $).
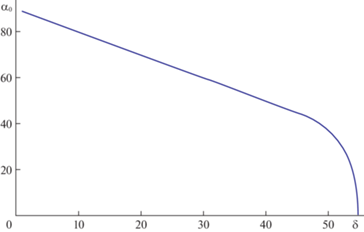
4. Высокоскоростные течения. Конус. Используя формулы (3.1) коэффициент подъемной силы конуса запишется [6]
(4.1)
$\begin{gathered} {{C}_{y}} = \left\{ {({{p}_{0}} - {{\tau }_{0}}){{{\sin }}^{2}}\delta \cos \alpha \left[ {{{{\cos }}^{2}}\alpha f(z) - g(z)} \right]} \right. + \\ + \;{{p}_{1}}\left. {\sin \delta \left[ {{{{\cos }}^{2}}\alpha g(z) - h(z)} \right]} \right\}\operatorname{ctg} \alpha ;\quad z = \operatorname{tg} \delta \operatorname{ctg} \alpha \\ \end{gathered} $При $z \geqslant 1$ $f(z) = 1 + \frac{3}{{2{{z}^{2}}}}$, $g(z) = 1 + \frac{1}{{2{{z}^{2}}}}$, $h(z) = 1$;
При $z < 1\quad \left\{ {\begin{array}{*{20}{l}} {f(z) = \frac{1}{\pi }\left[ {\left( {1 + \frac{3}{{2{{z}^{2}}}}} \right)\left( {\pi - \arccos z} \right) + \frac{1}{z}\left( {\frac{{11}}{6} + \frac{2}{{3{{z}^{2}}}}} \right)\sqrt {1 - {{z}^{2}}} } \right]} \\ {g(z) = \frac{1}{\pi }\left[ {\left( {1 + \frac{1}{{2{{z}^{2}}}}} \right)(\pi - \arccos z) + \frac{3}{{2z}}\sqrt {1 - {{z}^{2}}} } \right]} \\ {h(z) = \frac{1}{\pi }\left( {\pi - \arccos z + \frac{1}{z}\sqrt {1 - {{z}^{2}}} } \right)} \end{array}} \right.$
Для доказательства теоремы 1 из решения уравнения (2.5) находим значение ${{\delta }_{0}}$ = = 35.26°.
Для доказательства теоремы 2 решаем уравнение $Cy = 0$ при $\delta < {{\delta }_{0}}$. Результат решения на рис. 6.
Рис. 6.
Зависимость ${{\alpha }_{0}}\left( \delta \right)$ для кругового конуса в свободномолекулярной модели (${{\operatorname{Re} }_{0}} \to 0$) – кривая 1 и модель Ньютона (${{\operatorname{Re} }_{0}} \to \infty $) – кривая 2.
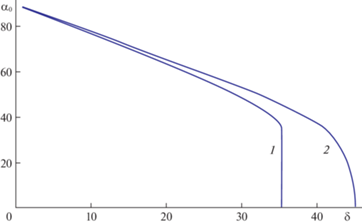
В случае модели Ньютона подставляем в эти выражения ${{p}_{0}} = 2$, ${{p}_{1}} = {{\tau }_{0}} = 0$ получаем формулы локального метода для конуса. Уравнение (2.5) дает
Заключение. В статье рассматриваются коэффициенты подъемной силы клина и кругового конуса для двух моделей течения: свободномолекулярная модель газа и модель основанная на гипотезе локальности высокоскоростных течений. Для данных случаев сформулированы и доказаны теоремы, согласно которым для любого угла полураствора найдется такой угол атаки, начиная с которого коэффициент подъемной силы становится отрицательным, и также существует угол полураствора, начиная с которого коэффициент подъёмной силы отрицателен для любого угла атаки.
Работа выполнена при поддержке РФФИ, грант № 20-08-00790.
Список литературы
Галкин В.С., Гладков А.А. О подъемной силе при гиперзвуковых скоростях // ПММ. 1961. Т. 25. Вып. 6. С. 1138–1139.
Галкин В.С. О подъемной силе в свободномолекулярном потоке // ПММ. 1962. Т. 26. Вып. 3. С. 567.
Василенко Д.А., Дорофеев Ф.Е., Дорофеев Е.А. Построение нейросетевого аппроксиматора для определения критического угла полураствора в эффекте смены знака коэффициента подъемной силы для затупленных конических тел // Тр. МАИ. 2021. Вып. 119.
Ньютон И. Математические начала натуральной философии. М.: Наука, 1989, 688 с.
Коган М.Н. Динамика разреженного газа. М.: Наука, 1967, 440 с.
Галкин В.С., Ерофеев А.И., Толстых А.И. Приближенный метод расчета аэродинамических характеристик тел в гиперзвуковом разреженном газе // Тр. ЦАГИ. 1977. Вып. 1833. С. 6–10.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика


