Прикладная математика и механика, 2022, T. 86, № 2, стр. 235-250

1. Введение. Контакт поверхностей во влажной атмосфере при определенных условиях сопровождается капиллярной конденсацией и образованием менисков жидкости, стягивающих отдельные контактирующие микронеровности двух поверхностей или удерживающих на поверхности микрочастицы износа и загрязнений. Силы капиллярной адгезии, возникающие в таких микроменисках, могут достигать значительных величин и существенно влиять на динамическую и статическую силы трения [1], что является одной из причин заедания и поломок в микромеханических системах [2], а также важным фактором в сцеплении биологических материалов [3].

Для моделирования контакта отдельного выступа или частицы износа с контртелом в условиях статического трения рассматривается решение контактной задачи для осесимметричного индентора и упругого полупространства под действием нормальной и тангенциальной сил, когда приложенная тангенциальная сила недостаточно велика, чтобы вызвать полное скольжение, и область контакта делится на зоны сцепления и проскальзывания. Исследование влияния мениска жидкости, окружающего область контакта, на решение такой задачи является целью настоящей работы.

Решение задачи о контакте с частичным проскальзыванием для двух упругих шаров было получено Каттанео [4] и Миндлиным [5] и обобщено для случая произвольных осесимметричных тел в работах Йегера [6] и позже Чиавареллы [7], а также обобщено для случая трансверсально изотропных тел [8]. Предположение об идентичности материалов контактирующих тел позволило рассматривать задачи о нормальном и тангенциальном нагружении отдельно друг от друга. При этом считалось, что в области скольжения нормальные $p$ и касательные $\tau $ напряжения связаны одночленным законом трения Амонтона $\tau = \mu p$, где $\mu $ – коэффициент трения. В такой постановке были в дальнейшем рассмотрены задачи для различной геометрии взаимодействующих тел, в частности, для текстурированных поверхностей [9, 10].

Влияние адгезии, вызванной межмолекулярными силами, в условиях контакта сухих поверхностей на решение задачи о частичном проскальзывании изучалось в [11–13] для случая плоской задачи и в [14–16] для пространственного осесимметричного контакта. В работах [11–15] решение строилось аналитически в рамках приближения об идентичности материалов взаимодействующих тел, а в [16] – численно для пары различных материалов. Заметим, что локальный закон трения в форме Амонтона $\tau = \mu p$ неприменим для задач с учетом адгезии, в которых контактное давление на части области контакта становится отрицательным, а значит, отрицательным должно быть и касательное напряжение в этой области, что физически невозможно. Поэтому в работах [11, 12, 14] касательное напряжение в области проскальзывания считалось постоянным $\tau = {{\tau }_{0}}$, а в работах [13, 15, 16] использовался закон трения $\tau = \mu p$, но предполагалось, что в области контакта действует только положительное нормальное давление $p$. Однако, закон трения в виде постоянного касательного напряжения $\tau = {{\tau }_{0}}$ не позволяет учесть влияние нормальных напряжений на касательные. Предположение о только положительном нормальном давлении в области контакта также не является физически достоверным, в частности, оно не позволяет исследовать случай отрицательной внешней нагрузки, когда контакт по конечной области существует благодаря адгезии, и контактные давления могут стать отрицательными в значительной части области контакта или во всей этой области.

В настоящей работе предлагается преодолеть эту трудность путем использования двучленного закона трения Кулона в области проскальзывания:

где величины ${{\tau }_{0}}$ и $\mu $ таковы, чтобы обеспечить неотрицательные касательные напряжения во всей области проскальзывания даже при отрицательных значениях нормального давления $p$. В работе рассмотрено контактное взаимодействие в условиях частичного проскальзывания с учетом капиллярной адгезии, вызванной наличием в зазоре между телами мениска жидкости.

2. Постановка задачи. Рассматривается контакт упругого полупространства и упругого индентора в присутствии мениска жидкости, стягивающего поверхности вне области контакта. Пусть ось $z$ декартовой системы координат ($x,y,z$) направлена вглубь упругого полупространства, а плоскость $z = 0$ совпадает с поверхностью полупространства. К индентору сначала приложена внешняя нормальная сила $P$, действующая вдоль оси $z$, и после этого приложена тангенциальная сила T, действующая в направлении оси x (рис. 1). Форма индентора описывается функцией $f(x,y)$ = = $A{{({{x}^{2}} + {{y}^{2}})}^{n}}$, где $n \geqslant 1$ – целое число.

Пусть внутри области ${{\Omega }_{c}}$ поверхности находятся в контакте, а мениск занимает область ${{\Omega }_{m}}$. Граничные условия при $z = 0$ для давления и перемещения в направлении оси $z$ определяются формой индентора $f(x,y)$ в области контакта и постоянным капиллярным давлением ${{p}_{0}}$ в области мениска:

где ${{u}_{z}} = {{u}_{{z1}}} + {{u}_{{z2}}}$ – суммарное нормальное смещение поверхностей взаимодействующих тел за счет их деформирования, ${{\delta }_{z}}$ – внедрение индентора в полупространство в направлении оси $z$. При этом капиллярное давление под искривленной поверхностью мениска ${{p}_{0}}$ определяется формулой Лапласа где $\gamma $ – поверхностное натяжение жидкости, ${{R}_{1}}$, ${{R}_{2}}$ – радиусы кривизны мениска в двух взаимно ортогональных плоскостях, определяемые начальной геометрией и упругой деформацией индентора и полупространства.

Считается, что величина тангенциальной силы T недостаточна для того, чтобы вызвать скольжение во всей области контакта ${{\Omega }_{c}}$, т.е. область контакта делится на области сцепления ${{\Omega }_{{st}}}$ и проскальзывания ${{\Omega }_{{sl}}}$. При этом граничные условия в направлении оси x определяются тангенциальным перемещением ${{\delta }_{x}}$ индентора в области сцепления и законом трения (1.1) в области проскальзывания:

Условия равновесия в нормальном и тангенциальном направлении имеют вид:

3. Метод решения. Решение задачи строится в предположении, что упругие постоянные материалов индентора и полупространства одинаковы, и уравнения, связывающие контактные напряжения и перемещения в нормальном и тангенциальном направлениях не зависят друг от друга [7, 18]:

где $E* = {E \mathord{\left/ {\vphantom {E {(1 - {{\nu }^{2}})}}} \right. \kern-0em} {(1 - {{\nu }^{2}})}}$, $E$ – модуль Юнга, $\nu $ – коэффициент Пуассона материалов индентора и полупространства. Таким образом, задача о нормальном контакте может решаться независимо от задачи о тангенциальном нагружении.

Задача о нормальном нагружении упругого осесимметричного контакта при наличии мениска определяется условиями (2.1) и (2.2), а также первыми уравнениями из (2.4) и (3.1). В этом случае задача является осесимметричной: форма индентора описывается функцией $f(r) = A{{r}^{{2n}}}$, где $r = \sqrt {{{x}^{2}} + {{y}^{2}}} $, контактное давление $p$ и перемещение ${{u}_{z}}$ также являются функциями радиальной координаты $r$, область контакта ${{\Omega }_{c}}$ представляет собой круг $r \leqslant a$, а область мениска ${{\Omega }_{m}}$ – кольцо $a \leqslant r \leqslant b$.

В предположении, что угол смачивания обеих поверхностей жидкостью равен нулю и пренебрегая силой натяжения пленки на внешней границе мениска, из формулы Лапласа (2.2) можно получить следующее условие, связывающее капиллярное давление с упругими перемещениями границ взаимодействующих тел, их формой и нормальным внедрением [17]:

Контактная задача о нормальном нагружении осесимметричного индентора, форма которого описывается степенной функцией, с условиями (2.1) и (3.2), а также при условии непрерывности контактного давления на границе области контакта

была рассмотрена и решена в [17]. В результате получены следующие соотношения для распределения контактного давления по радиальной координате rнормального внедрения индентора внешней нормальной силы а также уравнение, следующее из условия (3.2):

Если внешняя нормальная нагрузка P и капиллярное давление p₀ заданы, то соотношения (3.6) и (3.7) служат в качестве уравнений для численного определения радиуса области контакта a и внешнего радиуса мениска b. После этого распределение контактного давления и внедрение индентора определяются по формулам (3.4) и (3.5), соответственно.

Задача о тангенциальном нагружении задается условиями (2.3) и вторыми из соотношений (2.4) и (3.1). Поскольку распределение нормальных давлений (3.4) зависит только от радиальной координаты $r$, из условий (2.3) следует, что касательное напряжение $\tau $ в области проскальзывания ${{\Omega }_{{sl}}}$ и перемещение ${{u}_{x}}$ в области сцепления ${{\Omega }_{{st}}}$ также являются функциями только радиальной координаты $r$, откуда, в силу формы второго из уравнений (3.1), следует осесимметричность решения задачи о тангенциальном нагружении. Пусть область сцепления ${{\Omega }_{{st}}}$ представляет собой круг $r \leqslant c$, а область проскальзывания ${{\Omega }_{{sl}}}$ – кольцо $c \leqslant r \leqslant a$ (см. рис. 1). Касательное напряжение $\tau (r)$ считается непрерывным на границе областей сцепления и проскальзывания (при $r = c$).

Для определения касательного напряжения в области сцепления воспользуемся теорией Каттанео–Миндлина [4, 5], обобщенной [6, 7] для трехмерного индентора произвольной формы. Представим функцию $\tau (r)$ при $r \leqslant a$ в виде:

где для функции дополнительного касательного напряжения $\tau {\kern 1pt} *{\kern 1pt} (r)$ выполняется условие $\tau {\kern 1pt} *{\kern 1pt} (r) \equiv 0$ при $r \geqslant c$. Подставляя выражение (3.8) во второе соотношение (3.1) и переходя в интегралах к полярным координатам [18], получим где ${\mathbf{K}}(x)$ – полный эллиптический интеграл первого рода. Из первого соотношения (3.1) и граничных условий (2.1) следует

Подставляя выражение (3.10) в (3.9) и учитывая граничные условия (2.3), а также значение интеграла [18]

где ${\mathbf{E}}(x)$ – полный эллиптический интеграл второго рода, получим для функции дополнительного касательного напряжения $\tau {\kern 1pt} *{\kern 1pt} (r)$ уравнение где

Поскольку для функции $\tau {\kern 1pt} *{\kern 1pt} (r)$ выполняется условие $\tau {\kern 1pt} *{\kern 1pt} (c) = 0$, то интегральное уравнение (3.12) по форме совпадает с интегральным уравнением контактной задачи о внедрении в упругое полупространство осесимметричного штампа заданной формы $f{\kern 1pt} *{\kern 1pt} (r)$ (3.13) при действии на него нормальной внешней силы, равной по величине

а значит, для решения уравнения (3.12) можно использовать полученные ранее соотношения для решения задачи о нормальном внедрении осесимметричного штампа в полупространство.

Воспользуемся решением задачи о внедрении осесимметричного штампа заданной формы $f{\kern 1pt} *{\kern 1pt} (r)$ в упругое полупространство [19]. Полученное выражение для нормального давления под штампом [19], с учетом соотношений (3.12)–(3.14) и (3.8) приобретает вид следующего выражения для искомого касательного напряжения при $r \leqslant c$

Условие для определения нормального внедрения штампа [19], преобразуется в условие для определения тангенциального перемещения ${{\delta }_{x}}$

Воспользовавшись формулой, полученной Галиным [20] для силы, прижимающей осесимметричный штамп, получим

В соотношениях (3.15) и (3.17), $\Delta $ – оператор Лапласа в полярных координатах, $\Delta f(r)$ = = $\left( {\frac{1}{r}\frac{\partial }{{\partial r}} + \frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}}} \right)f(r)$. При этом искомая полная тангенциальная сила T, с учетом (3.8) и (3.14), а также условий (2.1), определяется как

После подстановки выражений (3.13) в соотношения (3.15)–(3.18) и взятия интегралов (используя методы интегрирования [17]), получим окончательно для касательного напряжения в области сцепления $r \leqslant c$:

а также для тангенциальных перемещения и силы:

Предельная тангенциальная сила, при которой начинается полное скольжение индентора относительно полупространства, получается из (3.21) при $c = 0$:

где $P$ определяется выражением (3.6).

Если величины $a$ и $b$ определены решением уравнений (3.6), (3.7) задачи о нормальном нагружении, то при заданной тангенциальной силе T численное решение уравнения (3.21) позволяет определить радиус области сцепления c, после чего касательные напряжения в области сцепления и тангенциальное перемещение определяются выражениями (3.19) и (3.20).

В случае $n = 1$ и $A = 1{\text{/}}\left( {2R} \right)$ (индентор в форме параболоида вращения c радиусом кривизны вершины $R$) и $\mu = 0$ (трение в зоне проскальзывания задано законом $\tau (r) = {{\tau }_{0}}$) соотношения (3.19)–(3.21) совпадают с выражениями [14].

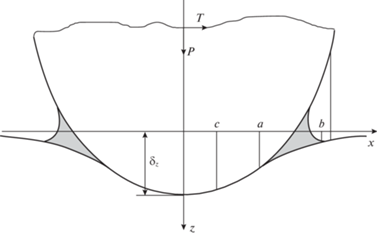
4. Результаты расчета. На рис 2,а приведены распределения безразмерного нормального давления $p{\text{/}}E{\kern 1pt} *$ по безразмерной радиальной координате $r{{A}^{{1/(2n - 1)}}}$, где ${{A}^{{ - 1/(2n - 1)}}}$ – характерный размер индентора. Результаты приведены для двух форм индентора, описываемых различными показателями степени n функции $f(r) = A{{r}^{{2n}}}$, и трех величин безразмерного капиллярного давления в мениске ${{p}_{0}}{\text{/}}E{\kern 1pt} *$. Остальные безразмерные параметры задачи считались постоянными – безразмерное поверхностное натяжение жидкости $\gamma {{A}^{{1/(2n - 1)}}}{\text{/}}E{\kern 1pt} *$ = 10^–4 и внешняя нормальная сила $P{{A}^{{2/(2n - 1)}}}{\text{/}}E{\kern 1pt} *$ = = 10^–3, действующая на индентор. Увеличение показателя n соответствует “уплощению” вершины индентора и, вследствие этого, расширению как области контакта, так и области мениска (область постоянного отрицательного давления на графике). Возрастание величины капиллярного давления в мениске приводит к увеличению размера области контакта и возрастанию контактного давления, что более выражено при больших значениях n, при этом ширина кольцевой области, занятой мениском, уменьшается.

На рис. 2,б приведены распределения безразмерного касательного напряжения $\tau {\text{/}}E{\kern 1pt} *$, соответствующие тем же величинам параметров, что и распределения давления на рис. 2,а. Параметры закона трения (1.1) – $\mu = 0.5$ и ${{\tau }_{0}}{\text{/}}E{\kern 1pt} * = 0.01$ – выбраны таким образом, чтобы касательные напряжения в области контакта оставались положительными, несмотря на то, что нормальные давления становятся отрицательными вблизи границы области контакта (см. рис. 2,а). При этом графики для $n = 1$ рассчитаны при значении безразмерной тангенциальной силы, действующей на индентор, $T{{A}^{{2/(2n - 1)}}}{\text{/}}E{\kern 1pt} *$ = 6 × 10^–4, а для $n = 3$ – при $T{{A}^{{2/(2n - 1)}}}{\text{/}}E{\kern 1pt} *$ = 7 × 10^–3. Точки излома на графиках распределения касательного напряжения соответствуют границе областей сцепления и проскальзывания. Результаты расчета показывают, что возрастание величины капиллярного давления в мениске приводит к расширению области сцепления, при этом величина максимального касательного напряжения ведет себя по-разному в зависимости от формы индентора: при $n = 1$ (индентор параболической формы) максимальное касательное напряжение убывает с возрастанием капиллярного давления, а при $n \geqslant 1$ (инденторы с “уплощенной” вершиной) максимальное касательное напряжение возрастает вместе с капиллярным давлением.

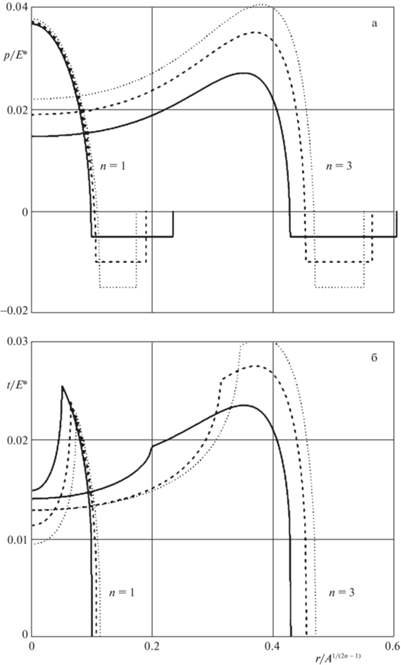
Чтобы проиллюстрировать влияние внешней нормальной силы на контактные характеристики, на рис. 3 приведены распределения контактного давления для различных значений безразмерной силы $P{{A}^{{2/(2n - 1)}}}{\text{/}}E{\text{*}}$. Графики построены при $n = 1$ и $\gamma {{A}^{{1/(2n - 1)}}}{\text{/}}E{\kern 1pt} *$ = 10^–3. Увеличение внешней нагрузки приводит к возрастанию площади контакта и максимального контактного давления, при этом, благодаря мениску, контакт существует не только при положительной (вдавливающей индентор) силе, но и в некотором диапазоне отрицательных (отрывающих индентор) внешних нагрузок. Контактные давления отрицательны вблизи границы области контакта, при уменьшении нагрузки область отрицательных давлений расширяется (кривые от 1 до 4). При некотором значении отрицательной нагрузки контактные давления могут стать отрицательными во всей области контакта (кривая 5).

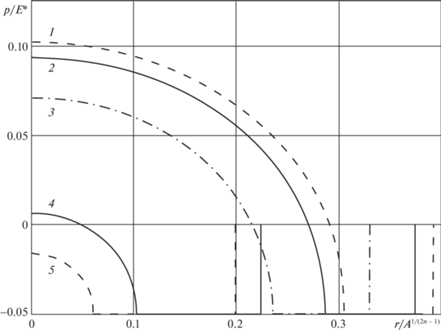
На рис. 4 показаны безразмерные радиусы областей контакта $a{{A}^{{1/(2n - 1)}}}$ и мениска $b{{A}^{{1/(2n - 1)}}}$ в зависимости от безразмерной внешней нормальной силы $P{{A}^{{2/(2n - 1)}}}{\text{/}}E{\text{*}}$ при величине капиллярного давления ${{p}_{0}}{\text{/}}E* = 0.01$ и $n = 1$. Параметры закона трения и безразмерное поверхностное натяжение жидкости равны тем же значениям, при которых построены кривые на рис. 2. Поскольку решение задачи о нормальном нагружении получено независимо от задачи о тангенциальном нагружении, размеры областей контакта и мениска не зависят от величины тангенциальной силы. Однако, размер области сцепления зависит от этой величины. На рис. 3 кривыми 3–5 показаны зависимости радиуса области сцепления от нормальной нагрузки для трех значений тангенциальной силы. При относительно малой величине тангенциальной силы область сцепления существует как при положительных, так и в некоторой области отрицательных значениях нормальной нагрузки (кривая 3). При увеличении тангенциальной силы область сцепления существует, только начиная с некоторого положительного значения нормальной нагрузки, которое возрастает с возрастанием тангенциальной силы (кривые 4 и 5).

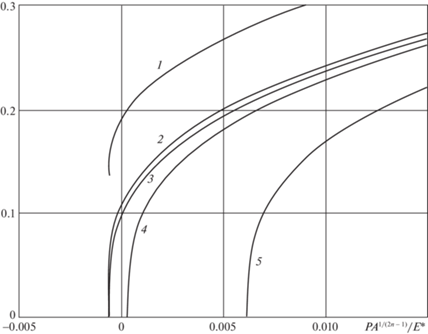
На рис. 5 представлены зависимости тангенциальной силы $T$, отнесенной к предельной силе ${{T}_{{\lim }}}$, при которой начинается полное скольжение, от отношения радиусов областей сцепления и контакта $c{\text{/}}a$ для двух форм индентора, определяемых показателем $n$, и различных значениях безразмерного поверхностного натяжения жидкости $\gamma {{A}^{{1/(2n - 1)}}}{\text{/}}E{\text{*}}$. Результаты получены при величинах безразмерной нормальной силы $P{{A}^{{2/(2n - 1)}}}{\text{/}}E{\kern 1pt} *$ = 0, капиллярного давления ${{p}_{0}}{\text{/}}E* = 0.1$ и при параметрах закона трения $\mu = 0.5$ и ${{\tau }_{0}}{\text{/}}E* = 0.1$. По мере увеличения тангенциальной силы $T$, относительный радиус области сцепления $c{\text{/}}a$ убывает вплоть до наступления полного скольжения, когда $T = {{T}_{{\lim }}}$ и $c = a$. При этом увеличение показателя n приводит к более медленному убыванию $c{\text{/}}a$ при малых $T$ и более быстрому – при больших $T$, близких к ${{T}_{{\lim }}}$. Увеличение поверхностного натяжения жидкости (или уменьшение модуля упругости взаимодействующих тел) приводит к увеличению зоны сцепления; этот эффект более заметен при $n = 1$, т.е., для индентора параболической формы, чем для форм с уплощенной вершиной.

На рис. 6 показаны графики внешнего радиуса мениска b и радиуса области сцепления c, отнесенные к радиусу области контакта a, в зависимости от величины безразмерного капиллярного давления в мениске ${{p}_{0}}{\text{/}}E{\text{*}}$ при безразмерном поверхностном натяжении $\gamma {{A}^{{1/(2n - 1)}}}{\text{/}}E* = {{10}^{{ - 4}}}$, нормальной нагрузке $P{{A}^{{2/(2n - 1)}}}{\text{/}}E* = {{10}^{{ - 4}}}$ и параметрах закона трения $\mu = 0.5$ и ${{\tau }_{0}}{\text{/}}E* = 0.01$, а также при двух разных показателях n, характеризующих форму индентора. Графики $b{\text{/}}a$ расположены в верхней половине рисунка, а графики $c{\text{/}}a$ – в нижней, поскольку во всем диапазоне значений параметров задачи выполняется $b{\text{/}}a \geqslant 1$, $c{\text{/}}a \leqslant 1$ (см. рис. 1). Величина $b{\text{/}}a$ определяется решением задачи о нормальном нагружении (3.6), (3.7), и поэтому не зависит от величины тангенциальной силы. Графики величины $c{\text{/}}a$ на рис. 6 построены для двух значений тангенциальной силы.

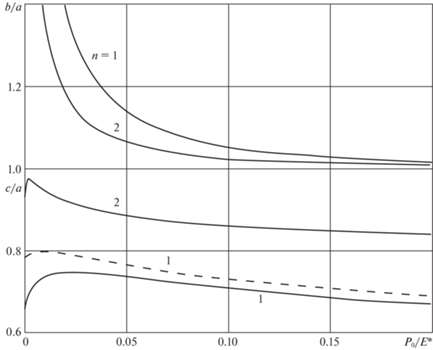
Результаты, представленные на рис. 6, показывают, что при увеличении величины капиллярного давления в мениске величина b/a уменьшается, т.е. уменьшается ширина кольцевой области, занятой мениском. Таким образом, увеличение адгезионного давления, стягивающего поверхности, сопровождается уменьшением области, по которой действует это давление. При этом относительный радиус области сцепления немонотонно зависит от ${{p}_{0}}{\text{/}}E{\text{*}}$: при очень малых величинах капиллярного давления величина c/a резко возрастает, достигает максимума и плавно уменьшается при дальнейшем повышении капиллярного давления ${{p}_{0}}{\text{/}}E{\text{*}}$. Увеличение показателя n (“уплощение” вершины индентора) приводит к уменьшению ширины мениска, но к увеличению радиуса области сцепления по отношению к контактному радиусу, при этом максимум c/a сдвигается в сторону меньших ${{p}_{0}}{\text{/}}E{\text{*}}$. Увеличение тангенциальной нагрузки приводит к уменьшению относительного радиуса области сцепления c/a, при этом ее максимум сдвигается в сторону больших значений капиллярного давления ${{p}_{0}}{\text{/}}E{\text{*}}$.

Безразмерная величина ${{T}_{{\lim }}}{{A}^{{2/(2n - 1)}}}{\text{/}}E{\text{*}}$ предельной тангенциальной силы, при которой возникает переход к полному скольжению, показана на рис. 7 как функция безразмерного капиллярного давления ${{p}_{0}}{\text{/}}E{\text{*}}$ для трех значений нормальной нагрузки – положительной (прижимающей индентор к полупространству), нулевой и отрицательной (отрывающей индентор от полупространства). Зависимость предельной тангенциальной силы от капиллярного давления также немонотонна. Контакт существует при нулевых и отрицательных нагрузках благодаря действию капиллярной адгезии. Однако, при отрицательной нагрузке увеличение капиллярного давления ${{p}_{0}}{\text{/}}E{\text{*}}$ может приводить к разрыву контакта (кривая 3).

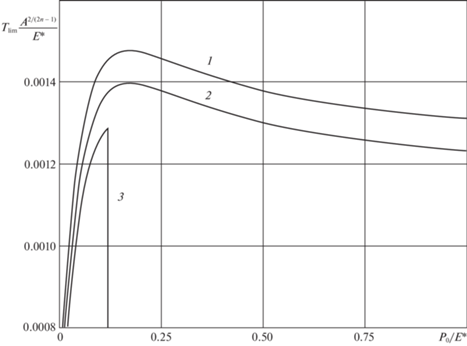
Заметим, что для мениска, образовавшегося за счет капиллярной конденсации из окружающего воздуха и находящегося с ним в термодинамическом равновесии, капиллярное давление определяется уравнением Кельвина [18]

где ${{T}_{0}}$ – абсолютная температура, ${{R}_{g}}$ – универсальная газовая постоянная, ${{V}_{m}}$ – молярный объем жидкости, $H$ – относительная влажность окружающего воздуха. Уравнение (3.1) описывает монотонное убывание величины ${{p}_{0}}$ с возрастанием относительной влажности $H$. Таким образом, в случае адгезии, вызванной капиллярной конденсацией из атмосферы, величины, немонотонно зависящие от капиллярного давления ${{p}_{0}}$ (относительный радиус области сцепления c/a и предельная тангенциальная сила ${{T}_{{\lim }}}$), будут немонотонно зависеть и от влажности $H$ – возрастать с увеличением $H$ до некоторого значения влажности, а затем убывать.

Заключение. Построено решение контактной задачи о нормальном и тангенциальном нагружении осесимметричного индентора, форма которого описывается степенной функцией, в контакте с упругим полупространством из такого же материала при наличии капиллярной адгезии. Задача рассмотрена в условиях частичного проскальзывания, когда область контакта делится на зоны сцепления и проскальзывания, при этом в области проскальзывания действует двучленный закон трения. Получены аналитические выражения для касательных напряжений в области сцепления, внешней тангенциальной нагрузки и тангенциального перемещения индентора, а также для предельной тангенциальной силы, при которой происходит переход к полному скольжению. Исследовано влияние на эти контактные характеристики формы индентора, поверхностного натяжения жидкости и капиллярного давления в мениске.

Установлено, в частности, что увеличение показателя n степенной функции, описывающей форму индентора (“уплощение” вершины индентора) и увеличение поверхностного натяжения жидкости приводят к возрастанию области сцепления и предельной тангенциальной силы, необходимой для перехода к полному скольжению. При этом величина предельной тангенциальной силы немонотонно зависит от капиллярного давления в мениске, определяемого относительной влажностью окружающего воздуха.

Работа выполнена при финансовой поддержке РФФИ, грант № 21-58-52006.