Прикладная математика и механика, 2022, T. 86, № 2, стр. 153-168
О стационарных движениях равногранного тетраэдра с неподвижной точкой в центральном поле сил
1 ФИЦ ИУ РАН
Москва, Россия
* E-mail: nikonova.ekaterina.a@gmail.com
Поступила в редакцию 22.05.2021
После доработки 30.12.2021
Принята к публикации 13.01.2022
- EDN: XGJHMJ
- DOI: 10.31857/S0032823522020096
Аннотация
Изучаются существование, устойчивость и ветвление стационарных движений равногранного тетраэдра вокруг неподвижной точки в центральном ньютоновском поле сил. Исследуется связь этих свойств стационарных движений со свойствами стационарных движений правильного тетраэдра, естественным геометрическим обобщением которого является равногранный тетраэдр.
1. Введение. В [1–3] были обнаружены достаточно неожиданные динамические свойства твердого тела в форме правильного тетраэдра и других платоновых тел, совершающих движение в центральном ньютоновском поле притяжения.
Исследование “чувствительности” динамических свойств платоновых тел восходит к публикации [4], в которой предложен оригинальный подход, опирающийся на эффективное использование симметрий в распределении масс при изучении стационарных движений в задачах динамики твердого тела (см. также [5–10]). Другое направление исследований динамики тетраэдральных тел, обусловленное потребностями механики космического полета, связано с предположением о наличии в них роторов [11–13].
2. Постановка задачи и основные обозначения. Рассмотрим движение твердого тела $\mathcal{T}$ вокруг неподвижной точки $O$ в поле сил ньютоновского притяжения с центром в точке $N$. Пусть $\gamma = {{({{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}})}^{T}}$ – единичный вектор, направленный от $N$ к $O$, ${\mathbf{I}} = {\text{diag}}\left( {{{I}_{1}},{{I}_{2}},{{I}_{3}}} \right)$ – тензор инерции тела относительно точки $O$, ${\mathbf{\omega }} = {{({{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}})}^{T}}$ – вектор угловой скорости тела. Здесь и далее все векторы и тензорные величины задаются в подвижной системе отсчета $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, оси которой направлены вдоль главных осей инерции тела, задаваемых собственными векторами тензора инерции ${\mathbf{I}}$.
Если ${{U}_{N}} = {{U}_{N}}\left( {\mathbf{\gamma }} \right)$ – потенциал силового поля, то описывающие движение уравнения Эйлера–Пуассона можно записать в виде
(2.1)
${\mathbf{I\dot {\omega }}} = {\mathbf{I\omega }} \times {\mathbf{\omega }} + {\mathbf{\gamma }} \times \frac{{\partial {{U}_{N}}}}{{\partial {\mathbf{\gamma }}}},\quad {\mathbf{\dot {\gamma }}} = {\mathbf{\gamma }} \times {\mathbf{\omega }}$Помимо интеграла энергии ${{\mathcal{J}}_{0}} = \frac{1}{2}\left( {{\mathbf{I\omega }},{\mathbf{\omega }}} \right) + {{U}_{N}}\left( {\mathbf{\gamma }} \right) = h$ и интеграла площадей ${{\mathcal{J}}_{1}} = \left( {{\mathbf{I\omega }},{\mathbf{\gamma }}} \right)$ = ${{p}_{\psi }}$, уравнения (2.1) допускают геометрический интеграл
задающий в пространстве ${{\mathbb{R}}^{3}}\left( {\mathbf{\gamma }} \right)$ т.н. сферу Пуассона $\mathcal{S}$.Как известно (см., например, [14]), система (2.1) может обладать перманентными вращениями вокруг оси $NO$ с постоянной по величине угловой скоростью ω. Положение оси перманентного вращения в теле согласно (2.1) задаются уравнениями
(2.3)
$0 = {\mathbf{\gamma }} \times \left( {\frac{{\partial {{U}_{N}}}}{{\partial {\mathbf{\gamma }}}} - {{\omega }^{2}}{\mathbf{I\gamma }}} \right);\quad \omega = {\text{const}}$Замечание. Согласно теории Рауса ([15, 16], см. также [17]) эти вращения могут быть найдены как критические точки приведенного (amended) потенциала
(2.4)
${{U}_{\psi }} = \frac{{p_{\psi }^{2}}}{{2I\left( {\mathbf{\gamma }} \right)}} + {{U}_{N}}\left( {\mathbf{\gamma }} \right),$Хорошо известно, что при описании движения твердого тела в центральном поле ньютоновского притяжения, как правило, достаточно воспользоваться разложением до слагаемых первого или второго порядка малости по параметру, характеризующему отношение размеров тела к его расстоянию до притягивающего центра. Однако, в случае, когда тензор инерции тела близок к шаровому, такие приближения, вообще говоря, оказываются недостаточными. В дальнейшем в качестве примера рассмотрим движение твердого тела $\mathcal{T}$ в виде равногранного тетраэдра с равными массами в вершинах.
3. Равногранный тетраэдр. Согласно [18], тетраэдр называется равногранным, если все грани – равные между собой треугольники. Как известно, у равногранного тетраэдра бимедианы попарно перпендикулярны и являются общими серединными перпендикулярами соответствующих скрещивающихся ребер. Пусть $\mathcal{T}$ – тело в форме равногранного тетраэдра с равными массами $m$ в вершинах. Будем считать, что оно совершает вращение вокруг неподвижной точки $O$, совпадающей с точкой пересечения бимедиан. Зададим жестко связанную с тетраэдром правую систему отсчета $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ с началом в точке $O$ и осями, направленными вдоль бимедиан. Если длины бимедиан равны $2r{{a}_{1}}$, $2r{{a}_{2}}$, $2r{{a}_{3}}$ соответственно, то вершины $A$, $B$, $C$ и $D$ тетраэдра $\mathcal{T}$ в этой системе отсчета задаются радиус-векторами
Оси $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ являются главными центральными осями инерции тела $\mathcal{T}$, в них главные центральные моменты $\mathcal{T}$ записываются как
(3.2)
${{I}_{k}} = 4m{{r}^{2}}I_{k}^{'},\quad k = 1,2,3,\quad I_{1}^{'} = a_{2}^{2} + a_{3}^{2},\quad I_{2}^{'} = a_{1}^{2} + a_{3}^{2},\quad I_{3}^{'} = a_{1}^{2} + a_{2}^{2}$4. Приближенное представление потенциала поля притяжения. Пусть $N$ – притягивающий центр, в котором сосредоточена масса $M$, $\left| {{\mathbf{NO}}} \right| = d$. Пусть единицы размерности выбраны так, что гравитационная постоянная, масса $M$, а также величина ${{r}_{ \star }}$ = = $\sqrt {{{d}^{2}} + {{r}^{2}}} $ равны единице (ср. [19]). Тогда потенциал притяжения имеет вид
(4.1)
${{U}_{N}} = - \mathop \sum \limits_{\left( {A,B,C,D} \right)} \rho _{A}^{{ - 1}},\quad {{\rho }_{A}} = {{\left( {1 + \varepsilon \left( {{\mathbf{\gamma }},{{{\mathbf{e}}}_{A}}} \right)} \right)}^{{1/2}}},\quad \varepsilon = 2dr,$(4.2)
${{U}_{0}} = - 4\quad {{U}_{1}} = 0,\quad {{U}_{2}} = - \frac{3}{2}\left( {a_{1}^{2}\gamma _{1}^{2} + a_{2}^{2}\gamma _{2}^{2} + a_{3}^{2}\gamma _{3}^{2}} \right),\quad {{U}_{3}} = \frac{{15}}{2}{{a}_{1}}{{a}_{2}}{{a}_{3}}{{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}}$Постоянная ${{U}_{0}}$ несущественная, она не играет роли в дальнейшем рассмотрении.
Замечание. Параметр разложения $\varepsilon $, предложенный ранее [19], удобно применять и в настоящем исследовании, поскольку он позволяет одновременно описывать случаи, когда тетраэдр располагается очень далеко от притягивающего центра $N$, и когда, наоборот, центр масс тетраэдра очень близок к притягивающему центру $N$.
5. Существование равновесий. Прежде всего, рассмотрим вопрос о существовании и устойчивости равновесий $\left( {{{p}_{\psi }} = 0} \right)$. Если ограничиться приближением потенциала (3.2) с точностью до членов третьего порядка с потенциалом U ' = $ - \frac{1}{2}((a_{1}^{2}\gamma _{1}^{2} + a_{2}^{2}\gamma _{2}^{2} + a_{3}^{2}\gamma _{3}^{2})$ – – $5\varepsilon {{a}_{1}}{{a}_{2}}{{a}_{3}}{{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}})$, то уравнения равновесий после преобразований примут вид
(5.1)
$\begin{array}{*{20}{c}} {{{\gamma }_{2}}{{\gamma }_{3}}\left( {{{b}_{3}} - {{b}_{2}}} \right) + {{\gamma }_{1}}\left( {\gamma _{3}^{2} - \gamma _{2}^{2}} \right) = 0} \\ {{{\gamma }_{3}}{{\gamma }_{1}}\left( {{{b}_{1}} - {{b}_{3}}} \right) + {{\gamma }_{2}}\left( {\gamma _{1}^{2} - \gamma _{3}^{2}} \right) = 0} \\ {{{\gamma }_{1}}{{\gamma }_{2}}\left( {{{b}_{2}} - {{b}_{1}}} \right) + {{\gamma }_{3}}\left( {\gamma _{2}^{2} - \gamma _{1}^{2}} \right) = 0,} \end{array}$(5.2)
${{b}_{1}} = \frac{2}{5}\;\frac{{{{a}_{1}}}}{{{{a}_{2}}{{a}_{3}}\varepsilon }}\quad \left( {1,2,3} \right)$Соотношение (3.1) в параметрах ${{b}_{i}}$, $i = 1,2,3$, записывается как
(5.4)
$\frac{1}{{{{b}_{1}}{{b}_{2}}}} + \frac{1}{{{{b}_{2}}{{b}_{3}}}} + \frac{1}{{{{b}_{3}}{{b}_{1}}}} = \frac{{25{{\varepsilon }^{2}}}}{4}$Уравнения (5.1) вместе с уравнением (2.2), выражающим единичность вектора ${\mathbf{\gamma }}$, станут основным предметом дальнейшего рассмотрения.
Эти уравнения всегда обладают решениями
(5.5)
$\begin{gathered} {{\mathcal{I}}_{1}}{\kern 1pt} :{{\gamma }_{1}} = \pm 1,\quad {{\gamma }_{2}} = 0,\quad {{\gamma }_{3}} = 0 \\ {{\mathcal{I}}_{2}}{\kern 1pt} :{{\gamma }_{1}} = 0,\quad {{\gamma }_{2}} = \pm 1,\quad {{\gamma }_{3}} = 0 \\ {{\mathcal{I}}_{3}}{\kern 1pt} :{{\gamma }_{1}} = 0,\quad {{\gamma }_{2}} = 0,\quad {{\gamma }_{3}} = \pm 1 \\ \end{gathered} $Этим шести решениям отвечают перманентные вращения, на которых тетраэдр “смотрит” на притягивающий центр серединой одного из своих ребер.
Пусть все ${{b}_{k}}$ различны (случай, когда две из трех величин ${{b}_{k}}$ равны, рассмотрен ранее [20]). Если на искомом решении ${{\gamma }_{1}} = 0$, тогда в силу первого уравнения (5.1) либо ${{\gamma }_{2}} = 0$, либо ${{\gamma }_{3}} = 0$, т.е. имеют место, либо решения ${{\mathcal{I}}_{3}}$, либо решения ${{\mathcal{I}}_{2}}$.
Далее, в предположении, что все ${{\gamma }_{k}} \ne 0$, систему (5.1) можно представить в виде
(5.6)
${{b}_{3}} - {{b}_{2}} = {{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}}\left( {\gamma _{3}^{{ - 2}} - \gamma _{2}^{{ - 2}}} \right)\quad \left( {1,2,3} \right)$На соотношения (5.6) можно смотреть как на уравнения относительно ${{b}_{k}}$. В этом случае говорят об обратной задаче. С другой стороны, на эти же соотношения можно смотреть как на уравнения относительно ${{\gamma }_{k}}$. В этом случае говорят о прямой задаче.
5.1. Решение обратной задачи. Если рассмотреть соотношения (5.6) как уравнения относительно bk, то их решение запишется как
(5.7)
${{b}_{k}} = \gamma _{k}^{{ - 2}}{{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}} + \nu {\kern 1pt} ';\quad \nu {\kern 1pt} ' \in \mathbb{R}$5.2. Решение прямой задачи. Если рассмотреть соотношения (4.6) как уравнения относительно ${{\gamma }_{k}}$, то их удобно представить как
(5.8)
${{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}} = \gamma _{1}^{2}\left( {{{b}_{1}} + \nu } \right)\quad \left( {1,2,3} \right);\quad \nu \in \mathbb{R}$Прежде всего заметим, что если, например, $\nu = - {{b}_{1}}$, то правая часть первого из уравнений (5.8) обращается в нуль, и должны обратиться в нуль левые части всех трех уравнений. В рамках сделанного предположения первое уравнение выполнено тождественно, а оставшиеся два уравнения примут вид
(5.9)
$0 = \gamma _{2}^{2}\left( {{{b}_{2}} - {{b}_{1}}} \right) = \gamma _{3}^{2}\left( {{{b}_{3}} - {{b}_{1}}} \right)$Но тогда, принимая во внимание предположение о том, что все ${{b}_{k}}$ различны, из соотношения (5.9) также имеем ${{\gamma }_{2}} = {{\gamma }_{3}} = 0$, и в силу геометрического интеграла (2.2) имеет место единственное решение вида ${{\mathcal{I}}_{1}}$.
В дальнейшем будем считать, что $\nu \notin \left\{ { - {{b}_{1}}, - {{b}_{2}}, - {{b}_{3}}} \right\}$. Перемножая левые и правые части равенств (5.8), имеем
Подстановка найденного произведения в (5.8) позволяет представить ответ задачи в виде:
(5.10)
$\gamma _{k}^{2} = \left( {{{b}_{1}} + \nu } \right)\left( {{{b}_{2}} + \nu } \right)\left( {{{b}_{3}} + \nu } \right){{\left( {{{b}_{k}} + \nu } \right)}^{{ - 1}}};\quad k = 1,2,3,$В силу (2.2) с учетом сделанных предположений относительно параметра $\nu $ он должен удовлетворять уравнению
(5.11)
$\begin{gathered} \left( {{{b}_{1}} + \nu } \right)\left( {{{b}_{2}} + \nu } \right)\left( {{{b}_{3}} + \nu } \right){{\left( {{{b}_{1}} + \nu } \right)}^{{ - 1}}} + \\ + \;\left( {{{b}_{1}} + \nu } \right)\left( {{{b}_{2}} + \nu } \right)\left( {{{b}_{3}} + \nu } \right){{\left( {{{b}_{2}} + \nu } \right)}^{{ - 1}}} + \\ + \;\left( {{{b}_{1}} + \nu } \right)\left( {{{b}_{2}} + \nu } \right)\left( {{{b}_{3}} + \nu } \right){{\left( {{{b}_{3}} + \nu } \right)}^{{ - 1}}} = 1, \\ \end{gathered} $(5.12)
$3{{\nu }^{2}} + 2\nu \left( {{{b}_{1}} + {{b}_{2}} + {{b}_{3}}} \right) + {{b}_{1}}{{b}_{2}} + {{b}_{1}}{{b}_{3}} + {{b}_{2}}{{b}_{3}} - 1 = 0$Дискриминант $D$ многочлена в (5.12) всегда строго положителен:
Таким образом, уравнение (5.11) имеет два вещественных корня
Подставляя эти значения в (5.10), в итоге имеем
(5.13)
$\gamma _{{1 \pm }}^{2} = \frac{1}{9}\left( {2{{b}_{2}} - \left( {{{b}_{1}} + {{b}_{3}} \pm b} \right)} \right)\left( {2{{b}_{3}} - \left( {{{b}_{1}} + {{b}_{2}} \pm b} \right)} \right)\quad \left( {1,2,3} \right)$Эти равновесия в дальнейшем обозначаются $\mathcal{I}{{\mathcal{I}}_{ \pm }}$.
Замечание. Общее решение прямой задачи о перманентных вращениях также имеет вид (5.13) с той лишь разницей, что в нем
(5.14)
${{b}_{1}} = \frac{2}{5}\frac{{{{a}_{1}}}}{{{{a}_{2}}{{a}_{3}}\varepsilon }}\left( {1 - \frac{4}{3}\frac{{{{r}^{2}}}}{{{{\varepsilon }^{2}}}}{{\omega }^{2}}} \right)\quad \left( {1,2,3} \right)$В этом случае наличие дополнительного параметра делает параметрическое исследование решений (5.13) гораздо более сложным. Такое исследование, равно как и исследование устойчивости перманентных вращений, в работе не осуществляется.
Для определения множества значений параметров, при которых решения (5.13) существуют, выполним переход к новым параметрам
(5.15)
${{\delta }_{1}} = \frac{{\sqrt 3 }}{3}\left( {{{b}_{1}} + {{b}_{2}} + {{b}_{3}}} \right),\quad {{\delta }_{2}} = \frac{{\sqrt 6 }}{6}\left( {2{{b}_{1}} - {{b}_{2}} - {{b}_{3}}} \right),\quad {{\delta }_{3}} = \frac{{\sqrt 2 }}{2}\left( {{{b}_{2}} - {{b}_{3}}} \right)$Замечание. Переход от параметров ${{b}_{i}}$, $i = 1,2,3$, к параметрам ${{\delta }_{i}}$, $i = 1,2,3$, инспирирован следующими обстоятельствами. Поверхность, задаваемая соотношением (4.4) в пространстве ${{\mathbb{R}}^{3}}\left( {{{b}_{1}},{{b}_{2}},{{b}_{3}}} \right)$ с ограничением (5.3), обладает осью симметрии с направляющим вектором ${{(1,1,1)}^{T}}$. В параметрах ${{\delta }_{i}}$, $i = 1,2,3$ ось симметрии рассматриваемой поверхности будет иметь направляющий вектор ${{(0,0,1)}^{T}}$, а ограничение (5.3) примет простейший вид ${{\delta }_{1}} > 0$. Кроме того, множества значений параметров, при которых решения (5.13) существуют, будет описываться лишь в терминах ${{\delta }_{2}}$ и ${{\delta }_{3}}$, что позволяет иллюстрировать эти множества на плоскости ${{\mathbb{R}}^{2}}\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$.
Во введенных параметрах $b = \frac{{\sqrt 6 }}{2}\;\sqrt {\delta _{2}^{2} + \delta _{3}^{2} + 2} $, и соотношение (5.13) принимает вид
(5.16)
$\gamma _{{2 \pm }}^{2} = - \frac{1}{6}\delta _{2}^{2} + \frac{1}{6}\delta _{3}^{2} - \frac{{\sqrt 3 }}{3}{{\delta }_{2}}{{\delta }_{3}} \mp \frac{1}{6}\left( {{{\delta }_{2}} - \sqrt 3 {{\delta }_{3}}} \right)\sqrt {\delta _{2}^{2} + \delta _{3}^{2} + 2} + \frac{1}{3}$Для решения $\mathcal{I}{{\mathcal{I}}_{ - }}$ правые части соотношений (5.16) неотрицательны, если выполнены неравенства
(5.17)
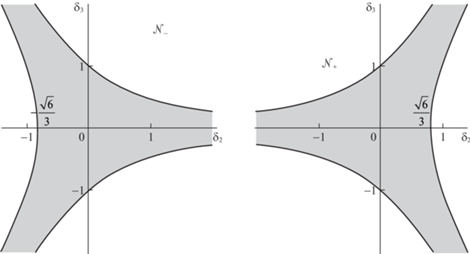
$\begin{array}{*{20}{c}} {\left( {\sqrt 3 {{\delta }_{2}} - {{\delta }_{3}}} \right)\left( {\sqrt 3 {{\delta }_{2}} + {{\delta }_{3}}} \right) \leqslant 2,\quad {{\delta }_{2}} \leqslant 0} \\ {{{\delta }_{3}}\left( {\sqrt 3 {{\delta }_{2}} + {{\delta }_{3}}} \right) \leqslant 1,\quad {{\delta }_{2}} + \sqrt 3 {{\delta }_{3}} \geqslant 0} \\ {{{\delta }_{3}}\left( {\sqrt 3 {{\delta }_{2}} - {{\delta }_{3}}} \right) \geqslant - 1,\quad {{\delta }_{2}} - \sqrt 3 {{\delta }_{3}} \geqslant 0} \end{array}$Параметр ${{\delta }_{1}}$ не входит в эти условия, в то время как на плоскости параметров $\Delta = {{R}^{2}}\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ условия (5.17) выполняются в области ${{\mathcal{N}}_{ - }}$, изображенной слева на рис. 1.
Граница области ${{\mathcal{N}}_{ - }}$ представима в виде $\partial {{\mathcal{N}}_{ - }}$ = $\partial {{\mathcal{N}}^{1}} \cup \partial{ \mathcal{N}}_{ - }^{2} \cup \partial{ \mathcal{N}}_{ - }^{3}$. В этой области произведение ${{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}}$ положительно и тройке $\left( {\gamma _{1}^{2},\gamma _{2}^{2},\gamma _{3}^{2}} \right)$ отвечают четыре решения $\left( {{{\gamma }_{1}}, - {{\gamma }_{2}}, - {{\gamma }_{3}}} \right)$, $\left( { - {{\gamma }_{1}}, - {{\gamma }_{2}},{{\gamma }_{3}}} \right)$, $\left( { - {{\gamma }_{1}},{{\gamma }_{2}}, - {{\gamma }_{3}}} \right)$, $\left( {{{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}}} \right)$.
Аналогично для решения $\mathcal{I}{{\mathcal{I}}_{ + }}$ правые части соотношений (5.16) неотрицательны, если параметры ${{\delta }_{k}}$, $k = 1,2,3$ удовлетворяют неравенствам
(5.18)
$\begin{array}{*{20}{c}} {\left( {\sqrt 3 {{\delta }_{2}} - {{\delta }_{3}}} \right)\left( {\sqrt 3 {{\delta }_{2}} + {{\delta }_{3}}} \right) \leqslant 2,\quad {{\delta }_{2}} \geqslant 0} \\ {{{\delta }_{3}}\left( {\sqrt 3 {{\delta }_{2}} + {{\delta }_{3}}} \right) \leqslant 1,\quad {{\delta }_{2}} + \sqrt 3 {{\delta }_{3}} \leqslant 0} \\ {{{\delta }_{3}}\left( {\sqrt 3 {{\delta }_{2}} - {{\delta }_{3}}} \right) \geqslant - 1,\quad {{\delta }_{2}} - \sqrt 3 {{\delta }_{3}} \leqslant 0} \end{array}$На том же рис. 1 область ${{\mathcal{N}}_{ + }}$ изображена справа. Граница области ${{\mathcal{N}}_{ + }}$ представима в виде $\partial {{\mathcal{N}}_{ + }}$ = $\partial {{\mathcal{N}}^{1}} \cup \partial{ \mathcal{N}}_{ + }^{2} \cup \partial{ \mathcal{N}}_{ + }^{3}$. В этой области ${{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}} < 0$ и тройке $\left( {\gamma _{1}^{2},\gamma _{2}^{2},\gamma _{3}^{2}} \right)$ отвечают четыре решения $\left( { - {{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}}} \right)$, $\left( {{{\gamma }_{1}},{{\gamma }_{2}}, - {{\gamma }_{3}}} \right)$, $\left( {{{\gamma }_{1}}, - {{\gamma }_{2}},{{\gamma }_{3}}} \right)$, $\left( { - {{\gamma }_{1}}, - {{\gamma }_{2}}, - {{\gamma }_{3}}} \right)$.
Замечание. Отметим, что границы области (5.17) переходят друг в друга при повороте на 120° около точки (0, 0). Это же верно и для границ области (5.18). Сами же области (5.17) и (5.18) переходят друг в друга при отражении координат относительно оси ${{\delta }_{2}} = 0$.
6. Устойчивость равновесий. Для исследования достаточных условий устойчивости равновесий, следуя методу Рауса ([15, 16], см. также [17]), выпишем функцию
(6.1)
$W = \sqrt 3 {{\delta }_{1}}U{\kern 1pt} '\; + \frac{\lambda }{2}\left( {\gamma _{1}^{2} + \gamma _{2}^{2} + \gamma _{3}^{2} - 1} \right)$(6.2)
$2{{\delta }^{2}}W = \left( {\frac{{{{\partial }^{2}}W}}{{\partial {{\gamma }^{2}}}}\delta {\mathbf{\gamma }},\delta {\mathbf{\gamma }}} \right);\quad \delta {\mathbf{\gamma }} = {{(\delta {{\gamma }_{1}},\delta {{\gamma }_{2}},\delta {{\gamma }_{3}})}^{T}}$(6.3)
${{\gamma }_{1}}\delta {{\gamma }_{1}} + {{\gamma }_{2}}\delta {{\gamma }_{2}} + {{\gamma }_{3}}\delta {{\gamma }_{3}} = 0$Неопределенный множитель Лагранжа ${{\lambda }}$ в общем случае имеет вид
Вторые производные
6.1. Тривиальные решения. Рассмотрим вопрос об устойчивости равновесий ${{\mathcal{I}}_{{\mathbf{k}}}}$ из (5.5).
На равновесии ${{\mathcal{I}}_{1}}$ неопределенный множитель $\lambda = \frac{{\sqrt 3 }}{3}\left( {{{\delta }_{1}} + \sqrt 2 {{\delta }_{2}}} \right)$, а линейное многообразие (6.3) имеет вид $\delta {{\gamma }_{1}} = 0$. Ограничение квадратичной формы на это линейное многообразие записывается как
(6.4)
${{\left. {2{{\delta }^{2}}W} \right|}_{{{{\mathcal{I}}_{1}}}}} = \frac{{\sqrt 2 }}{2}\left( {\sqrt 3 {{\delta }_{2}} - {{\delta }_{3}}} \right)\delta \gamma _{2}^{2} + \frac{{\sqrt 2 }}{2}\left( {\sqrt 3 {{\delta }_{2}} + {{\delta }_{3}}} \right)\delta \gamma _{3}^{2} \pm 2\delta {{\gamma }_{2}}\delta {{\gamma }_{3}}$Если ${{\delta }_{2}} > 0$ и $3\delta _{2}^{2} - \delta _{3}^{2} - 2 > 0$, то квадратичная форма (5.4) положительно определена, степень неустойчивости $\chi = 0$ и равновесие ${{\mathcal{I}}_{1}}$ устойчиво. Если $3\delta _{2}^{2} - \delta _{3}^{2}$ – 2 < 0, то квадратичная форма (6.4) знакопеременна, $\chi = 1$, и равновесие неустойчиво. Если ${{\delta }_{2}} < 0$ и $3\delta _{2}^{2} - \delta _{3}^{2}$ – 2 > 0, то квадратичная форма (6.4) отрицательно определена, степень неустойчивости $\chi = 2$ и равновесие ${{\mathcal{I}}_{1}}$ неустойчиво.
На равновесии ${{\mathcal{I}}_{2}}$ неопределенный множитель $\lambda = \frac{{\sqrt 6 }}{6}$ $(\sqrt 2 {{\delta }_{1}} - {{\delta }_{2}}$ + $\sqrt 3 {{\delta }_{3}})$, а линейное многообразие (6.3) имеет вид $\delta {{\gamma }_{2}} = 0$. Ограничение квадратичной формы на это линейное многообразие записывается как
(6.5)
${{\left. {2{{\delta }^{2}}W} \right|}_{{{{\mathcal{I}}_{2}}}}} = \frac{{\sqrt 2 }}{2}\left( { - \sqrt 3 {{\delta }_{2}} + {{\delta }_{3}}} \right)\delta \gamma _{1}^{2} + \sqrt 2 {{\delta }_{3}}\delta \gamma _{3}^{2} \pm 2\delta {{\gamma }_{1}}\delta {{\gamma }_{3}}$Если $ - {{\delta }_{2}} + \sqrt 3 {{\delta }_{3}} > 0$ и $ - \sqrt 3 {{\delta }_{2}}{{\delta }_{3}} + \delta _{3}^{2} > 1$, то квадратичная форма (6.5) положительно определена, степень неустойчивости $\chi = 0$ и равновесие ${{\mathcal{I}}_{2}}$ устойчиво. Если $ - \sqrt 3 {{\delta }_{2}}{{\delta }_{3}} + \delta _{3}^{2}$ < 1, то квадратичная форма (5.5) знакопеременна, $\chi = 1$, и равновесие неустойчиво. Если $ - {{\delta }_{2}} + \sqrt 3 {{\delta }_{3}} < 0$ и $ - \sqrt 3 {{\delta }_{2}}{{\delta }_{3}} + \delta _{3}^{2} > 1$, то квадратичная форма (6.5) отрицательно определена, степень неустойчивости $\chi = 2$ и равновесие ${{\mathcal{I}}_{2}}$ неустойчиво.
На равновесии ${{\mathcal{I}}_{3}}$ неопределенный множитель $\lambda = - \frac{{\sqrt 2 }}{2}\left( {\sqrt 3 {{\delta }_{2}} + {{\delta }_{3}}} \right)$, а линейное многообразие (6.3) имеет вид $\delta {{\gamma }_{3}} = 0$. Ограничение квадратичной формы на это линейное многообразие записывается как
(6.6)
${{\left. {2{{\delta }^{2}}W} \right|}_{{{{\mathcal{I}}_{3}}}}} = - \frac{{\sqrt 2 }}{2}\left( {\sqrt 3 {{\delta }_{2}} + {{\delta }_{3}}} \right)\delta \gamma _{1}^{2} - \sqrt 2 {{\delta }_{3}}\delta \gamma _{2}^{2} \pm 2\delta {{\gamma }_{1}}\delta {{\gamma }_{2}}$Если ${{\delta }_{2}} + \sqrt 3 {{\delta }_{3}} < 0$ и $\sqrt 3 {{\delta }_{2}}{{\delta }_{3}} + \delta _{3}^{2} > 1$, то квадратичная форма (6.6) положительно определена, степень неустойчивости $\chi = 0$ и равновесие ${{\mathcal{I}}_{3}}$ устойчиво. Если $\sqrt 3 {{\delta }_{2}}{{\delta }_{3}} + \delta _{3}^{2}$ < 1, то квадратичная форма (6.6) знакопеременна, χ = 1, и равновесие неустойчиво. Если ${{\delta }_{2}} + \sqrt 3 {{\delta }_{3}} > 0$ и $\sqrt 3 {{\delta }_{2}}{{\delta }_{3}} + \delta _{3}^{2} > 1$, то квадратичная форма (6.6) отрицательно определена, степень неустойчивости χ = 2 и равновесие ${{\mathcal{I}}_{3}}$ неустойчиво.
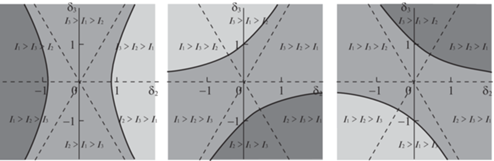
Замечание. Имеет место следующая связь между устойчивостью решений и порядком в неравенстве на моменты инерции тела. Если решение устойчиво, то момент инерции, соответствующий оси $O{{\gamma }_{i}}$ является наименьшим – или в терминах бимедиан – бимедиана ${{a}_{i}}$ — наибольшая. Если решение неустойчиво со степенью неустойчивости $\chi = 2$, то соответствующий момент инерции наибольший, и соответствующая бимедиана наименьшая. Обратное неверно, см. рис. 2, где плоскость ${{\mathbb{R}}^{2}}\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ с областями различных свойств устойчивости решения ${{\mathcal{I}}_{1}}$ приведена слева; для решения ${{\mathcal{I}}_{2}}$ аналогичная плоскость приведена по центру; для решения ${{\mathcal{I}}_{3}}$ – справа. Белым цветом изображены области, соответствующие устойчивому решению, светло-серым – неустойчивому решению со степенью неустойчивости $\chi = 1$ и серым – неустойчивому решению со степенью неустойчивости $\chi = 2$. Пунктирные линии разделяют области с различным порядком моментов инерции ${{I}_{k}}$, k = 1, 2, 3.
Замечание. Отметим, что решения $\mathcal{I}{{\mathcal{I}}_{ - }}$ и $\mathcal{I}{{\mathcal{I}}_{ + }}$ существуют одновременно лишь для тех значений параметров, при которых все три решения ${{\mathcal{I}}_{k}}$, $k = 1,2,3$, неустойчивы со степенью неустойчивости $\chi = 1$.
6.2. Общий случай. В общем случае изучения достаточных условий устойчивости во избежание громоздкости воспользуемся восходящим к Вейерштрассу подходом, опирающимся на рассмотрение окаймленной матрицы (ср. [21–26])
Коэффициенты Пуанкаре ${{\sigma }_{1}}$ и ${{\sigma }_{2}}$, определяющие знакоопределенность ограничения второй вариации (6.2) функции Рауса (6.1) на линейное многообразие (6.3), находятся из уравнения
гдеВыражения для ${{p}_{1}} = {{p}_{1}}\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ и ${{p}_{0}} = {{p}_{0}}\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ весьма громоздки и здесь не приводятся.
Оба корня многочлена (6.7) вещественны. При этом, если ${{p}_{0}} > 0$, ${{p}_{1}} < 0$, то эти корни положительны, степень неустойчивости равна нулю, и равновесие устойчиво по Ляпунову. Если ${{p}_{0}} < 0$, то эти корни имеют разные знаки, степень неустойчивости равна единице, и равновесие неустойчиво. Наконец, если ${{p}_{0}} > 0$, ${{p}_{1}} > 0$, то эти корни отрицательны, степень неустойчивости равна двум, и равновесие неустойчиво.
Для решения $\mathcal{I}{{\mathcal{I}}_{ - }}$ коэффициенты многочлена ${{P}_{2}}\left( \sigma \right)$ имеют вид
Покажем, что неравенство ${{p}_{0}} > 0$ выполнено в области ${{\mathcal{N}}_{ - }}$. Выражение в скобках, определяющее знак ${{p}_{0}}$, положительно тогда и только тогда, когда выполнена совокупность трех систем:
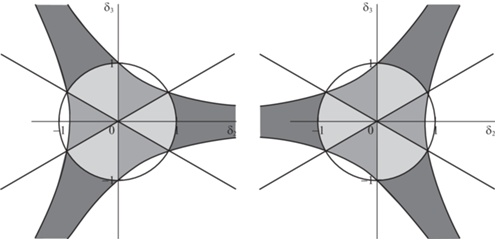
На плоскости ${{\mathbb{R}}^{2}}\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ системы 1, 2, 3 выделяют области, изображенные на рис. 3 слева. Решениям первой системы отвечают светло-серые области, второй системы – серые и третьей системы – темно-серые области. Таким образом, совокупность систем выполнена для любых $\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ из внутренних точек области ${{\mathcal{N}}_{ - }}$. На границе области коэффициент ${{p}_{0}}$ обращается в нуль.
Для определения знака коэффициента ${{p}_{1}}$ заметим, что
Из этого представления понятно, что ${{p}_{1}}\left( {{{\delta }_{2}},{{\delta }_{3}}} \right) > 0$ для любых $\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ из области ${{\mathcal{N}}_{ - }}$.
Итак, внутри области ${{\mathcal{N}}_{ - }}$ оба коэффициента ${{p}_{0}}$ и ${{p}_{1}}$ положительны, следовательно решение $\mathcal{I}{{\mathcal{I}}_{ - }}$ при этих значениях параметров $\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ неустойчиво со степенью неустойчивости $\chi = 2$. Для граничных точек области ${{\mathcal{N}}_{ - }}$ требуется дополнительное исследование устойчивости.
Для решения $\mathcal{I}{{\mathcal{I}}_{ + }}$ коэффициенты многочлена ${{P}_{2}}\left( \sigma \right)$ имеют вид
Покажем, что неравенство ${{p}_{0}} > 0$ выполнено в области ${{\mathcal{N}}_{ + }}$. Выражение в скобках, определяющее знак ${{p}_{0}}$, положительно, тогда и только тогда когда выполнена совокупность трех систем:
На плоскости ${{\mathbb{R}}^{2}}\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ системы 1, 2, 3 выделяют области, проиллюстрированные на рис. 3 справа. Решениям первой системы отвечают светло-серые области, второй системы – серые и третьей системы – темно-серые области. Таким образом, совокупность систем выполнена для любых $\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ из внутренних точек области ${{\mathcal{N}}_{ + }}$. На границе области коэффициент ${{p}_{0}}$ обращается в нуль.
Для определения знака коэффициента ${{p}_{1}}$ заметим, что
Из этого представления понятно, что ${{p}_{1}}\left( {{{\delta }_{2}},{{\delta }_{3}}} \right) < 0$ для любых $\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$ из области ${{\mathcal{N}}_{ + }}$.
Итак, внутри области ${{\mathcal{N}}_{ + }}$ коэффициент ${{p}_{0}}$ положительный, а ${{p}_{1}}$ – отрицательный, следовательно решение $\mathcal{I}{{\mathcal{I}}_{ + }}$ устойчиво при этих значениях параметров $\left( {{{\delta }_{2}},{{\delta }_{3}}} \right)$, степень неустойчивости $\chi = 0$. Для граничных точек области ${{\mathcal{N}}_{ + }}$ требуется дополнительное исследование устойчивости.
Замечание. Общие методы, касающиеся распределения свойств устойчивости вдоль ветвей стационарного движения, а также устойчивости стационарных движений, отвечающих точкам бифуркации, разработаны в [27, 28].
Замечание. Задача о существовании равновесий и перманентных вращений решается единообразно. Этого нельзя сказать о задаче устойчивости, которая сводится к анализу второй вариации приведенного потенциала (2.4), рассмотренного как функция на сфере (2.2). Исключение составляют перманентные вращения ${{\mathcal{I}}_{k}}$, $k = 1,2,3$, вокруг бимедиан из (6.5). В этом случае согласно теории, развитой в [29], рассуждение из разд. 6.1 остаются справедливыми и для перманентных вращений. При этом коэффициенты ${{b}_{k}}$ в условиях устойчивости определяются соотношениями (5.14).
7. О чувствительности равновесий к степени приближения гравитационного потенциала. К отысканию равновесий можно подходить, опираясь на введение новых переменных (ср. [30, 31]). Так если в качестве таких переменных использовать величины
(7.1)
${{g}_{1}} = \gamma _{1}^{2} + \gamma _{2}^{2} + \gamma _{3}^{2},\quad {{g}_{2}} = a_{1}^{2}\gamma _{1}^{2} + a_{2}^{2}\gamma _{2}^{2} + a_{3}^{2}\gamma _{3}^{2},\quad {{g}_{3}} = {{\gamma }_{1}}{{\gamma }_{2}}{{\gamma }_{3}},$(7.2)
${{U}_{N}} = {{\varepsilon }^{2}}{{u}_{N}},\quad {{u}_{N}} = - \frac{3}{2}{{g}_{2}} + \frac{{15}}{2}\varepsilon {{a}_{1}}{{a}_{2}}{{a}_{3}}{{g}_{3}} - \frac{{35}}{{32}}{{\varepsilon }^{2}}{{u}_{4}}\left( {{{g}_{1}},{{g}_{2}},{{g}_{3}}} \right) + ...$Пусть
Тогда уравнения равновесий примут вид
(7.3)
$\begin{gathered} \frac{{\partial w}}{{\partial {{g}_{1}}}} = \lambda + \frac{{\partial {{u}_{4}}}}{{\partial {{g}_{1}}}} + ... = 0 \\ \frac{{\partial w}}{{\partial {{g}_{2}}}} = - \frac{3}{2}\left( {1 - 5{{\varepsilon }^{2}}\frac{{\partial {{u}_{4}}}}{{\partial {{g}_{2}}}} + ...} \right) = 0 \\ \frac{{\partial w}}{{\partial {{g}_{3}}}} = \frac{{15}}{2}\varepsilon {{a}_{1}}{{a}_{2}}{{a}_{3}}\left( {1 - \frac{7}{{48}}\varepsilon \frac{{\partial {{u}_{4}}}}{{\partial {{g}_{3}}}} + ...} \right) = 0 \\ \frac{{\partial w}}{{\partial \lambda }} = {{g}_{1}} - 1 = 0 \\ \end{gathered} $Эти уравнения несовместны при достаточно малых значениях $\varepsilon \ne 0$, так как при выполнении этого условия уравнение (7.3) решения не имеет. Таким образом, равновесия имеют место лишь там, где замена $\left( {{{\gamma }_{1}},{{\gamma }_{2}},{{\gamma }_{3}}} \right)$ $ \to $ $\left( {{{g}_{1}},{{g}_{2}},{{g}_{3}}} \right)$ вырождена, т.е. в тех точках, для которых якобиан
(7.4)
$\mathcal{J}{\kern 1pt} ' = \gamma _{1}^{2}\left( {\gamma _{3}^{2} - \gamma _{2}^{2}} \right)a_{1}^{2} + \gamma _{2}^{2}\left( {\gamma _{1}^{2} - \gamma _{3}^{2}} \right)a_{2}^{2} + \gamma _{3}^{2}\left( {\gamma _{2}^{2} - \gamma _{1}^{2}} \right)a_{3}^{2} = 0$Нетрудно убедиться, что все найденные выше решения удовлетворяют равенству (7.4), определяющему поверхность в пространстве ${{\mathbb{R}}^{3}}\left( \gamma \right)$.
Замечание. При доказательстве данного утверждения явный вид зависимости u4 = = ${{u}_{4}}\left( {{{g}_{1}},{{g}_{2}},{{g}_{3}}} \right)$ не понадобился.
Выводы. Для твердого тела в форме равногранного тетраэдра, подвешенного в центре масс, выполнен параметрический анализ существования и устойчивости равновесий в центральном ньютоновском поле сил. Таким образом, прояснены вопросы, касающиеся установленных ранее [1, 2] свойств равновесий правильного тетраэдра, для которого равногранный тетраэдр является естественным обобщением, наследующим некоторые из дискретных симметрий. В дальнейшем естественно ставить вопрос о свойствах относительных равновесий равногранных тетраэдров на круговой орбите и о свойствах точек либрации равномерно вращающихся равногранных тетраэдров.
Выполнение аналогичного анализа равновесий для тетраэдров общего вида, вероятно, потребует разработки иных подходов, не опирающихся на использованные в работе свойства симметрии равногранных тетраэдров.
Список литературы
Суликашвили Р.С. О стационарных движениях тетраэдра и октаэдра в центральном поле тяготения // В сб.: Задачи исследования устойчивости и стабилизации движения. М.: ВЦ АН СССР, 1987. С. 57–66.
Суликашвили Р.С. Стационарные движения тел, допускающих группу симметрии правильных многогранников в ньютоновском поле сил // ПММ. 1989. Т. 53. Вып. 4. С. 582–586.
Burov A.A., Sulikashvili R.S. On the motion of a rigid body possessing a finite group of symmetry // Prépublication du C.E.R.M.A. Ecole Nationale des Ponts et Chaussées. 1993. № 17. P. 8.
Карапетян А.В., Нараленкова И.И. О бифуркации равновесий механических систем с симметричным потенциалом // ПММ. 1998. Т. 62. № 1. С. 12–21.
Нараленкова И.И. О ветвлении и устойчивости положений равновесия твердого тела в ньютоновском поле // В сб.: Задачи исследования устойчивости и стабилизации движения. М.: ВЦ РАН, 1995. С. 53–60.
Абрарова Е.В., Карапетян A.B. О стационарных движениях твердого тела в центральном гравитационном поле // ПММ. 1994. Т. 58. Вып. 5. С. 68–73.
Абрарова Е.В. Об устойчивости стационарных движений твердого тела в центральном поле // ПММ. 1995. Т. 59. Вып. 6. С. 947–955.
Буров А.А., Карапетян А.В. О движении крестообразных тел // Изв. РАН. МТТ. 1995. № 6. С. 14–18.
Абрарова Е.В. Об относительных равновесиях твердого тела в центральном поле // В сб.: Задачи исследования устойчивости и стабилизации движения. М.: ВЦ АН СССР, 1995. С. 3–28.
Абрарова Е.В., Карапетян A.B. О ветвлении и устойчивости стационарных движений и относительных равновесий твердого тела в центральном гравитационном поле // ПММ. 1996. Т. 60. Вып. 3. С. 375–387.
Буров А.А., Герман А.Д., Суликашвили Р.С. Об орбитальном движении тетраэдра-гиростата // ПММ. 2010. Т. 74. № 4. С. 594–609.
Буров А.А., Герман А.Д., Суликашвили Р.С. Об установившихся движениях гиростатов с равными моментами инерции в центральном поле сил // ПММ. 2011. Т. 75. № 5. С. 738–744.
Burov A.A., Guerman A.D., Sulikashvili R.S. Dynamics of a Tetrahedral Satellite–Gyrostat // AIP Conf. Proc. 2010. V. 1281. P. 465.
Рубановский В.Н., Самсонов В.А. Устойчивость стационарных движений в примерах и задачах. М.: Наука, 1988. 304 с.
Routh E.J. Treatise on the Stability of a Given State of Motion. Cambridge: Univ. Press, 1877. 108 p.
Routh E.J. The advanced part of a treatise on the dynamics of a system of rigid bodies. London: McMillan, 1884. 343 p.
Карапетян А.В. Устойчивость стационарных движений. М.: Эдиториал УРСС, 1998. 168 с.
Шарыгин И.Ф. Задачи по геометрии. Стереометрия. Сер. “Библиотечка Квант”, Вып. 31. М.: Наука, 1984. 160 с.
Vashkoviak M.A. On the stability of circular ’asteroid’ orbits in an N-planetary system // Celest. Mech. 1976. V. 13. № 3. P. 313–324.
Буров А.А., Никонова Е.А. Установившиеся движения симметричного равногранного тетраэдра в центральном поле сил // Изв. РАН. МТТ. 2021. № 5. С. 152–164.
Hancock H. Lectures on the Theory of Maxima and Minima of Functions of several Variables (Weierstrass Theory), McMicken Hall, Univ. Cincinnati, 1903.
Mann H.B. Quadratic forms with linear constraints // Am. Math. Monthly. 1943. V. 50. № 7. P. 430–433.
Шостак Р.Я. О признаке условной определенности квадратичной формы n переменных, подчиненных линейным связям, и о достаточном признаке условного экстремума функций n переменных // УМН. 1954. Т. 9 (60). № 2. С. 199–206.
Рубановский В.Н., Степанов С.Я. О теореме Рауса и методе Четаева построения функций Ляпунова из интегралов уравнений движения // ПММ. 1969. Т. 33. Вып. 5. С. 904–912.
Cтепанов С.Я. Симметризация критериев знакоопределенности симметричных квадратичных форм // ПММ. 2002. Т. 66. Вып. 6. С. 979–987.
Буров А.А. О необходимых условиях устойчивости установившихся движений систем со связями, реализуемыми большими потенциальными силами // ПММ. 2004. Т. 68. № 5. С. 870–877.
Возлинский В.И. О связи бифуркаций равновесий консервативных систем с распределением устойчивости на кривой равновесий // ПММ. 1967. Т. 31. Вып. 2. С. 418–427.
Возлинский В.И. Об устойчивости точек ветвления равновесий // ПММ. 1978. Т. 42. С. 259–267.
Карапетян A.B., Степанов С.Я. О стационарных движениях и относительных равновесиях механических систем с симметрией // ПММ. 1996. Т. 60. Вып. 5. С. 736–743.
Burov A.A., Nikonov V. I., Stability and branching of stationary rotations in a planar problem of motion of mutually gravitating triangle and material point // Russ. J. Nonlin. Dyn. 2016. V. 12. № 2. P. 179–196.
Буров А.А., Никонова Е.А. Вращение равногранного тетраэдра в центральном ньютоновском поле сил: конус Штауде // Вестн. МГУ. Сер. 1. Математика. Механика. 2021. № 5. С. 40–46.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика