Прикладная математика и механика, 2022, T. 86, № 3, стр. 313-328
О плоских резонансных вращениях спутника с шаровым демпфером на эллиптической орбите
1 Московский физико-технический институт
Москва, Россия
* E-mail: namelkin@mail.ru
Поступила в редакцию 02.12.2021
После доработки 11.02.2022
Принята к публикации 15.02.2022
- EDN: PLNGJN
- DOI: 10.31857/S003282352203002X
Аннотация
В рамках модели М.А. Лаврентьева изучается влияние внутренних диссипативных сил на вращательное движение спутника на эллиптической орбите. Получены эволюционные уравнения, описывающие плоские нерезонансные вращения спутника. Определены условия существования и устойчивости плоских резонансных вращений спутника. Получено аналитическое решение, описывающее плоские -периодические резонансные вращения спутника на эллиптической орбите.
1. Постановка задачи. Уравнения движения. Вращательное движение спутника, моделируемого одним твердым телом, в центральном гравитационном поле к настоящему времени хорошо изучено. В работах В.В. Белецкого, Ф.Л. Черноусько, А.П. Маркеева [1–6] и других авторов проведен подробный анализ вращений спутника на круговой и эллиптической орбите, изучены плоские и пространственные резонансные вращения спутника.
Влияние внутренних диссипативных сил на вращательное движение спутника в центральном гравитационном поле исследовалось в работах [7–11]. Здесь для описания диссипативных сил использовалась модель М.А. Лаврентьева [12]. В этой модели спутник (планета) моделируется системой из двух твердых тел – оболочки и шарового демпфера (ядра), при относительных перемещениях которого возникает диссипативный момент. В указанных работах проведено подробное исследование эволюции вращательного движения спутника на круговой орбите.
В настоящей работе изучается вращательное движение спутника с шаровым демпфером на эллиптической орбите.
В рамках используемой модели М.А. Лаврентьева спутник является гиростатом, т.е. его тензор инерции в базисе, связанном с оболочкой, остается неизменным. Пусть О – центр масс всего спутника, а $O{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}}$ – ортонормированный базис с началом в точке О и осями ${{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}},{{{\mathbf{e}}}_{3}}$, связанными с оболочкой. Обозначим через ${\mathbf{J}}$ тензор инерции всего спутника в этом базисе, а через ${\mathbf{J}}{\kern 1pt} * = {\mathbf{J}} - I{\mathbf{E}}$ – тензор инерции вспомогательного тела, образованного оболочкой и точечной массой, равной массе демпфера и расположенной в центре масс демпфера. Здесь $I$ – момент инерции демпфера относительно его центральной оси, ${\mathbf{E}}$ – единичная матрица.
Ниже будем полагать, что диссипативный момент пропорционален относительной угловой скорости демпфера и определяется формулой
где ω – вектор абсолютной угловой скорости оболочки, Ω – вектор абсолютной угловой скорости демпфера, $\tilde {\mu }$ – коэффициент демпфирования.Действующий на спутник гравитационный момент определяется формулой [1]
(1.2)
${{{\mathbf{M}}}_{g}} = {{3k{\mathbf{R}} \times {\mathbf{JR}}} \mathord{\left/ {\vphantom {{3k{\mathbf{R}} \times {\mathbf{JR}}} {{{R}^{5}},}}} \right. \kern-0em} {{{R}^{5}},}}$Динамические уравнения вращательного движения спутника записываются в виде
(1.3)
$\begin{gathered} {\mathbf{J}}{\kern 1pt} *{\kern 1pt} {\mathbf{\dot {\omega }}} + {\mathbf{\omega }} \times {\mathbf{J\omega }} = {{{\mathbf{M}}}_{g}} + \tilde {\mu }I({\mathbf{\Omega }} - {\mathbf{\omega }}) \\ I({\mathbf{\dot {\Omega }}} + {\mathbf{\omega }} \times {\mathbf{\Omega }}) = - \tilde {\mu }I({\mathbf{\Omega }} - {\mathbf{\omega }}) \\ \end{gathered} $Первое из этих уравнений представляет собой теорему об изменении кинетического момента вспомогательного тела, а второе – теорему об изменении кинетического момента демпфера. Все векторы в этих уравнениях заданы проекциями на оси базиса $O{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}}$.
Уравнения (1.3) дополняются до замкнутой системы кинематическими уравнениями вращательного движения оболочки спутника, записанными в тех или иных переменных. Для целей численного интегрирования целесообразно использовать уравнения Пуассона в кватернионах
Здесь ${\mathbf{\Lambda }}$ – кватернион единичной нормы, задающий положение базиса $O{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}}$ относительно базиса Кенига $O{{{\mathbf{i}}}_{1}}{{{\mathbf{i}}}_{2}}{{{\mathbf{i}}}_{3}}$. Для аналитического исследования могут быть использованы кинематические уравнения в углах Эйлера.
Оси базиса Кенига выберем так, чтобы ось ${{{\mathbf{i}}}_{3}}$ совпадала с нормалью ${\mathbf{n}}$ к плоскости орбиты, а ось ${{{\mathbf{i}}}_{1}}$ – с направлением на перигелий орбиты. Обозначим через ${\mathbf{r}} = {{\mathbf{R}} \mathord{\left/ {\vphantom {{\mathbf{R}} R}} \right. \kern-0em} R}$ единичный вектор, сонаправленный с радиус-вектором центра масс спутника, а через $\nu $ – истинную аномалию – угол между векторами ${\mathbf{r}}$ и ${{{\mathbf{i}}}_{1}}$. Угловая скорость орбитального базиса, образованного векторами ${\mathbf{r}}$, ${\mathbf{\tau }} = {\mathbf{n}} \times {\mathbf{r}}$ и ${\mathbf{n}}$, направлена по ${\mathbf{n}}$ и определяется выражением $\dot {\nu }\, = {c \mathord{\left/ {\vphantom {c {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}$, где $c$ – константа интеграла площадей ${{R}^{2}}\dot {\nu } = c$.
В качестве безразмерного времени будем использовать среднюю аномалию $\tau = {{\omega }_{0}}t$, где ${{\omega }_{0}}$ – средняя угловая скорость орбитального базиса, определяемая формулой
(1.5)
${{\omega }_{0}} = {{(k{\text{/}}{{a}^{3}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \frac{c}{{{{{(p{{a}^{3}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} = \frac{c}{{{{p}^{2}}}}{{(1 - {{e}^{2}})}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}},\quad p = \frac{{{{c}^{2}}}}{k}$Здесь a – большая полуось орбиты спутника, $p$ – параметр, e – эксцентриситет.
Введем безразмерные переменные ${\mathbf{U}}$ и ${\mathbf{V}}$ согласно формулам
(1.6)
${\mathbf{U}} = {{\mathbf{\omega }} \mathord{\left/ {\vphantom {{\mathbf{\omega }} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}},\quad {\mathbf{V}} = {{\mathbf{\Omega }} \mathord{\left/ {\vphantom {{\mathbf{\Omega }} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$В этих переменных уравнения (1.3) запишутся в виде
(1.7)
$\begin{gathered} {\mathbf{J}}{\kern 1pt} *{\kern 1pt} {\mathbf{U}}{\kern 1pt} '\; + {\mathbf{U}} \times {\mathbf{JU}} = \mu I({\mathbf{V}} - {\mathbf{U}}) + {{{\mathbf{m}}}_{g}} \\ {\mathbf{V}}{\kern 1pt} '\; + {\mathbf{U}} \times {\mathbf{V}} = - \mu ({\mathbf{V}} - {\mathbf{U}}) \\ \end{gathered} $Здесь штрихом обозначена производная по безразмерному времени $\tau = {{\omega }_{0}}t$, $\mu = {{\tilde {\mu }} \mathord{\left/ {\vphantom {{\tilde {\mu }} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$ – безразмерный коэффициент демпфирования, а безразмерный гравитационный момент ${{{\mathbf{m}}}_{g}}$ выражается формулой
(1.8)
${{{\mathbf{m}}}_{g}} = \frac{{{{{\mathbf{M}}}_{g}}}}{{\omega _{0}^{2}}} = \frac{{3{\mathbf{r}} \times {\mathbf{Jr}}}}{{{{{(1 - {{e}^{2}})}}^{3}}}}{{(1 + e\cos \nu )}^{3}}$Закон изменения истинной аномалии описывается уравнением
(1.9)
$\nu {\kern 1pt} ' = \frac{{{{{(1 + e\cos \nu )}}^{2}}}}{{{{{(1 - {{e}^{2}})}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}$Компоненты вектора $3{\mathbf{r}} \times {\mathbf{Jr}}$ в базисе главных центральных осей инерции спутника $O{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}}$ выражаются в виде
(1.10)
$3{\mathbf{r}} \times {\mathbf{Jr}} = 3[(C - B){{r}_{2}}{{r}_{3}},(A - C){{r}_{3}}{{r}_{1}},(B - A){{r}_{1}}{{r}_{2}}],$Если вместо переменной V ввести переменную ${\mathbf{W = V}} - {\mathbf{U}}$ (относительную угловую скорость демпфера), то уравнения (1.7) перепишутся в виде
(1.11)
$\begin{gathered} ({\mathbf{J}} - I{\mathbf{E}}){\mathbf{U}}{\kern 1pt} '\; + {\mathbf{U}} \times {\mathbf{JU}} = \mu I{\mathbf{W}} + {{{\mathbf{m}}}_{g}} \\ ({\mathbf{J}} - I{\mathbf{E}})\left( {{\mathbf{W}}{\kern 1pt} '\; + {\mathbf{U}} \times {\mathbf{W}}} \right) = - \mu {\mathbf{JW}} + {\mathbf{U}} \times {\mathbf{JU}} - {{{\mathbf{m}}}_{g}} \\ \end{gathered} $2. Плоские вращения спутника. В данной работе ограничимся анализом плоских вращений спутника с демпфером на эллиптической орбите. Такие вращения допускаются уравнениями (1.11) и представляют собой вращения вокруг одной из главных осей инерции спутника, сонаправленной с нормалью к плоскости орбиты. Не ограничивая общности, будем считать, что осью вращения является главная ось $O{{{\mathbf{e}}}_{3}}$. Такие вращения описываются следующей системой уравнений:
(2.1)
$\begin{gathered} {\text{W}}_{3}^{'} = - \mu (1 + \gamma ){{{\text{W}}}_{3}} - \varepsilon {{f}_{3}} \\ \varphi {\kern 1pt} ' = {{U}_{3}} \\ \end{gathered} $Здесь использованы обозначения
(2.2)
$\gamma = \frac{I}{{C - I}},\quad \varepsilon = \frac{{3(B - A)}}{{2(C - I)}},\quad {{f}_{3}} = \frac{{{{{(1 + e\cos \nu )}}^{3}}}}{{{{{(1 - {{e}^{2}})}}^{3}}}}\sin 2(\nu - \varphi ),$Отметим, что функцию ${{f}_{3}}$ можно записать в виде
(2.3)
${{f}_{3}} = \frac{{\partial F}}{{\partial \varphi }};\quad F = \frac{{{{{(1 + e\cos \nu )}}^{3}}\cos 2(\nu - \varphi )}}{{2{{{(1 - {{e}^{2}})}}^{3}}}},$Поскольку истинная аномалия $\nu $ является периодической по $\tau $ функцией с периодом $2\pi $, то этим же свойством обладает и функция $F$ (2.3). Поэтому ее можно представить рядом Фурье
(2.4)
$F(\tau ,\varphi ) = {{F}_{0}}(\varphi ) + \sum\limits_{k = 1}^\infty {{{A}_{k}}\sin (k\tau - 2\varphi ) + {{B}_{k}}\cos (k\tau - 2\varphi )} $Коэффициенты этого разложения определяются формулами
(2.5)
${{F}_{0}}(\varphi ) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {Fd\tau } = \frac{1}{{4\pi {{{(1 - {{e}^{2}})}}^{{3/2}}}}}\int\limits_0^{2\pi } {(1 + e\cos \nu )\cos 2(\nu - \varphi )d\nu } = 0$(2.6)
${{A}_{k}} = \frac{1}{\pi }\int\limits_0^{2\pi } {F\sin (k\tau - 2\varphi )d\tau } = - \frac{1}{2}{{\Phi }_{{ - k}}}\sin 4\varphi $(2.7)
${{B}_{k}} = \frac{1}{\pi }\int\limits_0^{2\pi } {F\cos (k\tau - 2\varphi )d\tau } = \frac{{{{\Phi }_{k}}(e)}}{2} + \frac{{{{\Phi }_{{ - k}}}(e)\cos 4\varphi }}{2}$Здесь ${{\Phi }_{k}}(e)$ и ${{\Phi }_{{ - k}}}(e)$ – интегралы Ф.Л. Черноусько [4], определяемые формулами
(2.8)
${{\Phi }_{k}}(e) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\frac{{{{{(1 + e\cos \nu )}}^{3}}\cos (k\tau - 2\nu )}}{{{{{(1 - {{e}^{2}})}}^{3}}}}d\tau } = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\frac{{(1 + e\cos \nu )\cos (k\tau - 2\nu )}}{{{{{(1 - {{e}^{2}})}}^{{3/2}}}}}d\nu } $(2.9)
${{\Phi }_{{ - k}}}(e) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\frac{{{{{(1 + e\cos \nu )}}^{3}}\cos (k\tau + 2\nu )}}{{{{{(1 - {{e}^{2}})}}^{3}}}}d\tau } = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\frac{{(1 + e\cos \nu )\cos (k\tau + 2\nu )}}{{{{{(1 - {{e}^{2}})}}^{{3/2}}}}}d\nu } $Явные выражения для этих функций в виде рядов по эксцентриситету можно найти в книге А.П. Маркеева [5]. Ниже выписаны первые члены этих разложений
(2.10)
$\begin{gathered} {{\Phi }_{1}}\, = - \frac{1}{2}e,\quad {{\Phi }_{2}}\, = 1 - \frac{5}{2}{{e}^{2}},\quad {{\Phi }_{3}} = \frac{7}{2}e,\quad {{\Phi }_{4}}\, = \frac{{17}}{2}{{e}^{2}},\quad {{\Phi }_{5}} = \frac{{845}}{{48}}{{e}^{3}},\quad {{\Phi }_{6}}\, = \frac{{533}}{{16}}{{e}^{4}},\; \ldots \\ {{\Phi }_{0}} = 0,\quad {{\Phi }_{{ - 1}}} = \frac{1}{{48}}{{e}^{3}},\quad {{\Phi }_{{ - 2}}} = \frac{1}{{24}}{{e}^{4}},\quad {{\Phi }_{{ - 3}}} = \frac{{81}}{{1280}}{{e}^{5}},\quad {{\Phi }_{{ - 4}}} = \frac{4}{{45}}{{e}^{6}},\; \ldots \\ \end{gathered} $Из таблицы (2.10) следует, что при $e \ll 1$ функции ${{\Phi }_{k}}(e)$ ($k \ne 0$) являются величинами порядка ${{e}^{{\left| {k - 2} \right|}}}$, а отношение между разными функциями можно описать неравенствами
(2.11)
$\Phi _{k}^{2} < {{(ae)}^{{2(k - s)}}}\Phi _{s}^{2};\quad k > s \geqslant 2,\quad \Phi _{{2 + k}}^{2} < {{(ae)}^{{2(k - 1)}}}\Phi _{1}^{2};\quad k \geqslant 2$(2.13)
$\Phi _{{n + s + 1}}^{2} < {{(ae)}^{2}}\Phi _{{n - s}}^{2};\quad n \geqslant 2,\quad 0 \leqslant s \ne n$(2.14)
$\Phi _{{n - s}}^{2} < {{(ae)}^{2}}\Phi _{{n + s + 1}}^{2};\quad n \leqslant 1,\quad 0 \leqslant s \ne - (n + 1)$Здесь $a > 0$ – ограниченная величина, зависящая от $k$, $s$ и $n$.
После подстановки выражений (2.5)–(2.7) в формулу (2.4) получим
(2.15)
$\,F(\tau ,\varphi ) = \frac{1}{2}\sum\limits_{k = 1}^\infty {[{{\Phi }_{k}}(e)\cos (k\tau - 2\varphi ) + {{\Phi }_{{ - k}}}(e)\cos (k\tau + 2\varphi )]} $Очевидно, что эту формулу можно переписать в виде
где суммирование ведется по всем целым положительным и отрицательным $k$.Для функции ${{f}_{3}}$ на основании (2.3) будем иметь
Резонансные вращения спутника определяются условиями
(2.18)
$\left\langle {\dot {\varphi }} \right\rangle = U = \frac{n}{2};\quad n = \pm 1, \pm 2, \pm 3, \ldots $Здесь через $U$ обозначено среднее значение ${{U}_{3}}$. Положительным значениям $n$ отвечают “прямые” вращения, а отрицательным – “обратные” вращения.
Условие отсутствия резонансов записывается в виде
(2.19)
$\left\langle {\dot {\varphi }} \right\rangle = U \ne \frac{n}{2};\quad n = \pm 1, \pm 2, \pm 3, \ldots $3. Нерезонансные плоские вращения спутника. Так как четвертое из уравнений (2.1) уже учтено при выводе формулы (2.12) для ${{f}_{3}}(\tau ,\varphi )$, то плоские вращения спутника с демпфером можно описать следующей замкнутой системой из трех уравнений:
Здесь и далее используются обозначения
Ниже будем полагать, что $0 < \varepsilon \ll 1$ (малый параметр), т.е. спутник близок к сферически симметричному.
Для анализа нерезонансных вращений используем метод осреднения [13, 14]. Сделаем замену переменных
в которой функции $S$ и $R$ найдем из системы уравнений(3.4)
$\begin{gathered} \sum\limits_k {\frac{{\partial S}}{{\partial {{\sigma }_{k}}}}} (k - 2U) = \mu \gamma R + \varepsilon {{f}_{3}} \\ \sum\limits_k {\frac{{\partial R}}{{\partial {{\sigma }_{k}}}}} (k - 2U) = - mR + \varepsilon {{f}_{3}} \\ \end{gathered} $Решения этой системы записывается гармоническими по переменным ${{\sigma }_{k}}$ функциями вида
(3.5)
$S = \sum\limits_k {{{a}_{k}}\sin {{\sigma }_{k}} + {{b}_{k}}\cos {{\sigma }_{k}}} ,\quad R = \sum\limits_k {{{p}_{k}}\sin {{\sigma }_{k}} + {{q}_{k}}\cos {{\sigma }_{k}}} $Коэффициенты при гармониках выражаются формулами
(3.6)
$\begin{gathered} {{q}_{k}} = \frac{{(k - 2U)\varepsilon {{\Phi }_{k}}}}{{{{{(k - 2U)}}^{2}} + {{m}^{2}}}},\quad {{p}_{k}} = - \frac{{m\varepsilon {{\Phi }_{k}}}}{{{{{(k - 2U)}}^{2}} + {{m}^{2}}}} \\ {{a}_{k}} = \frac{{\mu \gamma \varepsilon {{\Phi }_{k}}}}{{{{{(k - 2U)}}^{2}} + {{m}^{2}}}},\quad {{b}_{k}} = - \frac{{\mu m + {{{(k - 2U)}}^{2}}}}{{(k - 2U)[{{{(k - 2U)}}^{2}} + {{m}^{2}}]}}\varepsilon {{\Phi }_{k}} \\ \end{gathered} $После подстановки решений (3.5) в уравнения (3.1) получим
(3.7)
$\begin{gathered} U{\kern 1pt} '\left( {1 + \frac{{\partial S}}{{\partial U}}} \right) - 2S\sum\limits_k {\frac{{\partial S}}{{\partial {{\sigma }_{k}}}}} = \mu \gamma W \\ W{\kern 1pt} '\left( {1 + \frac{{\partial R}}{{\partial U}}} \right) - 2S\sum\limits_k {\frac{{\partial R}}{{\partial {{\sigma }_{k}}}}} = - mW \\ \end{gathered} $Из формул (3.5) и (3.6) следует, что в рассматриваемом нерезонансном случае функции $S$ и $R$ являются ограниченными функциями малого параметра $\varepsilon $. Этим же свойством обладают и фигурирующие в уравнениях (3.7) производные от этих функций. Обозначив среднее по времени угловыми скобками, получим
(3.8)
$\left\langle {\frac{{\partial S}}{{\partial U}}} \right\rangle = O({{\varepsilon }^{2}}),\quad \left\langle {\frac{{\partial R}}{{\partial U}}} \right\rangle = O({{\varepsilon }^{2}}),\quad \left\langle {2S\sum\limits_k {\frac{{\partial S}}{{\partial {{\sigma }_{k}}}}} } \right\rangle = O({{\varepsilon }^{3}})$(3.9)
$\left\langle {2S\sum\limits_k {\frac{{\partial R}}{{\partial {{\sigma }_{k}}}}} } \right\rangle = \sum\limits_k {({{p}_{k}}{{b}_{k}} - {{q}_{k}}{{a}_{k}})} = \sum\limits_k {\frac{{\mu {{\varepsilon }^{2}}\Phi _{k}^{2}}}{{(k - 2U)[{{{(k - 2U)}}^{2}} + {{m}^{2}}]}}} + O({{\varepsilon }^{3}})$При учете этих формул осредненные с точностью до $O({{\varepsilon }^{3}})$ уравнения (3.7) примут вид
(3.10)
$U{\kern 1pt} ' = \mu \gamma W,\quad W{\kern 1pt} '\; - \sum\limits_k {\frac{{\mu {{\varepsilon }^{2}}\Phi _{k}^{2}}}{{(k - 2U)[{{{(k - 2U)}}^{2}} + {{m}^{2}}]}}} = - mW$Из этих уравнений следует, что в установившемся режиме медленной эволюции средняя относительная угловая скорость демпфера выражается формулой
(3.11)
$W = \sum\limits_k {\frac{{\,\mu \,{{\varepsilon }^{2}}\Phi _{k}^{2}}}{{m(k - 2U)[{{{(k - 2U)}}^{2}} + {{m}^{2}}]}}} \,,$(3.12)
$U{\kern 1pt} ' = \frac{{\mu \gamma {{\varepsilon }^{2}}}}{{(1 + \gamma )}}\sum\limits_k {\frac{{\Phi _{k}^{2}}}{{(k - 2U)[{{{(k - 2U)}}^{2}} + {{m}^{2}}]}}} $Уравнение (3.12) описывает эволюцию плоского нерезонансного вращения спутника с демпфером на эллиптической орбите. Для круговой орбиты уравнение (3.12) принимает вид
(3.13)
$U{\kern 1pt} ' = \frac{{\mu \gamma {{\varepsilon }^{2}}}}{{2(1 + \gamma )(1 - U)[4{{{(1 - U)}}^{2}} + {{m}^{2}}]}}$Это уравнение было получено ранее [10]. Из него следует, что в случае круговой орбиты средняя угловая скорость оболочки спутника монотонно стремится к значению $U = 1$, т.е. спутник эволюционирует к положению относительного равновесия.
Исследуем поведение средней угловой скорости оболочки спутника в нерезонансном вращении для случая эллиптической орбиты. Рассмотрим вращение, для которого величина $2U$ лежит между резонансными значениями $n$ и $n + 1$, где $n \ne 0$ – целое число, которое может принимать как положительные, так и отрицательные значениями. Положим
Здесь $0 < \Delta \ll 1$ – величина, характеризующая удаленность рассматриваемых движений от резонансных вращений. Оценки для значений этой величины будут приведены ниже.
Обозначим через $\Sigma $ сумму в правой части уравнения (3.12). Ее можно записать в виде
(3.15)
$\Sigma = \sum\limits_{s = 0}^\infty {{{\Sigma }_{s}}} = \sum\limits_{s = 0}^\infty {\left( {\frac{{\Phi _{{n + s + 1}}^{2}}}{{(s + 1 - V)[{{{(s + 1 - V)}}^{2}} + {{m}^{2}}]}} - \frac{{\Phi _{{n - s}}^{2}}}{{(s + V)[{{{(s + V)}}^{2}} + {{m}^{2}}]}}} \right)} $Определим знак каждого слагаемого ${{\Sigma }_{s}}$ в сумме (3.15). Рассмотрим сначала случай $n \geqslant 2$ (вращения с угловой скоростью $U > 1$). Учитывая правое из неравенств (3.14), получим
(3.16)
$\begin{gathered} {{\Sigma }_{s}} < \frac{{\Phi _{{n + s + 1}}^{2}}}{{(s + \Delta )[{{{(s + \Delta )}}^{2}} + {{m}^{2}}]}} - \frac{{\Phi _{{n - s}}^{2}}}{{(s + 1)[{{{(s + 1)}}^{2}} + {{m}^{2}}]}} < \\ < \frac{1}{{(s + 1)[{{{(s + 1)}}^{2}} + {{m}^{2}}]}}\left( {\frac{{{{{(s + 1)}}^{3}}}}{{{{{(s + \Delta )}}^{3}}}}\Phi _{{n + 1 + s}}^{2} - \Phi _{{n - s}}^{2}} \right) \\ \end{gathered} $При учете неравенств (2.13) будем иметь
(3.17)
${{\Sigma }_{s}} < \frac{1}{{(s + 1)[{{{(s + 1)}}^{2}} + {{m}^{2}}]}}\left( {\frac{{{{{(s + 1)}}^{3}}}}{{{{{(s + \Delta )}}^{3}}}}{{{(ae)}}^{2}} - 1} \right)\Phi _{{n - s}}^{2};\quad 0 \leqslant s \ne n$Отсюда следует, что при $e \ll 1$ для значений $V$ из интервала (3.14), где
будут выполняться неравенства(3.19)
${{\Sigma }_{s}} < - \frac{1}{{2(s + 1)[{{{(s + 1)}}^{2}} + {{m}^{2}}]}}\Phi _{{n - s}}^{2} < 0;\quad 0 \leqslant s \ne n$Для $s = n$ имеем
(3.20)
${{\Sigma }_{s}} = {{\Sigma }_{n}} < \frac{{\,\Phi _{{2n + 1}}^{2}}}{{(\Delta + n)[{{{(\Delta + n)}}^{2}} + {{m}^{2}}]}} > 0$При этом для члена ${{\Sigma }_{{s - 1}}} = {{\Sigma }_{{n - 1}}}$ в силу (3.19) выполняется неравенство
В рассматриваемом случае $n \geqslant 2$. Поэтому на основании неравенства (2.11) имеем
а при учете формулы (3.18) получим(3.22)
${{\Sigma }_{n}} + {{\Sigma }_{{n - 1}}} < \left( {\frac{{{{\Delta }^{6}}}}{{4(\Delta + n)[{{{(\Delta + n)}}^{2}} + {{m}^{2}}]}} - \frac{1}{{2n({{n}^{2}} + {{m}^{2}})}}} \right)\Phi _{1}^{2} < 0$Из неравенств (3.19) и (3.22) следует $\Sigma < 0$. Это означает, что на нерезонансных вращениях с угловой скоростью $U > 1$ производная $U{\kern 1pt} ' < 0$, т.е. средняя угловая скорость спутника убывает.
Рассмотрим теперь случай $n \leqslant 1$ (вращения с угловой скоростью $U < 1$). Здесь $n$ может принимать значения +1, –1, –2, –3, …. Учитывая левое из неравенств (3.14), получим из (3.15)
(3.23)
$\begin{gathered} {{\Sigma }_{s}} > \frac{{\Phi _{{n + 1 + s}}^{2}}}{{(s + 1)[{{{(s + 1)}}^{2}} + {{m}^{2}}]}} - \frac{{\Phi _{{n - s}}^{2}}}{{(s + \Delta )[{{{(s + \Delta )}}^{2}} + {{m}^{2}}]}} > \\ \; > \frac{1}{{(s + 1)[{{{(s + 1)}}^{2}} + {{m}^{2}}]}}\left( {\Phi _{{n + 1 + s}}^{2} - \frac{{{{{(s + 1)}}^{3}}}}{{{{{(s + \Delta )}}^{3}}}}\Phi _{{n - s}}^{2}} \right) \\ \end{gathered} $При учете неравенства (2.14) будем иметь
(3.24)
${{\Sigma }_{s}} > \frac{1}{{(s + 1)[{{{(s + 1)}}^{2}} + {{m}^{2}}]}}\left( {1 - \frac{{{{{(s + 1)}}^{3}}}}{{{{{(s + \Delta )}}^{3}}}}a{{e}^{2}}} \right)\Phi _{{n + 1 + s}}^{2};\quad 0 \leqslant s \ne - (n + 1)$Отсюда следует, что при $e \ll 1$ для значений $V$ из интервала (3.14), где $\Delta $ определяется формулой (3.18), будут выполняться неравенства
(3.25)
${{\Sigma }_{s}} > \frac{1}{{(s + 1)[{{{(s + 1)}}^{2}} + {{m}^{2}}]}}\left( {1 - \frac{{{{{(s + 1)}}^{3}}}}{{2{{{(s + \Delta )}}^{3}}}}{{\Delta }^{3}}} \right)\Phi _{{n + 1 + s}}^{2} > 0;\quad 0 \leqslant s \ne - (n + 1)$Для $s = - (n + 1)$ из (3.23) имеем
(3.26)
${{\Sigma }_{s}} > - \frac{{\Phi _{{2n + 1}}^{2}}}{{(s + \Delta )[{{{(s + \Delta )}}^{2}} + {{m}^{2}}]}},$(3.27)
${{\Sigma }_{{s + 1}}} > \frac{1}{{(s + 2)[{{{(s + 2)}}^{2}} + {{m}^{2}}]}}\left( {1 - \frac{{{{{(s + 2)}}^{3}}}}{{2{{{(s + 1 + \Delta )}}^{3}}}}{{\Delta }^{3}}} \right)\Phi _{1}^{2}$Так как в формуле (3.15) $s \geqslant 0$, то случай $s = - (n + 1)$ возможен только при $n \leqslant - 1$. Для таких значений $n$ согласно (2.12) и (3.18) имеем
(3.28)
$\Phi _{{2n + 1}}^{2} < {{(ae)}^{4}}\Phi _{1}^{2} = {{\Delta }^{6}}\Phi _{1}^{2}{\text{/}}4;\quad n \leqslant - 1,$(3.29)
${{\Sigma }_{s}} + {{\Sigma }_{{s + 1}}} > \left( {\frac{1}{{2(s + 2)[{{{(s + 2)}}^{2}} + {{m}^{2}}]}} - \frac{{{{\Delta }^{6}}}}{{4(s + \Delta )[{{{(s + \Delta )}}^{2}} + {{m}^{2}}]}}} \right)\Phi _{1}^{2} > 0$Из неравенств (3.25) и (3.29) следует $\Sigma > 0$. Это означает, что на нерезонансных вращениях с угловой скоростью $U < 1$ производная $U{\kern 1pt} ' > 0$, т.е. средняя угловая скорость спутника возрастает.
Таким образом, и в случае эллиптической орбиты на нерезонансных вращениях при $U < 1$ средняя угловая скорость спутника возрастает, а при $U > 1$ – убывает. Но в отличие от случая круговой орбиты здесь в финале эволюции необязательно будет значение $U = 1$, поскольку возможны захваты в устойчивые резонансные вращения $2U = n$, где $n \ne 2$.
4. Плоские резонансные вращения спутника. Для изучения резонансных вращений спутника (2.18) положим
Вращение будет резонансным, если $X$ будет периодической функцией $\tau $. Функцию $X$ представим в виде двух составляющих
где $Y$ и $\tilde {X}$ эволюционная и осцилляционная составляющие, соответственно.При анализе резонансных вращений также, как и в разд. 3, будем пользоваться методом осреднения. Введем обозначение
Тогда система уравнений (3.1) запишется в виде
(4.4)
$\begin{gathered} U_{3}^{'} = \mu \gamma W + \varepsilon \sum\limits_{k \ne n} {{{\Phi }_{k}}\sin ({{\sigma }_{k}} - 2\tilde {X})} - \varepsilon {{\Phi }_{n}}\sin 2(Y + \tilde {X}) \\ W_{3}^{'} = - mW - \varepsilon \sum\limits_{k \ne n} {{{\Phi }_{k}}\sin ({{\sigma }_{k}} - 2\tilde {X})} + \varepsilon {{\Phi }_{n}}\sin 2(Y + \tilde {X}) \\ \tilde {X}{\kern 1pt} ' = {{U}_{3}} - n{\text{/}}2 \\ \end{gathered} $По аналогии с разд. 3 сделаем замену переменных
в которой функции $S$ и $R$ определим из системы уравнений(4.6)
$\begin{gathered} \sum\limits_{k \ne n} {\frac{{\partial S}}{{\partial {{\sigma }_{k}}}}} (k - n) = \mu \gamma R + \varepsilon \sum\limits_{k \ne n} {{{\Phi }_{k}}\sin {{\sigma }_{k}}} \\ \sum\limits_{k \ne n} {\frac{{\partial R}}{{\partial {{\sigma }_{k}}}}} (k - n) = - mR - \varepsilon \sum\limits_{k \ne n} {{{\Phi }_{k}}\sin {{\sigma }_{k}}} \\ \end{gathered} $Решения этой системы записываются гармоническими функциями вида
(4.7)
$S = \sum\limits_{k \ne n} {({{a}_{k}}\sin {{\sigma }_{k}} + {{b}_{k}}\cos {{\sigma }_{k}})} ,\quad R = \sum\limits_{k \ne n} {({{p}_{k}}\sin {{\sigma }_{k}} + {{q}_{k}}\cos {{\sigma }_{k}})} $Коэффициенты при гармониках выражаются формулами (3.6), в которых вместо $2U$ следует положить $n$, т.е.
(4.8)
$\begin{gathered} {{q}_{k}} = \frac{{(k - n)\varepsilon {{\Phi }_{k}}}}{{{{{(k - n)}}^{2}} + {{m}^{2}}}},\quad {{p}_{k}} = - \frac{{m\varepsilon {{\Phi }_{k}}}}{{{{{(k - n)}}^{2}} + {{m}^{2}}}} \\ {{a}_{k}} = \frac{{\mu \gamma \varepsilon {{\Phi }_{k}}}}{{{{{(k - n)}}^{2}} + {{m}^{2}}}},\quad {{b}_{k}} = - \frac{{\mu m + {{{(k - n)}}^{2}}}}{{(k - n)[{{{(k - n)}}^{2}} + {{m}^{2}}]}}\varepsilon {{\Phi }_{k}};\quad k \ne n \\ \end{gathered} $После подстановки этих решений в уравнения (4.4) получим систему
(4.9)
$W{\kern 1pt} '\; + \frac{{\partial R}}{{\partial Y}}Y{\kern 1pt} ' = - mW - \varepsilon \sum\limits_{k \ne n} {{{\Phi }_{k}}[\sin ({{\sigma }_{k}} - 2\tilde {X}) - \sin {{\sigma }_{k}}]} + \varepsilon {{\Phi }_{n}}\sin 2(Y + \tilde {X})$Здесь, записав третье уравнение системы (4.4) в виде двух уравнений, мы конкретизировали разделение переменной $X$ на эволюционную $Y$ и осцилляционную $\tilde {X}$ составляющие. При таком разделении выражение для осцилляционной составляющей запишется в виде
(4.10)
${{\tilde {X}}_{n}} = \int {Sd\tau } = \sum\limits_{k \ne n} {\frac{{({{b}_{k}}\sin {{\sigma }_{k}} - {{a}_{k}}\cos {{\sigma }_{k}})}}{{k - n}}} $Используя известные тригонометрические формулы и учитывая, что $S$ и $R$ являются ограниченными функциями малого параметра $\varepsilon $, получим после осреднения с точностью до $O({{\varepsilon }^{3}})$ следующую систему уравнений:
(4.11)
$W{\kern 1pt} '\; + \frac{{\partial R}}{{\partial Y}}Y{\kern 1pt} ' = - mW - \mu \gamma {{\varepsilon }^{2}}\sum\limits_{k \ne n} {\frac{{\Phi _{k}^{2}}}{{(k - n)[{{{(k - n)}}^{2}} + {{m}^{2}}]}}} + \varepsilon {{\Phi }_{n}}\sin 2Y$Здесь вторые члены в правых частях первых двух уравнений есть среднее от функций
Положения равновесия осредненной системы (4.11) соответствуют резонансным вращениям исходной системы (4.4) и определяются уравнениями
(4.12)
$U = \frac{n}{2},\quad W = 0,\quad \sin 2Y = {{Z}_{n}} = \frac{{\mu \gamma \varepsilon }}{{{{\Phi }_{n}}}}\sum\limits_{k \ne n} {\frac{{\Phi _{k}^{2}}}{{(k - n)[{{{(k - n)}}^{2}} + {{m}^{2}}]}}} $Очевидно, что для существования резонансного вращения $2U = n$ должно выполняться условие $\left| {{{Z}_{n}}} \right| \leqslant 1$. Величина $\left| {{{Z}_{n}}} \right|$ зависит от $\varepsilon $ (линейно), $e$, $n$, а также от значений параметров $\mu $ и $\gamma $. Зависимость от последних входит в выражение (4.12) через функции
Для этих функций при учете формулы (3.2) имеем
(4.14)
${{g}_{{nk}}} \to 0\quad {\text{при}}\quad \mu \gamma \to 0\quad {\text{и}}\quad \mu \gamma \to \infty ,\quad {{g}_{{nk}}} < \frac{m}{{{{{(k - n)}}^{2}} + {{m}^{2}}}} \leqslant \frac{1}{{2\left| {k - n} \right|}}$Из формулы (4.12) и таблицы (2.10) следует, что при $e \ll 1$ величина $\left| {{{Z}_{n}}} \right|$ обратно пропорциональна ${{e}^{{\left| {n - 2} \right|}}}$. Поэтому для каждого фиксированного набора значений параметров $\varepsilon $, $\mu $ и $\gamma $ при достаточно больших значениях $\left| {n - 2} \right|$ резонансных вращений $2U = n$ не существует. Сравнительный анализ функций ${{\Phi }_{n}}(e)$ для прямых и обратных вращений показывает, что с ростом $\left| {n - 2} \right|$ существенно быстрее “заканчиваются” обратные резонансные вращения. Число резонансных вращений уменьшается также по мере уменьшения эксцентриситета $e$, а при $e = 0$ (для круговой орбиты) имеется только резонансное вращение 1:1 ($n = 2$), соответствующее положениям равновесия спутника относительно орбитального базиса.
Из уравнений (4.11) следует, что условие асимптотической устойчивости положений равновесия (4.12), а, следовательно, и резонансных вращений спутника, выглядит следующим образом:
Если $0 < \left| {{{Z}_{n}}} \right| < 1$, то на полуинтервале $[0,\,\pi )$ существует два положения равновесия (4.12), одно из которых асимптотически устойчиво, а другое неустойчиво. Отметим, что здесь речь идет об устойчивости по отношению к плоским возмущениям.
Колебательная составляющая ${{\tilde {X}}_{n}}$ переменной ${{X}_{n}} = \varphi - n\tau {\text{/}}2$, определяемая рядом (4.10), для каждого $n$ содержит гармоники с частотами 1, 2, 3, … и поэтому является $2\pi $-периодической функцией $\tau $.
Для слабо эллиптических орбит ($e \ll 1$) при вычислении ${{Z}_{n}}$ и ${{\tilde {X}}_{n}}$ приемлемая точность достигается, если ограничиться членами наименьшего порядка по эксцентриситету $e$ в рядах (4.12), (4.10) и функциях (2.10). Для $n = 2$ такими “старшими” будут члены с номерами $k = 3$ и $k = 1$, а для $n \ne 2$ – член с номером $k = 2$.
Для “главного” резонанса $U = 1$ (резонанс 1:1 типа “Луна”, $n = 2$) старшие члены в рядах (4.12) и (4.10) записываются в виде
(4.16)
${{Z}_{2}} = \frac{{\mu \gamma \varepsilon }}{{{{\Phi }_{2}}}}\left( {\frac{{\Phi _{3}^{2}}}{{(1 + {{m}^{2}})}} - \frac{{\Phi _{1}^{2}}}{{(1 + {{m}^{2}})}}} \right) \approx \frac{{12\mu \gamma \varepsilon {{e}^{2}}}}{{(1 + {{m}^{2}})}} < 6\varepsilon {{e}^{2}}$(4.17)
$\begin{gathered} {{{\tilde {X}}}_{2}} = \frac{{7\varepsilon e}}{{2(1 + {{m}^{2}})}}\left( {(\mu m + 1)\sin (\tau + 2Y) + \mu \gamma \cos (\tau + 2Y)} \right) + \\ + \;\frac{{\varepsilon e}}{{2(1 + {{m}^{2}})}}\left( {(\mu m + 1)\sin (\tau - 2Y) + \mu \gamma \cos (\tau - 2Y)} \right) \\ \end{gathered} $В этом резонансном режиме спутник совершает $2\pi $-периодические колебания в окрестности относительного положения равновесия. Амплитуда этих колебаний пропорциональна произведению $\varepsilon e$.
Для резонансов $2U = n$, где $n \ne 2$, старшие члены в выражениях (4.12) и (4.10) имеют вид
(4.18)
${{Z}_{n}} = \frac{{\mu \gamma \varepsilon \Phi _{2}^{2}}}{{{{\Phi }_{n}}(2 - n)[{{{(2 - n)}}^{2}} + {{m}^{2}}]}},\quad \left| {{{Z}_{n}}} \right| < \frac{\varepsilon }{{2\left| {{{\Phi }_{n}}} \right|{{{(2 - n)}}^{2}}}}$(4.19)
${{\tilde {X}}_{n}} = - \frac{{\varepsilon {{\Phi }_{2}}}}{{{{{(2 - n)}}^{2}} + {{m}^{2}}}}\left( {\frac{{\mu m + {{{(2 - n)}}^{2}}}}{{{{{(2 - n)}}^{2}}}}\sin \left[ {(2 - n)\tau - 2Y} \right] + \frac{{\mu \gamma }}{{2 - n}}\cos \left[ {(2 - n)\tau - 2Y} \right]} \right)$Здесь амплитуда колебаний периодической составляющей пропорциональна $\varepsilon $.
В случаях, когда эксцентриситет $e$ не слишком мал, например, $e \geqslant 0.1$, для вычисления функций ${{Z}_{n}}$ и ${{\tilde {X}}_{n}}$ с хорошей точностью в рядах (4.10), (4.12) и функциях (2.10) необходимо помимо старших членов учитывать и несколько членов более высокого порядка малости по эксцентриситету $e$.
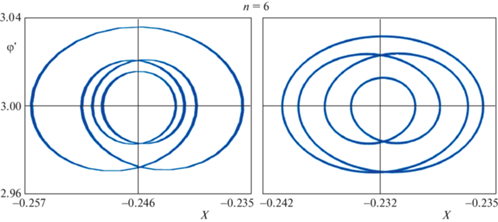
Полученные выше аналитические выводы о резонансных вращениях спутника подтверждаются результатами численного интегрирования точных уравнений движения (2.1). Для разных значений параметров соответствующим подбором начальных условий установлено существование устойчивых резонансных вращений $2U = n$ для n = 1, 2, 3, 4, 5, 6, –1, –2. При этом установлено, что если $e \leqslant 0.2$, то для вычисления значений ${{Z}_{n}}$ и функций ${{\tilde {X}}_{n}}$ с хорошей точностью достаточно в (4.12) и (4.10) учитывать не более четырех членов ряда. Соответствующий пример приведен на рис. 1 для резонансного вращения 3:1 ($n = 6$) для следующих значений параметров:
В левой части рисунка изображена фазовая траектория в плоскости $X,\varphi {\kern 1pt} '$, где $X = \varphi - 3\tau $, установившегося резонансного вращения, полученная по результатам численного интегрирования уравнений (2.1), а в правой части – фазовая траектория, вычисленная по формулам (4.12), (4.10) при сохранении в этих рядах членов с номерами $k = 1,2,3$.
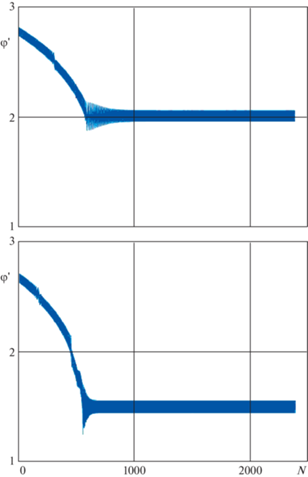
По результатам численного интегрирования уравнений (2.1) установлено также, что захват в существующие резонансные вращения $2U = n$, где $n \ne 2$, носит вероятностный характер. Т.е. для одних начальных значений $2U$ из интервала $(n,\,n + 1)$ захват в резонансное вращение $2U = n$ наблюдается, а для других происходит “проскакивание” мимо этого резонансного вращения и захват потом наблюдается в резонанс более низкого порядка. Соответствующий пример приведен на рис. 2, где приведены графики эволюции угловой скорости спутника для одной и той же комбинации значений параметров, но при разных начальных условиях. Здесь $N$ – число оборотов спутника вокруг притягивающего центра.
Вероятностный характер захвата в существующие резонансные вращения может объясняться неавтономностью рассматриваемой системы. На основании результатов численного интегрирования уравнений (2.1), проведенного для большого числа разных значений параметров и начальных условий, можно высказать предположение, что вероятность захвата в резонансы $2U = n$, где $n \ne 2$, пропорциональна некоторой положительной степени $\left| {{{\Phi }_{n}}} \right|$. Для обратных вращений эта вероятность существенно меньше, чем для прямых вращений. Например, указанные выше устойчивые обратные резонансные вращения $U = - 1{\text{/}}2$ и $U = - 1$ удалась обнаружить только специальным подбором начальных условий.
Численное интегрирование уравнений (2.1) показало также, что помимо резонансных вращений, описываемых $2\pi $-периодическими решениями (4.12), (4.10), возможны и другие, в которых решение $X = \varphi - n\tau {\text{/}}2$ содержит гармоники с дробными частотами. Этот факт обнаружен для резонанса 3:2 (резонанс типа “Меркурий”, $n = 3$) при интегрировании уравнений (2.1) для следующих значений параметров:
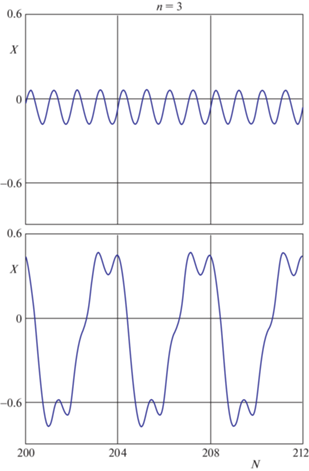
Установлено, что при задании начальных условий
наблюдается захват в резонансном вращении 3:2, для которого график переменной $X$ приведен на рис. 3 слева. А на рис. 3 справа приведен график $X$ для установившегося резонансного вращения 3:2, которое наблюдается, если начальные условия задать такими значениями фазовых переменных:В обоих случаях наблюдается захват в резонансное вращение 3:2. Но в первом случае переменная $X$ является $2\pi $-периодической по $\tau $, а во втором – $8\pi $-периодической по $\tau $. При этом амплитуда колебаний во втором случае отличается от амплитуды колебаний в первом случае более чем в четыре раза.
Следует отметить, что для подавляющего большинства начальных условий из окрестности резонанса 3:2 в процессе эволюции устанавливается резонансное вращение, для которого переменная $X = \varphi - 3\tau {\text{/}}2$ является $2\pi $-периодической по $\tau $, а обнаруженное $8\pi $-периодическое решение отвечает достаточно узкому множеству начальных условий. Не исключено, что в рассматриваемой задаче существуют и резонансные вращения 3:2, для которых переменная $X$ содержит гармоники с другими дробными частотами, например, является $4\pi $-периодической по $\tau $. Но для выявления таких резонансных вращений спутника требуется дополнительное исследование, которое выходит за рамки настоящей статьи.
Заключение. В работе проведено исследование плоских вращений спутника с шаровым демпфером на эллиптической орбите. Получены эволюционные уравнения, описывающие нерезонансные вращения спутника. Определены условия существования и устойчивости резонансных вращений спутника. Получено аналитическое решение, описывающее плоские $2\pi $-периодические резонансные вращения спутника с демпфером на эллиптической орбите. Аналитические выводы работы подтверждаются результатами численного интегрирования уравнений вращательного движения спутника с демпфером на эллиптической орбите.
Список литературы
Белецкий В.В. Движение спутника относительно центра масс в гравитационном поле. М.: Изд-во МГУ, 1975. 308 с.
Белецкий В.В., Лавровский Э.К. К теории резонансного вращения Меркурия // Астрон. ж. 1975. Т. 52. Вып. 6. С. 1299–1308.
Черноусько Ф.Л. О движении спутника относительно центра масс под действием гравитационных моментов // ПММ. 1963. Т. 27. Вып. 3. С. 473–483.
Черноусько Ф.Л. Резонансные явления при движении спутника относительно центра масс // ЖВММФ. 1963. Т. 3. № 3. С. 528–538.
Маркеев А.П. Линейные гамильтоновы системы и некоторые задачи об устойчивости движения спутника относительно центра масс. М.; Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2009. 396 с.
Маркеев А.П. К задаче о плоских периодических вращениях спутника на эллиптической орбите // Изв. РАН. МТТ. 2008. № 3. С. 102–115.
Амелькин Н.И., Холощак В.В. Об устойчивости стационарных вращений спутника с внутренним демпфированием в центральном гравитационном поле // ПММ. 2017. Т. 81. Вып. 2. С. 123–136.
Амелькин Н.И., Холощак В.В. О стационарных вращениях спутника при наличии внутренних упругих и диссипативных сил // ПММ. 2017. Т. 81. Вып. 6. С. 627–641.
Амелькин Н.И., Холощак В.В. Эволюция вращательного движения динамически симметричного спутника с внутренним демпфированием на круговой орбите // ПММ. 2019. Т. 83. Вып. 1. С. 3–15.
Амелькин Н.И., Холощак В.В. Вращательное движение несимметричного спутника с демпфером на круговой орбите // ПММ. 2019. Т. 83. Вып. 1. С. 16–31.
Амелькин Н.И. Эволюция вращательного движения планеты на круговой орбите под влиянием внутренних упругих и диссипативных сил // Изв. РАН. МТТ. 2020. № 2. С. 96–111.
Черноусько Ф.Л. О движении твердого тела, содержащего сферический демпфер // ПМТФ. 1968. № 1. С. 73–79.
Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1974. 503 с.
Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. М.: Наука, 1988. 326 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика