Прикладная математика и механика, 2022, T. 86, № 3, стр. 365-369

1. Введение. Волновые движения в прямоугольном канале заданной длины, постоянной ширины и глубины изменяющейся вдоль канала рассмотрены в классических монографиях [1, 2]. В рамках рассмотренных постановок были изучены волновые движения жидкости в частных случаях, когда профиль дна стремится к нулю таким образом, что решение задачи нахождения собственных частот и форм (сейш) колебаний можно найти аналитически. Сейшевые колебания в замкнутом водоеме, состоящем из длинного узкого канала постоянного сечения и широкого бассейна, соединенного с каналом без перемычки, изучались [3] численно и аналитически в рамках одно- и двумерной постановок. Результаты, полученные для одномерной модели хорошо согласуются с экспериментальными измерениями частот сейш низших мод.

Сравнение экспериментальных измерений сейш в сосуде наличием резких градиентов в профиле дна (модель озера Байкал) [4] с данными численных расчетов показало возможность использования линейной модели (теории длинных волн) для расчета собственных частот и форм колебаний. Было показано, что наличие резких неоднородностей в профиле дна слабо влияющее на собственные формы, становится заметным в профилях их пространственных производных даже в том случае, когда эта неоднородность существует на большой глубине от поверхности.

Волновые движения в канале переменной глубины – традиционный предмет изучения в океанологии и геофизики. Так, например, задачи о собственных колебаниях в озерах и других замкнутых водоемах оказываются важными с точки зрения возникновения катастрофических явлений (сели, волны большой амплитуды). Численному расчету собственных частот колебаний озер Швейцарии выполненному в рамках гидродинамического моделирования посвящена работа [5].

Аналитические также широко используются для решения качественных задач. В частности распространение волн в полузакрытом канале с линейным выходом профиля глубины на постоянную величину проанализирована аналитически [6]. В то же время вопрос о собственных формах сейш и их спектральных свойствах в канале конечной ширины и гладким профилем дна остался не исследованным. Ниже предложена модификация метода ускоренной сходимости [7] для анализа задач на собственные значения сейш, в каналах с такими профилями дна, когда аналитическое решение оказывается невозможным.

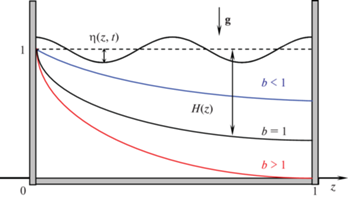
2. Постановка задачи. Обозначим через $\eta \left( {x,t} \right)$ возвышение свободной поверхности жидкости, заполняющей канал; $h\left( x \right)$ – глубина жидкости, $l$ – длина канала, ${\mathbf{g}}$ – ускорение силы тяжести (рис. 1). Показано, что возвышение свободной поверхности $\eta \left( {x,t} \right)$ удовлетворяет дифференциальному уравнению [1, 2]

и граничным условиям

Полагая $h\left( x \right) = {{h}_{0}}H\left( z \right)$, где $z = x{\text{/}}l$, будем искать периодические по времени решения уравнения (1.1) в виде

Подставляя представление (2.3) в уравнение (2.1) и граничные условия (2.2), приходим к следующей задаче Штурма–Лиувилля

где $\lambda = {{\omega }^{2}}{{l}^{2}}{\text{/}}\left( {g{{h}_{0}}} \right)$ – собственное число задачи Штурма–Лиувилля, формулируемая следующим образом: требуется найти такие значения параметра $\lambda $, при которых существуют нетривиальные решения краевой задачи (2.4). Искомые значения параметра $\lambda $ называются собственными числами задачи, а соответствующие им нетривиальные решения – собственными функциями или формами колебаний (сейши).

3. Выбор функции $H\left( z \right)$. При изучении сейш в каналах наиболее часто используется модель с вертикальными стенками (дно с обрывом), которые часто встречаются в искусственных сооружениях. В природных условиях, а также иногда и гидротехнических конструкциях и водохранилищах, в профиль дна обычно таков, что глубина канала плавно уменьшается до нуля при приближении к берегу. Учитывая приведенные соображения, а также предполагая монотонный характер профиля дна, выберем зависимость безразмерной глубины канала в виде

В точке $z = 0$, $H\left( 0 \right) = 0$, параметр $b$ описывает быстроту увеличения глубины при удалении от береговой линии. Значениям $b < 1$ соответствует пологий профиль дна, а $b > 1$ – крутой (см. рис. 1).

4. Метод решения. Задача (2.4) относится к классу задач, детально описанных в [7], однако применить метод ускоренной сходимости напрямую нельзя, поскольку ${{\left. {H\left( z \right)} \right|}_{{z = 0}}}$ = 0. Поступим следующим образом. Рассмотрим наряду с задачей (2.4) задачу вида

Здесь “регуляризирующий” параметр $a > 0$.

Учитывая, что $\forall z \in \left( {0,1} \right)$ имеет место неравенство

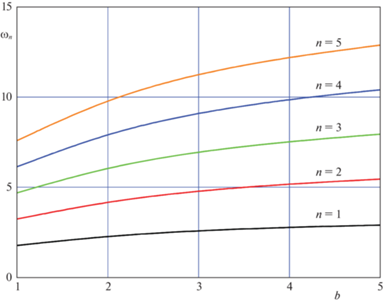
все собственные числа краевой задачи (4.1) будут больше, чем числа исходной задачи (2.4).

Будем решать методом ускоренной сходимости задачу Штурма–Лиувилля (4.1) для набора последовательно уменьшающихся параметров ${{a}_{k}} = {{10}^{{ - \left( {k + 2} \right)}}}$, $k = 1,2, \ldots $ Тогда набор найденных собственных значений задачи (4.1) ${{\tilde {\lambda }}_{n}}\left( {{{a}_{k}}} \right)$ при ${{a}_{k}} \to 0$ будет образовывать монотонно убывающую последовательность собственных чисел, сходящуюся сверху к искомым собственным числам задачи (2.4). Ограничивая проведение такой процедуры значением параметра $a = {{10}^{{ - 7}}}$, получаем значения пяти первых собственных чисел с относительной точностью ${{10}^{{ - 6}}}$. Построенные зависимости собственных частот ${{\omega }_{n}} = \sqrt {{{\lambda }_{n}}} $ (рис. 2) показывают их монотонно возрастающую зависимость от параметра пологости дна с выходом на предельное значение. Проведенные вычисления для больших $b = 10{\kern 1pt} - {\kern 1pt} 30$ показали, что предельная собственная частота, отвечающая случаю вертикальной стенке на левой границе канала, оказывается равной ${{\omega }_{ \bot }} = \pi n$.

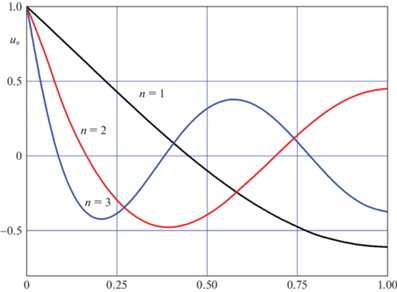
На рис. 3 изображены первая, вторая и третья собственные формы сейш для случая $b = 3$. Графики представляют собой знакопеременные функции с числом нулей, определяемых номером моды.

Таким образом, был разработан алгоритм, позволяющий применять метод ускоренной сходимости для краевых задач, с регулярными особенностями (H(z) = const · z + + $\underline{\underline O} ({{z}^{2}})$ на одной из граничных точек задачи.

Работа выполнена по теме государственного задания № АААА-А20-120011690132-4.