Прикладная математика и механика, 2022, T. 86, № 3, стр. 381-393
Об определении циркуляции вокруг цилиндра, обтекаемого вблизи плоскости
А. Г. Петров 1, *, Д. В. Маклаков 2, **
1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
2 Институт математики и механики им. Н.И. Лобачевского,
Казанский (Приволжский) федеральный университет
Казань, Россия
* E-mail: petrovipmech@gmail.com
** E-mail: dmaklak@kpfu.ru
Поступила в редакцию 07.01.2022
После доработки 31.03.2022
Принята к публикации 05.04.2022
- EDN: RDNVER
- DOI: 10.31857/S0032823522030092
Аннотация
Рассматривается плоская задача обтекания кругового цилиндра потенциальным потоком жидкости со скоростью, направленной параллельно плоскости. Циркуляция поля скорости определяется из постулата Гольдштика: максимальная скорость на границе круга должна быть минимальна. Строится точное решение этой задачи. Проводится сопоставление распределения давления на цилиндре и плоскости с экспериментальными данными и численными расчетами.
1. Введение. Плоской задаче потенциального обтекания кругового цилиндра около плоскости посвящено много работ. В монографии [1] показано, что линии тока двух точечных вихрей с противоположными циркуляциями яляются окружностями, а одна из них прямой линией. Таким образом, строится решение задачи о линиях тока циркуляционного обтекания кругового цилиндра около плоскости. Эта задача аналогична эквипотенциальным поверхностям между заряженным цилиндрическим проводником и плоскостью. Более сложной является задача обтекания кругового цилиндра около плоскости. В элементарных функциях строится решение только для случая контакта кругового цилиндра и плоскости. В общем случае задачи обтекания двух и более круговых цилиндров решение строится в виде рядов [2–8]. Интересно, что расход жидкости между круговыми цилиндрами, как показал Лагалли [2, 3], выражается достаточно простой аналитической формулой. Седов Л.И. [9] для задачи о бипланах выразил комплексный потенциал обтекания, через эллиптические функции, из которого можно получить и решение для двух круговых цилиндров.
В задаче обтекания цилиндра около плоскости величина циркуляции остается неопределенной, так как постулат Чаплыгина–Жуковского из-за отсутствия острой кромки здесь неприменим. В данной работе для определения циркуляции принимается минимаксный принцип Гольдштика: максимальное абсолютное значение скорости на поверхности цилиндра должно быть минимально [10]. Приводится [10] следующая аргументация в пользу выдвинутого постулата. “Согласно современной точке зрения циркуляция на крыловом профиле возникает вследствие отрыва и уноса вихря, после чего циркуляция устанавливается такой, чтобы обтекание было безотрывным. В начальной стадии обтекания гладкого профиля также отрываются и уносятся вихри, вследствие чего возникает циркуляция, уменьшающая возможность отрыва. В качестве основной гипотезы можно допустить, что взаимодействие тела с потоком вырабатывает циркуляцию, максимально препятствующую отрыву… Чтобы высказанная гипотеза приняла определенную форму принципа выбора циркуляции, должен быть решен вопрос о том, какая характеристика потока является наиболее адекватной мерой склонности потока к отрыву. Естественной характеристикой подобного рода является максимальное значение скорости на контуре; чем оно выше, тем больше перепад давления и тем более вероятен отрыв, обусловленный действием вязкости при восстановлении давления. Таким образом, в качестве возможного варианта обобщения постулата о циркуляции ниже рассматривается минимаксный вариационный принцип: при реальном обтекании циркуляция принимает такое значение, которое минимизирует максимальную скорость на контуре. Очевидно, что данный принцип в предельном случае крылового профиля дает классический результат, а при симметричном обтекании – нулевую циркуляцию”.
Приняв постулат Гольдштика, можно вычислить скорость на донной поверхности и на круговом цилиндре, а с помощью интеграла Бернулли определить давление на этих поверхностях. Давление может быть определено также из эксперимента или из прямого численного решения уравнений Навье–Стокса при больших числах Рейнольдса. Сравнение давлений покажет насколько приемлем принятый постулат.
Представлены [11, 12] результаты экспериментального и численного исследования обтекания круглого цилиндра, расположенного на различных высотах над границей плоскости. Изучалось [13, 14] движение цилиндра в потоке между двумя параллельными плоскостями. Развитие неустойчивости равновесия цилиндра приводит к автоколебаниям его между двумя стенками. Этот эффект качественно описывается в [13]. Из-за имеющейся циркуляции возникает аналог силы Жуковского, которая притягивает цилиндр к одной из плоскостей. При касании цилиндра циркуляция и сила Жуковского меняют знак, и цилиндр движется к противоположной стенке. Для некоторых частных случаев движение цилиндра подробно описано [14] с помощью прямого численного решения уравнений Навье–Стокса. Актуальность задачи обтекания кругового цилиндра около плоскости существенно повысилась в связи со строительством трубопроводов по дну водоемов. При течении в зазоре между трубой и дном может возникнуть донное напряжение, превышающее критическое значение, при котором начнется вымывание донной поверхности под трубой. Это может привести к аварии.
В настоящей работе рассматривается плоская задача обтекания кругового цилиндра потенциальным потоком жидкости, со скоростью, направленной параллельно плоскости. Выбор циркуляции из принципа Гольдштика определяет единственное течение, близкое к реальному. Из него можно получить максимальные скорости под цилиндром и, пользуясь теорией русловых процессов [15], определить возможность размыва дна.
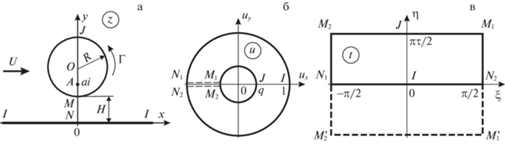
2. Постановка задачи. Аналитическое представление комплексного потенциала. Цилиндр радиуса $R$ обтекается слева направо вблизи плоской стенки двумерным установившимся безвихревым потоком идеальной несжимаемой жидкости. Скорость набегающего потока на бесконечности – $U$, циркуляция вокруг цилиндра – $\Gamma $, расстояние цилиндра от стенки – $H$. Начало декартовой системы координат расположено на стенке с осью ординат, проходящей через центр $O$ цилиндра (см. рис. 1а).
Рис. 1.
а) Схема обтекания цилиндра в физической плоскости $z = x + iy$. б) Параметрическая плоскость $u = {{u}_{x}} + i{{u}_{y}}$. в. Параметрическая плоскость $t = \xi + i\eta $.
В физической плоскости введем комплексную переменную $z = x + iy$ и комплексный потенциал течения $W(z) = \varphi (x,y) + i\psi (x,y)$, где $\varphi (x,y)$ – потенциал течения, а $\psi (x,y)$ – функция тока. Для аналитической функции $W(z)$ поставим следующую краевую задачу:
(2.4)
$\operatorname{Re} W[i(H + 2R)] = 0,\quad {{\left| {\frac{{dW}}{{dz}}} \right|}_{{z \to \infty }}} = U,$Отобразим конформно область течения на кольцо в параметрической плоскости $u$ с внешним радиусом единица, а внутренним $q$ (рис. 1б). Конформные отображения $u(z)$ и обратное $z(u)$ имеют вид
где(2.6)
$a = R\sqrt {{{{(h + 1)}}^{2}} - 1} ,\quad h = H{\text{/}}R,\quad q = h + 1 - \sqrt {{{{(h + 1)}}^{2}} - 1} $Отметим, что точка $A$ с комплексной координатой $z = ai$ всегда находится в нижней половине круга: $a \in (H,H + R)$. По величине параметр $a$ равен длине касательной, проведенной из начала координат к обтекаемой окружности. Кроме того, отображения (2.5) – дробнолинейные, и точка $z = ai$ является образом точки $u = 0$ при отображении $z = z(u)$. В плоскости $u$ преобразование инверсии относительно обеих окружностей переводит начало координат в бесконечно удаленную точку $u = \infty $, которая, в свою очередь, переходит в точку $z = - ai$. Следовательно, в плоскости $z$ точка $z = - ai$ будет симметрична точке $z = ai$ как относительно прямой $y = 0$, так и относительно обтекаемой окружности в смысле преобразования инверсии, то есть $(H + R - a)(H + R + a)$ = ${{R}^{2}}$. Из этого соотношения следует первая формула в (2.6).
Разрежем кольцо в плоскости $u$ по отрезку $MN$ и отобразим кольцо с разрезом на прямоугольник в плоскости $t$ (рис. 1в):
(2.7)
$t = \frac{1}{{2i}}\ln u = \frac{1}{{2i}}\ln \frac{{z - ai}}{{z + ai}} \Leftrightarrow z = - a{\kern 1pt} {\kern 1pt} {\text{ctg}}{\kern 1pt} {\kern 1pt} t$Основание прямоугольника равно $\pi $, а высота $\pi {\text{|}}\tau {\text{|/}}2$, где
Кроме того, легко доказать, что параметры $h$ и $a$ выражаются через $q$ так:
(2.9)
$h = \frac{1}{2}\left( {q + \frac{1}{q}} \right) - 1,\quad a = \frac{R}{2}\left( {\frac{1}{q} - q} \right)$Из (2.7) следует, что
(2.10)
$\frac{{dW}}{{dz}} = \frac{{dW}}{{dt}}{\text{/}}\frac{{dz}}{{dt}} = \frac{1}{a}{{\sin }^{2}}t{\kern 1pt} \frac{{dW}}{{dt}}$Функции $\frac{{dW}}{{dz}}(t)$ и ${{\sin }^{2}}t$ являются $\pi $-периодическими, поэтому $\frac{{dW}}{{dt}}(t)$ также $\pi $-периодическая функция. Кроме того, из граничных условий (2.1), (2.2) вытекает, что
Эти условия позволяют продолжить функцию $\frac{{dW}}{{dz}}(t)$ на всю комплексную плоскость $t = \xi + i\eta $ по принципу симметрии Римана–Шварца. Про этом
Следовательно, $\frac{{dW}}{{dt}}(t)$ – эллиптическая функция с периодами $\pi $ и $\pi \tau $. В качестве ячейки периодов возьмем прямоугольник с вершинами $ - \pi {\text{/}}2 - \pi \tau {\text{/}}2$, $\pi {\text{/}}2 - \pi \tau {\text{/}}2$, $\pi {\text{/}}2 + \pi \tau {\text{/}}2$, $ - \pi {\text{/}}2 + \pi \tau {\text{/}}2$. Комплексно сопряженная скорость $dw{\text{/}}dz$ всюду конечна в плоскости $z = x + iy$. Значит, функция $\frac{{dW}}{{dz}}(t)$ всюду конечна в прямоугольнике периодов. Функция ${{\sin }^{2}}t$ имеет в этом прямоугольнике единственный нуль второго порядка в точке $t = 0$. Отсюда и (2.10) заключаем, что $\frac{{dW}}{{dt}}(t)$ имеет в прямоугольнике периодов единственный полюс второго порядка в точке $t = 0$, и главная часть разложения в ряд Лорана $\frac{{dW}}{{dt}}(t)$ в окрестности $t = 0$ будет $A{\text{/}}{{t}^{2}}$, где $A$ – постоянная. Так как
Функции $\frac{{dW}}{{dt}}(t)$ и $W(t)$ построим с помощью теории тэта-функций Якоби ([16], гл. 21). Четыре тэта-функции определяются следующим образом:
(2.11)
$\begin{gathered} {{\vartheta }_{2}}(t,q) = 2\,\sum\limits_{n = 1}^\infty \,{{q}^{{{{{(n - 1/2)}}^{2}}}}}\cos (2n - 1)t \\ {{\vartheta }_{3}}(t,q) = 1 + 2\,\sum\limits_{n = 1}^\infty \,{{q}^{{{{n}^{2}}}}}\cos 2nt \\ \end{gathered} $Как видно из формул (2.11), при $q \ll 1$ эти функции являются быстро сходящимися рядами. Тэта-функции входят в ядро пакета Wolfram Mathematica [17] и их вычисление не представляет никаких затруднений. В дальнейшем для краткости параметр $q$ опускаем и будем писать ${{\vartheta }_{1}}(t)$ вместо ${{\vartheta }_{1}}(t,q)$, кроме того, как и в [16], условимся, что тэта-функция без аргумента, означает, что аргумент равен нулю, например, ${{\vartheta }_{2}} = {{\vartheta }_{2}}(0)$, $\vartheta _{1}^{'} = \vartheta _{1}^{'}(0)$.
Следует отметить, что тэта-функции не являются двоякопериодическими, а величины $\pi $ и $\pi \tau $ называют квазипериодами. Поэтому при добавлении к аргументу $t$ периодов $\pi $ и $\pi \tau $ и полупериодов $\pi {\text{/}}2$ и $\pi \tau {\text{/}}2$ тэта-функции переходят друг в друга и получают множители периодичности, аналогично формулам приведения для тригонометрических функций. Таблица приведения для тэта-функций приведена ниже.
В таблице 1 множители периодичности $M$ и $N$ принимают значения
где верхний знак минус берется при прибавлении, а нижний плюс – при вычитании $\pi \tau $ и $\pi \tau {\text{/}}2$.Таблица 1.
Таблица приведения для тэта-функций
| t | ${{\vartheta }_{1}}$ | ${{\vartheta }_{2}}$ | ${{\vartheta }_{3}}$ | ${{\vartheta }_{4}}$ |
|---|---|---|---|---|
| $ \pm \pi $ | $ - {{\vartheta }_{1}}$ | $ - {{\vartheta }_{2}}$ | ${{\vartheta }_{3}}$ | ${{\vartheta }_{4}}$ |
| $ \pm \pi \tau $ | $ - M{{\vartheta }_{1}}$ | $M{{\vartheta }_{2}}$ | $M{{\vartheta }_{3}}$ | $ - M{{\vartheta }_{4}}$ |
| $ \pm \pi {\text{/2}}$ | $ \pm {{\vartheta }_{2}}$ | $ \mp {{\vartheta }_{1}}$ | ${{\vartheta }_{4}}$ | ${{\vartheta }_{3}}$ |
| $ \pm \pi \tau {\text{/2}}$ | $ \pm iN{{\vartheta }_{4}}$ | $N{{\vartheta }_{3}}$ | $N{{\vartheta }_{2}}$ | $ \pm iN{{\vartheta }_{1}}$ |
Следуя ([16], c. 350), выводим
(2.12)
$\frac{{dW}}{{dt}} = Uaf(t) + B,\quad f(t) = - \frac{d}{{dt}}\frac{{\vartheta _{1}^{'}(t)}}{{\vartheta (t)}}$Все тэта-функции на действительной оси принимают действительные значения, поэтому в (2.12) константа $B$ – действительная. Циркуляция $\Gamma = W(t + \pi ) - W(t)$. С помощью формул приведения устанавливаем, что функция $\vartheta _{1}^{'}(t){\text{/}}{{\vartheta }_{1}}(t)$ является $\pi $-периодической. Интегрируя (2.12), находим $B = \Gamma {\text{/}}\pi $ и
(2.13)
$W(t) = UaF(t) + \frac{\Gamma }{\pi }t,\quad F(t) = - \frac{{\vartheta _{1}^{'}(t)}}{{{{\vartheta }_{1}}(t)}}$Расход жидкости между цилиндром и твердой стенкой
С помощью формул приведения для тэта-функций устанавливаем, что
Отсюда и (2.6), (2.8) выводим
Эта формула в несколько ином виде выведена Лагалли [2].
Теперь согласно (2.7) можем записать в явном виде функцию комплексного потенциала
(2.14)
$W(z) = UaF\left( {\frac{1}{{2i}}\ln \frac{{z - ia}}{{z + ia}}} \right) + \frac{\Gamma }{{2\pi }}\ln \frac{{z - ia}}{{z + ia}}$Отметим, что последний член в формуле (2.14) – это потенциал обтекания двух вихрей противоположной интенсивности $\Gamma $ и $ - \Gamma $, расположенных в точках $z = ia$ и $z = - ia$, соответственно.
3. Комплексно сопряженная скорость. Максимальная и минимальная циркуляции. Как видно из (2.10) и (2.13), комплексно сопряженная скорость $\frac{{d\,W}}{{d{\kern 1pt} z}}(t)$ выражается через эллиптическую функцию $f(t)$, вычисление которой требует вычисления первой и второй производной от функции ${{\vartheta }_{1}}(t)$. Получим два других представления этой функции, не содержащие производных. Введем следующие константы:
(3.1)
${{\beta }_{1}} = \frac{{{{{(\vartheta _{1}^{'})}}^{2}}}}{{\vartheta _{3}^{2}}},\quad {{\gamma }_{1}} = \frac{{\vartheta _{3}^{{''}}}}{{{{\vartheta }_{3}}}},\quad {{\beta }_{2}} = \frac{{{{{(\vartheta _{1}^{'})}}^{2}}}}{{\vartheta _{4}^{2}}},\quad {{\gamma }_{2}} = \frac{{\vartheta _{4}^{{''}}}}{{{{\vartheta }_{4}}}}$(3.2)
$f(t) = {{\beta }_{1}}\frac{{\vartheta _{3}^{2}(t)}}{{\vartheta _{1}^{2}(t)}} - {{\gamma }_{1}}\quad и\quad f(t) = {{\beta }_{2}}\frac{{\vartheta _{4}^{2}(t)}}{{\vartheta _{1}^{2}(t)}} - {{\gamma }_{2}}$В самом деле, с помощью формул приведения убеждаемся, что функции ${{\beta }_{1}}\vartheta _{3}^{2}(t){\text{/}}\vartheta _{1}^{2}(t)$ и ${{\beta }_{2}}\vartheta _{4}^{2}(t){\text{/}}\vartheta _{1}^{2}(t)$ являются двоякопериодическими с периоодами $\pi $ и $\pi \tau $. Их главные части разложений в ряд Лорана в окрестности точки $t = 0$ одинаковы и равны $1{\text{/}}{{t}^{2}}$. Поэтому согласно ([16], c. 350)
Функции ${{\vartheta }_{3}}(t)$ и ${{\vartheta }_{4}}(t)$ имеют нули первого порядка в точках $t = \pm \pi {\text{/}}2 + \pi \tau {\text{/}}2$ и $t = \pi \tau {\text{/}}2$, соответственно. Поэтому, если рассмотреть течения с комплексно сопряженными скоростями
(3.3)
${{f}_{1}}(t) = U{{\sin }^{2}}t\frac{{{{\beta }_{1}}\vartheta _{3}^{2}(t)}}{{\vartheta _{1}^{2}(t)}}\quad и\quad {{f}_{2}}(t) = U{{\sin }^{2}}t\frac{{{{\beta }_{2}}\vartheta _{4}^{2}(t)}}{{\vartheta _{1}^{2}(t)}},\quad t = \frac{1}{{2i}}\ln \frac{{z - ai}}{{z + ai}},$(3.4)
${{\Gamma }_{{\min }}} = Ua{{\gamma }_{1}}\pi ,\quad {{\Gamma }_{{\max }}} = Ua{{\gamma }_{2}}\pi ,$Замечаем, что
Теперь с помощью формулы (2.10) записываем комплексно сопряженную скорость в явном виде:
(3.5)
$\frac{{dW}}{{dz}}(z) = U\frac{{{{a}^{2}}}}{{{{z}^{2}} + {{a}^{2}}}}f\left( {\frac{1}{{2i}}\ln \frac{{z - ai}}{{z + ai}}} \right) + \frac{\Gamma }{\pi }\frac{a}{{{{z}^{2}} + {{a}^{2}}}}$Здесь для вычисления функции $f(t)$ можно использовать любую из формул (3.2).
В дальнейшем, при проведении числовых расчетов всегда полагаем, что $U = 1$ и $R = 1$. Отсюда $h = H$, а величины циркуляций относятся к $UR$.
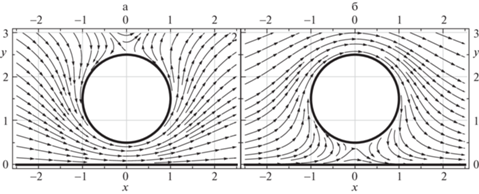
На рис. 2 показаны линии тока $\Psi (x,y)$ = $\operatorname{Im} (W(x + iy))$ = const при $h = 0.2$ для $\Gamma = {{\Gamma }_{{\max }}}$ (а) и $\Gamma = {{\Gamma }_{{\min }}}$ (б).
Рис. 2.
Линии тока при $h = 0.2$. a) ${{\Gamma }_{{\max }}} = 30.1268$, б) ${{\Gamma }_{{\min }}} = - 7.28855$.
При заданной циркуляции подъемная сила $L$, действующая на цилиндр, вычисляется по формуле Чаплыгина. Для коэффициента подъемной силы ${{C}_{L}} = 2L{\text{/}}(\rho {{U}^{2}}R)$ получим
4. Определение циркуляции по принципу Гольдштика. Пусть циркуляция $\Gamma = \alpha {{\Gamma }_{{\min }}}$ + + $(1 - \alpha ){{\Gamma }_{{\max }}}$, $\alpha \in [0,1]$. Ясно, что тогда $\Gamma \in [{{\Gamma }_{{\min }}},{{\Gamma }_{{\max }}}]$, а комплексно сопряженная скорость течения с такой циркуляцией имеет вид
Здесь в силу симметрии рассматриваем только левую половину окружности. Из равенств (2.8) и (2.9) следует, что
Использовав формулы приведения для тэта-функций, придем к следующей задаче
(4.1)
$\mathop {\max }\limits_{\xi \in [0,\pi /2]} \left| {\alpha {{V}_{1}}(\xi ) + (1 - \alpha ){{V}_{2}}(\xi )} \right| \to \min ;\quad \alpha \in [0,1],$Функции ${\text{|}}{{V}_{1}}(\xi ){\text{|}}$ и ${{V}_{2}}(\xi )$ определяют распределения скоростей по окружности для минимальной ${{\Gamma }_{{\min }}}$ и максимальной ${{\Gamma }_{{\max }}}$ циркуляций соответственно. Обозначим ${{V}_{{1\max }}} = - {{V}_{1}}(0)$, ${{V}_{{2\max }}} = {{V}_{2}}(\pi {\text{/}}2)$. С помощью тождества ${{\vartheta }_{{1'}}} = {{\vartheta }_{2}}{{\vartheta }_{3}}{{\vartheta }_{4}}$ (см. [16], c. 345) и формул приведения найдем
Обе функции ${{V}_{1}}(\xi )$ и ${{V}_{2}}(\xi )$ являются монотонно возрастающими на отрезке $[0,\pi {\text{/}}2]$. Функция ${{V}_{1}}(\xi )$ возрастает от $ - {{V}_{{1\max }}}$ до нуля, а ${{V}_{2}}(\xi )$ от нуля до ${{V}_{{2\max }}}$. Следовательно при $\alpha \in (0,1)$ функция $\alpha {{V}_{1}}(\xi )$ + $(1 - \alpha ){{V}_{2}}(\xi )$ также монотонно возрастает и принимает на концах отрезка значения разных знаков. Отсюда вытекает, что максимум модуля этой функции обязательно достигается на концах отрезка $[0,\pi {\text{/}}2]$. Минимаксная задача (4.1) упрощается и принимает вид:
(4.2)
$\max \left[ {\alpha {{V}_{{1\max }}},(1 - \alpha ){{V}_{{2\max }}})} \right]\; \to \min ;\quad \alpha \in [0,1]$Отметим, что ${{V}_{{1\max }}}$ и ${{V}_{{2\max }}}$ – максимальные скорости на поверхности цилиндра с минимальной ${{\Gamma }_{{\min }}}$ и максимальной ${{\Gamma }_{{\max }}}$ циркуляциями соответственно. Кроме того, эти величины определяют скорости в крайней верхней точке цилиндра $J$ и в крайней нижней нижней точке $M$:
Решение задачи (4.2) достигается, когда
Циркуляция, определенная по принципу Гольдштика, имеет вид
(4.3)
${{\Gamma }_{G}} = \frac{1}{2}\left( {{{\Gamma }_{{\min }}} + {{\Gamma }_{{\max }}} + \frac{{{{\Gamma }_{{\min }}} - {{\Gamma }_{{\max }}}}}{{h + 1}}} \right)$При такой циркуляции скорости в верхней и нижней точках цилиндра равны между собой:
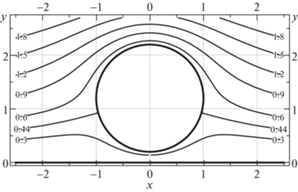
На рис. 3 показаны линии тока $\Psi (x,y)$ = $\operatorname{Im} [W(x + iy)]$ = const при $h = 0.2$ для $\Gamma = {{\Gamma }_{G}}$.
Рис. 3.
Линии тока для обтекания цилиндра с циркуляцией ${{\Gamma }_{G}} = - 2.27173$ при $h = 0.2$ ($Q = 0.438305$).
5. Асимптотические формулы для $0 < h \leqslant 1$. Когда расстояние цилиндра от стенки $h \to 0$, радиус внутренней окружности $q \to 1$, поэтому при малых $h$ ряды для тэта-функций (2.11) утрачивают свойство быстрой сходимости. Чтобы исправить эту ситуацию, воспользуемся мнимым преобразованием Якоби ([16], c. 351). Для рассматриваемого прямоугольника периодов эти преобразования приобретают вид:
(5.1)
$\begin{gathered} {{\vartheta }_{2}}(t,q) = A\exp ( - {{t}^{2}}{\text{/}}\delta ){{\vartheta }_{4}}(i\pi t{\text{/}}\delta ,{{q}_{1}}) \\ {{\vartheta }_{3}}(t,q) = A\exp ( - {{t}^{2}}{\text{/}}\delta ){{\vartheta }_{3}}(i\pi t{\text{/}}\delta ,{{q}_{1}}) \\ \end{gathered} $Замечаем, что если $h \leqslant 1$, то ${{q}_{1}} \leqslant 5.56277 \times {{10}^{{ - 4}}}$. Теперь в формулах (2.12), (2.13) и (3.1) преобразуем тэта-функции с помощью (5.1). Получаем новые представления для $f(t)$, $F(t)$, ${{\gamma }_{1}}$ и ${{\gamma }_{2}}$, которые раскладываем по степеням ${{q}_{1}}$ до членов $q_{1}^{2}$ включительно. В результате
(5.2)
$f(t) = {{\delta }^{{ - 2}}}\left[ {2\delta + {{\pi }^{2}}{{{\operatorname{csch} }}^{2}}\left( {\pi t{\text{/}}\delta } \right) + 8{{\pi }^{2}}\operatorname{ch} \left( {2\pi t{\text{/}}\delta } \right)q_{1}^{2}} \right]$(5.3)
$F(t) = {{\delta }^{{ - 1}}}\left[ {2t - \pi \operatorname{cth} \left( {\pi t{\text{/}}\delta } \right) + 4\pi \operatorname{sh} \left( {2\pi t{\text{/}}\delta } \right)q_{1}^{2}} \right]$(5.4)
${{\gamma }_{1}} = - \frac{2}{\delta } + \frac{{8{{\pi }^{2}}{{q}_{1}}}}{{{{\delta }^{2}}}} - \frac{{16{{\pi }^{2}}q_{1}^{2}}}{{{{\delta }^{2}}}},\quad {{\gamma }_{2}} = \frac{{{{\pi }^{2}} - 2\delta }}{{{{\delta }^{2}}}} + \frac{{8{{\pi }^{2}}q_{1}^{2}}}{{{{\delta }^{2}}}}$Теперь можно в формулах (2.14), (3.4) и (3.5) заменить $F(t)$, ${{\gamma }_{1}}$, ${{\gamma }_{2}}$ и $f(t)$ на их приближенные аналоги. При $h \leqslant 1$ соотношения (5.2)–(5.4) фактически дают точное аналитическое решение задачи, выраженное в элементарных функциях. Наихудшие по точности результаты получаются при $h = 1$. Представление о точности приближенных формул при $h \in (0,2.5)$ дает таблица 2.
Таблица 2.
Сравнение точных и приближенных характеристик течения при различных $h$
| Характ. | ${{\Gamma }_{G}}$ | Q | ${{C}_{L}}$ | ${{V}_{J}}$ | ${{V}_{M}}$ | ${{V}_{N}}$ |
|---|---|---|---|---|---|---|
| h | 0.7 | |||||
| Точн. | –0.701466 | 1.24937 | 0.865393 | 2.17162 | 2.17162 | 1.62772 |
| Прибл. | –0.701466 | 1.24937 | 0.865395 | 2.17162 | 2.17162 | 1.62772 |
| h | 1 | |||||
| Точн. | –0.419165 | 1.64419 | 0.492318 | 2.12448 | 2.12448 | 1.46697 |
| Прибл. | –0.419166 | 1.64419 | 0.492340 | 2.12448 | 2.12446 | 1.46696 |
| h | 2.5 | |||||
| Точн. | –0.0748012 | 3.33119 | 0.0792842 | 2.04080 | 2.04080 | 1.15987 |
| Прибл. | –0.0749209 | 3.33115 | 0.0823604 | 2.04081 | 2.03911 | 1.15910 |
C помощью формул (2.14) и (5.3) предельным переходом при $h \to 0$ для любой конечной циркуляции $\Gamma $ получим
Этот результат совпадает с решением, приведенным в монографии [1] при $h = 0$. Кроме того, если циркуляция определяется по принципу Гольдштика, то
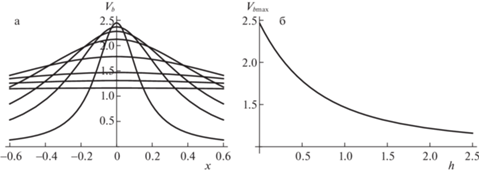
Распределения скорости ${{V}_{b}}(x)$ на плоскости $y = 0$, рассчитанные по точным и приближенным формулам для значений зазора
представлены на рис. 4 а. Для расчета использовались формулы (3.5) и (4.3), но точные значения $f(t)$ и $\Gamma $ находились c помощью (3.2) и (3.1), а приближенные – с помощью (5.2) и (5.4), соответственно. Как видно из рисунка, точные и приближенные графики неразличимы. Кроме того, скорость ${{V}_{b}}(x)$ имеет наибольшее значение в точке $x = 0$. С увеличением зазора максимальная скорость монотонно убывает.Рис. 4.
а) Графики скоростей на плоскости при различных $h$. б) Зависимость максимального значения скорости на плоскости от $h$.
С помощью соотношений (3.5), (5.2) и (5.4) выводится приближенная формула для максимальных значений скорости на дне
(5.5)
${{V}_{{b\max }}} = U\frac{{{{\pi }^{2}}\left[ {8(3h + 4){{q}_{1}} + h} \right]}}{{2{{\delta }^{2}}(h + 1)}}$Ее можно получить, из формулы (3.5), подставив в нее значение аргумента $z = 0 \Rightarrow t = \pi {\text{/}}2$
Правую часть с помощью (3.4), (5.2) и (5.4) следует выразить через параметры $\delta $ и ${{q}_{1}}$ и в асимптотических разложениях по $\delta $ и ${{q}_{1}}$ учесть только главные члены.
Полученная формула при $h = 2.5$ дает ${{V}_{{b\max }}} = 1.15903$, а для меньших значений $h$ все значащие цифры, полученные по этой формуле, совпадают с приведенными в таблице 2.
На рис. 4б показана зависимость от $h$ максимального значения скорости ${{V}_{{b\max }}} = {{V}_{b}}(0)$, рассчитанная по точным формулам и приближенной формуле (5.5). Как и на рис. 4а, графики полностью сливаются.
Для безразмерной зависимости ${{V}_{{b\max }}}(h)$ удобна интерполяционная формула ${{V}_{{b\max }}}$ = = $\frac{{2.47 + 1.144h}}{{1 + 1.44h}}$. По этой формуле ${{V}_{{b\max }}}(0.7) = 1.629,$ ${{V}_{{b\max }}}(1) = 1.481,$ ${{V}_{{b\max }}}(2.5) = 1.159$, а по данным таблицы 2: 1.627, 1.467 и 1.159.
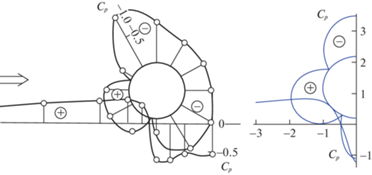
6. Обсуждение результатов. Выбор циркуляции по постулату Гольдштика приводит к обтеканию кругового цилиндра, при котором распределение давления по закону Бернулли на наветренной стороне кругового цилиндра и плоскости качественно согласуются с экспериментом. Экспериментальные и расчетные значения максимальных скоростей на плоскости и круговом цилиндре за счет вязкости примерно в полтора раза меньше приведенных выше по модели идеальной жидкости. С учетом коэффициента для скорости на окружности $k = 0.65$ и на дне $k = 0.7$, как видно из рис. 5, имеется даже и количественное согласие. На нем слева приведены экспериментально найденные [11] эпюры коэффициента давления ${{C}_{p}}$ на оси $x$ и окружности при зазоре между осью $x$ и границей круга $h = 0.2$. Число Рейнольдса было достаточно большим, порядка ${{10}^{4}}$. Справа приведены эпюры давления ${{C}_{p}} = 1 - {{(kV)}^{2}}$ на окружности и оси $x$.
Для других достаточно малых зазоров минимальное давление под цилиндром меняется в небольших пределах. Это соответствует малому изменению максимальной скорости в нижней точке цилиндра. По приведенной теории, как показывает рис. 3 в диапазоне относительных зазоров $h \in (0,0.5)$ отношение максимальной скорости под цилиндром к скорости на бесконечном удалении от него изменяется в небольших пределах от 1.8 до 2.4.
Работа выполнена по теме государственного задания (госрегистрации АААА-А20-120011690138-6), по теме РФФИ № 21-57-53019 ГФЕН_а и за счет средств Программы стратегического академического лидерства Казанского (Приволжского) федерального университета (“ПРИОРИТЕТ-2030”).
Список литературы
Милн-Томсон Л.М. Теоретическая гидродинамика. М.: Мир, 1964. 655 с.
Lagally M. The frictionless current in the outer areas of double circuits // Z. Angew. Math. Mech. 1929. V. 9. P. 299–305.
Lagally M. The frictionless flow in the region around two circles // NACA Technic. Memor. No. 626. 1931.
Мазур В.Ю. Движение кругового цилиндра вблизи вертикальной стенки // Изв. АН СССР. МЖГ. 1966. № 3. С. 75–79.
Wang Q.X. Interaction of two circular cylinders in inviscid flow // Phys. Fluids. 2004. V. 16. P. 4412–4425.
Crowdy D.G. Analytical solution for uniform potential flow past multiple cylinders // Eur. J. Mech. B/Fluids. 2006. V. 25. P. 459–470.
Crowdy D.G., Surana A., Yick K.-Y. The irrotational motion generated by two planar stirrers in inviscid fluid // Phys. Fluids. 2007. V. 19. P. 018103.
Alassar R.S., El-Gebeily M.A. Inviscid flow past two cylinders // J. Fluids Engng. Trans. ASME. 2009. V. 131.
Седов Л.И. Плоские задачи гидродинамики и аэродинамики. М.: Физматлит, 1980. 448 с.
Гольдштик М.А., Ханин В.М. Взаимодействие цилиндра со свободной поверхностью и струей // Изв. АН СССР. МЖГ. 1977. № 5. С. 50–58.
Bearman P.W., Zdravkovich M.M. Flow around a circular cylinder near a plane boundary // J. Fluid Mech. 1978. V. 89. Pt. 1. P. 33–47.
Price S.J., Sumner D., Smith J.G., Leong K., Paigdoussis M.P. Flow visualization around a circular cylinder near to a plane wall // J. Fluids&Struct. 2002. V. 16(2.2). P. 175–191.
Kharlamov A.A. Modeling of transverse self-oscillations of a circular cylinder in an incompressible fluid flow in a plane channel with circulation // J. Appl. Mech. Tech. Phys. 2012. V. 53(2.1). P. 38–42.
Andronov P.R., Dynnikov Y.A., Dynnikova G.Ya., Guvernyuk S.V. Flow-induced oscillations of circular cylinder in a narrow channel // Aerosp. Sci.&Technol. 2019. V. 93. P. 105348.
Петров А.Г., Потапов И.И. Избранные задачи русловых процессов. М.: Ленанд, 2019. 244 с.
Уиттекер Э.Т., Ватсон Дж.Н. Курс современного анализа. Ч. 2. М.: ГИФМЛ, 1963. 515 с.
Wolfram S. The Mathematica Book. New York: Wolfram Media, 2003.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика