Прикладная математика и механика, 2022, T. 86, № 3, стр. 424-444

При изучении контакта деформируемых тел силы межмолекулярного взаимодействия впервые учитывались применительно к герцевскому контакту [1]. В дальнейшем был разработан ряд эффективных подходов к решению контактных задач такого типа, среди которых следует отметить подходы, использующие концепцию поверхностной энергии – модели JKR и DMT [2, 3]. Эти подходы также использовались для расчета адгезионного контакта слоистых [4–7] и вязкоупругих тел [8–11].

Строгая постановка контактной задачи, учитывающая межмолекулярное взаимодействие, предполагает существование некоторого зазора $r$ между контактирующими телами. Величина этого зазора должна обеспечивать баланс сил, обусловленных контактной деформацией тел и их межмолекулярным взаимодействием (самосогласованный подход по Дерягину [12]). При таком подходе возможны постановки задачи с поверхностным (традиционная постановка [13–15]) и объемным (уточненная постановка [16–20]) приложением сил межмолекулярного взаимодействия.

Одной из характерных особенностей адгезионного контакта является возможность скачкообразного изменения его параметров. Впервые подобное изменение было теоретически описано применительно к подпружиненному контакту твердых тел при наличии сил Лондона–Ван-дер-Ваальса [21]. В дальнейшем скачкообразное изменение параметров адгезионного контакта упругих тел рассматривалось во многих исследованиях, среди которых отметим работы [12–14, 22], использующие самосогласованный подход при постановке задачи.

Аналогичная самосогласованному подходу концепция используется в теории бесконтактного трения, допускающей существование контактного зазора между трущимися поверхностями [23–27]. Были рассмотрены различные механизмы такого трения, например, эмиссия фононов, джоулева диссипация, эффекты сил Ван-дер-Ваальса.

Ранее был выполнен расчет напряженно-деформированного состояния (НДС) и диссипации энергии в вязкоупругом слое при наличии сил межмолекулярного взаимодействия (самосогласованный подход, традиционная и уточненная постановки задачи) при заданном контактном зазоре $r(t)$ [28], а также был выполнен расчет зазора $r(t)$ при заданном законе внедрения $\delta (t)$ индентора [29].

В данной работе, на основе полученных ранее результатов [28, 29], определяется диссипация энергии в вязкоупругом слое в режиме подвода/отвода индентора при заданном законе его внедрения. На основе решения этой задачи произведен расчет силы трения скольжения шероховатого контртела по вязкоупругому слою в режиме бесконтактного трения. Изучается влияние скачкообразного изменения контактного зазора во времени на диссипацию энергии и силу трения.

1. Постановка задачи. Рассмотрим контактное взаимодействие бесконечно протяженного плоского индентора и основания, состоящего из вязкоупругого слоя, связанного с подложкой, причем индентор и подложка являются абсолютно жесткими (рис. 1). Считается, что индентор и слой разделены контактным зазором $r$, обеспечивающим баланс сил вязкоупругого и межмолекулярного взаимодействий контактирующих тел (самосогласованный подход) [12]. Свяжем с основанием систему координат $Oxyz$, совместив ее плоскость $Oxy$ с границей раздела слоя и подложки. Контакт индентора и слоя считается плоскопараллельным, что обуславливает зависимость всех контактных характеристик только от координаты $z$ и времени $t$. Толщину слоя в недеформированном состоянии обозначим через ${{h}_{{{\kern 1pt} 0}}}$, а в деформированном – через $h$.

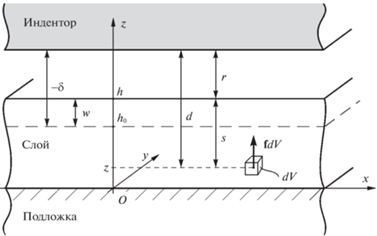
Межмолекулярное взаимодействие индентора и основания определяется парными взаимодействиями их молекул (гипотеза Гамакера). Соответствующая сила $F$ зависит от свойств пары молекул и расстояния $l$ между ними. Существуют разные формы такой зависимости, и в дальнейшем будет использоваться известный закон Леннард-Джонса [30]:

где ${{a}_{1}},{{a}_{2}},m,n$ – параметры взаимодействия, причем обычно полагают $m = 7,$ $n = 13$.

При определенных допущениях [14, 31] суммирование парных взаимодействий молекул позволяет для каждой точки слоя рассчитать объемную силу ${\mathbf{f}}$, обусловленную межмолекулярным взаимодействием. Эта сила направлена вдоль оси $z$ и зависит от расстояния $d = r + s = r + h - z$ между точкой ее приложения и индентором (рис. 1), причем толщину $h$ слоя здесь можно заменить постоянным значением ${{h}_{{{\kern 1pt} 0}}}$, что допустимо при малых деформациях. Таким образом, если обозначить через ${{f}_{i}}$, $i = 1,2,3$ компоненты объемной силы в системе координат $O{\kern 1pt} x{\kern 1pt} y{\kern 1pt} z$, то

Суммирование парных взаимодействий молекул позволяет также определить полную силу $p$ воздействия индентора на основание, приходящуюся на единицу площади его поверхности (верхней границы):

которая в рамках самосогласованного подхода интерпретируется как контактное давление [12–14, 19]. Кроме того, исключив из контактного давления $p$ силу воздействия индентора на подложку, можно определить фиктивное контактное давление ${{p}_{c}}$, обусловленное межмолекулярным воздействием индентора только на слой:

Выражения для функций $f(d)$ и $\Phi (r)$ в случае закона Леннард-Джонса приведены в [28, 29], тогда как функция ${{\Phi }_{c}}(r)$ имеет вид

где $k = m - 4$, $l = n - 4$, $H = {{h}_{0}} + r$, величины ${{A}_{{1c}}},{{r}_{{ec}}}$ выражаются известным образом через параметры закона (1.1) [28, 29].

Традиционная постановка контактной задачи при наличии межмолекулярного взаимодействия подразумевает, что определяемое по формуле (1.3) контактное давление прикладывается к поверхности слоя, в результате чего он деформируется [12–15]. Ниже также рассматривается уточненная постановка, в которой естественным образом предполагается, что деформация слоя порождается объемными силами (1.2), распределенными по его глубине, тогда как поверхность слоя свободна от нагрузок [16–20]. В качестве параметра нагружения слоя в обеих постановках выступает зазор $r$, однозначно определяющий объемную силу ${{f}_{i}}$ по формуле (1.2) и контактное давление $p$ по формуле (1.3).

Замечание 1. В работах [28, 29] расчет НДС слоя при традиционной постановке задачи выполнялся в предположении, что к его поверхности прикладывается контактное давление $p$. Однако это давление, согласно выражению (1.3), определяется межмолекулярным воздействием индентора не только на слой, но и на недеформируемую подложку. В связи с этим, представляется более корректным выполнять расчет НДС слоя, полагая, что он нагружается фиктивным контактным давлением ${{p}_{c}}$ вида (1.4), обусловленным межмолекулярным воздействием индентора только на слой.

Деформационные свойства слоя описываются линейным законом наследственного типа [32–34]

где ${{\delta }_{{ij}}}$ – символ Кронекера, ${{\varepsilon }_{{ij}}},{{\sigma }_{{ij}}}$ – компоненты тензоров деформаций и напряжений, $\theta = {{\varepsilon }_{{kk}}}$, причем здесь и далее применяется правило суммирования по повторяющимся индексам. Величины $\lambda $ и $\mu $ представляют собой мгновенные модули упругости (постоянные Ламе), а функции $\Lambda ,{\rm M}$ характеризуют вязкие свойства материала слоя и выражаются через ядра сдвиговой ${{R}_{1}}$ и объемной ${{R}_{2}}$ релаксации: причем $K = \lambda + 2\mu {\text{/}}3$ – мгновенный модуль объемной упругости.

Для построения полной системы уравнений НДС слоя соотношение (1.6) следует дополнить формулой Коши и уравнением равновесия [32, 33]:

в которых ${{u}_{i}}$ – компоненты вектора перемещений, объемная сила ${{f}_{i}}$ обусловлена межмолекулярным взаимодействием и определяется равенствами (1.2). Здесь и далее для записи частной производной функции используется общепринятое обозначение с запятой.

Для дальнейших выкладок потребуется конкретизировать ядра интегральных операторов в соотношении (1.6). Не ограничивая общности рассмотрения, пренебрежем объемной ползучестью материала слоя и положим [34]: ${{R}_{{{\kern 1pt} 1}}}(t) = {{R}_{{{\kern 1pt} 0}}}{{e}^{{ - \alpha {\kern 1pt} t}}},$ ${{R}_{{{\kern 1pt} 2}}}(t) \equiv 0$, так что, в силу соотношений (1.7):

где $\alpha ,{{R}_{0}}$ – заданные параметры, причем $\alpha = 1{\text{/}}{{t}_{r}}$, ${{t}_{r}}$ – время релаксации, ${{\Lambda }_{0}} = - 2\mu {{R}_{0}}{\text{/}}3$, ${{{\rm M}}_{0}} = \mu {\kern 1pt} {{R}_{{{\kern 1pt} 0}}}$. Кроме того, введем в рассмотрение длительные (равновесные) модули упругости ${{\lambda }^{\infty }},{{\mu }^{\infty }}$, а также мгновенный $B$ и длительный ${{B}^{\infty }}$ коэффициенты упругой податливости слоя: причем $\beta = \alpha - B{\kern 1pt} {{{\rm N}}_{0}} > 0,$ ${{{\rm N}}_{0}} = 4\mu {{R}_{{{\kern 1pt} 0}}}{\text{/}}3$ [28].

В качестве контактной характеристики будем использовать внедрение $\delta $ индентора в слой, отсчитываемое от поверхности слоя в недеформированном состоянии, т.е. от уровня $z = {{h}_{{{\kern 1pt} 0}}}$ (рис. 1). Отметим, что внедрение $\delta $ может принимать как положительные, так и отрицательные значения, причем последний случай изображен на рис. 1. Имеет место условие контакта

связывающее внедрение $\delta $ с зазором $r$ и перемещением $w = h - {{h}_{{{\kern 1pt} 0}}}$ поверхности слоя вдоль оси $z$.

Считается, что до момента времени $t = 0$ взаимодействие индентора с основанием является стационарным с постоянными во времени внедрением ${{\delta }^{s}}$ и зазором ${{r}^{s}}$, т.е.

Далее будет рассматриваться непрерывная зависимость $\delta (t)$, отвечающая переходу слоя из начального стационарного состояния (1.10) в другое стационарное состояние с конечным внедрением ${{\delta }_{m}}$ индентора, т.е.

где ${{t}_{m}}$ – время перемещения индентора, $0 < {{t}_{m}}$. Для такой зависимости будут рассмотрены режимы подвода индентора: и отвода индентора:

Здесь и далее точкой над символом функции обозначается ее производная по времени.

Подобный характер изменения внедрения $\delta (t)$ позволяет допустить асимптотическое поведение функции $r(t)$ на бесконечности:

где ${{r}_{m}}$ – значение контактного зазора в стационарном состоянии с внедрением ${{\delta }_{m}}$.

Начальное ${{r}^{s}}$ и конечное ${{r}_{m}}$ значения зазора, отвечающие начальному ${{\delta }^{s}}$ и конечному ${{\delta }_{m}}$ внедрению, находятся из уравнения [29]

Здесь и далее функция $Z(r)$ определяется по правилу

причем верхний/нижний вариант в круглых скобках отвечает традиционной/уточненной постановке задачи.

Изменение зазора $r$ во времени описывается дифференциальным уравнением:

в котором штрих у символа функции обозначает ее производную по аргументу.

Уравнение (1.16), как и прежде [29], получается путем дифференцирования по $t$ условия контакта (1.9), в котором граничное перемещение $w$, как компонента НДС слоя, известным образом выражается через функцию $r(t)$. Однако здесь для расчета НДС при традиционной постановке задачи используется фиктивное контактное давление ${{p}_{c}}$ (Замечание 1), поэтому в уравнении (1.16) присутствует функция ${{\Phi }_{c}}(r)$, тогда как прежде использовалась функция $\Phi (r)$.

Далее будет допускаться возможность существования у функции $r(t)$ нескольких точек разрывов первого рода [35], что, в свою очередь, обусловлено тем, что знаменатель в правой части дифференциального уравнения (1.16) может принимать нулевые значения [29]. Решение такого уравнения может быть построено при помощи известных численных методов (например, метода Рунге–Кутты четвертого порядка точности [36]) с привлечением специальной процедуры учета разрывов функции [29].

Как указывалось выше, при рассматриваемом плоскопараллельном контакте индентора и слоя (рис. 1), компоненты ${{\varepsilon }_{{ij}}},{{\sigma }_{{ij}}}$ НДС слоя зависят только от координаты $z$ и времени $t$, поэтом все они равны нулю, кроме ${{\varepsilon }_{{33}}}$, ${{\sigma }_{{11}}} = {{\sigma }_{{22}}}$, ${{\sigma }_{{33}}}$ [28]. Для этих компонент ранее были получены формулы [28], которые без труда переносятся на рассматриваемый случай функции $r(t)$ с несколькими точками разрыва первого рода:

где ${{\mu }_{*}} = [1 - (\alpha - {{R}_{0}}){\text{/}}\beta ]\mu $, ${{w}^{s}}(z) = - {{B}^{\infty }}{{X}^{s}}(z)$,

В равенствах (1.19), как и прежде, верхний/нижний вариант в круглых скобках отвечает традиционной/уточненной постановке задачи, причем записи верхнего варианта предполагают, что НДС слоя обусловлено фиктивным контактным давлением ${{p}_{c}}$, согласно Замечанию 1. Присутствующие в равенствах (1.19) функции ${{f}_{3}}(z,t)$ и ${{p}_{c}}(t)$ определяются по формулам (1.2) и (1.4), ${{f}^{s}}(z) = f({{r}^{s}} + {{h}_{0}} - z)$, $p_{c}^{s} = {{\Phi }_{c}}({{r}^{s}})$. Оператор $\mathcal{R}$ был определен ранее [28], здесь же только отметим, что он действует на функцию по аргументу $z$.

Из определения (1.6) величины $\sigma _{{ij}}^{{v}}$ и формул (1.17), (1.18) вытекает соотношение

которое будет использоваться в следующем разделе.

Важной особенностью формул (1.17), (1.18) является то, что их правые части и, следовательно, компоненты НДС слоя, выражаются через функцию $X(z,t)$. Согласно равенствам (1.2), (1.4) и (1.19), эта функция целиком определяется функцией $r(t)$, которая, будучи решением дифференциального уравнения (1.16), находится по известному внедрению $\delta (t)$ индентора. Указанные обстоятельства позволят нам в дальнейшем на основе формул (1.17), (1.18) рассчитать диссипацию энергии в вязкоупругом слое при заданном внедрении $\delta (t)$, ввиду того, что диссипация энергии целиком определяется эволюцией во времени НДС слоя [28]. В свою очередь, это позволит найти гистерезисные потери при подводе–отводе индентора и силу трения скольжения шероховатого индентора о вязкоупругий слой.

2. Расчет диссипации энергии. При деформировании некоторого объема $V = S{\kern 1pt} {{h}_{{{\kern 1pt} 0}}}$ вязкоупругого слоя площадью $S$ на промежутке времени $[{{t}_{1}},{{t}_{2}}]$ происходит диссипация энергии ${{D}_{{{\kern 1pt} [{{t}_{1}},{{t}_{2}}]}}}$, определяемая как теплота, выделенная объемом $V$ за это время. Согласно первому началу термодинамики [33]:

где $U$ – внутренняя энергия, которая является функцией состояния слоя и при неизменной температуре определяется эволюцией его НДС, – удельная работа деформации на промежутке $[{{t}_{1}},{{t}_{2}}]$. Здесь для простоты опускается аргумент $z$ у функций, интеграл (2.2) понимается в смысле Стилтьеса [35].

В дальнейшем также будет использоваться удельная потенциальная энергия $\Pi $ упругой деформации. Она определяется через компоненты ${{\varepsilon }_{{ij}}}$ по известной формуле [37], которая для рассматриваемого случая НДС имеет вид [28]

причем последнее выражение определяет потенциальную энергию с длительными модулями упругости ${{\lambda }^{\infty }}$ и ${{\mu }^{\infty }}$, которая отвечает стационарному состоянию слоя.

Как указывалось в предыдущем разделе, функция $r(t)$ может иметь разрывы первого рода. Учитывая это, допустим, что функции ${{\varepsilon }_{{ij}}}(t)$ и ${{\sigma }_{{ij}}}(t)$ тоже имеют точку разрыва $\hat {t} \in [{{t}_{1}},{{t}_{2}}]$ первого рода, являясь кусочно-гладкими.

Отметим, что при наличии у функций ${{\varepsilon }_{{ij}}}(t)$ и ${{\sigma }_{{ij}}}(t)$ разрывов в одной и той же точке $\hat {t}$, интеграл Стилтьеса (2.2), представляющий работу деформации, не существует [35]. Однако, исходя из физического смысла работы, можно выполнить регуляризацию этого интеграла. Для этого следует заменить скачкообразное изменение функции $r(t)$ в произвольно малой окрестности $(\hat {t} - \mu ,\hat {t} + \mu )$ точки $\hat {t}$ некоторым непрерывным изменением и вычислить соответствующие функции ${{\varepsilon }_{{ij}}}(t)$, ${{\sigma }_{{ij}}}(t)$ и интеграл (2.2). После этого для полученного интеграла необходимо выполнить предельный переход $\mu \to 0$, приводящий к исходным разрывам функций $r(t)$, ${{\varepsilon }_{{ij}}}(t)$ и ${{\sigma }_{{ij}}}(t)$ в точке $\hat {t}$. В результате, как и прежде [28], выражение (2.2) для удельной работы деформации можно представить в следующем виде

где $\varepsilon _{{ij}}^{ \pm }(\hat {t}) = \mathop {\lim }\limits_{t \to {\kern 1pt} {\kern 1pt} \hat {t} \pm {\kern 1pt} {\kern 1pt} 0} {{\varepsilon }_{{ij}}}(t)$, функция $\sigma _{{ij}}^{{v}}(t)$ определена в соотношении (1.6), а интеграл понимается в смысле Римана и берется отдельно по полуинтервалам $[{{t}_{1}},\hat {t})$ и $(\hat {t},{{t}_{2}}]$ непрерывности подынтегрального выражения. Выражение (2.4) без труда обобщается на случай нескольких точек разрыва первого рода функций ${{\varepsilon }_{{ij}}}(t)$ и ${{\sigma }_{{ij}}}(t)$ – в этом случае в правой части равенства (2.4) следует выполнить суммирование по всем точкам разрыва.

В соответствии с допущениями (1.11) и (1.14), далее будет рассматриваться процесс деформирования слоя из стационарного состояния ${{\varepsilon }_{{ij}}}(t) = \varepsilon _{{ij}}^{s}$, ${{\sigma }_{{ij}}}(t) = \sigma _{{ij}}^{s}$, $t \leqslant 0$, отвечающего $\delta (t) = {{\delta }^{s}}$, $r(t) = {{r}^{s}}$, в асимптотически стационарное состояние ${{\varepsilon }_{{ij}}}(t) \to \varepsilon _{{ij}}^{\infty }$, ${{\sigma }_{{ij}}}(t) \to \sigma _{{ij}}^{\infty }$, $t \to \infty $, отвечающее $\delta (t) = {{\delta }_{m}}$, $r(t) = {{r}_{m}}$. Для каждого такого состояния внутренняя энергия $U$ вязкоупругого слоя определяется по формуле [28]

Подстановка выражения (2.5) в равенство (2.1) позволяет получить следующее выражение для удельной диссипации энергии ${{d}^{\infty }}$ за время рассматриваемого процесса деформирования слоя:

причем ${{W}^{\infty }} = \mathop {\lim }\limits_{t \to \infty } {{W}_{{{\kern 1pt} [0,t]}}}$. При выводе этого выражения интегрирование по объему $V = S{\kern 1pt} {{h}_{{{\kern 1pt} 0}}}$ слоя было сведено к интегрированию по его толщине ввиду того, что компоненты ${{\varepsilon }_{{ij}}}$, ${{\sigma }_{{ij}}}$ НДС слоя зависят только от координаты $z$ и времени $t$.

В силу соотношений (2.3), (2.4), правая часть равенства (2.6) определяется эволюцией во времени компонент ${{\varepsilon }_{{ij}}}$, ${{\sigma }_{{ij}}}$ НДС слоя. Заменим в (2.6) эти компоненты их выражениями (1.18) и (1.20), отметив, что выражение (1.20) содержит непрерывную по $z$ функцию $\sigma _{{33}}^{{v}}(z,t)$ и, поэтому, позволяет эффективно определять скачки функций в правой части равенства (2.4). В результате можно установить, что

где

Формула (2.7) позволяет рассчитать диссипацию энергии в вязкоупругом слое при заданном внедрении $\delta (t)$. Действительно, правая часть равенства (2.7) целиком определяется функцией $r(t)$, т.к. через эту функцию, согласно формулам (1.2) и (1.4), определяются функции ${{f}_{3}}(z,t)$ и ${{p}_{c}}(t)$. В свою очередь, функция $r(t)$ находится из дифференциального уравнения (1.16) по заданному внедрению $\delta (t)$.

В качестве примера были выполнены расчеты диссипации энергии при линейном изменении внедрения $\delta $ индентора за время ${{t}_{m}}$ от начального ${{\delta }^{s}}$ до конечного ${{\delta }_{m}}$ значений:

где $\dot {\delta }$ – постоянная скорость внедрения. Целью расчетов было построение зависимости диссипации энергии ${{d}^{\infty }}$ от конечного внедрения ${{\delta }_{m}}$ при неизменном значении ${{\delta }^{s}}$. Время ${{t}_{m}}$ перемещения индентора определялось по формуле ${{t}_{m}} = ({{\delta }_{m}} - {{\delta }^{s}}){\text{/}}\dot {\delta }$, что обеспечивало одинаковую скорость $\dot {\delta }$ внедрения для каждого значения ${{\delta }_{m}}$. Для определенности рассматривался режим подвода (1.12).

Расчеты проводились при следующих значениях параметров задачи: $m = 7$, $n = 13$, ${{r}_{{ec}}} = 1$ нм, ${{r}_{{eb}}} = 0.5\,{{r}_{{ec}}}$, ${{h}_{{{\kern 1pt} 0}}} = $ 5 нм, ${{\delta }^{s}} = - \,4{\kern 1pt} {\kern 1pt} {{r}_{{ec}}}$, $\dot {\delta }$ = 2.625 мкм/с, $\lambda \simeq 2.08$ МПа, $\mu \simeq 3.13$ МПа, ${{R}_{{{\kern 1pt} 0}}} = 0.8 \times {{10}^{3}}$ с^–1, ${{t}_{r}} = $ ${{10}^{{ - 3}}}$ с, при этом значения мгновенного и длительного коэффициентов упругой податливости слоя составляли $B$ = 0.12 МПа^–1 и ${{B}^{\infty }}$ = 0.2 МПа^–1, соответственно. Кроме того, полагалось, что ${{A}_{{{\kern 1pt} 1c}}} = {{(6\pi )}^{{ - 1}}}{{A}_{H}}$ [12] и ${{A}_{{{\kern 1pt} 1b}}} = 10{{A}_{{{\kern 1pt} 1c}}}$, где ${{A}_{H}}$ – постоянная Гамакера, ${{A}_{H}} = {{10}^{{ - 19}}}$ Дж.

Для графического представления результатов расчетов здесь и далее будут использоваться безразмерные величины: $\tilde {t} = t{\text{/}}{{t}_{r}}$, $\tilde {r} = r{\text{/}}{{r}_{{ec}}}$, ${{\tilde {r}}_{m}} = {{r}_{m}}{\text{/}}{{r}_{{ec}}}$, ${{\tilde {\delta }}_{m}} = {{\delta }_{m}}{\text{/}}{{h}_{{{\kern 1pt} 0}}}$, ${{\tilde {d}}^{{{\kern 1pt} \infty }}} = {{d}^{\infty }}{\text{/}}{{d}_{*}}$, где ${{d}_{*}} = ({{B}^{\infty }} - B){{h}_{0}}p_{*}^{2}$, ${{p}_{*}} = {{A}_{{1c}}}{\text{/}}r_{{ec}}^{{m - 4}}$. Сплошная/штриховая линия на графиках отвечает уточненной/традиционной постановке задачи. Для обеспечения условия малости деформаций, при расчетах значения внедрения $\delta (t)$ полагались существенно меньшими толщины ${{h}_{{{\kern 1pt} 0}}}$ слоя.

Отметим, что величина $p_{*}^{{}}$ может быть использована в качестве оценки контактного давления, определяемого по формуле (1.3), причем ${{p}_{*}}$ выражается через постоянную Гамакера [12] или поверхностную энергию [14]. Величина ${{d}_{*}}$ совпадает с удвоенным значением диссипации энергии ${{d}^{\infty }}$ в случае ступенчатого изменения контактного давления от 0 до ${{p}_{*}}$ при традиционной постановке задачи [28]. Для выбранных параметров задачи ${{p}_{*}} \simeq 5.305$ МПа, ${{d}_{*}} \simeq 1.126 \times {{10}^{{ - 2}}}$ Дж/м².

На рис. 2 показаны расчетные зависимости диссипации энергии ${{d}^{\infty }}$ от конечного внедрения ${{\delta }_{m}}$ при уточненной и традиционной постановках задачи.

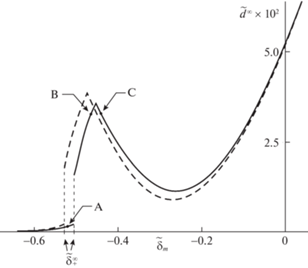
Представленные зависимости имеют особенности в виде разрывов и изломов, которые вызваны резкими изменениями вида функции $r(t)$ с ростом внедрения ${{\delta }_{m}}$. В свою очередь, эти изменения обусловлены немонотонным характером функции $Z(r)$ и могут быть объяснены с помощью графического описания эволюции контактного зазора $r$ в процессе подвода/отвода индентора [29]. Таким образом можно установить, что разрыв зависимости ${{d}^{\infty }}({{\delta }_{m}})$ происходит при ${{\delta }_{m}} = \delta _{ + }^{\infty }$, причем величина $\delta _{ + }^{\infty }$ известным образом определяется видом функции $Z(r)$ и ее значения в безразмерном виде $\tilde {\delta }_{ + }^{\infty } = \delta _{ + }^{\infty }{\text{/}}{{h}_{0}}$ показаны на рис. 2. Сам разрыв обусловлен появлением скачка у функции $r(t)$ с резким изменением ее конечного значения ${{r}_{m}}$, тогда как излом зависимости ${{d}^{\infty }}({{\delta }_{m}})$ связан с возникновением ситуации, когда скачок функции $r(t)$ происходит в период $(0,\;{{t}_{m}})$ изменения внедрения $\delta (t)$.

Подобные изменения вида функции $r(t)$ иллюстрируются рис. 3, на котором эта функция показана для точек A (${{\tilde {\delta }}_{m}} = - 0.52$), B (${{\tilde {\delta }}_{m}} = - 0.464$) и C (${{\tilde {\delta }}_{m}} = - 0.44$), расположенных на графике ${{d}^{\infty }}({{\delta }_{m}})$ до и после разрыва/излома (рис. 2). Для определенности используется уточненная постановка задачи.

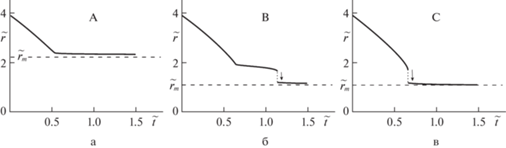
Согласно вышеизложенному, и это подтверждается расчетами, зависимость ${{d}^{\infty }}({{\delta }_{m}})$ представляется гладкой линией без разрыва и излома, если для каждого значения ${{\delta }_{m}}$ функция $r(t)$ не имеет скачков и значение ${{r}_{m}}$, как решение уравнения (1.15), непрерывно зависит от ${{\delta }_{m}}$. Для выполнения этих условий достаточно, чтобы [29]

Нарушение условия (2.10) приводит к скачкообразному росту диссипации энергии ${{d}^{\infty }}$ при достижении внедрением ${{\delta }_{m}}$ критического значения $\delta _{ + }^{\infty }$ (рис. 2).

Представленные на рис. 2 графики демонстрируют близость значений диссипации энергии ${{d}^{\infty }}$ для уточненной и традиционной постановок задачи при больших значениях ${{\delta }_{m}}$. Такая близость объясняется тем, что при больших внедрениях индентора зазор $r$ становится малым и межмолекулярное взаимодействие обуславливается главным образом малыми значениями аргумента функции $f(r + s)$, присутствующей в равенствах (1.2)–(1.4). В свою очередь, это приводит к тому, что функции $K(t,\tau )$ и, следовательно, значения диссипации энергии ${{d}^{\infty }}$ для уточненной и традиционной постановок задачи, определяемые по формулам (2.7), (2.8), становятся близкими друг к другу. Указанные обстоятельства подтверждают правомерность использования фиктивного контактного давления ${{p}_{c}}$  для расчета НДС слоя при традиционной постановке задачи (Замечание 1).

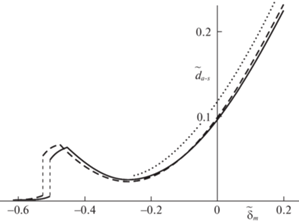
Замечание 2. В режиме подвода (1.12)/отвода (1.13) индентора, приложенная к нему внешняя сила совершает работу

причем, по закону сохранения энергии: где $\Delta U$ и $\Delta E$ – изменения внутренней энергии слоя и энергии поля межмолекулярного взаимодействия, приходящиеся на единицу площади слоя. Последнее равенство означает, что работа ${{A}^{{{\text{ext}}}}}$ внешней силы не может служить мерой диссипации энергии в слое.

3. Гистерезисные потери при индентировании определяются как суммарная диссипация энергии ${{d}_{{a - s}}}$ за цикл подвод–отвод индентора [38]:

где ${{\left. {{{d}^{\infty }}} \right|}_{{{\text{app}}}}}$ и ${{\left. {{{d}^{\infty }}} \right|}_{{{\text{ret}}}}}$ – величины диссипации энергии в режиме подвода (1.12) и отвода (1.13) индентора. Эти величины могут быть найдены на основе результатов предыдущего раздела, однако, при этом следует учитывать определенную специфику цикла подвод–отвод индентора.

Действительно, этот цикл подразумевает, что после подвода и формирования стационарного состояния слоя (формула (1.14)), происходит отвод индентора в стационарное состояние, совпадающее с начальным для режима подвода состоянием. Другими словами, между начальными и конечными значениями внедрения и зазора, отвечающими режимам подвода и отвода индентора имеют место следующие соотношения:

Таким образом, величины ${{\left. {{{d}^{\infty }}} \right|}_{{{\text{app}}}}}$ и ${{\left. {{{d}^{\infty }}} \right|}_{{{\text{ret}}}}}$ в выражении (3.1) для суммарной диссипации энергии находятся при помощи формулы (2.7) с учетом соотношений (3.2).

В качестве примера были выполнены расчеты гистерезисных потерь ${{d}_{{a - s}}}$ при линейном законе (2.9) изменения внедрения $\delta (t)$ в режимах подвода и отвода индентора. Расчеты проводились при значениях параметров задачи, указанных в предыдущем разделе.

На рис. 4 показаны расчетные зависимости гистерезисных потерь ${{d}_{{a - s}}}$ от конечного внедрения ${{\delta }_{m}} = {{\left. {\delta _{m}^{{}}} \right|}_{{{\text{app}}}}}$ с использованием безразмерной величины ${{\tilde {d}}_{{a - s}}} = {{d}_{{a - s}}}{\text{/}}{{d}_{*}}$. Как и следовало ожидать, имея ввиду результаты предыдущего раздела (рис. 2), при больших внедрениях ${{\delta }_{m}}$ уточненная и традиционная постановки задач дают близкие значения ${{d}_{{a - s}}}$.

Пунктирная линия на рис. 4 отвечает традиционной постановке задачи при допущении, что слой нагружается контактным давлением $p$, определяемым по формуле (1.3). Как видно, использование в качестве нагрузки фиктивного контактного давления ${{p}_{c}}$ приводит к более корректным результатам расчетов (штриховая линия на рис. 2), что вполне согласуется с замечанием 1.

Обращает на себя внимание то, что зависимости ${{d}_{{a - s}}}({{\delta }_{m}})$ являются немонотонными и имеют локальные максимумы и минимумы. Кроме того, эти зависимости имеют особенности в виде разрывов и изломов, причины появления которых указаны в предыдущем разделе.

4. Трение скольжения. Рассмотрим межмолекулярное взаимодействие вязкоупругого слоя с шероховатым контртелом, скользящим по нему с постоянной скоростью ${{V}_{s}}$ вдоль оси $x$ (рис. 5). Предполагается, что шероховатость контртела образована множеством одинаковых неровностей трапецеидальной формы. Неровности считаются пологими, а горизонтальные части профиля контртела достаточно протяженными, так что

Здесь и далее используются геометрические параметры неровностей, указанные на рис. 5.

Рассмотрим вначале взаимодействие со слоем единичной неровности контртела. Для этого выберем некоторый участок слоя произвольной ширины $b$ (вдоль оси $y$) и длины $\Delta {\kern 1pt} x$ (вдоль оси $x$), причем $\Delta {\kern 1pt} x \ll {{a}_{1}} - {{a}_{2}}$, $\Delta x \ll 2{{a}_{2}}$. Принимая во внимание сделанные допущения, взаимодействие такого участка с проходящей над ним неровностью можно представить как равномерный подвод и последующий равномерный отвод поверхности контртела, которую можно считать расположенной параллельно подложке слоя (первое допущение (4.1)). Кроме того, можно считать, что после подвода/отвода поверхности контртела вязкоупругий материал слоя успевает релаксировать и прийти в стационарное состояние (второе и третье допущения (4.1)).

Подобный характер взаимодействия скользящей неровности с выбранным участком слоя вполне соответствует постановке рассмотренной выше задачи о плоскопараллельном контакте индентора с вязкоупругим слоем при наличии режимов подвода (1.12) и отвода (1.13) с линейным законом (2.9) изменения внедрения $\delta (t)$ индентора. Параметры этой задачи связаны с параметрами задачи о скольжении контртела следующими равенствами:

где ${{H}_{1}},{{H}_{2}}$ – зазоры между подложкой и горизонтальными частями профиля контртела, причем ${{g}_{m}} = {{H}_{1}} - {{H}_{2}} = {{\delta }_{2}} - {{\delta }_{1}}$ – высота неровности (рис. 5).

С учетом вышесказанного, воспользуемся формулой (3.1) для определения диссипации энергии $\Delta {\kern 1pt} {{D}_{{{\kern 1pt} 1}}}$ на выбранном участке слоя при прохождении по нему единичной неровности, представив эту энергию в виде $\Delta {\kern 1pt} {{D}_{{{\kern 1pt} 1}}} = {{d}_{{a - s}}}{\kern 1pt} b\Delta {\kern 1pt} x$. Отсюда следует, что при прохождении неровностью пути $l$ диссипация энергии в слое на этом пути составит

Если ввести в рассмотрение силу ${{F}_{{{\kern 1pt} 1}}}$ трения неровности о слой, то по закону сохранения энергии, работа этой силы на пути $l$ должна равняться диссипации энергии, т.е. ${{F}_{{{\kern 1pt} 1}}}{\kern 1pt} l = {{D}_{{{\kern 1pt} 1}}}$. Подстановка в это равенство выражения (4.3) позволяет установить, что

Аналогичное выражение для силы трения через диссипацию энергии было получено ранее для классического вязкоупругого контакта скольжения [39].

Вернемся теперь к рассмотрению контртела с множеством неровностей. Выделим некоторый участок контртела длиной $a \gg L \equiv {{L}_{0}} + 2{{a}_{1}}$ и выбранной ранее шириной $b$, на котором располагается $N = a{\text{/}}L$ неровностей (рис. 5). В силу равенства (4.4), сила трения такого участка по слою составит $F = N{{F}_{1}}$ = $S{{L}^{{ - 1}}}{{d}_{{a - s}}}$, где $S = a{\kern 1pt} b$ – площадь выделенного участка контртела. В результате, можно найти силу трения $\bar {\tau }$, приходящуюся на единицу площади контакта (среднее напряжение трения):

Нагрузка на контртело, приходящаяся на единицу площади контакта (среднее контактное давление) определяется по формуле:

где $T = L{\text{/}}{{V}_{s}}$ – период циклических воздействий неровностей контртела на слой, $p$ – контактное давление, которое рассчитывается по известному зазору $r(t)$ с использованием формулы (1.3).

Располагая величинами $\bar {\tau }$ и $\bar {p}$, можно определить коэффициент трения скольжения [40]

который имеет физический смысл при положительных значениях давления $\bar {p}$.

На основе равенств (4.5), (4.6) и решения задачи о плоскопараллельном контакте индентора с вязкоупругим слоем (разд. 2 и 3), были выполнены расчеты величин $\bar {\tau }$ и $\bar {p}$ для различных значений максимального внедрения ${{\delta }_{2}}$ контртела.

Расчеты проводились при ${{a}_{1}}$ = 0.6 мкм, ${{a}_{2}}$ = 0.5 мкм, ${{g}_{m}} = 5 \times {{10}^{{{\kern 1pt} - 3}}}$ мкм, ${{L}_{{{\kern 1pt} 0}}}$ = 1 мкм, ${{V}_{s}}$ = 50 мкм/с. Величина ${{\delta }_{{{\kern 1pt} 1}}}$ определялась по формуле ${{\delta }_{{{\kern 1pt} 1}}} = {{\delta }_{{{\kern 1pt} 2}}} - {{g}_{m}}$ для каждого значения ${{\delta }_{2}}$. Значения остальных параметров принимались такими же, как в разд. 2.

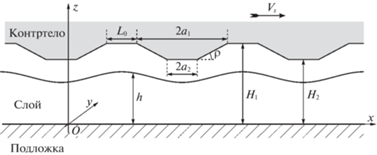
На рис. 6а и б изображены зависимости силы трения $\bar {\tau }$ и давления $\bar {p}$ от внедрения ${{\delta }_{2}}$ при уточненной и традиционной постановках задачи с использованием безразмерной величины ${{\tilde {\delta }}_{2}} = {{\delta }_{2}}{\text{/}}{{h}_{{{\kern 1pt} 0}}}$. На рис. 6в показаны кривые зависимости силы трения $\bar {\tau }$ от давления $\bar {p}$, построенные на основе графиков рис. 6а и б. Каждой точке на такой кривой отвечает некоторое значение внедрения ${{\delta }_{2}}$ из указанного на рис. 6а или б диапазона, причем стрелками обозначено направление роста величины ${{\delta }_{2}}$. Отметим, что неоднозначность зависимости $\bar {\tau }(\bar {p})$ обусловлена отсутствием монотонной зависимости давления $\bar {p}$ от внедрения ${{\delta }_{2}}$ (рис. 6б).

Показанные на рис. 6а зависимости $\bar {\tau }({{\delta }_{2}})$ имеют особенности в виде разрывов и изломов, причины появления которых указаны в разд. 2. В частности, разрыв происходит при ${{\delta }_{2}} = \delta _{ + }^{\infty }$ и обусловлен появлением скачка у функции $r(t)$ с резким изменением ее конечного значения ${{r}_{m}}$. Аналогичное поведение функции $r(t)$ имеет место, когда значение $\delta _{ + }^{\infty }$ принимает внедрение ${{\delta }_{{{\kern 1pt} 1}}}$. Однако, соответствующее внедрение ${{\delta }_{2}} = {{\delta }_{{{\kern 1pt} 1}}} + {{g}_{m}}$ = = $\delta _{ + }^{\infty } + {{g}_{m}}$ оказывается сравнимым с толщиной ${{h}_{{{\kern 1pt} 0}}}$ слоя, что противоречит условию малости деформаций. По этой причине, на рис. 6а дополнительные особенности зависимости $\bar {\tau }({{\delta }_{2}})$ не представлены.

Разрывы и изломы кривых зависимости силы трения $\bar {\tau }$ от давления $\bar {p}$ (рис. 6в) являются очевидным следствием наличия таких особенностей у соответствующих зависимостей $\bar {\tau }({{\delta }_{2}})$ (рис. 6а). Отметим, что ранее скачкообразное изменение силы трения при изменении нормальной нагрузки наблюдалась экспериментально для зонда атомно-силового микроскопа [41].

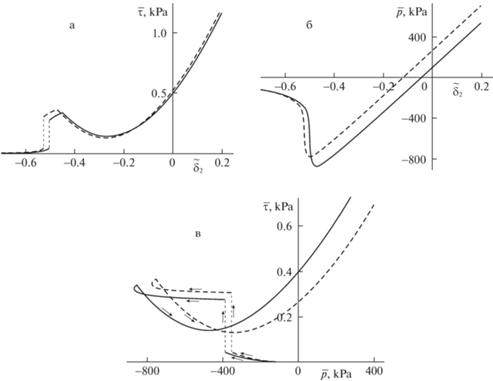
Как и прежде, можно утверждать, что зависимости $\bar {\tau }({{\delta }_{2}})$ и $\bar {\tau }(\bar {p})$ являются гладкими (без разрывов и изломов), если выполняется условие (2.10). Для проверки этого утверждения были выполнены расчеты при прежних значениях параметров задачи, но уменьшенной толщине слоя ${{h}_{{{\kern 1pt} 0}}}$ = 2 нм, когда имеет место неравенство (2.10). На рис. 7а и б изображены соответствующие зависимости $\bar {\tau }({{\delta }_{2}})$ и $\bar {p}({{\delta }_{2}})$, а на рис. 7в – зависимость $\bar {\tau }(\bar {p})$, которые, как и следовало ожидать, являются гладкими.

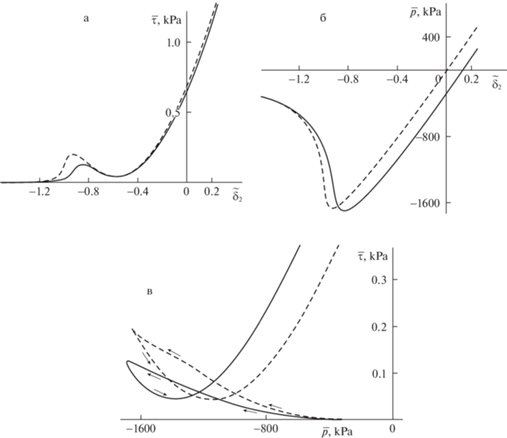
Сравнение рис. 6в и 7в указывает на то, что уменьшение толщины ${{h}_{{{\kern 1pt} 0}}}$ слоя приводит к существенному росту силы трения $\bar {\tau }$ в области больших (в частности, положительных) значений давления $\bar {p}$.

Располагая значениями силы трения $\bar {\tau }$ и давления $\bar {p}$ (рис. 6 и 7), можно выполнить оценку коэффициента трения ${{\mu }_{s}}$ по формуле (4.7). В таблице 1 приводятся значения ${{\mu }_{s}}$, полученные при давлении $\bar {p}$ = 1 МПа. Как видно, коэффициент трения в рассматриваемом случае имеет достаточно низкие значения, что отвечает режиму сверхнизкого трения [42, 43]. Обращает на себя внимание, что увеличение толщины ${{h}_{{{\kern 1pt} 0}}}$ слоя приводит к незначительному уменьшению коэффициента трения ${{\mu }_{s}}$. Использование традиционной постановки задачи вместо уточненной постановки приводит к существенному занижению оценки коэффициента трения.

Выводы

1. Выполнен расчет диссипации энергии в вязкоупругом слое в режиме подвода/отвода плоского индентора при наличии сил межмолекулярного взаимодействия (самосогласованный подход, традиционная и уточненная постановки задачи).

2. Выявлен эффект скачкообразного роста диссипации энергии ${{d}^{\infty }}$ при достижении конечным внедрением ${{\delta }_{m}}$ индентора критического значения $\delta _{ + }^{\infty }$ (рис. 2 и 4). Реализация этого эффекта зависит, в конечном счете, от упругой податливости слоя и характера межмолекулярного взаимодействия (условие (2.10)).

3. На основе решения задачи о подводе/отводе плоского индентора выполнен расчет силы трения скольжения шероховатого контртела по вязкоупругому слою в режиме бесконтактного трения. Продемонстрирована возможность скачкообразного роста силы трения при увеличении внедрения контртела.

Работа выполнена по теме государственного задания (№ госрегистрации АААА-А20-120011690132-4) и при финансовой поддержке РФФИ и БРФФИ в рамках научного проекта № 20-58-00007.