Прикладная математика и механика, 2022, T. 86, № 3, стр. 394-403

Периодические контактные задачи для полупространства с частично закрепленной границей

Н. Б. Золотов¹, Д. А. Пожарский^1, *

¹ Донской государственный технический университет
Ростов-на-Дону, Россия

Поступила в редакцию 03.03.2022
После доработки 29.03.2022
Принята к публикации 05.04.2022

EDN: LLPWJY
DOI: 10.31857/S0032823522030122

Аннотация

Рассматриваются две периодические контактные задачи с неизвестными областями контакта о бесконечной прямолинейной цепочке одинаковых жестких штампов на упругом полупространстве. Часть поверхности полупространства в виде полуплоскости находится в условиях скользящей или жесткой заделки, что позволяет получить корректные интегральные уравнения относительно контактного давления. Учитываются силы трения Кулона в направлении перпендикулярном границе закрепленной полуплоскости. Для решения задач применяется метод нелинейных интегральных уравнений, позволяющий одновременно определить область контакта и контактные давления. Рассчитаны механические характеристики, изучен переход от дискретной к непрерывной области контакта бесконечной длины.

Ключевые слова: периодический контакт, упругое полупространство, интегральные уравнения

Большинство публикаций в области периодического контакта посвящено плоским задачам [1, 2]. Для исследования пространственных периодических контактных задач для круговых инденторов разработан метод локализации [3, 4]. Рассматривались двоякопериодические контактные задачи [5–7]. Анализировались эффекты трения, износа, сцепления и адгезии при периодическом контакте упругих тел [8–10]. Изучалась периодическая система сферических инденторов на вязкоупругом полупространстве [11]. Для решения трехмерных периодических контактных задач применялись регулярный асимптотический метод [5, 12], численный метод быстрого преобразования Фурье с включением эффекта перколяции (слияния соседних областей контакта) [7], а также разработанный Б.А. Галановым [13] метод нелинейных граничных интегральных уравнений при заранее неизвестных областях контакта [12].

Интегральное уравнение трехмерной контактной задачи о прямолинейной периодической цепочке штампов на упругом полупространстве некорректно, поскольку ядро представляется расходящимся рядом. В настоящей статье для получения корректного интегрального уравнения предлагается фиксировать часть границы полупространства скользящей или жесткой заделкой с введением дополнительной линии раздела граничных условий, которая параллельна оси цепочки. В отличие от рассмотренных ранее аналогичных задач (несжимаемый клин с жестко заделанной гранью [12], полупространство без трения [2]) учитываются силы трения Кулона, действующие перпендикулярно границе зоны фиксации при произвольном коэффициенте Пуассона. Более того, привлекая аппарат обобщенных функций, можно показать, что для трехмерного клина скользящая заделка одной грани обеспечивает корректность интегрального уравнения периодической задачи для линейной цепочки на другой грани только для случая полупространства. Это связано с тем, что символ ядра должен быть типа тангенса гиперболического. Показано, что переход от дискретного к непрерывному пространственному линейно-периодическому контакту связан с образованием новых интегрируемых особенностей ядра на линии перехода.

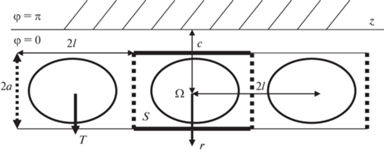
1. Постановка задач. Изучим квазистатические периодические контактные задачи о линейной цепочке одинаковых жестких штампов (период $2l$), внедренных в поверхность упругого полупространства на величину $\delta $ и начинающих достаточно медленно двигаться без перекоса перпендикулярно оси цепочки. В цилиндрических координатах $r$, $\varphi $, $z$ полупространство описывается неравенствами $r > 0$, $0 \leqslant \varphi \leqslant \pi $, ${\text{|}}z{\text{|}} < \infty $. Вне области контакта, расположенной на полуплоскости $\varphi = 0$, часть поверхности полупространства в виде полуплоскости $\varphi = \pi $ подчинена условиям скользящей или жесткой заделки (задачи А и Б соответственно). Граница закрепленной полуплоскости параллельна оси цепочки и удалена от нее на расстояние $c$ (рис. 1). Пусть штампы достаточно вытянуты вдоль оси цепочки, поэтому можно приближенно считать, что силы трения коллинеарны направлению движения (и направлены против движения). Задачи симметричны по координате $z$ (ось $z$ направлена по линии раздела граничных условий). К штампам приложены нормальные силы $P$ на расстоянии $H$ от линии раздела и касательные силы $T = \mu P$ ($\mu $ – коэффициент трения Кулона). Предполагается, что неизвестные области контакта априори содержатся в заданных соприкасающихся прямоугольниках со сторонами $2l$ и $2a$ (рис. 1). В прямоугольнике, содержащем начало координат и область контакта $\Omega $, форма основания штампа описывается функцией $f\left( {r,z} \right)$, которая продолжается периодическим образом по $z$ с периодом $2l$. Для определенности далее берем

(1.1)

$f(r,z) = \frac{{{{{(r - c)}}^{2}}}}{{2{{R}_{1}}}} + \frac{{{{z}^{2}}}}{{2{{R}_{2}}}}\quad ({{R}_{1}} < {{R}_{2}})$

Рис. 1.

Неизвестные области контакта содержатся в заданных прямоугольниках. Слияние областей возможно на точечных линиях. Ось z – линия раздела.

Граничные условия контактных задач имеют вид ($\Omega {\kern 1pt} *$ – объединенная область контакта; $r$, $\varphi $, $z$ – цилиндрические координаты)

(1.2)

$\begin{gathered} \varphi = 0{\kern 1pt} :{{u}_{\varphi }} = \delta - f(r,z),\quad {{\tau }_{{r\varphi }}} = \mu {{\sigma }_{\varphi }}{\text{,}}\quad {{\tau }_{{\varphi z}}} = 0,\quad {\text{(}}r,z{\text{)}} \in \Omega {\kern 1pt} * \\ {{\sigma }_{\varphi }} = {{\tau }_{{r\varphi }}} = {{\tau }_{{\varphi z}}} = 0,\quad (r,z) \notin \Omega {\kern 1pt} * \\ {\text{A)}}\quad \varphi = \pi {\kern 1pt} :{{u}_{\varphi }} = {{\tau }_{{r\varphi }}} = {\text{ }}{{\tau }_{{\varphi z}}} = 0 \\ {\text{Б)}}\quad \varphi = \pi {\kern 1pt} :{{u}_{\varphi }} = {{u}_{r}} = {{u}_{z}} = 0 \\ \end{gathered} $

При заданных параметрах упругости $G$ (модуль сдвига), $\nu $ (коэффициент Пуассона), величинах $a,c,l,\delta ,\mu $ и функции $f\left( {r,z} \right)$ требуется определить область контакта $\Omega $ и контактное давление $q\left( {r,z} \right)$ = $ - {{\sigma }_{\varphi }}\left( {r,0,z} \right)$, $\left( {r,z} \right) \in \Omega $, затем при использовании интегральных условий равновесия штампов могу быть найдены величины $P$ и $H$.

2. Интегральные уравнения. Упругое полупространство с закрепленной полуплоскостью является частным случаем трехмерного клина с углом раствора $\pi $, для которого в известных функциях Грина [14]¹ ¹ (а также в ядрах интегральных уравнений соответствующих контактных задач) исчезают интегральные уравнения Фредгольма второго рода. Используя эти функции для условий (1.2) ([14], с. 128), принцип суперпозиции и периодичность контактных задач, относительно контактного давления получим интегральное уравнение ($\theta = G{\text{/}}\left( {1 - \nu } \right)$)

(2.1)

$\iint\limits_\Omega {q(x,y)K(x,y,r,z)dxdy = 2\pi \theta [\delta - f(r,z)]},\quad (r,z) \in \Omega $

с ядром в форме

$\begin{gathered} K(x,y,r,z) = \frac{4}{{{{\pi }^{2}}}}\int\limits_0^\infty {\int\limits_0^\infty {{\text{sh}}(\pi u)W(u){{K}_{{iu}}}(\beta r)} } \left[ {{{K}_{{iu}}}(\beta x) + {{\mu }_{*}}\int\limits_0^\infty {{{W}_{1}}(t)\frac{{{\text{sh}}(\pi t){{K}_{{it}}}(\beta x)dt}}{{{\text{ch}}(\pi t) - {\text{ch}}(\pi u)}}} } \right] \times \\ \times \;\sum\limits_{k = - \infty }^\infty {\cos (\beta (z - y + 2lk))dud\beta } \\ \end{gathered} $

(2.2)

${{\mu }_{*}} = \mu \frac{{1 - 2\nu }}{{2(1 - \nu )}}$

$\begin{gathered} {\text{А)}}\quad W(u) = \operatorname{th} (\pi u),\quad {{W}_{1}}(t) = \operatorname{cth} (\pi t) \\ {\text{Б)}}\quad W(u) = \frac{{{\text{2}}\kappa \operatorname{sh} (2\pi u)}}{{{\text{2}}\kappa \operatorname{ch} (2\pi u) + {{\kappa }^{2}} + 1}},\quad \kappa = 3 - 4\nu ,\quad {{W}_{1}}(t) = \operatorname{th} (\pi t) \\ \end{gathered} $

Здесь ${{K}_{{iu}}}\left( r \right)$ – цилиндрическая функция Бесселя. Отметим, что символы $W\left( u \right)$ и ${{W}_{1}}\left( u \right)$ возникают также в ядре интегрального уравнения плоских контактных задачах с трением о действии одного штампа на упругую полуплоскость, часть границы которой (полуось) находится в условиях скользящей или жесткой заделки ([14], с. 31):

(2.3)

$K(x,r) = \int\limits_0^\infty {\frac{{{\text{ }}W(u)}}{u}\cos \left( {u\ln \frac{r}{x}} \right)} du - {{\mu }_{*}}\int\limits_0^\infty {\frac{{{\text{ }}W(u){{W}_{1}}(u)}}{u}\sin \left( {u\ln \frac{r}{x}} \right)} du$

Преобразуем ядро (2.2) к форме удобной для вычислений. Воспользуемся представлением [15]

(2.4)

$\sum\limits_{k = - \infty }^\infty {\cos (\beta (z - y + 2lk)) = 2\pi \cos (\beta (z - y))\sum\limits_{k = - \infty }^\infty {\delta (2\beta l - 2\pi k)} } ,$

где $\delta \left( x \right)$ – $\delta $-функция Дирака. Учитывая значения пределов

$\frac{2}{\pi }\mathop {\lim }\limits_{\beta \to 0} \int\limits_0^\infty {{\text{sh(}}\pi u){\text{ }}W(u){{K}_{{iu}}}(\beta x){{K}_{{iu}}}(\beta r)} du = \int\limits_0^\infty {\frac{{{\text{ }}W(u)}}{u}\cos \left( {u\ln \frac{r}{x}} \right)} du$

$\frac{2}{\pi }\mathop {\lim }\limits_{\beta \to 0} \int\limits_0^\infty {\int\limits_{\text{0}}^\infty {\frac{{W(u){{W}_{1}}(t){\text{ sh(}}\pi u){\text{sh(}}\pi t)}}{{{\text{ch}}(\pi t) - {\text{ch}}(\pi u)}}} {\text{ }}{{K}_{{it}}}(\beta x){{K}_{{iu}}}(\beta r)} dtdu = $

$ = - \int\limits_0^\infty {\frac{{{\text{ }}W(u){{W}_{1}}(u)}}{u}\sin \left( {u\ln \frac{r}{x}} \right)} {\kern 1pt} du,$

возникающих в ядре (2.2), (2.4) при $k = 0$ и соответствующих плоским задачам, преобразуем его к виду

$K(x,y,r,z) = \frac{1}{l}\int\limits_0^\infty {\frac{{{\text{ }}W(u)}}{u}\cos \left( {u\ln \frac{r}{x}} \right)} du - \frac{{{{\mu }_{*}}}}{l}\int\limits_0^\infty {\frac{{{\text{ }}W(u){{W}_{1}}(u)}}{u}\sin \left( {u\ln \frac{r}{x}} \right)} du + $

(2.5)

$ + \;\frac{4}{{\pi l}}\int\limits_0^\infty {\operatorname{sh} } (\pi u)W(u)\sum {(u,u)du + } \frac{{4{{\mu }_{*}}}}{{\pi l}}\int\limits_0^\infty {\int\limits_0^\infty {\frac{{W(u){{W}_{1}}(t)\operatorname{sh} {\text{(}}\pi u)\operatorname{sh} {\text{(}}\pi t)}}{{\operatorname{ch} (\pi t) - \operatorname{ch} (\pi u)}}} } \sum {(t,u)dtdu} $

$\sum {(t,u) = } \sum\limits_{k = 1}^\infty {{{K}_{{it}}}\left( {\frac{{\pi k}}{l}x} \right){{K}_{{iu}}}\left( {\frac{{\pi k}}{l}r} \right)\cos \left( {\frac{{\pi k}}{l}(z - y)} \right)} $

Для выделения главных членов из части ядра (2.5), не учитывающей силы трения (без ${{\mu }_{*}}$), используем интегралы и ряд [12, 16, 17] ($C$ – постоянная Эйлера)

$\int\limits_0^\infty {\frac{{\cos (ut) - \exp ( - u)}}{u}du = - \ln \left| t \right|} ,\quad \int\limits_0^\infty {\operatorname{ch} {\text{(}}\pi u){{K}_{{iu}}}(tx){{K}_{{iu}}}(tr)} du = \frac{\pi }{2}{{K}_{0}}(t{\text{|}}r - x{\text{|}})$

(2.6)

$\sum\limits_{k = 1}^\infty {{{K}_{0}}(kr)\cos (kz) = \frac{\pi }{{2\sqrt {{{r}^{2}} + {{z}^{2}}} }} + \frac{1}{2}\left( {{\text{C}} + \ln \frac{r}{{4\pi }}} \right) + } $

$ + \;\frac{\pi }{2}\sum\limits_{k = 1}^\infty {\left[ {\frac{1}{{\sqrt {{{{(2\pi k - z)}}^{2}} + {{r}^{2}}} }} + \frac{1}{{\sqrt {{{{(2\pi k + z)}}^{2}} + {{r}^{2}}} }} - \frac{1}{{\pi k}}} \right]} ,$

а для членов ядра, включающих ${{\mu }_{*}}$, возьмем интеграл ([14], с. 79),

$\frac{4}{{{{\pi }^{2}}}}\int\limits_0^\infty {\int\limits_0^\infty {\int\limits_0^\infty {\frac{{{{W}_{0}}(u,t)\operatorname{sh} {\text{(}}\pi u)\operatorname{sh} {\text{(}}\pi t)}}{{\operatorname{ch} (\pi t) - \operatorname{ch} (\pi u)}}{{K}_{{it}}}(\beta x)} } } {{K}_{{iu}}}(\beta r)\cos (\beta (z - y))d\beta dtdu = - \frac{{r - x}}{{{{R}^{2}}}}$

${{W}_{0}}(u,t) = \frac{1}{2}\left( {\operatorname{cth} \frac{{\pi u}}{{\text{2}}}\operatorname{th} \frac{{\pi t}}{{\text{2}}} + {\text{th}}\frac{{\pi u}}{{\text{2}}}\operatorname{cth} \frac{{\pi t}}{{\text{2}}}} \right),\quad R = \sqrt {{{{(r - x)}}^{2}} + {{{(z - y)}}^{2}}} ,$

значение которого встречается в контактной задаче с трением Кулона для полупространства со свободной поверхностью вне зоны контакта [4, 14].

В результате представим ядро (2.5) в форме

$\begin{gathered} K(x,y,r,z) = \frac{1}{R} - {{\mu }_{*}}\frac{{r - x}}{{{{R}^{2}}}} + \sum\limits_{k = 1}^\infty {\left[ {\frac{1}{{R_{k}^{ + }}} + \frac{1}{{R_{k}^{ - }}} - \frac{1}{{kl}} - {{\mu }_{*}}\left( {\frac{{r - x}}{{{{{(R_{k}^{ + })}}^{2}}}} + \frac{{r - x}}{{{{{(R_{k}^{ - })}}^{2}}}}} \right)} \right]} + \\ + \;\frac{1}{l}\int\limits_0^\infty {\left\{ {[W(u) - 1]\cos \left( {u\ln \frac{r}{x}} \right) + \exp ( - u)} \right\}} \frac{{du}}{u} - \frac{{{{\mu }_{*}}}}{l}\int\limits_0^\infty {[W(u){{W}_{1}}(u) - 1]\sin \left( {u\ln \frac{r}{x}} \right)} \frac{{du}}{u} + \\ \end{gathered} $

(2.7)

$\begin{gathered} + \;\frac{1}{l}\ln \frac{{\left| {r - x} \right|}}{{4l\left| {\ln (r{\text{/}}x)} \right|}} + \frac{{\text{C}}}{l} + \frac{4}{{\pi l}}\int\limits_0^\infty {{\text{[}}\operatorname{sh} {\text{(}}} \pi u)W(u) - \operatorname{ch} (\pi u)]\sum {(u,u)du + } \\ + \;\frac{{4{{\mu }_{*}}}}{{\pi l}}\int\limits_0^\infty {\int\limits_0^\infty {\frac{{[W(u){{W}_{1}}(t) - {{W}_{0}}(u,t)]\operatorname{sh} {\text{(}}\pi u)\operatorname{sh} {\text{(}}\pi t)}}{{\operatorname{ch} (\pi t) - \operatorname{ch} (\pi u)}}} } \sum {(t,u)dtdu} \\ R_{k}^{ \pm } = \sqrt {{{{(r - x)}}^{2}} + {{{(z - y \pm 2kl)}}^{2}}} \\ \end{gathered} $

В формуле (2.7) улучшена сходимость всех интегралов с учетом асимптотического поведения символов в бесконечности. Ядро (2.7) интегрального уравнения линейно-периодической контактной задачи включает члены, входящие в ядра известных интегральных уравнений как пространственных, так и плоских контактных задач с трением для одного штампа (см. формулу (2.3)) [4, 14]; в пределе при $l \to \infty $ оно переходит в известное для одного штампа. Однако логарифмическая особенность плоской задачи в формуле (2.7) нейтрализована рядом (2.6), поскольку ($x > 0$)

(2.8)

$\mathop {\lim }\limits_{r \to x} \ln \frac{{\left| {r - x} \right|}}{{\left| {\ln (r{\text{/}}x)} \right|}} = \ln \left| x \right|$

В задаче А в отличие от задачи Б

(2.9)

$W(u){{W}_{1}}(u) - 1 \equiv 0,$

что приводит к исчезновению второго интегрального слагаемого в формуле (2.7). Тождество (2.9) связано с совпадением символов $W(u){{W}_{1}}(u) \equiv 1$ в ядре (2.3) плоских задач с трением для полуплоскости при скользящей заделке по полуоси и при свободной границе вне зоны контакта ([14], с. 31). По этой же причине в задаче А в отличие от задачи Б последний интеграл в формуле (2.7) не является сингулярным, так как в этом случае

$\mathop {\lim }\limits_{t \to u} \frac{{[W(u){{W}_{1}}(t) - {{W}_{0}}(u,t)]\operatorname{sh} {\text{(}}\pi u)\operatorname{sh} {\text{(}}\pi t)}}{{\operatorname{ch} (\pi t) - \operatorname{ch} (\pi u)}} = - \frac{1}{{\operatorname{ch} (\pi u)}}$

Ядро (2.2) для задачи А может быть представлено в другой форме, в которой его часть, не учитывающая трение, свободна от квадратур и логарифмических членов. На основе разложения

$\operatorname{sh} (\pi u)W(u) = \operatorname{sh} (\pi u)\operatorname{th} (\pi u) = \operatorname{ch} (\pi u) - \frac{1}{{\operatorname{ch} (\pi u)}}$

и значений интегралов [14]

$\int\limits_0^\infty {\int\limits_0^\infty {\operatorname{ch} (\pi u)} } {{K}_{{iu}}}(\beta x){{K}_{{iu}}}(\beta r)\cos (\beta (z - y))d\beta du = \frac{{{{\pi }^{2}}}}{{4R}}$

$\int\limits_0^\infty {\int\limits_0^\infty {\frac{1}{{\operatorname{ch} (\pi u)}}} } {{K}_{{iu}}}(\beta x){{K}_{{iu}}}(\beta r)\cos (\beta (z - y))d\beta du = \frac{\pi }{{2R}}\operatorname{arctg} \frac{R}{{2\sqrt {xr} }}$

ядро (2.2) для задачи А приводится к виду

$K(x,y,r,z) = \frac{1}{R}\left( {1 - \frac{2}{\pi }\operatorname{arctg} \frac{R}{{2\sqrt {xr} }}} \right) - {{\mu }_{*}}\frac{{r - x}}{{{{R}^{2}}}} + $

(2.10)

$\begin{gathered} + \;\sum\limits_{k = 1}^\infty {\left[ {\frac{1}{{R_{k}^{ + }}}\left( {1 - \frac{2}{\pi }{\text{arctg}}\frac{{R_{k}^{ + }}}{{2\sqrt {xr} }}} \right) + \frac{1}{{R_{k}^{ - }}}\left( {1 - \frac{2}{\pi }{\text{arctg}}\frac{{R_{k}^{ - }}}{{2\sqrt {xr} }}} \right) - {{\mu }_{*}}\left( {\frac{{r - x}}{{{{{(R_{k}^{ + })}}^{2}}}} + \frac{{r - x}}{{{{{(R_{k}^{ - })}}^{2}}}}} \right)} \right]} + \hfill \\ + \;\frac{{4{{\mu }_{*}}}}{{\pi l}}\int\limits_0^\infty {\int\limits_0^\infty {\frac{{[W(u){{W}_{1}}(t) - {{W}_{0}}(u,t)]\operatorname{sh} (\pi u)\operatorname{sh} (\pi t)}}{{\operatorname{ch} (\pi t) - \operatorname{ch} (\pi u)}}} } \sum {(t,u)dtdu} \hfill \\ \end{gathered} $

Пример. Эквивалентность форм (2.7) и (2.10) проверим, отбрасывая член ${{R}^{{ - 1}}}$, в частном случае $r = x \ne 0$, $z = y$, $l = 1$, $\mu = 0$. При учете предела (2.8) и интеграла [17]

$\int\limits_0^\infty {\frac{{K_{{iu}}^{2}(x)}}{{\operatorname{ch} (\pi u)}}du = \frac{\pi }{2}{{E}_{1}}(2x),\quad {{E}_{1}}(x) = \int\limits_x^\infty {\frac{{\exp ( - t)}}{t}dt} } $

можно численно убедиться в справедливости равенства

$\ln \frac{x}{4} + {\text{C}} + \int\limits_0^\infty {[\operatorname{th} (\pi u) - 1 + \exp ( - u)]\frac{{du}}{u} - 2\sum\limits_{k = 1}^\infty {{{E}_{1}}(2\pi kx) = } } - \frac{1}{{\pi x}} + \sum\limits_{k = 1}^\infty {\frac{1}{k}\left( {1 - \frac{2}{\pi }\operatorname{arctg} \frac{k}{x}} \right)} $

3. Численный анализ. Для решения контактных задач применим метод, предложенный Галановым [13], позволяющий одновременно определить область контакта и давления в этой области. В этом методе интегрирование в уравнении (2.1), (1.1) распространяется на прямоугольник S, содержащий область $\Omega $ (рис. 1). Предположения об отсутствии контакта и обращения в нуль давления в дополнительной области $S{{\backslash }}\Omega $ приводят к системе интегрального уравнения и интегрального неравенства

$\int\limits_S {q(N)K(N,M)dN = d(M);\quad q(M) \geqslant 0,\quad M \in \Omega } $

(3.1)

$\int\limits_S {q(N)K(N,M)dN > d(M);\quad q(M) = 0,\quad M \in S{{\backslash }}\Omega } $

$N = x,y,\quad M = r,z,\quad d(M) = 2\pi \theta [\delta - f(M)]$

После введения нелинейных операторов

${{p}^{ + }}(M) = \sup \{ p(M),0\} ,\quad {{p}^{ - }}(M) = \inf \{ p(M),0\} $

и представления искомого давления в форме

$q = q(M) = {{q}^{ + }}(M) + {{q}^{ - }}(M)$

система (3.1) сводится к решению нелинейного операторного уравнения типа Гаммерштейна

(3.2)

$\Theta {\text{ }}p = 0{\text{ (}}M \in \Omega {\text{),}}\quad \Theta {\text{ }}p \equiv {{p}^{ - }} + K{{p}^{ + }} - d,$

где $p = p\left( M \right)$, ${{p}^{ \pm }} = {{p}^{ \pm }}\left( M \right)$, $d = d\left( M \right)$

(3.3)

$K{{p}^{ + }} = \int\limits_S {{{p}^{ + }}(N)K(N,M)dN} $

При этом интегральное неравенство (3.1) удовлетворяется автоматически. Можно доказать эквивалентность системы (3.1) и уравнения (3.2) [12–14].

При численном решении уравнения (3.2) применяется модифицированный метод Ньютона, основанный на построении последовательных приближений по формулам

${{p}_{{n + 1}}} = {{p}_{n}} - {{(F{\kern 1pt} '{\kern 1pt} {{p}_{n}})}^{{ - 1}}}{\text{ }}\Theta {\text{ }}{{p}_{n}},\quad {{p}_{n}} = {{p}_{n}}(M);\quad n = 0,{\text{ }}1, \ldots ,\quad {{p}_{0}} = d,$

где $F$ – дифференцируемый оператор, аппроксимирующий оператор $\Theta $ по равномерной метрике [12–14].

В отличие от задач для одного штампа [13, 14] ядра (2.7) и (2.10) в прямоугольнике $S$ имеют не только классическую особенность ${{R}^{{ - 1}}}$, но и дополнительные интегрируемые особенности ${{(R_{1}^{ \pm })}^{{ - 1}}}$ в точках $r = x$, $z - y = \pm 2l$ на сторонах $S$, обозначенных точками на рис. 1. При расчете значений ядра в интегралах типа (3.3) особенности сглаживались по формуле ($k = 0;1$)

${{(r - x)}^{2}} + {{(z - y \pm 2kl)}^{2}} \to {{(r - x)}^{2}} + {{(z - y \pm 2kl)}^{2}} + \frac{{{{h}_{1}}{{h}_{2}}}}{{16}},$

где ${{h}_{1}}$ и ${{h}_{2}}$ – шаги сетки соответственно по осям $r$ и $z$.

Введем безразмерные обозначения (штрихи далее опускаем)

$r{\kern 1pt} ' = \frac{{r - c}}{l},\quad x{\kern 1pt} ' = \frac{{x - c}}{l},\quad z{\kern 1pt} ' = \frac{z}{l},\quad y{\kern 1pt} ' = \frac{y}{l},\quad A = \frac{l}{{2{{R}_{1}}}},\quad B = \frac{l}{{2{{R}_{2}}}},\quad \lambda = \frac{c}{l}$

$q{\kern 1pt} '(r{\kern 1pt} ',z{\kern 1pt} ') = \frac{{q(r,z)}}{{2\pi \theta }},\quad \varepsilon = \frac{a}{l},\quad \delta {\kern 1pt} ' = \frac{\delta }{l},\quad P{\kern 1pt} ' = \frac{P}{{2\pi \theta {{l}^{2}}}}{\text{,}}\quad S{\kern 1pt} ' \leftrightarrow S,\quad \Omega {\kern 1pt} ' \leftrightarrow \Omega $

Параметр $\lambda $ характеризует относительную удаленность цепочки штампов от линии раздела.

Значения вдавливающей силы $P$ от осадки $\delta $ и от параметра $\lambda $ приведены соответственно в табл. 1 и 2 при разных коэффициентах трения. Значения $P$ растут при увеличении осадки и снижаются при отдалении цепочки от линии раздела. В задаче Б соответствующие значения силы больше, чем в задаче А, различие между решениями задач А и Б снижается с ростом $\lambda $. Трение слабо влияет на зависимости $P\left( \delta \right)$ и $P\left( \lambda \right)$. При $\mu > 0$, когда штампы начинают удаляться от линии раздела, значения $P$ несколько меньше, чем при $\mu < 0$, причем разница значений $P$ при изменении знака μ снижается с ростом $\lambda $. При $\nu \to 0.5$ решения контактных задач А и Б сближаются, что вызвано совпадением ядер (2.7) обеих задач при $\nu = 0.5$.

Таблица 1.

Значения вдавливающей силы P(δ), A = ε = 1, B = 0.2, λ = 2, ν = 0.25

δ	1	1.5	2	1	1.5	2
δ	Задача А			Задача Б
μ = 0.2	0.2348	0.3838	0.5465	0.2416	0.3959	0.5652
μ = 0	0.2354	0.3856	0.5487	0.2422	0.3978	0.5670
μ = –0.2	0.2355	0.3868	0.5497	0.2423	0.3990	0.5678

Таблица 2.

Значения вдавливающей силы P(λ), A = ε = 1, B = 0.2, ν = 0.25

λ	1.5	4	6	1.5	4	6
λ	Задача А			Задача Б
δ = 1
μ = 0.2	0.2578	0.1952	0.1782	0.2662	0.1997	0.1818
μ = –0.2	0.2588	0.1955	0.1784	0.2671	0.2000	0.1821
δ = 1.5
μ = 0.2	0.4273	0.3165	0.2878	0.4434	0.3241	0.2939
μ = –0.2	0.4328	0.3168	0.2879	0.4484	0.3244	0.2941

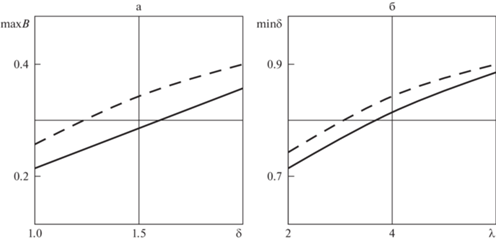
Для достаточно вытянутых вдоль линии раздела штампов (при малых B) при росте $\delta $ наблюдается выход области контакта на боковые стороны прямоугольника $S$ (показаны точками на рис. 1), что означает начало перколяции (слияние областей контакта). На рис. 2 показаны зависимости $\max B\left( \delta \right)$ и $\min \delta \left( \lambda \right)$, при которых начинается слияние областей контакта. При отдалении цепочки от линии раздела для начала перколяции при фиксированной осадке обычно необходимо сделать штампы более вытянутыми (уменьшить значение B). В задаче Б (жесткая заделка) для начала перколяции, как правило, требуется меньшая осадка, чем в задаче А (скользящая заделка).

Рис. 2.

Графики max B(δ) (а: задача А, A = ε = 1, μ = 0; λ = 4 – сплошная линия, λ = 1.2 – пунктир) и min δ(λ) (б: A = ε = 1, B = μ = 0.2, ν = 0.25; задача А – пунктир, задача Б – сплошная линия) для начала перколяции.

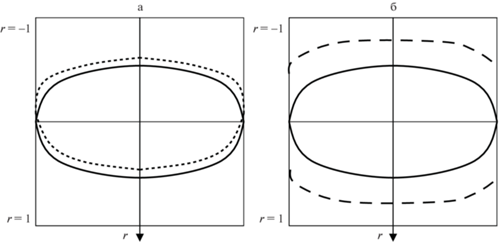
При отсутствии трения, а также при движении в сторону линии раздела ($\mu < 0$), область контакта смещается к линии раздела относительно оси цепочки, проходящей через точку начального касания. Движение в положительном направлении полуоси $r$ ($\mu > 0$) может выравнивать (симметризовать) область контакта относительно оси цепочки (рис. 3а, начало перколяции). Площадь области контакта существенно возрастает при увеличении осадки $\delta $, что может приводить к удлинению линии слияния соседних областей контакта (рис. 3б). При равных значениях осадки площадь области контакта, как правило, несколько больше в задаче Б, чем в задаче А.

Рис. 3.

Области контакта при A = ε = 1, B = 0.2, λ = 4, ν = 0.25; а) симметризация от трения (задача А, δ = 1; μ = 0 – точки, μ = 0.2 – сплошная линия); б) эволюция при росте осадки (задача Б, μ = 0.2; δ = 1 – сплошная линия, δ = 2 – пунктир).

Заключение. Закрепление части границы полупространства в виде полуплоскости позволяет получить корректные интегральные уравнения при линейно-периодическом пространственном контакте. Установлена структура ядер интегральных уравнений задач линейно-периодического контакта с трением при произвольной форме штампов, включающая известные члены ядер интегральных уравнений соответствующих плоских и пространственных контактных задач с трением для одного штампа. Порядок дополнительных интегрируемых особенностей ядра на линиях, где возможна перколяция, такой же, как у известной особенности ${{R}^{{ - 1}}}$. Трение перпендикулярно оси цепочки незначительно влияет на интегральную характеристику контактных давлений, вызывает изменение геометрии области контакта.

Работа выполнена при поддержке Российского научного фонда (код проекта 22-21-00013).

Список литературы

Xu Y., Jackson R.L. Periodic contact problems in plane elasticity: the fracture mechanics approach // ASME J. Trib. 2018. V. 140. № 1. P. 011404.
Пожарский Д.А. Периодические контактные и смешанные задачи теории упругости (обзор) // Изв. вузов. Сев.-Кавк. рег. Естеств. науки. 2021. № 2. С. 22–33.
Горячева И.Г. Периодическая контактная задача для упругого полупространства // ПММ. 1998. Т. 62. Вып. 6. С. 1036–1044.
Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука, 2001. 478 с.
Александров В.М. Двоякопериодические контактные задачи для упругого слоя // ПММ. 2002. Т. 66. Вып. 2. С. 307–315.
Jin F., Wan Q., Guo X. A double-Westergaard model for adhesive contact of a wavy surface // Int. J. Solids Struct. 2016. V. 102–103. P. 66–76.
Yastrebov V.A., Anciaux G., Molinari J.-F. The contact of elastic regular wavy surfaces revisited // Tribol. Lett. 2014. V. 56. P. 171–183.
Goryacheva I.G., Torskaya E.V. Modeling of fatigue wear of a two-layered elastic half-space in contact with periodic system of indenters // Wear. 2010. V. 268. № 11–12. P. 1417–1422.
Солдатенков И.А. Периодическая контактная задача теории упругости. Учет трения, износа и сцепления // ПММ. 2013. Т. 77. Вып. 2. С. 337–351.
Goryacheva I.G., Makhovskaya Y. Combined effect of surface microgeometry and adhesion in normal and sliding contacts of elastic bodies // Friction. 2017. V. 5. № 3. P. 339–350.
Goryacheva I., Yakovenko A. The periodic contact problem for spherical indenters and viscoelastic half-space // Tribol. Int. 2021. V. 161. P. 107078.
Пожарский Д.А. Периодическая контактная задача для упругого клина // ПММ. 2015. Т. 79. Вып. 6. С. 864–872.
Галанов Б.А. Метод граничных уравнений типа Гаммерштейна для контактных задач теории упругости в случае неизвестных областей контакта // ПММ. 1985. Т. 49. Вып. 5. С. 827–835.
Пожарский Д.А. Фундаментальные решения статики упругого клина и их приложения. Ростов-на-Дону: ООО “ДГТУ-Принт”, 2019. 312 с.
Гельфанд И.М., Г.Е. Шилов. Обобщенные функции и действия над ними. М.: Физматгиз, 1959. 486 с.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Элементарные функции. М.: Наука, 1981. 798 с.
Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. Специальные функции. М.: Наука, 1983. 752 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал