Прикладная математика и механика, 2022, T. 86, № 3, стр. 349-364

О кривизне граничных линий тока течений идеального газа в точках схода и присоединения

А. Н. Крайко^1, *, Н. И. Тилляева^1, **

¹ ФАУ ЦИАМ им. П.И. Баранова
Москва, Россия

^* E-mail: akraiko@ciam.ru
^** E-mail: ntill@ciam.ru

Поступила в редакцию 10.02.2022
После доработки 15.04.2022
Принята к публикации 15.04.2022

EDN: CVHHOK
DOI: 10.31857/S0032823522030146

Аннотация

Рассмотрены стационарные течения идеального (невязкого и нетеплопроводного) газа с линиями тока − границами текущей и неподвижной сред. В XIX в. такие границы появились в задачах истечения струй в затопленное пространство. При основном вкладе в их решение Н.Е. Жуковского до 1903 г. рассматривались только струи несжимаемой жидкости. В 1903 г. С.А. Чаплыгин начал изучение плоских дозвуковых струй идеального газа. В 1949 г. Л.В. Овсянников, решив задачу об истечении “критической” струи, обнаружил удивительные свойства течения со звуковой граничной линией тока. Вскоре отрезки таких линий тока, возникших в основном в задачах теории струйных течений, появились при построении тел, обтекаемых дозвуковыми потоками с наибольшими “критическими” числами Маха M*. При набегающем потоке с ${{\operatorname{M} }_{0}} < \operatorname{M} *$ всюду M < 1, нет ударных волн и волнового сопротивления. При ${{\operatorname{M} }_{0}} > \operatorname{M} *$ появляются сверхзвуковые зоны, возникают ударные волны и растущее с ростом ${{\operatorname{M} }_{0}}$ волновое сопротивление. Оказалось, что M* реализуют тела, при обтекании которых с ${{\operatorname{M} }_{0}} = \operatorname{M} *$ часть контуров − отрезки звуковых линий тока. Полезно знать их кривизну в точках схода и присоединения. У Н.Е. Жуковского для жидкости в точках схода она бесконечна. Бесконечность кривизны таких линий тока в идеальном газе установлена только через 100 лет. Ниже показано, как ведут себя параметры потока и их производные, включая кривизну линий тока, при приближении по разным направлениям к точкам схода и присоединения. Кривизна граничных линий тока в этих точках бесконечна, притом что кривизна звуковых линий тока при их пересечении с прямой звуковой линией перехода равна нулю.

Ключевые слова: стационарные течения идеального газа, переменные годографа, кривизна дозвуковых и звуковых граничных линий тока в точках схода и присоединения

1. Введение. Названные в аннотации гидро-аэро-газодинамики далеко не все выдающиеся ученые, которых заинтересовали стационарные течения идеальных жидкости или газа с изобарическими линиями тока − границами текущей и неподвижной сред. Еще нескольких назвал сам Н.Е. Жуковский [1]: “Начало решения таких задач было положено в 1868 г. Гельмгольцем. … В том же году Кирхгоф предложил общий прием решения подобных задач. … Более детальная разработка была сделана Релеем в 1876 г., напечатавшим две заметки.” Отметив затем вклад Герлаха (Gerlach, 1885 г.), Д.К. Бобылева (1881 г.), И.В. Мещерского (1886 г.), А.П. Котельникова (1889 г.) и Фохта (Voigt, 1886 г.), Н.Е. Жуковский пишет: “Критическую оценку метода Кирхгофа мы имеем в сочинении Бриллуэна”. И далее: “Во всех упомянутых работах авторы придерживались метода Кирхгофа и попытка видоизменить этот метод была сделана только Планком (в 1884 г.), который задался мыслью об освобождении метода от теории мнимого переменного с целью его распространения на пространство трех измерений. … Но, не говоря уже о задачах трех измерений, Планк не разрешил с помощью своего метода ни одной новой задачи. … главным недостатком метода Планка является то обстоятельство, что в нем, как и в первоначальном методе Кирхгофа, мы не можем направиться на решение определенной задачи. Конформное преобразование, введенное Кирхгофом, устраняет это затруднение, но зато вводит в задачу лишнюю, иногда очень трудную операцию. Ввиду того, что число известных конформных преобразований замкнутой области в область, ограниченную двумя параллельными прямыми, невелико, невелико и число задач, решаемых методом Кирхгофа … В предлагаемом (Н.Е. Жуковским – авт.) изменении метода Кирхгофа дана возможность обратиться к решению определенной задачи, не прибегая наперед к конформному преобразованию …” В результате “видоизмененным методом Кирхгофа”, а на самом деле, оригинальным “методом Жуковского” его автор решил много новых задач, которые не поддавались методу Кирхгофа. Предложенный метод и эти задачи – предмет двух статей Н.Е. Жуковского ([1] – 1890 г. и [2] – 1891 г.). Их общий объем − полторы сотни страниц.

Перечисленные выше авторы ограничивались несжимаемой жидкостью, точнее, − истечением жидкости из плоских каналов со стенками, составленными отрезками прямых. Если начало декартовых координат $xy$ совместить с одной из выходных кромок, то при подходе к ней по такому отрезку угол наклона $\theta $ вектора скорости потока ${\mathbf{V}}$ к оси $x$ не изменяется, скорость $V$ растет, а давление $p$ падает так, что производные от $V$ и $p$ вдоль контура на кромке обращаются в $ \pm \infty $. После выхода из канала при движении по граничной линии тока, наоборот, $V$ и $p$ постоянны, а угол $\theta $ меняется так, что кривизна границы при $x \to + 0$ обращается в бесконечность (для симметричных струй, текущих слева направо, в $ + \infty $ на верхней границе и в $ - \infty $ на нижней).

С середины ХХ в. течения с изобарической граничной линией тока стали интересны в связи с изучением отрыва вязкого пограничного слоя с искривленных стенок. Если начало декартовых координат $xy$ совместить с точкой отрыва, а ось $x$ направить по касательной к стенке при $x \to - 0$, то в приближении несжимаемой жидкости с исчезающей вязкостью [3–5] кривизна границы получается такой же, как выше.

Особый интерес к звуковой граничной линии тока, обязан неожиданному решению, найденному Л.В. Овсянниковым [6, 7]. Согласно этому решению выравнивание “критической” струи идеального газа происходит не асимптотически, как для несжимаемой жидкости, а в “прямой линии перехода” на конечном расстоянии от сечения выхода из канала. При натекании звуковой струи идеального газа на клиновидные препятствия [8, 9] прямых линий перехода три. Одна ограничивает натекающую звуковую струю, две (по одной с разных сторон от препятствия) – утекающие наклоненные звуковые потоки.

Известно, что в плоскопараллельных и осесимметричных течениях кривизна криволинейной звуковой линии тока в точке пересечения с прямой линией перехода равна нулю [10–12]. В общем случае анализ течений с дозвуковыми и звуковыми граничными линиями тока существенно упростил подход, развитый в [13] (см. также [14]). Этот же подход будет применен ниже.

Еще более интересны звуковые граничные линии тока стали после того, как было установлено [15], что отрезки таких линий образуют симметричные профили, тела вращения, головные и кормовые части полубесконечных пластины и кругового цилиндра, которые при ряде дополнительных ограничений обтекаются безграничным дозвуковым набегающим потоком под нулевым углом атаки с наибольшими критическими числами Маха M*. Типичными ограничениями здесь служат задание хорды профиля, длины тела или его головной (кормовой) частей, принимаемых за линейный масштаб, полутолщины пластины, радиуса кругового цилиндра, минимально допустимых “продольной” площади профиля или объема тела вращения и т.п. Простейшие примеры таких конфигураций − не возмущающие поток пластина под нулевым углом атаки и отрезок прямой (“осесимметричная игла”) в равномерном звуковом потоке с $\operatorname{M} \equiv {{\operatorname{M} }_{0}} \equiv \operatorname{M} *$ = 1. Отнесенная к квадрату заданной длины площадь их “продольных” сечений $S = 0$. Если в дополнение к фиксированной хорде или длине задать минимально допустимую величину $S > 0$, то согласно [15] контуры критических тел составят передний и задний торцы и соединяющие их без изломов верхняя и симметричная нижняя звуковые линии тока. При $S \to 0$ высота торцов стремится к нулю, ${{\operatorname{M} }_{0}}$ и M* стремятся к единице и получаются пластина и игла. Чтобы при $S > 0$ избавиться от неизбежных отрывов за телами, построенными в предположении безотрывного обтекания, вводится ограничение на углы наклона контуров их кормовых частей. В результате задний торец заменит пара прямолинейных отрезков, и плоская критическая конфигурация станет симметричным крыловым профилем.

В приведенных выше примерах критических конфигураций и в их обобщениях [16], у каждой звуковой линии тока наряду с точкой гладкого схода есть точка гладкого присоединения. Возможны критические конфигурации с точками схода или присоединения на прямых линиях перехода. При принципиальной простоте структуры плоских и осесимметричных критических конфигураций методы их построения [17–24] оказались достаточно сложными. Поэтому любая дополнительная информация, например, о кривизне граничных линий тока, будет полезна при построении критических конфигураций. Авторы [21–24], не останавливаясь на деталях далеко непростого анализа, констатируют, что найденная ими для идеального газа кривизна граничной линии тока в точке схода с прямолинейной стенки бесконечна. Ниже развитый в [13] подход привел к формулам, которые, подтверждая этот вывод, показывают, как в разных случаях кривизна линии тока растет при приближении к точкам схода и присоединения.

2. Плоскопараллельные потенциальные течения идеального газа в переменных годографа. Граничная линия тока вблизи прямой линии перехода. Плоскопараллельные изэнтропические и изоэнергетические стационарные течения идеального газа, будучи потенциальными, допускают переход к независимым переменным $V - \theta $. С точностью до произвольных аддитивной постоянной и положительного множителя k равенством

$d\psi = k\rho V(\cos \theta dy - \sin \theta dx)$

с плотностью газа $\rho = \rho \left( V \right)$ введем функцию тока $\psi $. Функция тока удовлетворяет уравнению Чаплыгина [14]

(2.1)

${{V}^{2}}{{\psi }_{{VV}}} + (1 + {{M}^{2}})V{{\psi }_{V}} + (1 - {{M}^{2}}){{\psi }_{{\theta \theta }}} = 0,$

в котором число Маха ${\text{M}} = {\text{M}}\left( V \right)$. Так для совершенного газа с постоянными теплоемкостями и их отношением (показателем адиабаты) $\gamma $

(2.2)

$M = \frac{{V\sqrt {1 - \varepsilon } }}{{\sqrt {1 - \varepsilon {{V}^{2}}} }} \Leftrightarrow 1 - {{M}^{2}} = \frac{{1 - {{V}^{2}}}}{{1 - \varepsilon {{V}^{2}}}},\quad \varepsilon = \frac{{\gamma - 1}}{{\gamma + 1}}$

В приведенных уравнениях и далее за масштабы скорости и плотности взяты их критические величины. После того как функция тока $\psi = \psi \left( {V,\theta } \right)$ найдена, координаты $x$ и $y$ определят дифференциальные равенства

(2.3)

$\begin{gathered} dx = - \frac{{V{{\psi }_{V}}\sin \theta + (1 - {{M}^{2}}){{\psi }_{\theta }}\cos \theta }}{{k\rho {{V}^{2}}}}dV + \frac{{V{{\psi }_{V}}\cos \theta - {{\psi }_{\theta }}\sin \theta }}{{k\rho V}}d\theta \\ dy = \frac{{V{{\psi }_{V}}\cos \theta - (1 - {{M}^{2}}){{\psi }_{\theta }}\sin \theta }}{{k\rho {{V}^{2}}}}dV + \frac{{V{{\psi }_{V}}\sin \theta + {{\psi }_{\theta }}\cos \theta }}{{k\rho V}}d\theta \\ \end{gathered} $

Эти равенства можно интегрировать по любой кривой плоскости $V - \theta $, в частности, по отвечающим изобарическим линиям тока вертикалям $V = \operatorname{const} $ или по горизонталям $\theta = \operatorname{const} $, отвечающим прямым отрезкам контуров обтекаемых стенок. Интегрирование по вертикалям определит зависимость координат $x$ и $y$ от угла наклона граничной линии тока, а затем ее кривизну. Покажем, как это делается, сначала для звуковой граничной линии тока вблизи точки ее пересечения с прямой линией перехода. Начать анализ со столь особой ситуации целесообразно по той причине, что в этом случае развитый в [13] и описанный в [14] подход применяется без изменений.

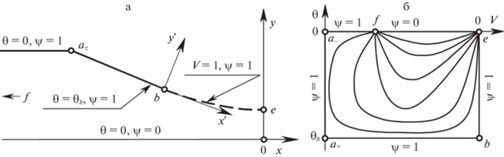
Верхняя половина струйного течения с точкой e пересечения граничной звуковой линии тока $b - e$ с прямой линией перехода $0 - e$ изображена в декартовых координатах на рис. 1а, а в переменных годографа на рис. 1б. На криволинейной линии тока $b - e$ и на прямом отрезке $0 - e$ линии перехода скорость потока $V = {{V}_{e}} = 1$. Вблизи точки $e$, где скорость $V$ и число Маха близки к единице, уравнение Чаплыгина (2.1) и равенства (2.3) примут вид

(2.4)

${{\psi }_{{VV}}} + 2{{\psi }_{V}} + {{\sigma }^{2}}\eta {{\psi }_{{\theta \theta }}} = 0,\quad \eta = 1 - V,\quad {{\sigma }^{2}} = {{\left. {d(1 - {{M}^{2}}){\text{/}}d\eta } \right|}_{{V = 1}}}$

(2.5)

$\begin{gathered} dx = - \frac{{{{\psi }_{V}}\sin \theta + {{\sigma }^{2}}\eta {{\psi }_{\theta }}\cos \theta }}{k}dV + \frac{{{{\psi }_{V}}\cos \theta - {{\psi }_{\theta }}\sin \theta }}{k}d\theta \\ dy = \frac{{{{\psi }_{V}}\cos \theta - {{\sigma }^{2}}\eta {{\psi }_{\theta }}\sin \theta }}{k}dV + \frac{{{{\psi }_{V}}\sin \theta + {{\psi }_{\theta }}\cos \theta }}{k}d\theta \\ \end{gathered} $

Рис. 1.

Струйное течение со звуковой граничной линией тока b–e и прямой линией перехода 0–e (а − в декартовых координатах, б − в переменных годографа).

Учтено, что $\rho \left( 1 \right) = 1$ в силу выбора масштаба плотности. Согласно формулам (2.2) для совершенного газа ${{\sigma }^{2}} = \gamma + 1$.

В точку $e$ плоскости $V - \theta $ приходят все линии тока, из-за чего ψ изменяется на конечную величину. Положив $\psi = 0$ на плоскости симметрии канала и струи (на оси х) и распорядившись произволом в выборе множителя $k$, сделаем $\psi = 1$ на стенке канала и на границе струи. Следовательно, вблизи точки е плоскости $V - \theta $ функцию тока следует искать в виде

(2.6)

$\psi = \chi (\omega ) + ...;\quad \omega = \frac{{ - \theta }}{{{{\eta }^{n}}}},\quad 0 \leqslant \chi (\omega ) \leqslant 1,\quad 0 \leqslant \omega \leqslant \infty ,\quad \chi (0) = 0,\quad \chi (\infty ) = 1$

с неизвестным показателем степени $n > 0$. Обозначив штрихом производные по $\omega $, получим

(2.7)

${{\psi }_{V}} = \frac{{n\omega }}{\eta }\chi {\kern 1pt} ',\quad {{\psi }_{{VV}}} = n\omega \frac{{n\omega \chi {\kern 1pt} '{\kern 1pt} '\; + (n + 1)\chi {\kern 1pt} '}}{{{{\eta }^{2}}}},\quad {{\psi }_{\theta }} = - \frac{{\chi {\kern 1pt} '}}{{{{\eta }^{n}}}},\quad {{\psi }_{{\theta \theta }}} = \frac{{\chi {\kern 1pt} ''}}{{{{\eta }^{{2n}}}}}$

Подстановка найденных производных в уравнение (2.4) при $\eta \ll 1$ дает уравнение

$n\omega \frac{{n\omega \chi {\kern 1pt} '{\kern 1pt} '\; + (n + 1)\chi {\kern 1pt} '}}{{{{\eta }^{2}}}} + {{\sigma }^{2}}\frac{{\chi {\kern 1pt} '{\kern 1pt} '}}{{{{\eta }^{{2n - 1}}}}} = 0,$

решения которого при $n \ne 3{\text{/}}2$ не позволяют удовлетворить условиям (2.6). При $n = 3{\text{/}}2$ придем к уравнению

$(9{{\omega }^{2}} + 4{{\sigma }^{2}})\chi {\kern 1pt} '{\kern 1pt} '\; + 15\omega \chi {\kern 1pt} ' = 0$

и к его решению

(2.8)

$\chi {\kern 1pt} '(\omega ) = \frac{C}{{{{{(9{{\omega }^{2}} + 4{{\sigma }^{2}})}}^{{5/6}}}}},\quad \chi (\omega ) = C\int\limits_0^\omega {\frac{{d\omega }}{{{{{(9{{\omega }^{2}} + 4{{\sigma }^{2}})}}^{{5/6}}}}}} ;\quad \frac{1}{C} = \int\limits_0^\infty {\frac{{d\omega }}{{{{{(9{{\omega }^{2}} + 4{{\sigma }^{2}})}}^{{5/6}}}}}} ,$

которое всем необходимым условиям (2.6) удовлетворяет.

Чтобы найти кривизну граничной линии тока вблизи точки $e$, положим в коэффициентах перед $d\theta $ равенств (2.5) $\sin \theta \approx \theta $, $\cos \theta \approx 1$, а ${{\psi }_{V}}$ и ${{\psi }_{\theta }}$ заменим выражениями из (2.7) с $\chi {\kern 1pt} '$ из (2.8). Это даст уравнения

$dx \approx \frac{{ - Cd( - \theta )}}{{{{3}^{{5/3}}}2k{{{( - \theta )}}^{{2/3}}}}},\quad dy \approx \frac{{C{{{( - \theta )}}^{{1/3}}}}}{{{{3}^{{2/3}}}2k}}d( - \theta ),$

выполняющиеся на вертикали $b - e$ вблизи точки $e$. Проинтегрировав их от точки $e$, в которой ${{\theta }_{e}} = {{\chi }_{e}} = 0$, придем к формулам

(2.9)

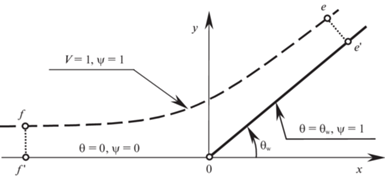
$ - \theta = 72\frac{{{{k}^{3}}}}{{{{C}^{3}}}}{{x}^{3}},\quad y - {{y}_{e}} \approx \frac{{{{3}^{{1/3}}}C{{{( - \theta )}}^{{4/3}}}}}{{8k}} \approx 54\frac{{{{k}^{3}}}}{{{{C}^{3}}}}{{x}^{4}},$

справедливым на линии тока $b - e$ вблизи точки $e$. Из них, помимо прочего, следует упомянутый выше известный полученный другими методами [10–12] результат о нулевой кривизне линии тока в точке пересечения с прямой линией перехода. В задаче о натекании звуковой струи на симметричное клиновидное препятствие с полууглом при вершине $0 < {{\theta }_{w}} < \pi $ [8, 9] таких точек четыре: $e$ и $f$ в изображенной на рис. 2 верхней половине течения и две в ее симметричной нижней половине.

Рис. 2.

Натекание звуковой струи идеального газа на клин: e–e' и f–f ' − прямые линии перехода, e–f − криволинейный участок звуковой граничной линии тока.

3. Течение в окрестности точки схода с обтекаемого контура дозвуковой граничной линии тока. Простой вариант плоской струи идеального газа, рассматриваемый в данном разделе, отличается от изображенного на рис. 1 тем, что на граничной линии тока $b - e$ скорость газа $V \equiv {{V}_{b}}$ и число Маха ${{\operatorname{M} }_{b}}$ меньше единицы. Следствия этого − выравнивание потока при $x \to \infty $, а в решении в форме (2.6) $n = 1$, т.е. $\omega = - \theta {\text{/}}\eta $, $\eta = {{V}_{b}} - V$ и ${{V}_{b}} < 1$. В рассматриваемой далее малой окрестности точки $b$ уравнение Чаплыгина (2.1) перепишем в форме

(3.1)

${{\psi }_{{VV}}} + {{\alpha }^{2}}{{\psi }_{V}} + {{\beta }^{2}}{{\psi }_{{\theta \theta }}} = 0;\quad {{\alpha }^{2}} = (1 + M_{b}^{2}){\text{/}}{{V}_{b}},\quad {{\beta }^{2}} = (1 - M_{b}^{2}){\text{/}}V_{b}^{2}$

Из двух появившихся в этом уравнении положительных констант в дальнейшем анализе участвует только вторая. В пределе малых дозвуковых скоростей она неограниченно растет, а при ${{\operatorname{M} }_{b}} = 1$ становится нулем.

В точке $b$ в отличие от точки $e$, исследованной выше, функция тока не рвется. Поэтому решение в ее окрестности будем искать в форме

(3.2)

$\begin{gathered} \psi = 1 + \varepsilon \chi (\omega ) + ...;\quad \omega = \frac{{\theta - {{\theta }_{b}}}}{{{{\eta }^{n}}}},\quad \eta = {{V}_{b}} - V;\quad 0 \leqslant \omega \leqslant \infty ,\quad {{\chi }_{0}} \equiv \chi (0) = 0 \\ {{\chi }_{\infty }} \equiv \chi (\infty ) = 0,\quad \varepsilon = {{[{{(\theta - {{\theta }_{b}})}^{2}} + {{\eta }^{{2n}}}]}^{m}} = {{({{\omega }^{2}} + 1)}^{m}}{{\eta }^{{2nm}}};\quad n > 0,\quad m > 0 \\ \end{gathered} $

Данные соотношения отличаются от (2.6), во-первых, одинаковыми (нулевыми) условиями для $\chi $ при $\omega = 0$ и $\omega = \infty $, а, во-вторых, двумя подлежащими определению показателями степени $n$ и $m$. Теперь вместо (2.7) получим

$\begin{gathered} {{\psi }_{V}} = n[({{\omega }^{2}} + 1)\omega \chi {\kern 1pt} '\; - 2m\chi ]{{({{\omega }^{2}} + 1)}^{{m - 1}}}{{\eta }^{{2mn - 1}}} \\ {{\psi }_{\theta }} = [({{\omega }^{2}} + 1)\chi {\kern 1pt} '\; + 2m\omega \chi ]{{({{\omega }^{2}} + 1)}^{{m - 1}}}{{\eta }^{{2mn - n}}} \\ \end{gathered} $

(3.3)

${{\psi }_{{VV}}} = n\{ \omega {{({{\omega }^{2}} + 1)}^{2}}[n\omega \chi {\kern 1pt} '{\kern 1pt} '\; + (n + 1)\chi {\kern 1pt} '] - 4mn({{\omega }^{2}} + 1)\omega \chi {\kern 1pt} '\; + $

$\begin{gathered} \, + 2m[2n({{\omega }^{2}} + m) - 1 - {{\omega }^{2}}]\chi \} {{({{\omega }^{2}} + 1)}^{{m - 2}}}{{\eta }^{{2mn - 2}}} \\ {{\psi }_{{\theta \theta }}} = \{ {{({{\omega }^{2}} + 1)}^{2}}\chi {\kern 1pt} '{\kern 1pt} '\; + 4m({{\omega }^{2}} + 1)\omega \chi {\kern 1pt} '\; + 2m[(2m - 1){{\omega }^{2}} + 1]\chi \} {{({{\omega }^{2}} + 1)}^{{m - 2}}}{{\eta }^{{2mn - 2n}}} \\ \end{gathered} $

Поскольку ${{\psi }_{V}} \ll {{\psi }_{{VV}}}$ при $\eta \ll 1$, то при подстановке этих производных в (3.1), опустив второе слагаемое, придем к уравнению

$\begin{gathered} \omega {{({{\omega }^{2}} + 1)}^{2}}[n\omega \chi {\kern 1pt} '{\kern 1pt} '\; + (n + 1)\chi {\kern 1pt} '] - 4mn({{\omega }^{2}} + 1)\omega \chi {\kern 1pt} '\; + 2m[2n({{\omega }^{2}} + m) - 1 - {{\omega }^{2}}]\chi + \\ + \;{{\beta }^{2}}\{ {{({{\omega }^{2}} + 1)}^{2}}\chi {\kern 1pt} '{\kern 1pt} '\; + 4m({{\omega }^{2}} + 1)\omega \chi {\kern 1pt} '\; + 2m[(2m - 1){{\omega }^{2}} + 1]\chi \} {{\eta }^{{2(1 - n)}}}{\text{/}}n = 0 \\ \end{gathered} $

Вблизи точки $b$ последнее слагаемое этого уравнения много меньше, равно или много больше прочих соответственно при $n < 1$, $n = 1$ или $n > 1$, а $\chi \left( \omega \right)$ и “собственные значения” $m$ определяет решение одной из трех краевых задач:

$n < 1{\kern 1pt} :\quad \chi {\kern 1pt} '{\kern 1pt} '\; + \frac{{(n + 1)({{\omega }^{2}} + 1) - 4mn}}{{n({{\omega }^{2}} + 1)\omega }}\chi {\kern 1pt} '\; + 2m\frac{{(2n - 1){{\omega }^{2}} - 1 + 2nm}}{{n{{{({{\omega }^{2}} + 1)}}^{2}}{{\omega }^{2}}}}\chi = 0$

$n = 1{\kern 1pt} :\quad \chi {\kern 1pt} '{\kern 1pt} '\; + 2\frac{{{{\omega }^{2}} + 1 + 2m({{\beta }^{2}} - 1)}}{{({{\omega }^{2}} + 1)({{\omega }^{2}} + {{\beta }^{2}})}}\omega \chi {\kern 1pt} '\; + 2m\frac{{{{\omega }^{2}} + {{\beta }^{2}} + (2m - 1)(1 + {{\beta }^{2}}{{\omega }^{2}})}}{{{{{({{\omega }^{2}} + 1)}}^{2}}({{\omega }^{2}} + {{\beta }^{2}})}}\chi = 0$

$n > 1{\kern 1pt} :\quad \chi {\kern 1pt} '{\kern 1pt} '\; + \frac{{4m\omega }}{{{{\omega }^{2}} + 1}}\chi {\kern 1pt} '\; + 2m\frac{{(2m - 1){{\omega }^{2}} + 1}}{{{{{({{\omega }^{2}} + 1)}}^{2}}}}\chi = 0$

с одинаковыми граничными условиями ${{\chi }_{0}} = 0$ и ${{\chi }_{\infty }} = 0$ в каждой из них.

При ${{\chi }_{0}} = 0$ и произвольных $n$ и $m$ решения приведенных линейных однородных уравнений, пропорциональные $\chi _{0}^{'}$, условию ${{\chi }_{\infty }} = 0$, естественно, не удовлетворяют. Как его выполнение определяет m, сначала покажем для $n = 1$, для которого с учетом условия ${{\chi }_{0}} = 0$ найдем

$\omega \ll 1{\kern 1pt} :\quad \chi {\kern 1pt} '{\kern 1pt} '\; + {{\lambda }^{2}}\chi = 0,\quad \chi = A\sin (\lambda \omega ) \approx \chi _{0}^{'}\omega ,\quad {{\lambda }^{2}} = 2m\frac{{{{\beta }^{2}} + 2m - 1}}{{{{\beta }^{2}}}},\quad \chi _{0}^{'} = A\lambda $

$\omega \gg 1{\kern 1pt} :\quad \chi {\kern 1pt} '{\kern 1pt} '\; + 2\frac{{\chi {\kern 1pt} '}}{\omega } = 0,\quad \chi {\kern 1pt} '\; = \frac{B}{{{{\omega }^{2}}}} \to \chi = {{\chi }_{\infty }} - \frac{B}{\omega }$

Здесь константа $\chi _{0}^{'}$ задается произвольно, а $B$, пропорциональное $\chi _{0}^{'}$, и ${{\chi }_{\infty }}$ находятся при численном решении полного уравнения (или системы двух уравнений для $\chi $ и $\chi {\kern 1pt} '$) до столь больших $\omega $, при которых значения $B = {{\omega }^{2}}\chi {\kern 1pt} '$ и ${{\chi }_{\infty }} = \chi + \omega \chi {\kern 1pt} '$ уже не изменяются.

Зафиксировав $n = 1$, $\chi _{0}^{'}$ и ${{\beta }^{2}}$ и проводя описанные выше расчеты при разных $m > 0$, построим кривую ${{\chi }_{\infty }} = {{\chi }_{\infty }}\left( m \right)$ с точкой, в которой ${{\chi }_{\infty }}\left( m \right)$ пересекает ось $m$. Она и дает решение. Если таких положительных значений $m$ не одно, то берется минимальное, дающее согласно представлению (3.2) наибольшую величину в разложениях по степеням малого “расстояния” до точки $b$ в переменных годографа. Расчеты, проведенные для $n = 1$, дали минимальное $m = 1$, не зависящее не только от величины $\chi _{0}^{'}$, как и должно быть, но и от значений ${{\beta }^{2}}$, что оказалось неожиданным. Выполненный в связи с этим анализ, не только подтвердил такую обнаруженную численно особенность, но и привел к полному аналитическому решению задачи. Чтобы понять, как получается решение, не зависящее от ${{\beta }^{2}}$, уравнение, отвечающее $m = n = 1$, перепишем, оставив ${{\beta }^{2}}$ только в знаменателе одного слагаемого

(3.4)

$\chi {\kern 1pt} '{\kern 1pt} '\; + 2\frac{{2\omega \chi {\kern 1pt} '\; + \chi }}{{{{\omega }^{2}} + 1}} - \frac{{2F}}{{{{\omega }^{2}} + {{\beta }^{2}}}} = 0,\quad F = \omega \chi {\kern 1pt} '\; + \frac{{{{\omega }^{2}} - 1}}{{{{\omega }^{2}} + 1}}\chi $

Функция $F = F(\omega ,\chi ,\chi {\kern 1pt} ')$ такова, что $F(0,0,\chi _{0}^{'}) = 0$. Найдя производную

$F{\kern 1pt} ' = \omega \left[ {\chi {\kern 1pt} '{\kern 1pt} '\; + \frac{{2\omega \chi {\kern 1pt} '}}{{{{\omega }^{2}} + 1}} + \frac{{4\chi }}{{{{{({{\omega }^{2}} + 1)}}^{2}}}}} \right],$

выразим отсюда $\chi {\kern 1pt} '{\kern 1pt} '$ и, подставив в уравнение (3.4), придем к уравнению для $F$ и к решению

$\frac{{F{\kern 1pt} '}}{\omega } - \frac{{2F}}{{{{\omega }^{2}} + {{\beta }^{2}}}} = 0 \to F = C({{\omega }^{2}} + {{\beta }^{2}})$

Поскольку $F(0,0,\chi _{0}^{'}) = 0$, то константа $C = 0$, $F = 0$, и справедливы уравнение

$F(\omega ,\chi ,\chi {\kern 1pt} ') \equiv ({{\omega }^{2}} + 1)\omega \chi {\kern 1pt} '\; + ({{\omega }^{2}} - 1)\chi = 0$

и его также не содержащее ${{\beta }^{2}}$ решение

(3.5)

$n = 1,\quad m = 1,\quad \chi = \frac{{\chi _{0}^{'}\omega }}{{{{\omega }^{2}} + 1}},\quad \chi {\kern 1pt} ' = \frac{{\chi _{0}^{'}(1 - {{\omega }^{2}})}}{{{{{({{\omega }^{2}} + 1)}}^{2}}}}$

Согласно выполненным расчетам ${{\chi }_{\infty }} = 0$ для $n = 1$ при любых положительных целых $m$, однако при $m \geqslant 2$ решение, например, убывающая с ростом $m$ константа $B$ от величины ${{\beta }^{2}}$ зависит.

Подстановка $\chi $ и $\chi {\kern 1pt} '$ из (3.5) в формулы (3.2) и (3.3) дает выражения

(3.6)

$\psi = 1 + \chi _{0}^{'}(\theta - {{\theta }_{b}})({{V}_{b}} - V) + ...,\quad {{\psi }_{V}} = - \chi _{0}^{'}(\theta - {{\theta }_{b}}),\quad {{\psi }_{\theta }} = \chi _{0}^{'}({{V}_{b}} - V)$

В этом и в последующих решениях $\psi $ − линейная функция $V$ и $\theta $, и уравнение Чаплыгина без ${{\psi }_{V}}$ выполняется в силу того, что ${{\psi }_{{VV}}}$ и ${{\psi }_{{\theta \theta }}}$ равны нулю по отдельности. При подстановке решения (3.5) в формулы (3.3) ${{\psi }_{{VV}}}$ и ${{\psi }_{{\theta \theta }}}$ также становятся нулями.

Чтобы найти кривизну граничной линии тока вблизи точки $b$, положим в равенствах (2.3) $dV = 0$ и, подставив ${{\psi }_{V}}$ и ${{\psi }_{\theta }}$ из (3.6), получим уравнения

$dx = - \chi _{0}^{'}\frac{{(\theta - {{\theta }_{b}})\cos {{\theta }_{b}}}}{{k{{\rho }_{b}}}}d\theta ,\quad dy = - \chi _{0}^{'}\frac{{(\theta - {{\theta }_{b}})\sin {{\theta }_{b}}}}{{k{{\rho }_{b}}}}d\theta $

Проинтегрировав их, придем к параметрическому представлению координат граничной линии тока с углом $\theta $ в качестве параметра

(3.7)

$x - {{x}_{b}} = - \chi _{0}^{'}\frac{{{{{(\theta - {{\theta }_{b}})}}^{2}}}}{{2k{{\rho }_{b}}}}\cos {{\theta }_{b}},\quad y - {{y}_{b}} = - \chi _{0}^{'}\frac{{{{{(\theta - {{\theta }_{b}})}}^{2}}}}{{2k{{\rho }_{b}}}}\sin {{\theta }_{b}}$

Следствие этих формул − верные вблизи точки $b$ зависимости $\theta $ и кривизны дозвуковой граничной линии тока $K$ от расстояния $\tau \geqslant 0$ до этой точки

(3.8)

$\theta = {{\theta }_{b}} + \frac{{{{{(2k{{\rho }_{b}}\tau )}}^{{1/2}}}}}{{{{{( - \chi _{0}^{'})}}^{{1/2}}}}},\quad K = \frac{{\partial \theta }}{{\partial \tau }} = \frac{{{{{(k{{\rho }_{b}})}}^{{1/2}}}}}{{{{{( - 2\chi _{0}^{'}\tau )}}^{{1/2}}}}},\quad \tau = \sqrt {{{{(x - {{x}_{b}})}}^{2}} + {{{(y - {{y}_{b}})}}^{2}}} $

Показано [21], что в идеальном газе кривизна дозвуковой граничной линии тока при приближении к точке схода стремится к бесконечности. Те же авторы при построении звуковых граничных линий тока [22], сходящих с круговых дисков (${{\theta }_{b}} = \pi {\text{/}}2$), пишут: “Более детальный анализ позволяет установить, что … в окрестности точки $b$: $y - {{y}_{b}} = O\left( {{{{\left( {\pi - \pi {\text{/}}2} \right)}}^{2}}} \right)$”. Это − все.

Аналогично, положив в равенствах (2.3) $d\theta = 0$, для $V$ и $\partial p{\text{/}}\partial \tau $ при подходе к точке $b$ по обтекаемой стенке получим формулы

(3.9)

$V = {{V}_{b}} - \frac{{{{V}_{b}}{{{(2k{{\rho }_{b}}\tau )}}^{{1/2}}}}}{{{{{[\chi _{0}^{'}(M_{b}^{2} - 1)]}}^{{1/2}}}}},\quad \frac{{\partial p}}{{\partial \tau }} = - \rho V\frac{{\partial V}}{{\partial \tau }} = \frac{{{{\rho }_{b}}V_{b}^{2}{{{(k{{\rho }_{b}})}}^{{1/2}}}}}{{{{{[2\chi _{0}^{'}(M_{b}^{2} - 1)\tau ]}}^{{1/2}}}}}$

Найдем $V$ и $\theta $ как функции $\nu = - y{\kern 1pt} '$ в координатах $x{\kern 1pt} '{\kern 1pt} y{\kern 1pt} '$ (рис. 1а), т.е. их изменение по нормали к $b - e$ в точке $b$. Для направленных по $x{\kern 1pt} '{\kern 1pt} $ и $ - y{\kern 1pt} '$ касательного ${\mathbf{t}}$ $\left( {\cos \theta ,\sin \theta } \right)$ и нормального ${\mathbf{n}}$ $\left( {\sin \theta , - \cos \theta } \right)$ ортов в этой точке: $\nu = \left( {x - {{x}_{b}}} \right)\sin {{\theta }_{b}}$ – $\left( {y - {{y}_{b}}} \right)\cos {{\theta }_{b}}$ и $dy$ = $ - \operatorname{ctg} {{\theta }_{b}}dx$ на ${\mathbf{n}}$. Подстановка в последнее равенство $dx$ и $dy$ из (2.3) с ${{\psi }_{V}}$ и ${{\psi }_{\theta }}$ из (3.6) дает дифференциальное уравнение, проинтегрировав которое придем к решению и его следствиям для малых $\theta - {{\theta }_{b}}$ и ${{V}_{b}} - V$:

(3.10)

$\begin{gathered} \theta - {{\theta }_{b}} = \frac{{{{{(1 - M_{b}^{2})}}^{{1/2}}}}}{{{{V}_{b}}}}({{V}_{b}} - V),\quad {{V}_{b}} - V = \frac{{{{V}_{b}}{{{(k{{\rho }_{b}}\nu )}}^{{1/2}}}}}{{{{{( - \chi _{0}^{'})}}^{{1/2}}}{{{(1 - M_{b}^{2})}}^{{1/4}}}}} \\ \theta - {{\theta }_{b}} = \frac{{{{{(1 - M_{b}^{2})}}^{{1/4}}}{{{(k{{\rho }_{b}}\nu )}}^{{1/2}}}}}{{{{{( - \chi _{0}^{'})}}^{{1/2}}}}},\quad \nu = (x - {{x}_{b}})\sin {{\theta }_{b}} - (y - {{y}_{b}})\cos {{\theta }_{b}} \ll 1 \\ \end{gathered} $

Вторая и третья формулы − результат интегрирования уравнений (2.3) с ${{\psi }_{V}}$ и ${{\psi }_{\theta }}$ из (3.6) и с $\theta - {{\theta }_{b}}$ из первой формулы.

Численному решению краевых задач, отвечающих значениям показателя степени $n < 1$, предпошлем рассмотрение малых и больших $\omega $, для которых

$\omega \ll 1 \to \chi = \frac{A}{l}{{\omega }^{l}},\quad \chi {\kern 1pt} '\; = A{{\omega }^{{l - 1}}},\quad l = \frac{{2m(1 - 2nm)}}{{n + 1 - 4mn}} > 0$

$\omega \gg 1 \to \chi {\kern 1pt} ' = \frac{{ - B}}{{{{\omega }^{{1 + 1/n}}}}} \to B = - {{\omega }^{{1 + 1/n}}}\chi {\kern 1pt} ',\quad \chi = {{\chi }_{\infty }} + \frac{{nB}}{{{{\omega }^{{1/n}}}}} \to {{\chi }_{\infty }} = \chi + n\omega \chi {\kern 1pt} '$

Численное решение этого уравнения при разных $0 < n < 1$ неизменно приводило к ${{\chi }_{\infty }} \approx 0$ при $m \approx \left( {n + 1} \right){\text{/}}2n$. Подстановка $m = \left( {n + 1} \right){\text{/}}2n$ в формулу для $l$ дает $l = 1$, $A = \chi _{0}^{'}$ и уравнение

$\chi {\kern 1pt} '{\kern 1pt} '\; + \frac{{(1 + n)({{\omega }^{2}} - 1)}}{{n({{\omega }^{2}} + 1)\omega }}\chi {\kern 1pt} '\; + (1 + n)\frac{{(2n - 1){{\omega }^{2}} + n}}{{{{n}^{2}}{{{({{\omega }^{2}} + 1)}}^{2}}{{\omega }^{2}}}}\chi = 0$

Записав его в форме $f\chi {\kern 1pt} '{\kern 1pt} '\; + g\chi {\kern 1pt} '\; + h\chi = 0$ с рациональными коэффициентами:

$f = {{n}^{2}}{{({{\omega }^{2}} + 1)}^{2}}{{\omega }^{2}},\quad g = n(1 + n)({{\omega }^{4}} - 1)\omega ,\quad h = (1 + n)[(2n - 1){{\omega }^{2}} + n],$

приведя к “нормальной форме” и решив согласно [25], получим

$\chi = u(\omega )\exp \left( {\frac{1}{2}\int {\frac{g}{f}d\omega } } \right) = u(\omega ){{\left( {\frac{\omega }{{{{\omega }^{2}} + 1}}} \right)}^{{(1 + n)/(2n)}}},\quad u{\kern 1pt} '{\kern 1pt} ' = - Iu,$

$I = \frac{h}{f} - \frac{1}{4}{{\left( {\frac{g}{f}} \right)}^{2}} - \frac{1}{2}{{\left( {\frac{g}{f}} \right)}^{'}} = \frac{c}{{{{\omega }^{2}}}},\quad c = \frac{{1 - {{n}^{2}}}}{{4{{n}^{2}}}},\quad s = \frac{{\sqrt {4c + 1} }}{2} = \frac{1}{{2n}}$

$u = {{C}_{1}}{{\omega }^{{1/2 + s}}} + {{C}_{2}}{{\omega }^{{1/2 - s}}} = {{C}_{1}}{{\omega }^{{(1 + n)/(2n)}}} + {{C}_{2}}{{\omega }^{{(n - 1)/(2n)}}}$

Затем, учтя условия ${{\chi }_{0}} = {{\chi }_{\infty }} = 0$, найдем

(3.11)

$n < 1,\quad m = \frac{{1 + n}}{{2n}},\quad \chi = \frac{{\chi _{0}^{'}\omega }}{{{{{({{\omega }^{2}} + 1)}}^{m}}}},\quad \chi {\kern 1pt} ' = \frac{{\chi _{0}^{'}(n - {{\omega }^{2}})}}{{n{{{({{\omega }^{2}} + 1)}}^{{m + 1}}}}}$

Подстановка этих $m$, $\chi $ и $\chi {\kern 1pt} '$ в (3.2) и (3.3) для $\psi $, ${{\psi }_{V}}$ и ${{\psi }_{\theta }}$, а ${{\psi }_{V}}$ и ${{\psi }_{\theta }}$ − в уравнения (2.3) дает те же выражения (3.6)–(3.9), что получены для $n = 1$.

Равенство $l = 1$ приводит к квадратному уравнению для $m$. Его второму корню $m = 1{\text{/}}2$ отвечает краевая задача

$\begin{gathered} n < 1,\quad m = \frac{1}{2}{\kern 1pt} :\quad \chi {\kern 1pt} '{\kern 1pt} '\; + \frac{{(n + 1){{\omega }^{2}} + 1 - n}}{{n({{\omega }^{2}} + 1)\omega }}\chi {\kern 1pt} '\; + \frac{{(2n - 1){{\omega }^{2}} + n - 1}}{{n{{{({{\omega }^{2}} + 1)}}^{2}}{{\omega }^{2}}}}\chi = 0, \\ {{\chi }_{0}} = 0,\quad {{\chi }_{\infty }} = 0 \\ \end{gathered} $

Поступив с ней так же, как с задачей для первого корня, сначала найдем

$\begin{gathered} \chi = \frac{{u(\omega )}}{{{{\omega }^{{(1 - n)/(2n)}}}{{{({{\omega }^{2}} + 1)}}^{{1/2}}}}},\quad u{\kern 1pt} '{\kern 1pt} ' = \frac{c}{{{{\omega }^{2}}}}u,\quad c = \frac{{1 - {{n}^{2}}}}{{4{{n}^{2}}}},\quad s = \frac{{\sqrt {4c + 1} }}{2} = \frac{1}{{2n}} \\ u = {{C}_{1}}{{\omega }^{{1/2 + s}}} + {{C}_{2}}{{\omega }^{{1/2 - s}}} = {{C}_{1}}{{\omega }^{{(1 + n)/(2n)}}} + {{C}_{2}}{{\omega }^{{(n - 1)/(2n)}}}, \\ \end{gathered} $

но затем при тех же граничных условиях ${{\chi }_{0}} = {{\chi }_{\infty }} = 0$ − лишь тривиальное решение: $\chi \equiv 0$.

Краевая задача

решается приведением уравнения к “нормальной” форме [25] еще проще, чем в рассмотренных случаях. Найдя

$\chi = \frac{{u(\omega )}}{{{{{({{\omega }^{2}} + 1)}}^{m}}}},\quad I = 0,\quad u{\kern 1pt} '{\kern 1pt} ' = - Iu = 0,\quad u(\omega ) = {{C}_{1}} + {{C}_{2}}\omega ,$

в силу граничных условий ${{\chi }_{0}} = {{\chi }_{\infty }} = 0$ получим

$n > 1,\quad m > \frac{1}{2},\quad \chi = \frac{{\chi _{0}^{'}\omega }}{{{{{({{\omega }^{2}} + 1)}}^{m}}}},\quad \chi {\kern 1pt} ' = \chi _{0}^{'}\frac{{1 + (1 - 2m){{\omega }^{2}}}}{{{{{({{\omega }^{2}} + 1)}}^{{m + 1}}}}}$

Формулы (3.6)–(3.10) оказываются следствием этого решения не при любых $m > 1{\text{/}}2$, а только при $m = \left( {n + 1} \right){\text{/}}2n$. Поэтому решением при n > 1 будет

(3.12)

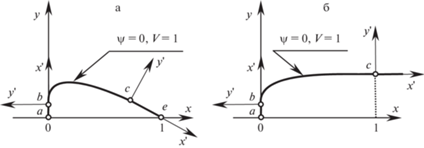
$n > 1,\quad m = \frac{{1 + n}}{{2n}} > \frac{1}{2},\quad \chi = \frac{{\chi _{0}^{'}\omega }}{{{{{({{\omega }^{2}} + 1)}}^{m}}}},\quad \chi {\kern 1pt} ' = \frac{{\chi _{0}^{'}(n - {{\omega }^{2}})}}{{n{{{({{\omega }^{2}} + 1)}}^{{m + 1}}}}}$

4. Течения в окрестностях точек схода и присоединения звуковых граничных линий тока. Данную тему начнем с течения вблизи точки схода звуковой линии тока на рис. 1. Иные примеры таких течений и течений с присоединением звуковой линии тока к обтекаемому контуру приведены на рис. 3, из которого можно получить представление о плоских и осесимметричных конфигурациях, обтекаемых дозвуковым потоком под нулевым углом атаки с наибольшими M*. Здесь это − симметричные профили и тела вращения (рис. 3а) и головные части полубесконечных пластины или кругового цилиндра (рис. 3б). Как уже отмечалось, при их построении кроме обычно задаваемой длины (для профиля − хорды) для тел рис. 3а фиксируется “продольная” площадь (в плоскости $xy$ декартовых или цилиндрических координат), а для головных частей − полувысота пластины или радиус цилиндра. У всех контуров рис. 3 есть отрезок $b{\kern 1pt} - {\kern 1pt} c$ звуковой линии тока с гладкими сходом и присоединением в точках $b$ и $c$ обтекаемой стенки. Вне отрезка $b{\kern 1pt} - {\kern 1pt} c$ почти всегда $\operatorname{M} < 1$. Исключения − внутренние течения с точкой $b$ или $c$ на нормальной оси $x$ прямой линии перехода [16]. При приближении к такой точке кривизна звуковой линии тока $K \to 0$ в силу решения (2.9).

Рис. 3.

Симметричный профиль или тело вращения (а) и головная часть пластины или кругового цилиндра (б), обтекаемые с наибольшими критическими числами Маха (b–c − отрезок звуковой линии тока).

Решение околозвукового уравнения Чаплыгина (2.4) вблизи точки $b$ рис. 1 ищется в форме (3.2) с ${{V}_{b}} = 1$, а для течений рис. 3 формулы для $\psi $ и $\omega $ заменены на $\psi = \varepsilon \chi \left( \omega \right) + ...$, $\omega = \left( {{{\theta }_{b}} - \theta } \right){\text{/}}{{\eta }^{n}}$. На уравнение

$\begin{gathered} \omega {{({{\omega }^{2}} + 1)}^{2}}[n\omega \chi {\kern 1pt} '{\kern 1pt} '\; + (n + 1)\chi {\kern 1pt} '] - 4mn({{\omega }^{2}} + 1)\omega \chi {\kern 1pt} '\; + 2m[2n({{\omega }^{2}} + m) - 1 - {{\omega }^{2}}]\chi + \\ + \;{{\sigma }^{2}}\{ {{({{\omega }^{2}} + 1)}^{2}}\chi {\kern 1pt} '{\kern 1pt} '\; + 4m({{\omega }^{2}} + 1)\omega \chi {\kern 1pt} '\; + 2m[(2m - 1){{\omega }^{2}} + 1]\chi \} {{\eta }^{{3 - 2n}}}{\text{/}}n = 0, \\ \end{gathered} $

определяющее $\chi $ при $\varepsilon \ll 1$, это, однако, не повлияло. При $\eta \ll 1$ его последнее слагаемое много меньше, равно или много больше остальных при $n < 3{\text{/}}2$, $n = 3{\text{/}}2$ или $n > 3{\text{/}}2$, а $\chi \left( \omega \right)$ и “собственные значения” $m$ определяет решение одной из трех краевых задач:

$n < \frac{3}{2}{\kern 1pt} :\quad \chi {\kern 1pt} '{\kern 1pt} '\; + \frac{{(n + 1)({{\omega }^{2}} + 1) - 4mn}}{{n({{\omega }^{2}} + 1)\omega }}\chi {\kern 1pt} '\; + 2m\frac{{(2n - 1){{\omega }^{2}} - 1 + 2nm}}{{n{{{({{\omega }^{2}} + 1)}}^{2}}{{\omega }^{2}}}}\chi = 0$

$\begin{gathered} n = \frac{3}{2}{\kern 1pt} :\quad \chi {\kern 1pt} '{\kern 1pt} '\; + \frac{{15({{\omega }^{2}} + 1) + 4m(4{{\sigma }^{2}} - 9)}}{{({{\omega }^{2}} + 1)(9{{\omega }^{2}} + 4{{\sigma }^{2}})}}\omega \chi {\kern 1pt} '\; + \\ + \;4m\frac{{[6 + (4m - 2){{\sigma }^{2}}]{{\omega }^{2}} + 9m - 3 + 2{{\sigma }^{2}}}}{{{{{({{\omega }^{2}} + 1)}}^{2}}(9{{\omega }^{2}} + 4{{\sigma }^{2}})}}\chi = 0 \\ \end{gathered} $

$n > \frac{3}{2}{\kern 1pt} :\quad \chi {\kern 1pt} '{\kern 1pt} '\; + \frac{{4m\omega }}{{{{\omega }^{2}} + 1}}\chi {\kern 1pt} '\; + 2m\frac{{(2m - 1){{\omega }^{2}} + 1}}{{{{{({{\omega }^{2}} + 1)}}^{2}}}}\chi = 0$

с одинаковыми граничными условиями ${{\chi }_{0}} = 0$ и ${{\chi }_{\infty }} = 0$.

Численное решение задачи, отвечающей $n = 3{\text{/}}2$, привело к результату, аналогичному, полученному для $n = 1$ в разд. 3. Минимальный показатель $m \approx 5{\text{/}}6$ теперь получался при любой величине ${{\sigma }^{2}}$. Понять, как такое возможно, помог опыт с уравнением (3.4). Перепишем уравнение, отвечающее $n = 3{\text{/}}2$ и $m = 5{\text{/}}6$, оставив ${{\sigma }^{2}}$ только в знаменателе одного из слагаемых

$\chi {\kern 1pt} '{\kern 1pt} '\; + \frac{{10\omega \chi {\kern 1pt} '}}{{3({{\omega }^{2}} + 1)}} + \frac{{5(2{{\omega }^{2}} + 3)\chi }}{{9{{{({{\omega }^{2}} + 1)}}^{2}}}} - \frac{F}{{9{{\omega }^{2}} + 4{{\sigma }^{2}}}} = 0,\quad F = 15\omega \chi {\kern 1pt} '\; + \frac{{5(2{{\omega }^{2}} - 3)}}{{{{\omega }^{2}} + 1}}\chi $

Как и в (3.4), функция $F\left( {\omega ,\chi ,\chi {\kern 1pt} '} \right)$ такова, что $F(0,0,\chi _{0}^{'}) = 0$. Найдя производную

$F{\kern 1pt} ' = 15\omega \left[ {\chi {\kern 1pt} '{\kern 1pt} '\; + \frac{{5\omega \chi {\kern 1pt} '}}{{3({{\omega }^{2}} + 1)}} + \frac{{10\chi }}{{3{{{({{\omega }^{2}} + 1)}}^{2}}}}} \right],$

выразим из этого равенства $\chi {\kern 1pt} '{\kern 1pt} '$ и, подставив в исходное уравнение, придем к уравнению для $F$ и к решению

$\frac{{F{\kern 1pt} '}}{{15\omega }} + \frac{F}{{9({{\omega }^{2}} + 1)}} - \frac{F}{{9{{\omega }^{2}} + 4{{\sigma }^{2}}}} = 0 \to F = C{{\left( {\frac{{9{{\omega }^{2}} + 4{{\sigma }^{2}}}}{{{{\omega }^{2}} + 1}}} \right)}^{{5/6}}}$

Так как $F(0,0,\chi _{0}^{'}) = 0$, то константа $C = 0$, $F = 0$, и справедливо уравнение

$\chi {\kern 1pt} ' = \frac{{(3 - 2{{\omega }^{2}})\chi }}{{3({{\omega }^{2}} + 1)\omega }}$

Решив его, получим

(4.1)

$n = \frac{3}{2},\quad m = \frac{5}{6}{\kern 1pt} :\quad \chi = \frac{{\chi _{0}^{'}\omega }}{{{{{({{\omega }^{2}} + 1)}}^{{5/6}}}}},\quad \chi {\kern 1pt} ' = \frac{{\chi _{0}^{'}(3 - 2{{\omega }^{2}})}}{{3{{{({{\omega }^{2}} + 1)}}^{{11/6}}}}}$

Согласно выполненным расчетам собственными значениями краевой задачи, отвечающей $n = 3{\text{/}}2$, наряду с $m = 5{\text{/}}6$ являются $m = 2l + 5{\text{/}}6$, $l = 1,2,...$ Для окрестности точки $b$ течения, изображенного на рис. 1, подстановка $\chi $ и $\chi {\kern 1pt} '$ из (4.1) в формулы для $\psi $, ${{\psi }_{V}}$ и ${{\psi }_{\theta }}$ приводит к выражениям

(4.2)

$\psi = 1 + \chi _{0}^{'}(\theta - {{\theta }_{b}})(1 - V) + ...,\quad {{\psi }_{V}} = - \chi _{0}^{'}(\theta - {{\theta }_{b}}),\quad {{\psi }_{\theta }} = \chi _{0}^{'}(1 - V),\quad \chi _{0}^{'} < 0$

Подставим эти ${{\psi }_{V}}$ и ${{\psi }_{\theta }}$ в уравнения (2.5), записанные на $b - e$ с $V = 1$ и $dV = 0$. Действуя далее, как в разд. 3, придем к формулам (3.7) и (3.8) с ${{\rho }_{b}} = {{\rho }_{*}} = 1$. Для $V$, ${{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial \tau }}} \right. \kern-0em} {\partial \tau }}$ и ${{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial \tau }}} \right. \kern-0em} {\partial \tau }}$ при подходе к точке $b$ по стенке получаются формулы

(4.3)

$V = 1 + \frac{{{{{(3k\tau )}}^{{1/3}}}}}{{{{{({{\sigma }^{2}}\chi _{0}^{'})}}^{{1/3}}}}},\quad \frac{{\partial p}}{{\partial \tau }} = - \frac{{\partial V}}{{\partial \tau }} = - \frac{{{{{(k{\text{/}}\chi _{0}^{'})}}^{{1/3}}}}}{{{{{(3\sigma \tau )}}^{{2/3}}}}},$

существенное отличие которых от (3.9) – иные степени $\tau $.

Для течений, изображенных на рис. 3,

(4.4)

$\psi = \chi _{0}^{'}({{\theta }_{b}} - \theta )(1 - V) + ...,\quad {{\psi }_{V}} = - \chi _{0}^{'}({{\theta }_{b}} - \theta ),\quad {{\psi }_{\theta }} = - \chi _{0}^{'}(1 - V);\quad \chi _{0}^{'} > 0,$

$\nu = y{\kern 1pt} '$, и вместо (3.7), (3.8) и (4.3) получаются близкие варианты:

(4.5)

$\begin{gathered} x{\kern 1pt} ' > 0{\kern 1pt} :\quad x - {{x}_{b}} = \chi _{0}^{'}\frac{{{{{({{\theta }_{b}} - \theta )}}^{2}}}}{{2k}}\cos {{\theta }_{b}},\quad y - {{y}_{b}} = \chi _{0}^{'}\frac{{{{{({{\theta }_{b}} - \theta )}}^{2}}}}{{2k}}\sin {{\theta }_{b}} \\ \theta = {{\theta }_{b}} - \frac{{{{{(2k\tau )}}^{{1/2}}}}}{{\chi {{{_{0}^{'}}}^{{1/2}}}}},\quad K = \frac{{\partial \theta }}{{\partial \tau }} = \frac{{ - {{k}^{{1/2}}}}}{{{{{(2\chi _{0}^{'}\tau )}}^{{1/2}}}}} \\ x{\kern 1pt} ' < 0{\kern 1pt} :\quad V = 1 - \frac{{{{{(3k\tau )}}^{{1/3}}}}}{{{{{(\chi _{0}^{'}{{\sigma }^{2}})}}^{{1/3}}}}},\quad \frac{{\partial p}}{{\partial \tau }} = - \frac{{\partial V}}{{\partial \tau }} = \frac{{{{{(k{\text{/}}\chi _{0}^{'})}}^{{1/3}}}}}{{{{{(3\sigma \tau )}}^{{2/3}}}}} \\ \end{gathered} $

Отличие от (3.10) формул, дающих изменение $V$ и $\theta $ по нормали к линии тока:

(4.6)

$\begin{gathered} {{(\theta - {{\theta }_{{b,c}}})}^{2}} = \frac{2}{3}{{\sigma }^{2}}{{(1 - V)}^{3}},\quad 1 - V = \frac{{{{{(3{\text{/}}2)}}^{{1/5}}}{{\nu }^{{2/5}}}}}{{{{{(\sigma \chi _{0}^{'}{\text{/}}k)}}^{{2/5}}}}} \to \theta = {{\theta }_{{b,c}}} - \frac{{{{{(2{{\sigma }^{2}}{\text{/}}3)}}^{{1/5}}}{{\nu }^{{3/5}}}}}{{{{{(\chi _{0}^{'}{\text{/}}k)}}^{{3/5}}}}} \\ \nu = (y - {{y}_{{b,c}}})\cos {{\theta }_{{b,c}}} - (x - {{x}_{{b,c}}})\sin {{\theta }_{{b,c}}} \ll 1, \\ \end{gathered} $

ожидаемо. Непринципиально отличие из-за иного направления нормали отвечающей рис. 3 формулы для $\nu $ при формуле из (3.10) в случае рис. 1.

Уравнения, отвечающие $n < 3{\text{/}}2$ и $n > 3{\text{/}}2$, совпадают с уравнениями разд. 3, которые там отвечали $n < 1$ и $n > 1$. В результате решения

$n < \frac{3}{2},\quad m = \frac{{n + 1}}{{2n}}{\kern 1pt} :\quad \chi = \frac{{\chi _{0}^{'}\omega }}{{{{{({{\omega }^{2}} + 1)}}^{m}}}},\quad \chi {\kern 1pt} ' = \frac{{\chi _{0}^{'}(n - {{\omega }^{2}})}}{{n{{{({{\omega }^{2}} + 1)}}^{{m + 1}}}}}$

$n > \frac{3}{2},\quad m = \frac{{n + 1}}{{2n}} > \frac{1}{2}{\kern 1pt} :\quad \chi = \frac{{\chi _{0}^{'}\omega }}{{{{{({{\omega }^{2}} + 1)}}^{m}}}},\quad \chi {\kern 1pt} ' = \frac{{\chi _{0}^{'}(n - {{\omega }^{2}})}}{{n{{{({{\omega }^{2}} + 1)}}^{{m + 1}}}}}$

отличаются от (3.11) и (3.12) только значениями $n = 3{\text{/}}2$. Их следствия для точек схода звуковых линий тока и точек их присоединения совпадают или практически совпадают с приведенными в (4.2)–(4.6).

Для осесимметричных течений в уравнении Чаплыгина появляется правая часть. Ее слагаемые, пропорциональные первым–третьим степеням ${{\psi }_{V}}$ и ${{\psi }_{\theta }}$, во всех изученных решениях имеют более высокий порядок малости по $\eta $, чем ${{\psi }_{{VV}}}$ и ${{\psi }_{{\theta \theta }}}$. Малы и дополнительные слагаемые в уравнениях, определяющих координаты $x$ и у. Как следствие, все полученные результаты переносятся на осесимметричные течения с единственной заменой: $k$ на $k{{y}_{b}}$.

Заключение. Выполненное исследование, первоначально имевшее некоторое отношение к построению тел, обтекаемых с наибольшими критическими числами Маха, неожиданно вывело авторов на практически забытые работы Н.Е. Жуковского по струям идеальной жидкости. Оказалось, что в XIX в. задачи, привлекшие его внимание, интересовали многих известных ученых-физиков, включая Гельмгольца, Кирхгофа, Релея, Бриллуэна, И.В. Мещерского и Планка. Однако ни одному из них не удалось продвинуться столь далеко, как Н.Е. Жуковскому всего в двух работах 1890–1891 гг. Желание напомнить об этом нашим современникам и понимание того, чье дело здесь продолжено, помогли завершить данный труд.

Авторы признательны А.М. Гайфуллину за полезную информацию.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (20-01-00100).

Список литературы

Жуковский Н.Е. Видоизменение метода Кирхгофа для определения движения жидкости в двух измерениях при постоянной скорости, заданной на неизвестной линии тока // в кн.: Жуковский Н.Е. Собр. соч. Т. II. Гидродинамика. М.; Л.: Гостехиздат, 1949. 764 с. С. 489–626.
Жуковский Н.Е. Определение движения жидкости при каком-нибудь условии, данном на линии тока // в кн.: Жуковский Н.Е. Собр. соч. Т. II. Гидродинамика. М.; Л.: Гостехиздат, 1949. 764 с. С. 640–653.
Imai I. Discontinuous potential flow as the limiting form of the viscous flow for vanishing viscosity // J. Phys. Soc. Japan. 1953. V. 8. № 3. P. 399–402.
Бетяев С.К. Эволюция вихревых пелен // в сб.: Динамика сплошной среды со свободными поверхностями. Чебоксары: Чуваш. гос. ун-т, 1980. С. 27–38.
Сычев В.В., Рубан А.И., Сычев Вик.В. и др. Асимптотическая теория отрывных течений. М.: Наука, 1987. 256 с.
Овсянников Л.В. Об одном газовом течении с прямой линией перехода // ПММ. 1949. Т. 13. Вып. 5. С. 537–542.
Овсянников Л.В. Исследование газовых течений с прямой звуковой линией // Тр. ЛКВВИА. 1950. Вып. 33. С. 3–24.
Шифрин Э.Г. К задаче обтекания бесконечного клина звуковой струей // Изв. АН СССР. МЖГ. 1969. № 2. С. 103–106.
Крайко А.Н., Мунин С.А. О натекании звуковой струи на клиновидные препятствия // ПММ. 1989. Т. 53. Вып. 3. С. 413–417.
Кацкова О.Н., Шмыглевский Ю.Д. Осесимметричное сверхзвуковое течение свободно расширяющегося газа с плоской переходной поверхностью // Вычисл. матем. М.: АН СССР. 1957. Вып. 2. С. 45–89.
Крайко А.Н., Тилляева Н.И. Метод характеристик и полухарактеристические переменные в задачах профилирования сверхзвуковых частей плоских и осесимметричных сопел // ЖВММФ. 1996. Т. 36. № 9. С. 159–176.
Крайко А.Н., Тилляева Н.И., Шамардина Т.В. Плоскопараллельные и осесимметричные течения с прямой звуковой линией // ЖВММФ. 2019. Т. 59. № 4. С. 649–669.
Крайко А.Н. Предельные свойства кусочно-потенциальных докритических и критических струйных течений идеального газа // ПММ. 2003. Т. 67. Вып. 1. С. 30–41.
Крайко А.Н. Теоретическая газовая динамика: классика и современность. М.: Торус пресс, 2010. 440 с.
Gilbarg D., Shiffman M. On bodies achieving extreme values of the critical Mach number. I // J. Ration. Mech.&Anal. 1954. V. 3. № 2. P. 209–230.
Крайко А.Н. Плоские и осесимметричные конфигурации, обтекаемые с максимальным критическим числом Маха // ПММ. 1987. Т. 51. Вып. 6. С. 941–950.
Fisher D.D. Calculation of subsonic cavities with sonic free streamlines // J. Math. Phys. 1963. V. 42. № 1. P. 14–26.
Брутян М.А., Ляпунов С.В. Оптимизация формы симметричных плоских тел с целью увеличения критического числа Маха // Уч. зап. ЦАГИ. 1981. Т. 12. № 5. С. 10–22.
Щербаков С.А. Расчет головной или кормовой части плоского тела, обтекаемого дозвуковым потоком с максимально возможным критическим числом Маха // Уч. зап. ЦАГИ. 1988. Т. 19. № 4. С. 10–18.
Schwendeman D.W., Kropinski M.C.A., Cole J.D. On the construction and calculation of optimal nonlifting critical airfoils // ZAMP. 1993. Bd 44. P. 556–571.
Зигангареева Л.М., Киселев О.М. О расчете кавитационного обтекания кругового конуса дозвуковым потоком сжимаемой жидкости // ПММ. 1994. Т. 58. Вып. 4. С. 93–107.
Зигангареева Л.М., Киселев О.М. Отрывное обтекание диска идеальным газом и тела с наибольшими критическими числами Маха // Изв. РАН. МЖГ. 1996. № 3. С. 166–172.
Зигангареева Л.М., Киселев О.М. О полубесконечных телах вращения, обтекаемых с максимальным критическим числом Маха // ПММ. 1997. Т. 61. Вып. 1. С. 97–107.
Зигангареева Л.М., Киселев О.М. О плоских конфигурациях, обтекаемых потоком идеального газа с максимальным критическим числом Маха // ПМТФ. 1998. № 5. С. 106–115.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976. 576 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал